Comparative Analysis of Basic and Extended Power Models of Boreholes Expansion Dependence on Explosive Charge in Blasting in Clay Soil
Abstract
1. Introduction
- Basic database—basic model
- Extended database—basic model
- Extended database—extended model
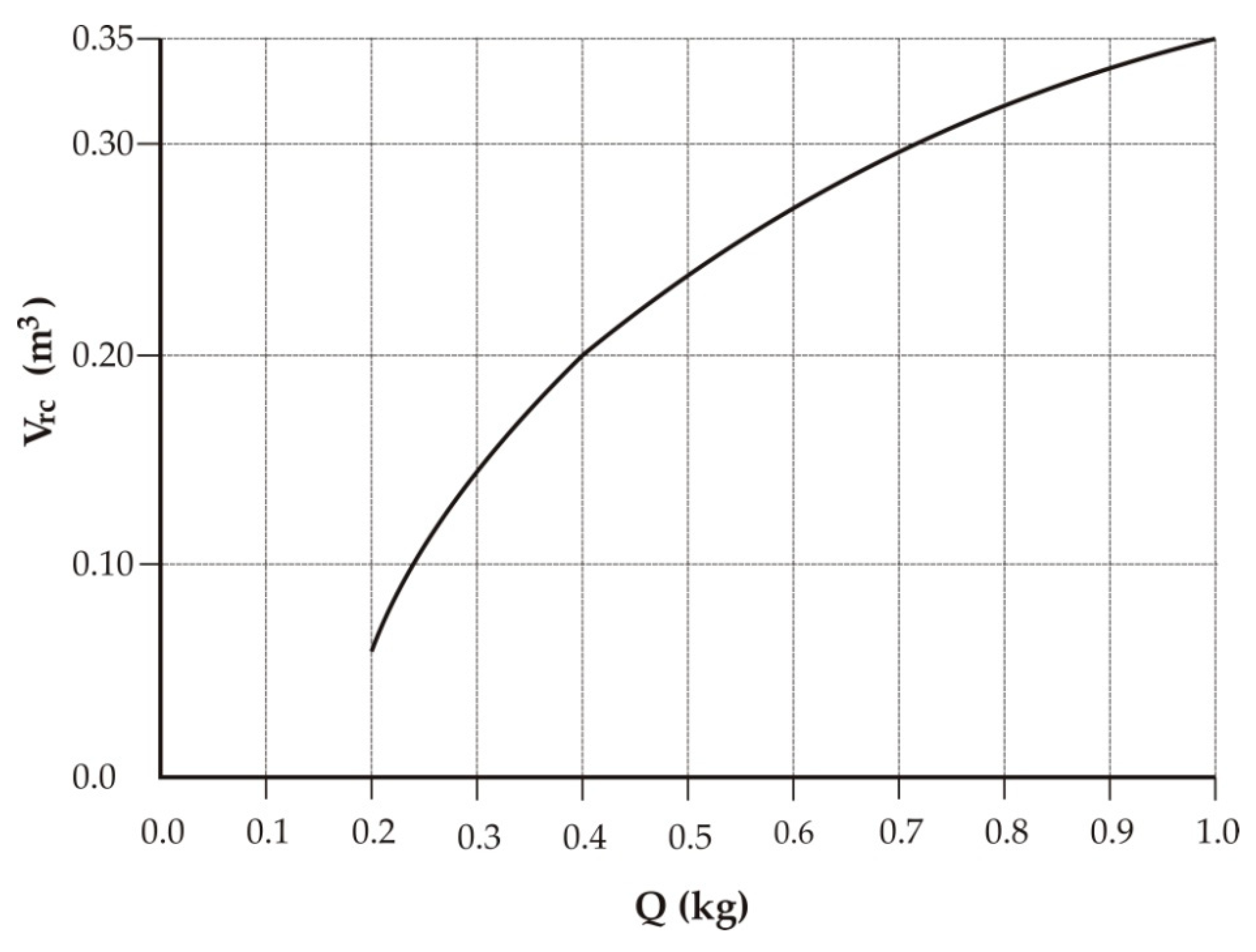
2. Previous Research
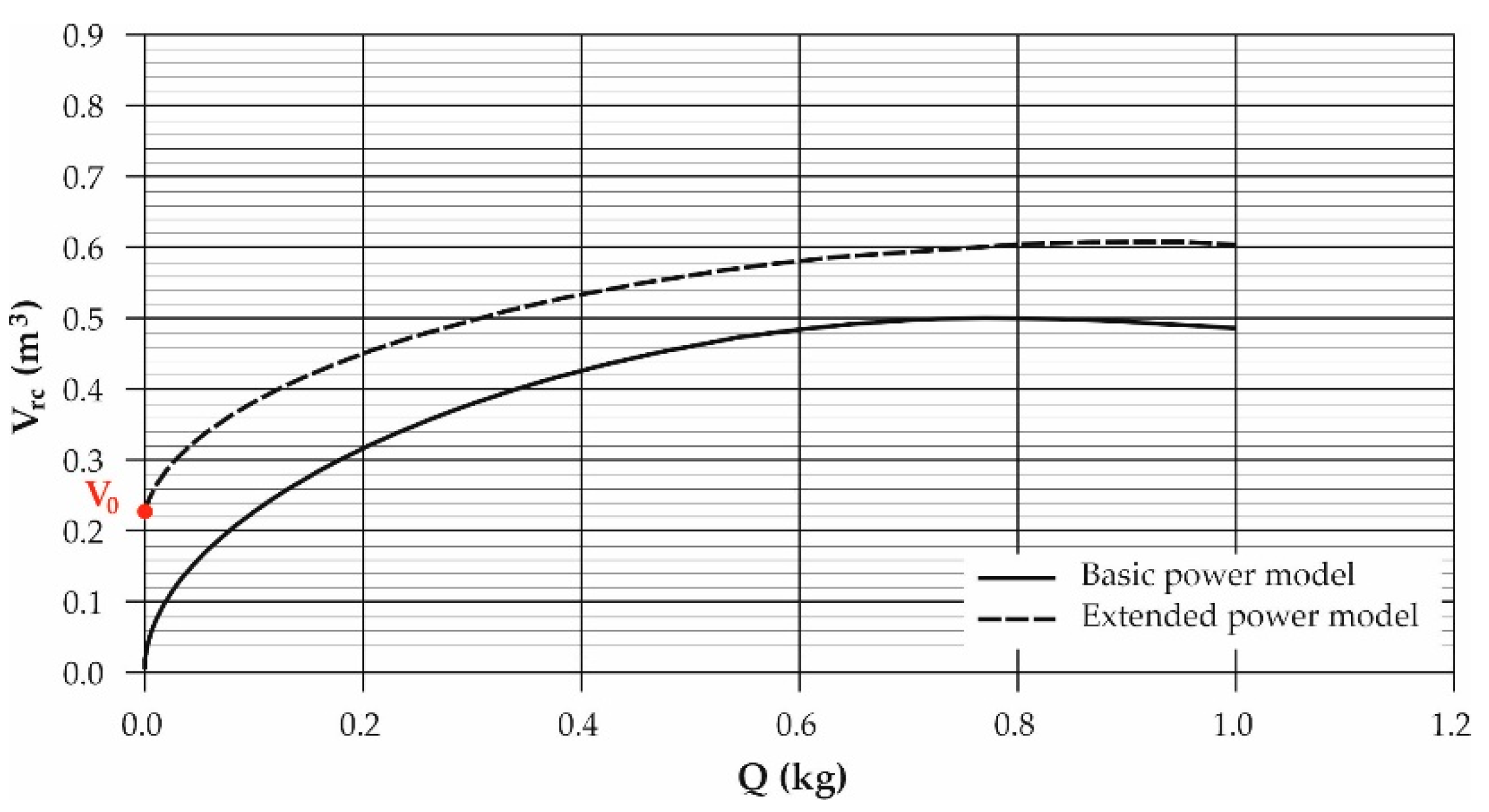
3. Extended Power Model
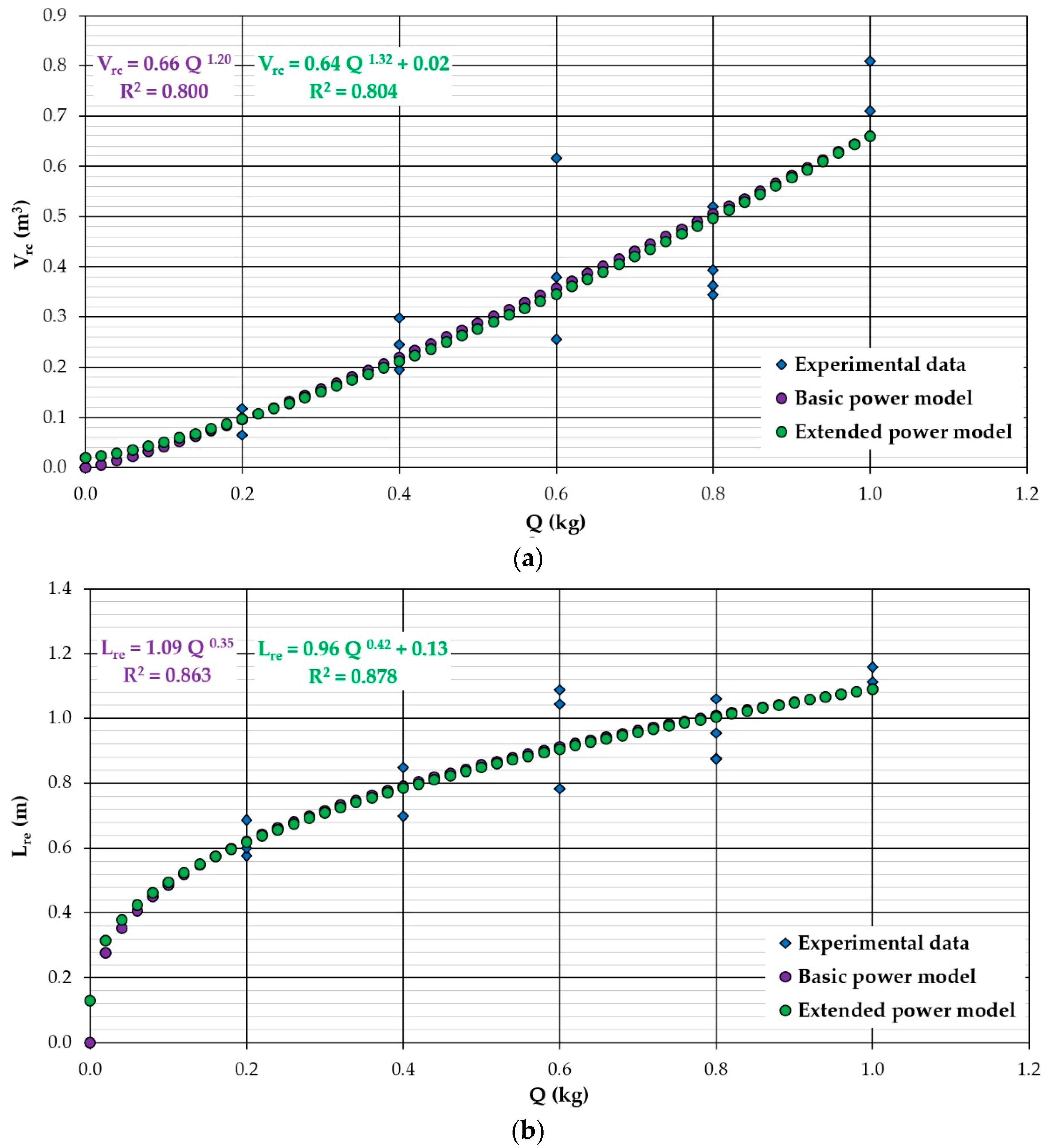
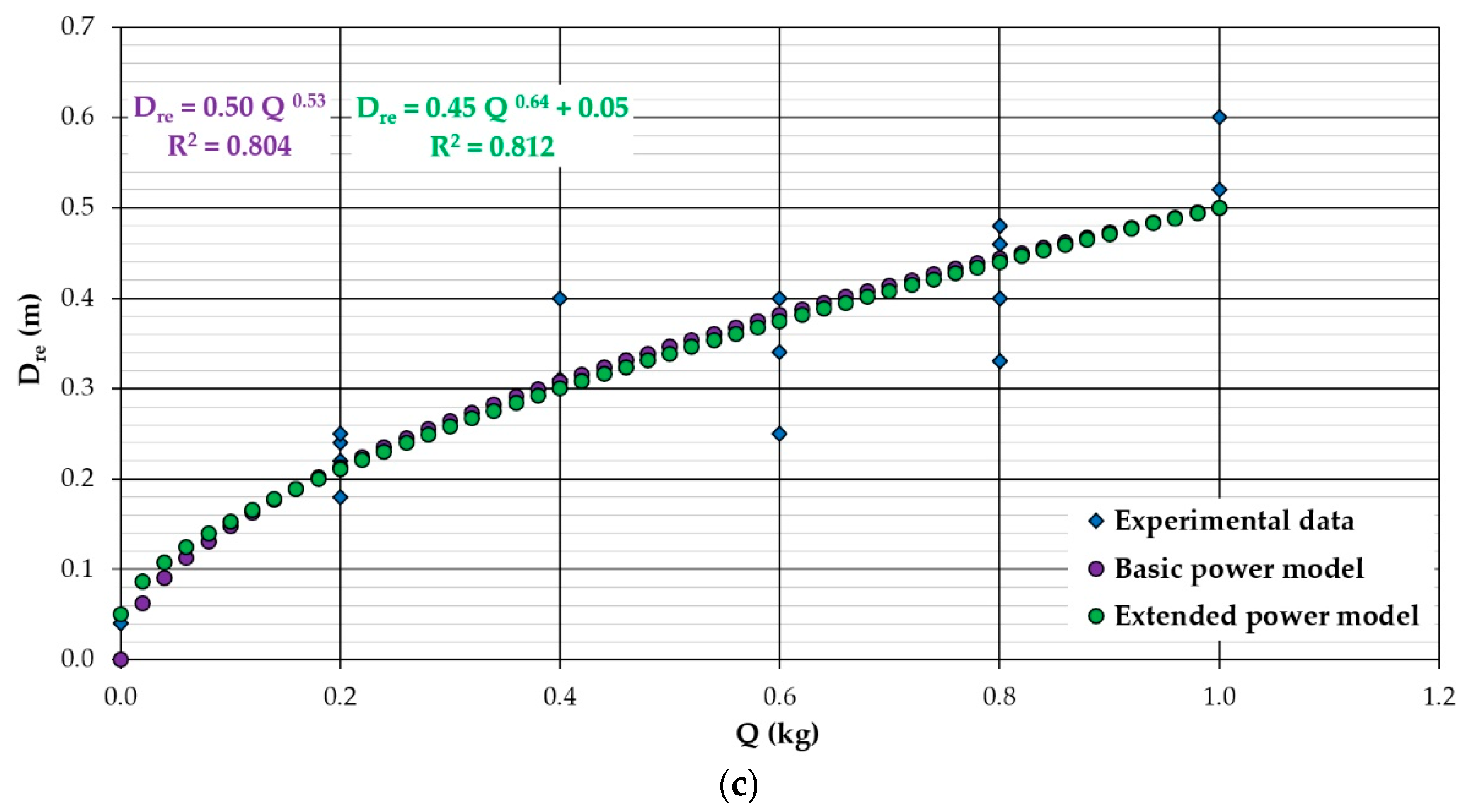
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Težak, D.; Stanković, S.; Kovač, I. Dependence Models of Borehole Expansion on Explosive Charge in Spherical Cavity Blasting. Geosciences 2019, 9, 383. [Google Scholar] [CrossRef]
- Krsnik, J. Miniranje; University of Zagreb: Zagreb, Croatia, 1989; ISBN 8680891088. [Google Scholar]
- Li, Q.; Li, Y.; Dasgupta, G.; Song, D.; Qiao, L.; Wang, L.; Dong, J. Analysis of the Blasting Compaction on Gravel Soil. J. Chem. 2015. [Google Scholar] [CrossRef]
- Dobrilović, M.; Bohanek, V.; Žganec, S. Influence of Explosive Charge Temperature on Velocity of Detonation of ANFO Explosive. Cent. Eur. J. Energetic Mater. 2014, 11, 191–198. [Google Scholar]
- Wang, Z.; Lu, Y. Numerical analysis on dynamic deformation mechanism of soils under blast loading. Soil Dyn. Earthqake Eng. 2003, 23, 705–714. [Google Scholar] [CrossRef]
- Težak, D. Influence of the Blasting Features on the Expansion in Clay Soil. Ph.D. Thesis, University of Zagreb, Faculty of Mining, Geology and Petroleum Engineering, Zagreb, Croatia, 2018. [Google Scholar]
- Frgić, L.; Hudec, M.; Krsnik, J.; Krajcer, M.; Mesec, J. Underground grounding by anchoring in soil. In Proceedings of the I Yugoslavian Symposium on Tunnels, Brijuni, Croatia, 24–26. November 1988; pp. 293–298. [Google Scholar]
- Bakr, R.M. The Impact of the unsupported excavation on the boundary of the active zone in medium, stiff and very stff clay. J. Civ. Environ. Eng. 2019, 9, 1–9. [Google Scholar]
- Soltani, A.; Deng, A.; Taheri, A.; Mirzababaei, M.; Vanapalli, S.K. Swell–Shrink Behavior of Rubberized Expansive Clays During Alternate Wetting and Drying. Minerals 2019, 9, 224. [Google Scholar] [CrossRef]
- Araya, K.; Gao, R.; Tsunematsu, S.; Ochi, K. Loosening of dense clay soils by linear blasting. J. Agric. Eng. Res. 1993, 54, 113–126. [Google Scholar] [CrossRef]
- Sućeska, M. Eksplozije i Eksplozivi-Njihova Mirnodopska Primjena; Brodarski Institut: Zagreb, Croatia, 2001; ISBN 953-6017-11-3. [Google Scholar]
- Dobrilović, M. Raspoloživa energija tlačnog udarnog vala udarne cjevčice i njezina primjena u iniciranju elektroničkog detonatora. Ph.D. Thesis, University of Zagreb, Zagreb, Croatia, 2008. [Google Scholar]
- Težak, D.; Soldo, B.; Đurin, B.; Kranjčić, N. Impact of Seasonal Changes of Precipitation and Air Temperature on Clay Excavation. Sustainability 2019, 11, 6368. [Google Scholar] [CrossRef]
- Žganec, S.; Bohanek, V.; Dobrilović, M. Influence of a Primer on the Velocity of Detonation of ANFO and Heavy ANFO Blends. Cent. Eur. J. Energ. Mater. 2016, 13, 694–704. [Google Scholar] [CrossRef]
- Mesec, J.; Težak, D.; Grubešić, M. The use of explosives for improvement of clay soils. Environ. Eng. 2015, 2, 95–101. (In Croatia) [Google Scholar]
- Shakeran, M.; Eslami, A.; Ahmadpour, M. Geotechnical Aspects of Explosive Compaction. Shock Vib. 2016, 2016, 6719271. [Google Scholar] [CrossRef]
- Wu, H.; Pollard, D.D. Imaging 3-D fracture networks around boreholes. Am. Assoc. Pet. Geol. 2002, 4, 593–604. [Google Scholar]
- Schepers, R.; Rafat, G.; Gelbke, C.; Lehmann, B. Application of borehole logging, core imaging and tomography to geotechnical exploration. Int. J. Rock Mech. Min. Sci. 2001, 38, 867–876. [Google Scholar] [CrossRef]
- McCarthy, J.D.; Graniero, P.A. A GIS-based borehole data management and 3D visualization system. Comput. Geosci. 2006, 32, 1699–1708. [Google Scholar] [CrossRef]
- Statistica V 13.5. Available online: http://www.statsoft.com/Products/STATISTICA-Features (accessed on 5 December 2019).
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, Tsahkadsor, Armenia, USSR, Budapest, Hungary, 2–8 September 1971; Akadémiai Kiadó: Budapest, Hungary; pp. 267–624. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Findley, D.F.; Parzen, E. A conversation with Hirotugu Akaike. Stat. Sci. 1995, 10, 104–117. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. Unifying the derivations of the Akaike and corrected Akaike information criteria. Stat. Probab. Lett. 1997, 31, 201–208. [Google Scholar] [CrossRef]
| Pakaex | Permonex V19 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Borehole | Explosive Charge Mass | Volume of the Resulting Cavity | Resulting Expansion of the Borehole | Deepening of the Resulting Expansion | Borehole | Explosive Charge Mass | Volume of the Resulting Cavity | Resulting Expansion of the Borehole | Deepening of the Resulting Expansion |
| Q (kg) | Vrc (m3) | Lre (m) | Dre (m) | Q (kg) | Vrc (m3) | Lre (m) | Dre (m) | ||
| MB20 | 1.00 | 0.7100 | 1.1570 | 0.5200 | MB24 | 0.80 | 0.6184 | 1.1900 | 0.3100 |
| MB41 | 1.00 | 0.8095 | 1.1110 | 0.6000 | MB26 | 0.80 | 0.5690 | 1.1310 | 0.3600 |
| MB34 | 0.80 | 0.3935 | 0.9530 | 0.3300 | MB45 | 0.80 | 0.7405 | 1.0700 | 0.4000 |
| MB18 | 0.80 | 0.3440 | 0.8770 | 0.4600 | PMB5 | 0.80 | 0.7227 | 1.0710 | 0.4200 |
| MB19 | 0.80 | 0.3626 | 0.8750 | 0.4800 | MB23 | 0.60 | 0.5276 | 1.1040 | 0.3500 |
| MB40 | 0.80 | 0.5190 | 1.0600 | 0.4000 | MB25 | 0.60 | 0.6330 | 1.0850 | 0.2900 |
| MB35 | 0.60 | 0.2555 | 0.7830 | 0.2500 | PMB6 | 0.60 | 0.6151 | 1.1520 | 0.3500 |
| MB17 | 0.60 | 0.6160 | 1.0430 | 0.3400 | MB36 | 0.40 | 0.1135 | 0.6930 | 0.2300 |
| MB39 | 0.60 | 0.3785 | 1.0880 | 0.4000 | MB21 | 0.40 | 0.2925 | 0.9360 | 0.2600 |
| MB15 | 0.40 | 0.2445 | 0.6980 | 0.3100 | MB27 | 0.40 | 0.2160 | 0.5850 | 0.3200 |
| MB16 | 0.40 | 0.1945 | 0.7870 | 0.3000 | MB43 | 0.40 | 0.2815 | 0.8660 | 0.3000 |
| MB38 | 0.40 | 0.2980 | 0.8480 | 0.4000 | MB22 | 0.20 | 0.0825 | 0.5570 | 0.2600 |
| MB13 | 0.20 | 0.1005 | 0.5760 | 0.1800 | MB28 | 0.20 | 0.0700 | 0.5050 | 0.2200 |
| MB14 | 0.20 | 0.0645 | 0.5770 | 0.2200 | MB42 | 0.20 | 0.1480 | 0.6620 | 0.2000 |
| MB29 | 0.20 | 0.0980 | 0.6870 | 0.2400 | - | 0.00 | 0.0005 | 0.1310 | 0.0390 |
| MB37 | 0.20 | 0.1175 | 0.6010 | 0.2500 | |||||
| - | 0.00 | 0.0007 | 0.1310 | 0.0390 | |||||
| Pakaex (N = 17) | a | b | c | K | SS | R2 | AIC | AICc | |
|---|---|---|---|---|---|---|---|---|---|
| Vrc | 1 | 0.66 | 0.66 | - | 2 | 0.170 | 0.770 | −68.700 | −67.900 |
| 2 | 0.66 | 1.20 | - | 2 | 0.170 | 0.800 | −74.278 | −73.528 | |
| 3 | 0.64 | 1.32 | 0.02 | 3 | 0.169 | 0.804 | −74.358 | −72.758 | |
| Lre | 1 | 1.09 | 0.35 | - | 2 | 0.130 | 0.780 | −72.920 | −72.120 |
| 2 | 1.09 | 0.35 | - | 2 | 0.148 | 0.863 | −76.667 | −75.917 | |
| 3 | 0.96 | 0.42 | 0.13 | 3 | 0.131 | 0.878 | −76.718 | −75.118 | |
| Dre | 1 | 0.50 | 0.53 | - | 2 | 0.060 | 0.720 | −85.920 | −85.120 |
| 2 | 0.50 | 0.53 | - | 2 | 0.060 | 0.804 | −92.130 | −91.380 | |
| 3 | 0.45 | 0.64 | 0.05 | 3 | 0.057 | 0.812 | −90.894 | −89.294 | |
| Permonex V19 (N = 15) | a | b | c | K | SS | R2 | AIC | AICc | |
|---|---|---|---|---|---|---|---|---|---|
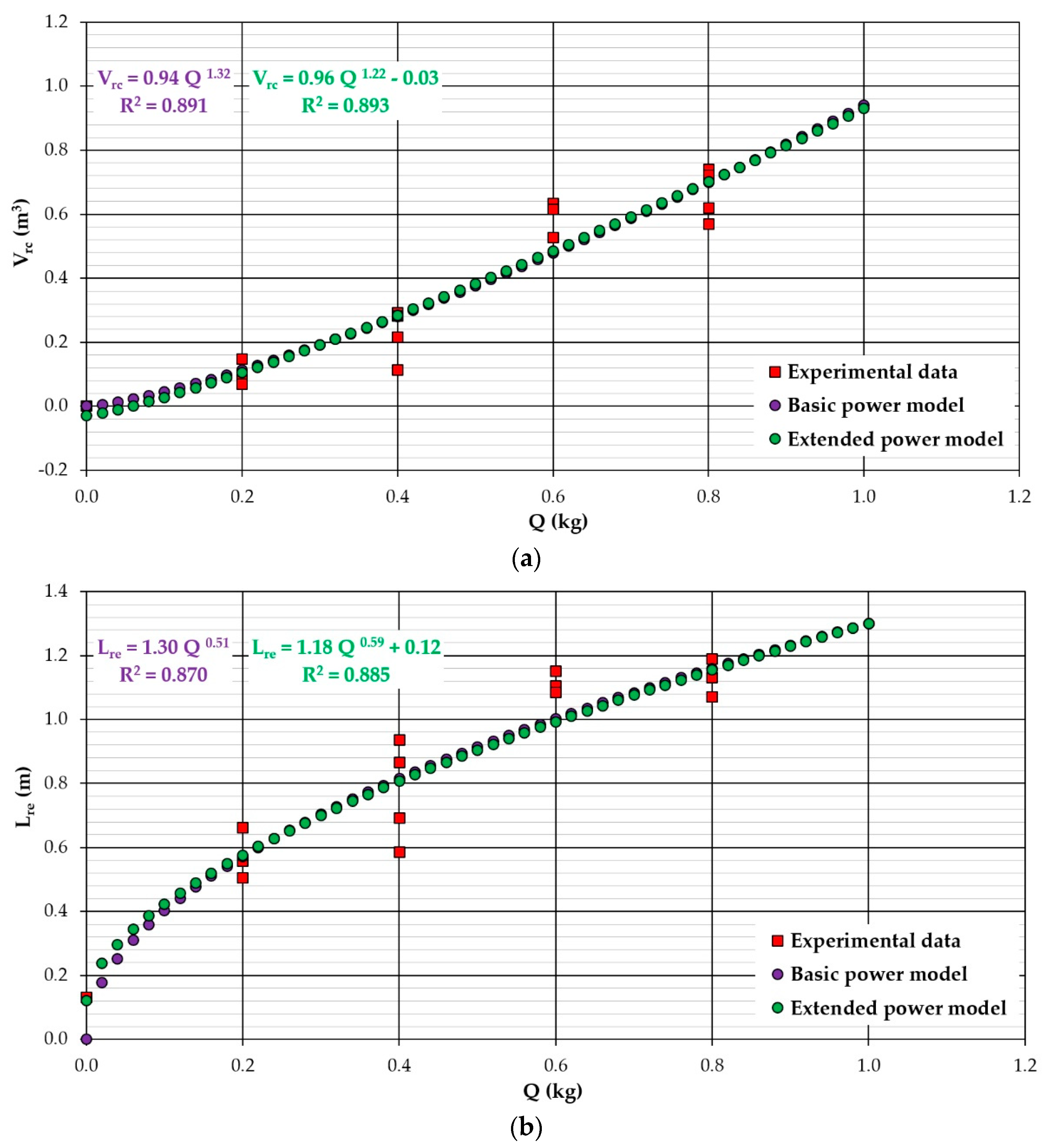
| Vrc | 1 | 0.94 | 0.21 | - | 2 | 0.110 | 0.870 | −64.260 | −63.340 |
| 2 | 0.94 | 1.32 | - | 2 | 0.110 | 0.891 | −70.173 | −69.316 | |
| 3 | 0.96 | 1.22 | −0.03 | 3 | 0.105 | 0.893 | −70.399 | −68.553 | |
| Lre | 1 | 1.30 | 0.51 | - | 2 | 0.160 | 0.810 | −59.010 | −58.090 |
| 2 | 1.30 | 0.51 | - | 2 | 0.170 | 0.870 | −62.972 | −62.115 | |
| 3 | 1.18 | 0.59 | 0.12 | 3 | 0.157 | 0.885 | −62.384 | −60.538 | |
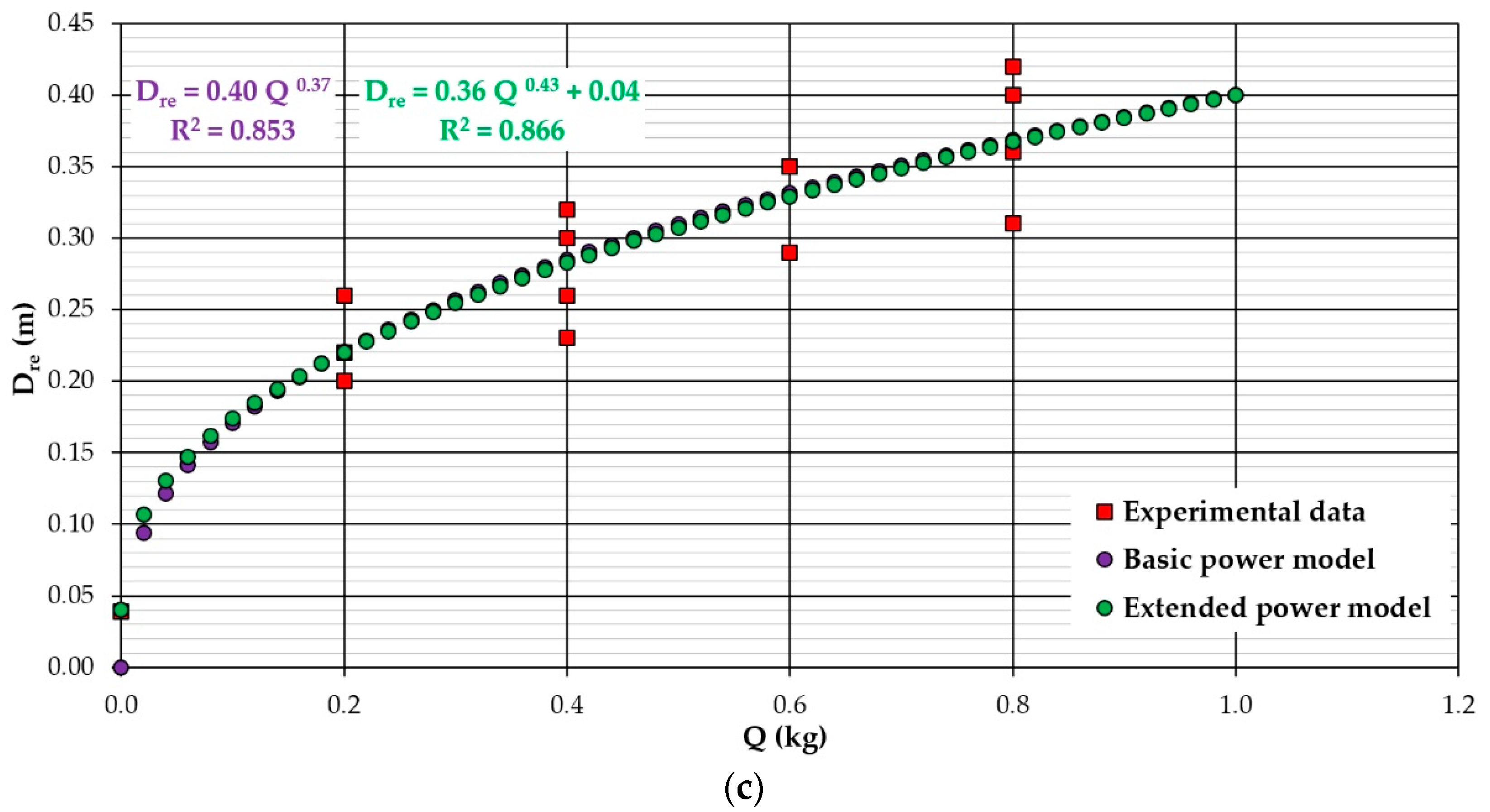
| Dre | 1 | 0.40 | 0.37 | - | 2 | 0.020 | 0.710 | −90.320 | −89.410 |
| 2 | 0.40 | 0.37 | - | 2 | 0.018 | 0.853 | −96.798 | −95.941 | |
| 3 | 0.36 | 0.43 | 0.04 | 3 | 0.017 | 0.866 | −96.187 | −94.472 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovač, I.; Težak, D.; Mesec, J.; Markovinović, I. Comparative Analysis of Basic and Extended Power Models of Boreholes Expansion Dependence on Explosive Charge in Blasting in Clay Soil. Geosciences 2020, 10, 151. https://doi.org/10.3390/geosciences10040151
Kovač I, Težak D, Mesec J, Markovinović I. Comparative Analysis of Basic and Extended Power Models of Boreholes Expansion Dependence on Explosive Charge in Blasting in Clay Soil. Geosciences. 2020; 10(4):151. https://doi.org/10.3390/geosciences10040151
Chicago/Turabian StyleKovač, Ivan, Denis Težak, Josip Mesec, and Ivica Markovinović. 2020. "Comparative Analysis of Basic and Extended Power Models of Boreholes Expansion Dependence on Explosive Charge in Blasting in Clay Soil" Geosciences 10, no. 4: 151. https://doi.org/10.3390/geosciences10040151
APA StyleKovač, I., Težak, D., Mesec, J., & Markovinović, I. (2020). Comparative Analysis of Basic and Extended Power Models of Boreholes Expansion Dependence on Explosive Charge in Blasting in Clay Soil. Geosciences, 10(4), 151. https://doi.org/10.3390/geosciences10040151





