A Compact Ionic Polymer Metal Composite (IPMC) System with Inductive Sensor for Closed Loop Feedback
Abstract
:1. Introduction
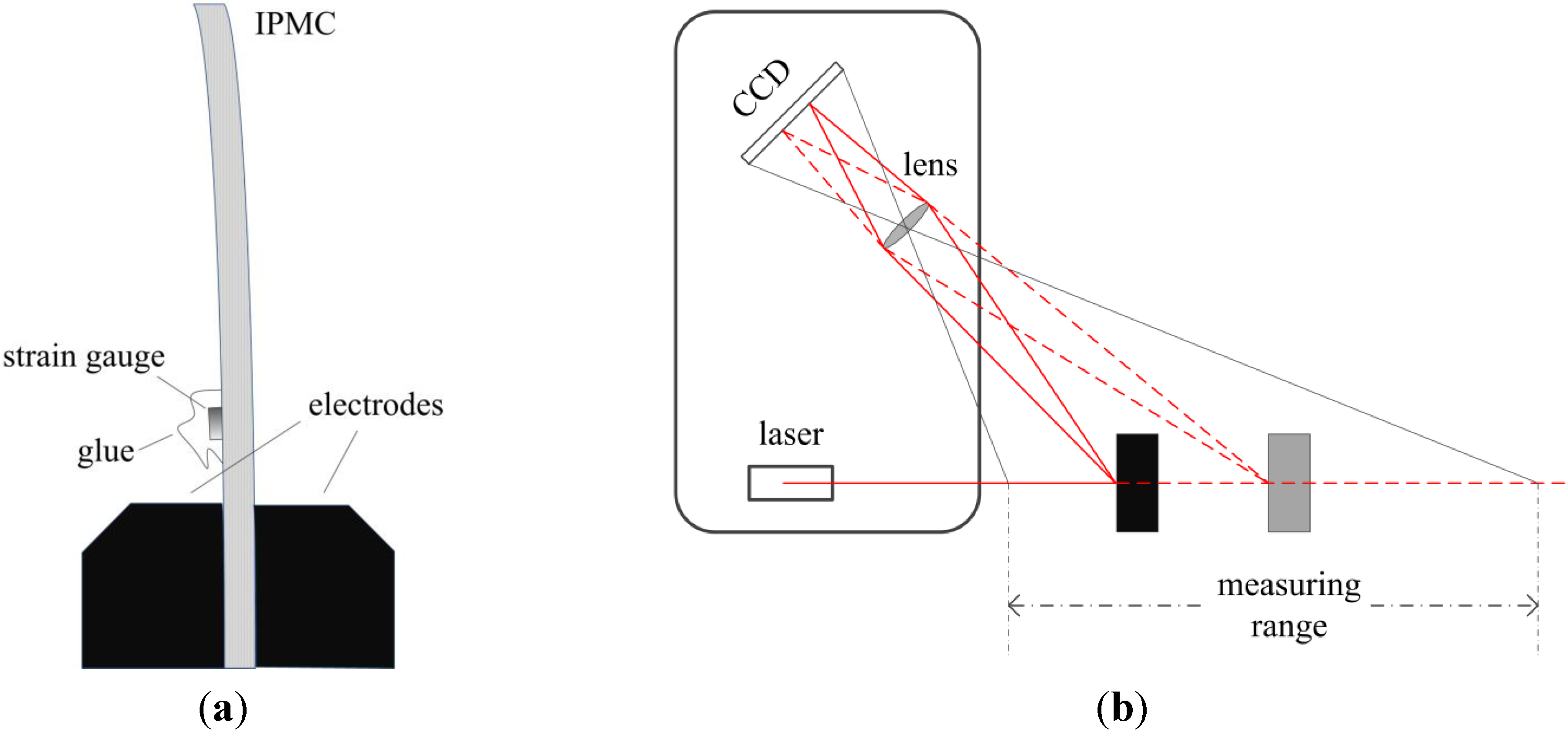
2. Inductive Sensing Principle
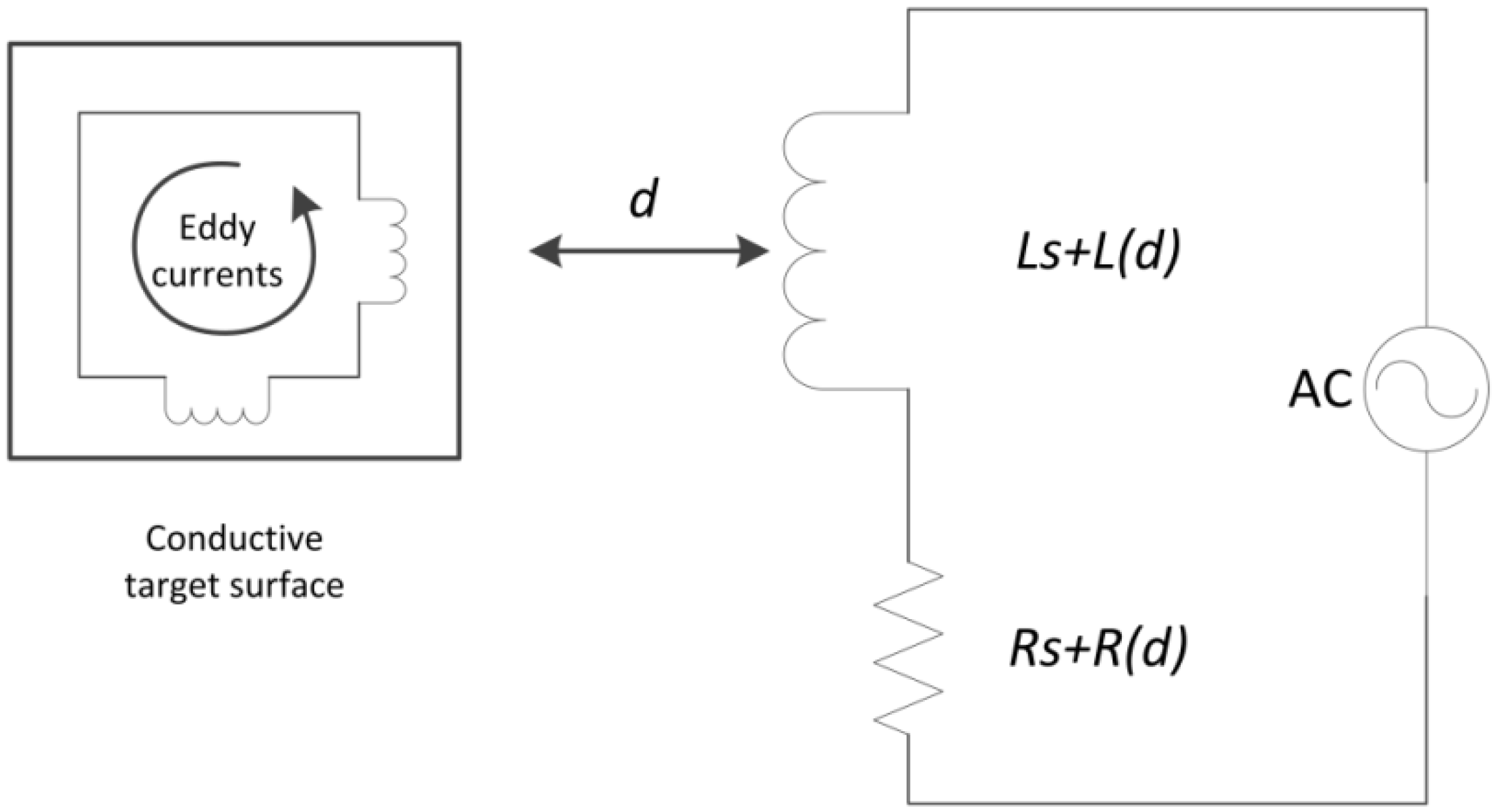
2.1. Target Material Selection
| Metal | Resistivity (10−6 Ω·m) | Penetration Depth (µm) | |||
|---|---|---|---|---|---|
| 10 kHz | 100 kHz | 1 MHz | 10 MHz | ||
| Copper | 0.017 | 660 | 210 | 66 | 21 |
| aluminium | 0.026 | 820 | 260 | 82 | 26 |
| Stainless steel | 0.77 | 4400 | 1400 | 440 | 140 |
| Titanium alloy | 1.69 | 6600 | 2100 | 660 | 210 |
2.2. PCB Coil Design
| Number | Outer Diameter (mm) | Inner Diameter (mm) | Turns | Free Field Frequency (kHz) | Free Field Inductance (uH) | Parallel Capacitance (pF) | Q Factor |
|---|---|---|---|---|---|---|---|
| 1 | 3.61 | 2 | 85 | 100 | 376.39 | 67.29 | 5.51 |
| 2 | 2.61 | 2 | 60 | 360 | 139.56 | 14 | 6.5 |
| 3 | 2.29 | 2 | 52 | 360 | 94.53 | 20.67 | 11 |
| 4 | 1.97 | 2 | 44 | 500 | 58.49 | 17.32 | 17 |
3. Performance of the Inductive Sensor
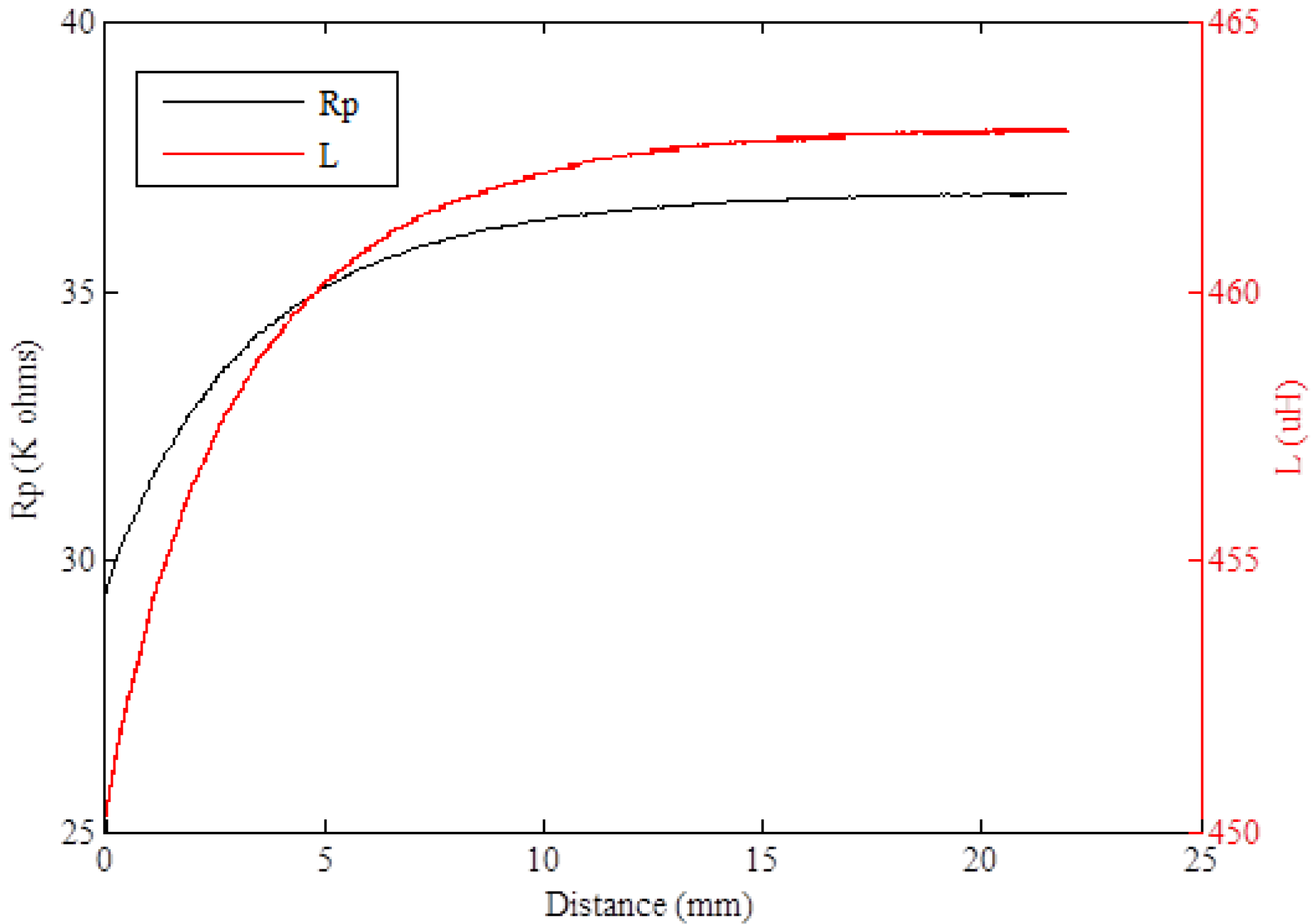
3.1. Resolution and Linearity of Inductive Sensors
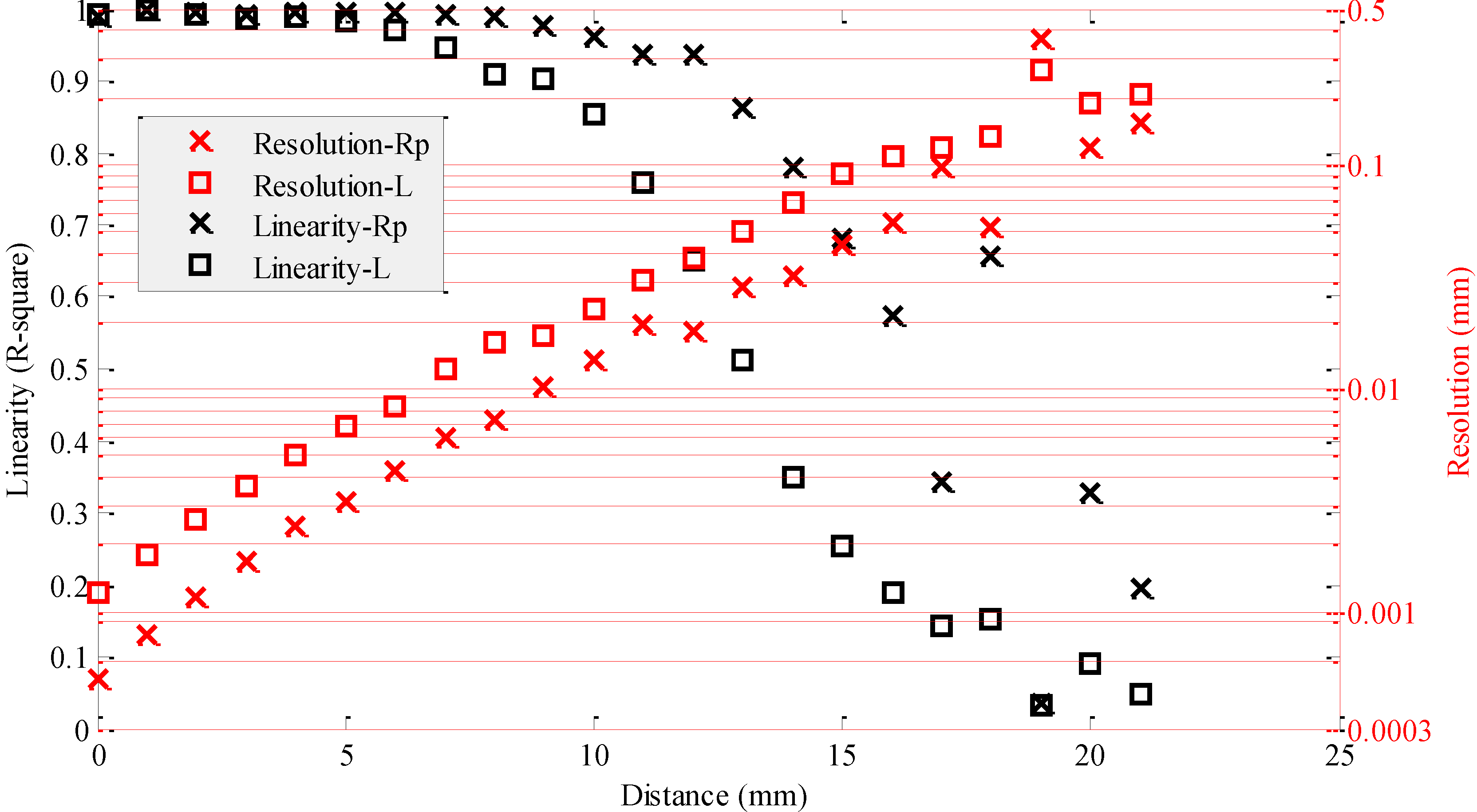
| Coil Number | Resolution-Rp | Resolution-L | Linearity-Rp | Linearity-L |
|---|---|---|---|---|
| 1 | 0.013 | 0.02 | 0.96 | 0.85 |
| 2 | 0.015 | 0.02 | 0.95 | 0.82 |
| 3 | 0.03 | 0.035 | 0.95 | 0.88 |
| 4 | 0.031 | 0.032 | 0.94 | 0.84 |
3.2. Measuring IPMC Frequency Response Driven by a Chirp Signal
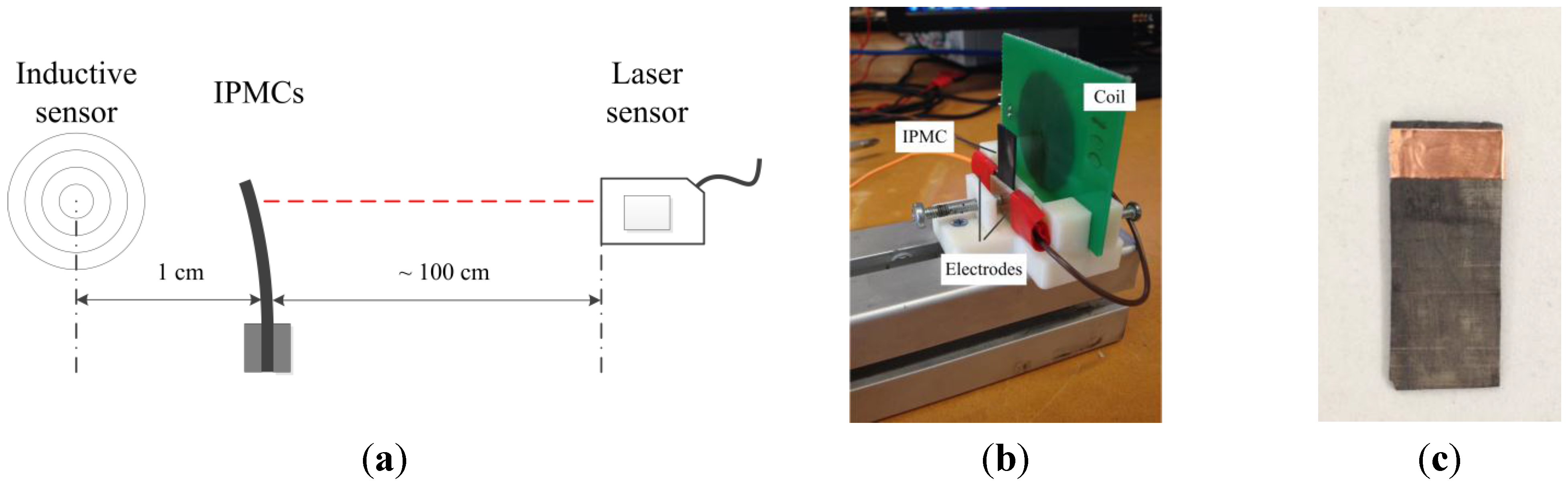
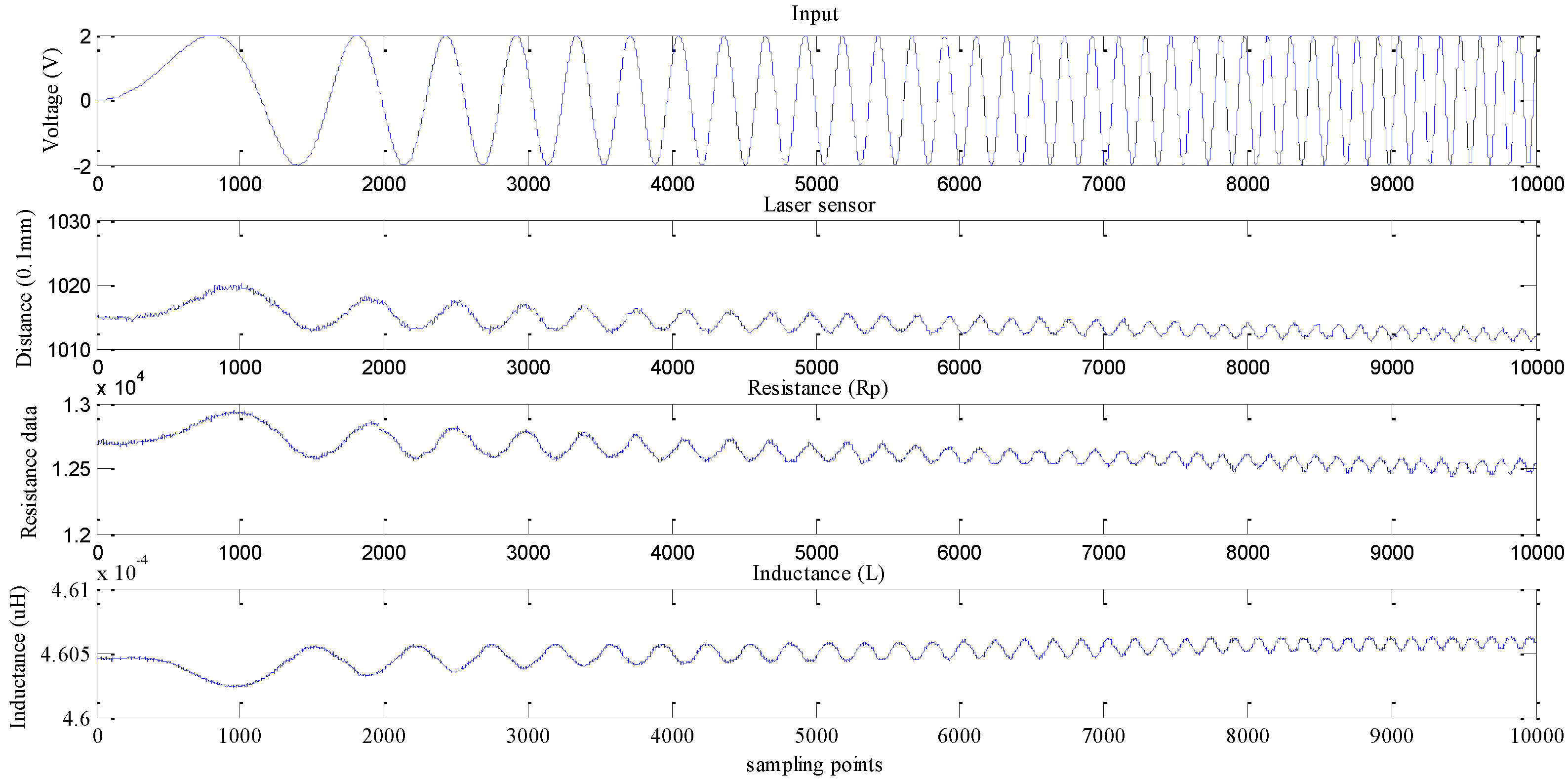
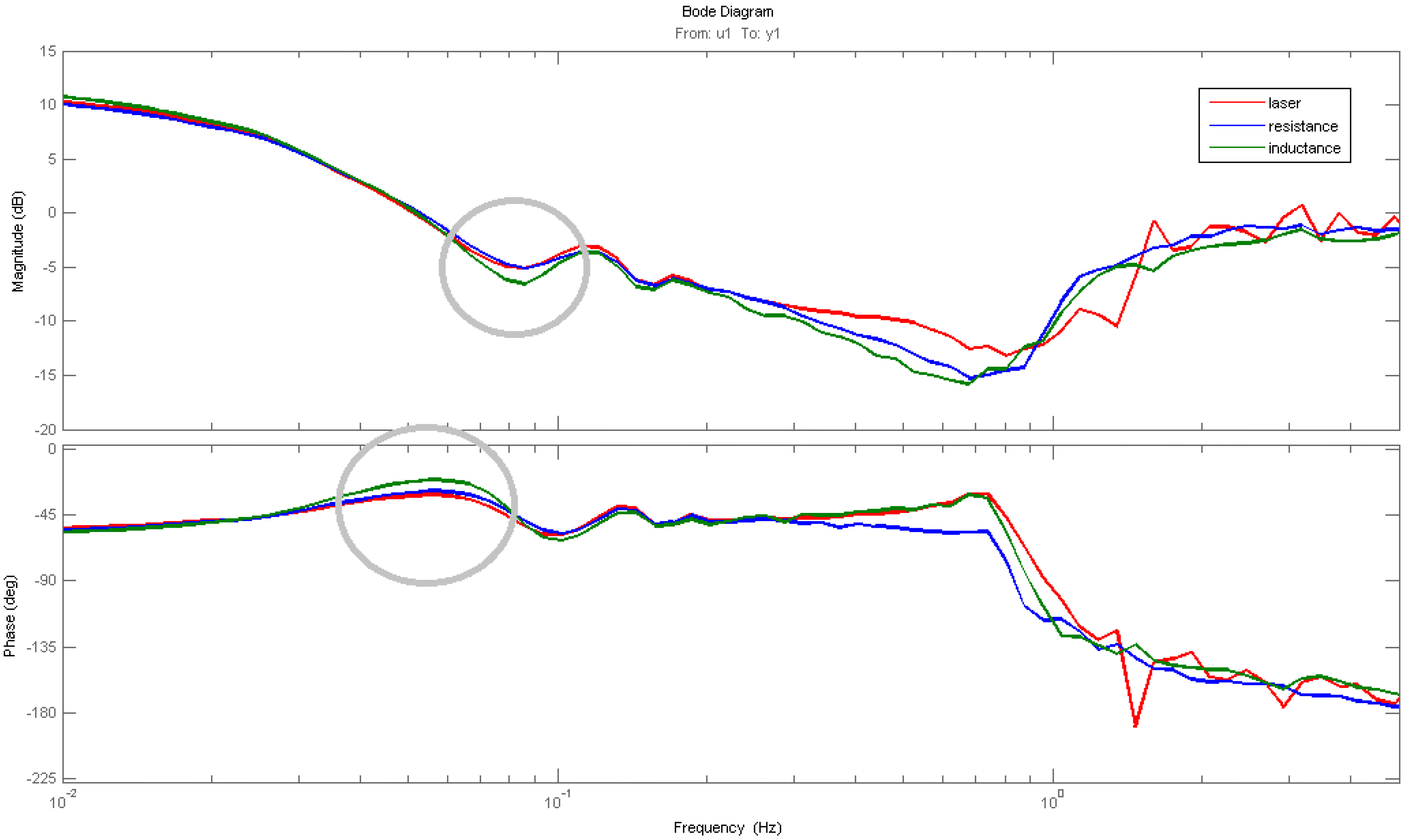
4. IPMC Deflection Controlled by a PID Controller
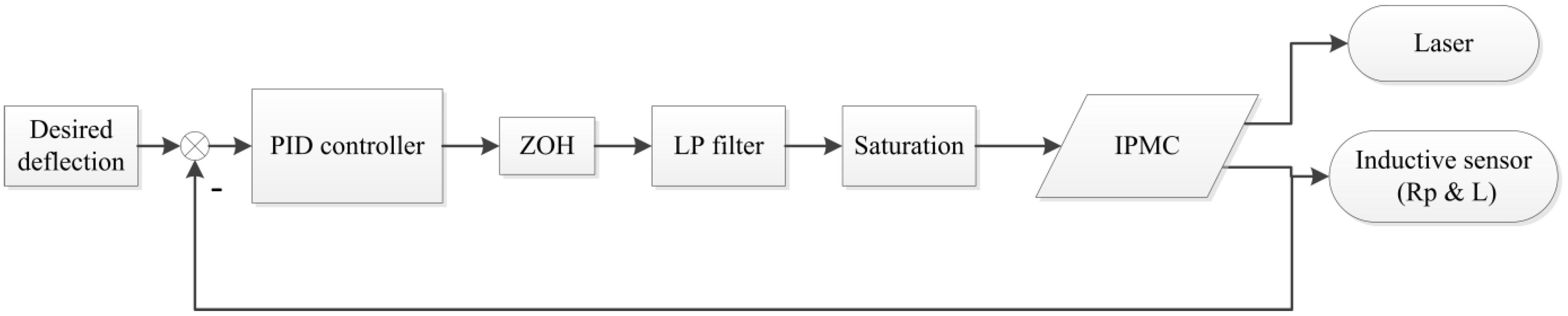
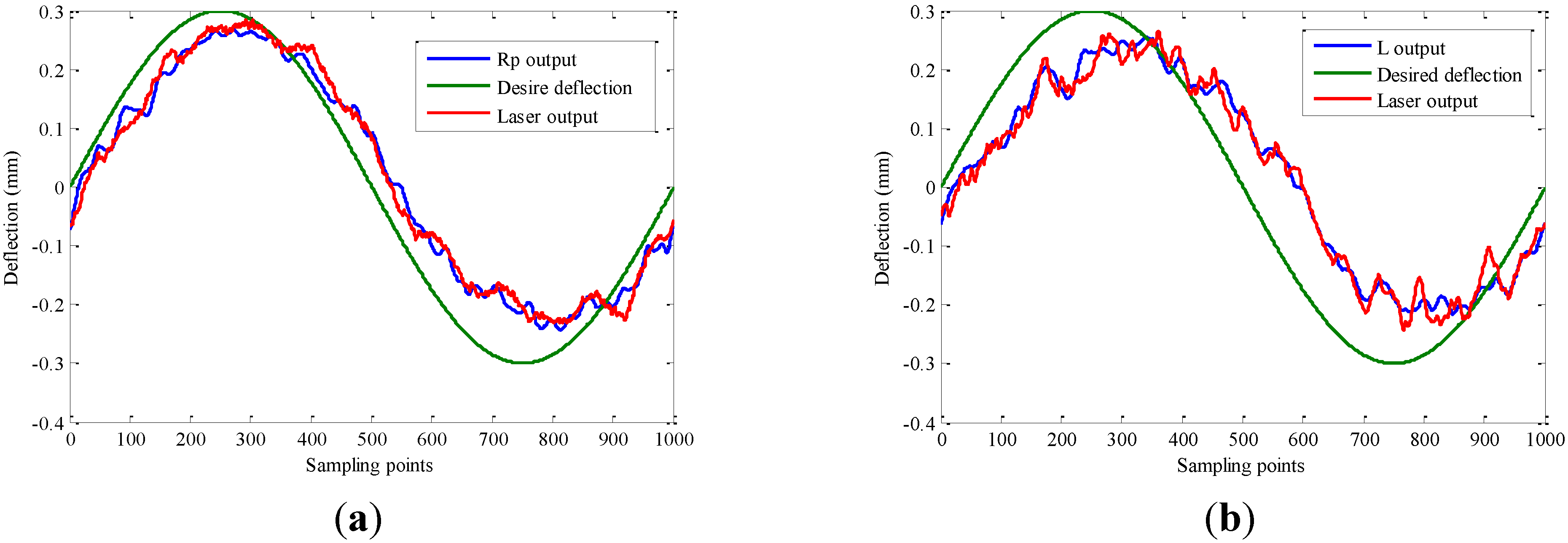
5. Conclusion
Author Contributions
Conflicts of Interest
References
- Hubbard, J.J.; Fleming, M.; Palmre, V.; Pugal, D.; Kim, K.J.; Leang, K.K. Monolithic IPMC fins for propulsion and maneuvering in bioinspired underwater robotics. IEEE J. Ocean. Eng. 2014, 39, 540–551. [Google Scholar] [CrossRef]
- Liu, D.; McDaid, A.; Aw, K.; Xie, S. Position control of an ionic polymer metal composite actuated rotary joint using iterative feedback tuning. Mechatronics 2011, 21, 315–328. [Google Scholar] [CrossRef]
- Ford, S.; Macias, G.; Lumia, R. Single active finger IPMC microgripper. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Amirouche, F.; Zhou, Y.; Johnson, T. Current micropump technologies and their biomedical applications. Microsyst. Technol. 2009, 15, 647–666. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.J. Design of IPMC actuator-driven valve-less micropump and its flow rate estimation at low Reynolds numbers. Smart Mater. Struct. 2006, 15. [Google Scholar] [CrossRef]
- McDaid, A.J.; Aw, K.C.; Haemmerle, E.; Xie, S.Q. Control of IPMC actuators for microfluidics with adaptive “online” iterative feedback tuning. IEEE/ASME Trans. Mechatron. 2012, 17, 789–797. [Google Scholar] [CrossRef]
- Fang, Y.; Tan, X.; Alici, G. Robust adaptive control of conjugated polymer actuators. IEEE Trans. Control Syst. Technol. 2008, 16, 600–612. [Google Scholar] [CrossRef]
- Kang, S.; Shin, J.; Kim, S.J.; Kim, H.J.; Kim, Y.H. Robust control of ionic polymer–metal composites. Smart Mater. Struct. 2007, 16. [Google Scholar] [CrossRef]
- Shan, Y.; Leang, K.K. Frequency-weighted feedforward control for dynamic compensation in ionic polymer–metal composite actuators. Smart Mater. Struct. 2009, 18. [Google Scholar] [CrossRef]
- Leang, K.K.; Shan, Y.; Song, S.; Kim, K.J. Integrated sensing for IPMC actuators using strain gages for underwater applications. IEEE ASME T. Mech. 2012, 17, 345–355. [Google Scholar] [CrossRef]
- Bonomo, C.; Fortuna, L.; Giannone, P.; Graziani, S. A sensor-actuator integrated system based on ipmcs [ionic polymer metal composites]. In Proceedings of IEEE Sensors, Vienna, Austria, 24–27 October 2004; pp. 489–492.
- Hao, L.; Sun, Z.; Li, Z.; Su, Y.; Gao, J. A novel adaptive force control method for IPMC manipulation. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Ruiz, S.; Mead, B.; Palmre, V.; Kim, K.J.; Yim, W. A cylindrical ionic polymer-metal composite-based robotic catheter platform: Modeling, design and control. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Mead, B.; Ruiz, S.; Yim, W. In Closed-loop control of a tube-type cylindrical IPMC. Proc. SPIE 2013, 8687. [Google Scholar] [CrossRef]
- Wilson, J.S. Sensor Technology Handbook; Elsevier: Oxford, UK, 2004. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems; Addison Wesley: Menlo Park, CA, USA, 1998. [Google Scholar]
- McDaid, A.; Aw, K.; Xie, S.; Haemmerle, E. Gain scheduled control of IPMC actuators with ‘model-free’ iterative feedback tuning. Sens. Actuators A. Phys. 2010, 164, 137–147. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; McDaid, A.; Sharma, R.; Aw, K.C. A Compact Ionic Polymer Metal Composite (IPMC) System with Inductive Sensor for Closed Loop Feedback. Actuators 2015, 4, 114-126. https://doi.org/10.3390/act4020114
Wang J, McDaid A, Sharma R, Aw KC. A Compact Ionic Polymer Metal Composite (IPMC) System with Inductive Sensor for Closed Loop Feedback. Actuators. 2015; 4(2):114-126. https://doi.org/10.3390/act4020114
Chicago/Turabian StyleWang, Jiaqi, Andrew McDaid, Rajnish Sharma, and Kean C. Aw. 2015. "A Compact Ionic Polymer Metal Composite (IPMC) System with Inductive Sensor for Closed Loop Feedback" Actuators 4, no. 2: 114-126. https://doi.org/10.3390/act4020114
APA StyleWang, J., McDaid, A., Sharma, R., & Aw, K. C. (2015). A Compact Ionic Polymer Metal Composite (IPMC) System with Inductive Sensor for Closed Loop Feedback. Actuators, 4(2), 114-126. https://doi.org/10.3390/act4020114







