A Novel DC Electroosmotic Micromixer Based on Helical Vortices

Abstract

This work introduces a novel direct current electroosmosis (DCEO) micromixer designed for rapid and efficient fluid mixing. This micromixer demonstrates excellent capability, achieving approximately 98.5% mixing efficiency within a one-second timespan and 99.8% efficiency within two seconds, all within a simple channel of only 1000 µm in length. A distinctive feature of this micromixer is its ability to generate robust and stable helical vortices by applying a controlled DC electric field. Unlike complex, intricate microfluidic designs, this work proposes a simple yet effective approach to fluid mixing, making it a versatile tool suitable for various applications. In addition, through simple modifications to the driving signal configuration and channel geometry, the mixing efficiency can be further enhanced to 99.3% in one second.

1. Introduction

The field of microfluidics is seeing accelerating growth as it finds new applications in various areas of micro-sciences. Indeed, the emergence and increasingly widespread use of microdevices such as Lab-on-Chips (LoCs), micro-total analysis systems (µTASs), and micro-fuel cells that handle fluidic materials, such as biological specimens, fuel, and coolants, have thrust microfluidics into the spotlight [1,2,3,4,5]. The miniaturization of fluidic functions has enabled a multitude of advantages, such as portability, reduced reagent consumption, faster reactions, and the suitability for direct integration with other microtechnologies, such as sensors, electronics, and/or optics. On the other hand, microfluidics, contrary to the macroscale, usually involve laminar flow dynamics due to the high surface-to-volume ratios involved. When dealing with laminar flows, achieving efficient mixing of fluid species constitutes a significant challenge because of the low advection naturally occurring in microchannels. As such, the unassisted mixing of microfluids is forced to rely on diffusion, which is inherently slow.

Consequently, micromixers are often necessary in order to achieve sufficiently homogeneous mixing of different miscible species. These devices can be categorized as either passive or active, depending on whether they require external energy to induce mixing (fluidic flow and pressure are considered internal to the microfluidic network). For passive micromixers, channel geometry plays a crucial role, as the high surface-to-volume ratio inherent to microfluidic systems allows various surface properties and forces to significantly influence flow physics. Various alternative mechanisms have been explored to create disturbances and vortices so as to accelerate the mixing of two merging miscible fluids, including electrohydrodynamics, magnetohydrodynamics, and acoustofluidics [6].

Electrohydrodynamic (or electrokinetic) techniques involve applying an external electric field to manipulate fluid motion as required. Since microfluidic systems typically handle aqueous solutions or solutions with specific ionic concentrations (e.g., salts in biofluids such as blood, urine, and sweat, as well as hydrogen and oxidants in fuel cells), electrokinetic methods have found extensive use. Two essential techniques within the realm of electrohydrodynamics are electroosmosis and electrothermal effects. Both methods are suitable for various types of solutions, with electroosmosis being more effective for low-conductivity solutions and small volumes and electrothermal effects thriving for high-conductivity solutions and larger volumes. Unlike electroosmosis, the electrothermal effect is reliant on temperature gradients formed in the bulk, for which appreciable fluid volume is required. Furthermore, the effectiveness of electrothermal actuation in producing strong vortices is dependent on fluid concentrations [7]. As such, this work focuses on introducing a novel electroosmosis method that, in addition to the aforementioned advantages, will be driven by low-frequency actuation signals.

Originally observed by Reuss in the movement of water through a clay plug under the effect of an electric field, electroosmosis was later explained by the formation of an electric double layer by Helmholtz, Gouy-Chapman, and Stern [8]. The electric double layer forms due to the accumulation of charges on the channel wall surface in response to an externally applied electric field. As a result, the ions in the solution are reconfigured so as to conserve the overall charge in the system. The resulting electric forces cause the free ions to move and disrupt the surrounding liquid. In turn, these disturbances may create vortices rupturing the liquid–liquid interface, thereby enhancing diffusion and promoting faster and more efficient mixing.

Electroosmosis can be classified into three major categories based on the nature of the driving electric field: direct current electroosmosis (DCEO), alternating current electroosmosis (ACEO) [9,10], and induced charge electroosmosis (ICEO) [11,12]. Among these methods, DCEO stands out for its simplicity and robustness. While ACEO can produce stronger mixing at a lower voltage, DCEO’s proportional relationship between the applied potential and velocity, combined with its inherent flow physics, can yield results superior to those of ACEO under certain conditions. Indeed, efficient and effective mixing relies on the generation of powerful vortices [13,14]. Three-dimensional vortices, such as those generated by spiral, helical, or toroidal structures, have the potential to be far more efficient than their planar counterparts owing to the complexity they introduce into the flow field [15,16].

This work intends to address the challenge of simple, rapid, and efficient microfluidic mixing over a minimal space footprint. As such, we introduce a novel DCEO micromixer design capable of generating strong helical vortices transversally to the flow, causing the fluid to spiral around the central channel axis. The proposed design leverages the simplicity (no moving parts, no driving circuitry) of DC actuation to implement an active mixing method and, thus, in general, more compact mixing action than purely passive implementations. Still, in essence, the presented approach is fully combinable with existing state-of-the-art passive mixing topologies (e.g., [17,18]) for even more efficient microfluidic mixing at the outlet. The proposed device relies on the implementation of microfluidic channels with custom hexagonal cross-sections, which is not a usual realization through standard microfabrication techniques. Although this article focuses on the presentation of a device topology and the simulation of its behavior, a preliminary fabrication process relying on grayscale lithography is suggested, along with an experimental validation of the feasibility of the steps critical for rendering a hexagonal profile. Future work is intended to present the fully realized mixer device. The simulation results indicate that the proposed device is able to achieve a mixing efficiency of 98.5% within just one second of activation. After a brief overview of the theoretical background, the designs of the device and fabrication process are presented, followed by an exploration of the effects of the design parameters on the mixer performance.

2. Theoretical Background

This section briefly provides an overview of the physical equations governing the fluidic dynamics within a DCEO mixer, as well as the definition of the mixing index that serves as a quality assessment metric in Section 4.

2.1. The Physics of DCEO

DCEO is a phenomenon whereby an externally applied electric field causes ionization at the wall–liquid interface, thus reorganizing the distribution of charges in the solution so as to maintain local charge neutrality near the charged microchannel walls. Given that most biological fluids of interest contain ionic salts, electroosmosis offers a versatile technique for manipulating flow dynamics. The mathematical model employed in this study encompasses three key equations governing the underlying physics.

Laminar flow in a microchannel is modeled using the Stokes creeping flow equation that considers inertial forces as negligible with respect to viscous forces:

$$\rho (\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}·\nabla \mathbf{u})=-\nabla p+\mu \left({\nabla }^2\mathbf{u}\right)+\mathbf{F}$$

(1)

where u represents the velocity, $\rho$ represents the density, p represents the pressure, $\mu$ represents the dynamic viscosity, and F represents the body force vector. Incompressibility and continuity conditions are maintained through the following continuity equation:

$$\nabla ·\mathbf{u}=0$$

(2)

The electric field in the bulk induced by ion concentration is governed by the following Laplace equation:

$${\nabla }^2{\varphi }_e=0$$

(3)

where ${\varphi }_e$ represents the electric potential.

The aforementioned body force F can be expressed as ${\rho }_e$E, where ${\rho }_e$ denotes the charge density and E is the applied electric field. For the simulations performed in this work, this condition is taken into account by applying electroosmotic slip velocity (${\mathbf{u}}_{slip}$) conditions on the electrode walls based on the Helmoltz–Smoluckowski velocity,

$${\mathbf{u}}_{slip}={\mu }_{eo}{\mathbf{E}}_t$$

(4)

$${\mu }_{eo}=-\frac{{ϵ}_0{ϵ}_r\zeta }{\mu }$$

(5)

$${\mathbf{E}}_t=\mathbf{E}-(\mathbf{E}·\mathbf{n})\mathbf{n}$$

(6)

where ${ϵ}_r$ is the relative permittivity of the liquid flowing in the channel, ${ϵ}_0$ is the vacuum permittivity, and $\zeta$ is the zeta potential of the wall. In order to model the effect of concentration diffusion occurring during the flow, under the applied field, the following advection–diffusion equation is also considered:

$$\frac{\partial c_i}{\partial t}+\nabla ·\left(\mathbf{u}{c}_i\right)=\nabla ·(D\Delta c_i),$$

(7)

where $c_i$ represents the local concentration of the species, and D is the diffusion coefficient of the liquid.

Channel dynamics are assessed for different flow rates and are generalized through the use of the non-dimensional parameter known as the Reynolds number:

$$Re=\frac{\rho uL}{\mu }$$

(8)

where L is the characteristic length, and it is assumed that the inlet and outlet maintain atmospheric pressure conditions.

2.2. Mixing Index

In order to assess the effectiveness of mixer designs, it is necessary to resort to an objective quantitative metric that can be applied to the simulation results. Specifically, the efficiency of a micromixer can be evaluated based on the uniformity of the mixing achieved in the liquid as it reaches a given channel cross-section; for instance, the outlet. In this work, the target applications involve the laminar combination of two distinct water-based solutions; hence, the quality of mixing can be quantified by calculating a mixing index (MI) based on the level of uniformity for the point-wise solute concentration all along that cross-section [19]:

$$MI=1-\sqrt{\frac{1}{N-1}\sum _{i=1}^N{\left(\frac{c_i-c_{av}}{c_{av}}\right)}^2}$$

(9)

where $c_i$ denotes the concentration at the ith point of the cross-section, and $c_{av}$ denotes the average concentration value over N study points. MI may range from 0 (indicating no mixing whatsoever) to 1 (indicating perfect mixing). However, the MI metric provides only information pertaining to the level of homogeneity at a certain cross-section of the device, without any consideration for the improvement provided with respect to the initial state.

As such, the degree of mixing (${\delta }_m$) can serve to quantify the extent to which the fluids merging at the channel inlet have been fully mixed once they reach the outlet [18,20]:

$${\delta }_m=1-\frac{\sigma }{{\sigma }_{max}}$$

(10)

which, for the proposed device, corresponds to

$${\delta }_m=1-\frac{{1-MI|}_{outlet}}{{1-MI|}_{inlet}}$$

(11)

3. Micromixer Design

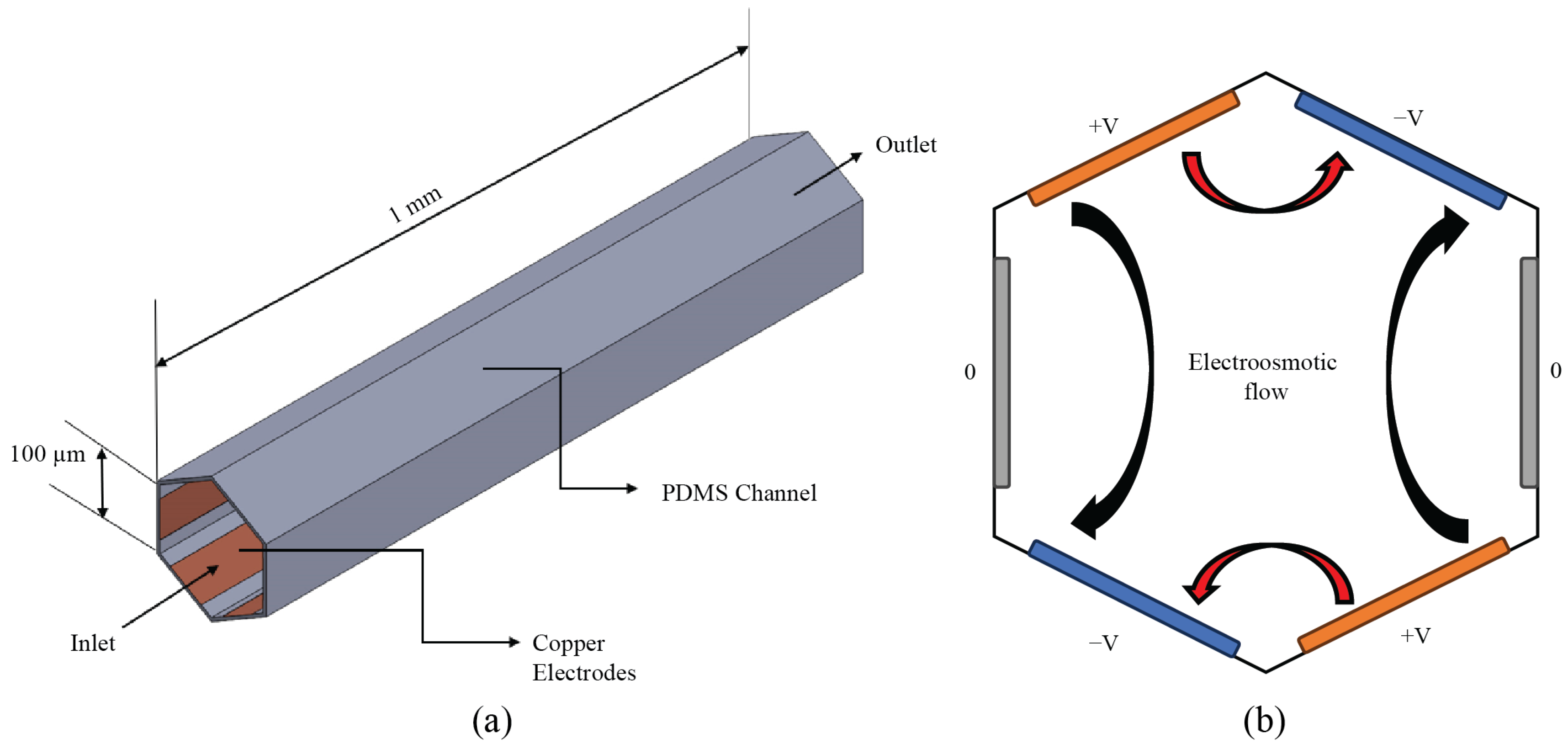
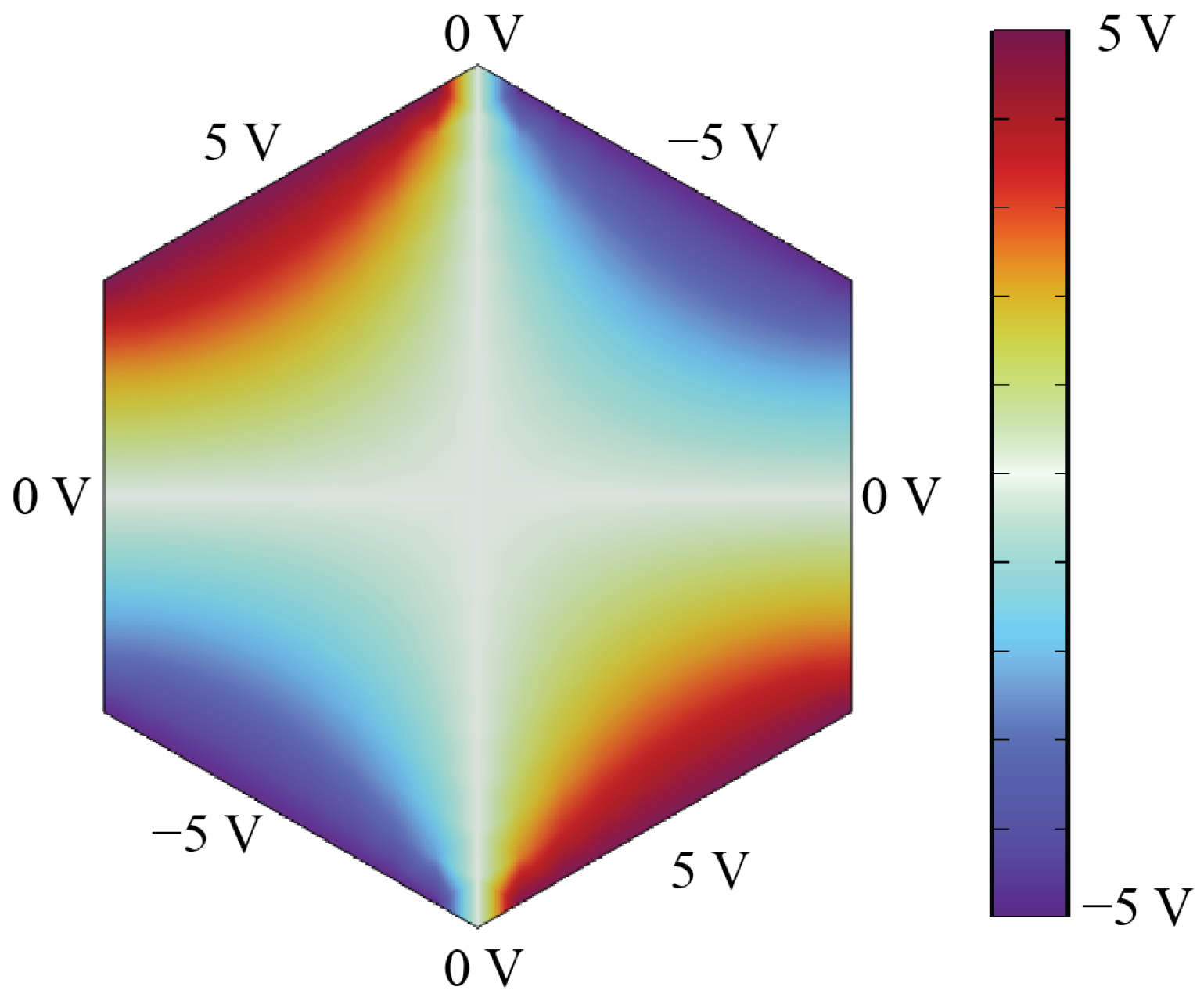
3.1. Device Topology and Working Principle

As depicted in Figure 1a, the proposed micromixer channel is made of polydimethylsiloxane (PDMS) and is designed as a regular hexagon with a side length of 100 µm and a nominal length of 1 mm. Distinct metal electrodes are positioned on the six faces of the hexagonal channel. Copper is selected as the metal for its excellent electrical conductivity and adhesion to PDMS [21].

Upon applying a positive electric potential to one pair of opposite electrodes and the same magnitude (but negative) potential to another pair while maintaining a neutral potential on the last pair, an asymmetric electric field is established throughout the channel cross-section. Through electroosmosis, the applied electric field drives the fluid bulk from one electrode to another in the direction of decreasing potential, as highlighted in Figure 1b. Due to the asymmetry (i.e., the electric force between adjacent electrodes is stronger than that between opposite electrodes), the fluid is expected to form persistent helical vortices that, combined with a longitudinal flow along the channel, will result in a spiral fluidic motion.

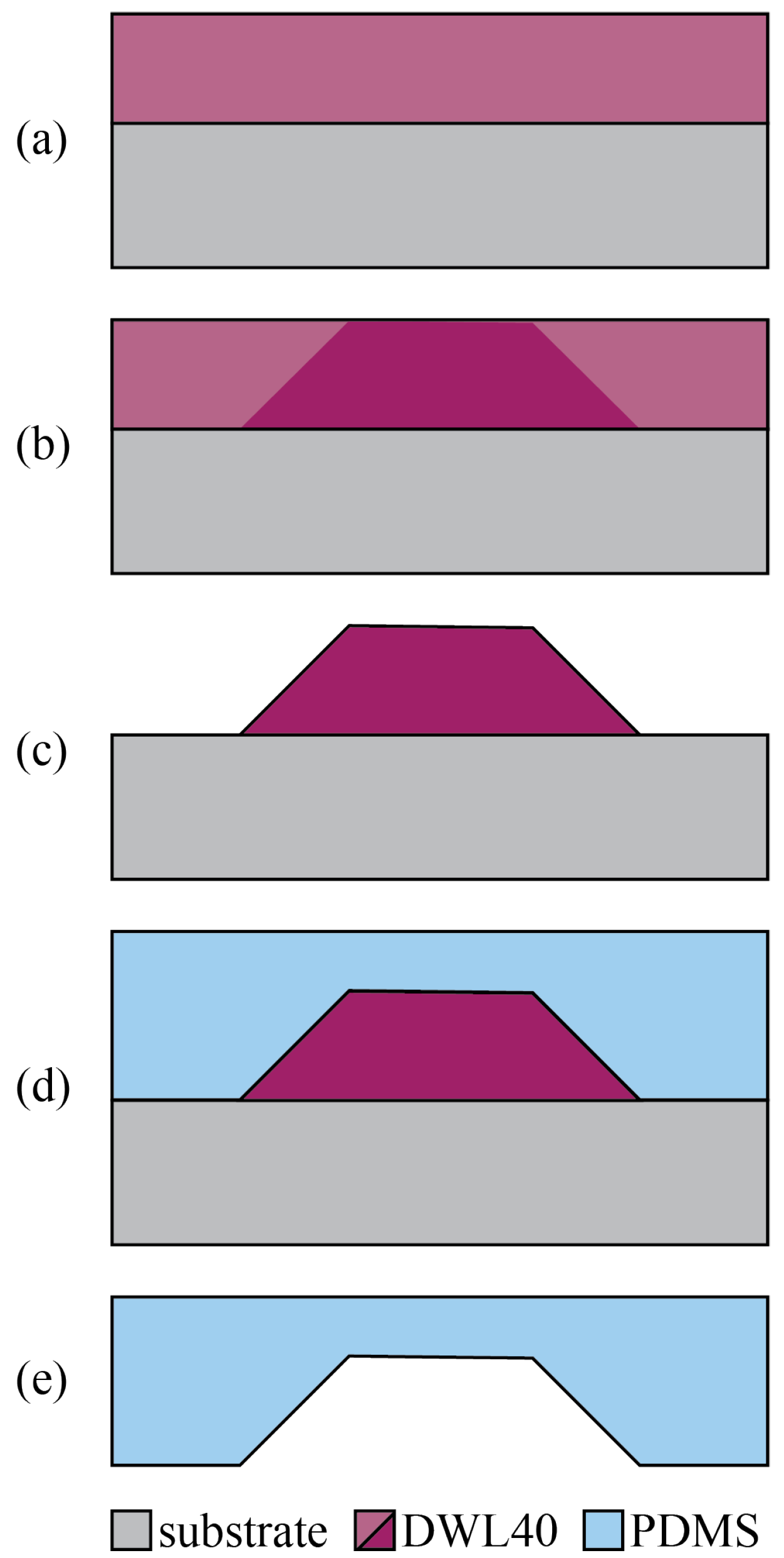
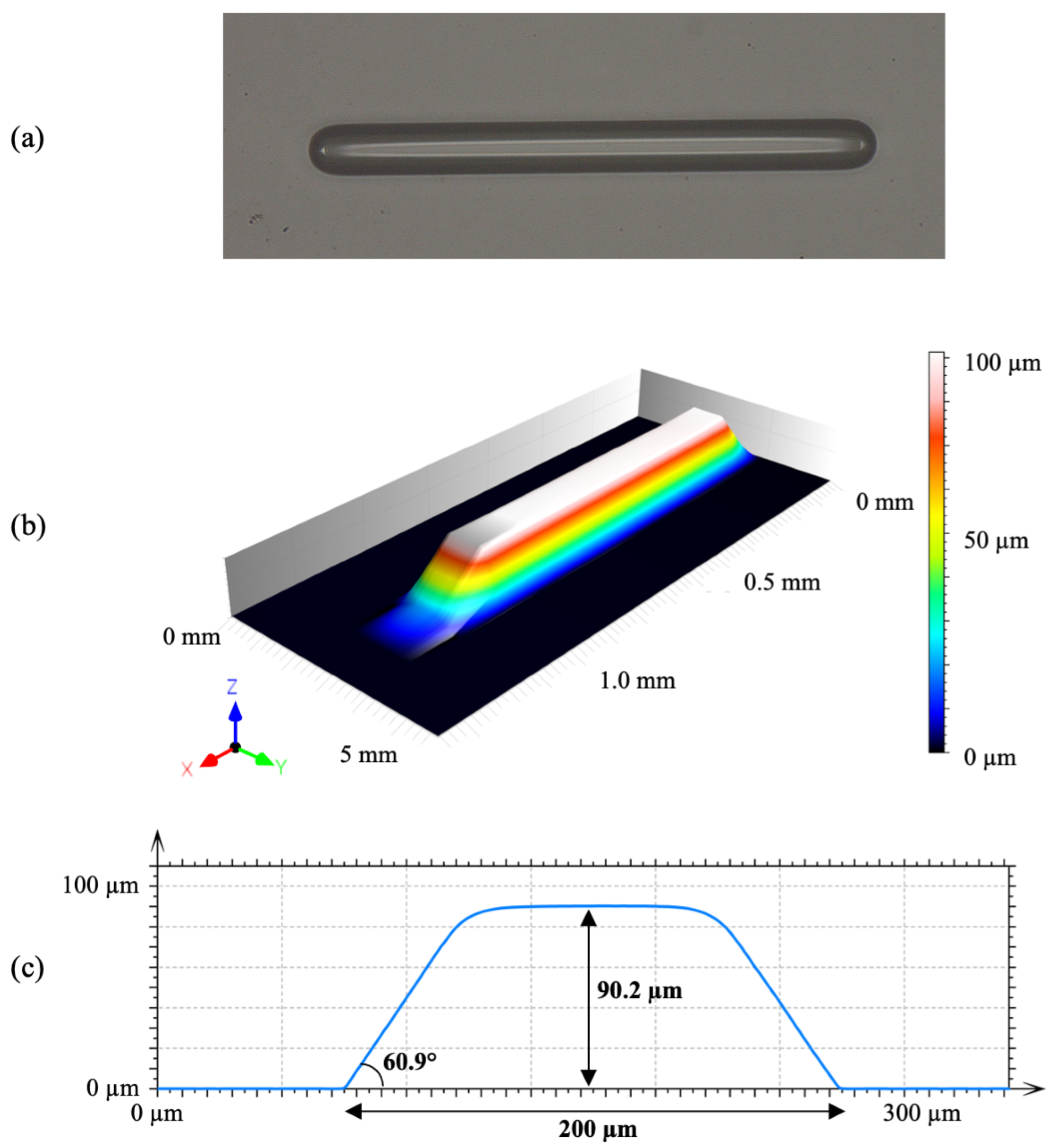
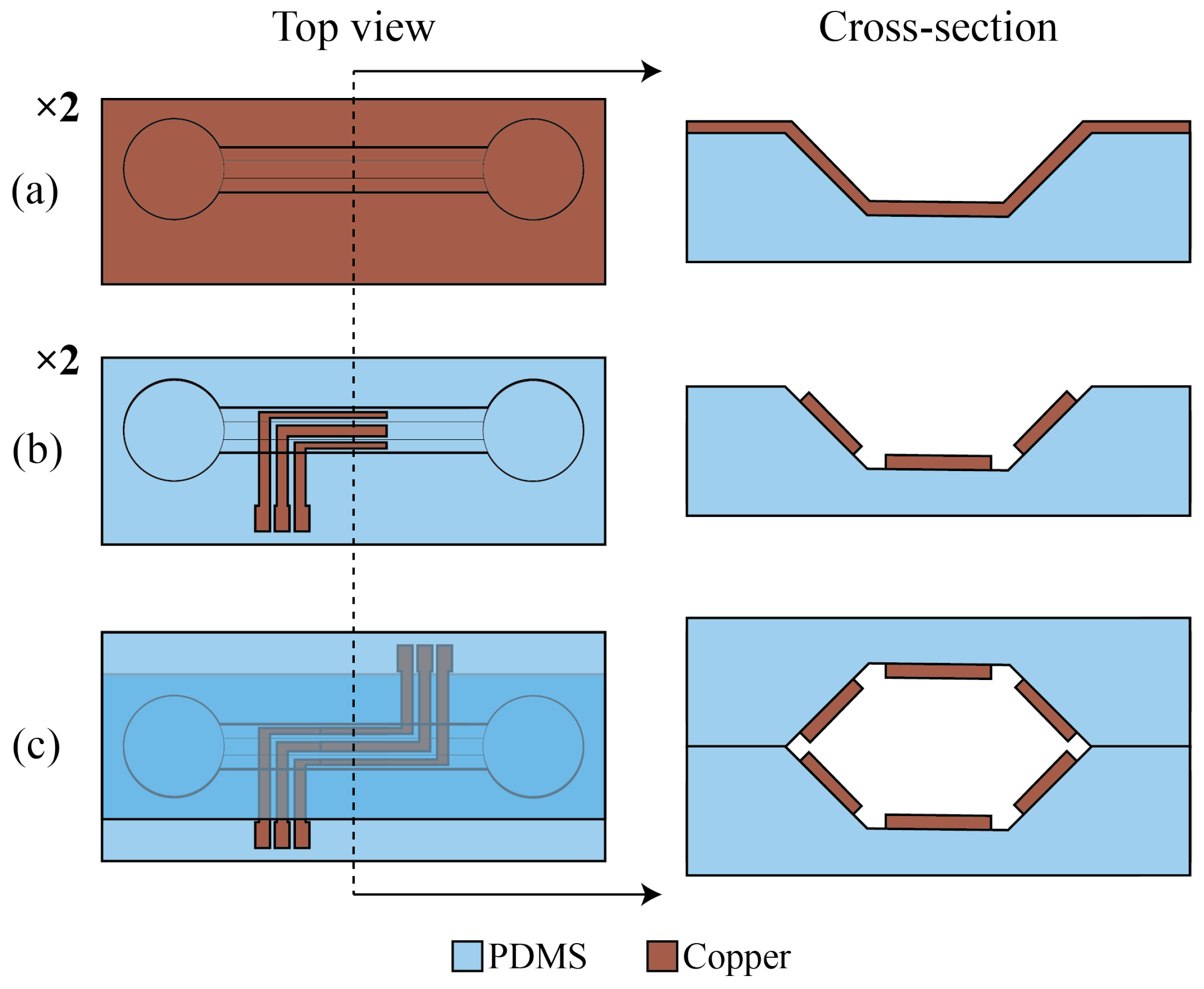
3.2. Fabrication Process

Recent advances in electroosmotic mixer fabrication have focused on improved mixing efficiency and reliability [22,23,24]. In order to benefit from effective DCEO, the proposed device topology requires an uncommon 3D hexagonal channel cross-section. This subsection details the intended fabrication process allowing the implementation of this geometry, which is constructed by attaching two identical channel halves.

The process begins with the realization of a casting mold for the two channel halves, which are to be implemented in PDMS. On a clean glass substrate, after oxygen plasma treatment, an 87 μm thick coat of negative mr-DWL 40 photoresist is applied by spin coating and soft baked at 100 °C (Figure 2a). Using the Raith PicoMaster 100 direct laser writing system, the photoresist is then subjected to maskless grayscale lithography through the modulation of the laser intensity to achieve a 60-degree slope for the developed pattern (Figure 2b,c). Figure 3 demonstrates the use of grayscale lithography to implement a channel mold with adequate shape and dimensions. This critical step validates the eventual viability of this approach for implementing hexagonal microfluidic channels.

This mold then serves twice to cast PDMS in order to form the two halves of the hexagonal microchannel (Figure 2d). The PDMS is heated at 100 °C for 35 min and then detached from the mold (Figure 2e).

For each of the two PDMS parts, copper is conformally deposited by DC sputtering inside the channel (Figure 4a) and is patterned via lithography using spray-coated Microposit S1813 positive photoresist. Spin coating is expressly avoided in order to circumvent the edge beading effect that would otherwise occur due to the channel recess profile. Once photolithography is complete, copper is etched using ferric chloride/hydrochloric acid wet etching [25] (Figure 4b). Finally, the two substrates are aligned and bonded together so as to form the hexagonal channels while leaving electric contact pads exposed. PDMS bonding is enabled by $O_2$ plasma activation (Figure 4c).

4. Results

The behavior of the proposed mixer is assessed using finite-element methods by means of COMSOL Multiphysics, which allows for the simulation of models combining fluid mechanics and electrostatic effects.

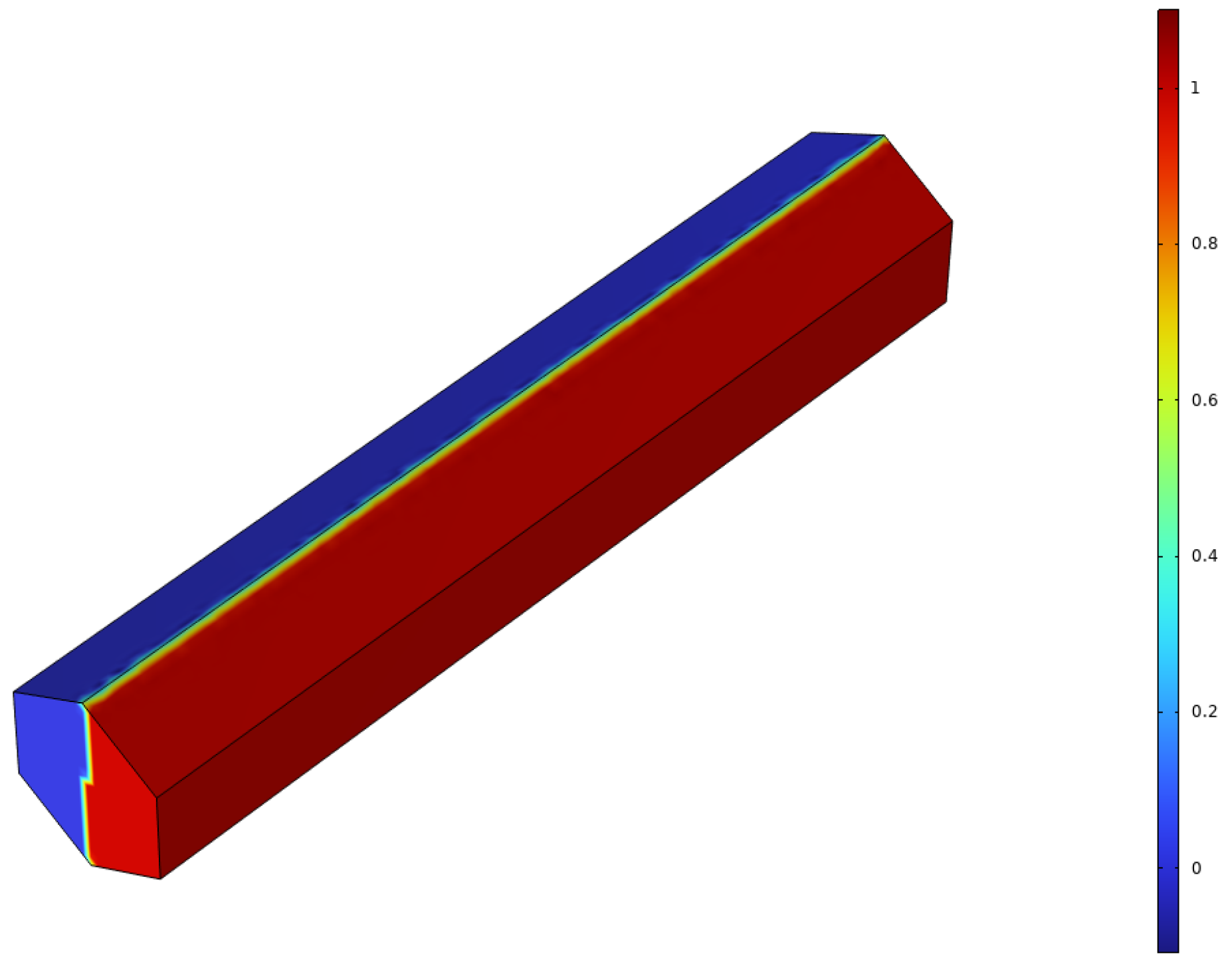
4.1. Initial and Boundary Conditions

The initial conditions of the model assume that the fluid inside the channel is at rest at time zero, with distinct concentrations in both halves of the channel, representing the laminar combination of two species, as shown in Figure 5.

Another initial condition imposed is that the electric charge be conserved throughout the system. As for the boundary conditions, they mainly consist of the inlet velocity and the electric potential applied across the electrode pairs. A simulation is carried out using the generalized minimal residual method (GMRES) with the quadratic discretization of the numerical model and uses the implicit generalized alpha method for time-stepping, with a constant time step of 100 ms.

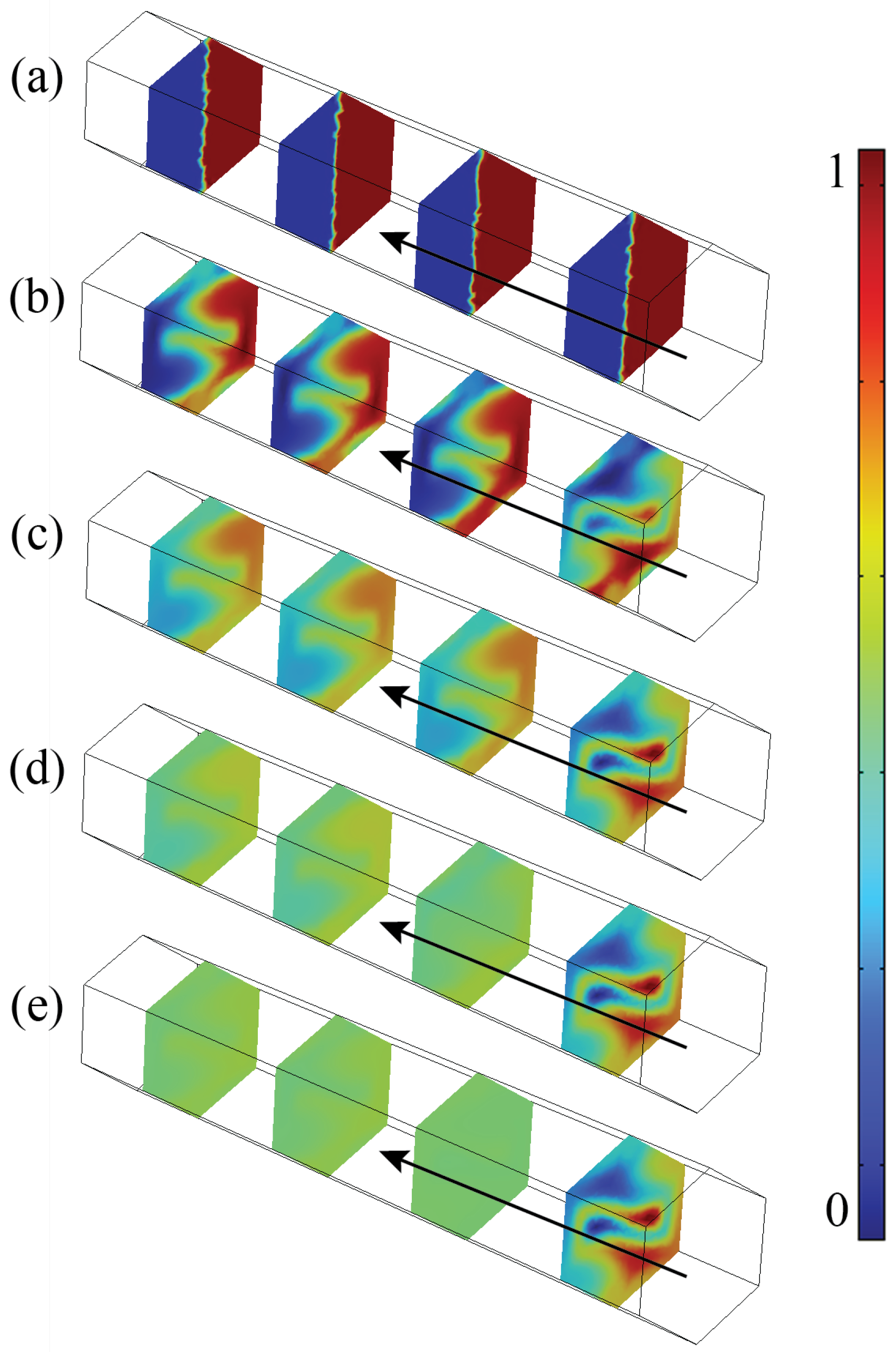
4.2. Vortex Formation and Mixing Action

Upon applying a positive potential of 5 V to one pair of opposite electrodes and a negative potential of −5 V to another pair while maintaining a zero potential on the final pair of electrodes (see Figure 6), combined with an inlet flow of 0.5 $\mathsf{\mu }$m/s, one observes the formation of helical vortices inducing a spiral mixing contour within the microchannel. Figure 7 shows the strong helical vortex along the channel boundary and a sub-axial vortex around its central axis.

Figure 8 shows the concentration profile along the channel for different delays after turning on the mixer for a Reynolds number of 0.0865. The concentration in the channel progressively converges to a uniform value of 0.5, indicating full mixing. At 1 s after activating the electrodes, $MI$ at the outlet of the channel is approximately 98.46%. The calculated ${\delta }_m$ of 98.44% confirms the effectiveness of the proposed mixing approach.

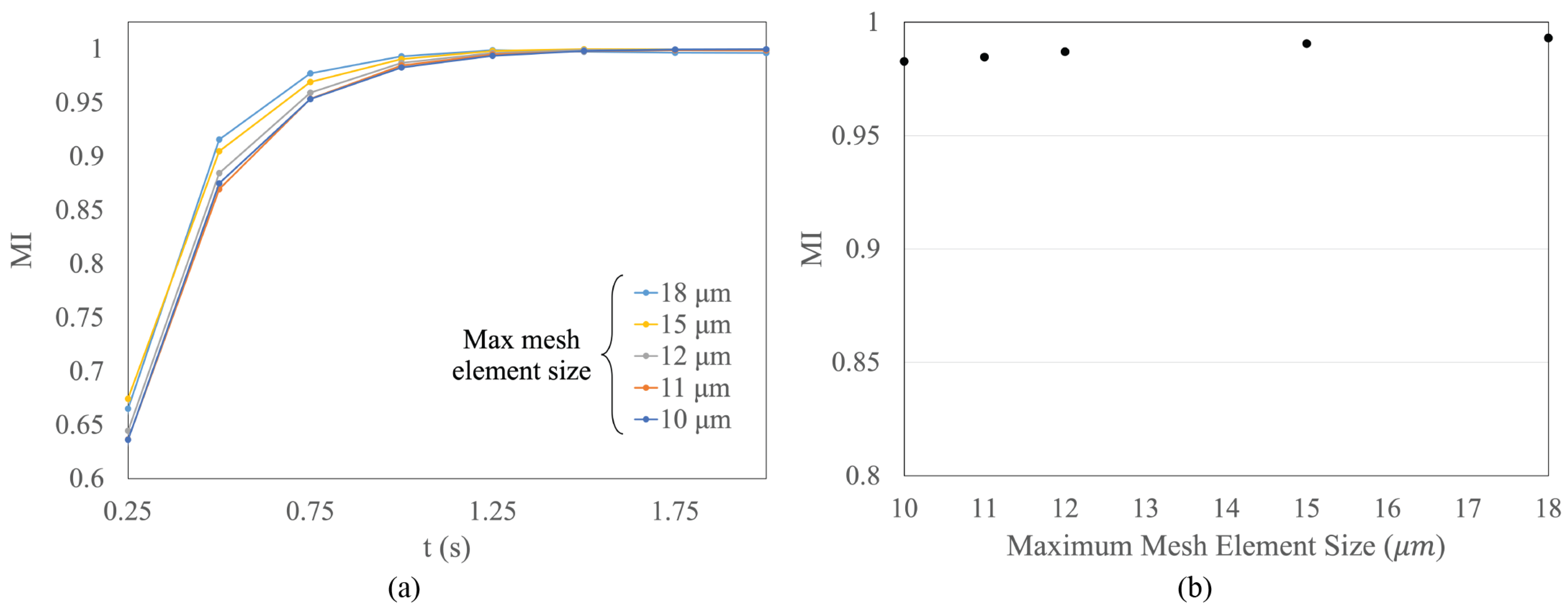
4.3. Model Mesh Independence Assessment

As presented in Figure 9, simulations were performed using the parameters from the previous section while varying the grid size of the finite-element mesh in order to ascertain the overall numerical reliability of the results. One can observe convergence for a maximum mesh element size of 11 $\mathsf{\mu }$m, which is, therefore, the value selected for all simulations in this work.

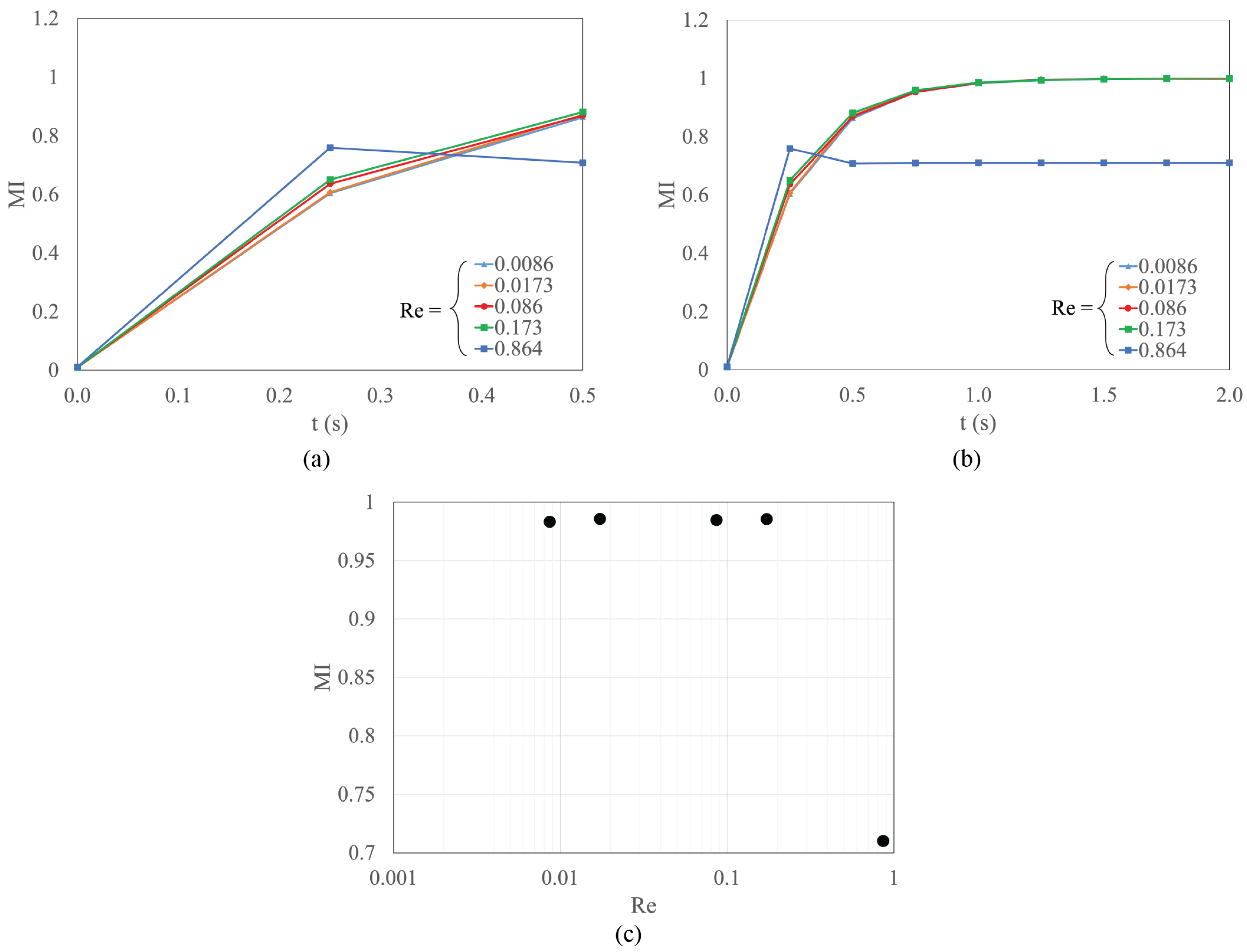
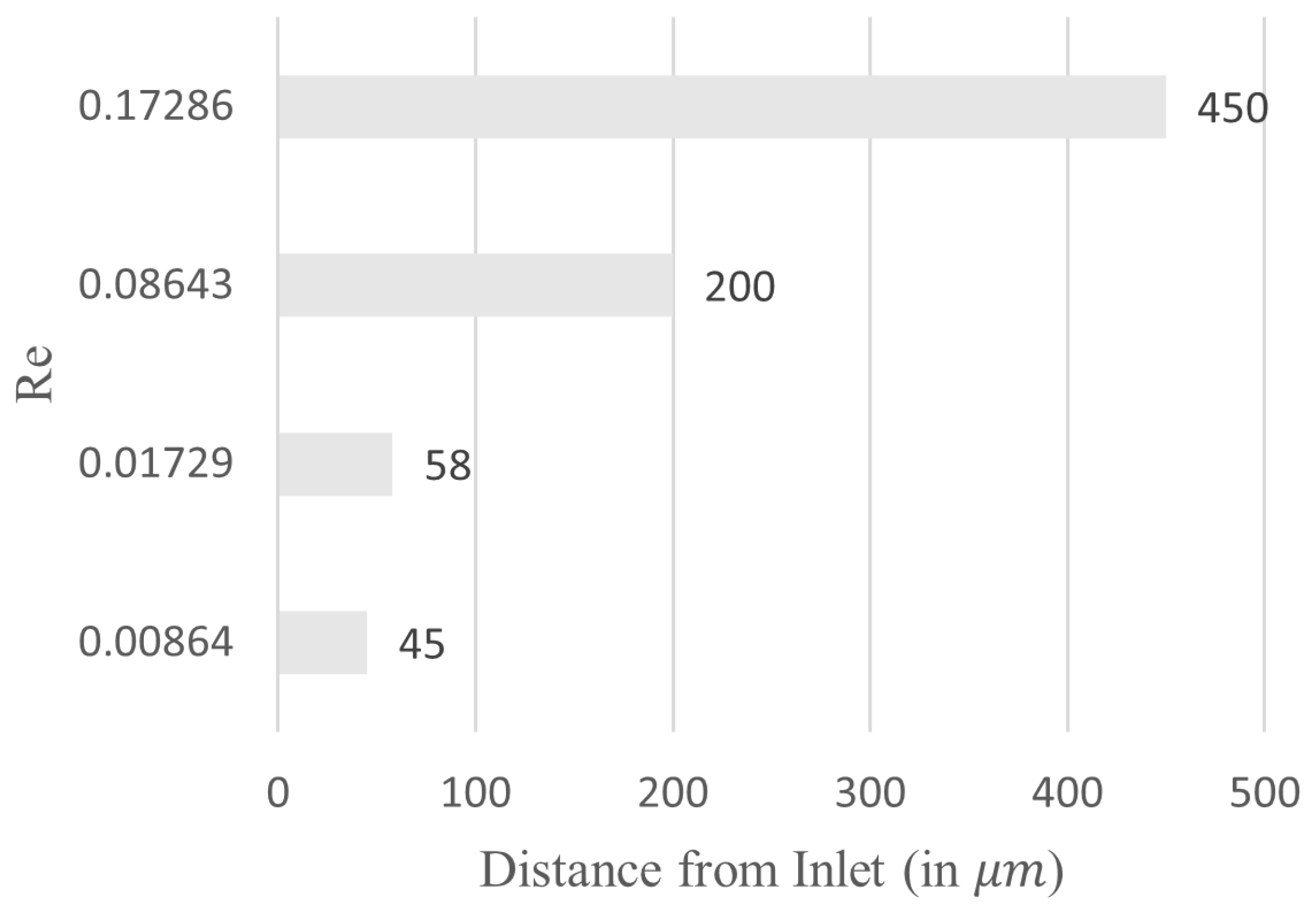
4.4. Effect of the Reynolds Number on Mixing Efficiency

This work studies the effectiveness of the proposed approach for different Reynolds numbers by varying the inlet velocity conditions. Reformulating Equation (8), the Reynolds number for a hexagonal channel of side length a may be obtained through

$$Re=\frac{u{D}_h}{\mu }$$

(12)

where the hydrodynamic diameter is

$$D_h=\frac{4A}{P}$$

(13)

while

$$A=\frac{3\sqrt{3}}{2}{a}^2$$

(14)

$$P=6a.$$

(15)

The electroosmotic effect relies both on the applied voltage and on the speed of the bulk flow. Hence, an increase in fluid velocity leads to a more pronounced electroosmotic effect, resulting in enhanced mixing. However, this effect is only detected up to a certain Reynolds number, beyond which the inertial forces begin to dominate, suppressing the formation of vortices. In Figure 10a, one can observe a significant reduction in the mixing index for Reynolds numbers beyond about 0.5. Furthermore, in Figure 10b, the mixing index at the channel outlet converges to a value well below that indicative of uniform mixing. This suggests that the fast flow velocity forces the fluid to reach the outlet before the electroosmotic effect has had time to induce complete mixing. Consequently, a longer active mixing portion of the channel would be required to achieve a similar degree of mixing as for lower Re in order to expose each traveling element of the fluid to an equivalent duration of mixing action before reaching the outlet.

The study also reveals a mixing index spike after around 0.25 s for a Reynolds number of 0.864, indicating that the high fluid velocity contributes itself to the mixing effect. For Reynolds numbers below 0.173, the mixing efficiency exceeds 99.85% after 2 s. Figure 10c, with its close-up on the early moments after mixing start, highlights the faster transient mixing effect for higher Re.

Figure 11 illustrates the minimum distance from the inlet required to achieve a mixing efficiency of 95% for different Reynolds numbers. As such, this dictates the minimum channel length to be able to achieve that level of mixing.

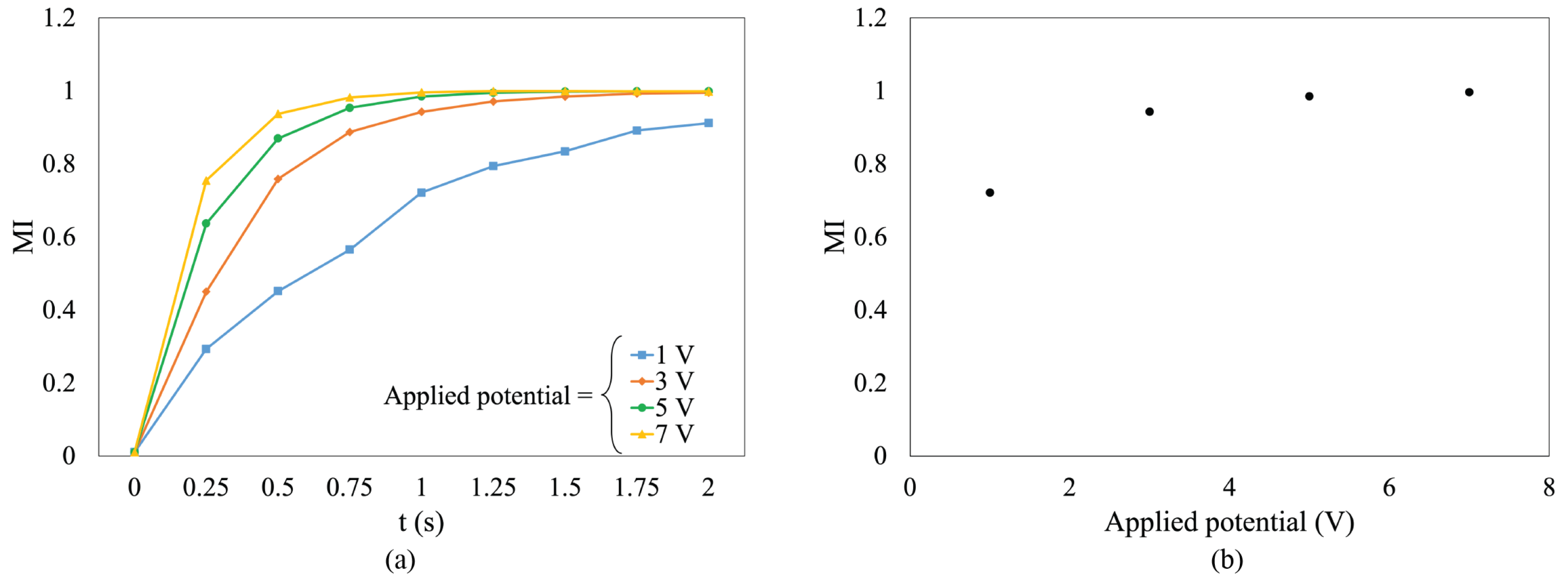
4.5. Effect of the Actuation Potential on Mixing Efficiency

A higher applied DC voltage is expected to lead to stronger electroosmosis. When a strong electric field is applied, the bulk electric force generated by ${\rho }_e$ E becomes significant, resulting in the formation of vortices that have a pronounced effect on fluid flow. Figure 12a shows how increasing the applied electric potential significantly speeds up the mixing action. As such, it is crucial to make use of an actuation voltage large enough to sufficiently mix the fluid before it reaches the mixer channel outlet, as highlighted in Figure 12b.

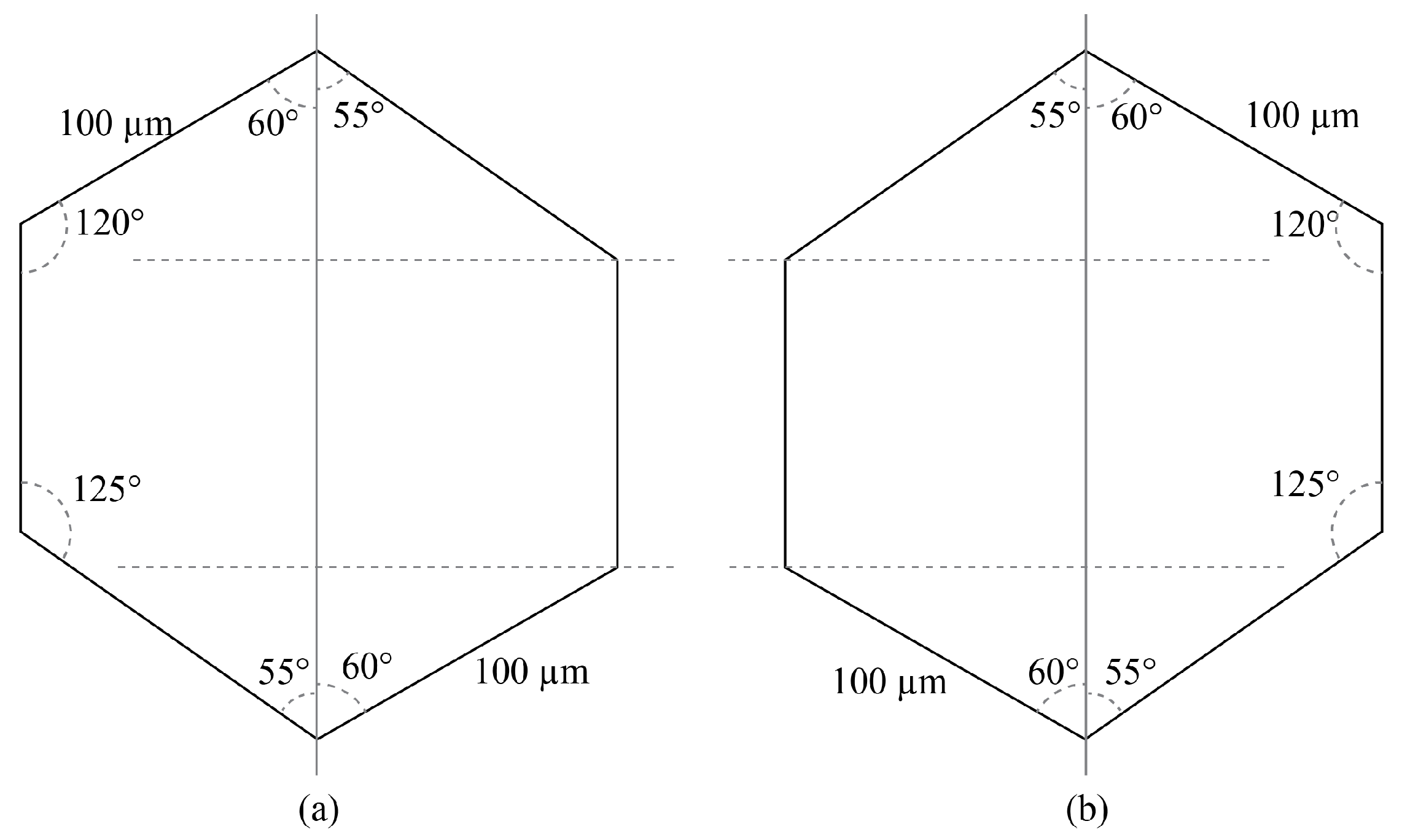
4.6. Effect of Channel Geometry

The selection of a hexagonal channel proves advantageous in guiding vortices to circulate fully within the channel. Geometrical differences, although subtle, may have a significant impact on mixing dynamics. As an investigation of the potential of this approach, a slight modification in the hexagonal cross-section is introduced, and its impact is studied. Indeed, the hexagonal shape of the cross-section is transformed to be slightly irregular by modifying some angles by 5° compared to the regular structure (Undef) in order to elongate two of the sides. Two geometries are investigated: one where the faces corresponding to positive electrodes are elongated (${\mathrm{Def}}_N$) and the other where the faces corresponding to negative electrodes are elongated (${\mathrm{Def}}_P$), as showcased in Figure 13.

The slight change in geometry brings the positive and negative electrodes closer together and modifies the electric potential distribution across the cross-section, as seen in Figure 14.

Since the intensity of the electric field is inversely proportional to the distance between the electrodes, these modified geometries lead to an average increase in the value of the y-component of the electric field by 5000 V/m, which accelerates the electroosmotic mixing, allowing the $MI$ to exceed 90% in just 500 ms, as shown in Figure 15. After 1 s, the $MI$ reaches 99.31%, compared to 98.46% for the undeformed case.

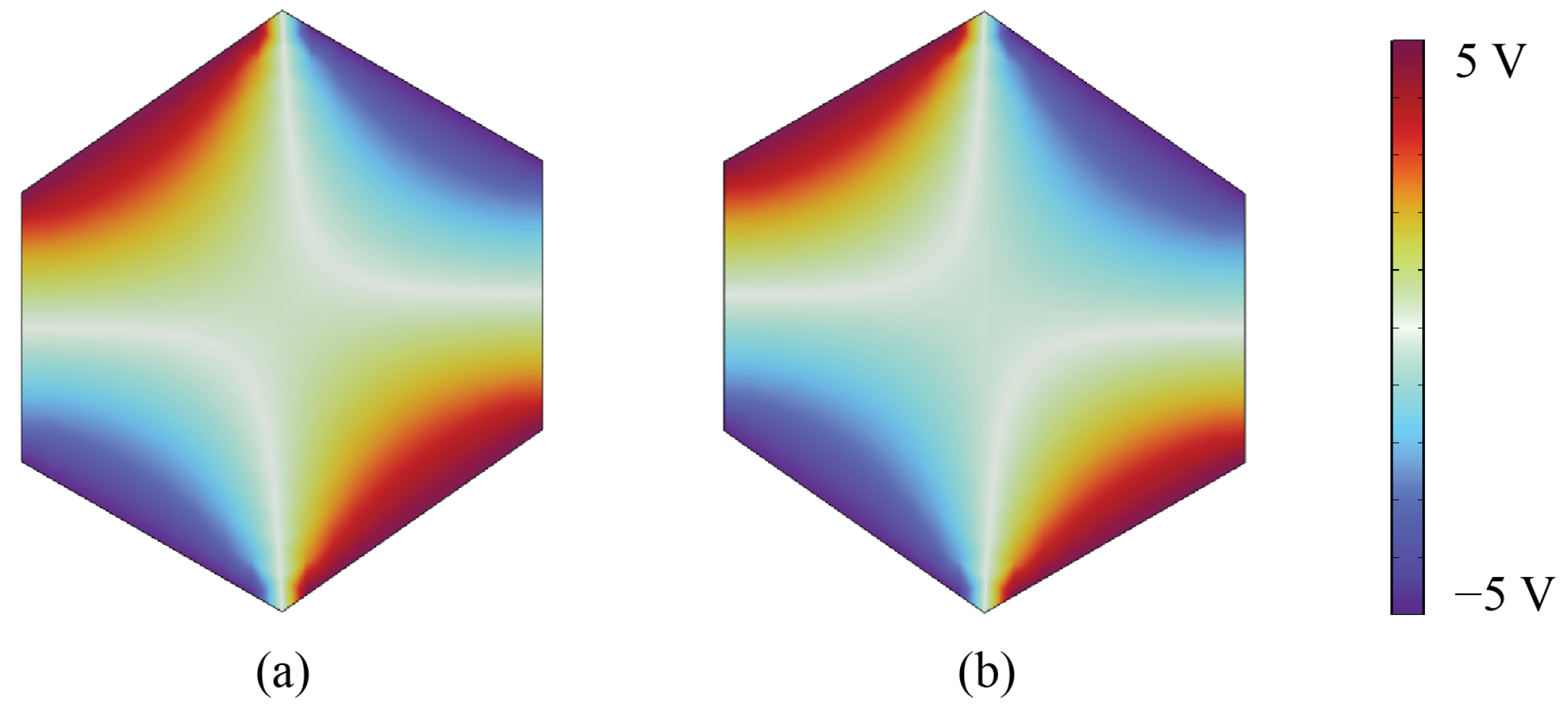
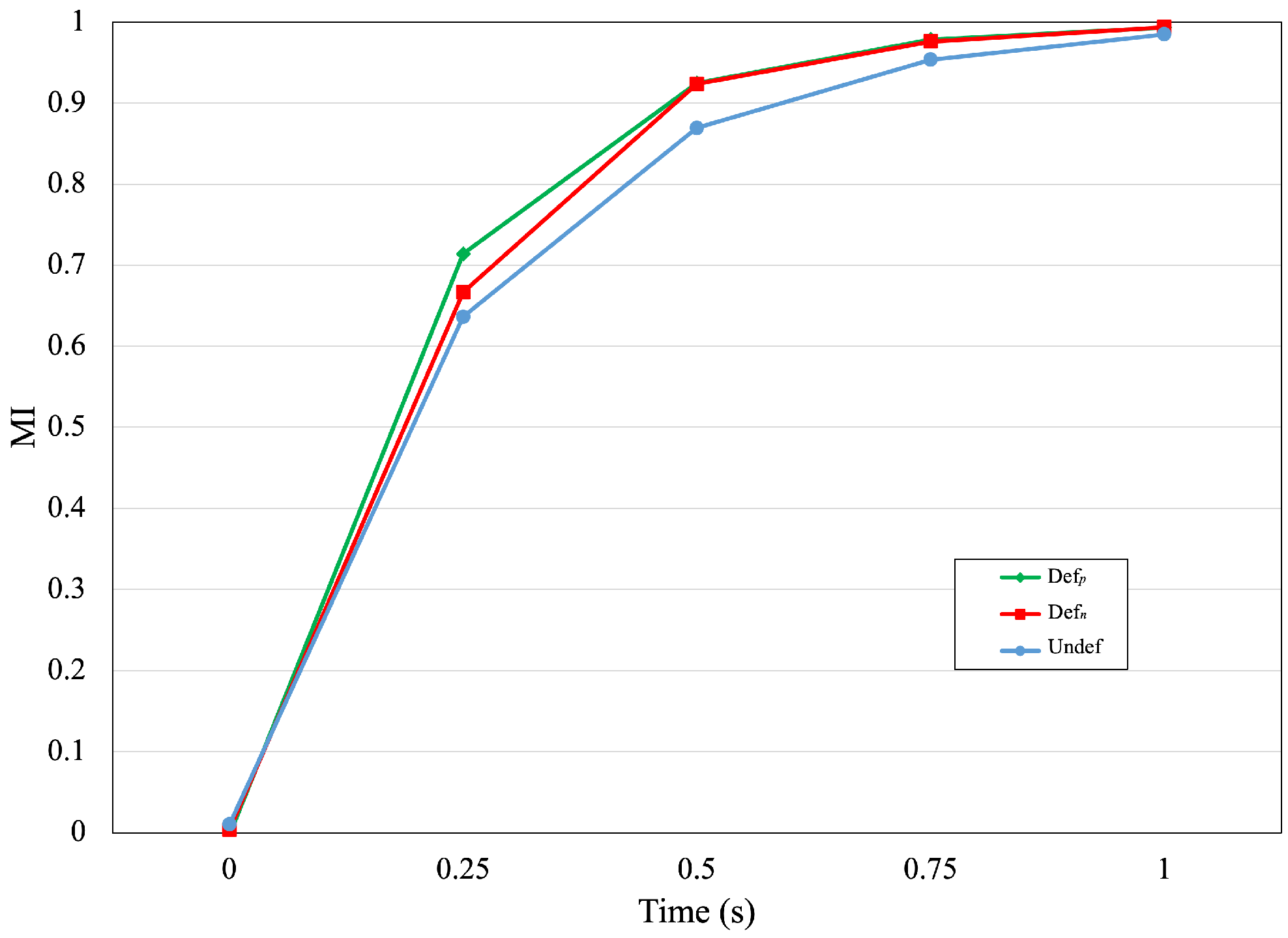
4.7. Effect of Asymmetric Voltage Configuration

This work also explores the impact of applying asymmetric voltage levels to the electrodes. In this scenario, the two left-hand electrodes are still driven by the same voltage levels (±5 V), while a different level is used for the right-hand electrodes in two alternate configurations: ±3 V (${\mathrm{Conf}}_{3V}$) and ±7 V (${\mathrm{Conf}}_{7V}$). The electric potential distributions across the cross-section of the channel are shown in Figure 16. After 1 s of flow, the mixing indices are 98.46% (base configuration), 97.72% (${\mathrm{Conf}}_{3V}$), and 99.25% (${\mathrm{Conf}}_{7V}$).

5. Discussion

While passive micromixers, such as EC cavity array micromixers, staggered herringbone mixers (SHMs), slanted groove mixers (SGMs), and barrier-embedded mixers (BEMs), have exhibited remarkable mixing efficiencies, their designs often involve intricate structures that can be challenging to fabricate [26,27]. Similarly, curved structures such as serpentine micromixers, which induce Dean Vortices, may necessitate additional effort to circulate the liquid through bends in the channel [28]. While complex elliptical curves have been implemented to improve the performance of serpentine micromixers and toroidal and helical channels have been introduced to introduce chaotic flow, all of these approaches require additional effort in terms of fabrication [29].

In contrast, the proposed DC electroosmotic (DCEO) micromixer features a streamlined design, free from the need for complex internal structures or additional sources to drive the bulk fluid through the channel. The electroosmosis effect efficiently agitates the fluid, allowing the micromixer to create strong helical vortices and chaotic flow without the need for complex helical or toroidal structures and without impeding fluidic flow.

While some micromixers make use of acoustic techniques to generate vortices or disturbances in the bulk fluid, either by actuating extended structures such as cantilever beams or membranes [30,31] or by creating complex vortices using the interference of effects from nearby structures [32,33], these methods can produce complex vortices and generate considerable heat. As a result, challenges exist in stabilizing and safely eliminating bubbles [34].

Among electrokinetic methods, alternating current electrothermal (ACET) micromixers have shown impressive results. However, ACET is not ideally adapted for situations with limited fluid volume, such as the one that our proposed micromixer addresses [35]. For such applications, the use of DC electroosmosis is more practical and reliable, as it allows for precise control of the potentials applied to the electrodes and produces strong vortices, enabling efficient mixing within a limited channel length. The proposed DCEO approach is particularly well-suited for optimizing mixing efficiency through cross-sectional geometry, which alters the distance between electrodes.

6. Conclusions

In the realm of microfluidics and micromixers, the proposed DCEO micromixer stands out as a novel and highly efficient solution. This microdevice showcases its remarkable mixing efficiency, achieving approximately 98.5% mixing efficiency in just one second and an impressive 99.8% mixing in two seconds, all within a remarkably compact channel length of only 1 mm. This efficiency is consistently achieved across a wide range of Reynolds numbers, typically ranging from 0.08 and 0.2, making it versatile for a variety of microfluidic applications.

One of the standout features of this micromixer is its ability to generate persistent and stable helical vortices through the controlled application of a constant DC electric field. Unlike more complex and intricate microfluidic designs, the proposed micromixer can be implemented using a simple fabrication process and conveniently integrated within a full lab-on-a-chip system.

It was demonstrated that channel cross-sectional geometry can be further optimized to target even greater mixing performance.

As a future development, it is envisioned that the device could potentially be improved by segmenting the electrodes and selectively activating sections according to the current Reynolds number. This enhancement could optimize power utilization according to the required mixing length.

In summary, the proposed DCEO micromixer not only meets but exceeds the needs of various microfluidic applications. Due to its generation of helical vortices, it has the potential to revolutionize microscale mixing and pave the way for new applications, such as serving as a foundation for innovative centrifugation techniques.