Abstract
The electro-mechanical brake is a new advancement in railway train braking. Ball-screws are important components of electro-mechanical braking units (EMBUs), and their wear can cause EMBUs to degrade in performance or even fail to function. In this paper, we present a framework for prediction of ball-screw wear with discrete operating conditions as inputs, taking into account the time-varying characteristics of EMBUs. The framework includes determining the contact type, analyzing relative motion, calculating contact deformations, and estimating wear. The contact type is determined based on the quasi-static approach of Hertz theory. A dynamics model using multiple coordinate systems is established to analyze how balls and raceways move in relation to each other. The contact deformations of the ball–raceway contact are determined using numerical calculation. Then, the wear depth increment is calculated using the Archard model. The results of the calculation and the endurance test indicate that the wear on the screw raceway is greater than that on the nut raceway. The effect of velocity is greater than the effect of axial force. The presented calculation framework is reasonable and can be used for predicting EMBU ball-screw wear.
1. Introduction
The electro-mechanical brake (EMB) is a novel braking mode for railway trains, which has advantages of shorter response time, higher control accuracy, simpler maintenance, and a more compact structure [1,2,3,4]. Currently, the EMB technology has been applied to aircraft, automotives, and rail vehicles [5,6,7,8,9,10] and is recognized as the next generation of braking technology.
The actuators of the EMB system are electro-mechanical brake units (EMBUs). Two crucial parts of the EMBU are the motor and ball-screw. Ball-screw wearing is an unavoidable deterioration of the EMBU, leading to higher friction and increased internal clearance. Ultimately, it results in functional failures, such as an inadequate response or brake failure. Therefore, the wear prediction of the ball-screw is an important issue for health monitoring of EMB systems.
The wear of ball-screws primarily comes from the sliding friction between the balls and the raceways. There have been some studies on the wear modeling of ball-screws. The researchers typically establish a kinematic model of a ball-screw in the Frenet–Serret coordinate system using the rolling element theory and the dynamic model of Jones and Harris [11,12]. They then study the wear accumulation, preload degradation, and accuracy loss under various preloading modes, loads, and angular velocities [13,14]. Wei et al. [14] extended the CEB elastic–plastic contact theory [15] to calculate the wear of the high-speed ball-screw with single-nut preload. Cheng et al. [16] proposed an improved Archard wear model considering time-varying loads and time-varying sliding distances for wear calculation. Zhao et al. [17,18] analyzed the loss of accuracy in the ball-screw with double-nut preload using Archard wear theory, fractal theory, and an iterative interpolation method. Shen et al. [19] further considered the two-stage wear characteristics of ball-screw with preload. In the first stage (running-in stage), the model is established based on macroscopic geometric principles, and in the second stage (steady wear stage), the model is established based on fractal theory. Zhang et al. [20] included the wear amount in the transmission efficiency model to analyze its impact on transmission efficiency. Cheng et al. [21] proposed a model to predict the accuracy loss and wear of ball-screws. There are dynamic modeling methods of ball-screw systems deserving attention. Zhang et al. [22] proposed an equivalent dynamic model of a ball-screw system with the hybrid element method. Okwudire et al. [23] established a hybrid finite element model considering the coupled axial, torsional, and lateral dynamics. In addition, the lumped mass method [24], dynamic stiffness model [25], and modified load distribution model with additional elastic units [26] are also interesting studies that are helpful for ball-screw calculation and analysis.
Most of the aforementioned studies focused on high length-to-diameter ratio ball-screws used in CNC machine tools. This type of ball-screw is different from the one used in EMBUs. The ball-screw used in CNC machine tools has a long lead length (10 mm or more) and operates at high velocity (300 rpm or more). The ball-screw of EMBUs is a slow-moving ball-screw with a small pitch. The motion stroke is small, but the axial force is large. The velocity and accuracy requirements are lower compared to CNC machine tools. There have also been some studies on the wear of the EMBU ball-screw.
The wear of the ball-screw leads to increased axial internal clearance of the actuator [27,28]. Isturiz et al. [29] used current and position signals as monitoring indicators for measuring clearance increase. Mansouri et al. [30] used the Kalman filtering method to estimate the wear gap. Fu et al. [31,32] modeled the electro-mechanical actuator using bond graph theory and conducted fault simulation to analyze the dynamic response of the actuator in the presence of wear clearance. The studies above mainly focused on the effects of failures after wear occurs instead of quantitatively analyzing the development of wear.
EMBUs operate at time-varying velocity and load; hence, the wear increments of ball-screws also vary dynamically. This paper introduces a wear prediction framework that combines the unsteady-state operating characteristics of EMBUs to predict the cumulative wear of ball-screws in EMBUs. The wear prediction framework uses the time-varying velocity and load as inputs. Then, the contact type and contact area are identified based on elastic–plastic contact theory. A multi-coordinate system dynamic model of the ball-screw is then established to numerically calculate the contact deformation and sliding velocity. Finally, the Archard model is used to calculate the incremental and cumulative wear. The proposed calculation framework is validated with the results of the endurance test.
The rest of the paper is organized as follows. The working principle of EMBUs is described in the next section. In Section 3, we present the methodology for the EMBU ball-screw wear prediction framework. In Section 4, we introduce the wear prediction framework and describe the endurance test used to validate the calculation. In Section 5, we discuss and compare the results of the calculation and test. Finally, we conclude the paper in Section 6.
2. Working Principle of EMBUs
The brake cylinder of the EMBU consists of the motor, the ball-screw, and other mechanical transmission components. A photograph of an EMBU and a simplified diagram of a brake cylinder are shown in Figure 1. When braking, the electronic brake control unit (EBCU) converts the desired clamping force into the appropriate command current. The driver circuit powers the stator windings to create a magnetic field, which in turn drives the rotor and the screw to rotate in sync. The nut converts rotational motion into linear motion, pushing out the clamp lever. The brake pads on the lever press against the brake disc to create the necessary clamping force. The clamping force is ultimately converted into a braking force by the friction between the pads and disc, as well as the adhesion between the wheels and rails. Similarly, during brake release, the rotor and the screw rotate in opposite directions. The nut then pulls the clamp lever back, releasing the clamp force.
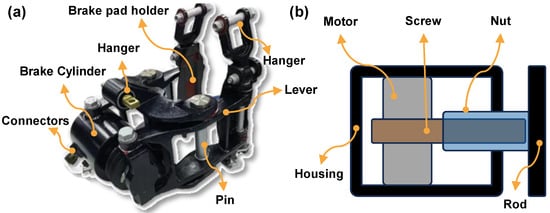
Figure 1.
Schematic diagrams of a disc EMBU and brake cylinder. (a) Photograph of a disc EMBU; (b) simplified diagram of brake cylinder.
According to the working principle of EMBUs, the braking and releasing process can be divided into four phases: clearance–elimination, force–generation, force–maintenance, and force–release. During these four phases, Figure 2 illustrates the interaction between the brake pads and the disc. When the EMBU is in any phase other than the force–maintenance phase, there is sliding friction between the balls and raceways of the ball-screw. Sliding friction causes the most wear during the steady wear stage of the ball-screw. The wear can lead to an increase in the axial clearance within the brake cylinder.
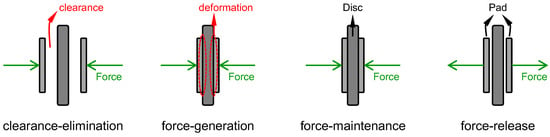
Figure 2.
Relationship between brake pads and disc in the four duty phases of the braking and releasing process.
3. Wear Modeling
This section presents the methodology used in the EMBU ball-screw wear prediction framework. The contact model is established to determine the contact type between the ball and the raceway and to calculate the contact area. The multi-coordinate system dynamics model is established to analyze the force relationship between the ball and the raceway, as well as the relative sliding velocity. The wear depth increment is calculated using the Archard model.
3.1. Contact Model
By the geometry and material properties of the ball-screw, the associated parameters of the ball–raceway contact can be calculated. As depicted in Figure 3, we can define the radius of ball, screw-raceway and nut-raceway as , , and , the contact angle between balls and raceways as , the helix angle as , and the screw nominal diameter as . Then, the principle curvature, sum of principle curvature, and effective curvature ratio can be calculated as shown in Table 1. A negative principle curvature indicates that the contact surface is concave.
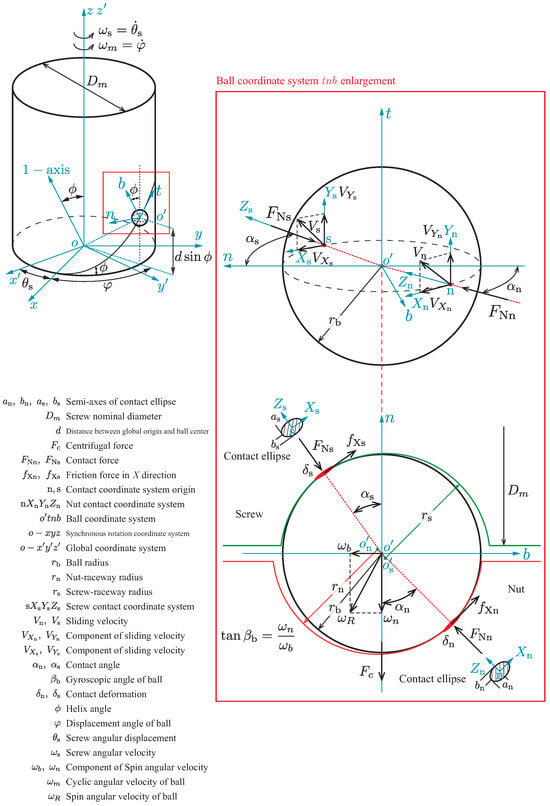
Figure 3.
Schematic diagram of dynamic model for ball-screw.

Table 1.
Symbols and formulas for principle curvature, sum of principle curvature, and effective curvature ratio of the ball–raceway contact.
According to the Hertz theory [33], the deformation of the ball–raceway contact can be obtained as follows,
where and are complete ellipticity integrals of the first and second kind, respectively. is the effective modulus. is the ratio of the long and short semi-axes of the contact ellipse. is the normal force at the ball–raceway contact. The subscripts s and n correspond to screw and nut, respectively.
Due to the computational complexity of elliptic integrals, the approximate fitting method proposed by Markho is used in this paper [34],
The normal force at the ball–raceway contact can be obtained as follows,
in which,
where is the axial force. Z is the effective number of balls. i is the number of loaded turns. is the number of unloaded balls in the recirculation system.
To determine the contact type between the balls and the raceways, we need to calculate the plasticity index. According to Tabor [35], plastic deformation begins to occur within the surface layer when the average contact pressure reaches 0.6H. Here, H represents the hardness of the softer of the two objects in contact. Chang et al. [15] accordingly proposed the critical interference for plastic deformation, which can be written as follows,
where and is the Poisson ratio of the softer object [36]. is the average effective curvature radius of asperities, which is equal to the composite roughness [14].
When , the contact is elastic. When , the contact is elastic–plastic. With the contact type identified, the contact area can be calculated from the following equation [37],
in which,
3.2. Dynamic Model
The dynamic model of the ball-screw is established in order to analyze its force and motion. Figure 3 shows the schematic diagram of the dynamic model.
The model contains three motion coordinate systems and two contact coordinate systems. is the global coordinate system. is the synchronous rotation coordinate system, which rotates with the screw. The -axis and z-axis of the two systems are coincident. is a Frenet coordinate system, the origin of which is at the center of the ball. The t-axis is along the direction of the ball trajectory. The n-axis and b-axis are in the plane of the ball–raceways contact.
The two contact coordinate systems are at the ball–raceways contact, which are and .
Define the cyclic angular velocity of the ball and the spin angular velocity as and , which are given as [38],
in which,
where is the rotational angular velocity of the screw and is the gyroscopic angle.
According to [38], the gyroscopic angle ranges between 46 and 48° for screw velocity below 1000 rpm. And the initial value taken between 40 and 50° has little effect on the wear prediction. Therefore, the initial value of gyroscopic angle is taken as 47° for numerical calculation.
After obtaining the spin angular velocity and ignoring its component along the t-axis [38], its components in the n-axis and b-axis can be obtained from the geometric relations depicted in Figure 3,
From the dynamics of the ball in the -plane in Figure 3, it can be found that the ball is subjected to centrifugal force and friction and normal contact force. The centrifugal force is generated by the cyclic angular velocity , parallel to the negative direction of the n-axis. Hence, the centrifugal force can be obtained from the following equation,
where is the mass of a ball.
The friction mainly comes from the viscous drag caused by the lubricating medium and sliding friction. The viscous drag between the ball and the raceway is [39],
in which,
where is the initial dynamic viscosity. is the ratio of equivalent radii. is the pressure–viscosity parameter. is the load.
The sliding friction arises from the shear stress in the contact area, which is directly proportional to the normal contact force and can be calculated using the following equation.
where is the boundary friction coefficient. is the load shared by asperities.
By adding the lubricant and asperity friction force, the final equivalent friction coefficient can be defined:
Combining the force analysis above, the force equilibrium equation for the ball in the -plane can be expressed as follows [38,40],
To solve the force equilibrium equation for the balls, we also need the contact angles between the ball and the raceways. Hence, the relationship without load and with load for the ball center and the curvature center of raceways is modeled, as shown in Figure 4.
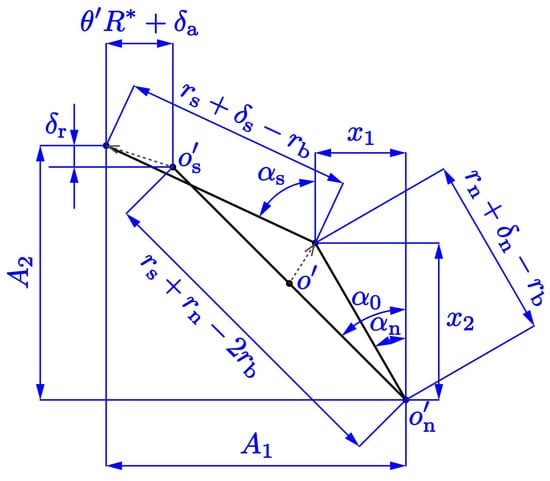
Figure 4.
Schematic diagram of ball center and raceway curvature center without load and with load.
, , are the ball center, the curvature center of the screw-raceway, and the nut-raceway, respectively, and the three are co-linear when there is no load. In this case, the contact angle is 45°, and this value will be used as the initial value for the numerical calculation later.
Fix the curvature center of the nut-raceway , the ball center and the curvature center of the screw-raceway will move in the arrow direction shown in Figure 4 when the ball-screw is subjected to an axial load.
The following equations can be obtained from the relationship in Figure 4,
where is the relative axial angular between the screw and nut after loading. and are the relative axial and radial displacements between the screw and nut after loading, respectively.
After obtaining the contact angles and the axis components of the angular velocity, the relative sliding velocity at the ball–raceway contact can be expressed as follows [41],
in which,
where is the component of the spin angular velocity in the t-axis, which is approximated to zero.
3.3. Wear Prediction Model
The Archard wear model [42] is used to calculate the amount of wear on the screw-raceway and the nut-raceway, assuming that all wear occurs on the softer contact object and the raceway is less hard than the ball.
The wear volume is related to the load and sliding distance as follows [43],
where is the increment of wear volume, is the increment of sliding distance, is the pressure yield limit for the softer material, and a dimensionless wear constant. For precision ball-screws made of bearing steel and under well-lubricated conditions, can be taken as 10−9 [43,44].
Let the discrete time step be , then the increment of wear depth and the relative sliding velocity are,
With Equations (21) and (22), divide both sides of equal sign of Equation (20) by and organize the result as follows,
To determine the incremental wear depth of the screw-raceway and the nut-raceway, it is necessary to calculate the contact area and relative sliding velocity using Equations (7) and (19), respectively.
Since the whole working cycle is relatively constant, the wear of the balls and the ball-screw working length involved is approximated to be considered uniformly distributed at the end of the endurance test. It is equivalent in terms of the final state.
4. Wear Calculation and Test Validation
This section introduces the wear prediciton framework, including the discretization of working conditions and the numerical calculation process. An EMBU endurance test used to validate the wear calculation is also presented.
4.1. Working Condition Discretization
The Archard wear theory assumes that when the yield limits of the materials of the two contacting objects are not the same, the wear is calculated only for the softer one and does not take into account the occurrence of wear in the harder contacting object. In ball–raceway contact, the screw-raceway and the nut-raceway are softer than the balls; therefore, it is assumed that wear occurs in the raceways. However, in practice, the balls will also wear out. The wear distribution ratio of raceway and ball is approximately 2/3 for the raceway and 1/3 for the ball [45,46].
Since the ball will move cyclically in the raceway, we consider the average wear increment generated at all contacts as the wear increment for that operating condition. The cumulative wear increment in the raceway is calculated by adding up the average wear increment values after each EMBU duty cycle. One duty cycle of an EMBU involves completing the actions of clearance–elimination, force–generation, force–maintenance, and force–release (see Figure 2). During the clearance–elimination, force–generation, and force–release phases, wear occurs due to the relative sliding of the balls and raceways.
According to the analysis of the EMBU working principle, the working conditions of the ball-screw in these three phases are shown in Figure 5. As illustrated by the figure,
- Clearance–elimination: the angular velocity of the screw rises from zero to the maximum velocity and stays at that velocity for a period of time. The axial force moves the nut and the clamp lever to eliminate the clearance between the brake disc and pads.
- Force–generation: the angular velocity of the screw decreases from the maximum velocity while the axial force increases. Finally, the axial force reaches its maximum value and the screw angular velocity decreases to zero.
- Force–release phase: the angular velocity of the screw is reversed from zero to a maximum velocity and is maintained for a specific period of time. The reverse rotation of the screw drives the nut and clamp lever back, reducing the axial force. Then, when the target current reaches zero, the screw angular velocity decreases and the axial force also continues to decrease. Finally, the screw angular velocity reduces to zero and the axial force also decreases to zero.
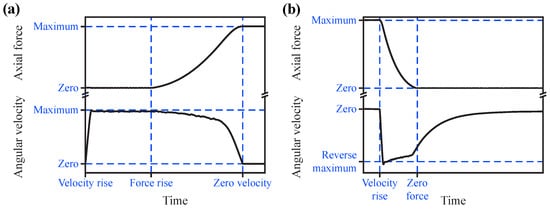
Figure 5.
Working condition of ball-screw in one duty cycle. (a) Clearance–elimination and force–generation phase; (b) force–release phase.
Therefore, the time-varying axial force and the angular velocity of the screw are discretized as and , which are used as inputs for the calculation of wear increment. Then, the average value of the wear increment resulting from all the ball–raceway contacts is calculated. And the average values of each time step are added together to calculate the wear of a duty cycle.
4.2. Numerical Calculation
The wear of ball-screw is calculated using component parameters, the axial force, and the screw angular velocity as inputs. The flow chart of the calculation process is illustrated in Figure 6. It is divided into two parts: the first part solves numerically for the contact deformation of the ball and raceways, and the second part calculates the wear depth increment.
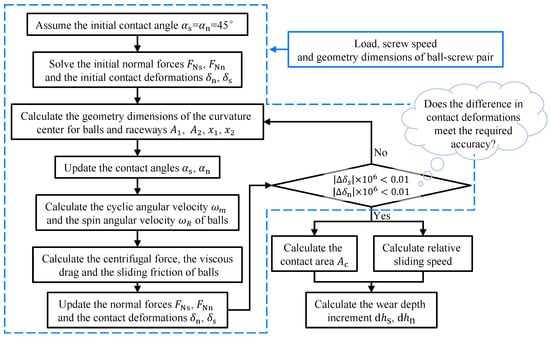
Figure 6.
Flow chart of the wear depth increment calculation.
The steps in the first part are shown in the blue box in Figure 6, which are,
- Repeat Steps 2 to 4 until the difference in contact deformations meets the required accuracy.
The input values of related symbols used for the numerical calculation are listed in Table 2.

Table 2.
Input values of related symbols used for the numerical calculation.
4.3. Test Validation
We designed an endurance test and conducted the test to gather the degradation data. The photograph and schematic diagram of the test are shown in Figure 7. The industrial PC calculates the current command and sends it to the motor driver via the CAN communication device. The motor driver produces the three-phase current to operate the motor in EMBUs. The measured signals are obtained using the data acquisition (DAQ) card.
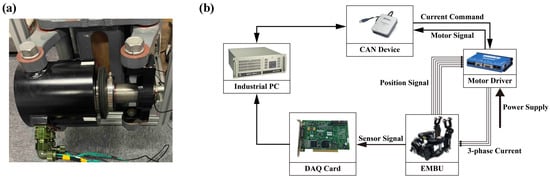
Figure 7.
Schematic diagram of endurance test. (a) Photograph; (b) test layout.
In addition, the endurance test applies and relieves the force according to a designed cycle and mainly examines the open-loop output force characteristics of the EMBU. It is a static test without a rotation disk and an actual vehicle braking process, so there is no wear on the brake discs and pads.
5. Results and Discussion
The endurance test conditions are designed according to the operating conditions of the EMBU. The time-varying axial force and the time-varying screw angular velocity are discretized using a time step as 0.01 s. Using the discrete results as the computational input, the incremental wear depth in each step is obtained as shown in Figure 8. The photographs in Figure 9 show the balls with normal wear and the screw after the endurance test.
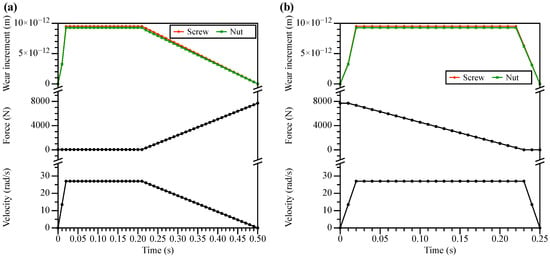
Figure 8.
Calculation results of incremental wear depth in one duty cycle. (a) Clearance–elimination and force–generation phase; (b) force–release phase.

Figure 9.
Photographs of the normal wear balls and the screw after the endurance test. (a) Balls; (b) Screw.
It can be found that the effect of angular velocity on the wear increment is greater than that of the axial force. And the wear on the screw-raceway is greater than that on the nut-raceway.
The diameter of the balls was measured after the test using a vernier scale. Each ball was measured five times from different angles and the average value was taken as the ball diameter after removing the maximum and minimum values. The measurement results for the ball diameter are shown in Figure 10. The initial diameter is 3.175 mm, and after approximately 200,000 duty cycles, the diameter ranges between 3.14 mm and 3.162 mm, with a median of 3.153 mm and a mean of 3.1518 mm. Inferred from the median, the depth of wear on the balls is 0.022 mm, and on one side is 0.011 mm. According to the wear distribution ratio of raceway and ball, the wear depth on one side of the raceway is 0.022 mm. Hence, the total wear depth on one side of the ball and the raceway is 0.033 mm. The test has been conducted for a total of 200,000 duty cycles; therefore, the total of the wear depth increment on one side of the ball and raceway for each cycle is 1.65 × 10−10 m.
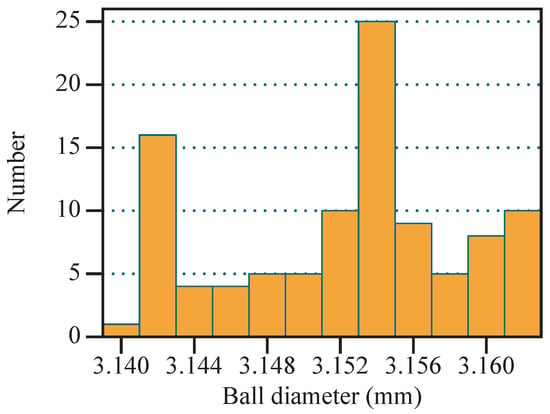
Figure 10.
Measurement results of ball diameter after the endurance test.
According to the test conditions, using the method outlined in Figure 6, the calculation results for the wear depth increment of the screw- and nut-raceway for one duty cycle are shown in Table 3. The test results and the calculation results are of similar magnitude and close in value. Other random factors may also influence the wear process, but they are not currently being considered. Thus, the calculations can be considered reasonable.

Table 3.
Calculation results for the wear depth increment of screw- and nut-raceway for one duty cycle.
The wear of ball-screws will affect the control accuracy of the EMBU in the braking and releasing process, resulting in the degradation of vehicle’s braking performance. When the wear increases to a certain level, the performance of the EMBU may deteriorate to the point where it cannot fulfil the braking task, i.e., failure of the EMBU.
6. Conclusions
For the railway transport system, the safety of train operation needs to be ensured by the brake system. Ball-screws play important roles in the EMBUs by converting rotational motion into translational motion and thus outputting force. They are the core components of the brakes and the key link for the effective execution of the braking and releasing functions. Wear is an inevitable degradation behavior of ball-screws. The wear will result in functional failures of EMBUs. The prediction of ball-screw wear allows for tracking and monitoring of the performance of the EMBUs as well as the operational performance of the entire system, which can help engineers and users to better use and maintain the system. The rotation angle, angular velocity, angular acceleration, and axial force of the screw can be taken as indicators used for health monitoring of EMB systems. This paper studied the wear process of EMBU ball-screws. Combined with the characteristics of time-varying working conditions of EMBUs, this paper presents a framework for ball-screw wear calculation and validates it with endurance test results. Summing up the above analysis, the following conclusions can be drawn:
- The load is dynamically varied during the duty cycle of the EMBU, which has an effect on the contact type and wear increment of the ball and raceway. In this paper, the load is discretized to determine the elastic–plastic contact type to calculate the wear increment.
- The calculation results and the endurance test show that the wear of the screw-raceway is greater than that of the nut-raceway and that the effect of velocity is greater than the effect of axial force.
- The test results show that the presented calculation framework in this paper is reasonable. It can be used for ball-screw wear and internal clearance prediction.
Author Contributions
Conceptualization, T.M. and M.W.; methodology, J.W. and T.M.; software, T.M.; validation, T.M. and J.W.; formal analysis, J.W.; investigation, J.W.; resources, M.W.; data curation, J.W. and T.M.; writing—original draft preparation, J.W.; writing—review and editing, T.M.; visualization, J.W.; supervision, M.W.; project administration, C.T.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the China Postdoctoral Science Foundation with grant number 2021M702476.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank editors and anonymous reviewers for their helpful comments and suggestions to improve the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
The following symbols are used in this paper.
| r | radius |
| nominal diameter | |
| contact angle between balls and raceways | |
| helix angle | |
| principle curvature | |
| principle curvature of screw-raceway (direction of sliding velocity) | |
| principle curvature of screw-raceway (orthogonal direction) | |
| principle curvature of nut-raceway (direction of sliding velocity) | |
| principle curvature of nut-raceway (orthogonal direction) | |
| effective curvature ratio of the contact between ball and screw-raceway | |
| effective curvature ratio of the contact between ball and nut-raceway | |
| complete ellipticity integrals of the first kind | |
| complete ellipticity integrals of the second kind | |
| effective modulus | |
| ratio of the long and short semi-axes of the contact ellipse | |
| normal force at the ball–raceway contact | |
| axial force | |
| Z | effective number of balls |
| i | number of loaded turns |
| number of unloaded balls | |
| H | hardness |
| Poisson ratio of the softer object | |
| average effective curvature radius of asperities | |
| rotational angular velocity of the screw | |
| gyroscopic angle | |
| spin angular velocity | |
| mass of the ball | |
| initial dynamic viscosity | |
| ratio of equivalent radii | |
| pressure–viscosity parameter | |
| load of the contact | |
| boundary friction coefficient | |
| load shared by asperities | |
| relative axial angular between the screw and nut after loading | |
| relative axial displacement between the screw and nut after loading | |
| relative radial displacement between the screw and nut after loading | |
| component of the spin angular velocity in t-axis | |
| increment of wear volume | |
| increment of sliding distance | |
| pressure yield limit for the softer material | |
| dimensionless wear constant | |
| discrete time step | |
| increment of wear depth | |
| relative sliding velocity | |
| Subscripts | |
| b | ball |
| s | screw |
| n | nut |
| s or n |
References
- Wu, M.; Ma, T.; Tian, C.; Yang, J.; Chen, M. Discussion on development trend of train braking technology. China Railw. Sci. 2019, 40, 134–144. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Miao, F. An adaptive backstepping nonsingular fast terminal sliding-mode control for the electromechanical brake system with backlash nonlinearity compensation. Proc. Inst. Mech. Eng. Part F J. Rail. Rapid. Transit. 2023, 237, 858–870. [Google Scholar] [CrossRef]
- Baek, S.K.; Oh, H.K.; Kim, S.W.; Seo, S.I. A clamping force performance evaluation of the electro mechanical brake using PMSM. Energies 2018, 11, 2876. [Google Scholar] [CrossRef]
- Baek, S.K.; Oh, H.K.; Park, J.H.; Shin, Y.J.; Kim, S.W. Evaluation of efficient operation for electromechanical brake using maximum torque per ampere control. Energies 2019, 12, 1869. [Google Scholar] [CrossRef]
- Sun, X.; Yang, Z.; Yang, J. Typical failure mode and effect analysis of flight control electromechanical actuation system. In Proceedings of the CSAA/IET International Conference on Aircraft Utility Systems (AUS 2018), Guiyang, China, 19–22 June 2018; IET: London, UK, 2018; pp. 1162–1169. [Google Scholar]
- Li, C.; Zhuo, G.; Tang, C.; Xiong, L.; Tian, W.; Qiao, L.; Cheng, Y.; Duan, Y. A Review of Electro-Mechanical Brake (EMB) System: Structure, Control and Application. Sustainability 2023, 15, 4514. [Google Scholar] [CrossRef]
- Qiao, G.; Liu, G.; Shi, Z.; Wang, Y.; Ma, S.; Lim, T.C. A review of electromechanical actuators for More/All Electric aircraft systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4128–4151. [Google Scholar] [CrossRef]
- Meitinger, K.H. NEW CHASSIS SYSTEMS–Das fahrwerk des AUDI R8 e-tron (The chassis of the AUDI R8 e-tron). In Proceedings of the 7th International Munich Chassis Symposium 2016: Chassis. Tech Plus; Springer: Berlin/Heidelberg, Germany, 2017; pp. 89–102. [Google Scholar]
- Chen, Q.; Lv, Z.; Tong, H.; Zeng, D.; Ouyang, L.; Liu, Q. Study on multi-closed loop control of electro-mechanical braking for electric vehicles based on clamping force. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023. [Google Scholar] [CrossRef]
- Zhao, Y.; Lin, H.; Elahi, H.; Miao, F.; Riaz, S. Clamping force sensor fault analysis and fault-tolerant control of the electromechanical brake system. Arab. J. Sci. Eng. 2023, 48, 6011–6023. [Google Scholar] [CrossRef]
- Jones, A.B. A General Theory for Elastically Constrained Ball and Radial Roller Bearings Under Arbitrary Load and Speed Conditions. J. Basic Eng. 1960, 82, 309–320. [Google Scholar] [CrossRef]
- Harris, T. An analytical method to predict skidding in high speed roller bearings. Asle Trans. 1966, 9, 229–241. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Wei, C.C.; Liou, W.L.; Lai, R.S. Wear analysis of the offset type preloaded ball–screw operating at high speed. Wear 2012, 292, 111–123. [Google Scholar] [CrossRef]
- Chang, W.; Etsion, I.; Bogy, D.B. An elastic-plastic model for the contact of rough surfaces. J. Tribol. 1987, 109, 257–263. [Google Scholar] [CrossRef]
- Cheng, Q.; Qi, B.; Liu, Z.; Zhang, C.; Xue, D. An accuracy degradation analysis of ball screw mechanism considering time-varying motion and loading working conditions. Mech. Mach. Theory 2019, 134, 1–23. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Song, X.; Wei, N. A modeling method for predicting the precision loss of the preload double-nut ball screw induced by raceway wear based on fractal theory. Wear 2021, 486, 204065. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, M.; Song, X.; Guo, Q. Analysis of the precision sustainability of the preload double-nut ball screw with consideration of the raceway wear. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 1530–1546. [Google Scholar] [CrossRef]
- Shen, J.W.; Feng, H.T.; Zhou, C.G.; Chen, Z.T.; Ou, Y. A new two-stage degradation model for the preload of ball screws considering geometric errors. Wear 2022, 500, 204352. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, C.; Ren, S.; Qian, C.; Feng, H. An analysis method for the transmission efficiency of the preloaded ball screw based on wear volume calculation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 236, 2392–2405. [Google Scholar] [CrossRef]
- Cheng, Q.; Qi, B.; Liu, Z.; Yang, C.; Zheng, J. Positioning accuracy degradation and lifetime prediction of the ball screw considering time-varying working conditions and feed modes. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 235, 943–957. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Liu, H.; Liang, T.; Zhao, W. Dynamic modeling and analysis of the high-speed ball screw feed system. Proc. Inst. Mech. Eng. Part B J. Eng. Manufac. 2015, 229, 870–877. [Google Scholar] [CrossRef]
- Okwudire, C.E.; Altintas, Y. Hybrid Modeling of Ball Screw Drives With Coupled Axial, Torsional, and Lateral Dynamics. J. Mech. Des. 2009, 131, 071002. [Google Scholar] [CrossRef]
- Xu, M.; Li, C.; Zhang, H.; Liu, Z.; Zhang, Y. A comprehensive nonlinear dynamic model for ball screw feed system with rolling joint characteristics. Nonlinear Dyn. 2021, 106, 169–210. [Google Scholar] [CrossRef]
- Jin, L.; Li, C.; Wang, X.; Xie, L. A dynamic stiffness model for high-speed ball screw pair with the mass center of screw nut considered. Mech. Ind. 2023, 24, 21. [Google Scholar] [CrossRef]
- Zhou, C.G.; Xie, J.L.; Feng, H.T. Investigation of the decompression condition of double-nut ball screws considering the influence of the geometry error and additional elastic unit. Mech. Mach. Theory 2021, 156, 104164. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, N.; Chen, J.; Yang, Y.; Shen, G. A review of fault diagnosis, prognosis and health management for aircraft electromechanical actuators. IET Electr. Power App. 2022, 16, 1249–1272. [Google Scholar] [CrossRef]
- Bodden, D.S.; Clements, N.S.; Schley, B.; Jenney, G. Seeded failure testing and analysis of an electro-mechanical actuator. In Proceedings of the 2007 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 1–8. [Google Scholar]
- Isturiz, A.; Vinals, J.; Abete, J.M.; Iturrospe, A. Health monitoring strategy for electromechanical actuator systems and components, screw backlash and fatigue estimation. In Proceedings of the Recent Advances in Aeropsace Actuation Systems and Components, Toulouse, France, 13–14 June 2012. [Google Scholar]
- Mansouri, B.; Piaton, J.; Guyamier, A. The backlash gap size estimation for electromechanical actuator in an operational behavior. In Proceedings of the Third European Conference of the Prognostics and Health Management Society 2016, Bilbao, Spain, 5–8 July 2016; PHM Society: Rochester, NY, USA, 2016; pp. 1–6. [Google Scholar]
- Fu, J.; Maré, J.C.; Yu, L.; Fu, Y. Multi-level virtual prototyping of electromechanical actuation system for more electric aircraft. Chin. J. Aeronaut. 2018, 31, 892–913. [Google Scholar] [CrossRef]
- Fu, J.; Maré, J.C.; Fu, Y. Modelling and simulation of flight control electromechanical actuators with special focus on model architecting, multidisciplinary effects and power flows. Chin. J. Aeronaut. 2017, 30, 47–65. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper (On the contact of elastic solids). J. Reine Angew. Math. 1882, 92, 156–171. [Google Scholar] [CrossRef]
- Markho, P. Highly accurate formulas for rapid calculation of the key geometrical parameters of elliptic Hertzian contacts. J. Tribol. 1987, 109, 640–647. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Chang, W.R.; Etsion, I.; Bogy, D.B. Static Friction Coefficient Model for Metallic Rough Surfaces. J. Tribol. 1988, 110, 57–63. [Google Scholar] [CrossRef]
- Horng, J.H. An elliptic elastic-plastic asperity microcontact model for rough surfaces. J. Tribol. 1998, 120, 82–88. [Google Scholar] [CrossRef]
- Wei, C.C.; Lin, J.F. Kinematic analysis of the ball screw mechanism considering variable contact angles and elastic deformations. J. Mech. Des. 2003, 125, 717–733. [Google Scholar] [CrossRef]
- Houpert, L. Ball bearing and tapered roller bearing torque: Analytical, numerical and experimental results. Tribol. Trans. 2002, 45, 345–353. [Google Scholar] [CrossRef]
- Xu, X.; Tang, W.; Yu, T.; Yin, M. Wear prediction of ball screw using Archard model. Modul. Mach. Tool Autom. Manuf. Tech. 2016, 2016, 54–59. [Google Scholar] [CrossRef]
- Lin, M.; Ravani, B.; Velinsky, S. Kinematics of the ball screw mechanism. J. Mech. Design 1994, 116, 849–855. [Google Scholar] [CrossRef]
- Archard, J. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Xu, X.H.; Wang, Y.H.; Xu, D. Wear prediction of ball screw based on adhesive wear. In Proceedings of the 4th International Conference on Advanced Design and Manufacturing Engineering (ADME 2014), Hangzhou, China, 26–27 July 2014; Trans Tech Publications, Ltd.: Stafa-Zurich, Switzerland, 2014; pp. 261–265. [Google Scholar]
- Fein, R.S. Boundary lubrication. In Handbook of Lubrication Theory and Practice of Tribology; CRC Press: Boca Raton, FL, USA, 1984; Volume 2, pp. 49–68. [Google Scholar]
- Zhao, G.; Fan, Y.; Luo, X.; Li, L. Elastic-plastic contact deformation of precise ball screw pair in overload condition. J. Nanjing Univer. Sci. Tech. 2014, 38, 192–198. [Google Scholar]
- Palmgren, A. Ball and Roller Bearing Engineering; SKF Industries Inc.: Lansdale, PA, USA, 1959. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).