Abstract
Parallel elastic actuation is a highly promising concept for assisting preplanned trajectories such as repetitive tasks in industrial machines and robots. Nevertheless, due to the persisting challenges on spring lifetime, its full potential has yet to be leveraged in the industry. We propose a novel adaptive magnetic spring as a fatigue-free spring mechanism to enable variable stiffness actuators in long lifetime applications. The spring is designed to flexibly deal with variations in operating conditions, i.e., mass customization. We propose a co-design methodology which simultaneously optimizes the sizing of the magnetic spring (for the given machine and its operating conditions), together with the controls and ideal dynamic response of the system. This mechanism and the methodology are applied to a design problem of a weaving machine drivetrain, where the benefits of the adaptive magnetic spring are highlighted with respect to a fixed stiffness magnetic spring, and the current industrial benchmark without springs. Experimentally validated findings show a consistent and considerable improvement with respect to energy consumption and peak torque reduction of up to 47% and 64%, respectively, when comparing to the current industrial benchmark.
1. Introduction
Parallel elastic actuators (PEA) and variable stiffness actuators (VSA) [1,2], by virtue of high torque/force density of the springs, are a successful means to improve the value of actuators in applications with repetitive highly dynamic loads in one of the following aspects:
- Improved energy efficiency;
- Improved actuator density or reduced actuator size and cost;
- Faster operation, i.e., increased production rate.
This is achieved by changing the impedance of the mechanical subsystem, i.e., adding stiffness in the form of springs in order to reduce the reactive power flow between the mechanical and electrical subsystems in a mechatronic drivetrain. As a result, the exchange of energy in acceleration and deceleration takes place between the potential energy of the spring and the kinetic energy of the moving mass/inertia. It has also been suggested that for a broader family of industrial actuators, aside from serial robots, pre-planned trajectories can be assisted by a spring-based system for the same beneficial effects [3].
Many industrial applications feature highly dynamic drivetrains with repetitive motions, such as textile machinery, pick and place robots, and similar lower complexity industrial automation tasks in packaging, but also widespread high-end applications such as lithography scanning [4]. These systems require a relatively high peak power due to the fast reciprocating or intermittent motion, while consuming a considerably lower process power. Resulting high peak loads can have a detrimental impact on the drivetrain performance, cost (through oversizing of components), energy efficiency, lifetime, user comfort and can produce unwanted sound radiation. Additionally, in systems driven from the electrical grid, the pulsating power can have a detrimental effect on the electricity grid, i.e., a sub-harmonic reactive power [5].
Most of the electro-mechanic actuators in the automation industry are driven by rotational servo motors, typically a geared permanent magnet synchronous motor (PMSM). In such a configuration the above-mentioned power oscillation manifests as a torque ripple—a periodic increase or decrease in output torque as a shaft rotates, caused by the previously mentioned oscillating masses driven through non-linear mechanisms such as cam-followers and bar-linkages. To use an integrated PEA (motor–spring–gearbox) in this configuration, a motion conversion mechanism (allowing for continuous rotation of the driven shaft) is required, which can add significant complexity to the actuator. Even more importantly, direct use of PEA concepts from the literature in industrial machinery is not desired due to the lifetime limitations of mechanical springs (fatigue failure) combined with highly stringent lifetime requirements [6]. As a side note, torque ripple can also be caused by other dynamic effects, such as gear meshing [7], aerodynamic effects in fans and wind turbines, system flexibilities, and discrete combustion times of an ICE, all of which are not directly addressed in this manuscript.
Magnetic spring concepts were introduced in 1980s, enabled by the introduction of rare-earth magnets with high energy density, as a fatigue-free replacement for mechanical springs, e.g., for use in linear piston compressors [8]. A combination of magnetic arrays, although not always referred to as magnetic springs, has been researched for gravity compensation, specifically in robotics applications [9,10,11,12,13]. To the knowledge of the authors, the only known commercially available magnetic spring [14] is supposedly to be used exactly for quasi-static load compensation, i.e., gravity compensation, instead of requiring a pneumatic cylinder. For assisting linear motors, operating in the vertical direction, this linear motion spring disposes of a quasi-constant force with respect to the displacement. Additionally, magnetic springs have been studied for gravity compensation in lithography scanner heads within the semiconductor industry [10,12]. Alternatively, in a high dynamic range, magnetic springs have been proposed for vibration isolation [9,10,11,12,13,15,16,17] mostly in their linear range. Furthermore, non-linear spring characteristics have been researched in which simple magnetic springs have been designed for the purposes of proof-of-concept [18]. In a similar manner, non-linear magnetic springs have also been proposed for use in small-sized energy harvesters to expand the frequency range of the harvester [19], due to the so-called energy pumping effect. Between these two extremes (static and high-frequency isolation), most pertinent to the subject matter, higher stiffness magnetic springs have been studied for application in reciprocating linear motion [20,21,22] and rotary reciprocating and intermittent motion [11,23,24].
Instead of relying on complex locking mechanisms, the use of stable and unstable equilibria of the magnetic spring in order to achieve a bi-stable PEA was first introduced by King et al. [11]. This concept was further expanded as reported in a patent application [24], where a combination of multiple magnetic springs were used to create small stable equilibria within unstable ones, making it feasible for magnetic springs to have stable zero-power energy storage [23]. The use of sinusoidal characteristic magnetic springs was also proposed as an option in a compliant actuation system in bio-robotic actuators. Comparing the work of [25,26] to mechanical counterparts [27], we can conclude that at the low frequencies necessary for bio-robotic applications, the added value of magnetic springs is limited, i.e., have a significant added cost and weight compared to mechanical springs, while the benefits of lifetime are not as prominent as in highly dynamic and heavy-duty motion systems. As an extension to this work, [26] mentioned an idea for variable amplitude using a secondary actuator to vary axial overlap of the stator and rotor of concentric magnetic disks. More recently, in [28], this concept was further developed into an early lab test embodiment proof-of-concept.
Recent efforts [29] have focused on the integration of an electric motor with magnetic springs for a weaving loom application. Such integration leads to a smaller print of a motor with a passive magnetic spring, but this does not reduce the cost of the active material or allow for the adaptation of the spring, which is critical for its use in applications of interest (e.g., different operational speeds of the weaving loom). Moreover, the integrated concept severely limits the use of gearing between the motor and the load, as the minimum torque ripple order that a magnetic spring can compensate for is N = 1, which for bar-linkages and cam-followers used in point-to-point motions limits the reduction ratio to only 2. As a result, a rather large high-torque low-speed motor is necessary, which somewhat contradicts the stated objectives.
In [30], a miniature actuator, a simple magnet geometry of millimetre scale, was used to exploit the possibility of tailoring the spring by combining multiple discrete elements. The design methodology in [31] was based on an analytical/integral magnetic dipole force calculation model and the principle of superposition. This is an interesting concept but rather limited due to the intrinsic non-linearity of realistic magnetic devices, i.e., it only works for magnetic springs made exclusively from permanent magnets and no soft magnetic materials. This is a significant weakness, as assemblies with back irons are necessary to guide the flux, i.e., limit the stray flux that causes inefficient designs and magnetic disturbance in the surroundings of the actuator, possibly attracting unwanted metallic particles or even generating external forces. In [32], we exploited the available computational power and a finite elements model (FEM) combined with the notions of topology optimization, giving a more general approach to spring tailoring. As its main weakness, this approach only included limited notions of manufacturability, e.g., operates at the tens of centimetres scale where the design freedom is expected to be larger, and would require either limited shaping capabilities or advanced manufacturing technology (e.g., additive manufacturing or metal injection moulding).
Overall, it can be said that machine builders are in the early exploration stage regarding PEA. To better frame the benchmarking approach followed in this article we need to consider the following statements:
- Mechanical springs are not suitable for industrial applications, due to fatigue failure, see, e.g., [7].
- Magnetic spring are promising for industrial applications, see, e.g., [33]; they can significantly reduce the energy consumption and/or increase the production rate, with a virtually unlimited lifetime.
Therefore, we compare the usage of a magnetic spring PEA vs. a case without (i.e., current state of practice), as currently no magnetic springs or mechanical springs are used in state-of-the art machines.
The use of a basic PEA faces problems when applied in industrial settings, one passive spring results in globally optimal behaviour for only one specific operating condition, while most industrial manufacturing machines need to operate in different conditions, e.g., different speeds, load weights and motion profiles. Motivated by this challenge, we invented a new concept for a parallel elastic actuator, featuring a novel, patented adaptive magnetic spring (AMS) [34]. We exploited the AMS for different working conditions of the machine. Next to this, to answer the lack of systematic and industrially relevant design methodologies on the topic, we developed industry-focused magnetic spring design tools. Hence, the contributions and the main building blocks of this article are the following:
- Novel adaptive magnetic spring (AMS) concept and prototype.
- Model-based co-design toolchain for magnetic-spring-equipped systems, aiming to optimize system dynamics, controls and sizing/configuration of the magnetic springs. To do so, we build on the workflow as considered in [35] (DriveTrain Co-Design Toolchain), by employing Simscape [36], CasADi [37] and IPOPT [38].
- Magnetic spring component design tool, employing Matlab in tandem with FEMM [39].
- Demonstration of the added value of the AMS on an industrially relevant weaving loom use case, in a simulation and via experiments.
The novel AMS concept is introduced in Section 2.2 and compared with fixed sinusoidal magnetic springs. Next, in Section 3, the model-based co-design toolchain for spring-assisted drivetrain is presented. This toolchain addresses both the sizing of the spring to fit the existing drivetrain dynamic behaviour as well as the control design in the presence of the magnetic springs. Both are optimized simultaneously (in the same problem), guaranteeing a system-level optimum [40]. Afterwards, a number of simulation studies are conducted, showing the added benefits of the AMS over fixed magnetic springs, in case multiple operation conditions are considered. In Section 4, first the AMS component is designed (FEMM) and second, the resulting AMS prototype is illustrated. Section 5 then experimental validates the proposed AMS as well as the controls optimized by the toolchain. Last, Section 6 wraps up the paper.
2. Proposed Innovative Concepts and Problem Definition
2.1. Passive Magnetic Spring Concepts
A magnetic spring (Figure 1) is a passive magneto-mechanical device with two mechanical interfaces, exhibiting a torque (or force in case of linear springs) dependent on relative displacement between the two interfaces. Within this publication we focus on torsional magnetic springs, specifically for reasons of easier practical implementation in applications of interest. Typically in the manufacturing machines mentioned above, several rotational joints are available and are therefore preferred for torsional spring installation. In magnetic springs the origin of the torque is the interaction between permanent magnet materials and/or soft magnetic iron. When observed from the outside, the functionality of the magnetic spring can be compared to that of a mechanical spring. However, the underlying physical principles are utterly different and no elastic deformation is required to store energy in a magnetic spring. Instead, the energy is stored in a reversible magnetic field variation of permanent magnets. Due to this difference, magnetic springs do not succumb to fatigue failure, even after a very long operational lifetime. Moreover, as we demonstrated previously [6], the energy density of magnetic springs surpasses that of mechanical springs for very long lifetime requirements, which is typically the case in the applications of interest.
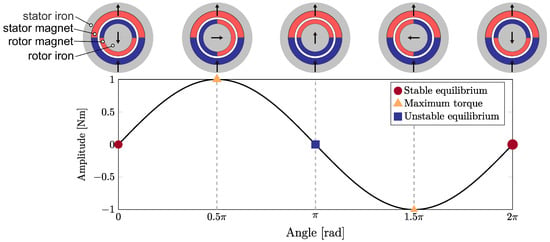
Figure 1.
Torsional magnetic spring consisting of diametrically magnetized stator and rotor NdFeB ring—simplistic PEA concept for efficient motion between unstable equilibria (counter-aligned magnetic field of rotor and stator) through the stable equilibrium (aligned rotor and stator magnetic field) without fatigue failure and locking mechanism.
On top of the virtually unlimited lifetime, the magnetic spring allows for energy storage concepts without locking mechanisms as its intrinsic unstable equilibria can be exploited (Figure 1). This way a stabilizing controller with infinitesimally low energy input can be used to keep the motion system stable in an unstable equilibrium () and then moved to another one () when desired.
For such a fixed sinusoidal characteristic spring, we can write the resulting torque as:
Here, denotes the angle of the rotating axis, the amplitude and the phase of a single-sine of order .
Additionally, the design flexibility demonstrated in a recent publication [32] allows for shaping of the magnetic spring torque. The shaping is achieved through two different approaches: (i) Fourier decomposition of the desired characteristic, combining several springs with sinusoidal characteristics into a single assembly; (ii) re-shaping of the magnetic domains, resulting in a free-shape limited only by magnet and back iron manufacturability (e.g., minimum thickness, air gap size, feasible magnetizations, etc.). For the sake of simplicity, and given the fact that shaping optimization has been covered in previous publications we intentionally omit it herein.
2.2. Adaptive Magnetic Spring Concepts
Together with the above-described passive magnetic springs, we study adaptive magnetic springs, which allow for changes in torque amplitude and phase, i.e., exploit the adaptive spring characteristic for different working conditions of the use case.
In addition to already known ones [26], several AMS concepts have been invented [34] to circumvent their limitations and bring the AMS closer to industrial applications. These novel concepts are made as a combination of conventional mechanical devices (e.g., brake, screw, bearings) and magnetic springs.
2.2.1. Novel Concept 1: Adaptive Phase
The simplest novel concept is that of a phase adaptive magnetic spring (see Figure 2 top). It combines the passive concept presented above (Section 2.1) with an additional bearing that allows for free rotation of the “stator”, and a locking mechanism that can fix the stator in any given position and prevent it from moving. In this device we can distinguish between two operational phases:
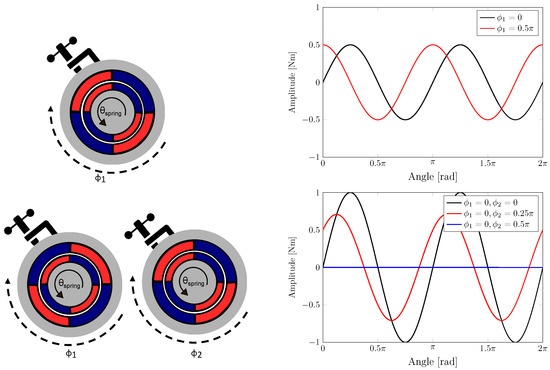
Figure 2.
Patented magnetic spring concept and the resulting torque characteristics: phase adaptive concept (top) and concept of operation relying on two sinusoidal phase adaptive units for adaptive phase and amplitude (bottom).
- Spring setting. The stator is unlocked, for which energy expenditure is required in the locking mechanism. The stator then follows the motion of the rotor due to the magnetic coupling between the stator and rotor. This allows for the primary mover, i.e., the servo motor used to control the process, to change the orientation of the stator without requiring a secondary high-performance mover.
- Machine operation. The stator is fixed with the locking mechanism (which from then on does not consume energy). Then, the desired machine motion can be executed with an optimal phase alignment of the magnetic spring.
2.2.2. Novel Concept 2: Adaptive Phase and Amplitude
This concept consists of two adaptive phase springs mentioned above (see Figure 2 bottom). To achieve both phase and amplitude variability, it relies on the simple fact that the sum of two sines with a phase offset is equal to a single sine characteristic with the same periodicity, but with a modified amplitude. The resulting amplitude and phase can be calculated based on a general trigonometric identity:
with a, b and c scalar constants, angle and scalar phase offsets , and . Then, c and satisfy:
In this specific case, a and c are equal in order to be able to annihilate the spring torques of the two sub-assemblies and have the resulting amplitude equal to zero. Therefore, we can reduce the expression above to:
where denotes the amplitude, the pole pair number of the stator and rotor, i.e., the periodicity of the torque, and the (adaptive) phase [34] of each pair , as shown in Figure 2.
For example, the embodiment of the concept shown in Figure 2 relies on two locking devices that can each unlock one of the stators. Released stators can be re-positioned by the principal actuator of the drivetrain (e.g., PMSM servo), due to the coupling rotor–stator, to a desired position where the stators are locked again. The main consequence of this innovation is that no secondary actuators are required apart from low-power, low-cost brake actuators to vary the spring characteristic. Take note, this concept is feasible for only sinusoidal spring characteristics.
For the purposes of our study, and to distinguish active from adaptive, we assume that adaptive springs properties can only be varied at a significantly slower rate than the principal motion dynamics of the drivetrain. A practical constraint follows from this: an adaptive magnetic spring needs to be pre-set before operation. Alternatively, an active spring would be a device capable of adjusting its stiffness at the same rate as the principal motion dynamics of the drivetrain or faster. For this reason an active spring would be equivalent to a secondary actuator driving this motion, acting as a spring purely by the definition of its control. As interesting as such concept might be from academic perspective, it would also add to system energy losses and cost, which is the opposite of this work’s motivation.
2.3. Weaving Loom Drivetrain Use Case
In this section, we illustrate a motivating industrial example: a weaving loom. Afterwards, we introduce the lab-scale four-bar linkage experimental setup considered in this paper, which has similar working principles as the weaving loom. This lab-scale setup is equipped with a prototype of the AMS.
Industrial weaving looms require multiple oscillating reciprocating drivetrains for functions such as shedding, insertion, beat-up and auxiliaries (e.g., selvedge). As with many other manufacturing machines, the reciprocating motion is achieved through a motion conversion mechanism, i.e., a bar-linkage mechanism or a cam-follower, driven by a combination of an inverter and a servo motor. The requirements for this configuration correspond roughly to a peak power range of 100 W–100 kW and a speed range of 0–1000 RPM on the driven shaft. Such machines encounter multiple operational scenarios such as:
- Nominal operation. When the machine is operating around a required average speed, motor torque ripple is encountered due to oscillating masses (e.g., shedding mechanisms) combined with the non-linearity of the mechanism.
- Start-stop behaviour. Typically, the goal is to start or stop the machine within a given amount of machine cycles, requiring a fast ramp-up or ramp-down of the speed (limited by peak motor torque). When failing to do so, woven products might have a lower quality due to the so-called “starting marks” from a too low speed at beat-up.
Therefore, from the application perspective, these processes are subject to the following constraints:
- Maximally allowed speed fluctuations during continuous operations, since these fluctuations affect the process quality, i.e., the quality of the woven fabric.
- Actuator torque limits (peak and RMS), due to thermal limitations of the servo motor depending on the cooling approach.
The total cost of ownership (TCO) of the drivetrain can be roughly split into (i) investment costs, where peak motor torque is indicative of the motor size, and (ii) operating costs, with RMS motor torque indicative of energy consumption.
For research purposes, we have defined a corresponding setup based on the weaving application introduced above. The considered setup is shown in Figure 3. It consists of a four-bar linkage mechanism that connects a permanent magnet synchronous motor (PMSM) with an oscillating load (flywheel). Furthermore, the prototype adaptive magnetic spring (AMS) is attached on the side of the PMSM. Note that on this setup no actual weaving takes place, but the working principles, dynamics, loads and speeds are representative of a down-scaled industrial weaving loom. In Table 1, the specifications of the setup are shown. The real-time control is executed by a Triphase real-time target running on Xenomai at a sampling frequency of 4000 Hz. The rotation of the PMSM is measured using a rotary incremental encoder with 8192 CPR.
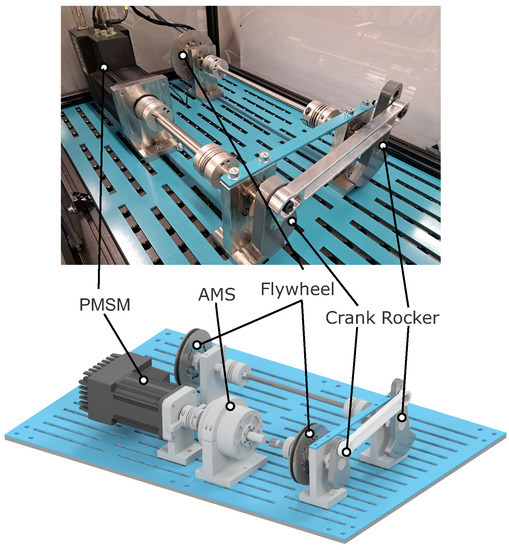
Figure 3.
Experimental setup with adaptive magnetic spring (AMS) at the crank side: photo (top) and CAD rendering (bottom).

Table 1.
Specifications of the four-bar linkage setup including its modelled parameters.
3. Model-Based Co-Design Toolchain for Magnetic-Spring Equipped Systems
In this section, we introduce the proposed model-based co-design toolchain for magnetic-spring equipped systems (building on the results of [35]) and apply it to the four-bar linkage model in a simulation. The goal of the toolchain is optimize the controls and dynamic response of the model given a cost function and a set of constraints, through solving an optimal control problem (OCP). Furthermore, the architecture and sizing of the magnetic spring is directly accounted for in the optimization as well, yielding a co-design problem. The workflow of the toolchain is as follows:
- Model generation (including the magnetic spring). The system is modelled in Simscape. Afterwards, symbolic model equations are extracted to white-box CasADi symbolics [37] using the tool Simscape2CasADi [41]. These symbolic equations enable efficient (high-order) derivative evaluation through algorithmic differentiation, and are used to facilitate optimization of the system design and controls in the next step.
- Optimal system and control design. Employing the model obtained in the previous step, the dynamics and controls of the system are optimized, along with the desired magnetic spring profile, sizing and configuration.
Remark 1.
The control input derived in the second step is a (non-parameterized) feed-forward motor torque input signal. This input can be applied directly to the considered system, as performed in a simulation, but we consider a feedback controller as well for experimental validation, providing robustness for non-modelled components and disturbances. This feedback controller then tracks a reference signal (desired motor speed), which is a direct outcome of the optimization problem as well. Alternatively, the found feed-forward motor torque control law can serve as a benchmark for other well-tuned control laws, ranging from simple PID controllers, to parameterized feed-forwards [42], as well as model-predictive control (MPC) techniques [43].
3.1. Model Generation
The use case under consideration is a four-bar linkage system (crank-rocker mechanism), as introduced in Section 2.3. A schematic overview is shown in Figure 4, showing the system modelled in Simscape. The motor is modelled as an ideal torque source, and is coupled with an inertia and a block implementing friction. The magnetic spring is added on the motor-side, which is parameterized as either a sinusoidal magnetic spring or the proposed adaptive magnetic spring. Note that alternative magnetic spring parameterizations can be considered as well (e.g., free-shape), although these are not considered in this study. A custom Simscape block is created which implements the kinematic transformation of the linkage mechanism. On the load-side, an inertia and damper are added, connected to the rocker-side of the linkage.
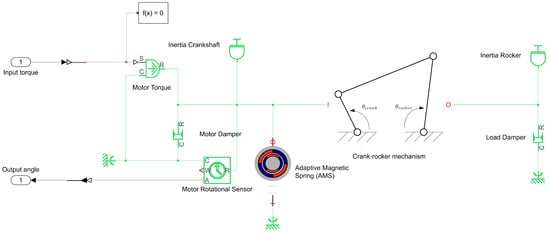
Figure 4.
Simscape model of the four-bar linkage experimental setup, with a magnetic spring on the crankshaft.
Using Simscape2CasADi [41], white-box symbolic model equations are extracted from the Simscape model. In Table 2, the states, inputs and outputs of the CasADi model extracted from Simscape are shown (see Section 3).

Table 2.
The states, inputs and outputs of the CasADi model extracted from Simscape.
The output is a set of differential algebraic equations (DAE), formulated in CasADi symbolics [37]. The continuous-time model is given in the form of:
where denotes time, the differential state variables, the algebraic state variables, the inputs, the parameters, and the outputs. Function denotes the ordinary differential equation (ODE) function, denotes the algebraic residual function, and h denotes the output function. The model extracted from the Simscape diagram, depicted in Figure 4, has differential states, algebraic states, input (motor torque ), outputs (motor angle , motor angular velocity and the in-going angle of the linkage mechanism ), and several tunable model parameters. More details can be found in Table 2. The tunable model parameters are the lengths of the components, as well as the friction and inertia terms, as shown in Table 1. Furthermore, we consider two parameterizations of the magnetic spring (with corresponding tunable parameters): (i) a sinusoidal characteristic magnetic spring, see Equation (1), where amplitude A and phase are optimized, with fixed order ; (ii) an adaptive magnetic spring, see Equation (4), with tunable model parameters A and with . Since the spring is rigidly connected to the crank axle, = .
Magnetic Spring: Scaling Inertia Model
In order to approximate the inertia of the magnetic spring, we use a simplified model, yielding the inertia as a function of the dimensions of the spring (fixed form factor), the magnet material density kg/m, the magnet energy density J/m (42H) and an empirical factor [6] that takes into account the imperfect use of magnetic material . The approximation of is then given by:
The energy of the magnetic spring, , can be for an -order sinusoidal magnetic spring with amplitude A expressed as .
3.2. Optimal System and Control Design
In this section, the dynamic behaviour and controls of the four-bar linkage model are optimized, along with the design of the magnetic spring. First, the generic formulation of the discrete-time co-design problem is provided. Second, we solve a number of co-design problems for several operating conditions of the system.
3.2.1. Generic Discrete-Time Co-Design Problem Formulation
We consider a time horizon , with the end time, divided over intervals (samples). The index of a single sample is denoted as . The discrete-time co-design problem is then formulated as:
Matrix contains all optimization variables over the entire horizon: (and similarly for , and ). It is assumed that is not a function of time. In the above, Equation (7a) implements the cost function. Equations (7b)–(7d) embed the discretized model dynamics (Equations (5a)–(5c)) in the optimization problem. The state propagation (Equation (7b)) is implemented using multiple shooting [44], with integrator function F, e.g., implemented as a central Euler integrator: , with sampling time . Equation (7e) can be used to implement multiple types of constraints, such as initial condition constraints, input and path constraints, boundary constraints, etc. The resulting discrete-time optimization problem is a large, sparse non-linear program (NLP), containing continuous optimization variables, to be solved using the interior point optimizer IPOPT: an open-source software package for large-scale non-linear optimization [38], which is interfaced with CasADi used to implement the NLP [37].
Note that a single optimization problem is used to find both the optimal inputs and trajectories (, and ) as well as the optimal set of design parameters p. Although a more complicated problem has to be solved, it can yield the optimal results significantly faster compared to a nested approach ([45,46]), since the optimization problem only has to be solved once. Furthermore, the application of a good initial guess for the optimization variables, or by even employing a multi-start approach (see, e.g., [47]), can aid the solver in finding a good solution.
3.2.2. Fixed Sinusoidal Magnetic Springs
In this section, we solve a co-design problem for a given drivecycle: run-up from standstill, nominal operation around a given speed, run-down to standstill. In this case, the magnetic spring is modelled as a single sinusoidal spring (Equation (1)). We benchmark this case to the case where no magnetic spring is considered. Furthermore, we show that the limited adaptivity of this magnetic spring design hampers performance in the case where varying operating conditions are considered.
3.3. Simulation Example: Benefits of Fixed Sinusoidal Magnetic Springs
The optimization problem is formulated as:
In the above, denotes a scalar (adding slight regularization to the problem). The main control goal is to minimize the required motor torque (ripple) (), while meeting the constraints on the motor speed (), see Equation (8b), limiting the allowed speed fluctuations. This velocity constraint requires the motor to ramp up from standstill to the desired mean speed in ½ a rotation (and vice versa for ramp-down). Furthermore, a speed fluctuation of 10% is allowed, and lower and upper bounds on the allowed motor torque are provided (Equation (8c)), equal to ± 20 Nm. Equation (8d) ensures that in total 10 rotations of the motor are made. The initial conditions are implemented according to Equation (8e). The sampling time s.
The problem is solved for a mean speed of 600 RPM, with initial linkage angle rad, for the case without a magnetic spring and with a sinusoidal magnetic spring. The length of the control horizon samples. The results of the optimization problems are shown in Figure 5. It can be seen that the addition of the magnetic spring (with torque ) reduces the required motor torque, while still meeting the constraints on the motor speed. Details on the RMS and maximum motor torques, with and without a spring, are shown in Table 3. The magnetic spring is able to reduce the RMS and peak motor torques by 60% and 45%, respectively, throughout the considered profile. Last, it can be seen that the energy consumption of the system:
with the motor resistance and torque constant , see Table 1, reduced by 26% over the entire range. In particular, the electrical losses are reduced significantly in the case where a magnetic spring is considered, as is also shown in Figure 5. The amplitude A of the magnetic spring is optimized to 18.7 Nm, with phase rad. For this example, the inertia of the magnetic spring is found to equal kg/m (see Equation (6e)).
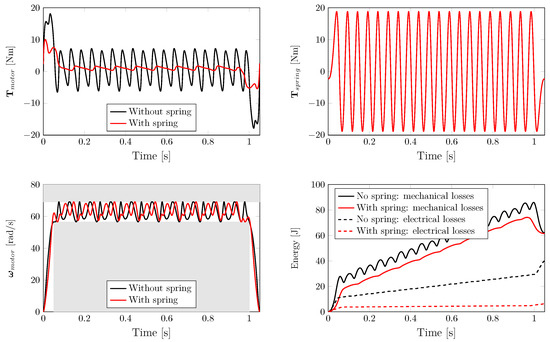
Figure 5.
Simulation results for 600 RPM, comparing the case with a sinusoidal magnetic spring and without a magnetic spring, for rad.

Table 3.
Resulting motor torques and energy consumption, with a sinusoidal magnetic spring and without magnetic spring, given a mean speed of 600 RPM. Significant reductions are achieved in the case where the system is equipped with a magnetic spring.
3.4. Simulation Counter-Example: Limitations of Fixed Sinusoidal Magnetic Springs
If we solve the above optimization problem for a mean speed of 400 RPM instead, we obtain reductions in RMS and maximum motor torque of 56% and 42%, respectively. A key difference however is the optimized design of the magnetic spring. The amplitude A of the magnetic spring is optimized to 8.6 Nm, with phase rad, while the phase is similar to the result for the 600 RPM case, the amplitude reduced drastically, since lower torques are required due to the lower operating speed.
The limited adaptivity of the sinusoidal magnetic spring can be highlighted by re-solving the same optimization problem (with a mean speed of 400 RPM), but using the spring design found for the 600 RPM case. Upon doing so, the required RMS motor torques are significantly higher (≥) than the case if no spring was be considered at all, since the motor now has to counter-act the high torques of the spring, see Figure 6. Hence, the currently considered fixed magnetic spring design is sub-optimal in the case where multiple operation conditions have to be accounted for. In the next section, we study the proposed adaptive magnetic spring in a simulation, aiming to overcome the identified limitations.
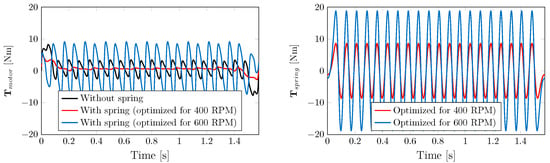
Figure 6.
Simulation results for 400 RPM. The left plot shows the motor torque and the right plot shows the magnetic spring torque. Three cases are compared: (i) without spring; (ii) with sinusoidal magnetic spring, optimized for 400 RPM; (iii) with sinusoidal magnetic spring, but optimized for 600 RPM.
Novel Adaptive Magnetic Springs
Herein, we solve similar co-design problems as denoted in Equation (8), but here we consider the proposed adaptive magnetic spring as denoted in Equation (4). We consider a range of varying operating conditions to demonstrate the adaptability of the proposed magnetic spring. First, the speed of the system is varied between 300 and 600 RPM for a fixed initial crank angle and the results are assessed. Second, the crank angle is varied between 0 and for a speed of 600 RPM.
In Figure 7 and Figure 8, the results are shown for a range of speeds between 300 and 600 RPM, with rad. The figures show that the magnetic spring is able to significantly outperform the case without a magnetic spring, even when the RPM is varied. This is possible due to the flexible adaptation of the adaptive magnetic spring angles (shown in the bottom-right plot of Figure 8). For lower speeds, the angle difference is larger, yielding a lower spring torque (since the pairs are more in anti-phase), and vice versa for higher speeds. For this example, the amplitude of each pair Nm. Figure 7 shows the resulting , and for the case with an adaptive magnetic spring (with a re-scaled time axis). As expected, the higher the RPM, the higher the resulting and , but the ripples in remain minimal. Note that the results for 400 and 600 RPM are equal to the results reported in the previous section (where a single sinusoidal spring was individually optimized for each case). Note that when the RPM increases, the energy reduction is the highest. This is due to the fact that the electrical losses (see Equation (9)) scale with the square of the motor torque, which is higher for increased speeds.
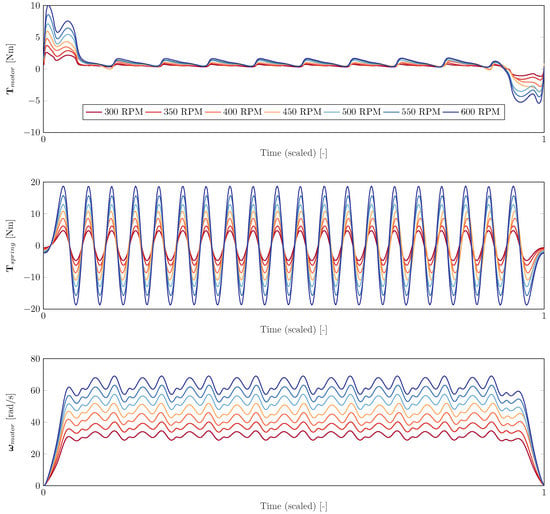
Figure 7.
Simulation results varying speeds: 300–600 RPM, with rad, considering the proposed adaptive magnetic spring. From top to bottom: The resulting , and for the case with an adaptive magnetic spring (with a re-scaled time axis).
Next, we vary the initial condition of the crank . In doing so, the required motor torque to drive the system varies, as well as the ideal corresponding spring configuration, due to the non-linearity of the linkage mechanism. In Figure 9, we vary between 0 and and assess the reductions in motor torque (RMS, peak) and energy consumption for the case with vs. without a magnetic spring, for a mean speed of 600 RPM. The following observations were made:
- The RMS motor torque is reduced by 13–62%. The energy consumption is reduced by 8–32%.
- The peak motor torque is in some cases kept constant (for both cases equal to the allowed maximum of ±20 Nm), whereas in some other cases the peak motor torques are reduced by up to 60%.
- The peak magnetic spring torque varies between approximately 5–20 Nm. When considering an amplitude Nm for each pair, the pairs are fully aligned for the case where the peak spring torque is 20 Nm, and close to anti-phase in the case of 5 Nm.
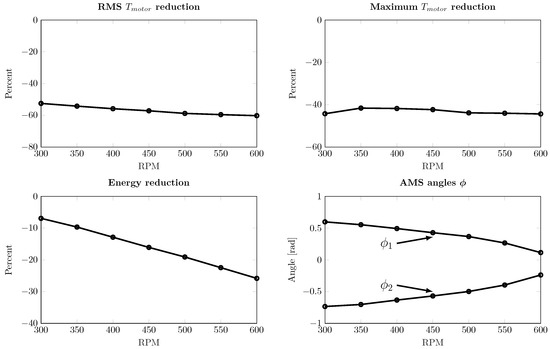
Figure 8.
Simulation results varying speeds: 300–600 RPM, with rad, considering the proposed adaptive magnetic spring. The reductions in RMS motor torque, peak motor torque and energy (with vs. without magnetic spring) are shown as a function of RPM. Furthermore, the resulting AMS angles are shown.
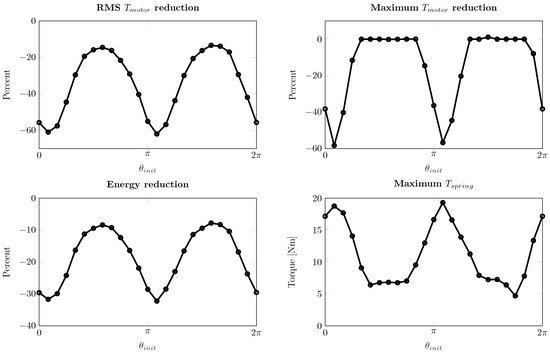
Figure 9.
Results for the case with the adaptive magnetic spring versus without the magnetic spring, while varying between 0 and , given a mean speed of 600 RPM. Reductions in RMS and maximum motor torque are shown, as well as the resulting energy consumption. Furthermore, the maximum torque of the magnetic spring is shown.
4. Novel Adaptive Magnetic Spring: Component Design
This section covers the mechanical design of the adaptive magnetic spring. First, we optimize the design of the component through a finite element magnetics method (FEMM). Second, the resulting prototype is detailed.
4.1. Optimal Component Design
In this section, the magnetic spring geometry is optimized, given a physical parameterization. Herein, the most pertinent details of the magnetic optimization are covered, while for a more general overview of the methodology the reader is directed to [32].
The goal of the magnetic optimization is to match the torque profile obtained in the previous step. Here, denotes the number of discrete samples considered, covering one rotation of the magnetic spring (with a linearly increasing angle). In order to do so, we approximate the magnetic spring radial flux geometry and resulting magnetic field as a 2D magnetostatic FEM problem. The cost function is then given by:
where is the FEM 2D torque of a 1 mm slice, is the axial length and is the parameter set describing the spring geometry. The relevant parameter list is available in Table 4.

Table 4.
Extended parameter space for the optimal component design step.
The parameters tuned in the optimization are both discrete (e.g., no. of pole pairs) and continuous (e.g., magnet thickness), which can further complicate the optimization. In order to deal with these caveats, (i) a black-box optimizer is used and (ii) the parameter space is initialized using smart guesses based on characteristic features of the torque profile: attractors, repellers and zero torque regions. The former can deal with mixed integer optimization, and non-convex problems while the latter leads to faster convergence. Initialization can alternatively be performed as fully symmetric or even random. In both cases we observed that our initial guess outperformed these, due to the mentioned link between the magnet positions and characteristic features. Practically speaking, the number of features and the nature of force creation can lead to either or 2 for the number of required pole pairs. Therefore, the parameter space is allocated accordingly to the biggest possible parameter vector dimension, and then manipulated as required by discrete/topological parameters. More specifically, the length of the parameter vector is determined based on the number of attractors and repellers in the torque characteristic requirements and parameters per magnet, as described in Table 4, where the number of magnets on the stator and rotor are calculated as follows:
In specific cases where magnet segmentation is desired, leading to more than one magnets per magnetic pole, the user still needs to override this allocation. This approach builds on previous publications [6,32], and integrates it into the system design approach.
For each calculation, we (i) translate the set to 2D geometry in FEMM through a planar straight line graph (PSLG), and (ii) run batch parallel calculations for transformed rotor angles, i.e., desired position vector to determine the torque profile . Finally, l is calculated so that the energy contents of the desired and optimized springs match:
and as such is not optimized as a geometry parameter, but follows from the 2D geometry. Set is an extended parametrization compared to a typical PMSM, as it allows for varying magnet locations, thicknesses, magnetization, and pole pitch coverage for each of the magnets, i.e., breaking symmetrical design.
For a single rotor–stator pair in the adaptive magnetic spring, the desired spring torque profile is selected as a second-order sine with an amplitude A = 10 Nm, so that a peak torque of 20 Nm can be delivered if both pairs are fully aligned. This peak torque matches the maximum spring torque found in the simulation study in Section 3. We solve the problem from Equation (10) using NOMAD [48], a direct search method for gradient-free optimization. We initialize the solver using a smart initial guess, using nominal geometry (sized through the energy density scaling law [6]) and initial magnet positions around the perimeter based on repeller and attractor locations in . The problem is terminated at either the maximum time, maximum number of iterations or when the cost function (10) is converged given the predefined tolerances.
In Figure 10, the results of the optimal component design step are shown. A torque match of 95.9% is obtained, as can be seen in Figure 10a. In Figure 10b, the geometry is shown. Herein, the magnets are NdFeB with grade 42H and the back iron is electrical steel M-19, for other structural parts (shaft, housing) M18 steel is assumed in the FEMM simulation.
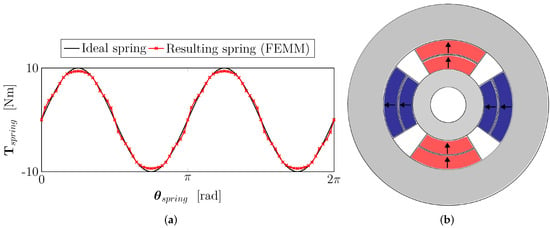
Figure 10.
Simulated spring torque from optimal component design, as well as the designed geometry. (a) Sinusoidal spring torque (incl. FEMM). (b) 2D geometry.
4.2. Prototype Adaptive Magnetic Spring
In the previous section, we have designed each rotor–stator pair as a sinusoidal spring with two pole pairs and an amplitude of 10 Nm, as shown in Figure 10. Thereafter, the resulting geometry was manufactured and the adaptive magnetic spring was assembled, conforming with the CAD diagram shown in Figure 11. The mechanical design surrounding the simulated magnetic assemblies, i.e., the active parts, are based standard off-the-shelf friction brakes with power-off braking action that act as two independent locking mechanisms. Take note that the brakes are standard off-the-shelf components and as such they use 70% of the total AMS volume. Stator bearings were selected as roller bearings, purely based on the dimensions available, even though in further designs a plain bearing might lead to further space reduction. Similarly, the brakes used could be reduced in size by changing the locking concept and the power of the actuator, resulting in a more compact design at the expense of locking speed. Currently, the majority of the AMS volume was taken up by the solenoid actuator of the brake.

Figure 11.
Patented magnetic spring concept with adaptive phase and amplitude. The left shows the tested prototype assembly, the right shows the CAD cross-section rendering.
However, due to manufacturing limitations an additional parasitic fourth-order ripple appeared in each rotor–stator pair of the prototype, on top of the desired second-order sine. This is due to the fact that the magnets were sunk into the back iron on the rotor and stator side, which gives a harmonic in the torque, which is expected given that the forces between the magnets and iron shoes are always attractive, unlike forces between magnetic poles which can be both attractive and repulsive. Although this effect can be reduced, and even almost completely removed (as performed in several other produced prototypes, e.g., the one presented in [6]), it is interesting to point it out here as a possible side-effect of the non-sinusoidal characteristics of the sub-assemblies. The described effect is phase locked and therefore not controllable. The resulting torque is modelled as:
where denotes the (fixed) gain, for the second- and fourth-order sine, respectively. and denote the angles of each rotor–stator pair (which can be varied, as was previously demonstrated in the simulation study). An example of the resulting torque profiles is shown in Figure 12. It shows the magnetic spring torque profile obtained using two different angle configurations: a solution yielding the maximally possible spring torque (), as well as the a solution yielding minimal torque (). The maximum amplitude of the latter case is approximately 4 Nm even when two spring units are counter-aligned, due to the parasitic effects.
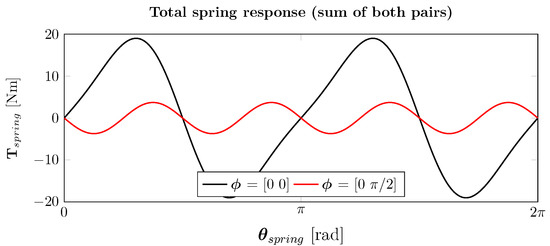
Figure 12.
Modelled magnetic spring torque profile of the prototype for two different angle configurations.
5. System Experimental Validation
The proposed adaptive magnetic spring was experimentally validated on the four-bar linkage setup, as shown in Figure 3 and introduced in Section 2.3. We used the model-based co-design toolchain detailed in Section 3 to optimize the control inputs and the configuration of the adaptive magnetic spring.
5.1. Experiment Description
The controls of the four-bar linkage model, as well as the angles of the magnetic spring (see Equation (13)) were optimized and applied to the experimental setup. We considered a similar profile as in the simulation: run-up, nominal operation around a given speed, run-down. The speed was varied between 350 and 600 RPM in steps of 50 RPM. In order to find the optimal controls as well as the spring configuration, we solved a comparable optimization problem as defined in Equation (8). The control goal was to minimize the required RMS motor torque, but the achievable energy reduction was measured a posteriori. The setup had to ramp-up from standstill to the desired regime speed in 14bevelledtrue of a rotation (and vice versa for ramp-down), given a maximum motor torque of 28.7 Nm. During continuous operation, a speed fluctuation of 10% was allowed. In total, eight rotations were made. The magnetic spring torque profile was parameterized according to Equation (13), and the angles were be optimized. The initial angle of the linkage mechanism was set to rad.
As mentioned previously, the optimized control input is a non-parameterized feed-forward control signal. Parallel to this feed-forward input, we considered a feedback controller as well (PI controller), which tracks a speed reference signal . For the purpose of comparison, we also solved an optimization problem where is defined to be minimal (). Additionally, we benchmarked the solutions with the case where only a feedback controller was considered, along with a non-optimized reference signal (consisting of simply linear segments).
5.2. Results
In this section, we show the results of the experiments defined in Section 5.1. As introduced previously, four cases were considered, as shown in Table 5. First, we show the performance improvement over the entire considered range of speeds (350–600 RPM). Second, we highlight the results of two speeds: 400 and 550 RPM.

Table 5.
The four considered cases for experimental validation.
In Figure 13, the measured RMS and peak values of motor torque are shown, as well as the consumed energy over the considered speed range (350–600 RPM). The resulting motor torques include the feed-forward input (computed by the OCP) as well as the input applied by the feedback controller. Additionally, the resulting optimized angles of the adaptive magnetic spring are shown for the OCP + AMS case. In Figure 14, the reductions are assessed as a percentage with respect to either the benchmark (top row of plots) or the OCP case (bottom row of plots). We make the following observations:
- It can be seen that the benchmark case demands high peak and RMS torques from the motor and consumes the most energy. For the higher operating speeds, the peak motor torque reaches a maximum of 28.7 Nm.
- When the controls are optimized and the feed-forward control signal is added (OCP), we can reduce the required motor torques and the energy consumption with respect to the benchmark.
- Optimizing the angles of the magnetic spring (AMS), while only using a PI controller, further reduces the required energy and RMS motor torque. For higher speeds, the required peak motor torque is higher than for the OCP case.
- When both the angles of the magnetic spring and the controls are optimized (OCP + AMS), the best performance is obtained. With respect to the benchmark, we reduce the RMS motor torque by 41–77% and the peak motor torque by 53–75%. The energy consumption is reduced by 44–58%. With respect to the OCP case, we obtain reductions of 22–71% (RMS motor torque), 39–64 % (peak motor torque) and 32–47% (energy consumption). Hence, due to the flexibility of the adaptive magnetic spring, combined with the optimized controls, significant reductions are achieved throughout the considered speed range.
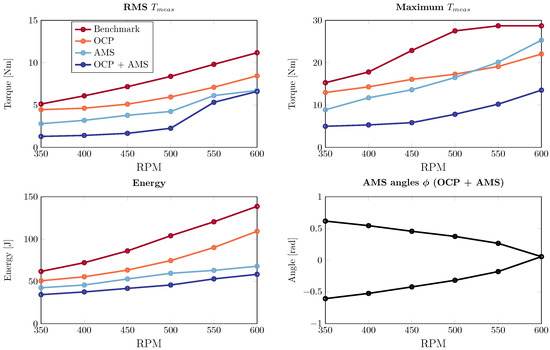
Figure 13.
RMS motor torque, peak motor torque and energy as a function of RPM. Furthermore, the resulting AMS angles are shown for the OCP + AMS case.
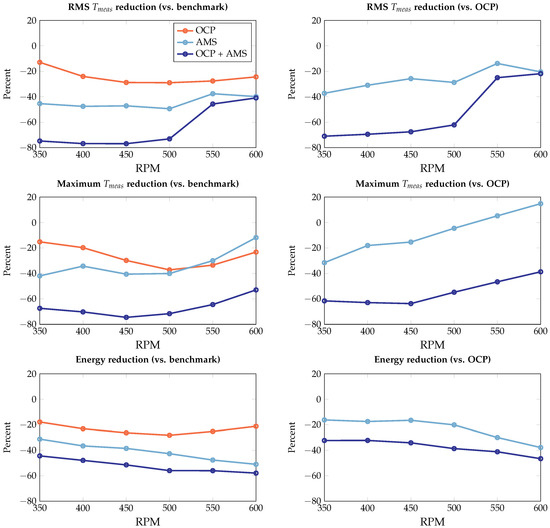
Figure 14.
Reductions in RMS motor torque, peak motor torque and energy as a function of RPM. The left column of plots shows the difference with respect to the benchmark, and the right column of plots with respect to the OCP case.
The results for the 400 RPM case are shown in Figure 15 as follows: the speed reference signals , the resulting measured motor speed and the applied constraints on the speed for each of the four cases. Especially for the benchmark, the speed constraints are violated regularly. In the top right plot, the resulting motor torques are shown, indicating the OCP + AMS case requires a significantly reduced torque with respect to the benchmark. The bottom right plot shows the mechanical and electrical losses for both the benchmark and the OCP + AMS case. In particular, the electrical losses are reduced significantly in the latter case. For the 550 RPM case, the results are shown in Figure 16. Similar conclusions can be drawn for the 400 RPM case.
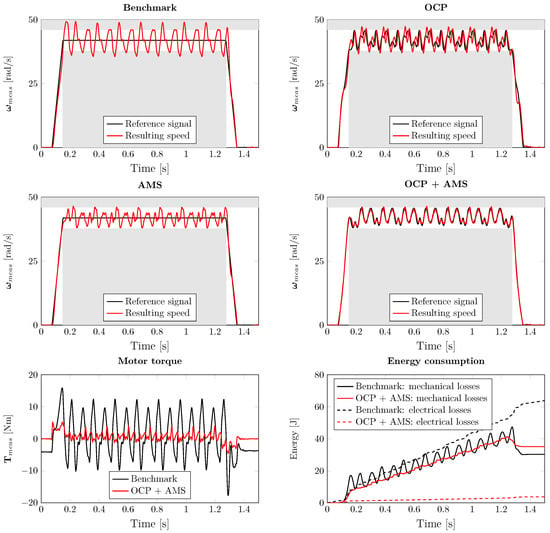
Figure 15.
Results of the experimental validation at 400 RPM: reference and measured speed for each of the four cases, including the measured motor torque and energy consumption for the benchmark and OCP + AMS cases.

Figure 16.
Results of the experimental validation at 550 RPM: reference and measured speed for each of the four cases, including the measured motor torque and energy consumption for the benchmark and OCP + AMS cases.
If we compare the reductions obtained in the simulation (see Figure 7) with the experimental results (bottom rows of Figure 14, OCP + AMS case), similarities in the obtained reductions can be seen: a consistent reduction in RMS and maximum motor torque, and an energy reduction that increases with higher operational speeds of the system. Remaining differences can be attributed to, e.g., variations in the magnetic spring response (see, e.g., Equation (13)), slight variations in and miscellaneous mismatches between the considered model and the true system (e.g., unmodelled flexibilities).
5.3. Energy Consumption for Spring Pre-Setting
Pre-setting a magnetic springs requires energy and time, which is another trade-off we have to account for when using magnetic springs to assist repetitive motion. In all of the design variants we can simply define the minimum pre-setting energy as:
where for the proposed concept this is the same for the maximum amplitude setting where the two phases are aligned, but can be reduced to 50% of the nominal case, since in best case scenario (0% overlap in Figure 2) we only have to move against one of the locked stator–rotor pairs during the pre-setting. This value can then be compared to the energy savings made with magnetic springs, which for our prototype is J. Compared to the savings of 17 J and 37 J (see difference between OCP and OCP + AMS in Figure 13), the results break-even after approximately s and s of operation, respectively. In contrast, most typical production machines considered run at the same time scale rate of minutes to hours. The time required to set the spring at this rate can be roughly approximated by 2–4× the maximum time constant of the reciprocating motion (i.e., inertial forces are much lower than the static spring force), which is RPM s for our example.
6. Conclusions and Outlook
We have presented an innovative adaptive magnetic spring (AMS) concept and its embodiment in a form of a functional prototype. Furthermore, a toolchain for the co-design of magnetic spring-assisted drivetrains was developed, addressing the optimization of both the desired torque profile of the magnetic spring (including its physical geometry), as well as the dynamics and controls of the considered (magnetic-spring-equipped) drivetrain. We demonstrated the results on a four-bar linkage system, which resembles the operation of a weaving loom, both in the simulation and on an experimental setup equipped with the AMS functional prototype. In the simulation, we have shown the benefit of the usage of magnetic springs over using no spring at all, and we have shown the need for adaptivity of the magnetic spring in case multiple operating conditions have to be accounted for. Concerning the experimental setup, we demonstrated a considerable reduction in energy consumption (up to 47%), peak torque (up to 64%) and RMS torque (up to 71%), showing that due to the adaptivity of the spring, good performance is obtained for a wide range of operational speeds.
The novel concepts and methodology presented here open a number of opportunities to be exploited in the future. In the section below, we discuss how this technology could create value in a broader range of problems through the use of the novel concepts and developed design tools, and address further improvements. The future work can be split into the following groups:
- Other applications. Apart from weaving, the AMS could find its application in other above-mentioned highly dynamic and repetitive motions in machines (point-to-point machines, punching, stamping, printing, oscillating piston compressors, packaging etc.). On top of the mentioned one-degree-of-freedom systems, AMS could allow the use of PEA concepts in industrial robotics with multiple degrees of freedom, in particular in high-speed parallel pick-and-place robots (e.g., delta-bots, parallel SCARA robots), where the full actuator mass is concentrated at the base of the robot.
- Linear or rotational magnetic springs. Although the focus of this article is on rotational actuators, our findings, especially ones related to the underlying physics and design methodology, can be extended to linear motion systems. Nevertheless, it has previously been noted [21,49] that linear systems have higher losses due to the limitations of prismatic bearings, even though this conclusion might not hold on smaller scales, as suggested in a recent publication [50]. In future, a more systematic comparison of rotational and linear motion systems with magnetic spring-assisted actuators is expected.
- Iterative learning control. The model used to solve the optimal control problems contains slight mismatches with respect to the actual dynamics of the experimental setup. These mismatches result in imperfections in the obtained control signals and determined magnetic spring settings. In order to deal with this, iterative learning control (ILC) could be employed to iteratively reduce the model–plant mismatch, thereby further improving the control performance [51].
- General use of the co-design toolchain. The toolchain introduced in Section 3 is applicable to solving co-design / optimal control problems for various system types where dynamic model equations are available. These tools have so far been already applied to several domains, e.g., mechanical, thermal, electromagnetic and multi-physics, see e.g., [35].
As a final note, we would like to draw a parallel with standardized brakes in servo systems, a prevalent approach for static load balancing in assisting robotic joints and industrial drivetrains at standstill (e.g., to oppose gravitational forces). In our opinion the findings presented in this article could lead the way towards dynamic load balancing, relying on the magnetic springs employed similarly in a modular fashion.
Author Contributions
Conceptualization and implementation, B.M., J.W., J.B. and C.G.; methodology, B.M., J.W. and C.G.; experimental validation; J.B. and J.W.; resources, C.G.; writing—review and editing, B.M., J.W., J.B. and C.G.; supervision C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out within the framework of Flanders Make’s ICON project “Torque Ripple Reduction”, funded by the Flanders Innovation & Entrepreneurship (VLAIO). Flanders Make is the Flemish strategic research centre for the manufacturing industry.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented within this study result from activities within the acknowledged projects and are available therein.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spyrakos-Papastavridis, E.; Childs, P.R.N.; Dai, J.S. Passivity Preservation for Variable Impedance Control of Compliant Robots. IEEE/ASME Trans. Mechatron. 2020, 25, 2342–2353. [Google Scholar] [CrossRef]
- Wolf, S.; Grioli, G.; Eiberger, O.; Friedl, W.; Grebenstein, M.; Höppner, H.; Burdet, E.; Caldwell, D.G.; Carloni, R.; Catalano, M.G.; et al. Variable Stiffness Actuators: Review on Design and Components. IEEE/ASME Trans. Mechatron. 2016, 21, 2418–2430. [Google Scholar] [CrossRef]
- Plooij, M.; Wisse, M.; Vallery, H. Reducing the energy consumption of robots using the bidirectional clutched parallel elastic actuator. IEEE Trans. Robot. 2016, 32, 1512–1523. [Google Scholar] [CrossRef]
- Csencsics, E.; Schitter, G. Exploring the Pareto Fronts of Actuation Technologies for High Performance Mechatronic Systems. IEEE/ASME Trans. Mechatron. 2021, 26, 1053–1063. [Google Scholar] [CrossRef]
- Bertoldi, P.; Hirl, B.; Labanca, N. Energy Efficiency Status Report 2012; JRC Technical Reports; European Union: Luxembourg, 2012; p. 143. [Google Scholar] [CrossRef]
- Mrak, B.; Lenaerts, B.; Driesen, W.; Desmet, W. Optimal magnetic spring for compliant actuation-validated torque density benchmark. Actuators 2019, 8, 18. [Google Scholar] [CrossRef]
- Mrak, B.; Adduci, R.; Weckx, S.; Driesen, W.; Desmet, W. Novel phase-bound magnetic vibration absorber for improved NVH performance of a wind turbine gearbox. In Proceedings of the ISMA 2018—International Conference on Noise and Vibration Engineering, Leuven, Belgium, 17–19 September 2018; pp. 4833–4845. [Google Scholar]
- Patt, P.J. Design and Testing of a Coaxial Linear Magnetic Spring with Integral Linear Motor. IEEE Trans. Magn. 1985, MAG-21, 1759–1761. [Google Scholar] [CrossRef]
- Boisclair, J.; Richard, P.L.; Laliberté, T.; Gosselin, C. Gravity Compensation of Robotic Manipulators Using Cylindrical Halbach Arrays. IEEE/ASME Trans. Mechatron. 2017, 22, 457–464. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.J.H.; Lomonova, E.A.; Delinchant, B.; Yonnet, J.P. Design study on a magnetic gravity compensator with unequal magnet arrays. Mechatronics 2013, 23, 197–203. [Google Scholar] [CrossRef]
- King, C.; Beaman, J.J.; Sreenivasan, S.V.; Campbell, M. Multistable Equilibrium System Design Methodology and Demonstration. J. Mech. Des. 2004, 126, 1036. [Google Scholar] [CrossRef]
- Janssen, J.L.G.; Paulides, J.J.H.; Lomonova, E.A. Study of Magnetic Gravity Compensator Topologies Using an Abstraction in the Analytical Interaction Equations. Prog. Electromagn. Res. 2012, 128, 75–90. [Google Scholar] [CrossRef]
- Robertson, W.; Cazzolato, B.; Zander, A. A multipole array magnetic spring. IEEE Trans. Magn. 2005, 41, 3826–3828. [Google Scholar] [CrossRef]
- LinMot Inc. Data Book 0185-0124 (EN): LinMot Data Book, 24th ed.; Technical Report; LinMot: Spreitenbach, Switzerland.
- Mizuno, T.; Takasaki, M.; Kishita, D.; Hirakawa, K. Vibration isolation system combining zero-power magnetic suspension with springs. Control. Eng. Pract. 2007, 15, 187–196. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Xu, D.; Hu, J.; Min, W.; Pang, L. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J. Mech. Sci. Technol. 2013, 27, 813–824. [Google Scholar] [CrossRef]
- Snamina, J.; Habel, P. Magnetic spring as the element of vibration reduction system. Mech. Control. 2010, 29, 40–44. [Google Scholar]
- Zhong, J.; Cheng, Z.; Ge, Z.; Zhang, Y.; Lu, W.; Song, F.; Li, C. Nonlinear vibration of a magnetic spring. Phys. Educ. 2012, 47, 444. [Google Scholar] [CrossRef]
- Foisal, A.R.M.; Hong, C.; Chung, G.S. Multi-frequency electromagnetic energy harvester using a magnetic spring cantilever. Sens. Act. Phys. 2012, 182, 106–113. [Google Scholar] [CrossRef]
- Poltschak, F. A high efficient linear motor for compressor applications. In Proceedings of the Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), 2014 International Symposium, Ischia, Italy, 18–20 June 2014; pp. 1356–1361. [Google Scholar] [CrossRef]
- Poltschak, F.; Ebetshuber, P. Design of Integrated Magnetic Springs for Linear Oscillatory Actuators. IEEE Trans. Ind. Appl. 2018, 54, 2185–2192. [Google Scholar] [CrossRef]
- Boldea, I.; Congxiao, W.; Bin, Y.; Nasar, S.A. Analysis and design of flux-reversal linear permanent magnet oscillating machine. In Proceedings of the Industry Applications Conference Thirty-Third IAS Annual Meeting, St. Louis, MO, USA, 12–15 October 1998; Volume 1, pp. 136–143. [Google Scholar] [CrossRef]
- Paden, B.A.; Fiske, O.J.; Ricci, M.R.; Okcuoglu, M.; Paden, D.B.; Paden, B.E. Electromagnetic Valve Apparatus with Nonlinear Spring. U.S. Patent No 9,395,012, 19 July 2016. [Google Scholar]
- Paden, B.E.; Chen, C.; Fiske, J.F. Magnetic Spring and Actuators with Multiple Equilibrium Positions. U.S. Patent US7265470B1, 4 September 2007. [Google Scholar]
- Sudano, A.; Tagliamonte, N.L.; Accoto, D.; Guglielmelli, E. A resonant parallel elastic actuator for biorobotic applications. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 2815–2820. [Google Scholar] [CrossRef]
- Sudano, A.; Accoto, D.; Zollo, L.; Guglielmelli, E. Design, development and scaling analysis of a variable stiffness magnetic torsion spring. Int. J. Adv. Robot. Syst. 2013, 10, 372. [Google Scholar] [CrossRef]
- Verstraten, T.; López-García, P.; Lenaerts, B.; Mrak, B.; Lefeber, D.; Vanderborght, B. Improving the performance of industrial machines with variable stiffness springs. Mech. Based Des. Struct. Mach. 2022, 50, 115–134. [Google Scholar] [CrossRef]
- Che, D.; Bird, J.Z.; Hagmüller, A.; Hossain, M.E. An Adjustable Stiffness Torsional Magnetic Spring with a Linear Stroke Length. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 5944–5948. [Google Scholar] [CrossRef]
- Ibrahim, M.; Sergeant, P. Dynamic Modelling and Analysis of Electric Motor with Integrated Magnetic Spring Driving Weaving Loom Application. IEEE Trans. Ind. Electron. 2022, 70, 2329–2338. [Google Scholar] [CrossRef]
- Woodward, M.A.; Sitti, M. Tailored Magnetic Springs for Shape-Memory Alloy Actuated Mechanisms in Miniature Robots. IEEE Trans. Robot. 2019, 35, 589–601. [Google Scholar] [CrossRef]
- Woodward, M.A.; Sitti, M. Universal Custom Complex Magnetic Spring Design Methodology. IEEE Trans. Magn. 2018, 54, 8200213. [Google Scholar] [CrossRef]
- Mrak, B.; Wex, B.; Mitterhofer, H. Methodology for Shape Optimization of Magnetic Designs: Magnetic Spring Characteristic Tailored to Application Needs. Actuators 2022, 11, 37. [Google Scholar] [CrossRef]
- Coemelck, D.; Delboo, E.; Roelstraete, K. Driving Device for a Weaving Machine with a Supporting Device. BE Patent BE1026177A1, 28 October 2019. [Google Scholar]
- Mrak, B.; Lenaerts, B.; Jeurgen, M.; Driesen, W. Magnetic Spring. NL Patent NL2020783B1, 24 October 2019. [Google Scholar]
- Adduci, R.; Willems, J.; Kikken, E.; Gillis, J.; Croes, J.; Desmet, W. An Integrated Co-Design Optimization Toolchain Applied to a Conjugate Cam-Follower Drivetrain System. Machines 2023, 11, 486. [Google Scholar] [CrossRef]
- Hassell, T.J.; Weaver, W.W.; Oliveira, A.M. Using Matlab’s Simscape modeling environment as a simulation tool in power electronics and electrical machines courses. In Proceedings of the 2013 IEEE Frontiers in Education Conference (FIE), Oklahoma City, OK, USA, 23–26 October 2013; pp. 477–483. [Google Scholar]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi—A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Wächter, A.; Biegler, L.T. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Meeker, D. Finite element method magnetics. FEMM 2010, 4, 162. [Google Scholar]
- Kamadan, A.; Kiziltas, G.; Patoglu, V. Co-design strategies for optimal variable stiffness actuation. IEEE/ASME Trans. Mechatron. 2017, 22, 2768–2779. [Google Scholar] [CrossRef]
- Gillis, J.; Kikken, E. Symbolic Equation Extraction from SimScape. In Proceedings of the Benelux Meeting on Systems and Control, Soesterberg, The Netherlands, 27–29 March 2018. [Google Scholar]
- van de Wijdeven, J.; Bosgra, O.H. Using basis functions in iterative learning control: Analysis and design theory. Int. J. Control. 2010, 83, 661–675. [Google Scholar] [CrossRef]
- Camacho, E.F.; Alba, C.B. Model Predictive Control; Springer Science & Business Media: Singapore, 2013. [Google Scholar]
- Bock, H.; Plitt, K. A Multiple Shooting Algorithm for Direct Solution of Optimal Control Problems. IFAC Proc. Vol. 1984, 17, 1603–1608. [Google Scholar] [CrossRef]
- Rayner, R.M.; Sahinkaya, M.N.; Hicks, B. Improving the design of high speed mechanisms through multi-level kinematic synthesis, dynamic optimization and velocity profiling. Mech. Mach. Theory 2017, 118, 100–114. [Google Scholar] [CrossRef]
- Ouyang, T.; Wang, P.; Huang, H.; Zhang, N.; Chen, N. Mathematical modeling and optimization of cam mechanism in delivery system of an offset press. Mech. Mach. Theory 2017, 110, 100–114. [Google Scholar] [CrossRef]
- Vikse, M.; Watson, H.A.; Kim, D.; Barton, P.I.; Gundersen, T. Optimization of a dual mixed refrigerant process using a nonsmooth approach. Energy 2020, 196, 116999. [Google Scholar] [CrossRef]
- Audet, C.; Le Digabel, S.; Tribes, C. NOMAD User Guide; Technical Report G-2009-37; Les Cahiers du GERAD: Montreal, QC, Canada, 2009. [Google Scholar]
- Mrak, B.; Driesen, W.; Desmet, W. Magnetic Springs—Fast Energy Storage for Reciprocating Industrial Drivetrains. In Proceedings of the ABCM International Congress of Mechanical Engineering, Rio de Janeiro, Brazil, 6–11 December 2015; Volume 23. [Google Scholar]
- Bhushan, B.M.; Yoon, J.Y.; Griffith, L.G.; Trumper, D.L. Flux-Biased, Energy-Efficient Electromagnetic Micropumps Utilizing Bistable Magnetic Latching and Energy-Storage Springs. IEEE/ASME Trans. Mechatron. 2021, 26, 2362–2372. [Google Scholar] [CrossRef]
- Steinhauser, A.; Swevers, J. An Efficient Iterative Learning Approach to Time-Optimal Path Tracking for Industrial Robots. IEEE Trans. Ind. Inform. 2018, 14, 5200–5207. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).