LESO-Based Nonlinear Continuous Robust Stabilization Control of Underactuated TORA Systems
Abstract
:1. Introduction
- (1)
- The control algorithms developed by the passivity-based control method are computationally simple but they are difficult to deal with unknown disturbances. In other words, when these controllers are applied for TORA systems in practice where unknown disturbances widely exist, the control performances of the controllers would deteriorate and even unstable results may be caused.
- (2)
- By introducing a coordinate transformation, the model of TORA systems becomes a relatively simple cascaded form, based on which the uncertain issue can be addressed by incorporating neural network/fuzzy system or sliding model control techniques. However, the transient control performances of the control system under these control schemes cannot be guaranteed as the corresponding inherent problems of computational complexity and chatting phenomenon cannot be avoided.
- (1)
- By borrowing the idea from the backstepping methodology, a hyperbolic tangent virtual control law is designed to obtain an integral chain error subsystem, which makes the well-known LESO technique easy to implement for the control design of TORA systems.
- (2)
- By employing the LESO, the unknown lumped matched disturbances are accurately estimated and timely compensated by augmenting the feedback controller with the estimate of disturbances, which guarantees the controller a strong robustness against disturbances.
- (3)
- Unlike some existing intelligent or sliding model control methods, the developed controller can generate robust and continuous control inputs to stabilize the rotation and translation of TORA systems smoothly and efficiently, without any learning mechanisms.
2. Control Problem Formulation
3. LESO-Based Backstepping Controller Design
3.1. Virtual Control Law
3.2. Linear Extended State Observer (LESO)
3.3. Continuous Nonlinear Feedback Control Law
4. Stability Analysis
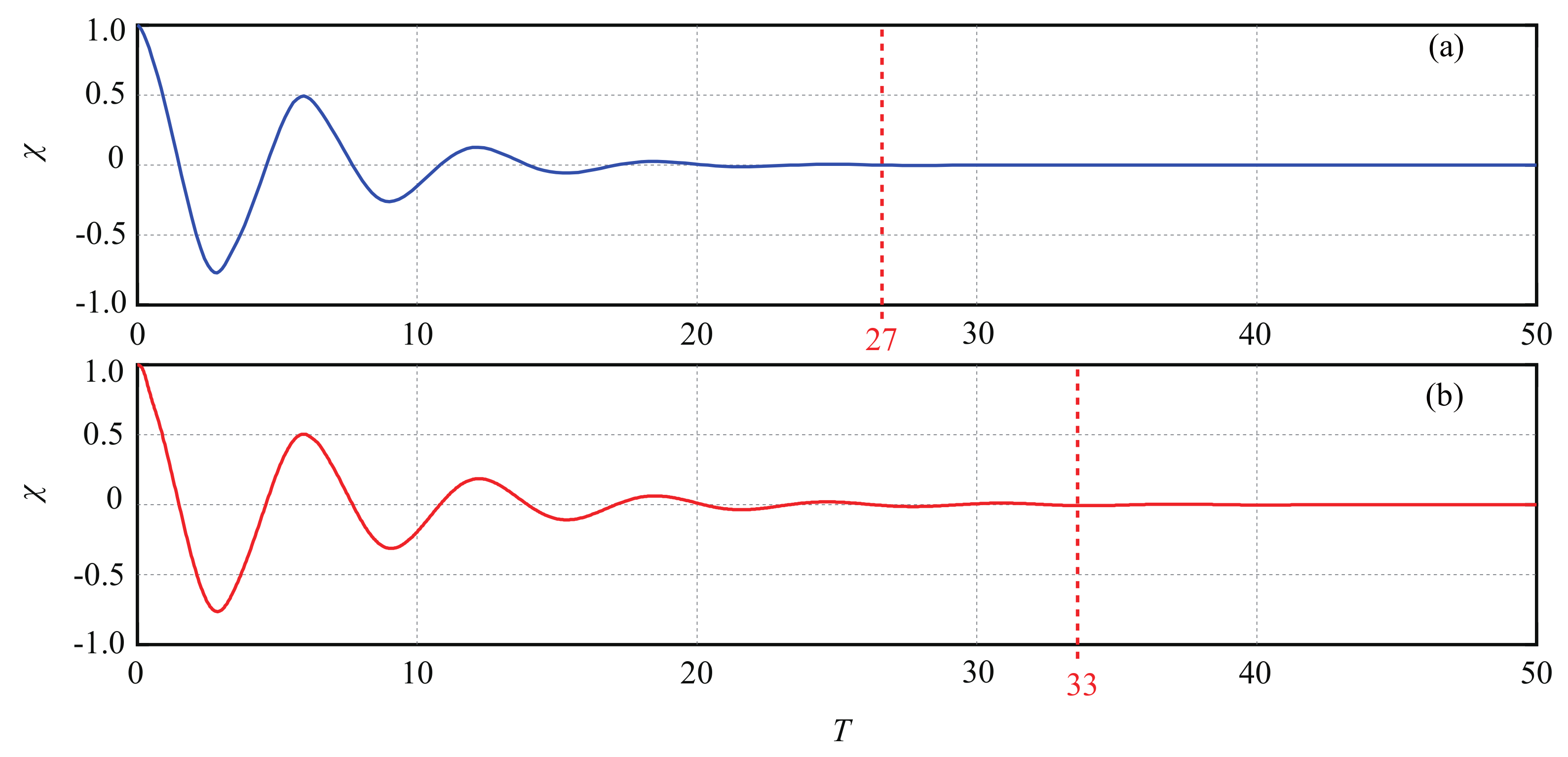
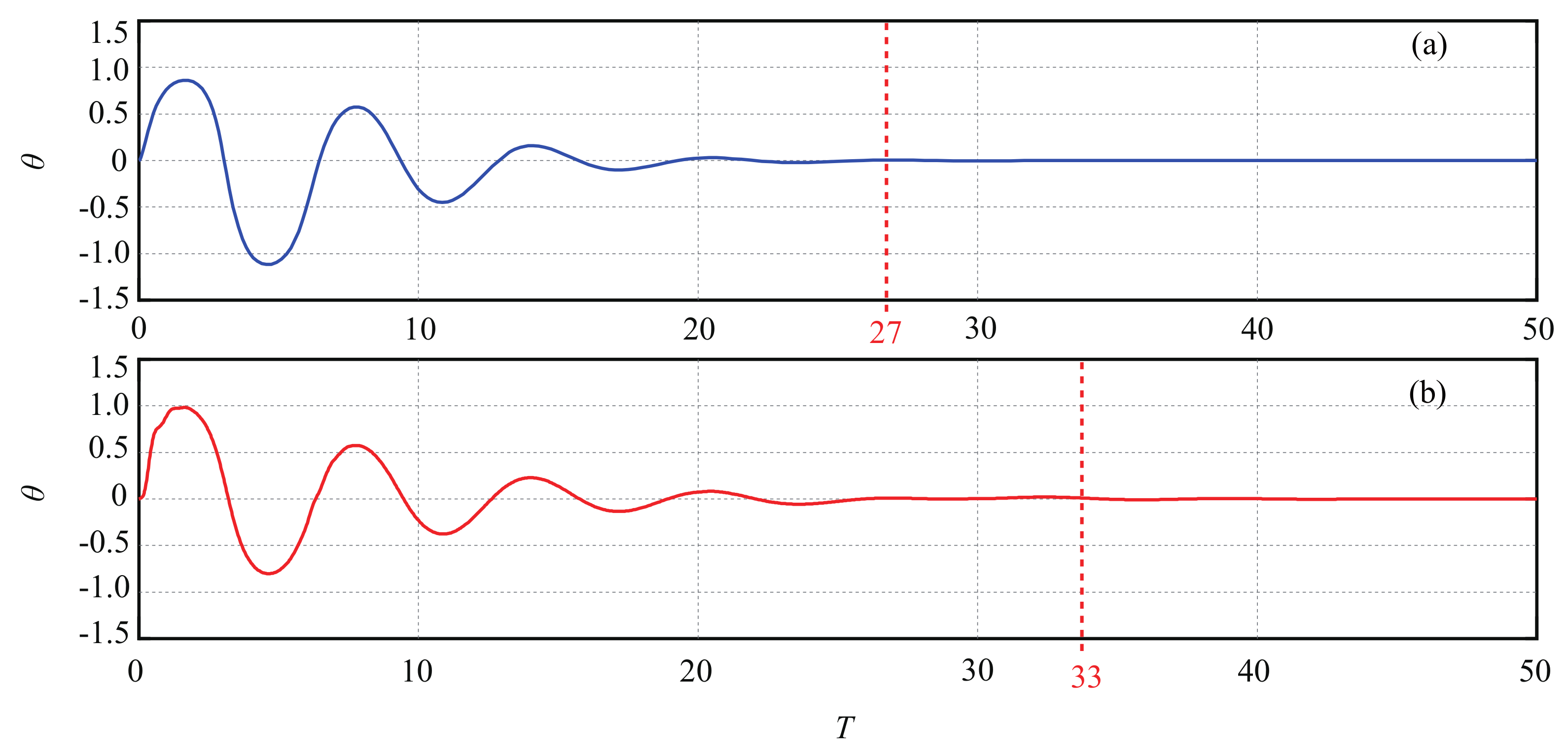
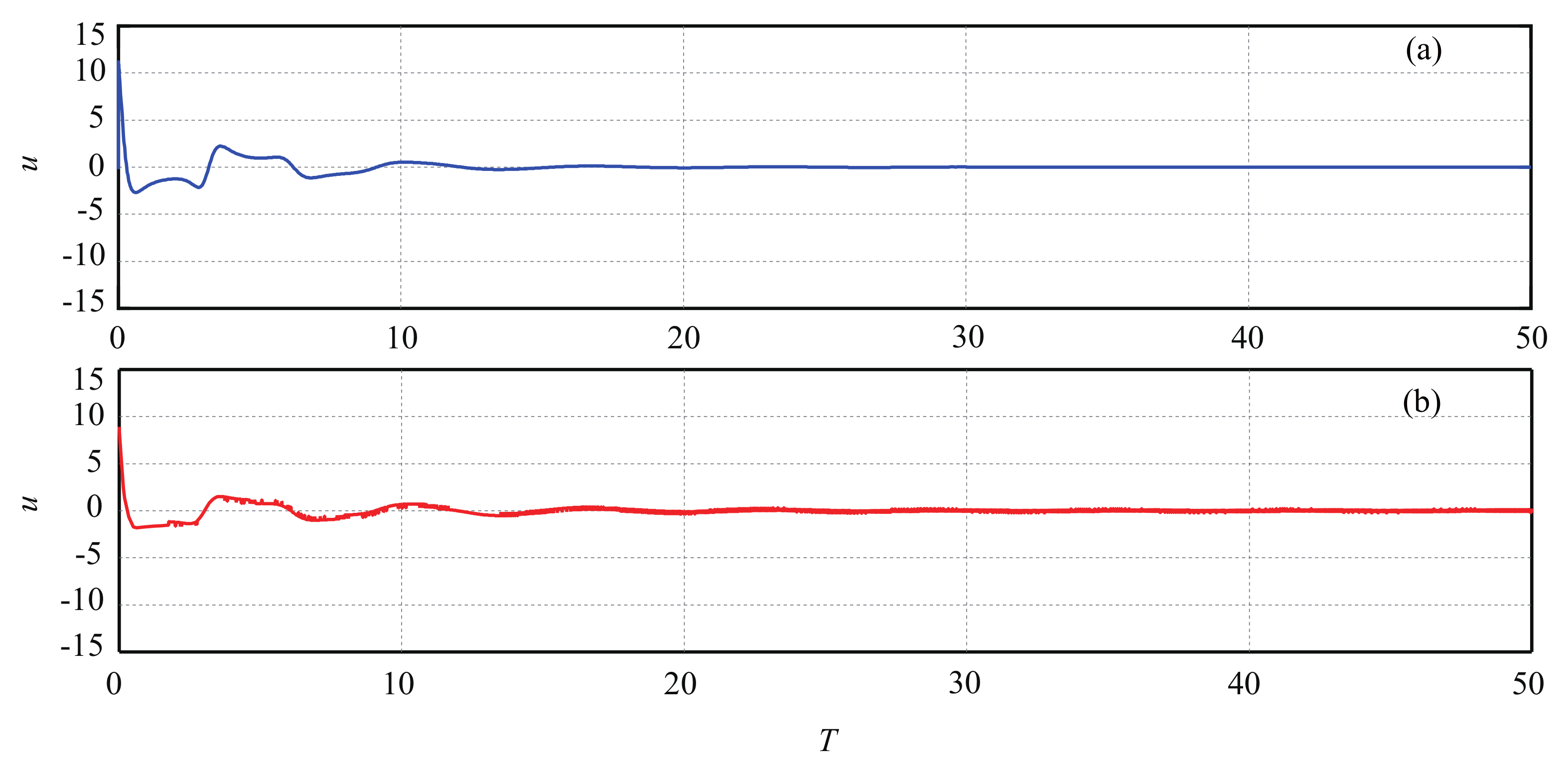
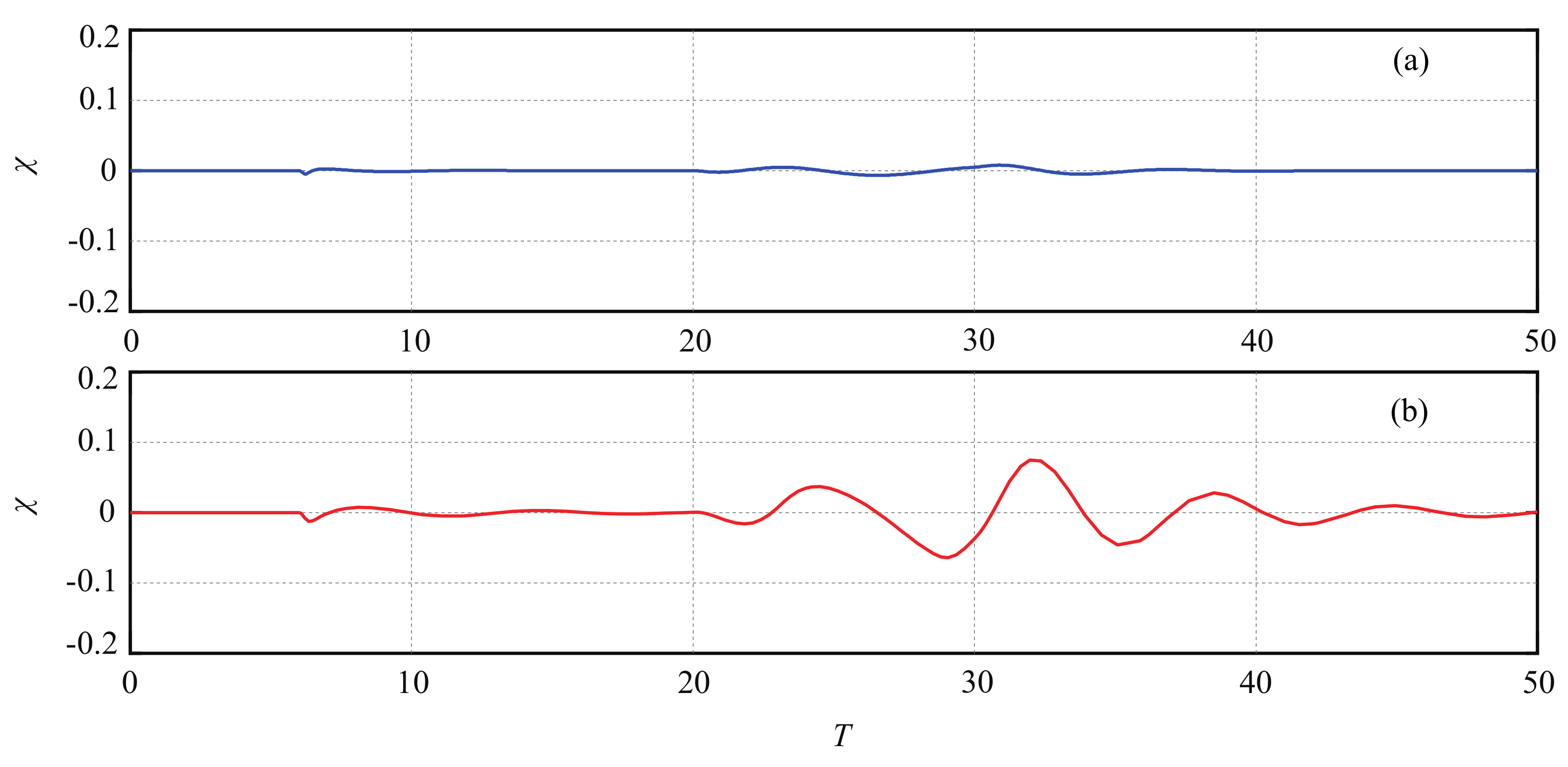
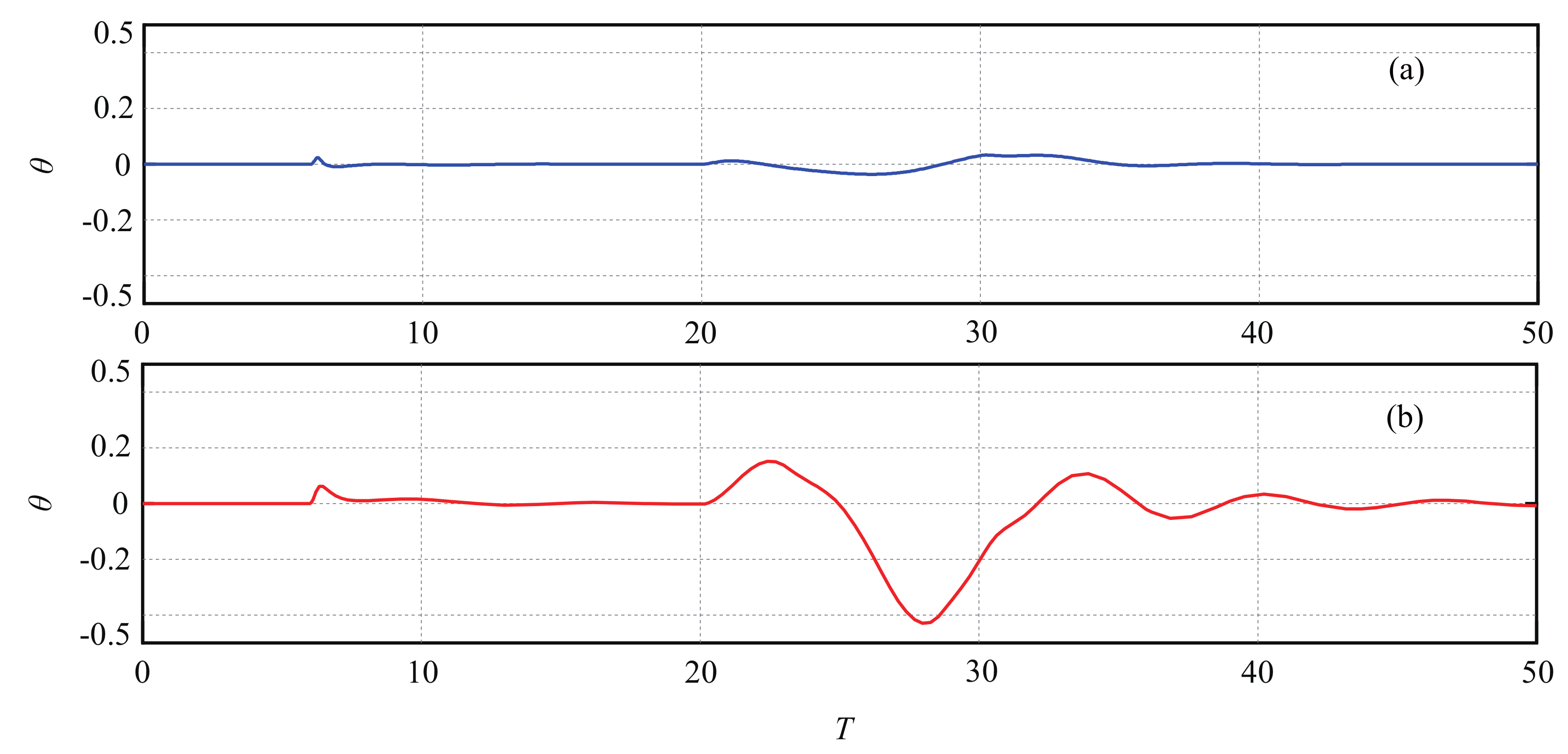
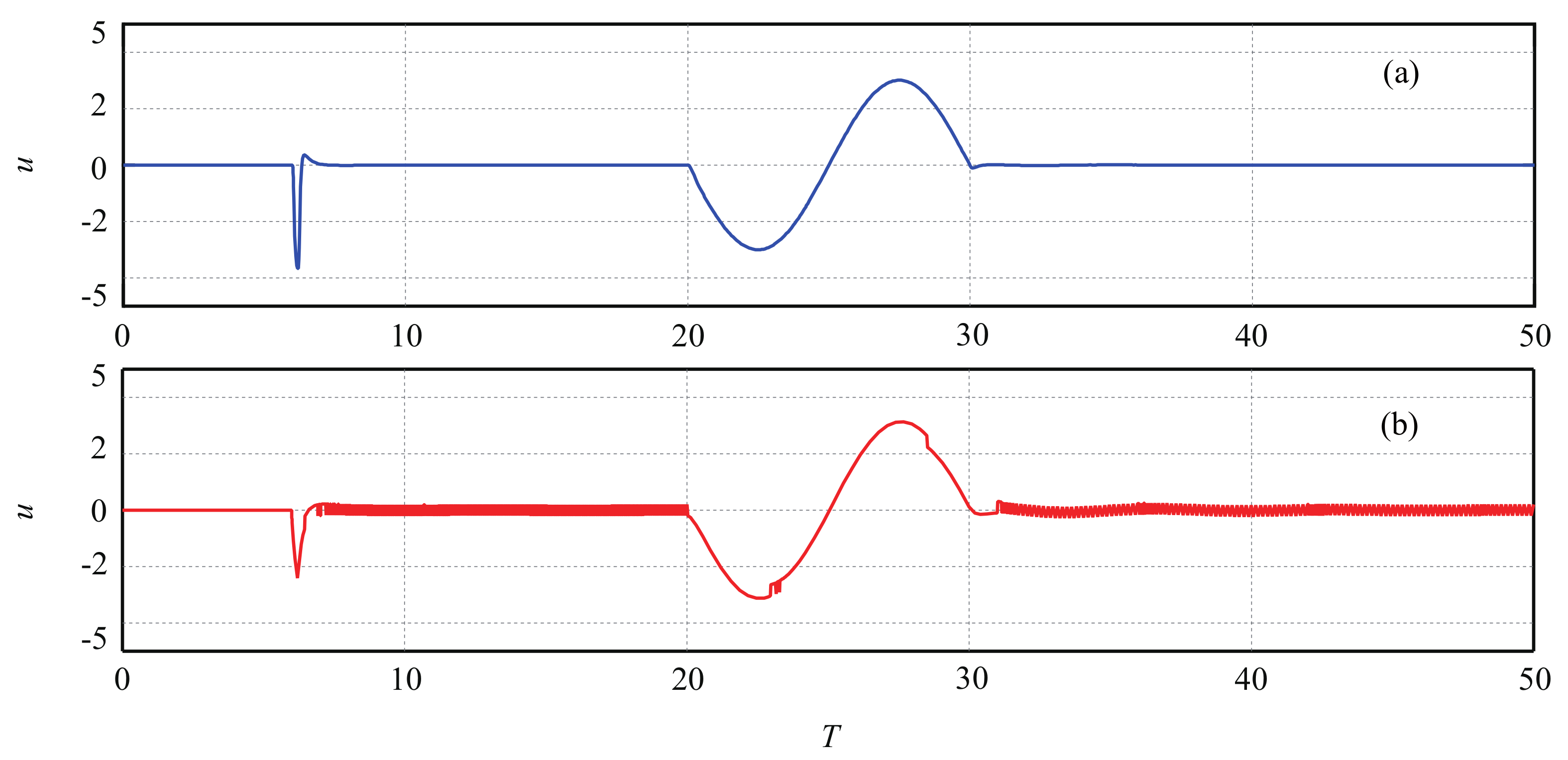
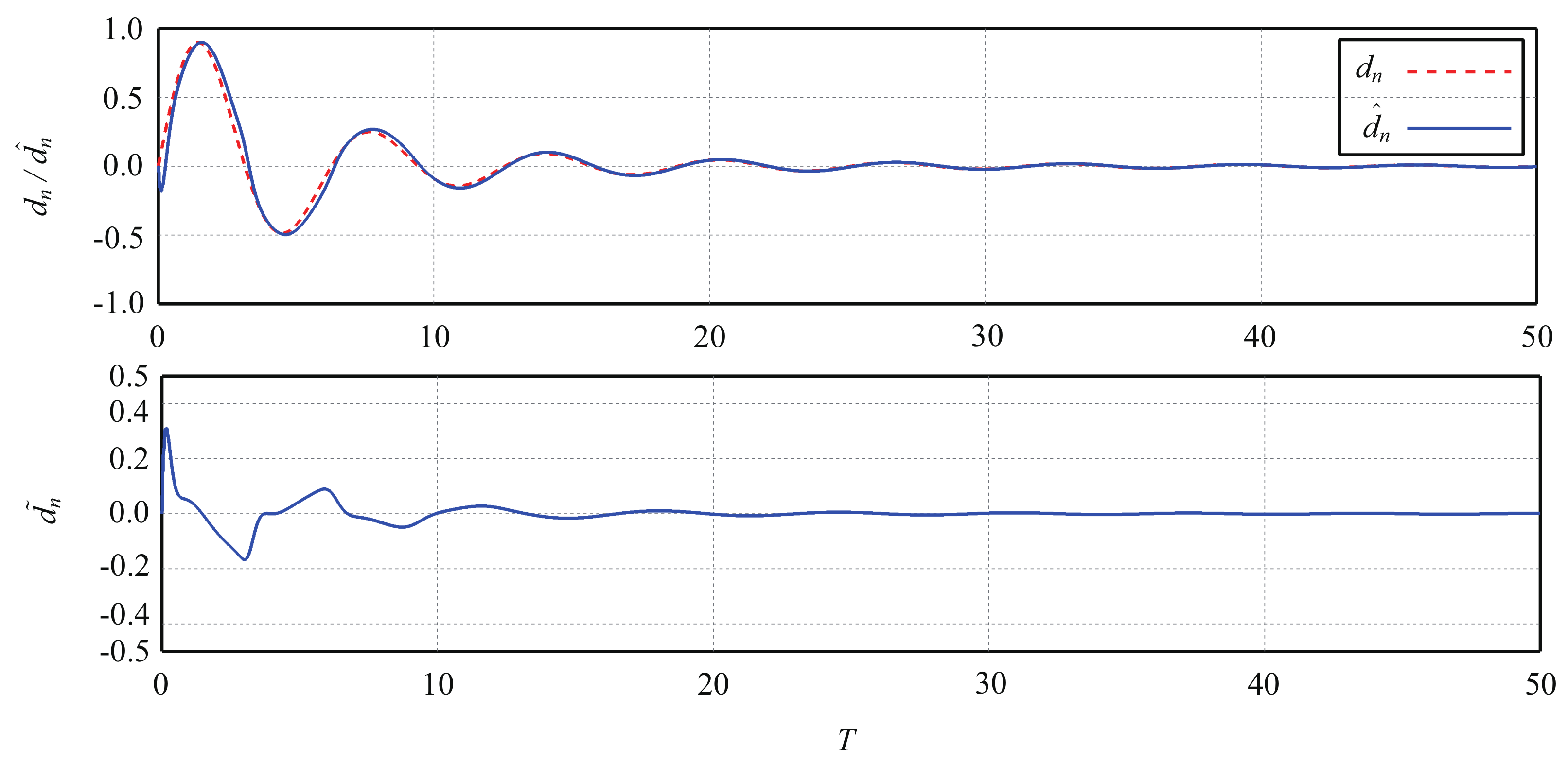
5. Simulation Results
5.1. Case 1: Robustness to Continuous Disturbance
5.2. Case 2: Robustness Test to Different Disturbances
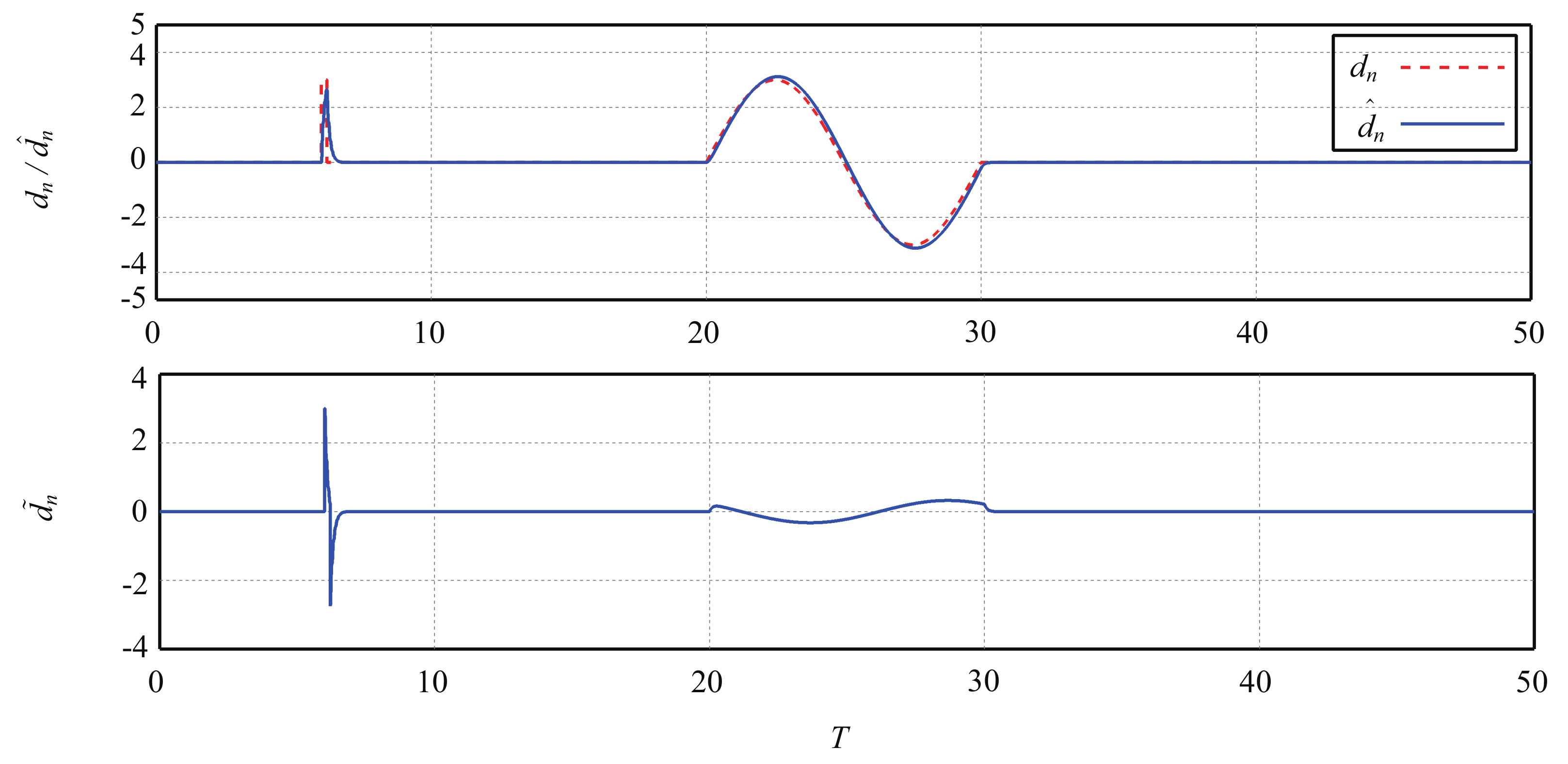
5.3. Estimation Performance of LESO
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, B.; Wang, S.; Liu, Y.J. Underactuated robotics: A review. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419862164. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, H.; Tian, Z.; Yu, L.; Zhang, G. Partial enhanced-coupling control approach for trajectory tracking and swing rejection in tower cranes with double-pendulum effect. Mech. Syst. Signal Process. 2021, 156, 107613. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Fang, Y. Neuroadaptive control for complicated underactuated systems with simultaneous output and velocity constraints exerted on both actuated and unactuated states. IEEE Trans. Neural Netw. Learn. Syst. 2021. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Chen, H.; Sun, N.; Fang, Y. Adaptive neural network output feedback control of uncertain underactuated systems with actuated and unactuated state constraints. IEEE Trans. Syst. Man Cybern. Syst. 2021. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Fang, Y. Adaptive fuzzy control for a class of MIMO underactuated systems with plant uncertainties and actuator deadzones: Design and experiments. IEEE Trans. Cybern. 2021. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Y.; Zhang, P.; Su, C.Y. Continuous control strategy of planar 3-linkage underactuated manipulator based on broad neural network. Actuators 2021, 10, 249. [Google Scholar] [CrossRef]
- Robert, T.B.; Dennis, S.B.; Vincent, T.C. A benchmark problem for nonlinear control design. Int. J. Robust Nonlinear Control 1998, 8, 307–310. [Google Scholar]
- Fradkov, A.; Tomchina, O.; Tomchin, D. Controlled passage through resonance in mechanical systems. J. Sound Vib. 2011, 330, 1065–1073. [Google Scholar] [CrossRef]
- Sun, N.; Wu, Y.M.; Fang, Y.C.; Chen, H. Nonlinear stabilization control of multiple-RTAC systems subject to amplitude-restricted actuating torques using only angular position feedback. IEEE Trans. Ind. Electron. 2017, 64, 3084–3094. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.Y.; Cheng, B.W.; Zhang, X. An active mass damper using rotating actuator for structural vibration control. Adv. Mech. Eng. 2016, 8, 1687814016657730. [Google Scholar] [CrossRef] [Green Version]
- Shah, S.A.A.; Gao, B.; Ahmed, N.; Liu, C. Advanced robust control techniques for the stabilization of translational oscillator with rotational actuator based barge-type OFWT. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2021, 235, 327–343. [Google Scholar] [CrossRef]
- He, M.E.; Hu, Y.Q.; Zhang, Y. Optimization design of tuned mass damper for vibration suppression of a barge-type offshore floating wind turbine. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 302–315. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, N.; Fang, Y.; Liang, D. An increased nonlinear coupling motion controller for underactuated Multi-TORA systems: Theoretical design and hardware experimentation. IEEE Trans. Syst. Man, Cybern. Syst. 2019, 49, 1186–1193. [Google Scholar] [CrossRef]
- Pan, C.; Cui, C.; Zhou, L.; Xiong, P.; Li, Z. A model-free output feedback control approach for the stabilization of underactuated TORA system with input saturation. Actuators 2021, 11, 97. [Google Scholar] [CrossRef]
- Pertres, Z.B.; Aranyi, P.; Korondi, P.; Hashimoto, H. Trajectory tracking by TP model transformation: Case study of a benchmark problem. IEEE Trans. Ind. Electron. 2007, 54, 1654. [Google Scholar] [CrossRef]
- Quan, Q.; Cai, K.Y. Additive-state-decomposition-based tracking control for benchmark. J. Sound Vib. 2013, 332, 4829–4841. [Google Scholar] [CrossRef] [Green Version]
- Sun, N.; Wu, Y.; Fang, Y.; Chen, H.; Lu, B. Nonlinear continuous global stabilization control for underactuated RTAC systems: Design, analysis, and experimentation. IEEE/ASME Trans. Mechatron. 2017, 22, 1104–1115. [Google Scholar] [CrossRef]
- Jankovic, M.; Fontaine, D.; Kokotović, P.V. TORA example: Cascade- and passivity-based control designs. IEEE Trans. Control. Syst. Technol. 1996, 4, 292–297. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.P.; Kanellakopoulos, I. Global output feedback tracking for a benchmark nonlinear system. IEEE Trans. Autom. Control 2000, 45, 1023–1027. [Google Scholar] [CrossRef]
- Wu, X.Q.; Xu, K.X.; Ma, M.; Ke, L.T. Output feedback control for an underactuated benchmark system with bounded torques. Asian J. Control 2020, 23, 1466–1475. [Google Scholar] [CrossRef]
- Avis, J.M.; Nersesov, S.G.; Nathan, R. A comparison study of nonlinear control techniques for the RTAC system. Nonlinear Anal. Real World Appl. 2010, 11, 2647–2658. [Google Scholar] [CrossRef]
- He, S.M.; Ji, H.B.; Yang, K.H. Semi-global output feedback tracking to reference system with input for a benchmark nonlinear system. Asian J. Control 2019, 21, 749–758. [Google Scholar] [CrossRef]
- Gao, B.T. Dynamic modeling and energy-based control design of TORA. Acta Autom. Sin. 2008, 34, 1221–1224, (In Chinese with an English Abstract). [Google Scholar] [CrossRef]
- Wu, X.Q.; Gu, M.M. Adaptive control of the TORA system with partial state constraint. Trans. Inst. Meas. Control 2019, 41, 1172–1177. [Google Scholar] [CrossRef]
- Burg, T.; Dawson, D. Additional notes on the TORA example: A filtering approach to eliminate velocity measurements. IEEE Trans. Control Syst. Technol. 1997, 5, 520–523. [Google Scholar] [CrossRef]
- Escobar, G.; Ortega, R.; Sira-Ramrez, H. Output-feedback global stabilization of a nonlinear benchmark system using a saturated passivity-based controller. IEEE Trans. Control Syst. Technol. 1999, 7, 289–293. [Google Scholar] [CrossRef]
- Wu, X.Q.; Xu, K.X.; Zhang, Y.B. Output-based feedback control of underactuated TORA systems by bounded inputs. Acta Autom. Sin. 2020, 46, 200–204, (In Chinese with an English Abstract). [Google Scholar]
- Gao, B.T.; Jia, Z.Y.; Chen, H.J.; Zhang, X. Dynamic modeling and backstepping control of TORA. Control Decis. 2007, 22, 1284–1288, (In Chinese with an English Abstract). [Google Scholar]
- Liu, D.T.; Guo, W.P. Nonlinear backstepping design for the underactuated TORA system. J. Vibroeng. 2014, 16, 552–559. [Google Scholar]
- Guo, W.P.; Liu, D.T. Nonlinear dynamic surface control for the underactuated translational oscillator with rotating actuator system. IEEE Access 2019, 7, 11844–11853. [Google Scholar] [CrossRef]
- Lee, C.H.; Chang, S.K. Experimental implementation of nonlinear TORA system and adaptive backstepping controller design. Neural Comput. Appl. 2012, 21, 785–800. [Google Scholar] [CrossRef]
- She, J.; Zhang, A.; Lai, X.; Wu, M. Global stabilization of 2-DOF underactuated mechanical systems-an equivalent-input-disturbance approach. Nonlinear Dyn. 2012, 69, 495–509. [Google Scholar] [CrossRef]
- Wu, T.B.; Gui, W.H.; Hu, D.; Du, C. Adaptive fuzzy sliding mode control for translational oscillator with rotating actuator: A fuzzy model. IEEE Access 2018, 6, 55861–55869. [Google Scholar] [CrossRef]
- Hung, L.C.; Lin, H.P.; Chung, H.Y. Design of self-tuning fuzzy sliding mode control for TORA system. Expert Syst. Appl. 2007, 32, 201–212. [Google Scholar] [CrossRef]
- Wu, X.Q.; Zhao, Y.J.; Xu, K.X. Nonlinear disturbance observer based sliding mode control for a benchmark system with uncertain disturbances. ISA Trans. 2021, 110, 63–70. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.Q.; Xu, K.X. Global sliding mode control for the underactuated translational oscillator with rotational actuator system. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2021, 235, 540–549. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Wang, S.; Li, S.; Su, J.; Li, J.; Zhang, L. Extended state observer-based nonsingular terminal sliding mode controller for a DC-DC buck converter with disturbances: Theoretical analysis and experimental verification. Int. J. Control 2022. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Cunningham, F., Jr.; Grossman, N. On Young’s Inequality. Am. Math. Mon. 1971, 78, 781–783. [Google Scholar] [CrossRef]
- Sussmann, H.J.; Kokotovic, P.V. The peaking phenomenon and the global stabilization of nonlinear systems. IEEE Trans. Autom. Control 1991, 36, 424–440. [Google Scholar] [CrossRef]
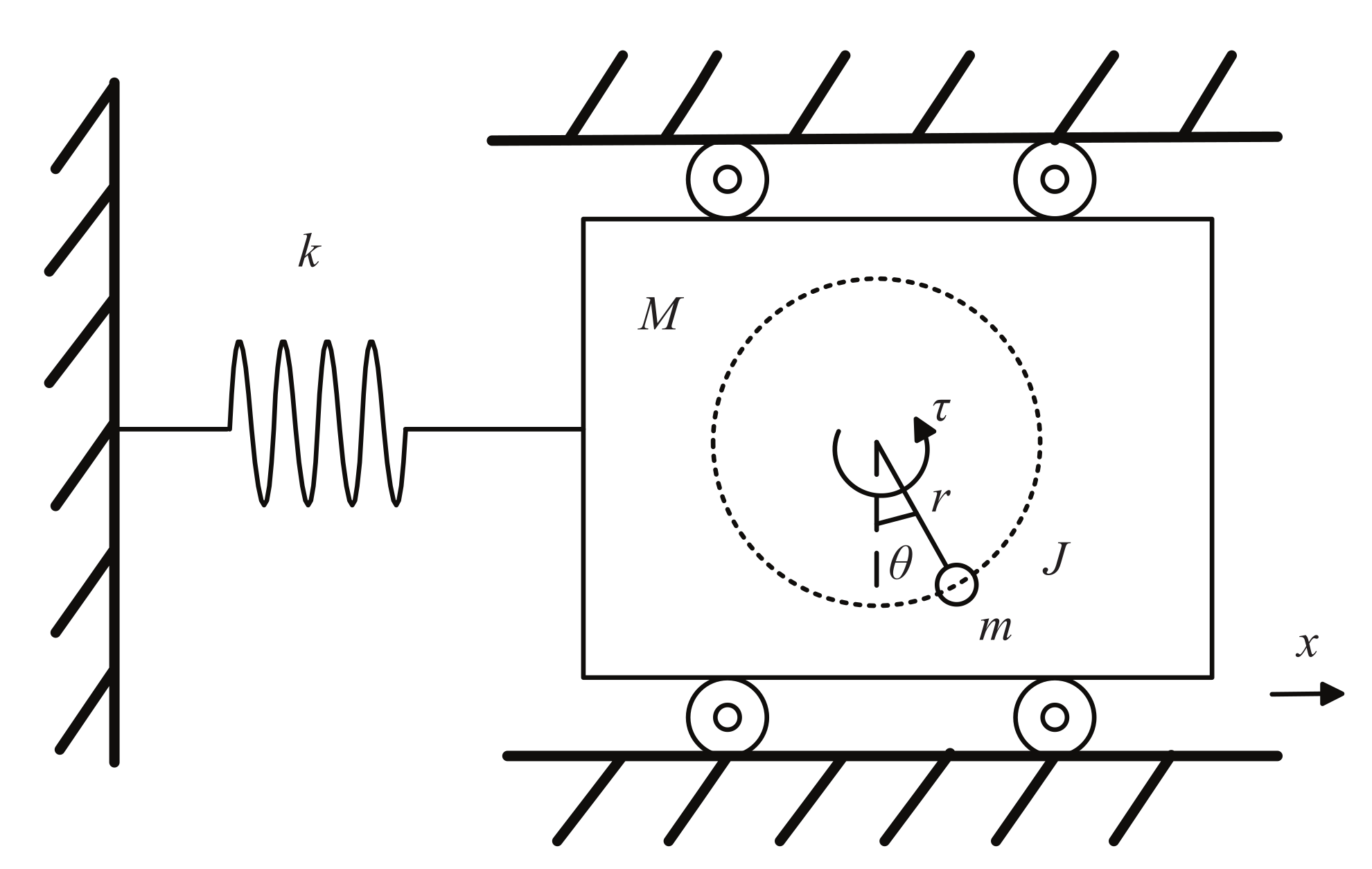

| Parameters/Variables | Meaning | Unit |
|---|---|---|
| M | Mass of the translational trolley | |
| m | Mass of the rotational ball | |
| k | Stiffness coefficient of the spring | |
| r | Rotational radius of the ball | |
| x | Translational displacement of the trolley | |
| Rotational angle of the ball with respect to the vertical position | ||
| J | Moment of inertia of the ball | |
| Control torque applied on the ball |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Pan, C.; Xiao, J.; Li, Z.; Cui, C. LESO-Based Nonlinear Continuous Robust Stabilization Control of Underactuated TORA Systems. Actuators 2022, 11, 220. https://doi.org/10.3390/act11080220
Wang Y, Pan C, Xiao J, Li Z, Cui C. LESO-Based Nonlinear Continuous Robust Stabilization Control of Underactuated TORA Systems. Actuators. 2022; 11(8):220. https://doi.org/10.3390/act11080220
Chicago/Turabian StyleWang, Yihao, Changzhong Pan, Jinsen Xiao, Zhijing Li, and Chenchen Cui. 2022. "LESO-Based Nonlinear Continuous Robust Stabilization Control of Underactuated TORA Systems" Actuators 11, no. 8: 220. https://doi.org/10.3390/act11080220
APA StyleWang, Y., Pan, C., Xiao, J., Li, Z., & Cui, C. (2022). LESO-Based Nonlinear Continuous Robust Stabilization Control of Underactuated TORA Systems. Actuators, 11(8), 220. https://doi.org/10.3390/act11080220






