Relationship Prediction Based on Graph Model for Steam Turbine Control Valve
Abstract
1. Introduction
2. Methods
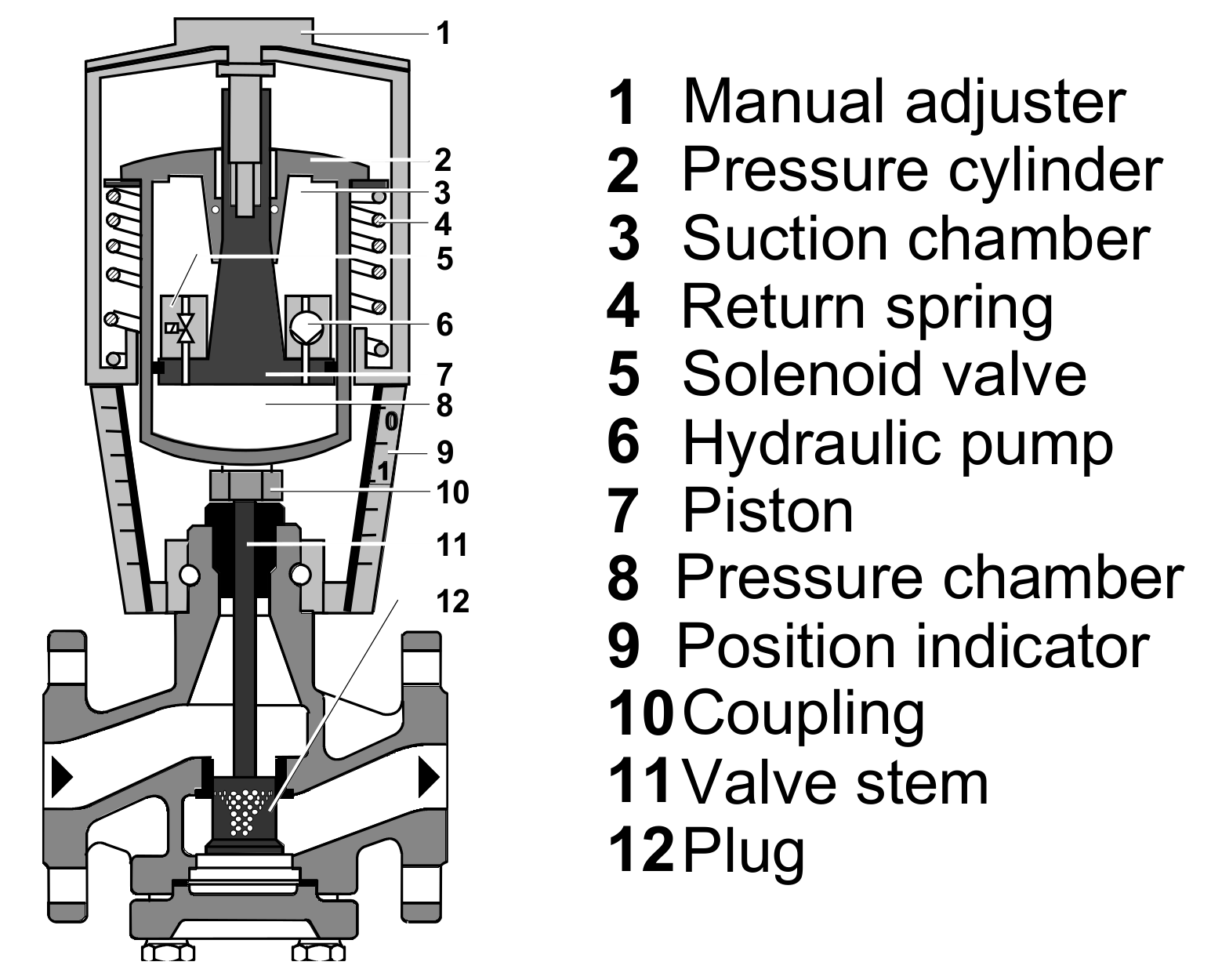
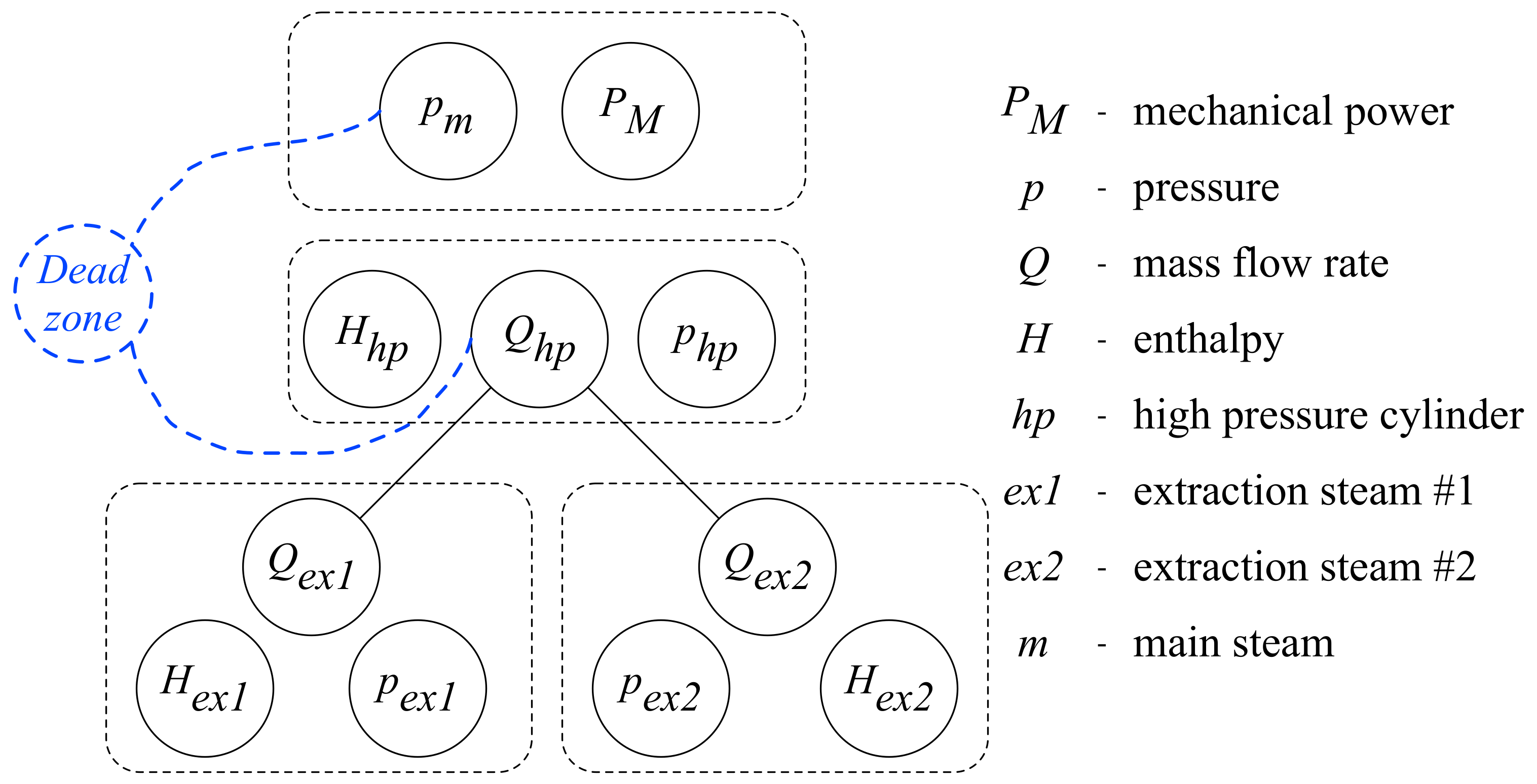
2.1. Problem Definition
2.2. Mathematical Preliminaries
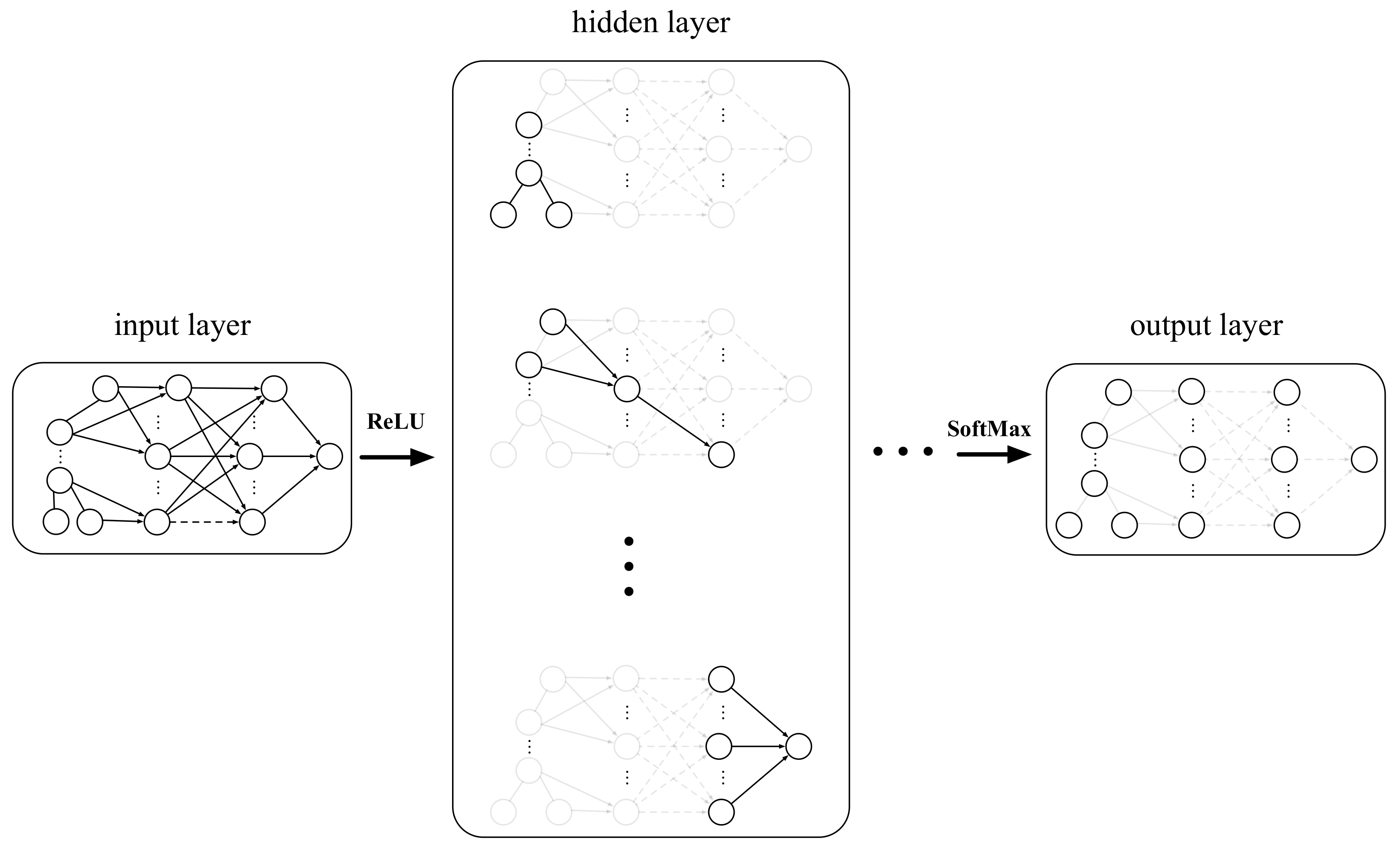
2.3. The Link Prediction Algorithm
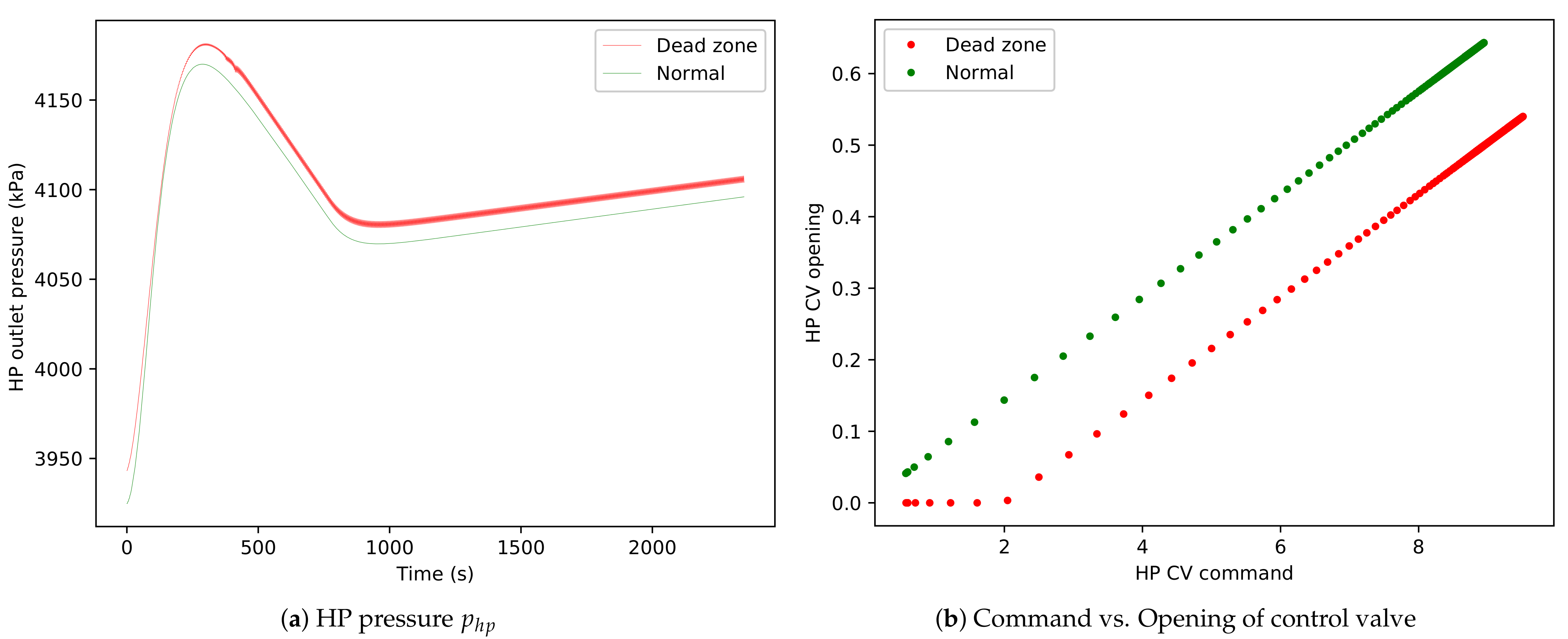
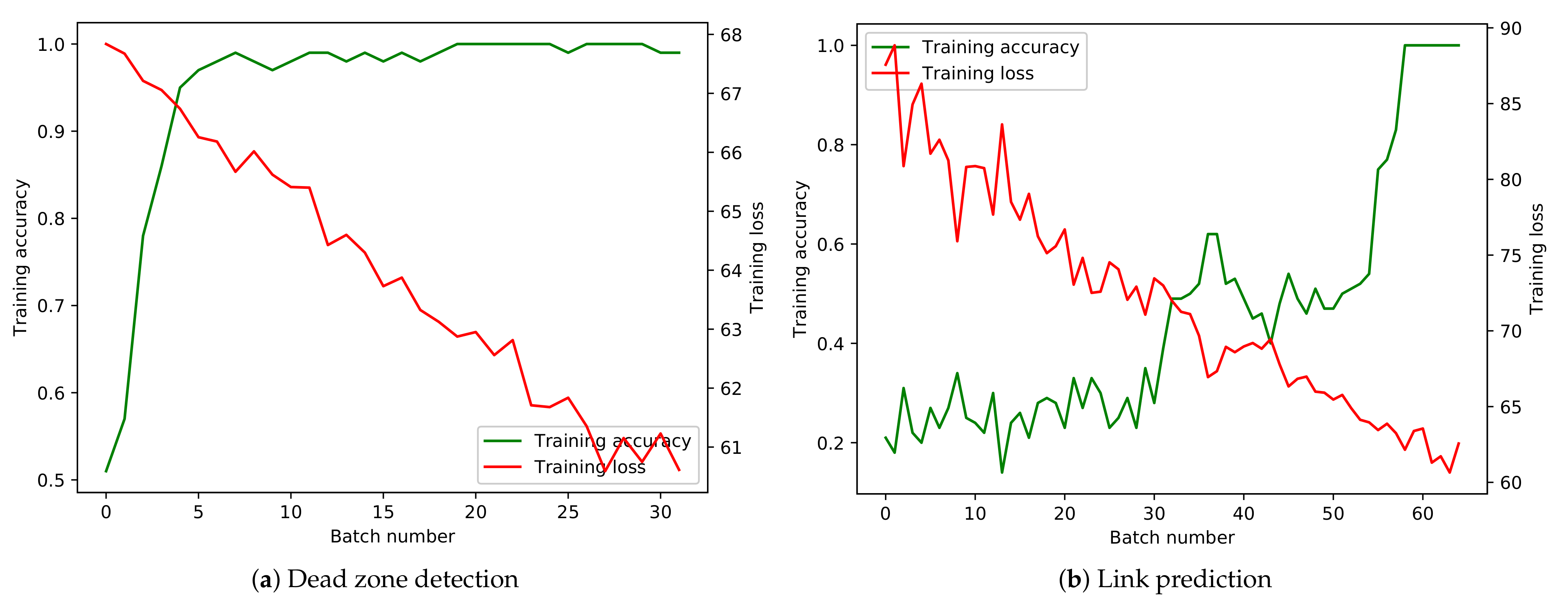
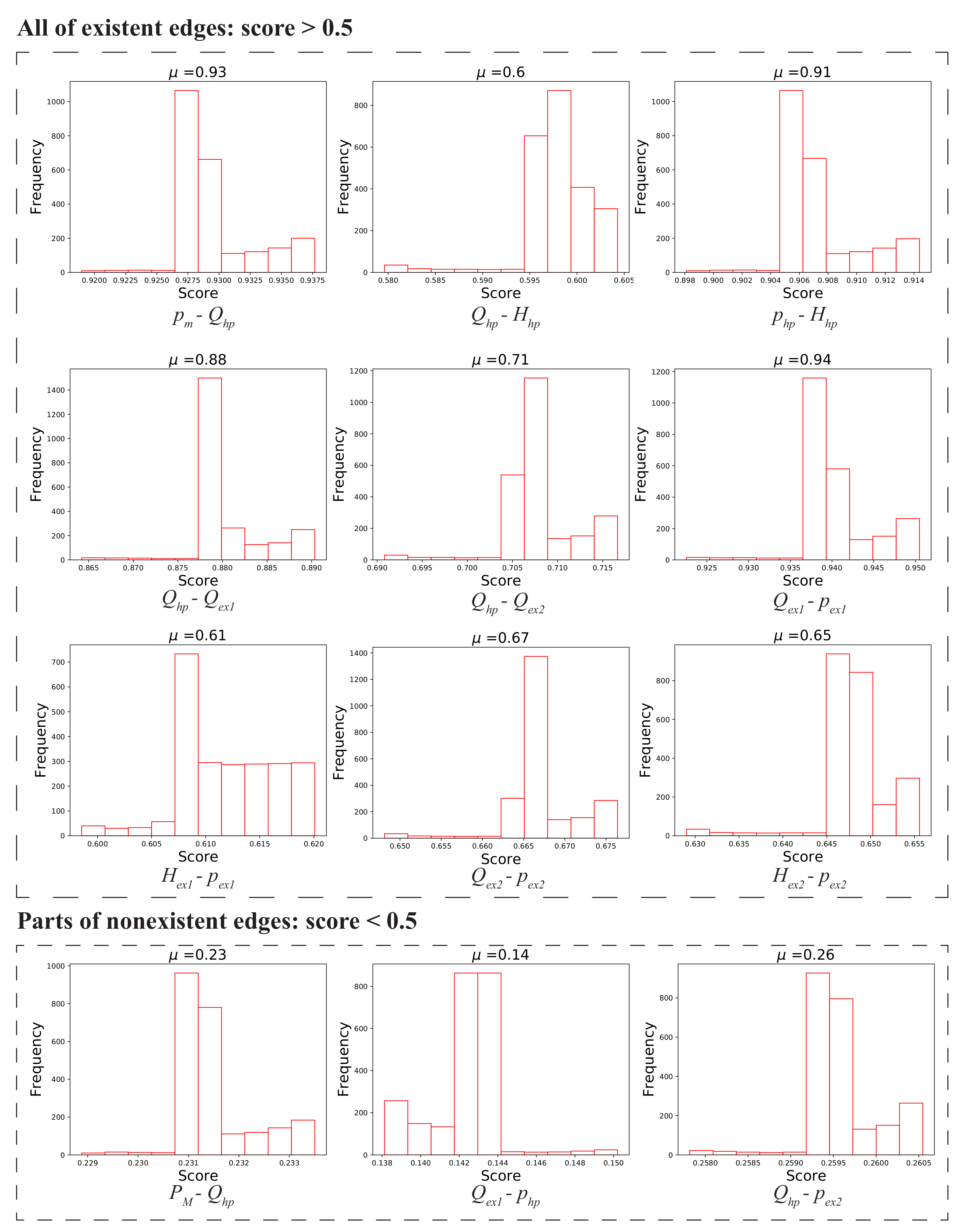
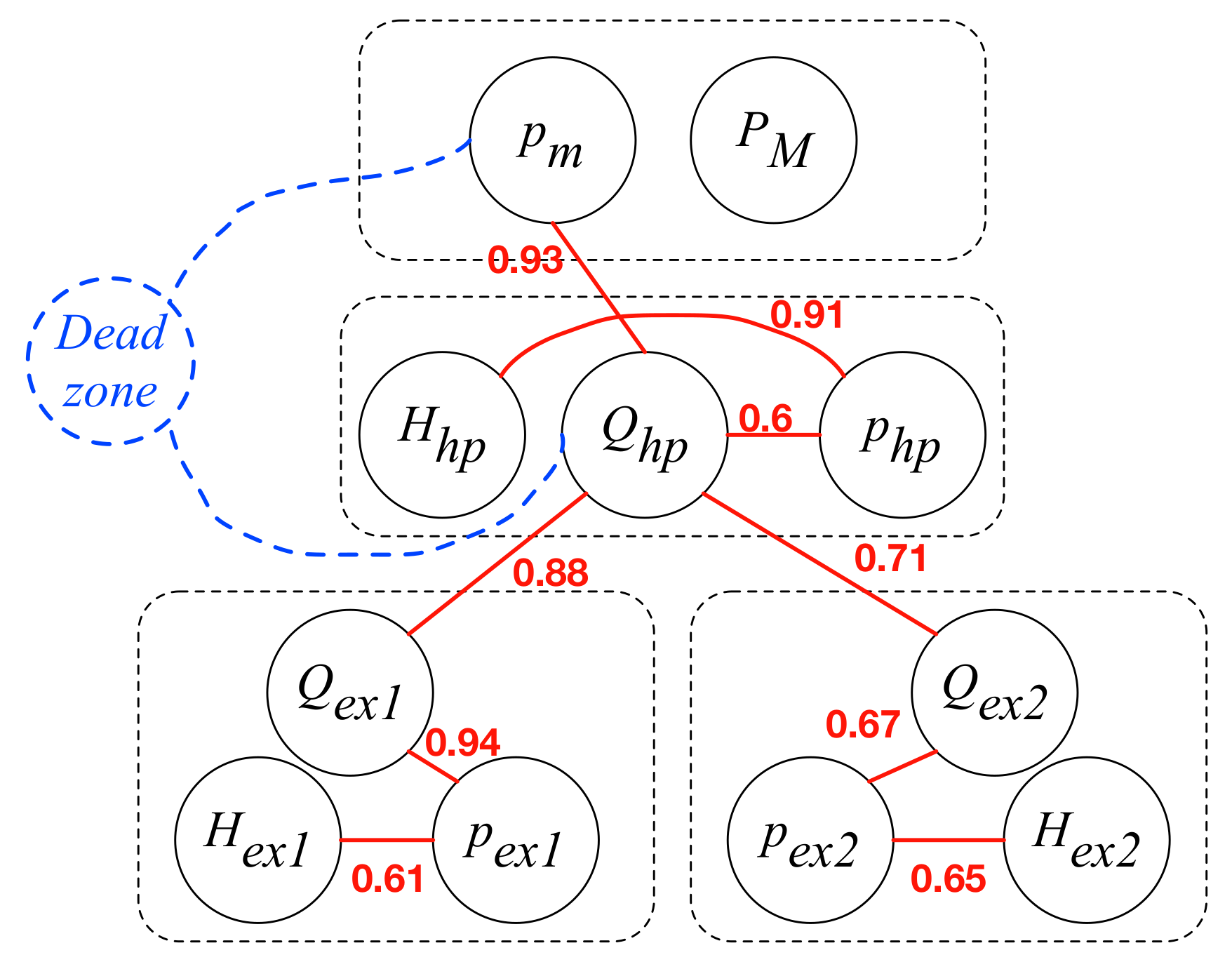
3. Numerical Examples
4. Conclusions Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HP | High Pressure Turbine |
| Mechanical power | |
| P | Pressure |
| Q | Mass flow rate |
| H | Enthalpy |
References
- Vazquez, N.R.; Fernandes, D.P.; Chen, D.H. Control Valve Stiction: Experimentation, Modeling, Model Validation and Detection with Convolution Neural Network. Int. J. Chem. Eng. Appl. 2019, 10, 195–199. [Google Scholar] [CrossRef]
- Amiruddin, A.A.A.M.; Zabiri, H.; Jeremiah, S.S.; Teh, W.K.; Kamaruddin, B. Valve stiction detection through improved pattern recognition using neural networks. Control Eng. Pract. 2019, 90, 63–84. [Google Scholar] [CrossRef]
- Trinh, H.A.; Truong, H.V.A.; Ahn, K.K. Fault Estimation and Fault-Tolerant Control for the Pump-Controlled Electrohydraulic System. Actuators 2020, 9, 132. [Google Scholar] [CrossRef]
- De la Guerra, A.; Jimenez-Mondragon, V.M.; Torres, L.; Escarela-Perez, R.; Olivares-Galvan, J.C. On-Line Open-Phase Fault Detection Method for Switched Reluctance Motors with Bus Current Measurement. Actuators 2020, 9, 117. [Google Scholar] [CrossRef]
- Quattrocchi, G.; Berri, P.C.; Dalla Vedova, M.D.L.; Maggiore, P. Innovative Actuator Fault Identification Based on Back Electromotive Force Reconstruction. Actuators 2020, 9, 50. [Google Scholar] [CrossRef]
- Athanasatos, P.; Costopoulos, T. Proactive fault finding in a 4/3-way direction control valve of a high pressure hydraulic system using the bond graph method with digital simulation. Mech. Mach. Theory 2012, 50, 64–89. [Google Scholar] [CrossRef]
- Li, S.; Huang, J.; Zhang, Z.; Liu, J.; Huang, T.; Chen, H. Similarity-based future common neighbors model for link prediction in complex networks. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Clauset, A.; Moore, C.; Newman, M.E. Hierarchical structure and the prediction of missing links in networks. Nature 2008, 453, 98–101. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Satuluri, V.; Parthasarathy, S. Local probabilistic models for link prediction. In Proceedings of the Seventh IEEE International Conference on Data Mining (ICDM 2007), Omaha, NE, USA, 28–31 October 2007; pp. 322–331. [Google Scholar]
- Lü, L.; Zhou, T. Link prediction in complex networks: A survey. Phys. A Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Pandey, B.; Bhanodia, P.K.; Khamparia, A.; Pandey, D.K. A comprehensive survey of edge prediction in social networks: Techniques, parameters and challenges. Expert Syst. Appl. 2019, 124, 164–181. [Google Scholar] [CrossRef]
- Haghani, S.; Keyvanpour, M.R. A systemic analysis of link prediction in social network. Artif. Intell. Rev. 2019, 52, 1961–1995. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Mohar, B.; Alavi, Y.; Chartrand, G.; Oellermann, O. The Laplacian spectrum of graphs. Graph Theory Comb. Appl. 1991, 2, 12. [Google Scholar]
- Yang, B.; Yih, W.t.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 2787–2795. [Google Scholar]
- Socher, R.; Chen, D.; Manning, C.D.; Ng, A. Reasoning with neural tensor networks for knowledge base completion. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 926–934. [Google Scholar]
- Affandi, M.; Abdullah, I.; Khalid, N.S. MATLAB as a Tool for the Teaching of Rankine Cycle with Simulation of a Simple Steam Power Plant. J. Teknol. 2015, 77. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-J.; Hu, L.-S. Relationship Prediction Based on Graph Model for Steam Turbine Control Valve. Actuators 2021, 10, 91. https://doi.org/10.3390/act10050091
Zhang Y-J, Hu L-S. Relationship Prediction Based on Graph Model for Steam Turbine Control Valve. Actuators. 2021; 10(5):91. https://doi.org/10.3390/act10050091
Chicago/Turabian StyleZhang, Yi-Jing, and Li-Sheng Hu. 2021. "Relationship Prediction Based on Graph Model for Steam Turbine Control Valve" Actuators 10, no. 5: 91. https://doi.org/10.3390/act10050091
APA StyleZhang, Y.-J., & Hu, L.-S. (2021). Relationship Prediction Based on Graph Model for Steam Turbine Control Valve. Actuators, 10(5), 91. https://doi.org/10.3390/act10050091






