A Novel Adaptive Super-Twisting Sliding Mode Control Scheme with Time-Delay Estimation for a Single Ducted-Fan Unmanned Aerial Vehicle
Abstract
1. Introduction
- A novel control scheme (ASTSMC-TDE) is proposed to guarantee better performance and system stability;
- The introduction of the TDE technique, which is the key to cancel out the disturbances the DUAV system is subjected to—the high nonlinearity [32,33,34], parametric uncertainties [35,36], and unknown disturbances. Nonetheless, the TDE technique results in errors since the estimation is delayed by one sample time [37].
- An adaptive sliding mode controller (ASMC) is introduced to suppress the TDE errors. However, when the switching gains of the ASMC become somewhat larger, the “parameter drift” phenomenon occurs [38].
- Hence, a smooth adaptive version of the ASMC with a dead-zone modification technique is introduced to guarantee system robustness.
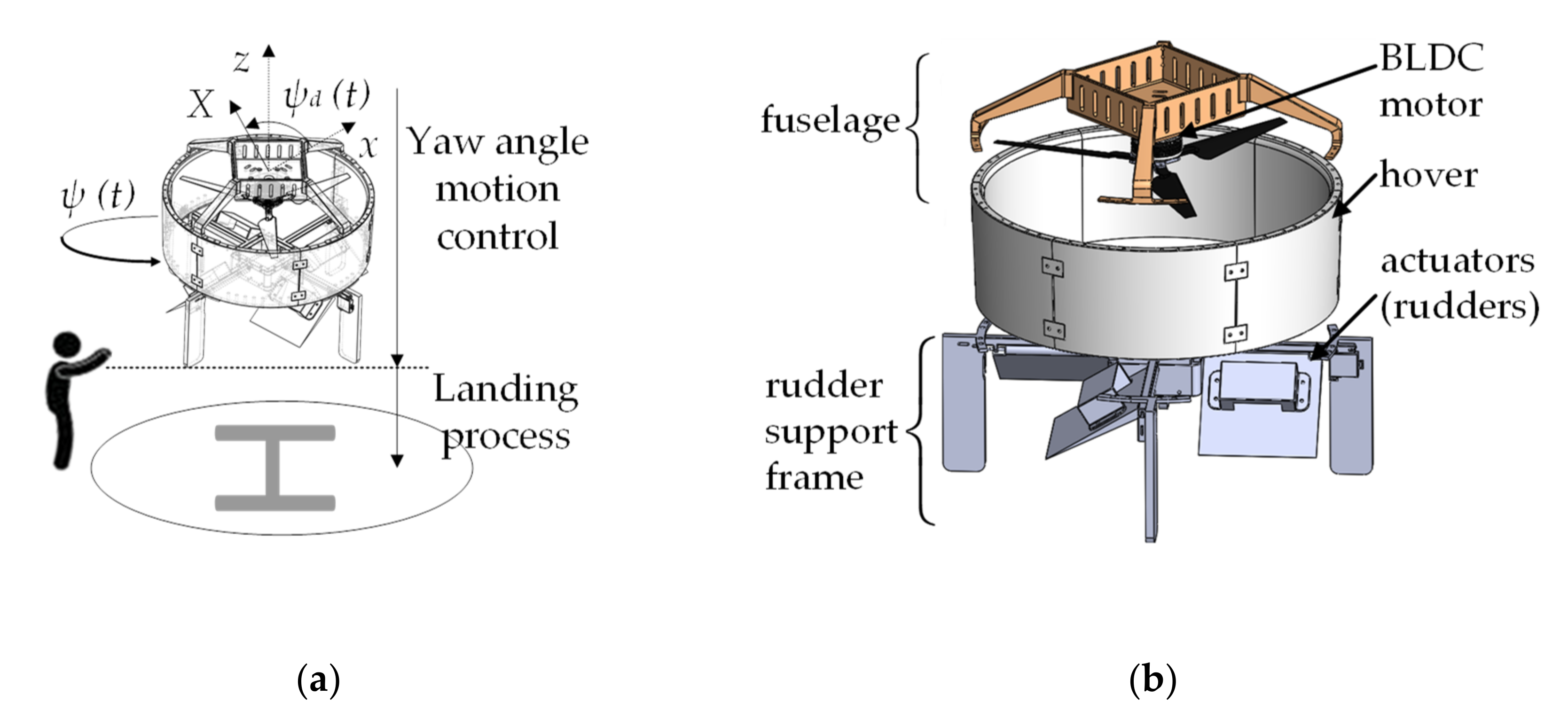
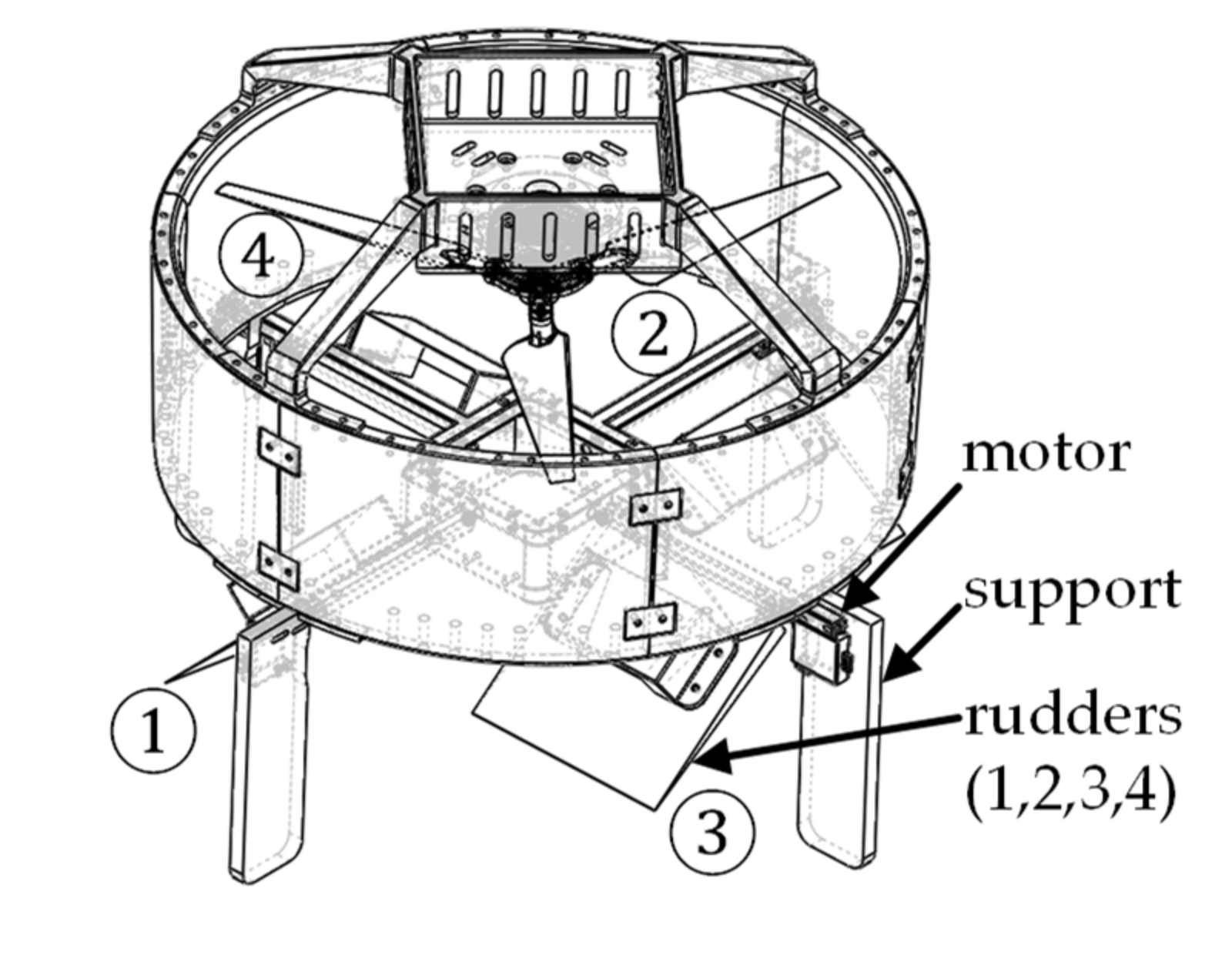
2. Description and Modeling of DUAV System
2.1. Description of the DUAV System
2.2. Modeling of the DUAV System
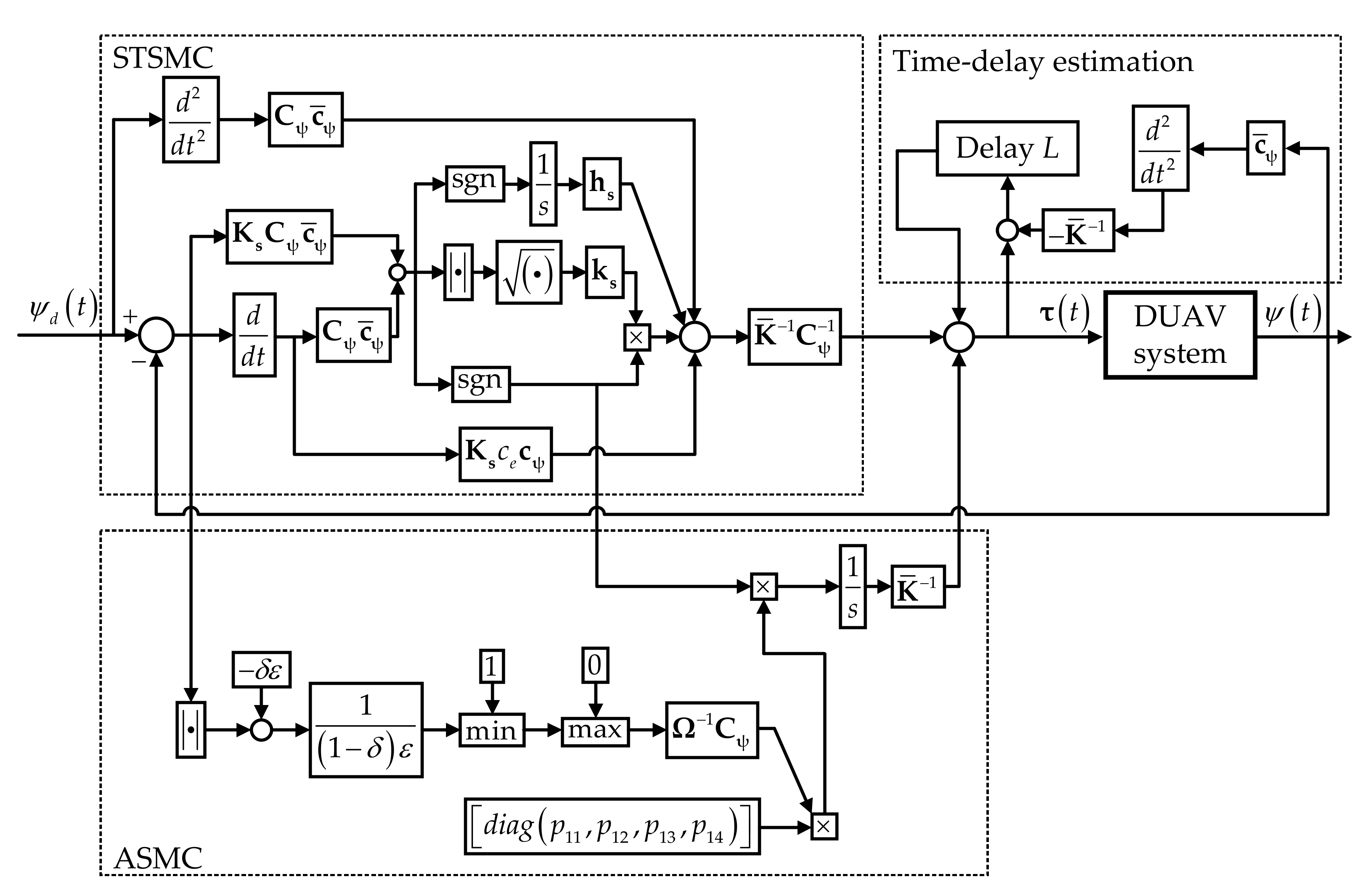
3. Novel Adaptive Super-Twisting Sliding Mode Control with Time-Delay Estimation
3.1. Control System Design
3.2. Stability Analysis
4. Evaluation Methods
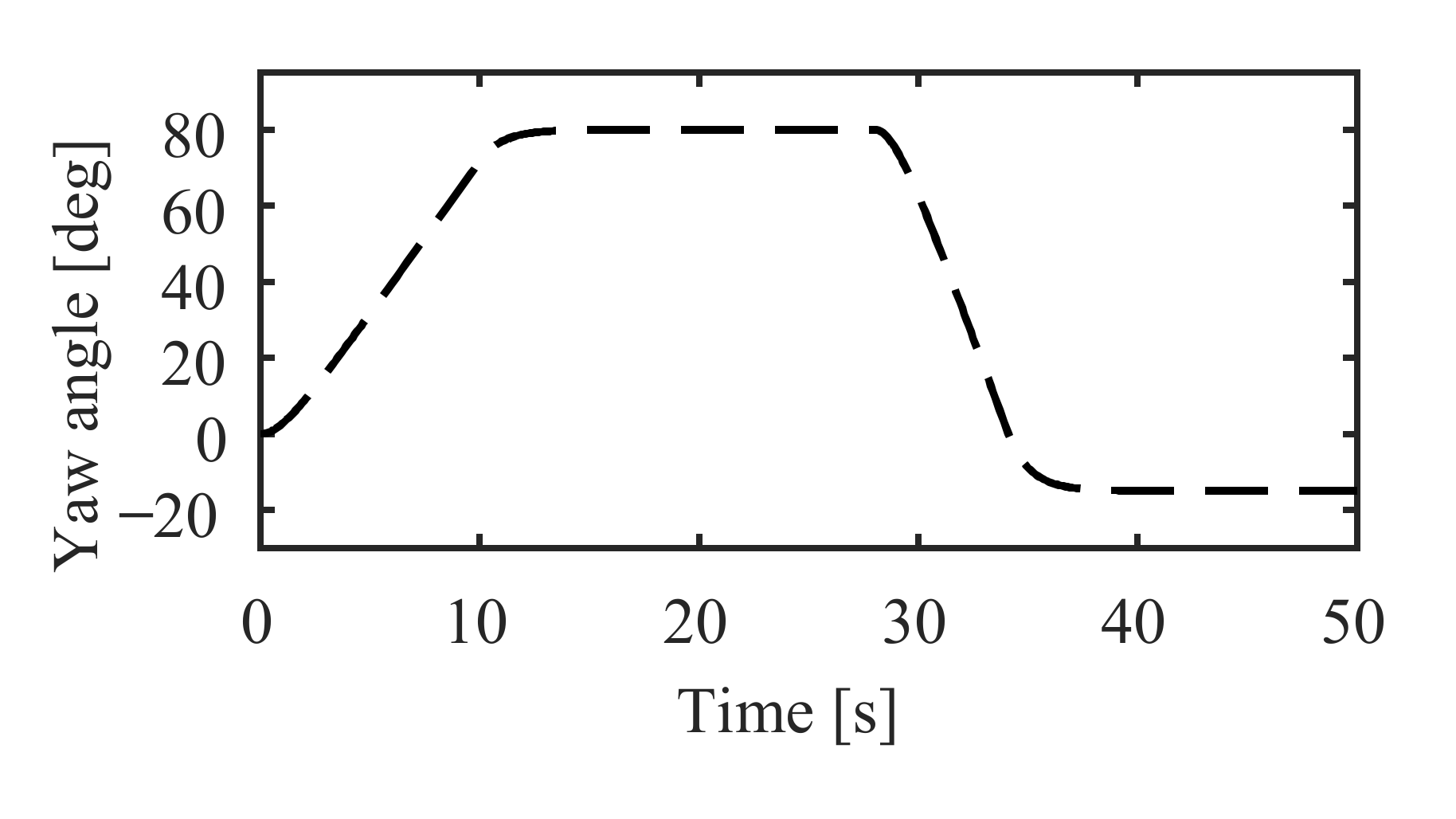
5. Simulation Studies
5.1. Simulation Setup
5.2. Simulation Results
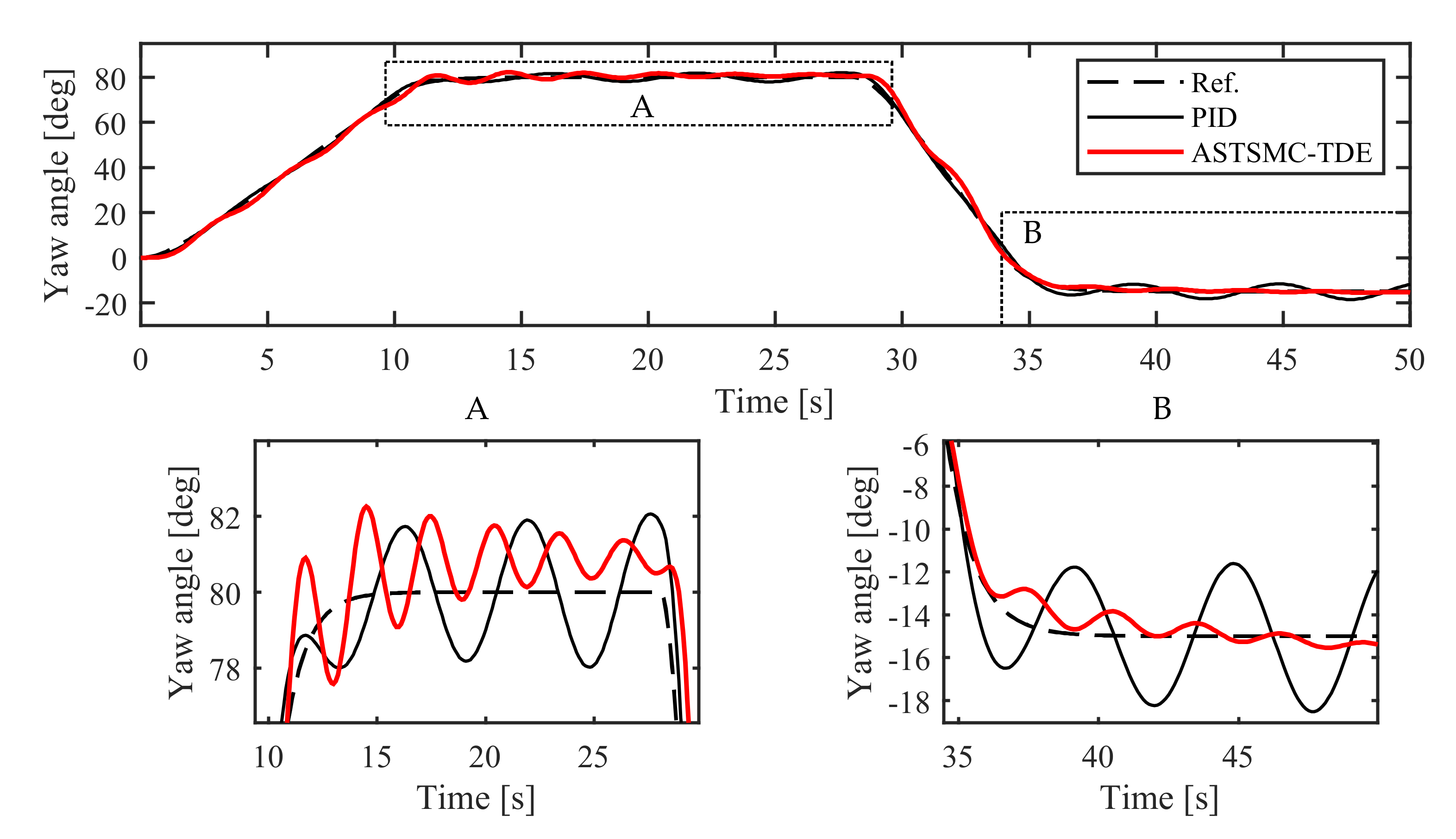
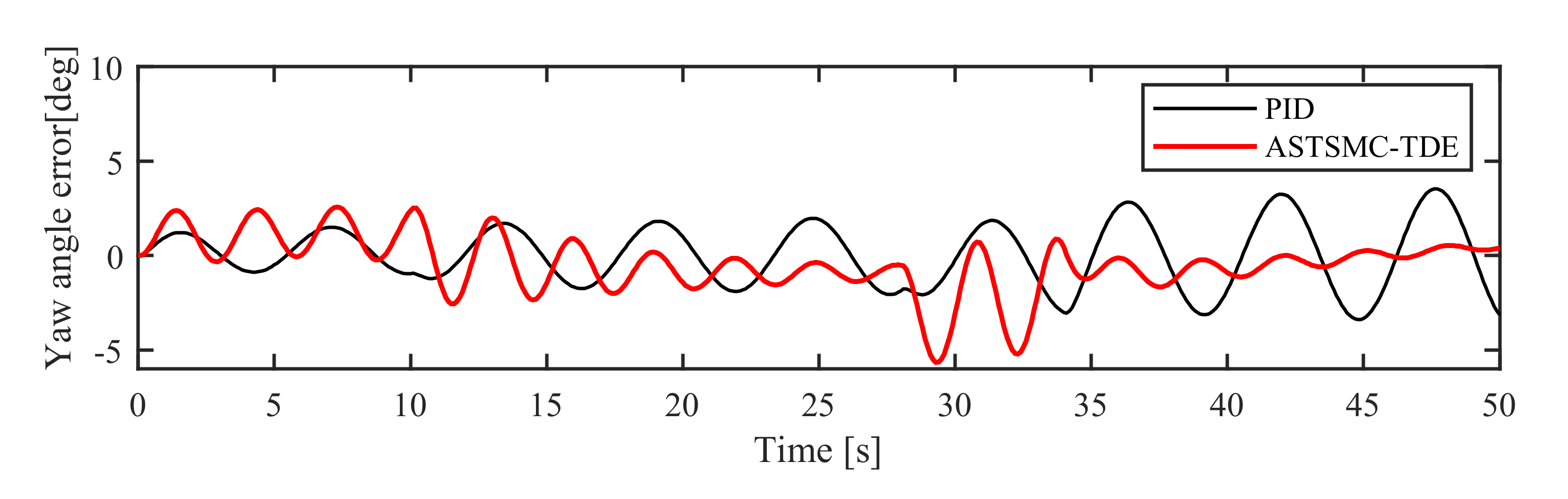
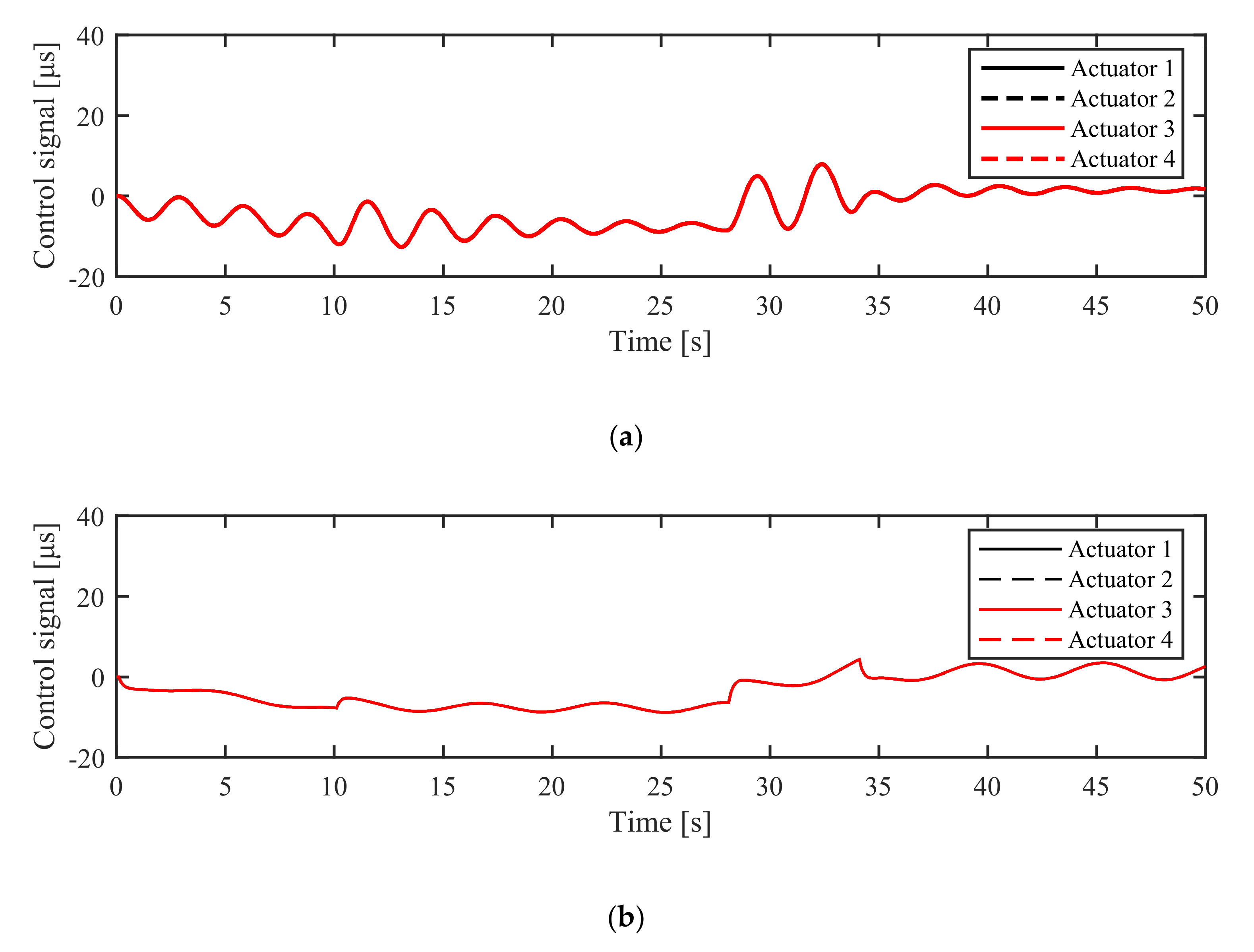
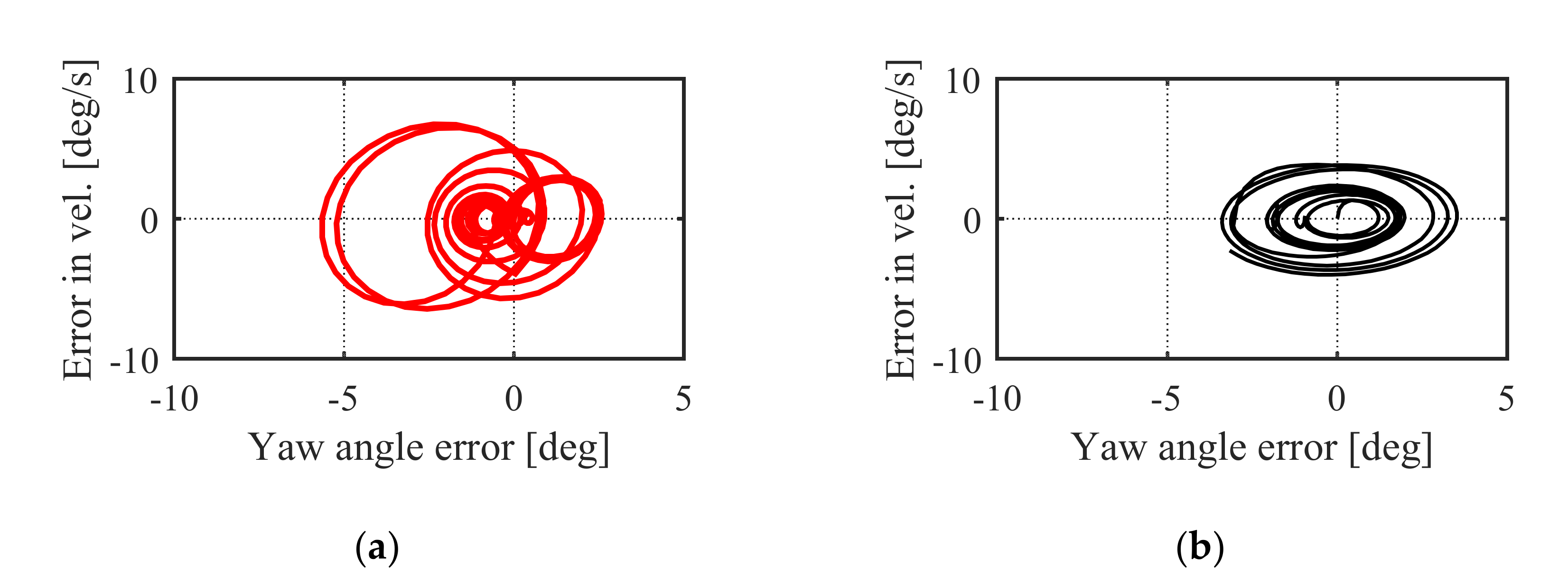
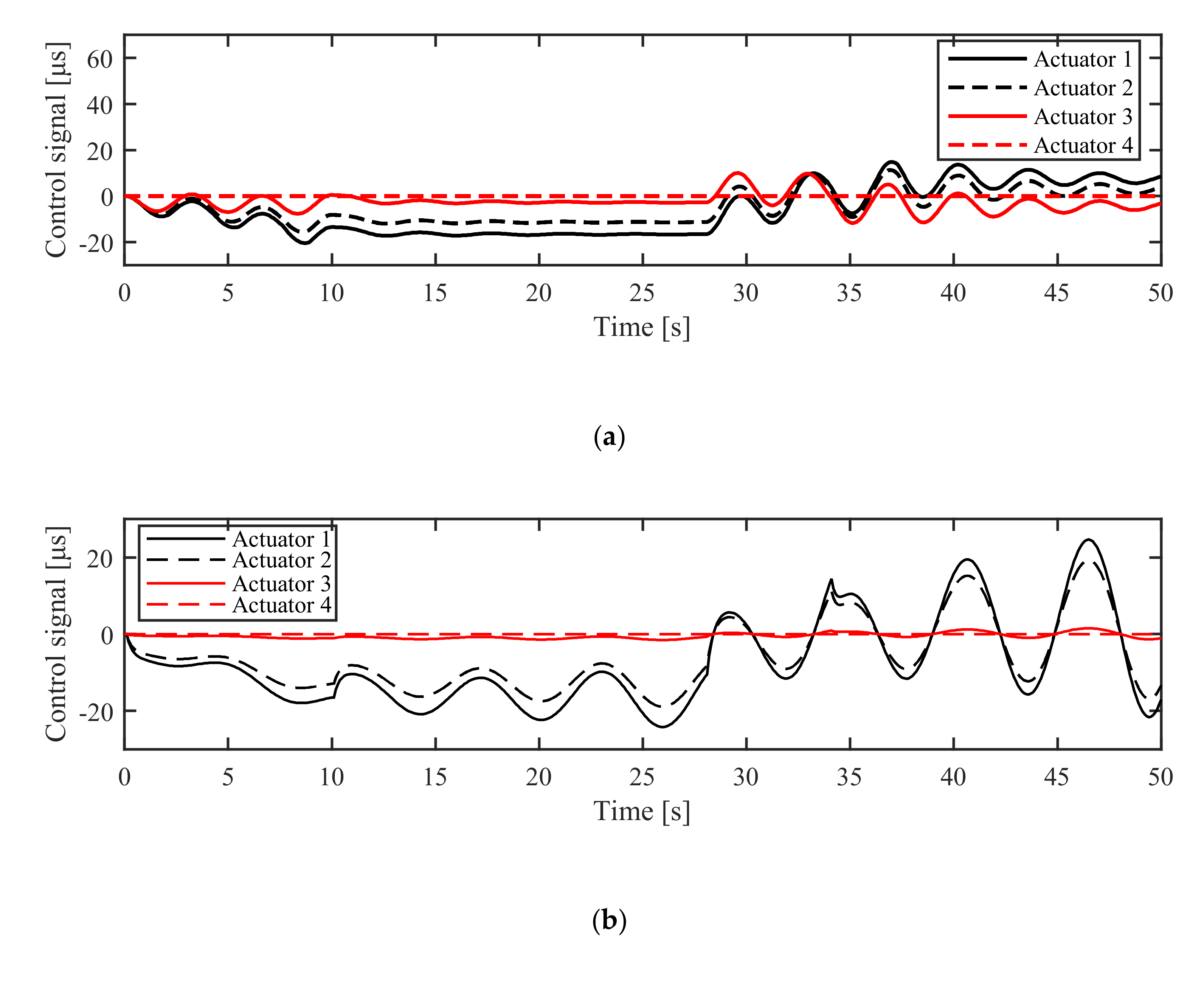
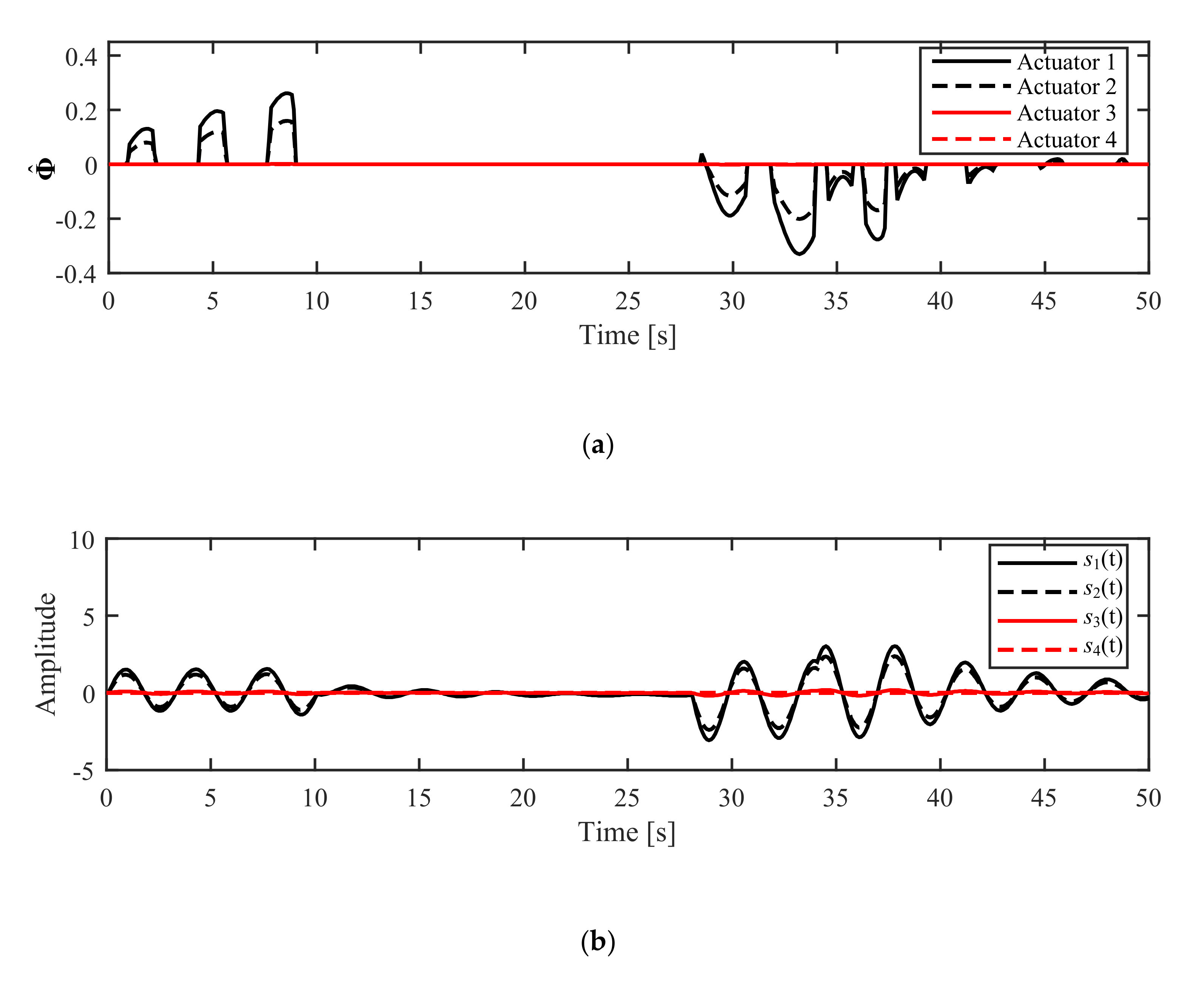
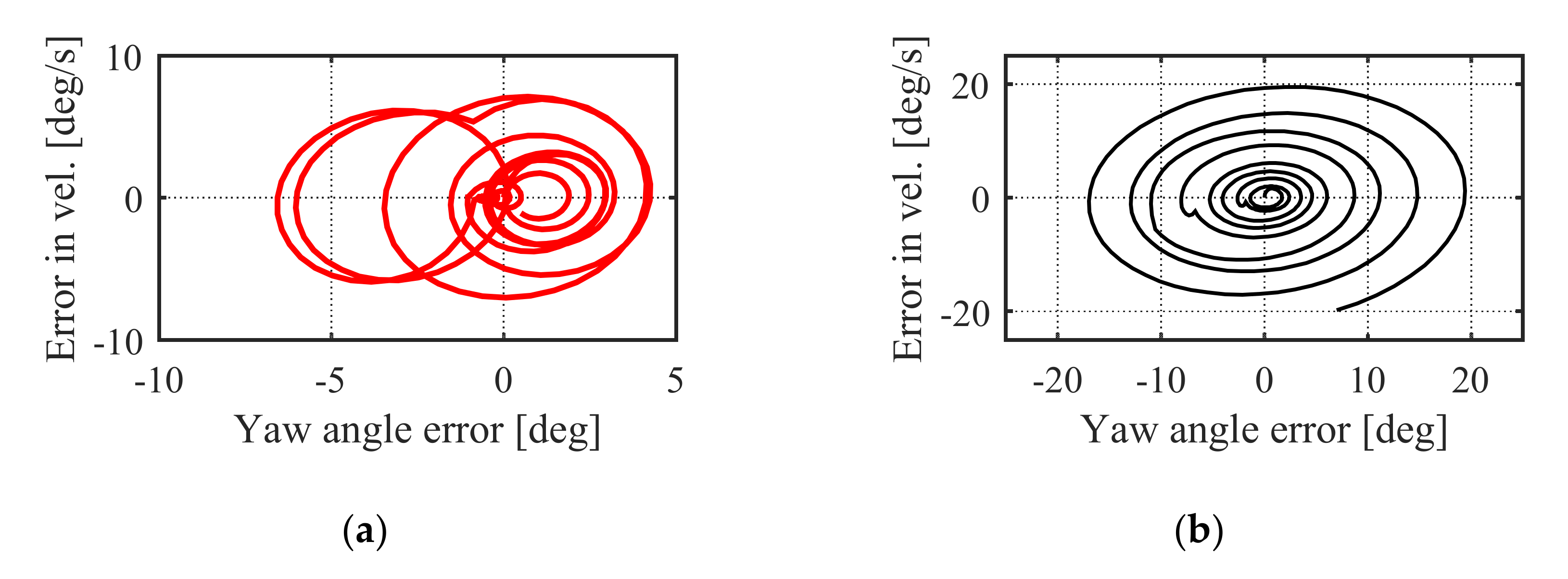
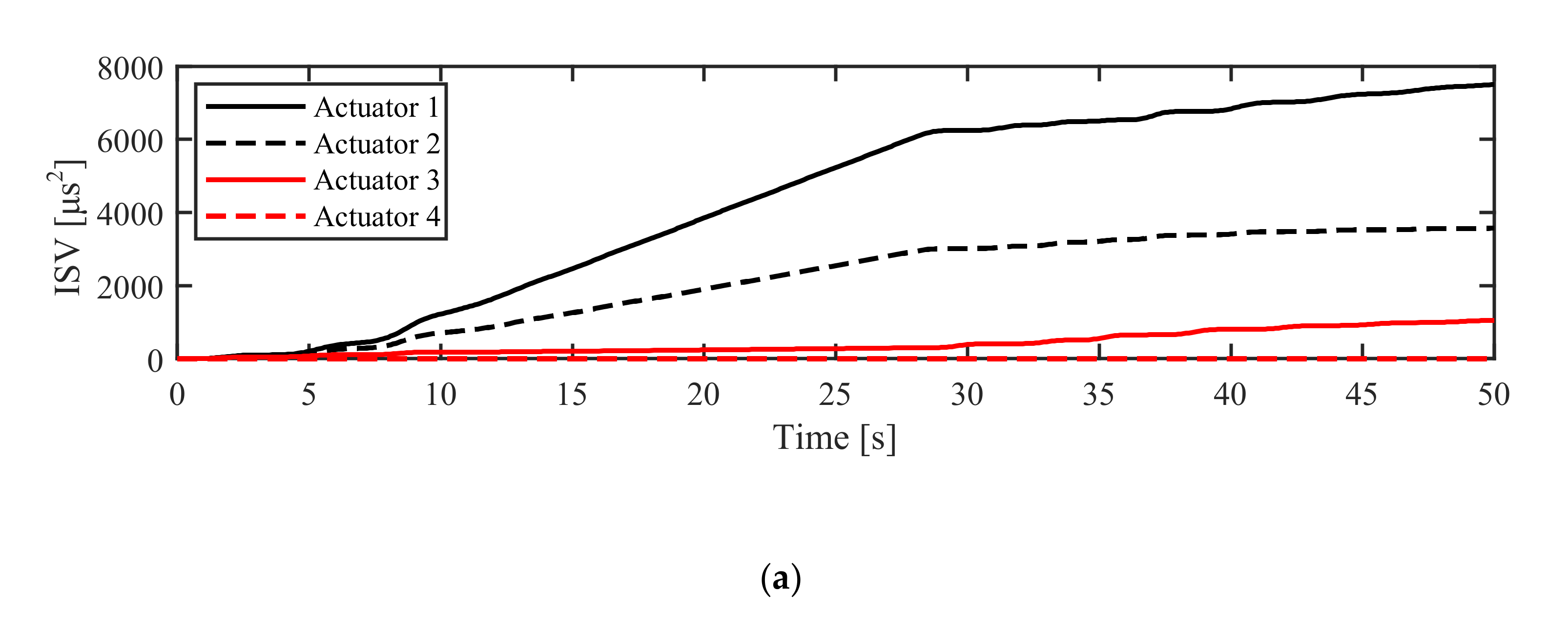
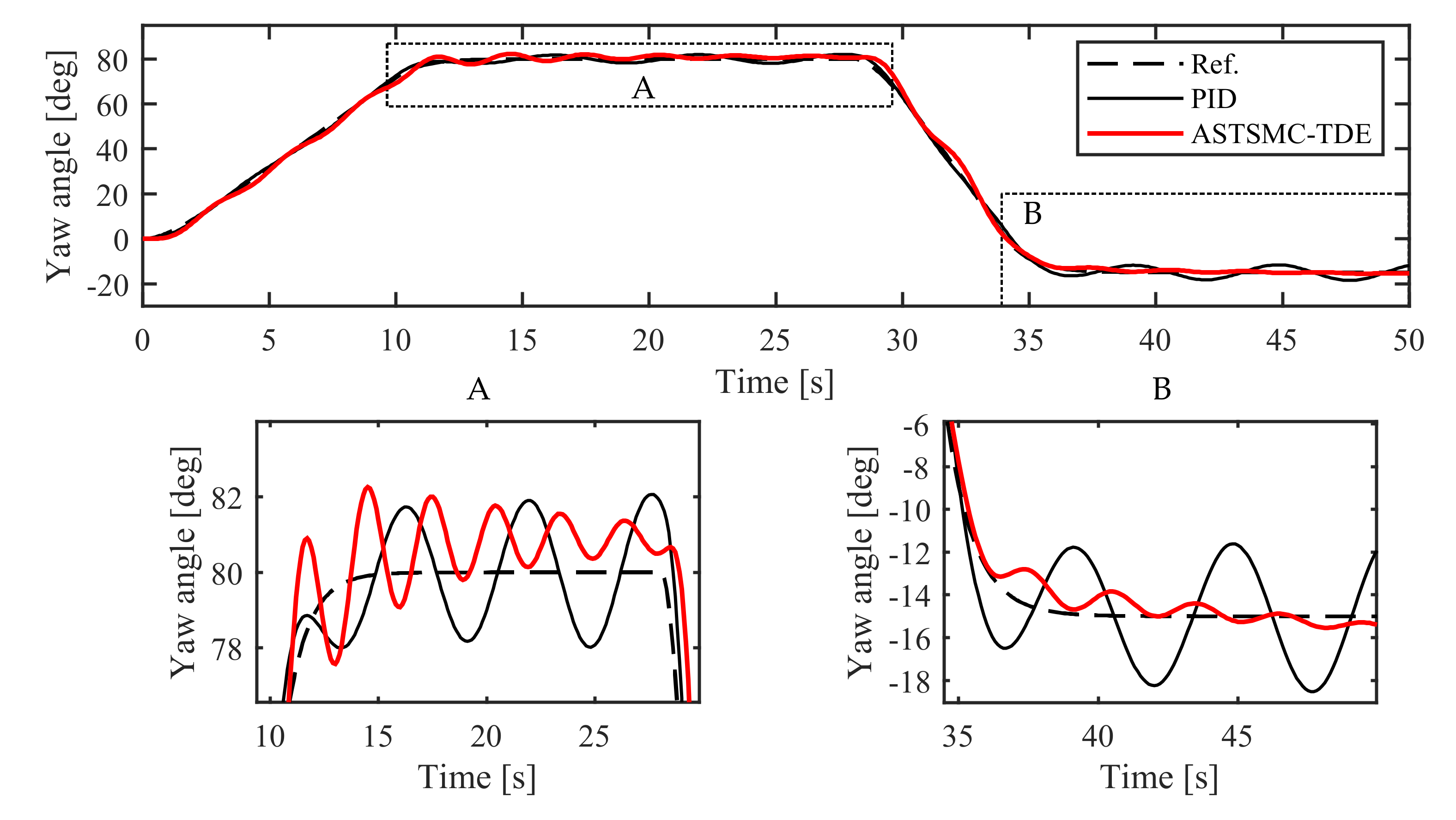
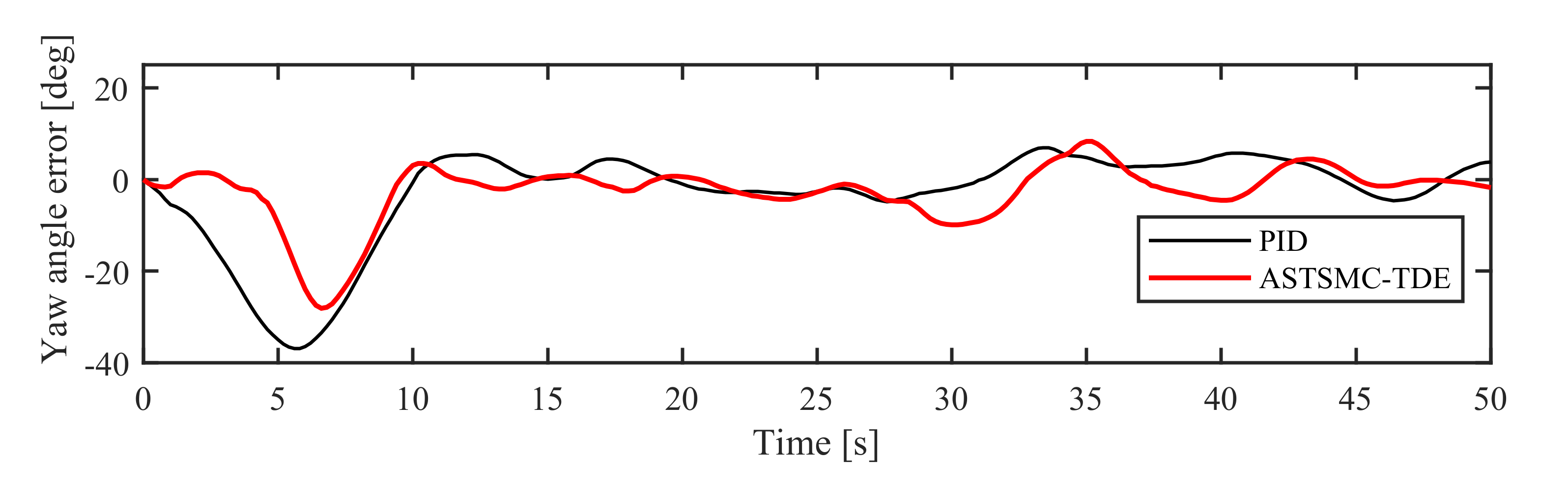
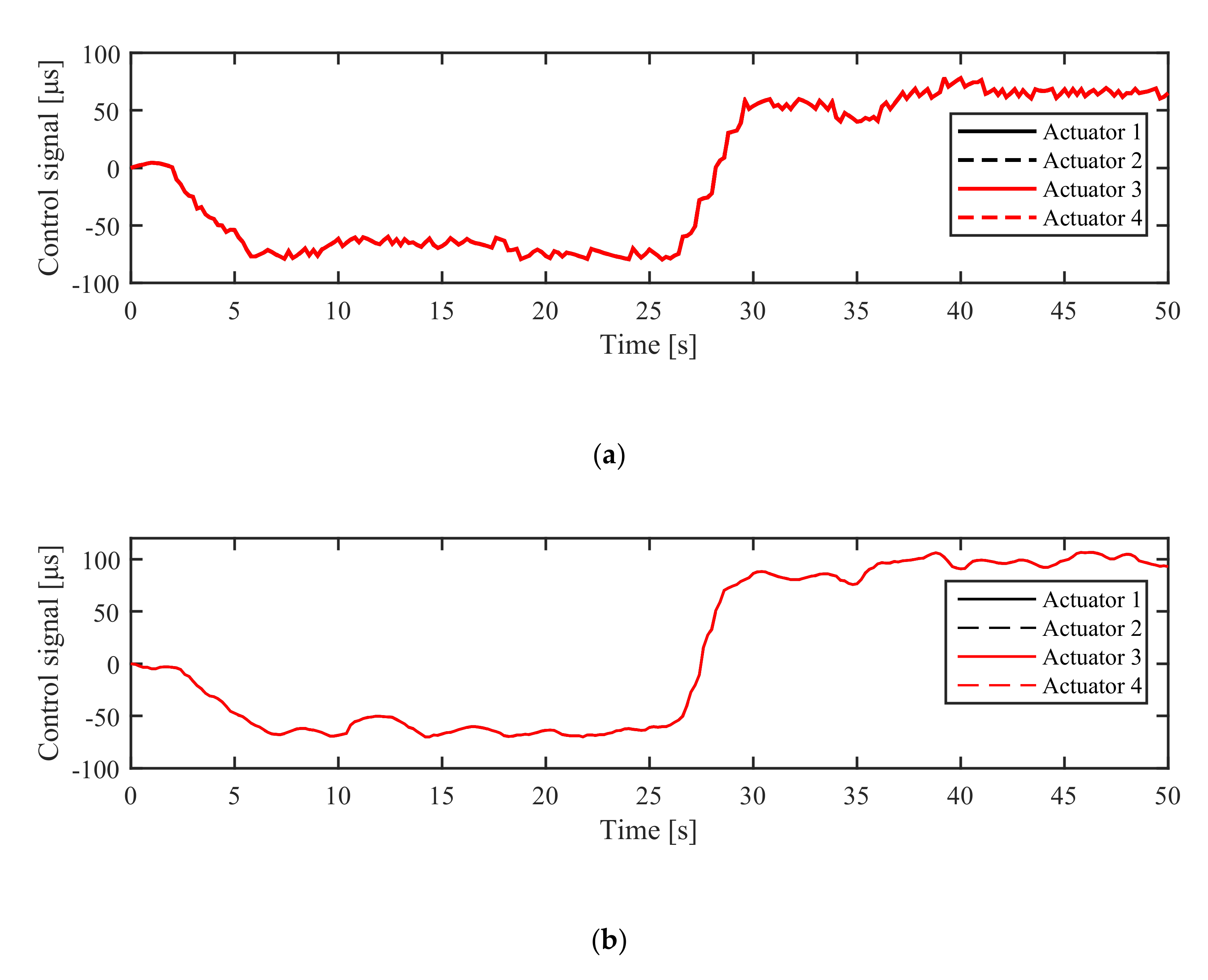
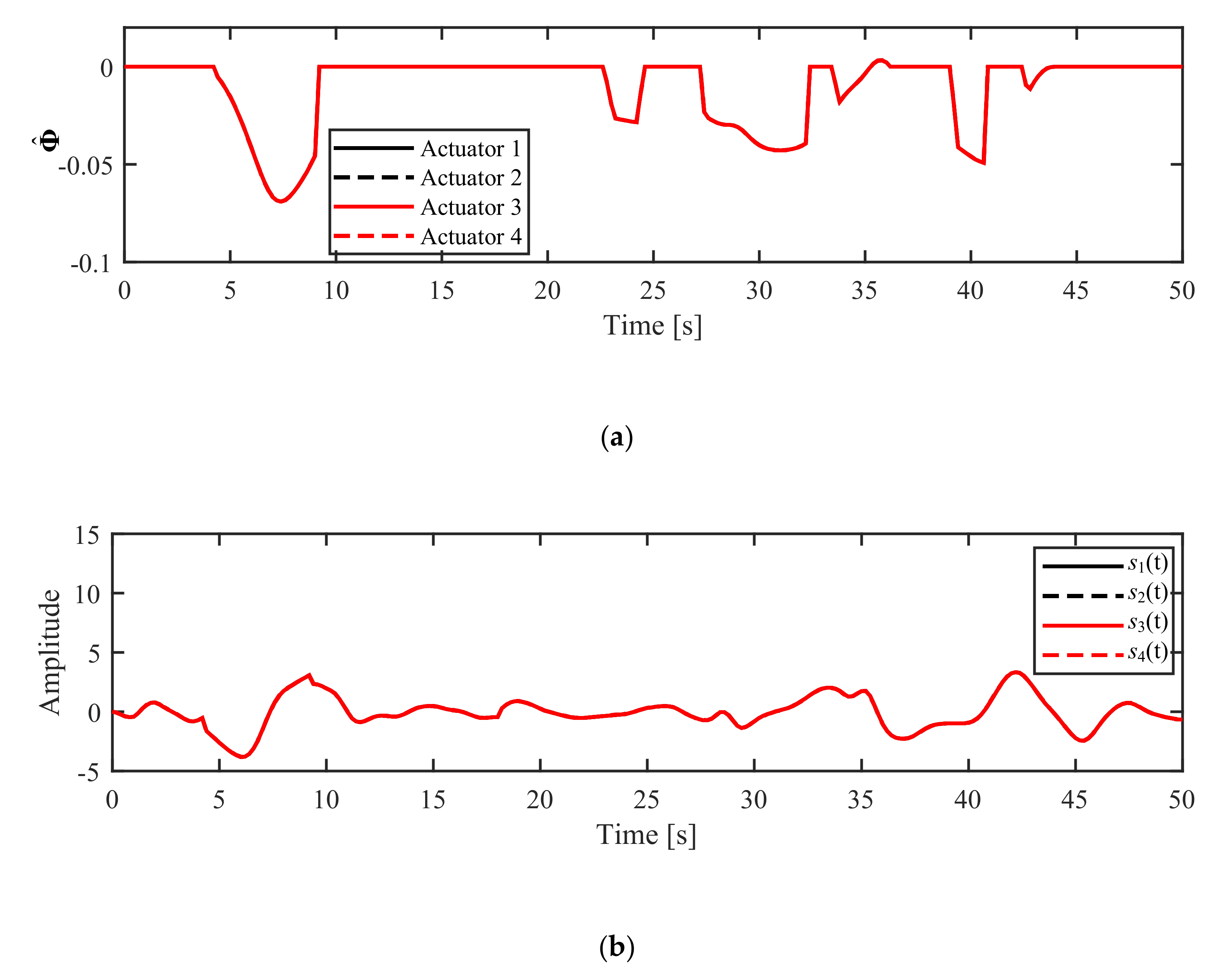
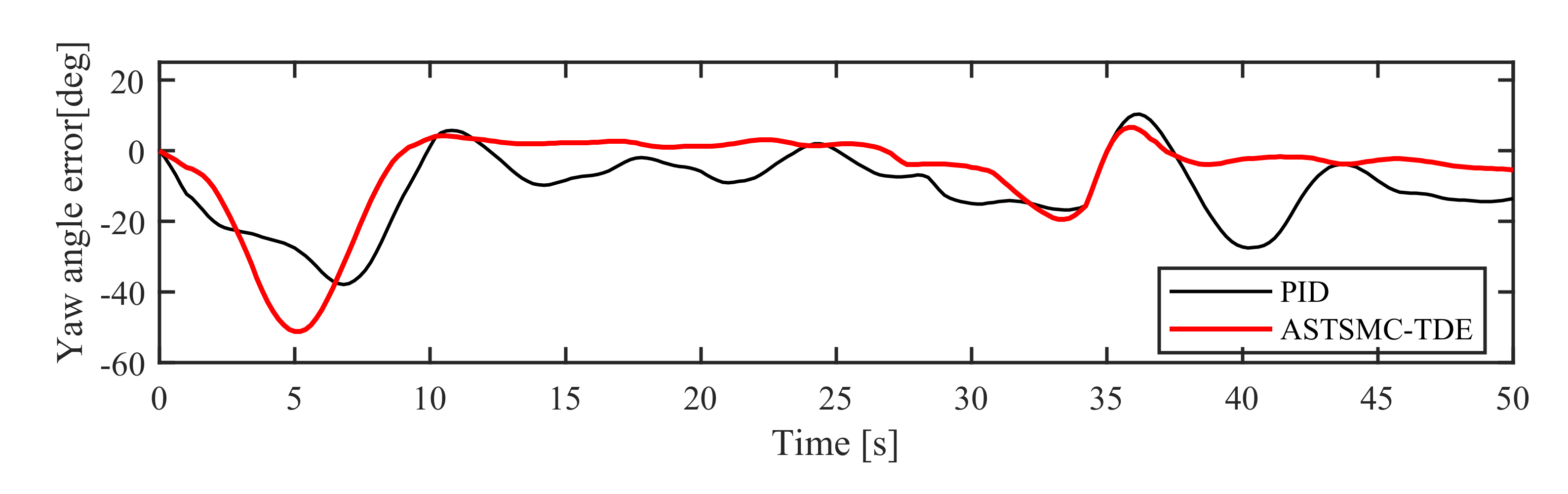
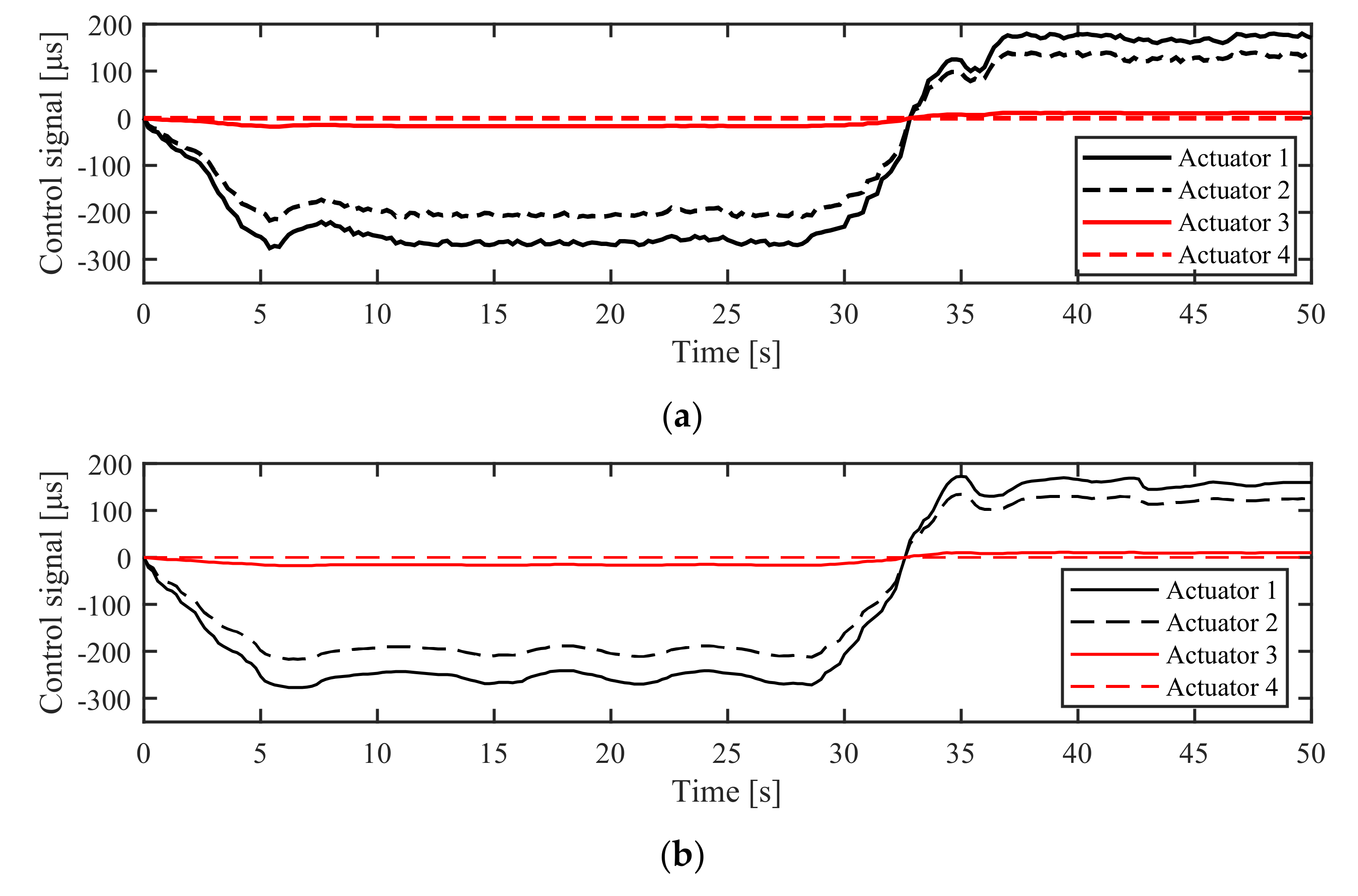
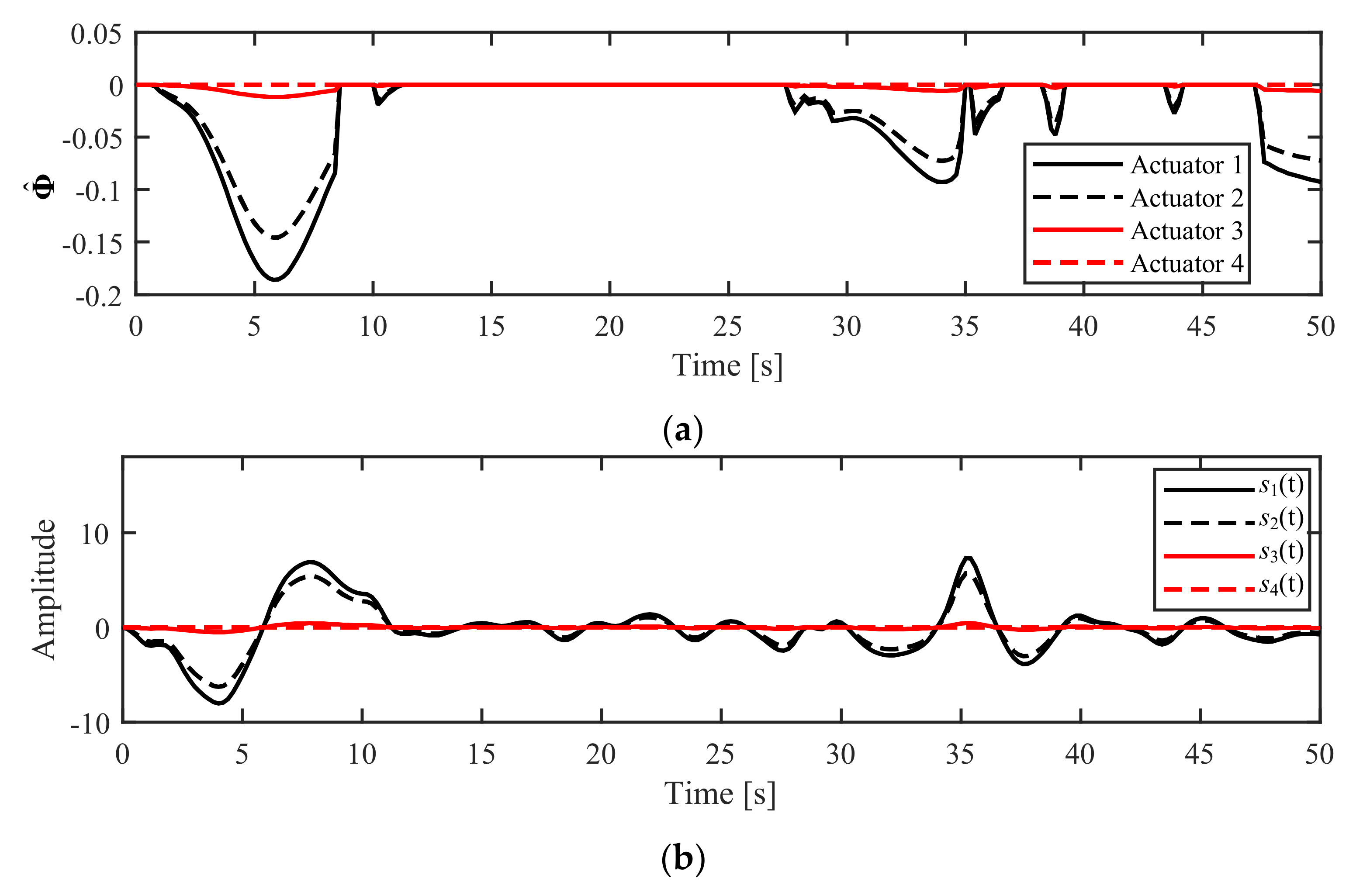
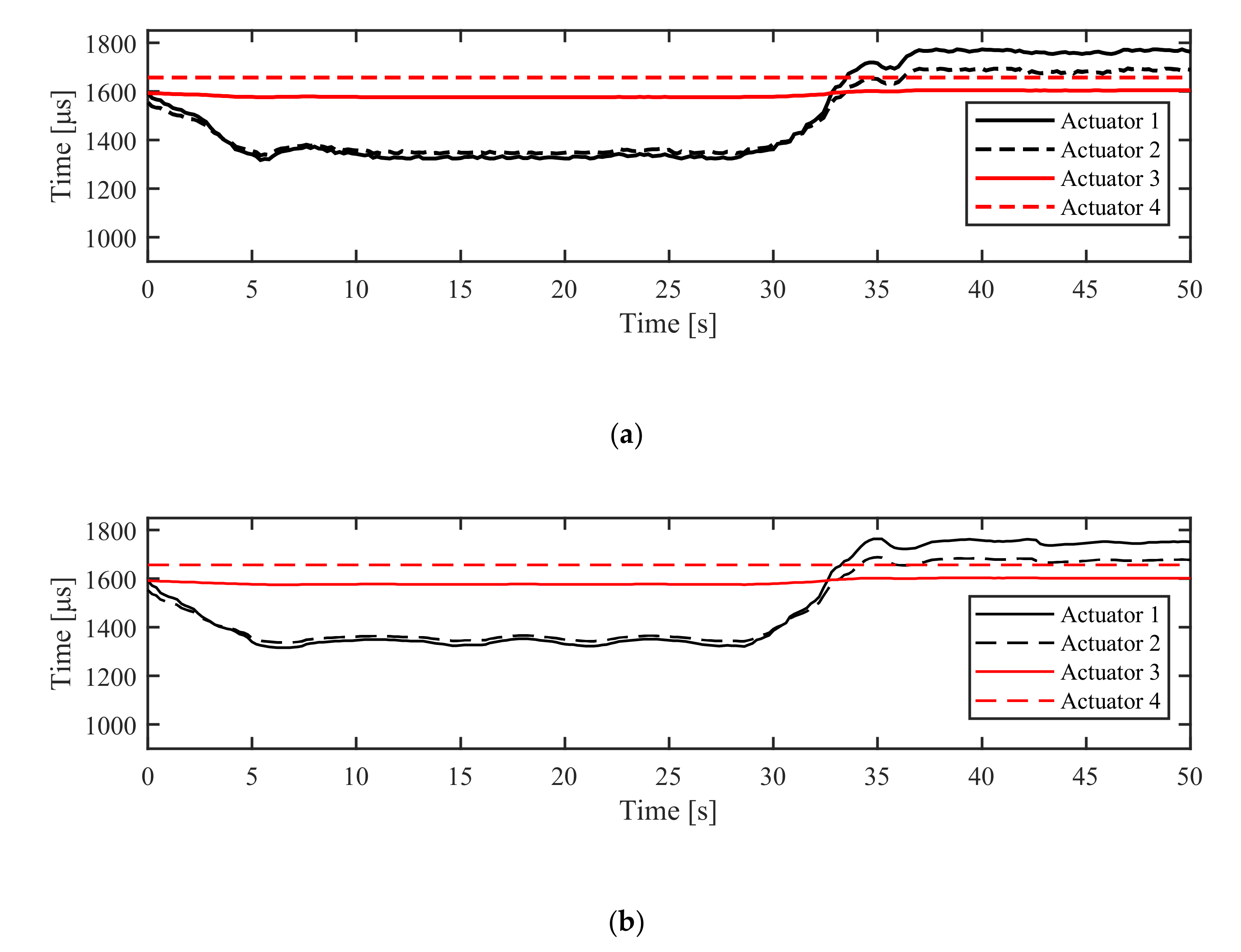
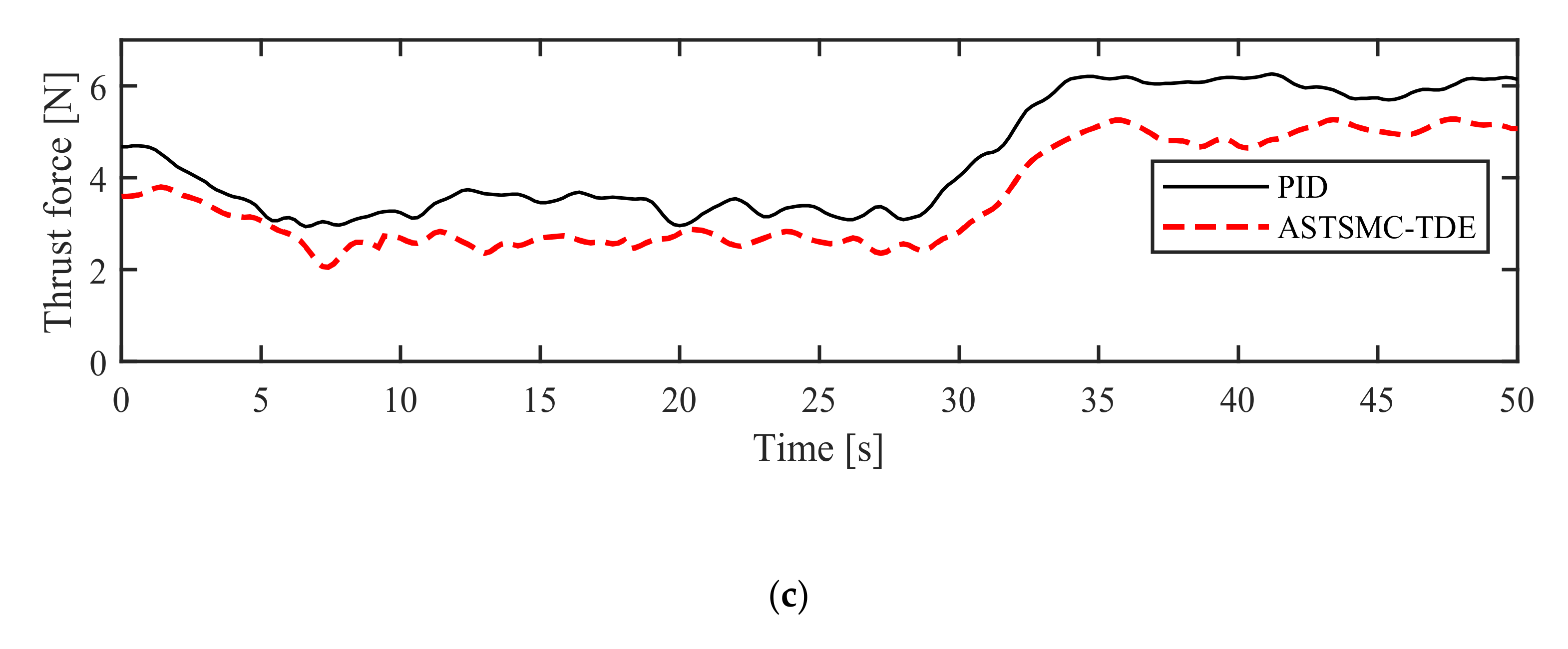
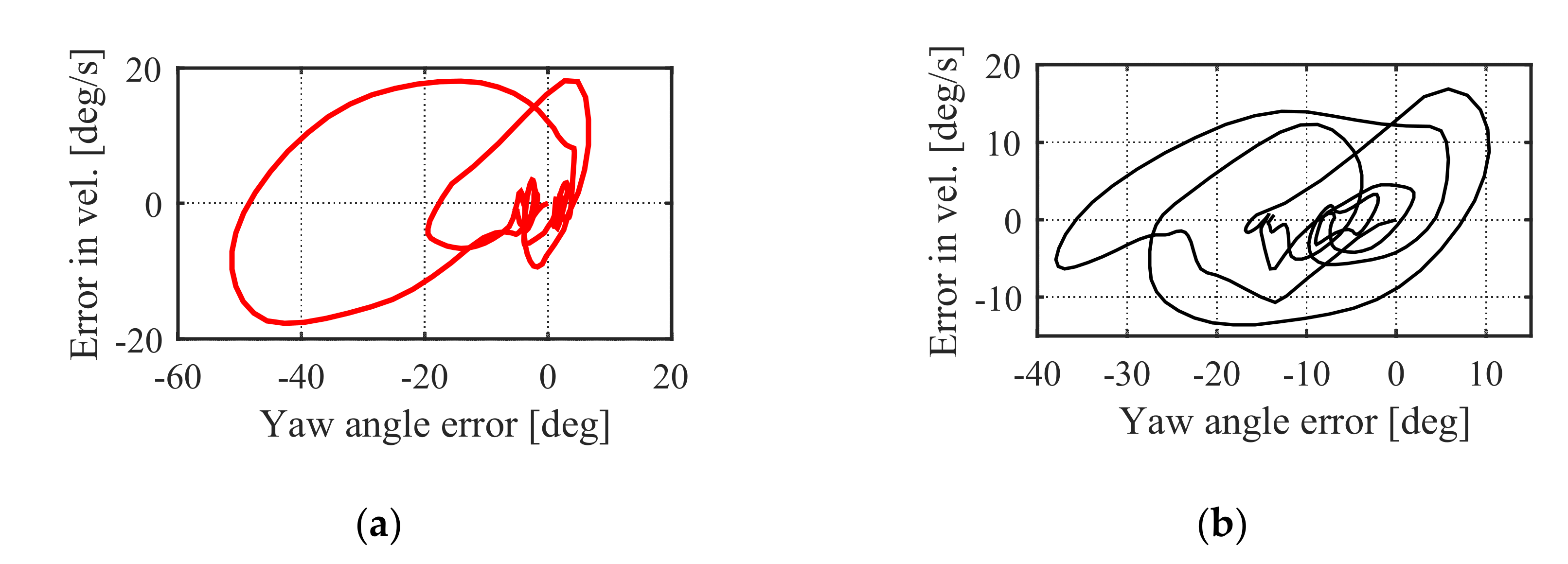
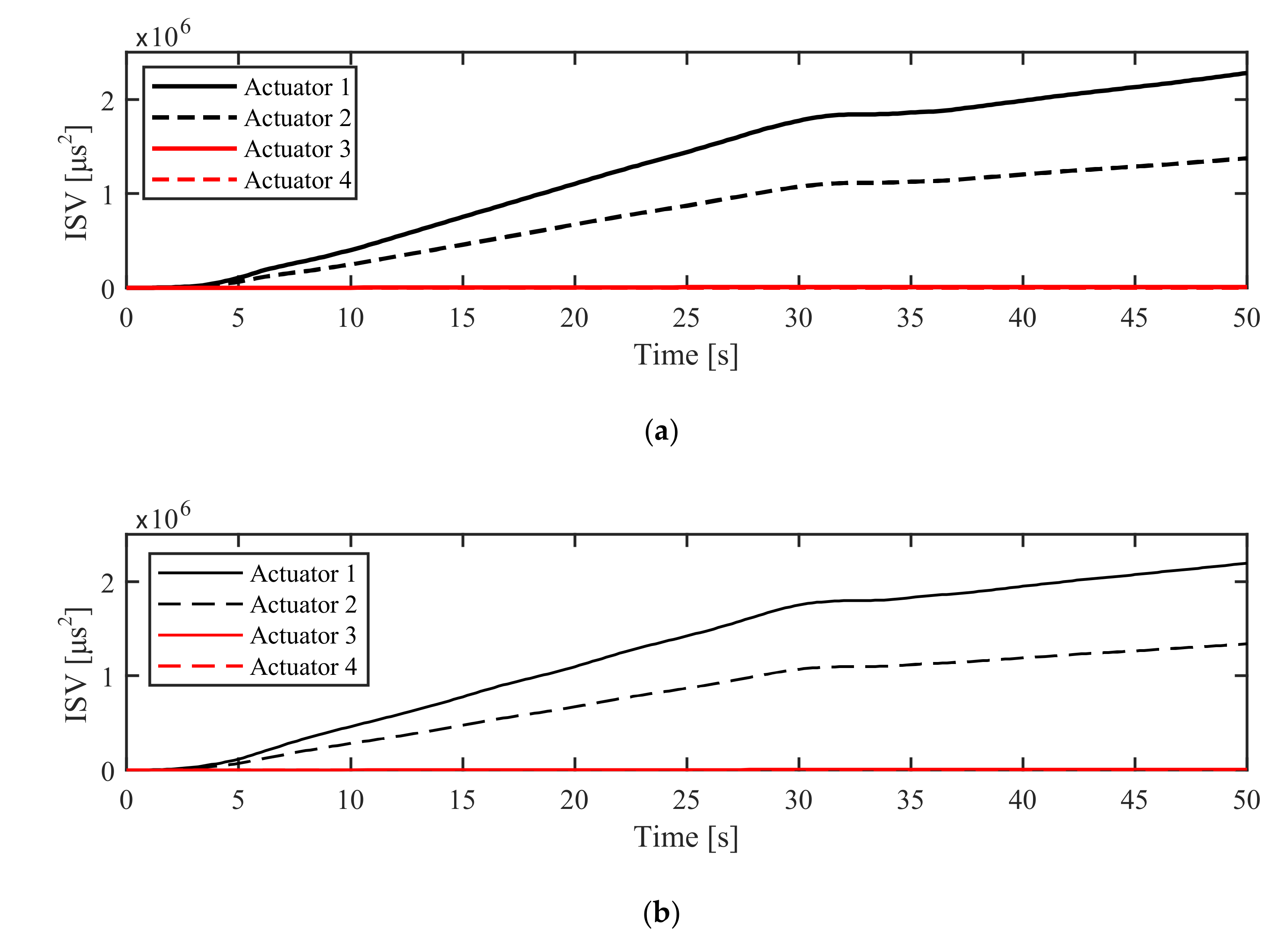
5.2.1. Simulation in NM Mode
5.2.2. Simulation in AM Mode
6. Experimental Studies
6.1. Experiment Setup
6.2. Experiment Results
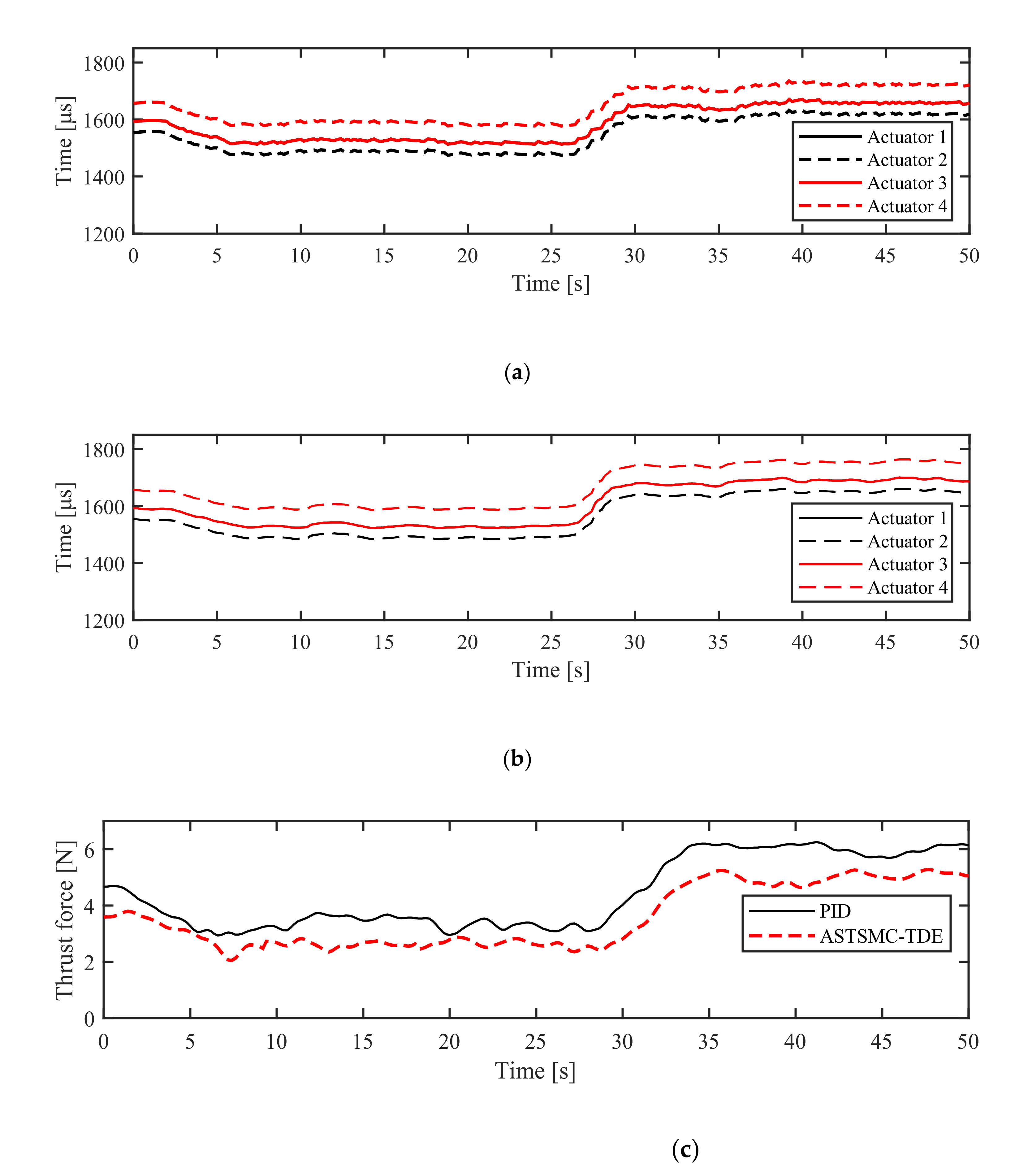
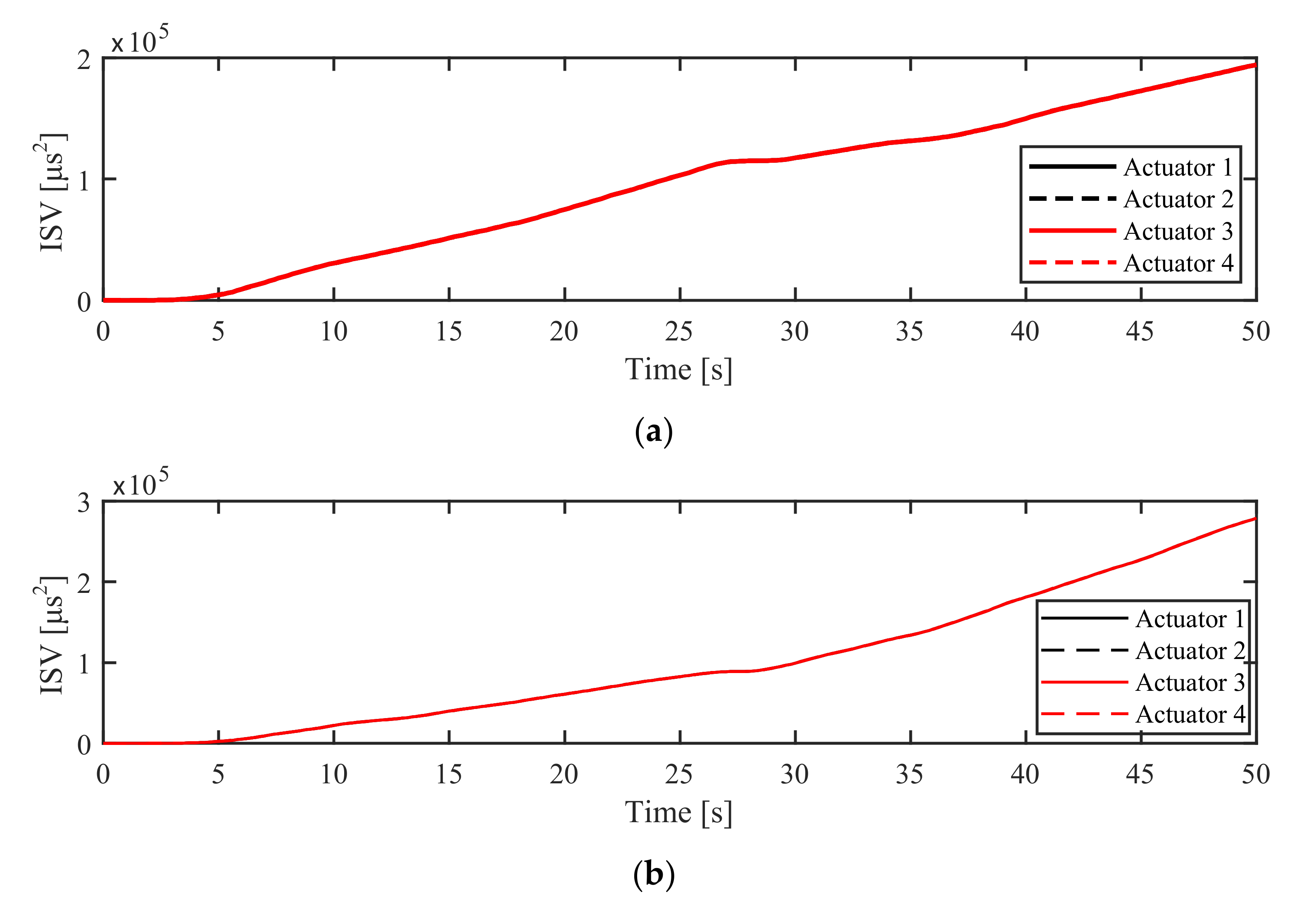
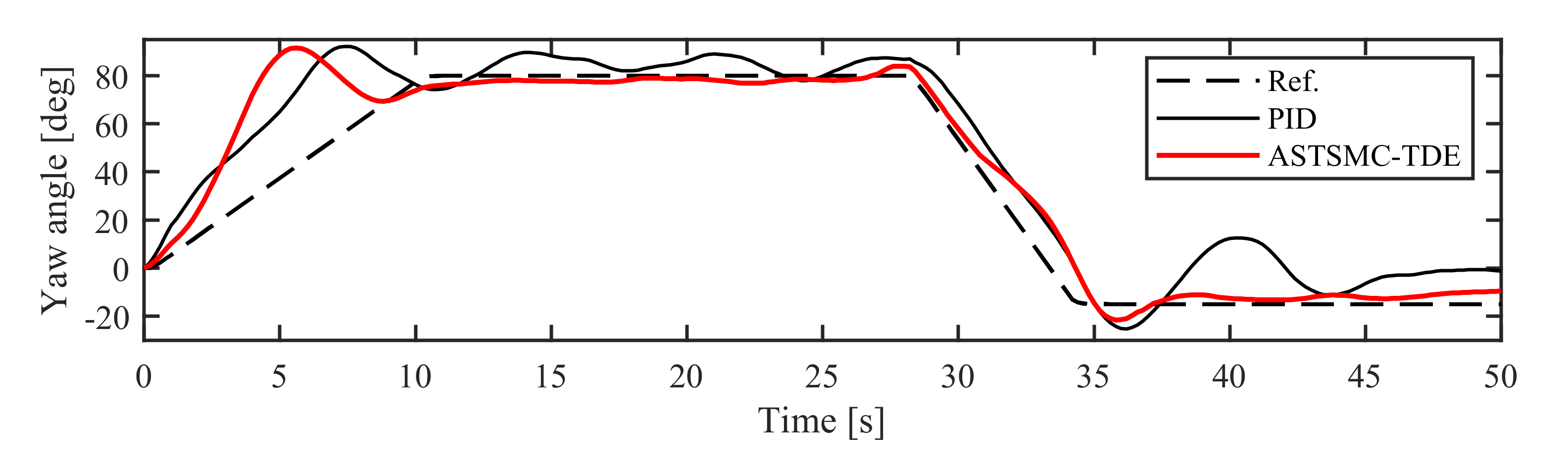
6.2.1. Experiment in NM Mode
6.2.2. Experiment in AM Mode
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Jo, D.; Kwon, Y. Analysis of VTOL UAV Propellant Technology. J. Comput. Commun. 2017, 5, 76–82. [Google Scholar] [CrossRef][Green Version]
- Akturk, A.; Camci, C. Tip Clearance Investigation of a Ducted Fan Used in VTOL Unmanned Aerial Vehicles—Part I: Baseline Experiments and Computational Validation. J. Turbomach. 2014, 136, 0210041–02100410. [Google Scholar] [CrossRef]
- Akturk, A.; Camci, C. Tip Clearance Investigation of a Ducted Fan Used in VTOL Unmanned Aerial Vehicles—Part II: Novel Treatments via Computational Design and Their Experimental Verification. J. Turbomach. 2014, 136, 0210051–02100510. [Google Scholar] [CrossRef]
- Fan, W.; Xiang, C.; Xu, B. Modelling, Attitude Controller Design and Flight Experiments of a Novel Micro-ducted-fan Aircraft. SAGE Adv. Mech. Eng. 2018, 10, 1–16. [Google Scholar] [CrossRef]
- Sheng, S.; Sun, C. A Near-hover Adaptive Attitude Control Strategy of a Ducted Fan Micro Aerial Vehicle with Actuator Dynamics. Appl. Sci. 2015, 5, 666–681. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T.; Pflimlin, J.M. Nonlinear Complementary Filters on the Special Orthogonal Group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B.; Huang, T. CFD Study of an Annular-ducted Fan Lift System for VTOL Aircraft. Aerospace 2015, 2, 555–580. [Google Scholar] [CrossRef]
- Choi, Y.H.; Suk, J.; Hong, S.H. Static Analysis of a Small Scale Ducted-fan UAV Using Wind Tunnel Data. Int. J. Aeronaut. Space Sci. 2012, 13, 34–42. [Google Scholar] [CrossRef]
- Gelhausen, P.; Enns, D. Improving Control System Effectiveness for Ducted Fan VTOL UAVs Operating in Crosswinds. In Proceedings of the 2nd AIAA “Unmanned Unlimited” Systems, Technologies, and Operations—Aerospace, San Diego, CL, USA, 15–18 September 2003. [Google Scholar]
- Naldi, R.; Gentili, L.; Marconi, L.; Sala, A. Design and Experimental Validation of a Nonlinear Control Law for a Ducted-fan Miniature Aerial Vehicle. Elsevier Control Eng. Pract. 2010, 18, 747–760. [Google Scholar] [CrossRef]
- Lipera, L.; Colbourne, J.D.; Rotkowitz, M.C.; Patangui, P. The Micro Craft iSTAR Micro Air Vehicle: Control System Design and Testing. In Proceedings of the American Helicopter Society 57th Annual forum, Washington, DC, USA, 9–11 May 2001. [Google Scholar]
- Ko, A.; Ohanian, O.J.; Gelhausen, P. Ducted Fan UAV Modeling and Simulation in Preliminary Design. In Proceedings of the AIAA Modeling and Simulation Technologies Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar]
- Muehlebach, M.; D’Andrea, R. The Flying Platform–A Testbed for Ducted Fan Actuation and Control Design. Elsevier Mechatron. 2017, 42, 52–68. [Google Scholar] [CrossRef]
- Spurgeon, S.K. Sliding Mode Observers: A survey. Int. J. Syst. Sci. 2008, 39, 751–764. [Google Scholar] [CrossRef]
- Mironova, A.; Mercorelli, P.; Zedler, A. A multi Input Sliding Mode Control for Peltier Cells Using a Cold-hot Sliding Surface. Elsevier J. Frankl. Inst. 2018, 355, 9351–9373. [Google Scholar] [CrossRef]
- Hsia, T.C.; Lasky, T.A.; Guo, Z. Robust Independent Joint Controller Design for Industrial Robot Manipulators. IEEE Trans. Ind. Electron. 1991, 38, 21–25. [Google Scholar] [CrossRef]
- Jin, M.; Kang, S.H.; Chang, P.H.; Lee, J. Robust Control of Robot Manipulators Using Inclusive and Enhanced Time delay Control. IEEE ASME Trans. Mechatron. 2017, 22, 2141–2152. [Google Scholar] [CrossRef]
- Youcef-Toumi, K.; Ito, O. A Time Delay Controller for Systems with Unknown Dynamics. ASME J. Dyn. Syst. Meas. Control 1990, 112, 133–142. [Google Scholar] [CrossRef]
- Hua, M.D.; Hamel, T.; Morin, P.; Samson, C. Introduction to Feedback Control of Underactuated VTOL Vehicles. IEEE Control Syst. Mag. 2013, 33, 61–75. [Google Scholar]
- Filipescu, A.; Mincă, E.; Filipescu, A.; Coandă, H.G. Manufacturing Technology on a Mechatronics Line Assisted by Autonomous Robotic Systems, Robotic Manipulators and Visual Servoing Systems. Actuators 2020, 9, 127. [Google Scholar] [CrossRef]
- Aggumus, H.; Guclu, R. Robust H∞ Control of STMDs Used in Structural Systems by Hardware in the Loop Simulation Method. Actuators 2020, 9, 55. [Google Scholar] [CrossRef]
- Li, B.; Zhou, W.; Sun, J.; Wen, C.Y.; Chen, C.K. Development of Model Predictive Controller for a Tail-sitter VTOL UAV in Hover Flight. Sensors 2018, 18, 2859. [Google Scholar] [CrossRef]
- Enders, E.; Burkhard, G.; Munzinger, N. Analysis of the Influence of Suspension Actuator Limitations on Ride Comfort in Passenger Cars Using Model Predictive Control. Actuators 2020, 9, 77. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control Theory and Applications; International Ltd: Padstow, UK, 1998. [Google Scholar]
- Levant, A. Sliding Order and Sliding Accuracy in Sliding Mode Control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Barth, A.; Reichhartinger, M.; Reger, J.; Horn, M.; Wulff, K. Lyapunov-design for a Super-twisting Sliding-mode Controller Using the Certainty-equivalence Principle. Elsevier Int. Fed. Autom. Control 2015, 48, 860–865. [Google Scholar] [CrossRef]
- Tran, M.T.; Kim, K.H.; Park, H.C.; Kim, Y.B. A Study on an Adaptive Super-twisting Sliding Mode Control Design with Perturbation Estimation. J. Power Syst. Eng. 2020, 24, 53–63. [Google Scholar] [CrossRef]
- Huynh, T.; Kim, Y.B. A Study on Gimbal Motion Control System Design Based on Super-twisting Control Method. J. Korean Soc. Precis. Eng. 2021, 38, 115–122. [Google Scholar] [CrossRef]
- Humaidi, A.J.; Hasan, A.F. Particle Swarm Optimization-based Adaptive Super-twisting Sliding Mode Control Design for 2-degree-of-freedom Helicopter. Sage Meas. Control 2019, 52, 1–17. [Google Scholar] [CrossRef]
- Morioka, H.; Wada, K.; Sabanovic, A. Sliding Mode Control Based on the Time Delay Estimation. IEEE Workshop Var. Struct. Syst. 1996, 102–107. [Google Scholar]
- Tseng, M.L.; Chen, M.S. Chattering Reduction of Sliding Mode Control by Low-pass Filtering the Control Signal. Asian J. Control 2010, 12, 392–398. [Google Scholar] [CrossRef]
- Cho, G.R.; Chang, P.H.; Park, S.H.; Jin, M. Robust Tracking Under Nonlinear Friction Using Time-delay Control with Internal Model. IEEE Trans. Control Syst. Technol. 2009, 17, 1406–1414. [Google Scholar]
- Lee, J.; Chang, P.H.; Jin, M. An Adaptive Gain Dynamics for Time Delay Control Improves Accuracy and Robustness to Significant Payload Changes for Robots. IEEE Trans. Ind. Electron. 2020, 67, 3076–3085. [Google Scholar] [CrossRef]
- Jin, M.; Jin, Y.; Chang, P.H.; Choi, C. High-accuracy Trajectory Tracking of Industrial Robot Manipulators Using Time Delay Estimation and Terminal Sliding Mode. In Proceedings of the 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009. [Google Scholar]
- Youcef-Toumi, K.; Ito, O. A Time Delay Controller for Systems with Unknown Dynamics. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988. [Google Scholar]
- Zheng, G.; Polyakov, A.; Levant, A. Delay Estimation via Sliding Mode for Nonlinear Time-delay System. Elsevier Autom. 2018, 2018, 266–273. [Google Scholar] [CrossRef]
- Baek, J.; Jin, M.; Han, S. A New Adaptive Sliding-mode Control Scheme for Application to Robot Manipulators. IEEE Trans. Ind. Electron. 2016, 63, 3628–3637. [Google Scholar] [CrossRef]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control with Aerospace Applications; Springer: London, UK, 2013. [Google Scholar]
- Cook, M.V. Flight Dynamics Principles, 2nd ed.; Elsevier Ltd.: Cambridge, MA, USA, 2007. [Google Scholar]
- Caro-Lopera, F.J.; Leiva, V.; Balakrishnan, N. Connection Between the Hadamard and Matrix Products with an Application to Matrix-variate Birnbaum–Saunders Distributions. Elsevier J. Multivar. Anal. 2012, 104, 126–139. [Google Scholar] [CrossRef]
- Styan, G.P.H. Hadamard Products and Multivariate Statistical Analysis. Linear Algebra Its Appl. 1973, 6, 217–240. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. Strict Lyapunov Functions for the Super-Twisting Algorithm. IEEE Trans. Autom. Control 2012, 57, 1035–1040. [Google Scholar] [CrossRef]


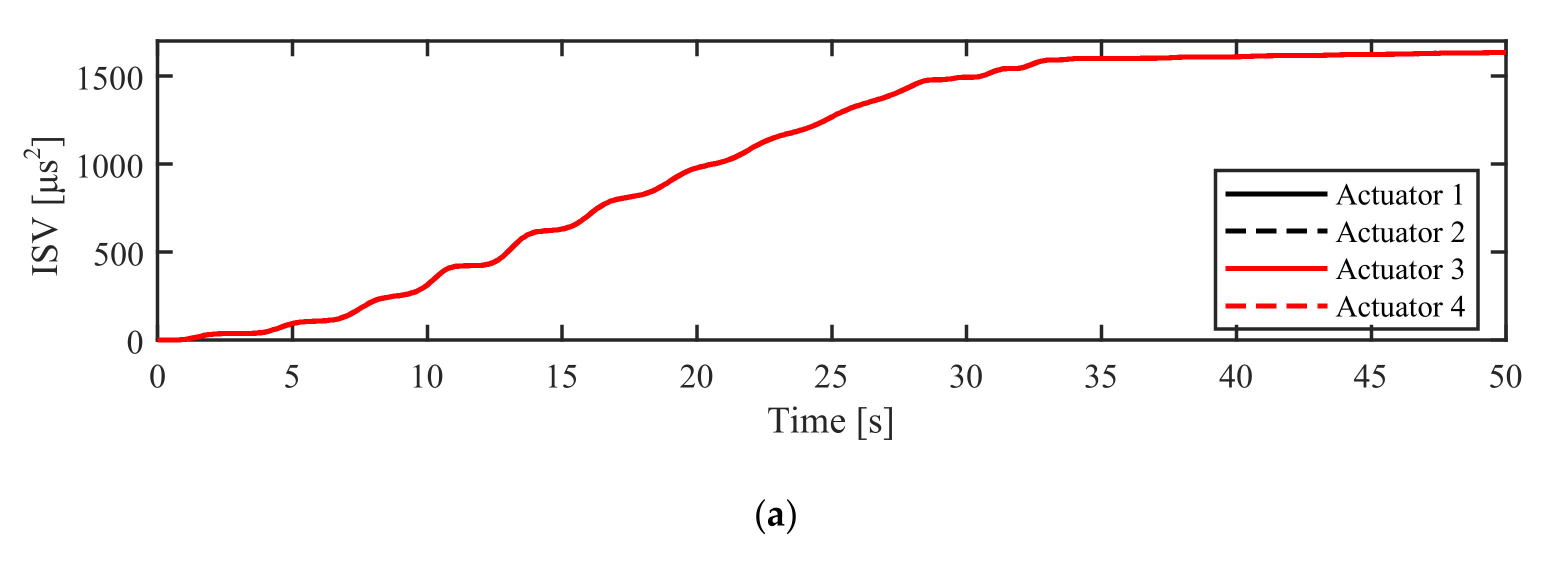
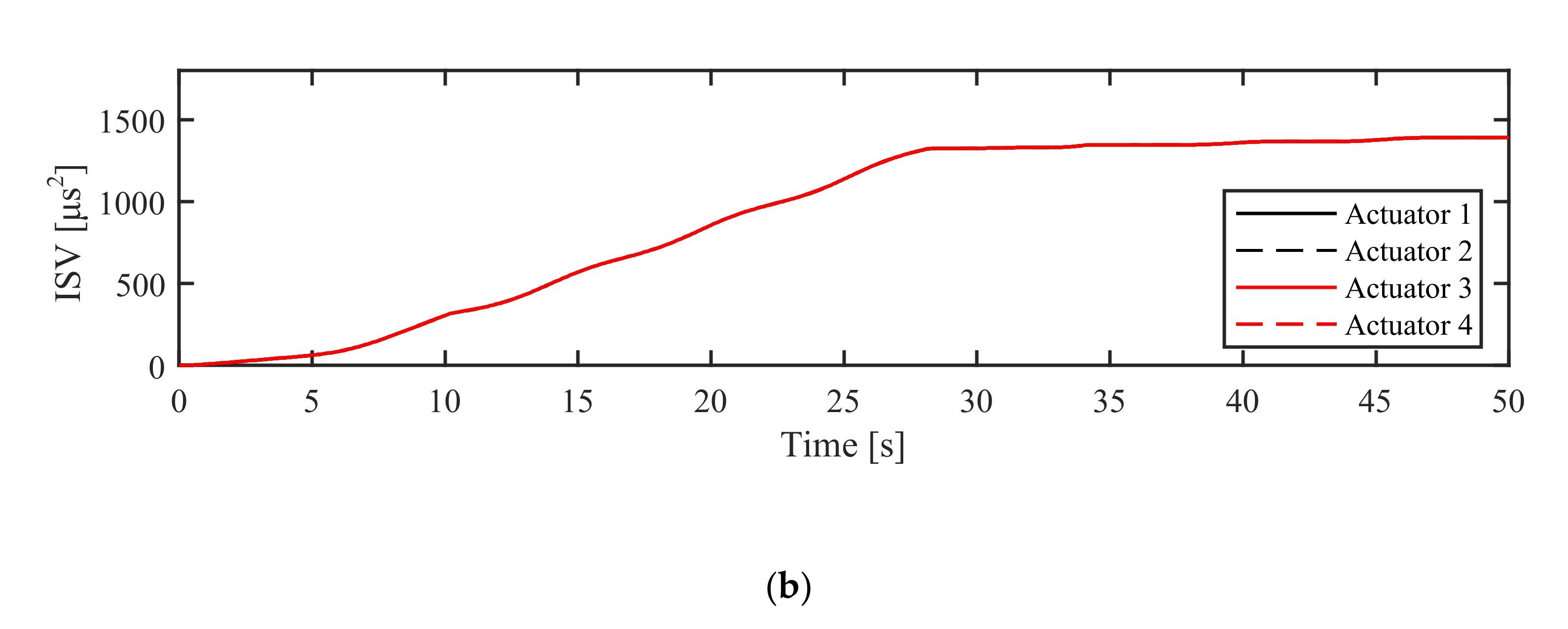
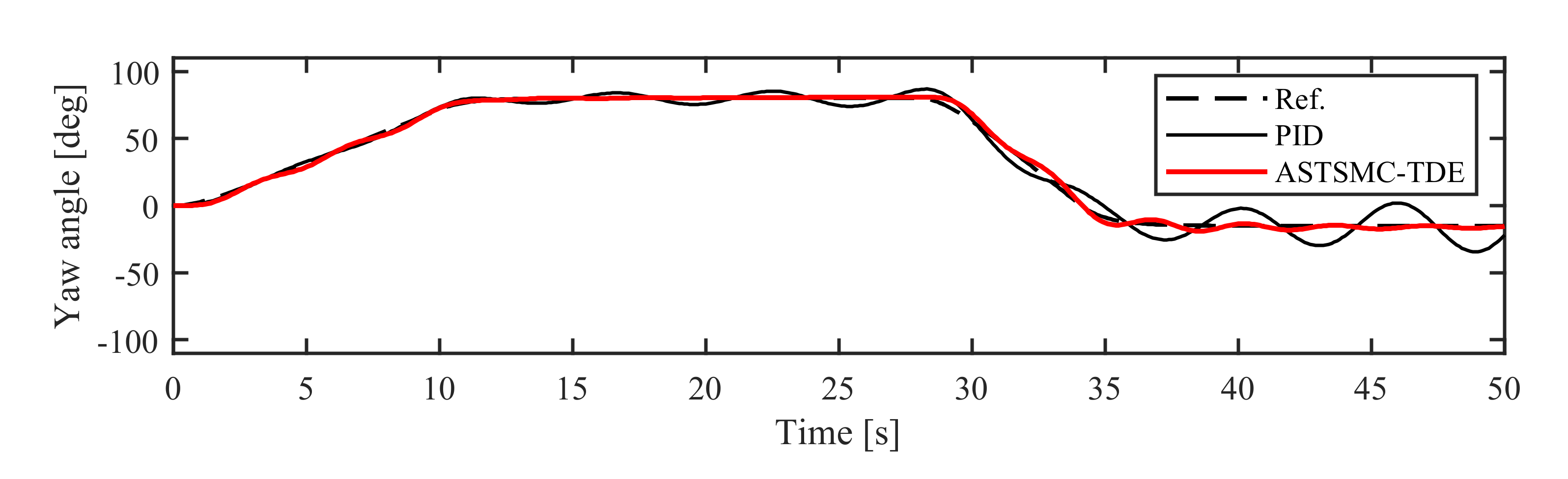
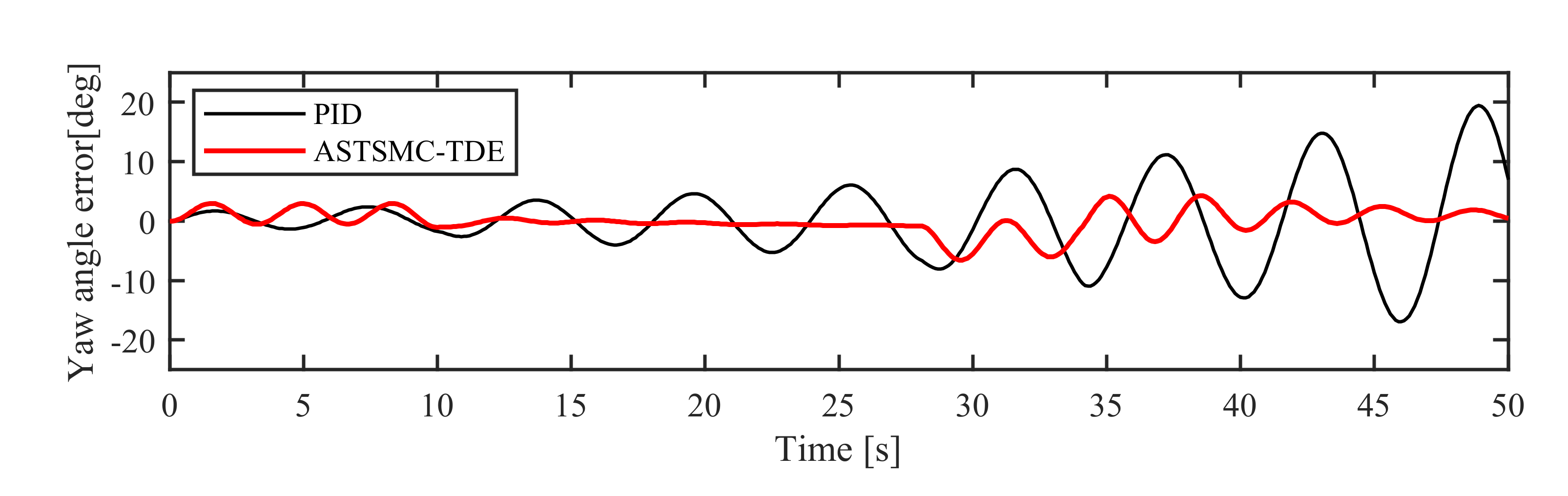
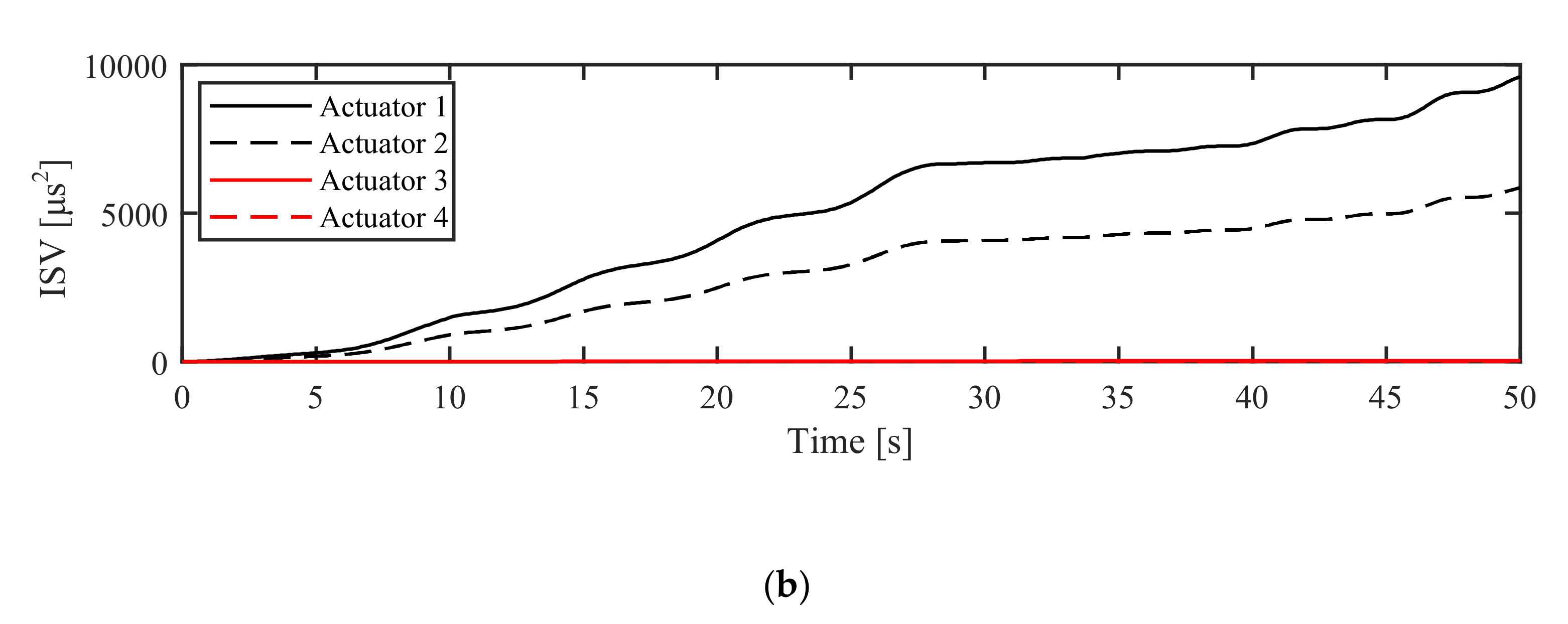


| RMSE [deg] | ITAE [s.deg] | ISV [μs2] | |
|---|---|---|---|
| ASTSMC-TDE | 1.5422 | 5.4977 | 1635.1 |
| 1635.1 | |||
| 1635.1 | |||
| 1635.1 | |||
| PID | 1.6469 | 6.9611 | 1392 |
| 1392 | |||
| 1392 | |||
| 1392 |
| RMSE [deg] | ITAE [s.deg] | ISV [μs2] | |
|---|---|---|---|
| ASTSMC-TDE | 2.0114 | 7.0281 | 7507 |
| 3569.8 | |||
| 1051.7 | |||
| 0 | |||
| PID | 6.7549 | 24.9629 | 9597.4 |
| 5857.8 | |||
| 37.49 | |||
| 0 |
| Devices | Specification Parameters |
|---|---|
| Hover diameter | d = 410 [mm] |
| Propeller diameter | dp = 393.7 [mm] |
| BLDC power | P = 2.4 [kW] |
| DUAV mass | m = 2.01132 [kg] |
| Communication method of Arduino board | RS-232 (COM) |
| Communication method of the gyro sensor | Bluetooth |
| I/O devices | Arduino Mega 2560 |
| Control software | Labview 2016 |
| Load-cell sensor (max) | F = 20 [kgf] ~ Vout = 10 [V] |
| Gyro sensor | ± 2000 (0/s) |
| Servo motor | 0.17sec 600 at 4.8[V] |
| RMSE [deg] | ITAE [s.deg] | ISV [μs2] | |
|---|---|---|---|
| ASTSMC-TDE | 6.8753 | 41.0508 | 1.9437 × 105 |
| 1.9437 × 105 | |||
| 1.9437 × 105 | |||
| 1.9437 × 105 | |||
| PID | 10.7277 | 64.1518 | 2.7873 × 105 |
| 2.7873 × 105 | |||
| 2.7873 × 105 | |||
| 2.7873 × 105 |
| RMSE [deg] | ITAE [s.deg] | ISV [μs2] | |
|---|---|---|---|
| ASTSMC-TDE | 13.7254 | 75.932 | 2.2801 × 106 |
| 1.3751 × 106 | |||
| 9.4316 × 103 | |||
| 0 | |||
| PID | 14.9606 | 119.7465 | 2.1967 × 106 |
| 1.3395 × 106 | |||
| 8.5648 × 103 | |||
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, M.-T.; Lee, D.-H.; Chakir, S.; Kim, Y.-B. A Novel Adaptive Super-Twisting Sliding Mode Control Scheme with Time-Delay Estimation for a Single Ducted-Fan Unmanned Aerial Vehicle. Actuators 2021, 10, 54. https://doi.org/10.3390/act10030054
Tran M-T, Lee D-H, Chakir S, Kim Y-B. A Novel Adaptive Super-Twisting Sliding Mode Control Scheme with Time-Delay Estimation for a Single Ducted-Fan Unmanned Aerial Vehicle. Actuators. 2021; 10(3):54. https://doi.org/10.3390/act10030054
Chicago/Turabian StyleTran, Minh-Thien, Dong-Hun Lee, Soumayya Chakir, and Young-Bok Kim. 2021. "A Novel Adaptive Super-Twisting Sliding Mode Control Scheme with Time-Delay Estimation for a Single Ducted-Fan Unmanned Aerial Vehicle" Actuators 10, no. 3: 54. https://doi.org/10.3390/act10030054
APA StyleTran, M.-T., Lee, D.-H., Chakir, S., & Kim, Y.-B. (2021). A Novel Adaptive Super-Twisting Sliding Mode Control Scheme with Time-Delay Estimation for a Single Ducted-Fan Unmanned Aerial Vehicle. Actuators, 10(3), 54. https://doi.org/10.3390/act10030054







