Morrku Mangawu—Knowledge on the Land: Mobilising Yolŋu Mathematics from Bawaka, North East Arnhem Land, to Reveal the Situatedness of All Knowledges

Abstract

Yolŋu mathematics refers to the complex matrix of patterns, relationships, shapes, motions and rhythms of time and space that underpin the ways that Yolŋu people, Indigenous people of North East Arnhem Land in northern Australia, nourish and are nourished by their environments. Through its fundamental reliance on human and more-than-human connectivity and situatedness, Yolŋu people mobilise the concept of Yolŋu mathematics to challenge Western knowledges, including Western ideas of mathematics and environment. This paper discusses Yolŋu mathematics and the relationships between humans and more-than-humans, which co-produce a world that is living and interconnected, and which reveals all knowledge as situated.

1. Introduction

Gänma is where the salt water and the fresh water meet and mingle, at Bawaka and throughout Yolŋu North East Arnhem Land in the north of Australia. As the fresh water comes off and out of the land and sky, it meets the salt water of the sea. There is a mixing, a meeting and mingling, that brings difference together without erasing it. Gänma thus means new life and new ideas. It evokes knowledges coming together. There is power and knowledge with two waters mixing1.

Gänma is an important concept for Yolŋu people and has been used to describe and understand Yolŋu-ŋapaki (non-Yolŋu) intercultural relationships and learnings in a range of environmental, educational and other contexts (for example, see [1,2,3,4,5,6,7]). One important aspect of gänma is Yolŋu mathematics, a concept put forward by Yolŋu to encourage gänma, meeting and mingling, as it prompts a coming together of ontologies, of ways of being in and with the environment or ecological systems more broadly. Yolŋu mathematics refers to the complex matrix of patterns, relationships, shapes, motions and rhythms of time and space that underpin the ways that Yolŋu people nourish and are nourished by their environments.

In this paper we write as a human and more-than-human collective of Yolŋu and ŋapaki, with and as Bawaka homeland to elaborate some aspects of gänma and Yolŋu mathematics. In doing so, we aim to introduce some aspects of Yolŋu ontology within which humans and more-than-humans co-become with and as Country [8,9]. Within Yolŋu ontology, relationships between humans and more-than-humans co-produce a world which is living and interconnected, and which admits no ontological division between humans and their environments or ecologies [10]. As such Bawaka Country is the lead author and heart of this paper. Bawaka has enabled our learning, our meeting, the stories that guide us, the connections we discuss and has brought us into being today.

Bawaka Country is a known place/space, located in North East Arnhem Land, a large area of Yolŋu Aboriginal land in the far north of Australia. Richly nourished and attended, Bawaka is Country, as encompassed by the Aboriginal English term Country, a term that includes humans, more-than-humans and all that is tangible and non-tangible, and that co-becomes with humans as an active, vibrant, sentient and sapient presence. Country is sentient and communicative, it can know and be known, and can take action. Debbie Rose ([11], p. 7) explains, “Country is a living entity with a yesterday, today and tomorrow, with a consciousness, and a will toward life. Because of this richness, Country is home, and peace; nourishment for body, mind, and spirit; heart’s ease.” Our research collective that writes this paper is part of Country too, is part of its vibrant knowing and being. Together we co-become through webs of responsibility and reciprocity with all Country’s fellow beings and becomings.

As in the title of the paper, morrku mangawu, knowledge is on, with and as the land. Bawaka cannot be separated, as we humans cannot be separated, from being part of Country. It is these intense, ordered and patterned connectivities—Yolŋu mathematics—that this paper focuses on. We look to these connectivities to highlight one of the many ways Yolŋu people have generously created space for gänma, for two ways learning, for a shift in power relationships, for recognition and respect. However our contribution is not an ethnography of Yolŋu knowledge. It is not an example of academics coming in to an “authentic” and separate Yolŋu world, discovering it and exposing it to others. Rather, our contribution is itself an example of gänma, of knowledges and ontologies that mix and mingle, and that is what we share with you. For as we write as Bawaka, we write as Laklak, an Indigenous Datiwuy elder and caretaker of Gumatj (including Bawaka) Country, as her sisters Ritjilili, Merrkiyawuy and Banbapuy, teachers and community leaders, their daughter Djawundil, who hosts tourists for their family-owned business, and, as Sandie, Kate and Sarah, three academic human geographers who, through their work at and with Bawaka, have been adopted into the family.

In this paper we share with you some of the ways the world works in a Yolŋu way of thinking and being, in particular how the rules are mathematical. To Yolŋu, there are logical orders in the land. There are rules and patterns, like the rules of gurrutu (kinship) that are part of the cycles of the universe. There is counting and sharing, physics and measurement, and there are cycles of growth and harvesting. Yolŋu look at the water, at the tides coming and going, at the flows of the rivers and the movement of light through the sea, and see order and system. There is mathematics in the moon and the seasons, in the rain and the clouds. Yolŋu know these things through the land—morrku mangawu. When a wind starts or a flower opens, that is the land teaching. That is Yolŋu mathematics, a mathematics that places Yolŋu in, with and as Country.

As the land has been teaching Yolŋu people, Yolŋu have been teaching ŋapaki. As discussed below, two ways learning has been occurring in North East Arnhem Land, however the waters are yet to mix and mingle in many broader contexts. As such, the paper argues that Yolŋu mathematics in the context of gänma has to be actually be two ways. Western knowledges too need to learn. Indeed, the challenge of Yolŋu mathematics opens a space for multidirectional, more-than-human centred learnings—a recognition of environmental and educational situatedness, diversity and plurality. It is a pluralistic approach that unsettles universalisations, homogeneity and human-centred authority and agency.

In making this argument, the paper firstly outlines the emergence of Yolŋu mathematics as a concept within the context of empowerment and gänma in North East Arnhem Land. It goes on to discuss how Yolŋu mathematics is the connectivities between humans and more-than-humans, which co-become a world that is living and situated. Here, notions of “the environment” or ecologies are expanded beyond reductionist notions that see humans as the only beings able to act, think and acknowledge. Instead, the Aboriginal Australian notion of Country enables conceptualisations of more-than-human, co-emergent co-becomings. This is then illustrated by the co-becomings of Yolŋu mathematics in the context of the Yirrkala Community School and cultural tourism in North East Arnhem Land. The paper concludes by arguing that this generous sharing of knowledge, this engagement with Yolŋu mathematics, reveals all knowledges as situated and issues a profound challenge to western-centred environmental and educational discourses and practices.

2. Two Way Learning

In writing of gänma and Yolŋu mathematics, we position ourselves within a long history of Yolŋu empowerment and resistance to colonialism. Yolŋu have been at the forefront of assertions of sovereignty in a wide range of realms including in art, science, religion and politics [7,12,13,14,15,16]. Yolŋu launched the first land rights case in Australian history and in 2008, won a landmark sea rights case that saw recognition of their sovereignty into the sea [17]. They have led efforts at bilingual learning, and have been widely acknowledged for their work in art, music, cultural tourism, writing and dance. In all these spheres, whether dance or mathematics or tourism or through overt political action, they have been engaged in putting forward a diverse way of being in and with the world, asserting Yolŋu ontologies and Yolŋu sovereignty.

These assertions of sovereignty are set against enduring legacies of colonization which have included European dismissal of non-European, and Indigenous, ways of being and thinking. In Australia, for example, Aboriginal people were serially denied recognition of their knowledges and rights over land, even their very existence [18]. In the 1960s, Yolŋu played an important role in the fight for land rights in Australia, in the effort to overturn concepts of Terra Nullius (the legal assertion of Indigenous absence upon which British colonial claims over Australia proceeded). In the 1970s and beyond, the homelands movement presented a powerful response to European understandings of people’s relationships to land as alienable. The homelands movement was thus a movement asserting Indigenous rights over and with their homelands as well as an expression of cultural strength and continuity [12,13]. As Laklak states:

It was about us being in our home, having a right to belong where we are. We can be equal Australians. We can be Australians and have culture. We should have rights to be Yolŋu. For us, the homelands cannot be ignored. We can’t run away from the kinship we have with Country and all the animals, plants, winds and spirits that dwell there. We have a place where we belong. That movement that we started forty-plus years ago, it still goes on.

For Yolŋu people, any understanding of order or patterns in the universe, that is, mathematics, cannot be understood outside Country or kinship. Country, as Laklak states, “cannot be ignored”. The powerful land rights and homelands movements that begun in the 1960s, strengthened and extended in the 1970s and beyond, to focus on a wide range of domains including an insistence on recognizing Yolŋu ways of knowing and being, including mathematics and relationships with/as Country.

Yolŋu first used the notion of Yolŋu mathematics in the 1970s as a way of countering the idea that Western practices of mathematics had no equivalent in pre-colonial Yolŋu society [15,19,20,21]. Indeed, Helen Verran, a key contributor to the emergence of the Yolŋu mathematics curriculum at Yirrkala, makes a case that mathematics and land ownership are intimately related. Verran argues that mathematics of Aboriginal land ownership has historically been ignored, marginalised and denigrated in Australian (and international) politics, law, academia and practice [22]. She goes on to reveal Yolŋu mathematics as both analogous to western mathematics, yet significantly different, and she re-imagines the implications of this for the politics, negotiation and co-existence of land ownership/s in Australia.

Not only have legal and political systems been unable to grapple with the challenge of Yolŋu mathematics but mainstream education systems have also been unable to recognise alternative mathematics and their importance for Indigenous rights and education [22]. Yolŋu mathematics thus presents a challenge, and critiques the development and pedagogical domination of Western mathematical traditions [23]. The establishment of the Gänma mathematics programme at the Yirrkala Community School in the 1970s was primarily concerned with providing a cognitive link between Yolŋu and western mathematical practices and terminologies as well as bridging a gap between two distinct knowledge systems [19]. The development of the Gänma mathematics programme is epistemologically dependent upon a number of Yolŋu metaphors, in particular gänma, that highlight the potential for a two-way system of equal knowledge exchange. As explained above, this exchange is not limited to educational reform but is also implicit in land-rights [22] and is embedded in the wider socio-political desire for autonomy [16]. We explore Yolŋu mathematics in the school context later in the paper. Firstly, we discuss in more detail the connectivities and situatedness of Yolŋu mathematics.

3. Yolŋu Mathematics

Yolŋu mathematics, like Western mathematics, is the science of patterns, groups, relationships, rhythms and space. To understand Yolŋu mathematics, however, it has to be linked to place. For us, as we write this paper, that place is Bawaka. So it is important to know that as we discuss Yolŋu mathematics, we are telling it through Bawaka, through, with and as our homeland.

At the back of the beach at Bawaka is a big raŋan, a big paperbark tree. If you open it you will see there are layers and layers, layers and layers of bark. As the bark peels away, there is more bark. It is all intertwined together. That is Yolŋu knowledge—there are layers and layers of it. These layers are mathematics. Mathematics is about the patterns and the rhythms, about counting and time and space. It is about how things are connected to other things and about the relationships between them.

This vision of mathematics is one that is absolutely situated. As Donna Haraway asserted in her influential work on situated knowledges, there is no objective knowledge, all knowledge is indeed situated [24]. Bawaka reminds us that it is not only situated, but that this situatedness is place-based in a profound way. This is knowledge intimately embedded in Country, in what it means to live, to be, on this earth and to be connected within more-than-human communities. Put simply, nothing can be understood without reference to its waŋa—its special place. It literally buries down in layers like charcoal in the Australian landscape.

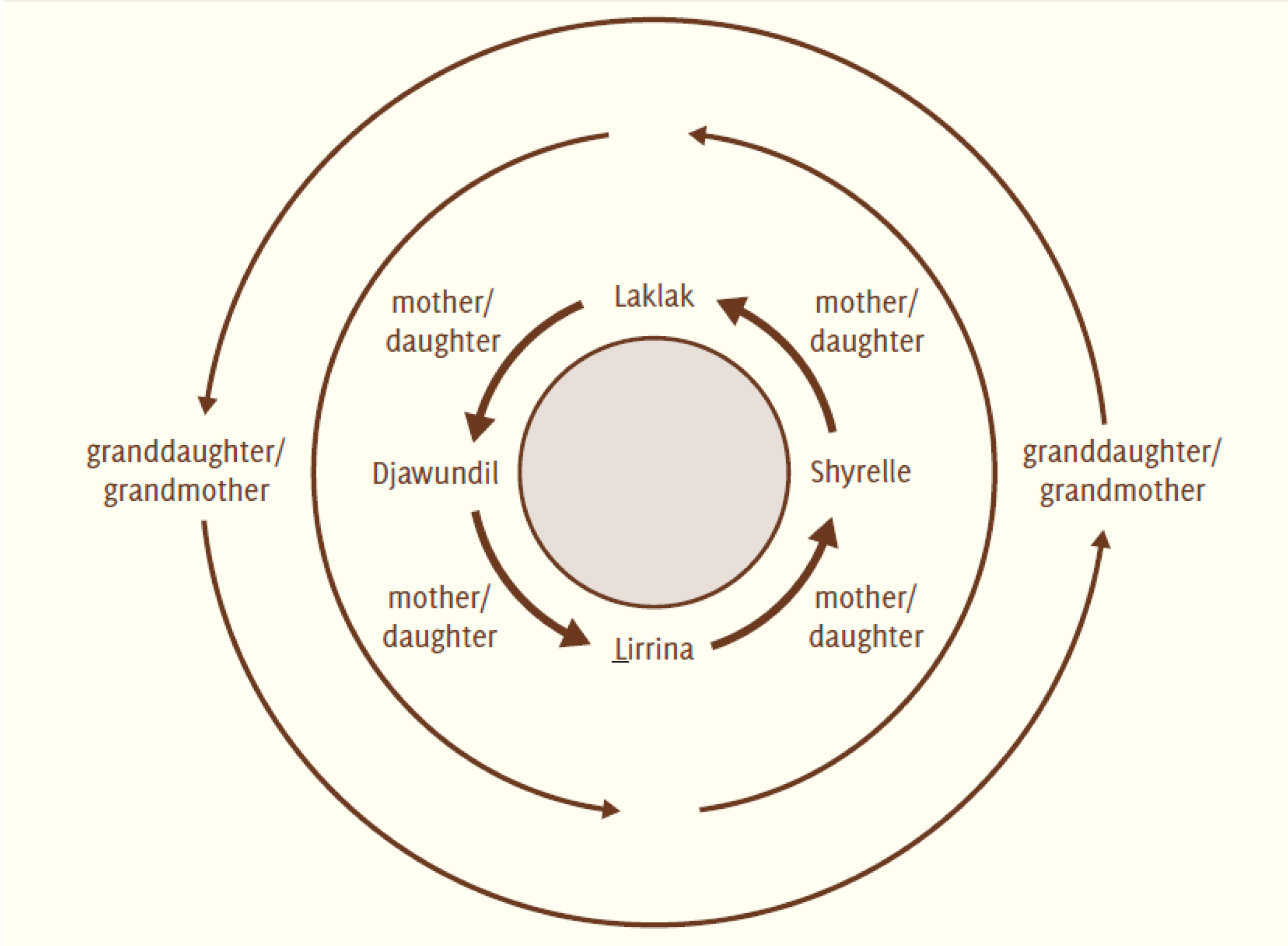
Yolŋu mathematics is very complex. It talks about place and it talks about the ordering of numbers, the infinite cycles and patterns that hold the world together. The ordering of numbers is like this mat (see Figure 1). It is woven, and in the middle is its starting point. Every child who is born is in the system. They have a place. They have a family [25]. They have totems. They have a language. Kate, Sarah and Sandie’s adoption as Bawaka family embodies this situatedness—is an ongoing aspect of Yolŋu mathematics’ co-emergence, co-becoming through infinite patterns of recursion that loop and fold, making and remaking people and Country, time and place/space [8]. As Merrkiyawuy states:

So here we are—Banbapuy is yapa (sister) for me, and so is Sandie. So they’ve (Sandie, Kate and Sarah) now been put into our place, and they are like family; they can’t be moved to another. Everyone who comes to our communities we put into place, if you are not put in a place, then you are nothing. You’re not there. So Banbapuy and I and Sandie are here. Our children—waku—are Kate and Karina. So they’ve got a place. Everything and everyone has a place.

The specificities of place and relationships are understood through gurrutu, kinship. Gurrutu is a complicated pattern that holds all people and more-than-humans in relationship with each other in ways that circumscribe roles and responsibilities. As Laklak describes:

Gurrutu is cyclical, like a helix, going up and around and up. For example, we have a märi, a grandmother. She has her waku, daughter, and her gutharra, granddaughter. Now the daughter of the granddaughter is not the märi’s great-granddaughter but rather her mother. See the pattern? The new-born baby is the mother of the old woman. The old woman is the new-born baby’s daughter (see Figure 2).

Gurrutu is underpinned by the patterns of Yirritja-huwa and Yothu-Yindi (child-mother). Everything in the Yolŋu universe—Yolŋu, non-Yolŋu who have been adopted into families, animals, rocks, plants, winds, songs, cycles, clan estates—is either Yirritja or Dhuwa. Together, Yirritja and Duwa make up the cosmos. Yirritja and Dhuwa also interrelate with another fundamental pattern of gurrutu, the Yothu-Yindi relationship. Here Yirritja gives rise to Dhuwa and Dhuwa to Yirritja as Yothu-Yindi (child-mother) so that all beings are either a mother or child within a relationship. If a child is Yirritja and madirriny, the South Wind, is Yirritja, that wind would be their sister or cousin. The ritjilili, choppy water, which is Dhuwa, would be their mother and their child.

Gurrutu takes these recursive patterns and layers upon them. It brings complex roles and specific kinship relations that follow the patterns of Yirrtija and Dhuwa, and Yothu and Yindi, and build upon them in ways that dictate, for example, who may marry whom, who will care for a certain piece of Country, who has responsibility for a certain song-cycle or sacred art, and who/what you might avoid out of respect. The complex mathematical aspects of these patterns—and it is worth pointing out here that we have only touched upon the most basic patterns of kinship, have been documented by Rudder, Verran, Christie and others [6,7,19,26,27]. As these authors point out, while these mathematical formulations may be recognisable as complex mathematical frameworks within a Western perspective, they are more than abstractions. For Yolngu, relationships and relationality take precedence over ideas of discreteness or abstract quantity [27]. Mathematical patterns bind people to each other and to Country in relationships of co-becoming and as manifestation of strong ethical frameworks. Here, then, is an effort to go beyond superficial renderings of Indigenous mathematics so that, rather than picking certain examples that easily map onto a Western understanding, a more profound ontological view is embraced. For a Yolŋu view of knowledge, of mathematics, comes from a relational ontology, from connectiveness and relationality [8,9,28,29]. In Yolŋu mathematics, people are not separated from nature. The earth is not separated from the sky. Songs and stories are not separated from people and objects. All these things exist as part of one another and come into being together [29,30]. It is a form of relativity.

Coming-into-being-together implies a co-emergence of humans and more-than-humans. As such, Yolŋu mathematics acknowledges non-humans as important, active agents with their own knowledges and with important roles to play in the functioning of the cosmos. This is not a human-centred vision but one that recognises non-human agencies as sapient and purposeful. Bawaka Country is active. It is knowledgeable. The land and the spirits, the sea and all beings have their own mathematics—their own languages, rules, and relationships, their own gurrutu and their own places within the cycles of gurrutu that make up Country. The sea has its own wäŋa, its own mathematics. The guya, the fish, stingray and the miyapunu, the turtle have all got their own language, they have their own rules, style of talking and living with one another. The birds and animals know where to sleep, where to put their babies, where to build their nests, and how and when to migrate. The same for trees and bushes. The land knows what their language is.

These mathematics are constantly being brought into being through song and story, through manikay. They are performative and the performance of Yolŋu mathematics is essential for nurturing and (re)creating the cosmos. As Laklak explains:

When manikay start you have to start from the place—whoever, whatever clan you are you start from your own land. And then you sing what’s there in the land, how it was made, the creation of the land, and then you move from there to where the creator beings or the spirit beings that created that land, the creators journey you’re singing, how he or she, found or created on the way, like animals, or where his or her foot, the soil the sand the land the waterholes the rivers.

Laklak tells us that manikay, Yolŋu songs of Yolŋu mathematics, which underpin Yolŋu life worlds, weave through the web and bring it all together. The shape of all things—valleys, mountains, plains, people, actions, and events—can all be sung. There are songs for the sea and for the freshwater and the land. Trees, spirits, land, animals, plants, winds, waters, people are sung. They are kept alive through manikay even when they have passed on.

There are Bawaka songs: songs about going out with the boat, songs about people sitting in the shade of the djomula (casuarinas trees), looking at Bawaka and the nice and calm water (marrawulwul), the naykuna (flat) water, and all the rocks. The rocks up here are called rirralin and bakitju—where the kids swim in the water hole in the rocks. The rocks have lots of names of significance to Gumatj and they sing about them 3–4 times and then stop, and then sing about the calm water. Then they sit and see the islands from Bawaka and sing the names of places like Nanukala, each beach and island has got a name.

Gurrutu, manikay and the mathematics they perform are multilayed, complex and interwoven in and through time and space. They constantly co-become through the co-emergence of these ongoing relationships. We now explore this co-becoming in the context of gänma, of two-way learning in schools and with tourists.

4. Co-Becoming Yolŋu Mathematics

4.1. In Schools

Yolŋu have been particularly strong in integrating principles from Yolŋu mathematics, including gurrutu, into the Yirrkala Community School curriculum and teaching practices. Incorporating a Yolŋu perspective, including Yolŋu language, Yolŋu concepts and Yolŋu mathematics into educational curriculums is seen as an important part of sovereignty and the assertion of Yolŋu rights, and an important part of cultural maintenance. Yolŋu mathematics reflects a Yolŋu worldview in the classroom, and provides a way of supporting and validating Yolŋu knowledges and ontologies. It also provides a cognitive bridge between students’ cultural milieu and the purportedly abstract world of Western mathematics [31,32,33].

The Gänma mathematics curriculum at Yirrkala Community School revolves around mapping western and Yolŋu thinking together in two ways. Firstly, there is the linkage between the western numeracy system and the Yolŋu gurrutu system as recursive ordering systems. Secondly, there is the mapping of the logical orders located in the land; the western system of quantification or measurement and the Yolŋu system of Djalkiri in which value is inherent in the land due to action of creation and sacred sites.

Yolŋu mathematics is taught everyday and in ongoing ways at the Yirrkala Community School. Merrkiyawuy and Banbapuy, principal and senior teacher at the school, teach Yolŋu mathematics as they want the students to learn two ways. Learning becomes gänma, an exchange between Yolŋu and ŋapaki knowledges and ontologies. Instead of knowledge flowing in one direction, from ŋapaki to Yolŋu (as in most of the mainstream education system in Australia), Yolŋu are recognized and valued for their knowledge. For Merrkiyawuy and Banbapuy, as well as other staff, that is important for teachers, for Yolŋu and for Yolŋu kids. It is also important for Country and for human-more-than-human co-becoming.

The Gänma curriculum is based on learning on Country. As such it is constantly emerging and co-becoming through intense interrelationships between children, teachers, family members and Country. Teachers take the children out onto the land, for example to collect turtle eggs from the beach. As Merrkiyawuy and Banbapuy explain:

To find the eggs we use Yolŋu mathematics. We look at the tracks of the turtle—it’s important we don’t just dig anywhere, because when turtles come up onto the beach they turn around and then they dig over here, dig over there—we need to look at the shape of the track, learning the tracks, to see exactly where the eggs were laid in the buried hole. So we don’t just go up there and start digging—otherwise it’s just ruining the land, we have a look first—the shape of the track, and then try and find where it is. So the kids learn this and they look at the hole and they dig. By digging the kids learn how to identify the air pockets, about depth and length. Then when we bring the eggs out we use a Yolŋu way of counting—waŋgany, marrma, lurrkun, dämbu miriw, one, two, three, four—and then one on the top, that’s one rulu—and then there’s two rulu, three rulu—and that’s how the children are counting there—so learning their way of mathematics. Then they decide, how many will I be taking—how many eggs shall I take home to my mum and dad. It’s a living maths. Garma2 is living maths (see Figure 3).

Learning mathematics is thus a way of learning Country, of learning how to listen to Country, to care for Country and be cared for by Country. Most profoundly, learning mathematics reinforces for students that they are not and cannot be separated from Country, but rather they come into being with it.

4.2. With Tourists

Conceptualisations of Yolŋu mathematics have been taken up by many Yolŋu as a way of interpreting and communicating their relationships with each other and with the environment, and as a way of asserting the importance of Yolŋu knowledge and authority for non-Yolŋu people, ŋapaki. While Yolŋu mathematics at Yirrkala community school largely speaks to Yolŋu children (and Yolŋu and ŋapaki teachers), Yolŋu people have found other ways to specifically reach ŋapaki, including through tourism.

A range of Yolŋu tourism businesses, including corporate, educational and custom-made tours, engage visitors with Yolŋu kinship, traditional lore and language, both spoken and sign. One business—Bawaka Cultural Experiences (BCE) is owned by the Burarrwanga family3. BCE’s focus is on sharing Yolŋu knowledge, through gänma, two-way learning: “The business is about Bawaka people sharing knowledge with the world. It is how Bawaka people are, sharing knowledge with the world, learning from each other, Indigenous and non-Indigenous” ([34], p. 27). Through this sharing BCE helps visitors develop an understanding of the holistic nature of Yolŋu knowledge and offer glimpses into some of layers of patterns, rhythms and relationships with and as Country that underpin it. This is fundamentally about reasserting control over how Yolŋu knowledge is communicated to ŋapaki audiences. As Laklak argues:

We’ve got to stand on our two feet. Yolŋu should be in charge of the politics that affect us. It is time for a yuta (new) generation. Bäpa [Laklak fathers], he taught all the other Elders how ŋapaki work, their knowledge. And he taught Yolŋu knowledge to ŋapaki, so they could be equal. Ŋapaki politics and Yolŋu politics. Ŋapaki could see Yolŋu knowledge and Yolŋu could see ŋapaki knowledge. That is the most important thing, for young people of the future, to understand politics and Rom (Law/Lore).

Tourists are immersed in Yolŋu mathematics from the moment they step out of their vehicle onto Bawaka sand. Through the welcome smoking ceremony, through activities that give them a skin name and through the diverse ways they are guided—doing, talking, being, and becoming—by Yolŋu hosts, they are invited to understand how Yolŋu mathematics connects all. Tourists are encouraged to understand the centrality of Country to all knowing and being, including mathematics. As one tourist reflected:

…it was the fact that we were on their land, hearing their stories, told their way in their time and having being invited to be part of that. You know, I really felt they were sharing something very important and special to them with us.

[35]

BCE often invoke lirrwi, charcoal, to emphasise their connections in, with and as place. As Laklak explains:

Everywhere you dig in Australia you’ll find some charcoal from the fires of Indigenous people. It shows that Indigenous people lived there, that we are from this place. There are layers and layers of it too, just like the raŋan and just like our knowledge. When you first dig, you’ll see one layer of lirrwi; when you’ll dig more, you’ll see more. It’s significant knowledge that goes down deep. It’s from our ancestors. It’s knowledge that’s embedded in the land and that has been part of the lives of Aboriginal people for generations, forever.

([1], p. 190)

This is done in ways that emphasise the place-based and situated nature of Yolngu mathematics, but also in ways that may challenge tourists’ conceptualisations of Indigenous knowledge as something located in the past, without reference to contemporary realities. The puzzle designed by Merrkiyawuy (see Figure 4) makes the vibrant, contemporary and practical ramifications of gurrutu abundantly clear.

The layers of lirrwi, like the layers of rangan, are Yolŋu knowledge and Yolŋu mathematics co-becoming with and as Country. Tourism, then, provides an opportunity for Yolŋu to share some layers of Yolŋu mathematics and to engage in gänma, co-becoming together, in a different context. Tourism brings Yolŋu into relationship with people from across Australia and from around the world to share Indigenous ways of being, knowledges and practices. Through this gänma, Bawaka becomes for tourists more than “the environment”, it becomes Country, knowledgeable, sentient and caring, not a static background to culture or a canvas on which to write abstract knowledge, but an intimate part of what it means to know, live and co-become.

5. Mixing, Mingling and Concluding

From its birth in the Yirrkala Community School, Yolŋu mathematics has been mobilised to encourage mixing and mingling. Despite these intentions, ŋapaki have much to learn from Yolŋu mathematics and there is a persistent and widespread lack of knowledge around Indigenous mathematics and land management systems, and the ways these may interact. As Laklak reflects:

Many people have worked so hard to get a curriculum that builds on Yolŋu knowledge and ŋapaki knowledge. But the government is trying to take it out, to make Yolŋu children foreigners in their own school even though they are the first people. We could learn from each other. Why can’t the government see that?

Echoing Verran’s work analysing pre-native title attitudes towards Indigenous mathematics in Australia [22], continuing debates in Australia reinforce the ontological arrogance of thinking there is only one form of mathematics—either through the dismissal of Indigenous knowledges or expressions of surprise as other knowledges are “suddenly dis-covered”:

I don’t understand why we are including these [Indigenous] perspectives in these subjects. Science and maths are universal. (The head of the Prime Minister’s indigenous council, Warren Mundine, cited in [36], in response to the Federal Government’s review of the new national curriculum which sought to embed Aboriginal and Torres Strait Islanders Cultures and Histories as a cross-curriculum priority).

While English speakers may talk of infinite possibilities, ancient Australian Aboriginal languages very rarely stretched past number five. However, a study published today shows that far from being simple, Aboriginal numeral systems “lost and gained” numbers over time.

[37]

Such comments point to the lack openness towards “infinite possibilities” not of Yolŋu or other Indigenous knowledge systems, but of those unable or unwilling to see beyond one-way learning [38]. While gänma has always been understood by Yolŋu and their allies as about intercultural exchange, this kind of pluralistic approach eludes most mainstream knowledges. Thus, as critical as it is to teach Indigenous students through appropriate Indigenous approaches [39], principles of gänma could be adopted more broadly in mainstream educational practices throughout Australia and ideas of environment opened up to and respectfully recognise and engage with alternate ways of knowing—a true two ways learning.

Knowledge on, with and as the land, morrku mangawu, has much to offer understandings of human-environmental relations, ideas of knowledge and of mathematics. If, for Yolŋu, things and being can only be understood in relation to other things and beings—what might be called relationality or relativity—an insistence that a thing or being can be understood in an abstract, discrete way, as unrelated to others, is revealed as deeply culturally embedded. Indeed dominant Western ways of knowing, and mainstream mathematics, are often dependent upon such abstractions. These abstractions tell us as much about cultural understandings and preoccupations as they do about the objects of that knowledge, which, after all, only come into being with others.

Within Yolŋu mathematics, there can be no human that sits separate from their environment, from other humans or from other more-than-human becomings. Humans can no more act on a separate, discrete or unknowing environment than they may act upon their own selves. In place of environment, Yolŋu mathematics is knowledge of, with and as Country. Yolŋu mathematics is the multi-species, more-than-human knowledges and practices that emerge through our co-becoming, assertions of knowing, being and becoming-together. Such assertions underscore the situatedness of all knowledges and challenge universalist claims around abstract mathematics, human subjectivities, or ideas of environmental management that perceive the environment as something that exists separately from people, as something to acted upon.

However, understanding Yolŋu mathematics as morrku mangawu points to more than knowledge two ways. It points to radical more-than-human multiplicity and multidirectionality. There is no singular Yolŋu mathematics—as knowledge with/of/as the land is dependent upon different homelands and contexts. Similarly, Western mathematics is plural and diverse, with the mathematics taught in schools and integrated into most people’s daily life bearing little resemblance to the complex and relational ideas of mathematics explored (and contested) within and between pure mathematics and quantum physics. For Yolŋu, furthermore, it is not just humans who understand, generate and interpret patterns and relationships—more-than-humans too have law, language, knowledge and logic. Knowledge, mathematics, is indeed multi-centric and multi-directional. Yolŋu mathematics, morrku mangawu, underscores this plurality, this situatedness, this more-than-human diversity.

In this paper, we have attended to Bawaka Country, and its mathematics, by acknowledging its place as author, and acknowledging our co-constitution as part of each other and of Country. We speak of morrku mangawu. In doing so, Bawaka has guided, shaped and taught us. We have tried to practice gänma in a different context, in an academic world, by taking seriously Yolŋu ontologies and inviting new forms of mixing and mingling, within our Indigenous-ŋapaki-more-than-human collective and with you. As you read this paper, the salt water and fresh water, the diverse currents, different temperatures, carrying different lives, different knowledges and different becomings over time and space, come together again in new ways. This is living mathematics.