A Geometrical Method for Sound-Hole Size and Location Enhancement in Lute Family Musical Instruments: The Golden Method
Abstract
:1. Introduction
- The method is described in an itemized flowchart form in chapter two.
- Two well-known instruments will be checked with this approach as case studies in order to show the effectiveness of the Golden Method.
- A new musical instrument will be developed using the proposed method and its damping capability would be compared with that of two well-known instruments to confirm the effectiveness of the golden method in optimizing the sound-hole size and location in lute family musical instruments from a damping point of view.
2. Methodology
“Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures such as Oxford physicist Roger Penrose, have spent endless hours over this simple ratio and its properties. But the fascination with the Golden Ratio is not confined just to mathematicians. Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.”
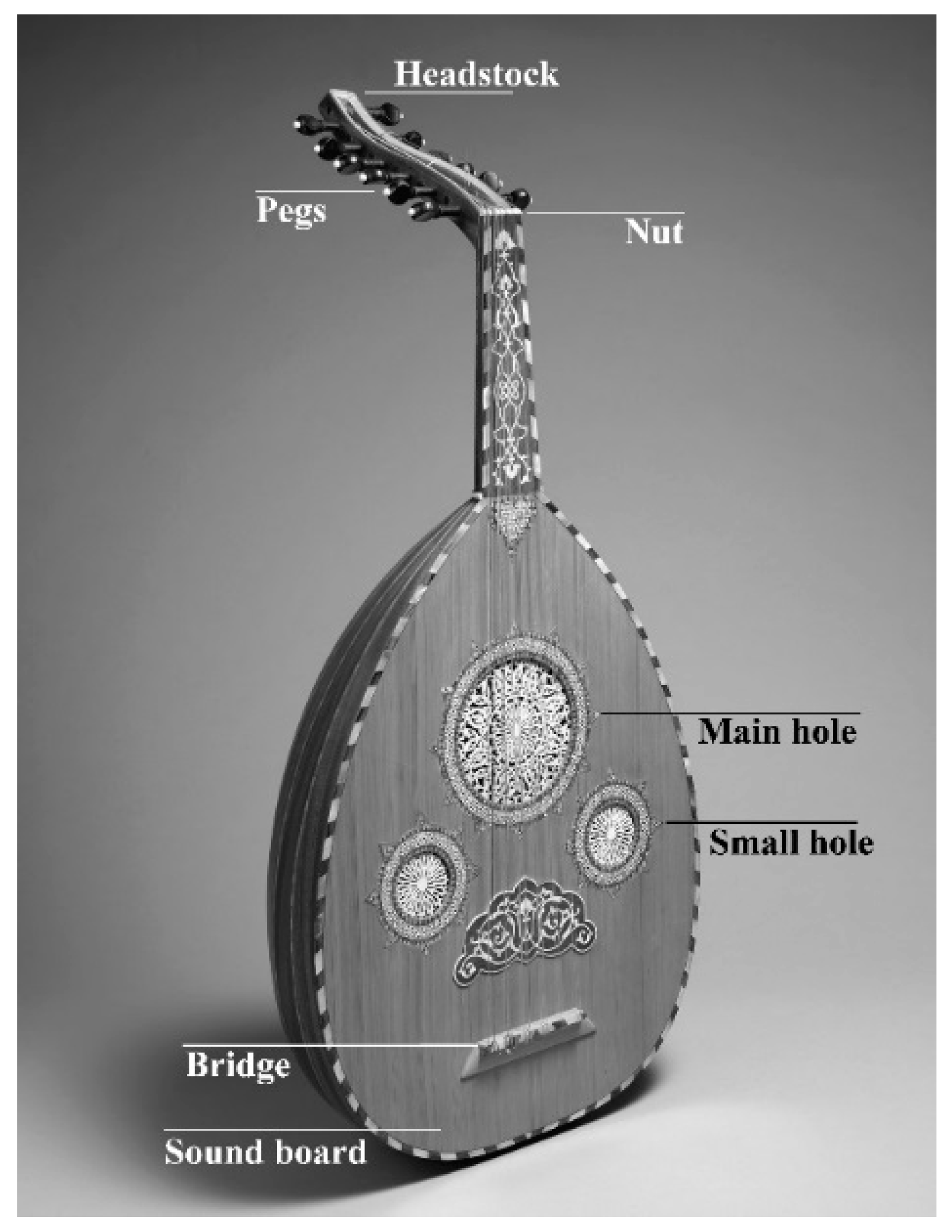
- The circular sound-hole has been assumed as the optimized shape for the lute family (based on the literature).
- The material and mechanical properties of the instrument are not discussed in this paper because of their dynamic-index nature. These parameters can be studied in a separate standalone research work.
- The main objective of the proposed method is to enhance the musical note keeping capability of the instrument for orchestral consideration.
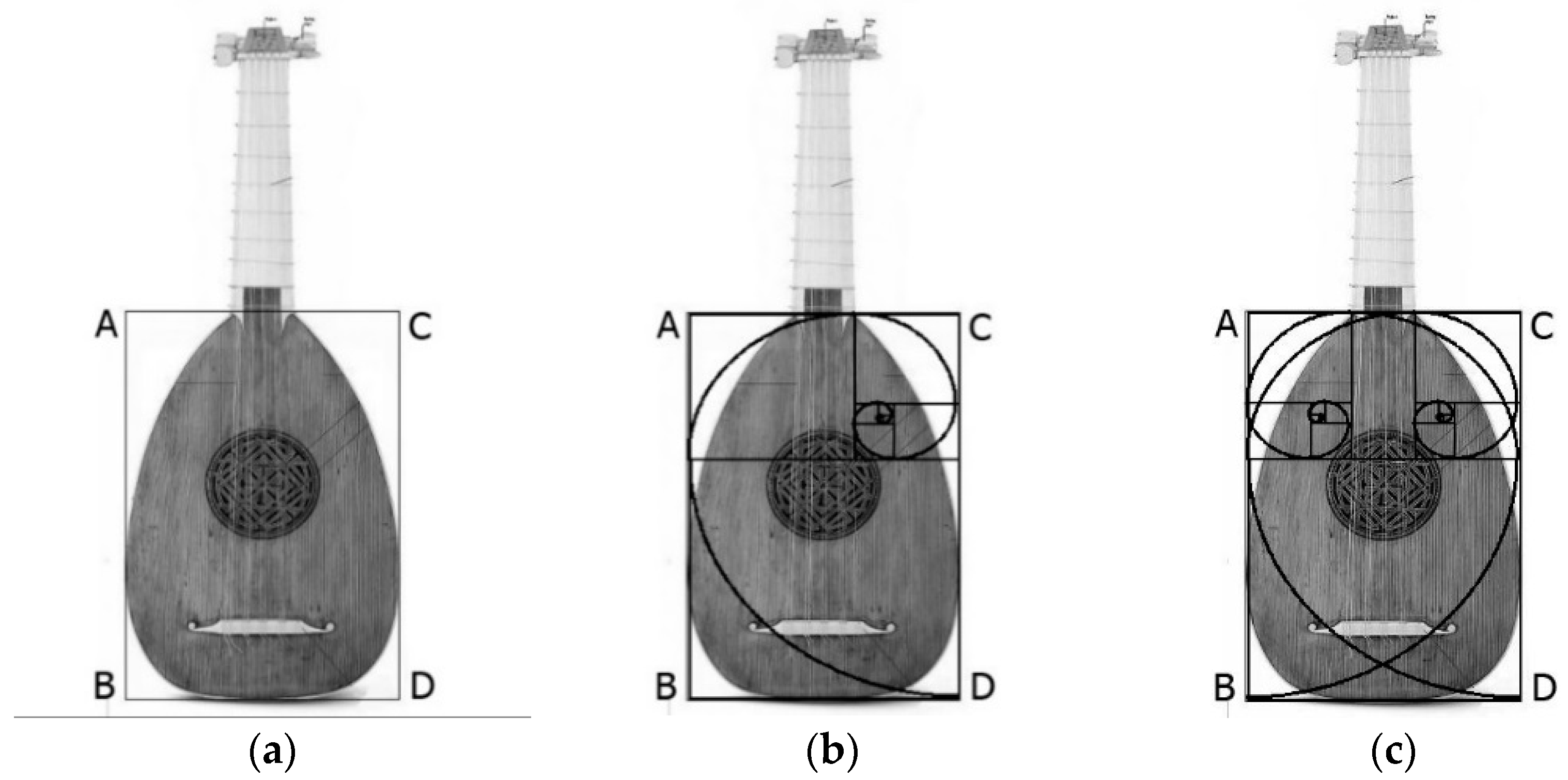
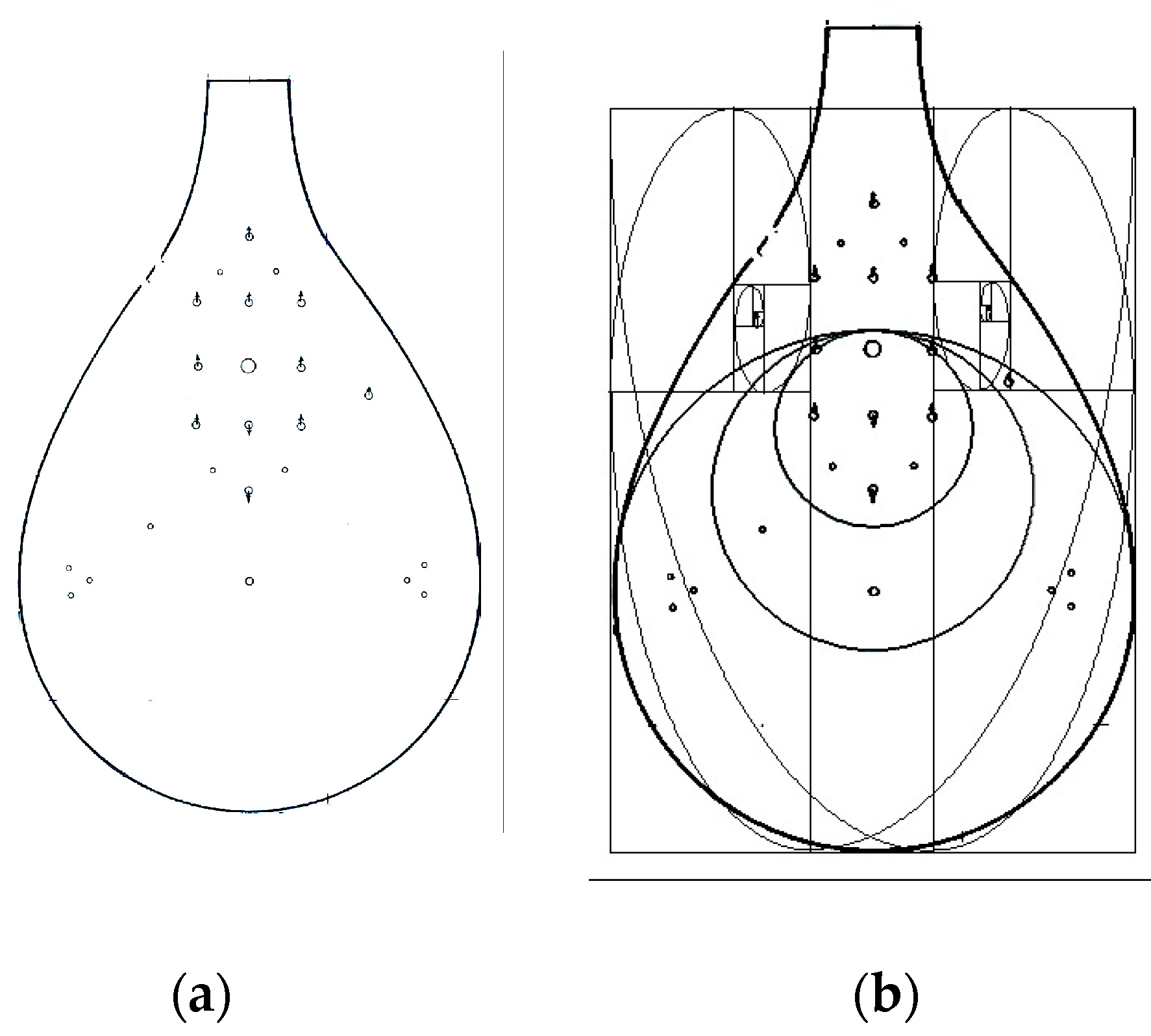
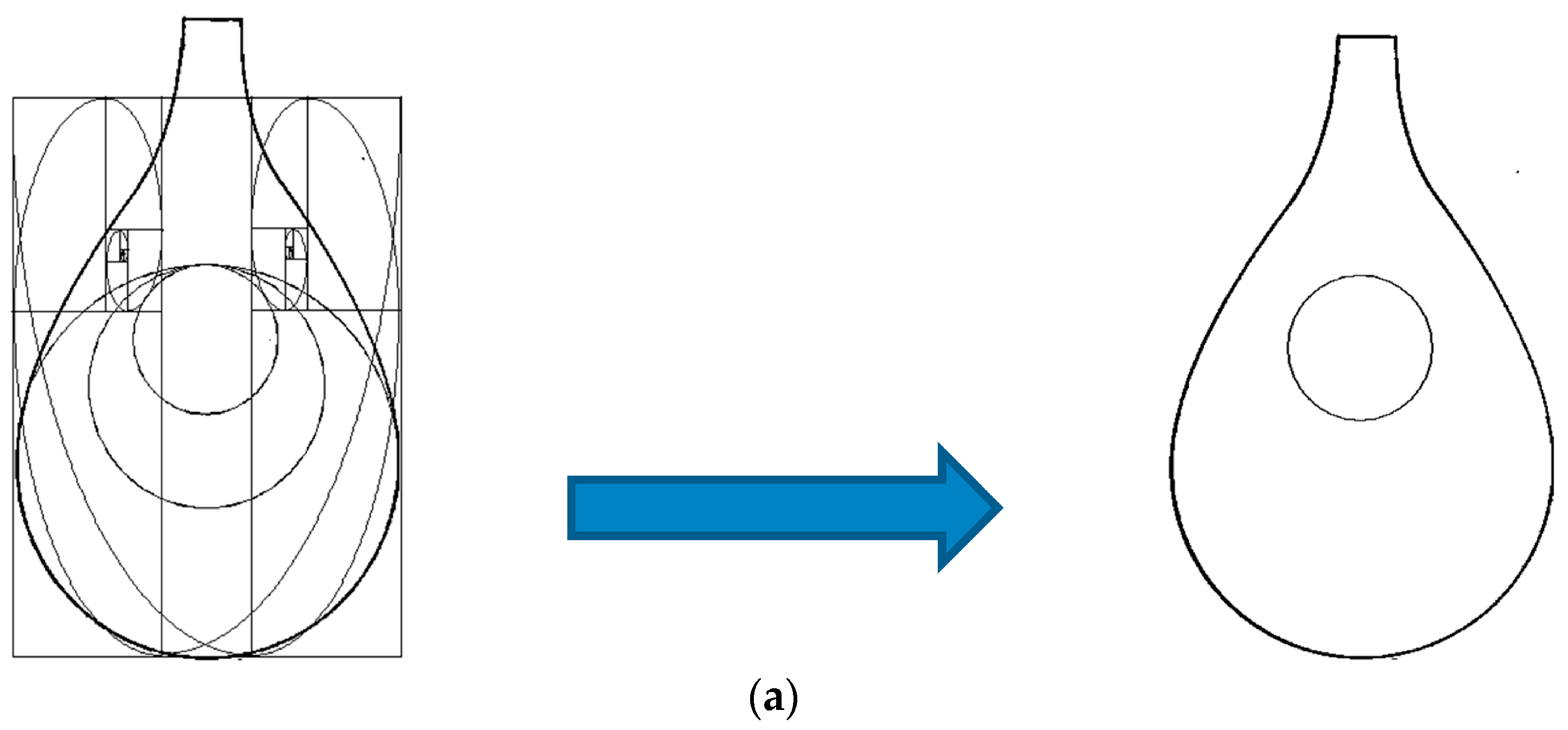
- Plot the rectangle ABCD covering the instrument soundboard and tangent to it as shown in Figure 3a.
- Plot the golden rectangle and its logarithmic spiral from one side of the ABCD as shown in Figure 3b. Full details on how to plot such a golden rectangle and spiral are very straightforward and can be found in (Chang 2002, Hemenway 2005).
- Repeat step 2 from another side of the ABCD as shown in Figure 3c and draw another golden rectangle and logarithmic spiral that mirror those of step 2.
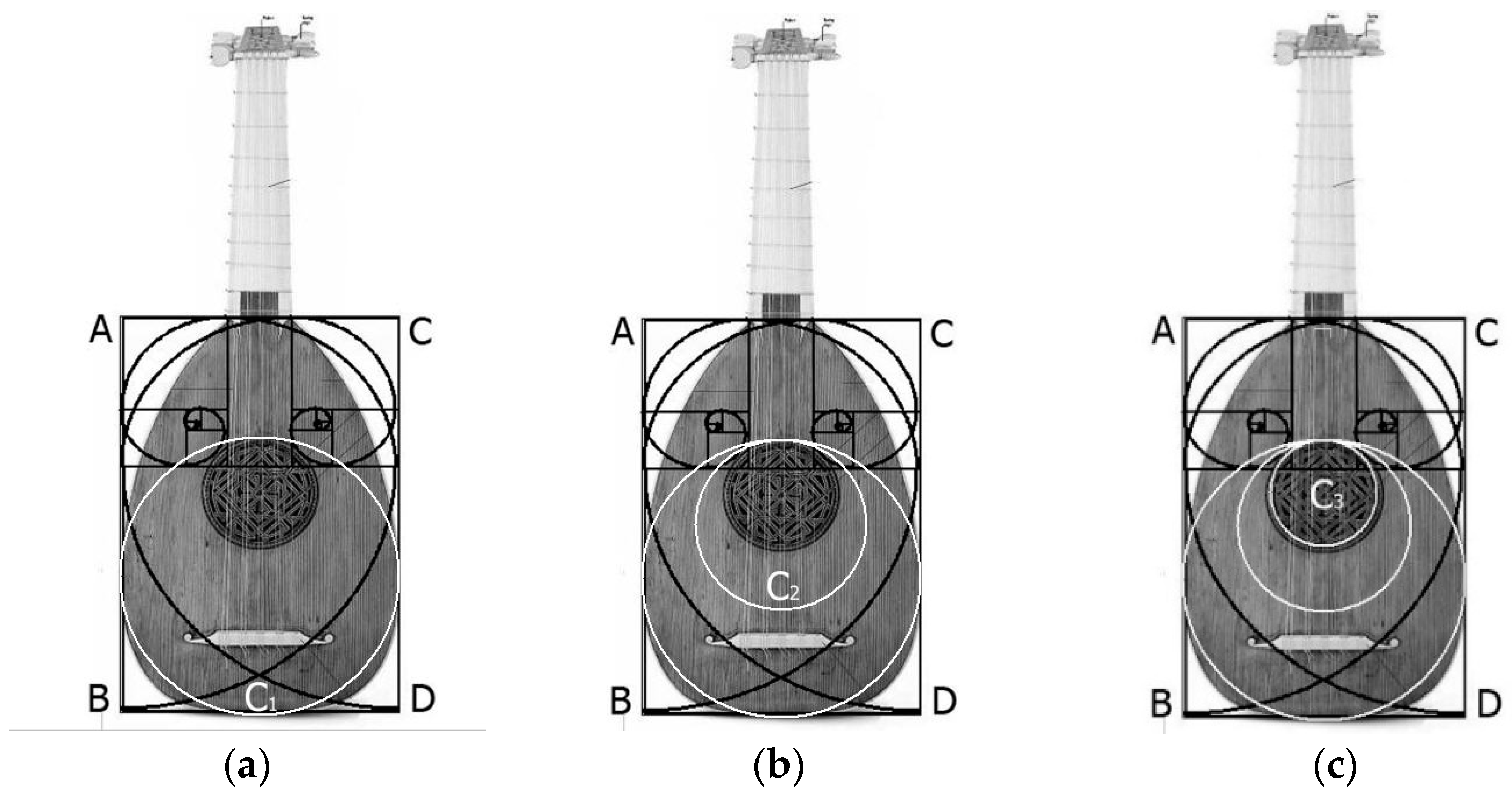
- Plot a circle C1 tangent over the 3 lines AB, BD, and CD as shown in Figure 4a.
- Plot the first golden circle C2 so that
- The vertical diameters and upper vertex of the two circles are common.
- The diameter ratio:
- Plot the second golden circle C3; this circle is drawn like C2 (but C3 should follow the above-mentioned conditions for C2) (Figure 4c).
- Now, if C3 touches the two golden spirals (Figure 5a), this can locate the precise location and size of the optimized sound-hole.
3. Experimental Evaluation
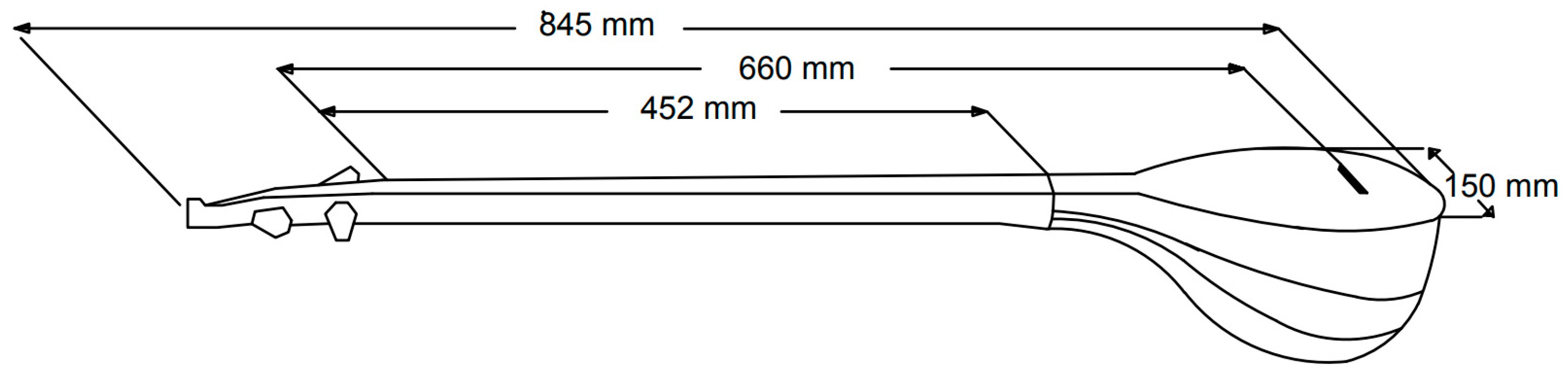
3.1. Case Study I: Delroba2
3.2. Case Study II: Eshghi3
3.3. Case Study III: Mahava4
4. Experimental Apparatus and Procedure
4.1. Data Acquisition System
4.2. Test Procedure
5. Results and Analysis
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Baines, Anthony. 1992. The Oxford Companion to Musical Instruments. New York: Oxford University Press. [Google Scholar]
- Barber, Stephen, and Sandi Harris. 2016. Eleven Course Lutes. Available online: http://www.lutesandguitars.co.uk/htm/cat06.htm (accessed on 7 March 2016).
- Bissinger, George. 1992. Effect of f-hole shape, area, and position on violin cavity modes below 2 KHz. Journal of Catgut Acoustical Society 2: 603–8. [Google Scholar]
- Chang, Yu-Sung. 2002. “Golden Spiral” from the Wolfram Demonstrations Project. Available online: http://demonstrations.wolfram.com/GoldenSpiral/ (accessed on 1 February 2015).
- Coates, Kevin. 1985. Geometry, Proportion and the Art of Lutherie. Oxford: Clarendon Press. [Google Scholar]
- Cremer, Lothar. 1984. The Physics of the Violin. Cambridge: MIT Press. [Google Scholar]
- Encyclopaedia Iranica. 1988. “Encyclopaedia Iranica—Barbatl”. Available online: http://www.iranicaonline.org/articles/barbat (accessed on 4 February 2012).
- Engel, Carl. 1883. Researches into the Early History of the Violin Family. London: Novello, Ewer & Company. [Google Scholar]
- Hemenway, Priya. 2005. Divine Proportion: Φ Phi in Art, Nature, and Science. New York: Sterling Publishing Co., pp. 127–9. [Google Scholar]
- Hutchins, Carleen M. 1990. A study of the cavity resonances of a violin and their effects on its tone and playing qualities. The Journal of the Acoustical Society of America 87: 392. [Google Scholar] [CrossRef]
- Hideo, Itakawa, and Chichi Kumagai. 1952. Researches on Violin Making. Tokyo: Institute of Industrial Science, The University of Tokyo. [Google Scholar]
- Kamalian, Mohammad M., and Behzad Mobasseri. 2015. Said and Unsaid. Tehran: Ney Press, p. 56. [Google Scholar]
- Khaleghi, Reza. 1963. The History of Persian Music. Tehran: Mahour Press, p. 128. [Google Scholar]
- King, Alvin Thomas. 2004. The Cremonese System for Positioning the F-Holes. The Strad. December. Available online: http://www.fiddleheadstrings.com/microsoft_word___for_the_strad_part_1_8_sept.pdf (accessed on 15 November 2014).
- King, Alvin Thomas. 2005. How Stradivari Positioned the F-Holes. The Strad. January. Available online: http://www.fiddleheadstrings.com/microsoft_word___for_the_strad_part_2_8_sept.pdf (accessed on 15 November 2014).
- Lamb, Horace. 1932. Hydrodynamics. New York: Dover. [Google Scholar]
- Livio, Mario. 2002. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number. New York: Broadway, p. 6. [Google Scholar]
- Marcel-Dubois, Claudie. 1941. Les Instruments de Musique de l’Inde Ancienne. Paris: Presses Universitaires de France, pp. 89, 205. [Google Scholar]
- Markowsky, George. 1992. Misconceptions about the Golden Ratio”. The College Mathematics Journal 23: 2–19. [Google Scholar] [CrossRef]
- Mcpherson, Mathew. 2002. Arrangement of a Sound Hole and Construction of a Sound Board in an Acoustic. U.S. Patent 20020043146 A1, April 18. [Google Scholar]
- MIT News. 2015. Power Efficiency In The Violin. Hadi Tavakoli Nia, Cambridge: Jennifer Chu|MIT News Office, February 10. [Google Scholar]
- Nia, Hadi T., Ankita D. Jain, Yuming Liu, Mohammad-Reza Alam, Roman Barnas, and Nicholas C. Makris. 2015. The Evolution of air Resonance Power Efficiency in the Violin and Its Ancestors. London: The Royal Society. [Google Scholar]
- Rault, Christian Luthier. 2014. Mediaeval. Available online: http://www.christianrault.com/en/workshop/mediaeval (accessed on 15 November 2014).
- Rayleigh, John William Strutt Baron. 1945. The Theory of Sound. London: Macmillan, Volume 1, pp. 1877–8, Reprinted by New York: Dover, 1945. [Google Scholar]
- Sandys, William, and Simon A. Forster. 1884. History of the Violin. John Russell Smith: London: Addison and Lucas. [Google Scholar]
- Savart, Felix. 1976. Memoire sur la construction des Instruments ‘a cordes et ‘a archet. In Musical Acoustics, Part I (Violin Family Components) and II (Violin Family Functions). Volume 5–6 of Benchmark Papers in Acoustics. Paris: Deterville. [Google Scholar]
- Shaw, Edgar A.G. 1990. Cavity resonance in the violin: Network reperesentation and effect of damped and undamped rib holes. Journal of the Acoustical Society of America 87: 398–410. [Google Scholar] [CrossRef]
- Shirazi, Naser. 1990. Setar Making. Tehran: p. 92. [Google Scholar]
- Takegawa, Akito. 2008. Golden Ratio Air Vent Holes. U.S. Patent 7485791 B2. [Google Scholar]
- Tavakoli Nia, Hamid. 2010. Acoustic Function of Sound Hole Design in Musical Instruments. Master’s Thesis, Department of Mechanical Engineering in Partial Fulfillment of the Requirements for the Degree of Master of Science in Mechanical Engineering at the Massachusetts Institute Of Technology, Massachusetts, USA, June. [Google Scholar]
- Van der Straeten, Edmund Sebastian Joseph. 1968. The History of the Violin, Its ancestors and Collateral Instruments From Earliest Times. New York: Da Capo Press. [Google Scholar]
- Von Helmholtz, Hermann L. 1860. Thoery of Air Oscillations in Tubes with Open ends. Journal fur die Reine und Angewandte Mathematik 57: 1–72. [Google Scholar]
- Von Helmholtz, Hermann L. 1954. On the Sensations of Tone as a Physiological Basis for the Theory of Music. New York: Dover. [Google Scholar]
- Tamara Semenovna Vyzgo. 1980. Muzykal’nye Instrumenty Sredneĭ Azii (Musical Instruments of Central Asia). Moskva: Izd-vo “Muzyka”, Moscow. p. XIX. [Google Scholar]
| 1 | Setar is a Persian member of lute family musical instruments. |
| 2 | Mean enchanting; one of the most famous Setar designs. |
| 3 | Means “related to love”; one of the most famous Setar designs. |
| 4 | Means “like the moos sound”. |



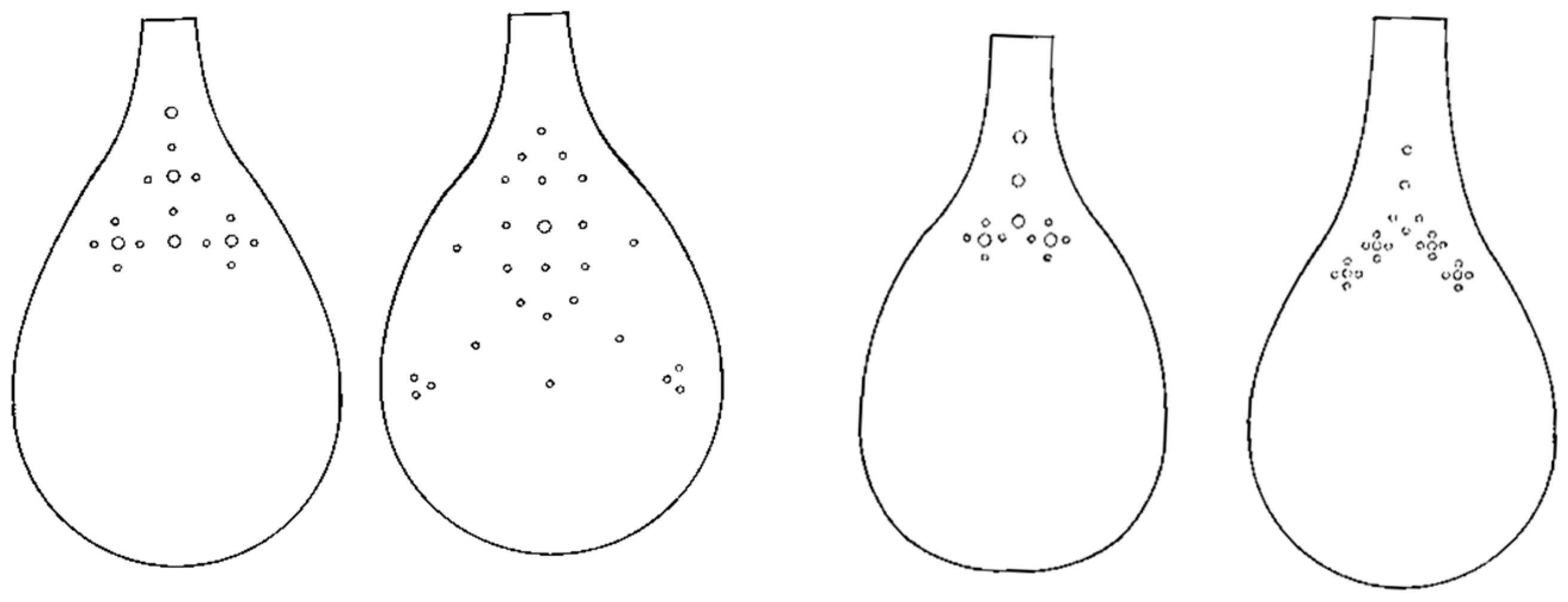



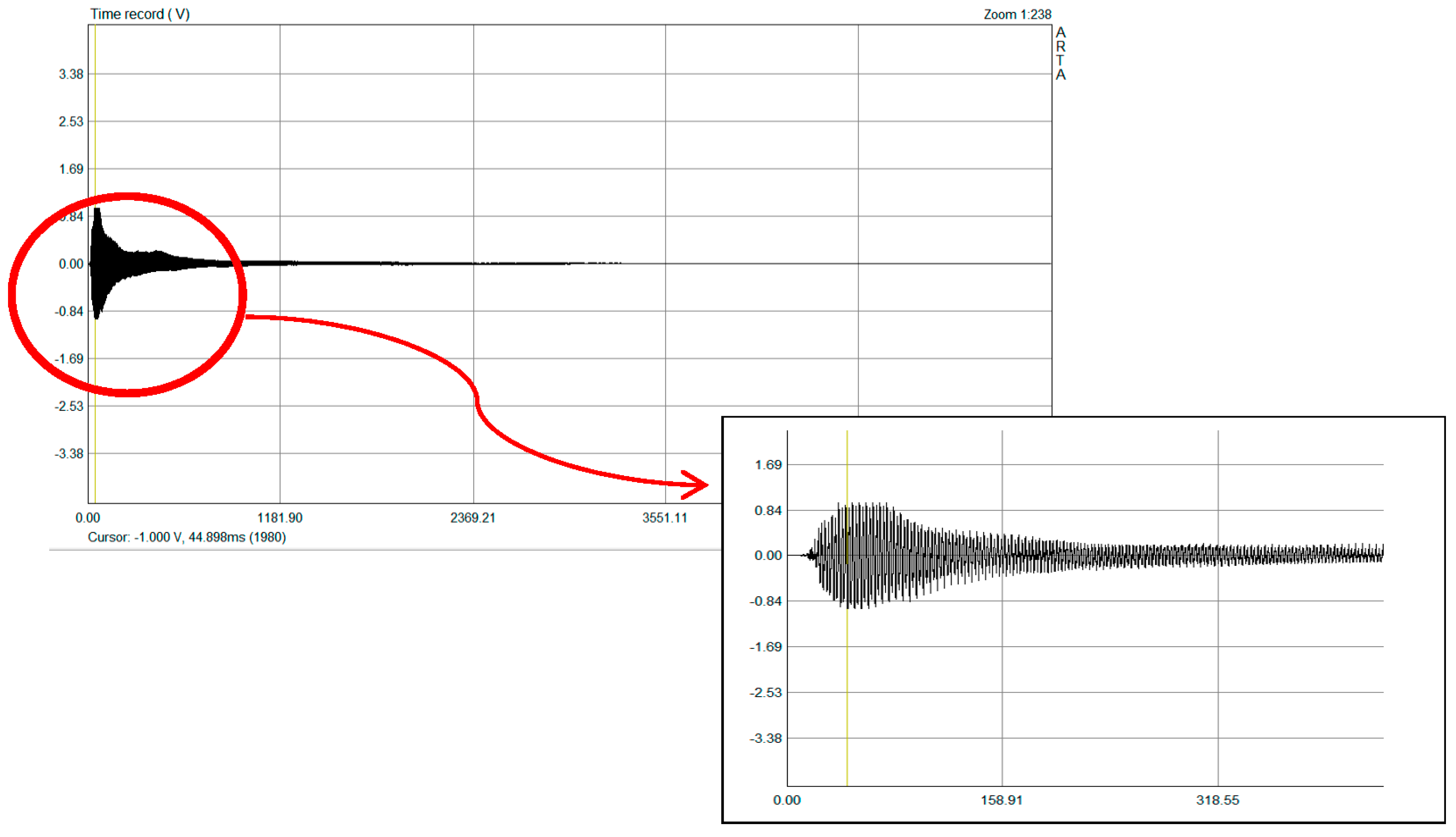
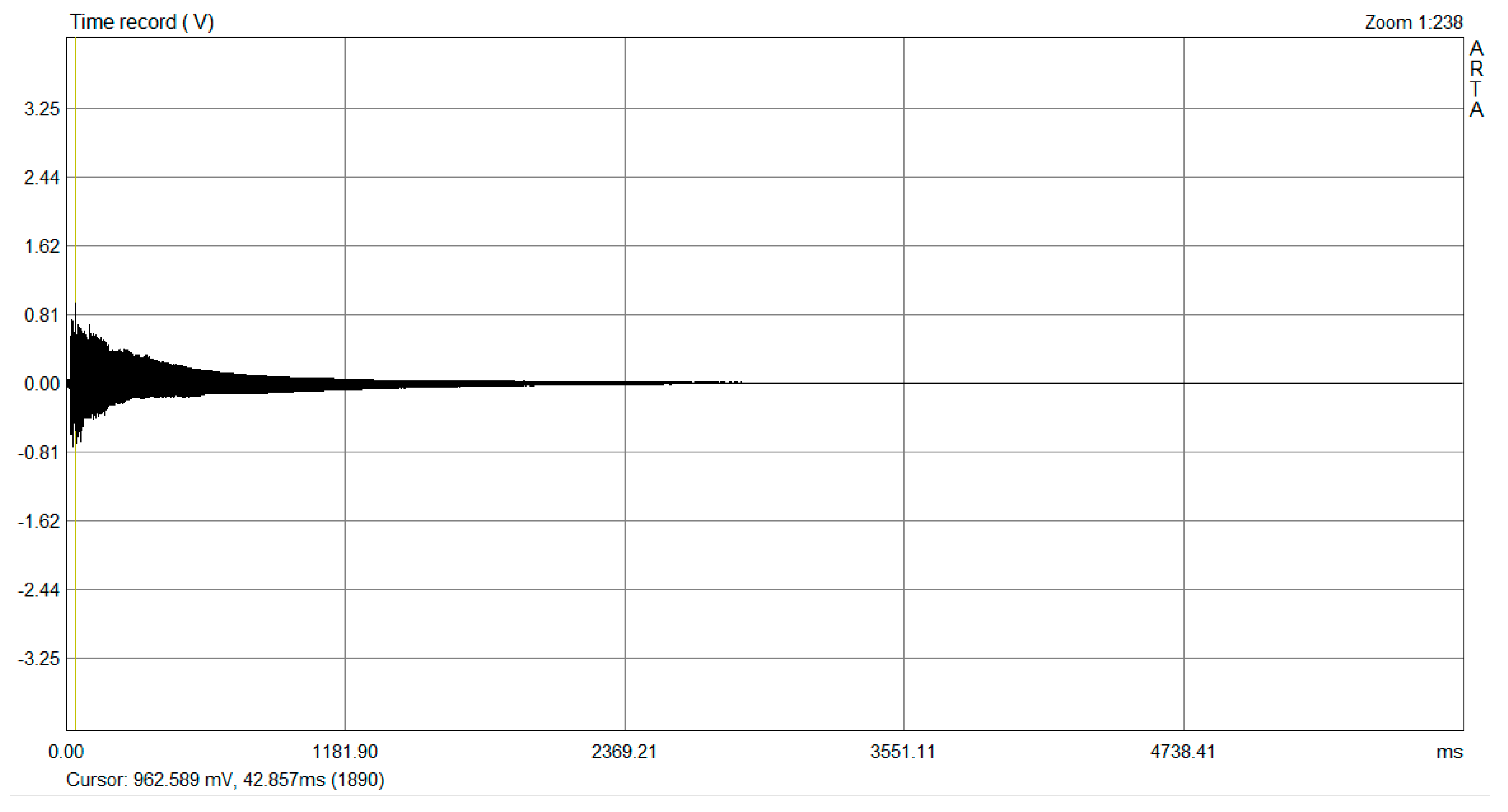
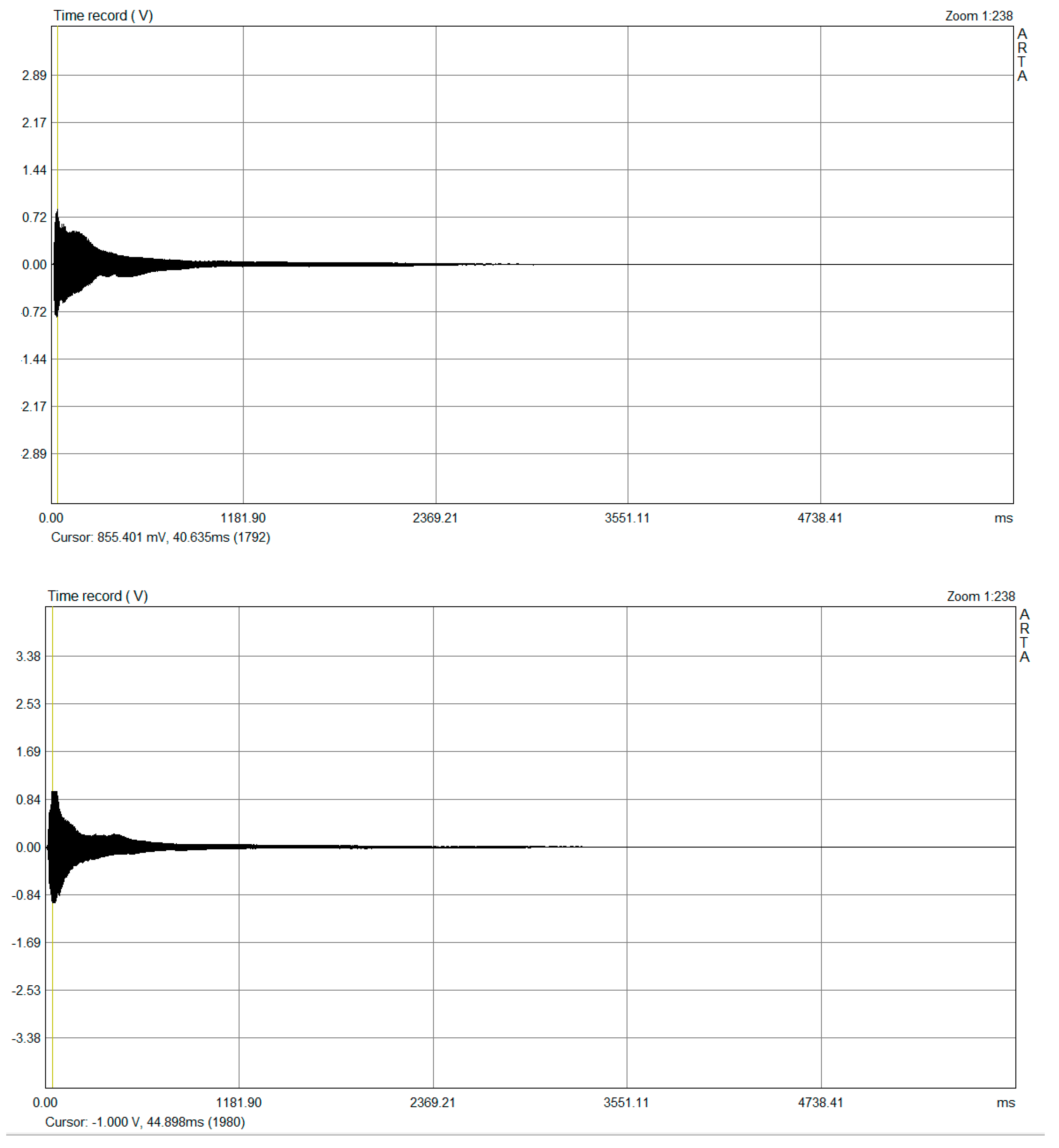

| Maximum Amplitude (mV) | Maximum Amplitude Time (ms) | Damping Time (ms) § | |
|---|---|---|---|
| Delroba | 962 | 42.9 | 3004 |
| Eshghi | 855 | 40.6 | 2955 |
| Mahava | 1000 | 44.8 | 3155 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jafari, S.; Karbasbaf, M.M. A Geometrical Method for Sound-Hole Size and Location Enhancement in Lute Family Musical Instruments: The Golden Method. Arts 2017, 6, 20. https://doi.org/10.3390/arts6040020
Jafari S, Karbasbaf MM. A Geometrical Method for Sound-Hole Size and Location Enhancement in Lute Family Musical Instruments: The Golden Method. Arts. 2017; 6(4):20. https://doi.org/10.3390/arts6040020
Chicago/Turabian StyleJafari, Soheil, and Mohammad Mahdi Karbasbaf. 2017. "A Geometrical Method for Sound-Hole Size and Location Enhancement in Lute Family Musical Instruments: The Golden Method" Arts 6, no. 4: 20. https://doi.org/10.3390/arts6040020
APA StyleJafari, S., & Karbasbaf, M. M. (2017). A Geometrical Method for Sound-Hole Size and Location Enhancement in Lute Family Musical Instruments: The Golden Method. Arts, 6(4), 20. https://doi.org/10.3390/arts6040020





