1. Introduction
Public policy on genetics and insurance is typically perceived as a balancing act between two competing considerations. On the one hand, there are social, ethical and public health arguments, which suggest that the ability of insurers to decline particular customers or charge higher prices on the basis of predictive genetic tests should be severely limited. On the other hand, there are economic arguments under the rubric of ‘adverse selection,’ which suggest that limiting insurance discrimination has costs, not just for insurers, but for society as a whole. Under this framing, public policy always involves a trade-off of two ills, genetic discrimination versus adverse selection: how much genetic discrimination can we tolerate, and what level of adverse selection costs are we prepared to pay?
The main point of this article is that this trade-off is often illusory. From the viewpoint of society as a whole, not all adverse selection is adverse, and public policy should not aim to eliminate all adverse selection. Limits on insurance discrimination, which induce the right amount of adverse selection (but not too much adverse selection) can increase ‘loss coverage’, and so make insurance work better for society as a whole. My argument is one of simple arithmetic, which is demonstrated in this paper by simple examples. For a more discursive treatment, see the recent book
Thomas (
2017), and for technical details see the papers (
Thomas 2008;
Hao et al. 2016a,
2016b,
2018).
In order to critique insurers’ usual argument, I first need to explain what is meant by ‘adverse selection’ in the context of genetics and insurance. Start with the observation that, if permitted, insurers will seek to obtain the results of any genetic tests which insurance applicants may have taken, and then charge applicants low or high prices depending on their individual results. If instead insurers are banned from asking about test results and have to quote a common (or ‘pooled’) price to all applicants, they might initially set the price as a population-weighted average of the high and low risk prices. This pooled price will seem expensive to low risks, and cheap to high risks; and so (the argument goes) low risks will have lower propensity to buy insurance, and high risks will have higher propensity. Compared to the whole population, the pool of insurance purchasers will be skewed towards higher risks. To avoid losses, insurers will then need to reset the pooled price higher than a population-weighted average of the high and low risk prices. In addition, since low risks are usually more numerous than high risks, reduced purchasing propensity by low risks combined with increased purchasing propensity by high risks implies that the total number of risks insured will usually fall. This triad of phenomena—insurance purchasing skewed towards higher risks, higher insurance prices, and reduced numbers insured—collectively constitute ‘adverse selection’.
Adverse selection is clearly ‘adverse’ in the sense that the skew towards higher risks could be disadvantageous to the insurance company (but only if it failed to reflect this skew in the price set). However, insurers (and also most economists) go further: they say that adverse selection is also adverse to society as a whole. This view starts from an intuitive premise that the compensation of losses by insurance is a ‘good thing’ (I agree with this premise). On this premise, insurers argue that the higher insurance prices and reduction in numbers insured implied by adverse selection represent a bad outcome for society as a whole.
However, in a competitive market, the higher insurance price under adverse selection is matched by higher claim payouts; there is no loss to society as a whole. Furthermore, the reduction in numbers insured under adverse selection is not equivalent to a reduction in losses compensated. Losses compensated depend not just on numbers insured, but on which people are insured: the low risks (who arguably need insurance less), or the high risks (who arguably need insurance more). This distinction about which people are insured under adverse selection leads to a novel insight: if the shift in coverage towards higher risks is large enough, it might more than outweigh the fall in numbers insured. The expected quantum of losses compensated by insurance—a quantity I call ‘loss coverage’—might then be increased by adverse selection.
In cases where the shift in coverage towards higher risks more than outweighs the fall in numbers insured, adverse selection implies that more risks are voluntarily transferred to insurers, and more losses are compensated. In this scenario, I argue that adverse selection is not adverse at all; on the contrary, it represents a better outcome for society as a whole.
The rest of this paper proceeds as follows. In
Section 2, I give simple examples that illustrate how the shift in coverage towards higher risk under adverse selection might more than outweigh the fall in numbers insured (and also how it might not). In
Section 3, I discuss the broader application of these examples, and give some empirical evidence.
Section 4 discusses some considerations which the simple examples leave out.
Section 5 gives conclusions.
2. Simple Examples of Adverse Selection
This section elaborates on the argument sketched in
Section 1 that some adverse selection (but not too much adverse selection) can be a good thing for society as a whole. The method is illustration by examples, in the same spirit as dice-rolling examples to illustrate probability laws. The examples are simplified and exaggerated for clarity, but the underlying point is quite general.
In life or health insurance in the context of genetics, the usual population pattern we observe is majority of ‘standard’ risks, and a smaller number of much higher risks (say people with a genetic test result indicating a predisposition to illness). To represent this, consider a population of just ten people, comprising eight lower risks and two higher risks. Assume that all losses and insurance cover are for unit amounts (this simplifies the discussion, but it is not necessary). Then, consider three alternative scenarios for insurance risk classification and adverse selection.
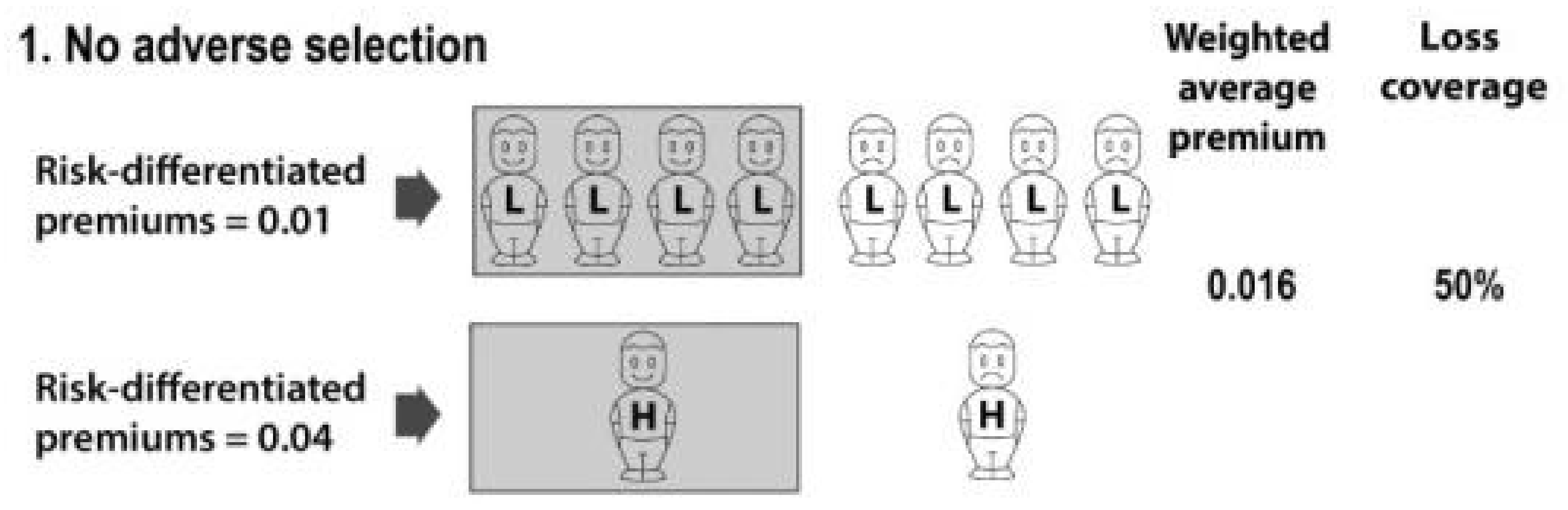
The first scenario—risk-differentiated premiums, with no adverse selection—is represented in
Figure 1. Each ‘L’ represents one lower risk, and each ‘H’ represents one higher risk (say with a genetic predisposition to illness). The lower risk-group of eight risks each have probability of loss 0.01, and the higher risk-group of two risks each have probability of loss 0.04.
In Scenario 1, members of each risk-group are charged a risk-differentiated price equal to their true probability of loss. The response of each risk-group to a risk-differentiated price is the same: exactly half the members of each risk-group buy insurance.
1 The shading over five risks represents that those five risks buy insurance.
The weighted average of the premiums paid is (4 × 0.01 + 1 × 0.04)/5 = 0.016. Since higher and lower risks are insured in the same proportions as they exist in the population, there is no adverse selection. Exactly half of the population’s expected losses are compensated by insurance. I describe this as ‘loss coverage’ of 50%. The calculation is:
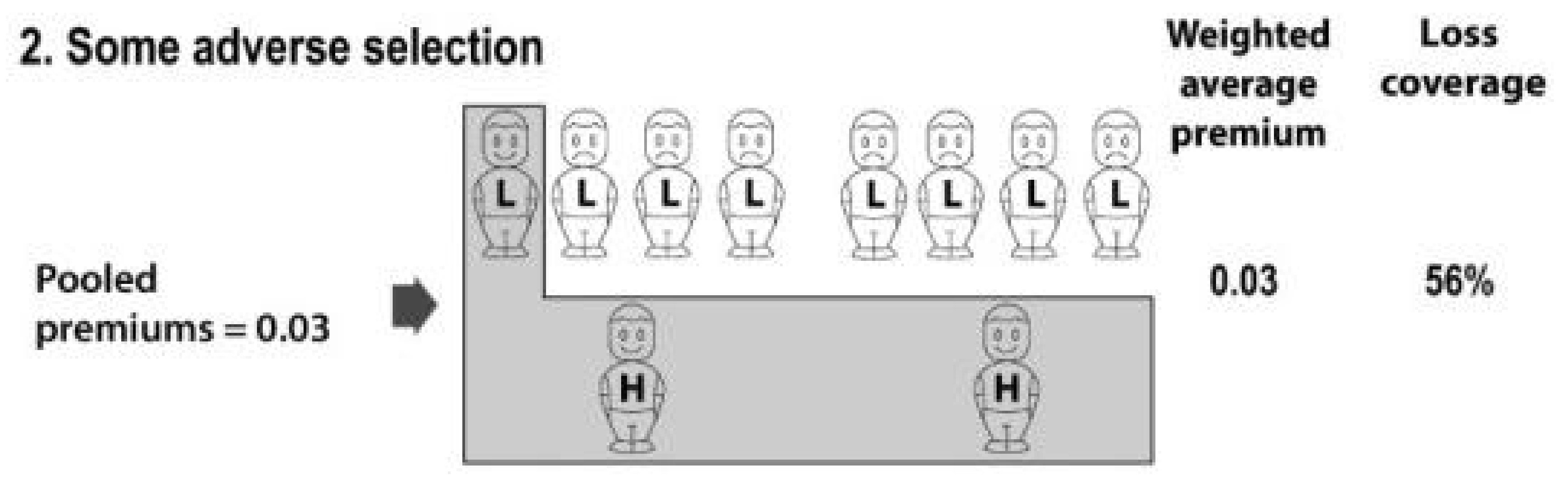
Now consider Scenario 2 in
Figure 2. Risk classification has been banned, and so insurers have to charge a common pooled premium to both higher and lower risks. Higher risks buy more insurance, and lower risks buy less (this is adverse selection). The pooled premium is set as the weighted average of the true risks, so that expected profits on low risks exactly offset expected losses on high risks. This weighted average premium is (1 × 0.01 + 2 × 0.04)/3 = 0.03. The shading symbolises that three risks (compared with five previously) buy insurance.
Note that, in Scenario 2, purchasing is skewed towards higher risks, the weighted average premium is higher, and the number of risks insured is lower. This triad comprises the essential features of adverse selection, which Scenario 2 accurately and completely represents. However, there is a surprise: despite the adverse selection in Scenario 2, the expected losses compensated by insurance for the whole population are now higher. That is, 56% of the population’s expected losses are now compensated by insurance, compared with 50% before. The calculation is:
Scenario 2, with a higher expected fraction of the population’s losses compensated by insurance—higher loss coverage—seems superior from a social viewpoint to Scenario 1. The superiority of Scenario 2 arises not despite adverse selection, but because of adverse selection.
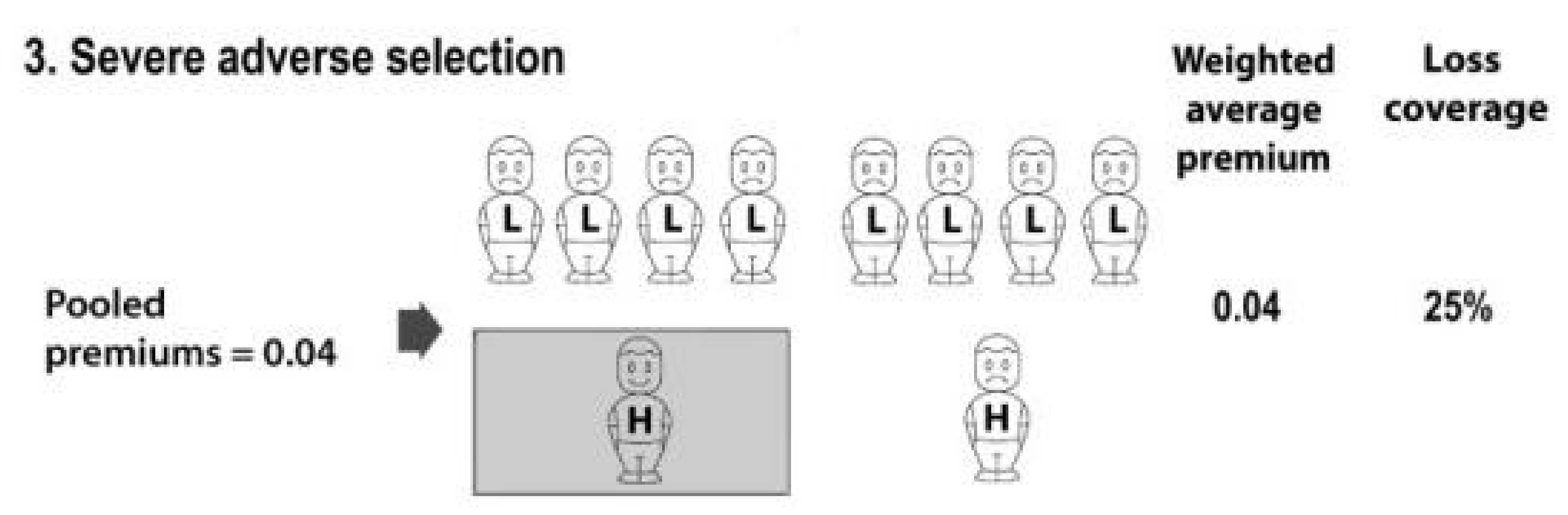
A ban on risk classification can also reduce loss coverage, if the adverse selection which the ban induces becomes too severe. This possibility is illustrated in Scenario 3 in
Figure 3.
In
Figure 3, adverse selection has progressed to the point where only one higher risk, and no lower risks, buys insurance. The expected losses compensated by insurance for the whole population are now lower. That is, 25% of the population’s expected losses are now compensated by insurance, compared with 50% in Scenario 1, and 56% in Scenario 2. The calculation is:
Taken together, the three scenarios suggest that banning risk classification can increase loss coverage if it induces the ‘right amount’ of adverse selection (Scenario 2), but reduce loss coverage if it generates ‘too much’ adverse selection (Scenario 3). Whether Scenario 2 or Scenario 3 actually prevails depends on the response of higher and lower risks to changes in prices—that is, the ‘demand elasticities’ of higher and lower risks.
3. Discussion
3.1. Discussion of Examples
The argument illustrated by the examples applies broadly. It does not depend on the specific context of life insurance, nor on any unusual choice of numbers for the examples. The key idea is that loss coverage—expected losses compensated by insurance for the whole population—is increased by a degree of adverse selection.
I argue that, for a public policymaker or regulator, loss coverage is a good metric for the social efficacy of insurance. I say this because compensation of the population’s losses is the main social purpose of insurance, which policymakers often seek to promote—by public education, by exhortation and sometimes by incentives such as tax relief on premiums. Policymakers may therefore prefer risk classification regimes that lead to higher loss coverage. This typically means regimes with some restrictions on risk classification, leading to some degree of adverse selection, and somewhat lower numbers insured than if adverse selection were eliminated.
My argument contrasts with orthodox economic arguments that public policymakers should either seek to minimise adverse selection, or make a trade-off against other policy preferences such as an ethical aversion to genetic discrimination. The orthodox arguments highlight that adverse selection leads to a rise in the average price of insurance and fall in numbers insured. What these arguments overlook is that adverse selection also leads to a shift in coverage towards higher risks (those who need insurance most). If this shift in coverage is large enough, it can more than outweigh the fall in numbers insured, so that loss coverage is increased.
One way to maximise loss coverage is to make insurance compulsory. Public policymakers sometimes adopt this solution (e.g., third-party liability insurance in many jurisdictions for road vehicles, or social insurance for risks such as unemployment). In other markets (e.g., life insurance), loss coverage is socially important, but arguably not enough to justify the infringement of freedom which compulsory insurance implies. In these markets, public policymakers may seek to raise loss coverage to the maximum level consistent with individual freedom of choice in insurance decisions. This can be achieved by limiting risk classification to the degree necessary to induce the ‘right’ level of adverse selection—the level which maximises loss coverage.
3.2. Comparison with Empirical Demand Elasticities
Which of Scenario 2 (good) or Scenario 3 (bad) in
Section 2 above will actually prevail if we restrict risk classification, say by banning use of genetic tests to set prices? This depends on the response of higher and lower risks to changes in the prices they face—that is, the demand elasticities of higher and lower risks. Generally speaking, it is helpful (in the sense of promoting Scenario 2) if two conditions are satisfied, First, lower risks should have lower elasticity (lower responsiveness to price), and higher risks should have higher elasticity (higher responsiveness to price). This combination implies that, when differentiation of prices by risk is restricted, low risks (who face a higher price than before) will tend to remain in the market, and high risks (who face a lower price than before) will tend to join the market, thus increasing loss coverage overall. Second, it is helpful if all demand elasticities have absolute value less than one; in other words, a given percentage rise in price causes a smaller percentage fall in demand (e.g., if price increases say 10%, demand falls only 5%).
2 There is a good deal of evidence that insurance demand elasticities are indeed often of absolute value less than 1.
Table 1 shows some relevant empirical estimates for insurance demand elasticities. Whilst the various contexts in which the estimates were made do not correspond exactly to the scenarios I use in
Section 2 above, the figures are at least suggestive of the possibility that the condition ‘demand elasticity of absolute value less than one” may often be satisfied in practice.
4. Some Considerations Which the Examples in Section 2 Leave Out
The possibility illustrated in
Section 2 that a degree of adverse selection increases loss coverage is quite general, but it may seem surprising in the light of traditional negative perceptions of adverse selection. The present section discusses a number of considerations which were omitted in
Section 2, and shows that they do not fundamentally change the validity of my main point.
4.1. Insurer Expenses and Profits
The examples abstract from all the loadings which insurers add to pure risk premiums to cover expenses and profits. Including the loadings makes the results more complicated, but without changing the main insight that some adverse selection (and hence some restriction on risk classification) is needed to maximise loss coverage.
4.2. Adverse Selection Involving Unusually Large Insurance Policies
For insurances such as life insurance where the amount of the potential claim (the ‘sum insured’) can be chosen by the customer, selection may involve not just a higher propensity to buy, but also the selective choice of a larger sum insured. This may be a serious concern if insurance can be bought in circumstances where a claim is more likely than not (e.g., life insurance when the purchaser has already been diagnosed with a terminal illness); in these circumstances, choosing a large sum insured (and paying the correspondingly large premium) may represent a very attractive investment opportunity. However, in circumstances where a genetic test result implies that a claim is more probable, but still unlikely, the perception that a customer can exploit any under-pricing by choosing a larger sum insured is often exaggerated by many commentators.
To understand this exaggeration, suppose that an insurer offers a life insurance premium based on an assumed risk of dying of p = 5% over the term of an insurance policy (say the next 25 years), but I have private information (e.g. a genetic test result), which indicates that my real risk is four times the normal level, which is p* = 20%. If I ‘invest’ in over-insurance, then my private knowledge means that I pay a ‘favourable’ price (5% rather than 20%). However, despite the ‘favourable’ price, it is still very likely (80% likely, with the true probabilities) that I will just pay all the premiums and not die in the term, so that no payout is made.
This one-shot gamble against long odds seems to me an unattractive investment proposition for the customer for a large bet. It would remain unattractive for a wide range of plausible probabilities and premiums. It may be worth buying a ‘normal’ level of cover
for insurance purposes, such as ensuring dependents have an adequate income in the unlikely event of my early death. However, the notion that over-insurance based on a private genetic test is a no-brainer
for investment purposes is not mathematically valid, if the loss event remains unlikely on the true probabilities.
3 4.3. Insurance as Probabilistic Good versus Reassurance Good
Loss coverage was defined above as expected losses compensated by insurance. Another way of characterising loss coverage is that it represents the coverage of insurance, weighted by the risks of those who are covered—that is, loss coverage is risk-weighted coverage.
The risk-weighted nature of loss coverage is predicated on the notion that the good provided by insurance is the contingent compensation of losses. This good materialises only in a particular future state of the world, which has different probabilities for higher and lower risks. That is, insurance is a probabilistic and individually heterogeneous good. For such a good, one unit of sales to a higher risk individual is a different (more valuable) good compared with one unit of sales to a lower risk individual. In loss coverage, this difference is reflected in the risk-weighting of coverage.
This framing of insurance as a probabilistic good is implicit in most commentary on risk classification, and it seems appropriate when considering public policy at a population and objective level. However, at an individual and subjective level, insurance can also be framed as a non-probabilistic good, where insurance represents certain ‘freedom from worry’ in the present, rather than as contingent compensation of losses in the future. Insurance framed as ‘freedom from worry’ is a non-probabilistic good. In the specific insurance context, we might call it a reassurance good.
If insurance is framed as a reassurance good, is it still more valuable for higher risks in proportion to their risk (as the definition of loss coverage implies)? I would argue yes: four times the risk means four times the worry. However, another argument is that the value of reassurance provided by a particular class of insurance (say life insurance) is broadly the same for all customers, and largely invariant to individual variations in probabilities of loss. If the latter argument is favoured, then the risk-weighted nature of loss coverage may overstate the benefits of covering higher risks.
4.4. Other Rationales for Restrictions on Insurance Risk Classification
Restrictions on risk classification may be justified by concerns quite different from the aggregate insurance market outcomes, which are the focus of this paper. These concerns may include perceptions of unfairness, inaccuracy, prejudice, pre-existing disadvantage, controllability, transparency, consent, and perverse incentives (e.g., not to undergo clinically useful tests because of worry about insurance consequences). These concerns do not in any way detract from the main point of this paper; they provide
additional reasons for considering some restrictions on risk classification.
4 4.5. Loss Coverage: The Insurer’s Perspective
Whilst this paper focuses mainly on a public policy perspective, the loss coverage concept can also be viewed from the insurer’s perspective. Maximising loss coverage is equivalent to maximising insurers’ premium income. If profit loadings are proportional to premiums, maximising loss coverage could be a desirable objective for insurers. Thus, even from the insurer’s perspective, adverse selection is not always a bad thing.
5. Conclusions
Public policy on genetics and insurance is typically perceived as a balancing act between two competing considerations. On the one hand, there are social, ethical and public health arguments, which suggest that the ability of insurers to discriminate on the basis of predictive genetic tests should be limited. On the other hand, there are economic arguments under the rubric of ‘adverse selection’, which suggest that limiting insurance discrimination has costs, not just for insurers, but for society as a whole. I argue that this trade-off is often illusory. From the viewpoint of society as a whole, not all adverse selection is adverse; public policy should not aim to eliminate all adverse selection. Limits on insurance discrimination that induce the right amount of adverse selection (but not too much adverse selection) can increase the expected losses compensate by insurance—that is, increase ‘loss coverage’—and so make insurance work better.
The right amount of restriction depends on the response of higher and lower risks to changes in the prices they face, that is the demand elasticities of higher and lower risks. Some restrictions on genetic tests may well be helpful in inducing the right amount of adverse selection (that is, the level that maximises loss coverage); on the other hand, restrictions on age as well might ‘go too far’, and so induce too much adverse selection and lower loss coverage.
The argument of this article is distinct from deontological arguments that it is morally wrong for insurers to discriminate on the basis of genetic tests, or consequentialist arguments that such discrimination will deter people from seeking clinically useful tests, or lead to stigmatisation affecting employment and other relations. These wider arguments may have merit. However, the argument in this article is based solely on aggregate insurance market outcomes; it is a matter of arithmetic, not of ethics.