Neighborhoods and Racial Inequality in Assortative Mating and Fertility in the United States

Abstract

While racial inequalities in assortative mating and fertility have been well documented, the role of neighborhoods has frequently been overlooked in explaining these disparities. In this study, I use restricted birth record data from the state of California with neighborhood-level socioeconomic and demographic data to explore the roles of neighborhoods and structural neighborhood inequality in mediating racial inequality in assortative mating and fertility in 2018 and 2019. Overall, neighborhood disadvantage, particularly disadvantage measured in a neighborhood’s mobility network, mediated a substantial proportion of the disparity in fathers’ educational attainment between White and Black or Hispanic mothers in California in 2018 and 2019. Additionally, while I observe evidence of Black and Hispanic neighborhoods having significantly greater fertility rates than White neighborhoods, this gap can be entirely explained by neighborhood disadvantage. Lastly, a significant share of the fertility gap between less-educated White and Black women is mediated by neighborhood disadvantage. This study motivates more research at the intersection of assortative mating and fertility at the neighborhood scale.

1. Introduction

Assortative mating and fertility are central concepts at the intersection of social stratification and demography. The strongest intergenerational correlations concern education [1]. Assortative mating leads to the concentration of investments children receive, strengthening the transmission of advantages and household resources over generations and amplifying intragenerational inequality.

Children born to educated parents generally receive substantially more education than children born to uneducated parents or only one educated parent [2]. A higher education level is valuable to children and constitutes the central mediator behind numerous stratification processes. According to the results of certain studies, individuals who receive a higher level of education tend to have higher incomes and enjoy better health than those with a lower level of education [3,4,5,6]. Additionally, assortative mating is consequential for intragenerational inequality because spousal education considerably influences wealth accumulation and health [7,8,9,10].

Furthermore, recent scholarship, particularly Maralani has proposed assortative mating as contributing to the perpetuation of racial inequality between generations [11]. Assortative mating generally leads to the concentration of parental resources and amplifies inequality in the investment made into children [12,13,14,15,16,17]. Maralani found that, compared with well-educated White women, well-educated Black women tend to marry less-educated men [11]. The association between the education levels of fathers and children appears to be weaker for Black children. However, Maralani found that lower levels of educational attainment among fathers of children born to Black women still contribute substantially to racial inequality among children [11].

Differences in fertility between Black and White women also contribute to intergenerational racial stratification. Maralani found that Black women with a lower level of education have substantially higher fertility rates than equally educated White women [11]. However, well-educated Black women have similar levels of fertility as White women. One consequence of these fertility patterns is that a disproportionately higher number of Black than White children are born to less-educated women.

Fertility rates can be broadly consequential for families and neighborhoods. Studies have shown that children born to families with many siblings have worse life outcomes [18,19,20,21,22]. Meanwhile, criminological research has also demonstrated that neighborhoods in the United States with younger populations—particularly, large, young, male populations—are plagued with substantially more crime and disorder [23,24].

Although demographers commonly study the causes of assortative mating, disentangling these causal factors poses significant challenges owing to endogeneity issues. For example, neighborhoods are endogenous to assortative mating to the extent that women who marry well-educated men tend to live in neighborhoods with a high SES because of their union directly contributing to the level of SES in the neighborhood. However, non-marital childbearing—fewer children being born to married and cohabiting parents [14] has increased substantially over the last few decades, especially among less-educated non-White women [12].

Methodologically, an increase in non-marital, non-cohabiting childbearing suggests that neighborhoods are less endogenous to assortative mating (as indicated by the educational association between parents). Rather, neighborhoods may increasingly serve as relevant mating markets for individuals to meet. In this sense, neighborhood residence may become a cause rather than a consequence of mating outcomes. Some recent research has examined assortative mating as it contributes to residential sorting, though evidence is still rather limited on its impact [25,26].

Data on everyday mobility patterns, which can capture the everyday exposures of neighborhood residents and explain substantial variation in various adverse neighborhood outcomes, such as violence, COVID-19 incidence, fatal police shootings, and adverse birth outcomes, have been increasingly used in sociological studies of neighborhoods [24,27,28,29,30]. Neighborhoods connected to socioeconomically disadvantaged neighborhoods experience worse outcomes in various ways. The visit-weighted level of disadvantage of the neighborhoods from which another neighborhood receives and sends visitors is termed mobility-based disadvantage. It contrasts with the mean SES of a neighborhood’s residents, known as residential disadvantage. Generally, for most adverse neighborhood outcomes, mobility-based disadvantage has substantially more predictive power than residential disadvantage [27].

I jointly focus on neighborhood disadvantage, assortative mating, and fertility as both concepts are of central importance to racial inequality and social stratification [31], and have been jointly studied before [11]. I hypothesize that well-educated mothers in mobility-disadvantaged neighborhoods are more likely to have children with less-educated men. If a woman is not already in a relationship, her everyday mobility patterns likely determine the mating market available. Consequently, well-educated women who reside in mobility-disadvantaged neighborhoods likely have fewer options for well-educated men, making them more likely to enter into relationships with less-educated men. Additionally, non-marital fertility may be more significant for women living in mobility-disadvantaged neighborhoods. Past research has suggested that fertility tends to be higher among women in more disadvantaged circumstances [32,33,34,35]. Additionally, short-term sexual relationships tend to be more common in mobility-disadvantaged neighborhoods, as past research has revealed that the exact neighborhood mechanisms linked to mobility-based disadvantage are associated with a higher occurrence of such relationships [36]. However, testing these mechanisms is beyond the scope of the analysis.

Current Study and Hypotheses

This study investigates whether structural neighborhood inequalities help explain racial disparities in assortative mating and fertility. I hypothesize the following:

1.

Well-educated mothers in mobility-disadvantaged neighborhoods are more likely to have children with less-educated men, due to restricted exposure to highly educated partners.

2.

Fertility rates will be higher in racially disadvantaged neighborhoods, and these differences will be mediated by both residential and mobility-based neighborhood disadvantages.

In this paper, I combine restricted birth record data from California with neighborhood-level socioeconomic and demographic data to explore the relationship between race, educational attainment, neighborhoods, and assortative mating and fertility. I center on and measure assortative mating around the birth of a child, deviating from the conventional focus on formalized unions (e.g., marriage) in past research. Furthermore, while substantial research has investigated assortative mating at broader levels of geography, few studies have carefully examined the role of neighborhoods. Studies that have investigated assortative mating and the role of fertility and family formation in terms of neighborhoods have performed so in a limited manner, failing to consider modern approaches to measuring neighborhood socioeconomic status (SES), such as mobility-based disadvantage [37,38,39]. In this paper, I explore neighborhoods to determine the variation in assortative mating (in terms of education) and understand how neighborhood-level factors contribute to such disparities. Notably, this paper is the first to combine novel (mobility-based) measures of neighborhood disadvantage with assortative mating and fertility data—providing an updated and more advantaged understanding of how neighborhood contexts might shape these important outcomes.

2. Method

2.1. Data

This study relies on data from three different sources. First, birth record data were obtained from the state of “California’s Comprehensive Birth File”, a dataset containing records of all births registered in California that occurred in 2018 and 2019. It includes almost all the fields on California birth certificates and various demographic data on mothers and fathers, such as age, race or ethnicity, and educational attainment. The dataset also mentions the census tract where the mother resides at the time of a child’s birth. One notable limitation of this dataset is that it does not contain data on births outside of California. Presumably, some women who reside in California give birth in other states, although it seems unlikely that this would be a large enough number to substantially bias estimates. This analysis utilizes the entire record of births to mothers residing in California, with the criterion being that both parents were at least 25 years of age (cases where the father or mother had missing age, race, or education data are also excluded). It should be noted that similar analyses were performed among cases with parents under age 25, revealing the same substantive findings. These results are available upon request to the author. The 25-year cutoff is preferred because individuals under the age of 25 are substantially less likely to have reached their maximal educational attainment, and this cutoff aligns with how the American Community Survey reports educational attainment data at the neighborhood level.

The second dataset was the “2015–2019 American Community Survey (ACS) five-year estimates”, constituting a random sample of 5% of all American households surveyed during 2015–2019, and the most recent version available for 2010 census tract definitions (which are necessary for linking purposes). I draw on this data to create several demographic and socioeconomic variables for census tracts, estimating a nationwide residential disadvantage score for all. Drawing from past research, this residential disadvantage score is estimated as a principal component of seven neighborhood attributes: percentages of poverty, unemployment, single-headed households, public assistance receipt, adults without a high school diploma, adults with a bachelor’s degree or higher, and workers who are managers or professionals [40].

The third dataset was the Safegraph “Social Distancing Metrics” dataset. Safegraph is a company that aggregates mobility data from a panel dataset of 45 million mobile devices. Its Social Distancing Metrics dataset provides census block group-level data on individuals’ everyday mobility patterns for each day in 2019. It estimates the number of residents in each US census block group who visit other census block groups, including specific information on the visited census block groups. Home locations for smartphones are estimated based on the device’s mean nighttime (6 p.m. to 7 a.m.) location over the preceding six weeks, to the measurement of the device’s mobility. A device owner’s visit to another neighborhood is estimated based on a cluster of pings in a census block group for at least a one-minute duration. As census block groups nest perfectly in census tracts, the former’s everyday mobility patterns are aggregated into the latter. This study followed the exact methodology used by [27].

I generated a mobility network with values. ${V(n}_{ij})$, representing the volume of mobility of residents of census tract i to census tract j over all days (a) in 2019. This operation can be written as follows:

$${V(n}_{ij})=\left.{\displaystyle \frac{\sum _{a=1}^D{n}_{aij}}{\sum _{a=1}^D\sum _{j=1}^N{n}_{aij}}} \right|i\ne j$$

Next, I estimated measures of mobility-based disadvantage following recent research [27]. I combined directed mobility patterns with the measure of residential neighborhood disadvantage (RND) to estimate a neighborhood’s IND (Indegree neighborhood disadvantage) score as the visit-weighted average RND scores of the other neighborhoods from which it receives visits. Following past methodology, I restricted visits to only those between census tracts within the same commuting zone. For counties bordering commuting zones, my approach allowed adjacent counties in other commuting zones to contribute to neighborhood mobility patterns. I accounted for variation in the sending neighborhood’s population sizes and visit probabilities in the following equation:

$${IND}_i={\displaystyle \frac{\sum _{j=1}^N{RND}_j\times V\left(n_{ji}\right)\times P_j}{\sum _{j=1}^{N}V\left(n_{ji}\right)\times P_j}}, i\ne j$$

where $P_j$ is the population of a sending neighborhood.

Additionally, I estimated a symmetric measure: outdegree neighborhood disadvantage (OND). This is the weighted average disadvantage level of neighborhoods to which any neighborhood $n_i$ is structurally connected through its residents’ within-Commuting zone mobility visit patterns to these neighborhoods, as follows:

$$OND=\sum _{j=1}^N\left({\displaystyle \frac{{V(n}_{ij})}{{V(n}_i)-{V(n}_{ii})}}\times {RND}_j\right), i\ne j$$

In this equation, ${V(n}_i)$ represents the total number of visits from tract i, ${V(n}_{ii})$ represents visits within tract i (loops), and ${RND}_j$ represents the residential disadvantage score of the visited neighborhood.

As I theoretically expected that both OND and IND are important to assortative mating, I combined them into a single measure using simple averaging (mobility-based neighborhood disadvantage; MND):

$$MND={\displaystyle \frac{IND+OND}{2}}$$

All three datasets are merged by linking using FIPS codes from the US Census Bureau 2010 Census Tract definitions.

2.2. Analysis

This methodological analysis is divided into two sections. First, this study explores assortative mating regarding individual race and neighborhood variables by utilizing linear multilevel models. The primary outcome of interest was whether a father had at least a bachelor’s degree, conditional on the mother’s education, race, and neighborhood attributes. The following model(s) were estimated using the lme4 package in R:

$${FBACH}_{ij}={\beta }_{0j}+{\beta }_1\left({MLESS}_{ij}\right)+{\beta }_2\left({MBACH}_{ij}\right)+{\beta }_3\left({MBLACK}_{ij}\right)+{\beta }_4\left({MHISP}_{ij}\right)+{\beta }_5\left({MASIAN}_{ij}\right)+{\beta }_6\left({MOTHER}_{ij}\right)+{\epsilon }_{ij}$$

$${\beta }_{0j}={\gamma }_{00}+{\gamma }_1\left({RND}_j\right)+{\gamma }_2\left({MND}_j\right)+u_{0j}$$

In the above equation, the dummy variables $FBACH$, $MLESS$, $MBACH$, $MBLACK$, $MHISP$, $MASIAN$, and $MOTHER$ indicate whether the father holds at least a bachelor’s degree, the mother has less than a high school education, the mother holds at least a bachelor’s degree, the mother is non-Hispanic Black, the mother is Hispanic (of any race), the mother is non-Hispanic Asian, and the mother is non-Hispanic Other, respectively. The omitted reference category for the mother’s education is high school or some college education (without a bachelor’s degree), and the omitted reference category for race is non-Hispanic White. This equation represents a simple multilevel random-intercept model wherein individuals are nested within neighborhoods, with the individual-level predictors being educational attainment and the mother’s race, and the neighborhood-level predictor being neighborhood disadvantage.

Table 1. Assortative Mating Analysis Summary Statistics.

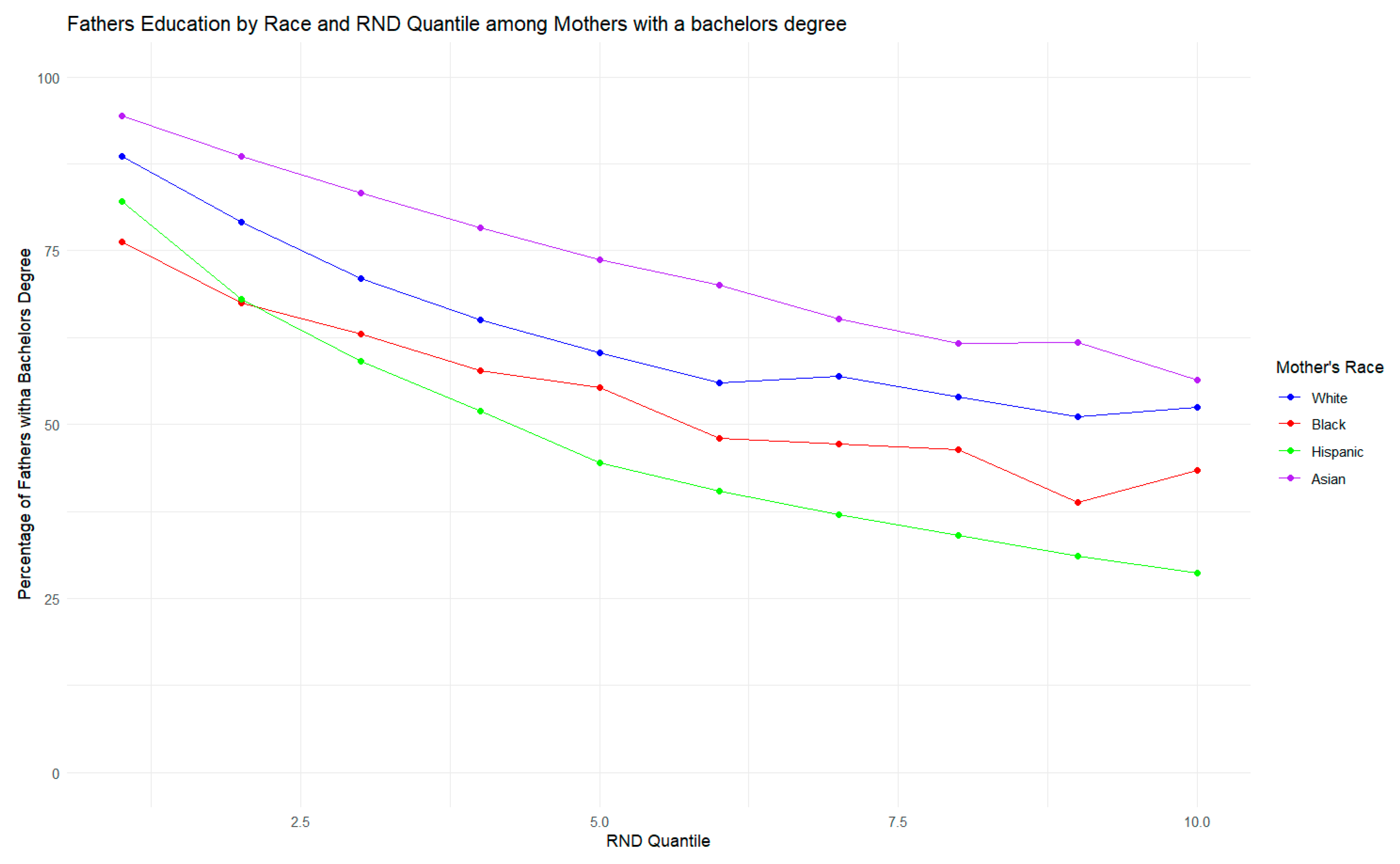
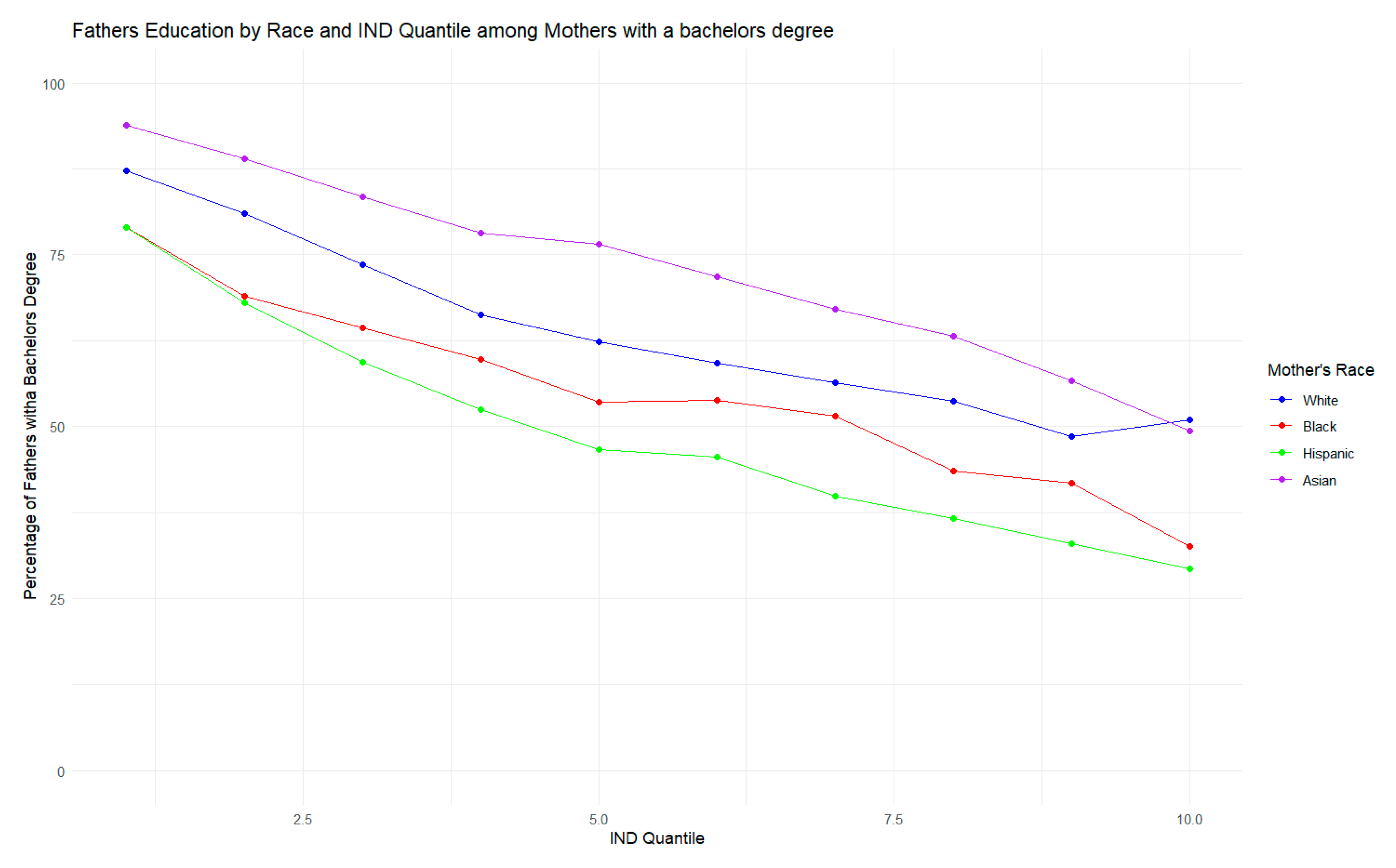
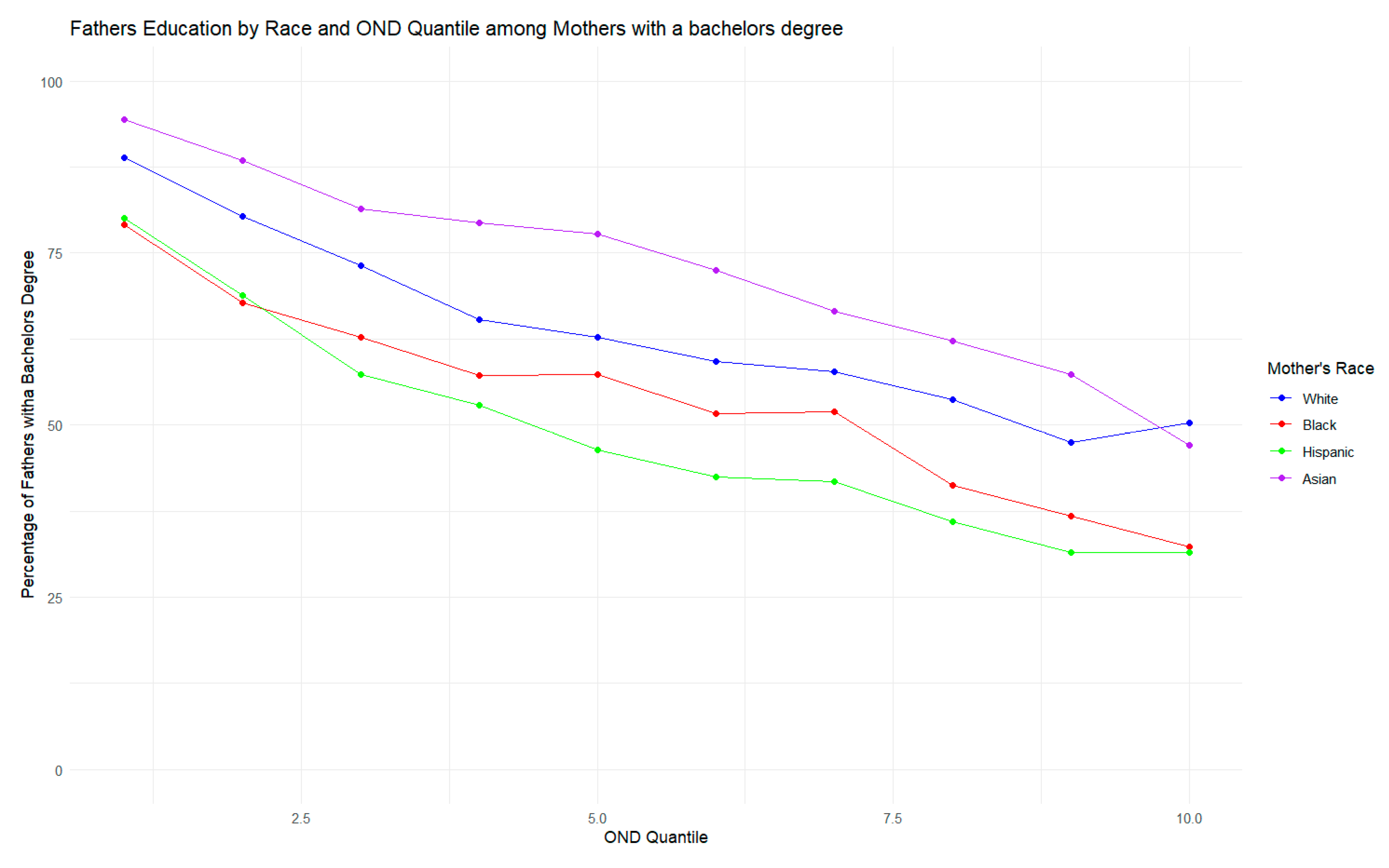
Variable	Mean	SD	Min	Pctile [25]	Pctile [75]	Max
White	0.3	0.47	0	0	1	1
Black	0	0.207	0	0	0	1
Hispanic	0.4	0.493	0	0	1	1
Asian	0.2	0.398	0	0	0	1
Other	0	0.101	0	0	0	1
Mother < HS	0.1	0.293	0	0	0	1
Mother = HS	0.5	0.498	0	0	1	1
Mother ≥ Bach.	0.4	0.497	0	0	1	1
MND	0	0.634	−1.617	−0.482	0.451	1.813
RND	0	1.078	−2.371	−0.821	0.807	3.725
Father ≥ Bach.	0.4	0.486	0	0	1	1
NH Men’s Educ.	0.3	0.223	0	0.137	0.475	0.96

Note. RND: residential neighborhood disadvantage, MND: mobility-based neighborhood disadvantage, HS: High school or equivalent education, NH Men’s Educ.: proportion of men aged 25 years in the census tract who held at least a bachelor’s degree.

summarizes the statistics for this analysis.

Although, two alternative variations were explored: a linear multilevel model predicting the father’s education as an integer variable and the two aforementioned models with the father and mother switched (estimating the mother’s ed-ucation based on the father’s attributes).

Fertility Analysis

Negative binomial models were used for the second analysis to estimate fertility among neighborhood subpopulations. Negative binomial models are appropriate here, given the nature of birth totals as a potentially over-dispersed count variable [41]. Specifically, the female population in each census tract was divided into six categories: women with less than a high-school education aged 25–34 and 35–44 years; women with a high-school education aged 25–34 and 35–44 years; and women with at least a bachelor’s degree aged 25–34 and 35–44 years. It should be noted that similar analyses were performed among cases with parents under age 25, revealing the same substantive findings. These results are available upon request to the author.

A dataset involving unique combinations of one of the six subpopulations and census tracts was constructed. The outcome variable of interest was the number of births in the dataset for each subpopulation. A logged population offset equivalent to the estimated size of the subpopulation was also included within the neighborhood based on the ACS 2015–2019 5-year estimates, as well as two-way fixed effects of adjusting the effect of educational attainment and age category on fertility rates within the subpopulation. Subsequently, standard errors at the census tract level were clustered to account for the correlation in errors between observations. The model was estimated using the “fixest” package in R. My primary model can be represented as follows:

$$\mathrm{l}\mathrm{n}\left({\mu }_{ijk}\right)={\beta }_1\left({BLACK}_i\right)+{\beta }_1\left({HISP}_i\right)+{\beta }_1\left({ASIAN}_i\right)+{\beta }_1\left({OTHER}_i\right)+{\beta }_1\left({RND}_i\right)+{\beta }_1\left({MND}_i\right)+\mathrm{l}\mathrm{n}\left({pop}_{ijk}\right)+{∆}_j+{\nabla }_k+{\epsilon }_i$$

where ${\mu }_{ijk}$ is the count of births to mothers in the neighborhood i who have education j and are in age category k; ${BLACK}_i$, ${HISP}_i$, and ${ASIAN}_i$ are indicator variables denoting whether neighborhood i is more than 50% non-Hispanic Black, more than 50% Hispanic (of any race), or more than 50% Asian, respectively; ${OTHER}_i$ is an indicator variable denoting if neighborhood i does not fall into any of the aforementioned categories (or is more than 50% non-Hispanic White); ${RND}_i$ is a continuous variable representing the residential disadvantage score associated with neighborhood i; ${MND}_i$ is a continuous variable representing the mobility-based disadvantage score associated with neighborhood i; $\mathrm{l}\mathrm{n}\left({pop}_{ijk}\right)$ represents a logged offset term based on the estimated size of the subpopulation in the neighborhood; ${∆}_j$ represents fixed effects for the educational category; ${\nabla }_k$ represents fixed effects for age category; and ${\epsilon }_i$ represents an error term clustered at the census tract level.

Table 2. Fertility Analysis Summary Statistics.

Variable	Mean	Sd	Min	Pctile [25]	Pctile [75]	Max
Births	9	11.392	0	2	12	389
Population	118.1	115.698	0	36.194	165.612	2636.133
White	0.4	0.481	0	0	1	1
Black	0	0.089	0	0	0	1
Hispanic	0.3	0.467	0	0	1	1
Asian	0	0.212	0	0	0	1
Other	0.3	0.438	0	0	1	1
RND	0	1.079	−2.371	−0.868	0.775	3.725
MND	0	0.624	−1.617	−0.493	0.413	1.813

Note. RND: residential neighborhood disadvantage, MND: mobility-based neighborhood disadvantage.

presents the summary statistics for this analysis.

3. Results

3.1. Father’s Education

To examine patterns of educational assortative mating, Figure 1, Figure 2 and Figure 3 display the probability that fathers hold a bachelor’s degree among births to mothers who themselves have a bachelor’s degree, disaggregated by the mother’s race and neighborhood disadvantage. Figure 1 illustrates these associations using residential neighborhood disadvantage (RND), while Figure 2 and Figure 3 capture analogous patterns using indegree (IND) and outdegree (OND) mobility-based disadvantage, respectively. These figures collectively demonstrate substantial racial gradients in the association between neighborhood disadvantage and assortative mating. While all racial groups of women are likely to have children with less-educated men in more disadvantaged neighborhoods, the intercepts vary by race. Additionally, the slope appears steeper for IND and OND compared to RND.

Table 3. Multilevel Linear Probability Models Predicting Father’s Educational Attainment.

	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
(Intercept)	0.138 ***	0.226 ***	0.243 ***	0.236 ***	0.235 ***	0.083 ***
	(0.001)	(0.001)	(0.002)	(0.001)	(0.001)	(0.002)
<HS	−0.118 ***	−0.063 ***	−0.051 ***	−0.038 ***	−0.039 ***	−0.041 ***
	(0.002)	(0.002)	(0.002)	(0.002)	(0.002)	(0.002)
≥Bach.	0.579 ***	0.498 ***	0.418 ***	0.411 ***	0.411 ***	0.409 ***
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Black		−0.126 ***	−0.084 ***	−0.067 ***	−0.067 ***	−0.067 ***
		(0.003)	(0.003)	(0.003)	(0.003)	(0.003)
Hispanic		−0.164 ***	−0.120 ***	−0.103 ***	−0.101 ***	−0.098 ***
		(0.001)	(0.002)	(0.002)	(0.002)	(0.001)
Asian		0.088 ***	0.074 ***	0.079 ***	0.078 ***	0.077 ***
		(0.002)	(0.002)	(0.002)	(0.002)	(0.002)
Other		−0.097 ***	−0.069 ***	−0.064 ***	−0.065 ***	−0.064 ***
		(0.006)	(0.005)	(0.005)	(0.005)	(0.005)
RND				−0.099 ***	−0.060 ***
				(0.001)	(0.002)
MND					−0.079 ***	−0.029 ***
					(0.003)	(0.002)
NH Men’s Educ.						0.469 ***
						(0.006)
Random Intercepts			X	X	X	X
N	441,096	441,096	441,096	441,096	441,096	441,096
Log-likelihood	−202,907.194	−190,504.645	−179,132.229	−175,674.355	−175,293.132	−173,942.173
AIC	405,822.389	381,025.290	358,282.457	351,368.711	350,608.265	347,906.346

Note: *** p < 0.001. RND: residential neighborhood disadvantage, MND: mobility-based neighborhood disadvantage, HS: High school education or equivalent, NH Men’s Educ.: proportion of men aged 25 years in the census tract who held at least a bachelor’s degree.

presents the results of the first set of analyses using a linear probability model for straightforward interpretation. Similar models were tested with different functional forms. Notably, however, the predicted probabilities of this linear model were well between 0 and 1 (not near the margins), constituting a relatively appropriate use of the linear probability model. The same general results can be replicated with a multilevel logit model.

Model 1 provides a simple one-level model of whether fathers held at least a bachelor’s degree based on the mothers’ education. It reveals that, relative to a mother only having a high school diploma, a mother having at least a bachelor’s degree is a significantly positive predictor (p < 0.001) of a father also having a bachelor’s degree. This model also reveals that, relative to a mother having only a high school education, a mother having less than a high school education is a significantly negative predictor (p < 0.001) of a father having a bachelor’s degree.

Model 2 includes the mother’s race, which slightly attenuates the effect of the mother’s education, although both these indicator variables remain highly significant (p < 0.001). Additionally, the results of the model reveal racial inequalities in assortative mating. Controlling for educational attainment, Black women are significantly (p < 0.001) less likely to have children with men who hold a bachelor’s degree than are White women. Notably, the inequality between Black and White women is smaller than that between Hispanic and White women. Further, controlling for educational attainment, Hispanic women are also significantly (16.4%; p < 0.001) less likely to have children with men who have bachelor’s degrees than are White women. Controlling for educational attainment, Model 2 reveals that Asian women are significantly (p < 0.001) more likely to have children with men who have bachelor’s degrees than are White women, and that Other women are significantly (p < 0.001) less likely to have children with men who held a bachelor’s degree than are White women.

Model 3 adds neighborhood random intercepts, producing substantially different Level 1 coefficients than Model 2. However, this should not be interpreted to mean that neighborhood mediates the association between mothers’ and fathers’ educational attainment. Rather, neighborhoods should be viewed as endogenous to assortative mating. Women who enter into relationships with well-educated men tend to live in certain high-SES neighborhoods directly because of their spouses’ SES (or because of their unmeasured attributes).

Additionally, Model 3 has substantially different racial coefficients from Model 2. In the latter, Black women were significantly less likely to have children with men who held bachelor’s degrees than were White women. However, Model 3 suggests that controlling for educational attainment and neighborhood, Black women are significantly more likely to have children with men holding bachelor’s degrees than are White women. Again, this result does not necessarily indicate that one’s neighborhood mediates the association between mothers’ race and fathers’ educational attainment.

Model 4 includes a neighborhood-level variable to examine the factors affecting variation in educational assortativity between neighborhoods. Specifically, it includes the RND variable, which measures the SES associated with a neighborhood’s residents, with greater values indicating lower SES (more neighborhood disadvantage). Generally, fathers in neighborhoods with higher RND are less likely to hold a bachelor’s degree. In this application, RND can be considered relatively endogenous to assortative mating, assuming that most fathers and mothers live in the same neighborhoods. As expected, RND is negatively and significantly (p < 0.001) associated with the probability of a father holding a bachelor’s degree.

Although RND is highly endogenous to fathers’ educational attainment, mobility-based disadvantage appears much less endogenous. However, residing in a high-SES neighborhood may suggest that a woman has already entered into a relationship with a well-educated man, while residing in a mobility-based disadvantaged neighborhood does not inherently imply this. Thus, the primary way whereby mobility-based disadvantage is associated with a spouse’s educational attainment may be through this disadvantage’s association with the mating market available to women.

Model 5 includes the same predictors as Model 4, as well as incorporates the mobility-based disadvantage measure. As expected, mobility-based disadvantage is a strongly significant (p < 0.001) negative predictor of a father holding at least a bachelor’s degree. Model 6 is similar to Model 5, except that, instead of measuring RND, it directly measures the proportion of men aged 25 years who held at least a bachelor’s degree. This model provides a more accurate assessment of whether the SES of mobility-connected neighborhoods impacts assortative mating. As anticipated, the model reveals that the proportion of men in the neighborhood with at least a bachelor’s degree is an extremely strong predictor of the probability of a father holding at least a bachelor’s degree. However, it also reveals that mobility-based disadvantage remains a highly significant (p < 0.001) negative predictor of the probability of a father holding a bachelor’s degree.

3.2. Fertility Differences Between Neighborhoods

This study also explores the neighborhood-level factors associated with fertility (

Table 4. Predicting the Number of Births to Neighborhood Subpopulations of Women.

	Model 1	Model 2	Model 3
Black	0.11 **	0.00	−0.02
	(0.04)	(0.04)	(0.04)
Hispanic	0.14 ***	−0.03 *	−0.03 *
	(0.01)	(0.01)	(0.01)
Asian	0.01	0.00	0.03
	(0.04)	(0.04)	(0.04)
Other	0.02	−0.04 ***	−0.03 **
	(0.01)	(0.01)	(0.01)
RND		0.10 ***
		(0.01)
MND			0.20 ***
			(0.01)
Population Offset	X	X	X
Age FE	X	X	X
Education FE	X	X	X
N	45,792	45,792	45,792
AIC	242,814.28	242,242.36	241,885.50
BIC	242,884.13	242,320.94	241,964.09
Pseudo R2	0.18	0.18	0.19

Note: *** p < 0.001; ** p < 0.01; * p < 0.05. Alpha parameters vary from 3.90 to 4.05 and are highly significant in all models. RND: residential neighborhood disadvantage, MND: mobility-based neighborhood disadvantage.

). Model 1 is a simple negative binomial model predicting the number of births in a particular neighborhood’s subpopulation based on its racial categorization. It is offsetting for population size, with fixed effects for age and educational attainment, and standard errors clustered at the neighborhood level. Model 1 reveals that, compared with White neighborhoods, Black and Hispanic neighborhoods exhibit significantly higher birth rates. All else remaining equal, Black and Hispanic neighborhood subpopulations experience approximately 12% and 15% more births, respectively, than do White neighborhood subpopulations. The difference between Asian/Other and White neighborhoods is not statistically significant.

Model 2 includes the same predictors as Model 1, and additionally includes the RND measure. Introducing this single variable completely diminishes the initially strong positive coefficients for Black and Hispanic women in Model 1, transforming them into negative coefficients. This can be interpreted as residential disadvantage mediating entire differences in birth rates between Black, Hispanic, and White neighborhoods. Model 3 includes the same predictors as Model 2, with the exception that MND is substituted for RND. MND is an even stronger predictor of birth rates than is RND, which can also fully mediate the effect of a Black or Hispanic neighborhood on birth rates. These results suggest that inequalities in fertility based on neighborhood racial composition can be fully explained by neighborhood disadvantage.

3.3. Fertility Among Less-Educated Women

This study augments prior studies by exploring even more specific subpopulations. Rather than examining the age–education subpopulations of women, this section investigates the age–race subpopulations of high-school-educated women. Prior research has revealed that high fertility rates among less-educated Black women contribute to educational inequality between racial groups [11]. This short analysis determines neighborhoods’ role in fertility differences between Black and White women (

Table 5. Predicting the Number of Births to Neighborhood High-School Educated Subpopulations of Women.

	Model 1	Model 2	Model 3	Model 4
Black	0.13 ***	0.07 ***	0.06 ***	0.07 ***
	(0.01)	(0.01)	(0.01)	(0.01)
Hispanic	0.34 ***	0.28 ***	0.27 ***	0.28 ***
	(0.01)	(0.01)	(0.01)	(0.01)
Asian	0.08 ***	0.07 ***	0.08 ***	0.08 ***
	(0.01)	(0.01)	(0.01)	(0.01)
Other	−0.99 ***	−1.01 ***	−1.01 ***	−1.00 ***
	(0.02)	(0.02)	(0.02)	(0.02)
RND		0.11 ***		−0.03 ***
		(0.01)		(0.01)
MND			0.27 ***	0.32 ***
			(0.01)	(0.02)
N	74,715	74,715	74,715	74,715
AIC	224,866.30	223,983.87	223,152.87	223,126.76
BIC	224,921.63	224,048.42	223,217.42	223,200.53
Pseudo R2	0.26	0.26	0.26	0.26

Note: *** p < 0.001; Alpha parameters vary from 3.70 to 4.07 and are highly significant in all models. Note. RND: residential neighborhood disadvantage, MND: mobility-based neighborhood disadvantage.

).

Model 1 is a simple negative binomial model predicting the birth count of a particular neighborhood’s subpopulation based on its racial categorization, offsetting for population size, with fixed effects for age and standard errors clustered at the neighborhood level. Compared with White female high-school-educated subpopulations, Black and Hispanic subpopulations exhibit substantially higher birth rates. Asian women exhibit significantly (p < 0.001) higher birth rates as well, although this difference is much smaller. Notably, high school-educated “Other” women exhibit substantially lower birth rates. I hypothesize that this powerful effect for “Other” is likely a result of “Other” women more often being miscoded as “missing” in the birth record data. Consequently, it perhaps does not seem as though many “Other” women are giving birth.

Model 2 adds neighborhood residential disadvantage. Notably, the coefficients for Black and Hispanic women are substantially attenuated owing to conditioning on residential disadvantage. Model 1 indicates that all else remaining equal, Black women recorded 14% more births than did White women, which fell to 7% in Model 2. Residential disadvantage appears to be a highly significant (p < 0.001) positive predictor of birth rates among high-school-educated women. Models 3 and 4 explore mobility-based disadvantage, another highly significant, positive predictor of birth rates among high-school-educated women. Model 4 indicates that it is a dominant predictor of birth rates among them. Ultimately, these models suggest that much of the increased fertility among high-school-educated Black and Hispanic women can be attributed to their tendency to reside in highly disadvantaged neighborhoods.

4. Discussion

This study reveals two main findings. First, neighborhoods are highly relevant to racial disparities in educational assortative mating. Compared with White women, Black and Hispanic women in California were found to be far more likely to have children with less-educated men, even after controlling for women’s educational attainment. A substantial share of disparities can be attributed to neighborhood inequalities. In particular, women residing in lower-SES neighborhoods or neighborhoods connected to low-SES neighborhoods through mobility patterns are significantly more likely to have children with less-educated fathers. In this study, these neighborhood attributes explained a considerable share of the gap between Black and White women related to the father’s education, which has substantial implications for social stratification processes [11].

Second, neighborhood processes are highly relevant to understanding racial inequality in fertility. Compared with White neighborhoods, Black and Hispanic neighborhoods exhibited substantially higher birth rates, although measures of residential and mobility-based neighborhood disadvantage can explain the entire relationship. In more specific subpopulations, a substantial share of the fertility gap between high-school-educated Black and White women can be explained by neighborhood disadvantage.

The results highlight the importance of neighborhood processes in assortative mating and fertility. Although newer, more precise measures of neighborhood disadvantage have emerged, demographers must take advantage of these measures to better understand complex demographic processes. Past research has highlighted assortative mating and fertility as key mechanisms in the reproduction of racial inequality [11]. These results directly build on this past work by highlighting neighborhoods as a secondary mechanism that further explains the stratifying role of these demographic processes.

While this research is not causal, these results invite more work that is, as well as work that investigates the attributes of these demographic processes more comprehensively. This study can be directly extended by investigating the attributes of fathers more carefully, including how neighborhood fertility rates are associated with different levels of education among men. Examining more specific educational categories may help determine how these factors affect racial variation in assortative mating.

This analysis was limited by the data type (birth record data), leaving ample opportunity for demographers to further explore this topic. A similar methodological approach would likely yield more informative findings in examining richer longitudinal datasets (such as the Panel Study on Income Dynamics) [42], wherein distinctions between marital, non-marital, cohabiting, and non-cohabiting fertility can be made. Specific fertility rates can be more precisely estimated, enabling scholars to better understand the exact forms of fertility associated with certain types of neighborhoods, potentially yielding more explicit policy recommendations to address disparities. Additionally, running similar analyses of assortative mating and fertility trends on quasi-experimental neighborhood data (such as the Moving-to-Opportunity experiment) [43], may yield more causally viable conclusions. Neighborhoods are highly endogenous to numerous other social processes, making it unreasonable to draw causal conclusions using observational data regarding the effect of neighborhood residence on assortative mating and fertility.