The Role of a PMI-Prediction Model in Evaluating Forensic Entomology Experimental Design, the Importance of Covariates, and the Utility of Response Variables for Estimating Time Since Death
Abstract
:1. Introduction
Some Specialized Terminology
2. Lesson 1: Employ an Unbiased Sampling Technique for Generating Training Data
3. Lesson 2: Exceed the Minimum Sample Size for a Categorical Response
4. Lesson 3: The Practical Significance of a Covariate, or the Practical Value of a Response, Should Be Evaluated by Predictive Model Performance
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IP | Inverse prediction |
| PMI | Postmortem interval |
| PMImin | Minimum postmortem interval |
| SI | Succession interval |
| TD | Training data |
| MS | Mystery specimen |
References
- Catts, E.P. Analyzing entomological data. In Entomology & Death. A Procedural Guide; Haskell, N.H., Catts, E.P., Eds.; Joyce’s Print Shop: Clemson, SC, USA, 1990; pp. 124–137. [Google Scholar]
- Goff, M.L. Estimation of postmortem interval using arthropod development and succession patterns. Forensic Sci. Rev. 1993, 5, 81–94. [Google Scholar] [PubMed]
- Catts, E.P. Problems in estimating the postmortem interval in death investigations. J. Agric. Entomol. 1992, 9, 245–255. [Google Scholar]
- Amendt, J.; Campobasso, C.P.; Gaudry, E.; Reiter, C.; LeBlanc, H.N.; Hall, M.J.R. Best practice in forensic entomology-standards and guidelines. Int. J. Leg. Med. 2007, 121, 90–104. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.E.; Haskell, N.H.; Wells, J.D. Evaluating the utility of hexapod species for calculating a confidence interval about a succession based postmortem interval estimate. Forensic Sci. Int. 2014, 241, 91–95. [Google Scholar] [CrossRef] [PubMed]
- National Research Council. Strengthening Forensic Science in The United States: A Path Forward; National Academies Press: Washington, DC, USA, 2009; p. 352. [Google Scholar]
- Roe, A.; Higley, L.G. Development modeling of Lucilia sericata (Diptera: Calliphoridae). Peer J. 2015, 3, e803. [Google Scholar] [CrossRef] [PubMed]
- Avila, F.W.; Goff, M.L. Arthropod succession patterns onto burnt carrion in two contrasting habitats in the Hawaiian Islands. J. Forensic Sci. 1998, 43, 581–586. [Google Scholar] [CrossRef] [PubMed]
- Bourel, B.; Hédouin, V.; Martin-Bouyer, L.; Bécart, A.; Tournel, G.; Deveaux, M.; Gosset, D. Effects of morphine in decomposing bodies on the development of Lucilia sericata (Diptera: Calliphoridae). J. Forensic Sci. 1999, 44, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Mądra-Bielewicz, A.; Frątczak-Lagiewska, K.; Matuszewski, S. Sex- and size-related patterns of carrion visitation in Necrodes littoralis (Coleoptera: Silphidae) and Creophilus maxillosus (Coleoptera: Staphylinidae). J. Forensic Sci. 2016. [Google Scholar] [CrossRef]
- Wells, J.D.; LaMotte, L.R. Estimating maggot age from weight using inverse prediction. J. Forensic Sci. 1995, 40, 585–590. [Google Scholar] [CrossRef]
- LaMotte, L.R.; Wells, J.D. P-values for postmortem intervals from arthropod succession data. J. Agric. Biol. Environ. Stat. 2000, 5, 58–68. [Google Scholar] [CrossRef]
- Wells, J.D.; LaMotte, L.R. Estimating the postmortem interval. In Forensic Entomology. The Utility of Arthropods in Legal Investigations; Byrd, J.H., Castner, J.L., Eds.; CRC Press: Boca Raton, FL, USA, 2001; pp. 263–285. [Google Scholar]
- LaMotte, L.R.; Wells, J.D. Inverse prediction for heteroscedastic response using mixed models software. Commun. Stat. Simul. Comput. 2015. [Google Scholar] [CrossRef]
- LaMotte, L.R.; Wells, J.D. Inverse prediction for multivariate mixed models with standard software. Stat. Papers 2016, 57, 929–938. [Google Scholar] [CrossRef]
- LaMotte, L.R.; Roe, A.L.; Wells, J.D.; Higley, L.G. A statistical method to construct confidence sets on carrion insect age from development stage. J. Agric. Biol. Environ. Stat. 2017. [Google Scholar] [CrossRef]
- Dytham, C. Choosing and Using Statistics. A Biologist’s Guide; Blackwell Science: Oxford, UK, 1999; p. 218. [Google Scholar]
- Wells, J.D.; Lecheta, M.C.; Moura, M.O.; LaMotte, L.R. An evaluation of sampling methods used to produce insect growth models for postmortem interval estimation. Int. J. Leg. Med. 2015, 129, 405–410. [Google Scholar] [CrossRef] [PubMed]
- Steel, R.G.D.; Torrrie, J.H. Principles and Procedures of Statistics: A Biometrical Approach, 2nd ed.; McGraw Hill: New York, NY, USA, 1980; p. 633. [Google Scholar]
- LaMotte, L.R.; Wells, J.D. Commentary on J.-P. Michaud, G. Moreau, Predicting the visitation of carcasses by carrion-related insects under different rates of degree-day accumulation, Forensic Sci. Int. 185 (2009) 78–83. Forensic Sci. Int. 2017, 270, e16–e19. [Google Scholar] [CrossRef] [PubMed]
- Moreau, G.; Michaud, J.-P. On the mishandling of probabilities in Lamotte & Wells’ commentary on J.P. Michaud, G. Moreau, Predicting the visitation of carcasses by carrion-related insects under different rates of degree-day accumulation. Forensic Sci. Int. 2017, 270, e20–e25. [Google Scholar] [PubMed]
- Kaneshrajah, G.; Turner, B. Calliphora vicina larvae grow at different rates on different body tissues. Int. J. Leg. Med. 2004, 118, 242–244. [Google Scholar] [CrossRef] [PubMed]
- Goff, M.L.; Miller, M.L.; Paulson, J.D.; Lord, W.D.; Richards, E.; Omori, A.I. Effects of 3,4-methylenedioxymethamphetamine in decomposing tissues on the development of Parasarcophaga ruficomis (Diptera: Sarcophagidae) and detection of the drug in postmortem blood, liver tissue, larvae, and puparia. J. Forensic Sci. 1997, 42, 276–280. [Google Scholar] [PubMed]
- Harnden, L.M.; Tomberlin, J.K. Effects of temperature and diet on black soldier fly, Hermetia illuscens (L.) (Diptera: Stratiomyidae), development. Forensic Sci. Int. 2016, 266, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S. The Practical Effect of Rearing Substrate on Development of Chrysomya Megacephala; M.F.S. Report; Florida International University: Miami, FL, USA, 2016; p. 39. [Google Scholar]
- Teder, T. Sexual size dimorphism requires a corresponding sex difference in development time: A meta-analysis in insects. Funct. Ecol. 2014, 28, 479–486. [Google Scholar] [CrossRef]
- Concha, C.; Scott, M.J. Sexual development of Lucilia cuprina (Diptera: Calliphoriae) is controlled by the transformer gene. Genetics 2009, 182, 785–798. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Vensko, S.P.; Belikoff, E.J.; Scott, M.J. Conservation and sex-specific splicing of the transformer gene in the calliphorids Cochliomyia hominivorax, Cochliomyia macellaria, and Lucilia sericata. PLoS ONE 2013, 8, e56303. [Google Scholar] [CrossRef] [PubMed]
- Picard, C.J.; Deleblois, K.; Tovar, F.; Bradley, J.L.; Johnston, J.S.; Tarone, A. Increasing precision in development-based postmortem interval estimates: What’s sex got to do with it? J. Med. Entomol. 2013, 50, 425–431. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.L.; Wells, J.D. Isolation of the male specific Transformer exon as a method for immature specimen sex identification in Chrysomya megacephala (Diptera: Calliphoridae). J. Med. Entomol. 2017, 54, 496–500. [Google Scholar] [CrossRef] [PubMed]
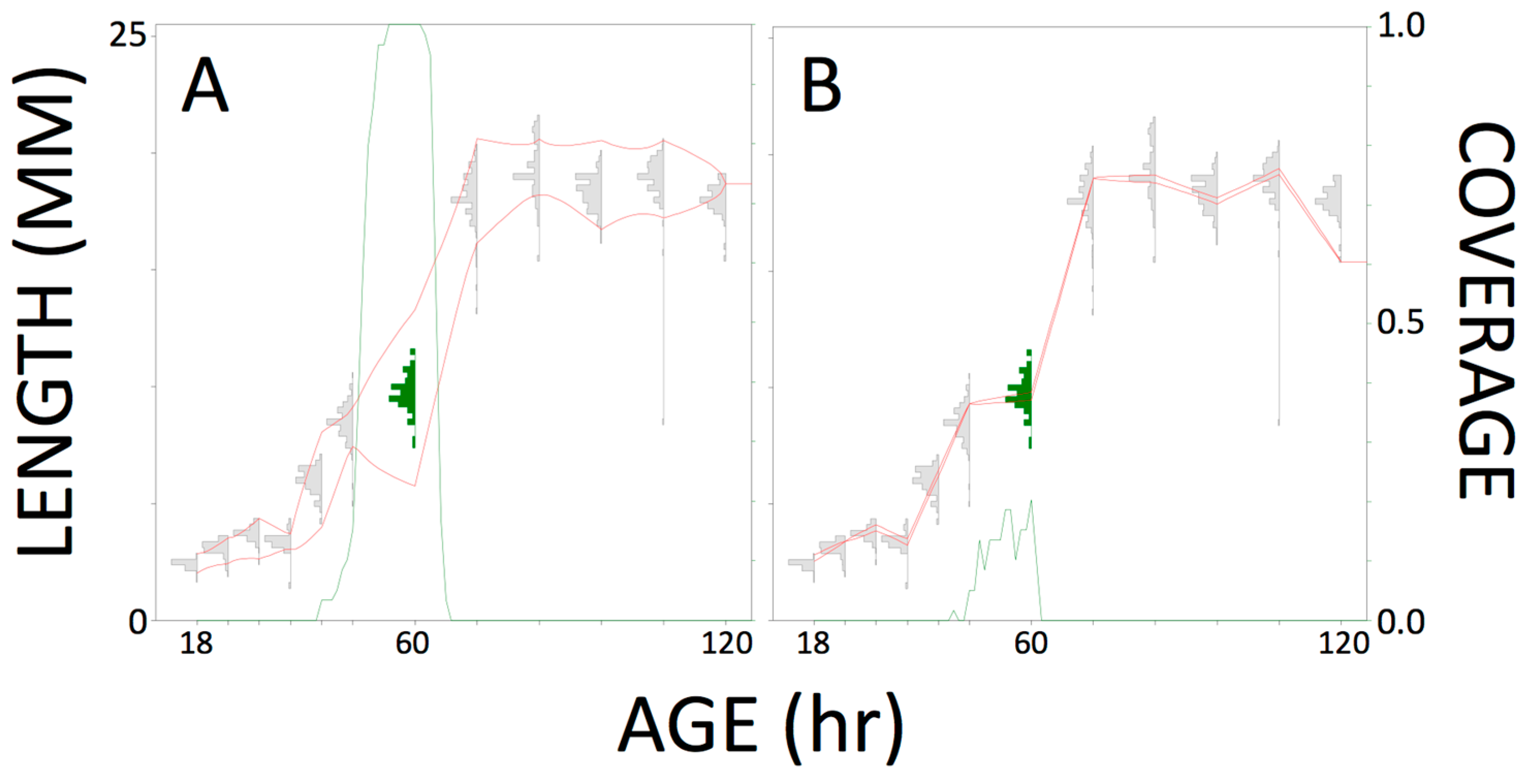
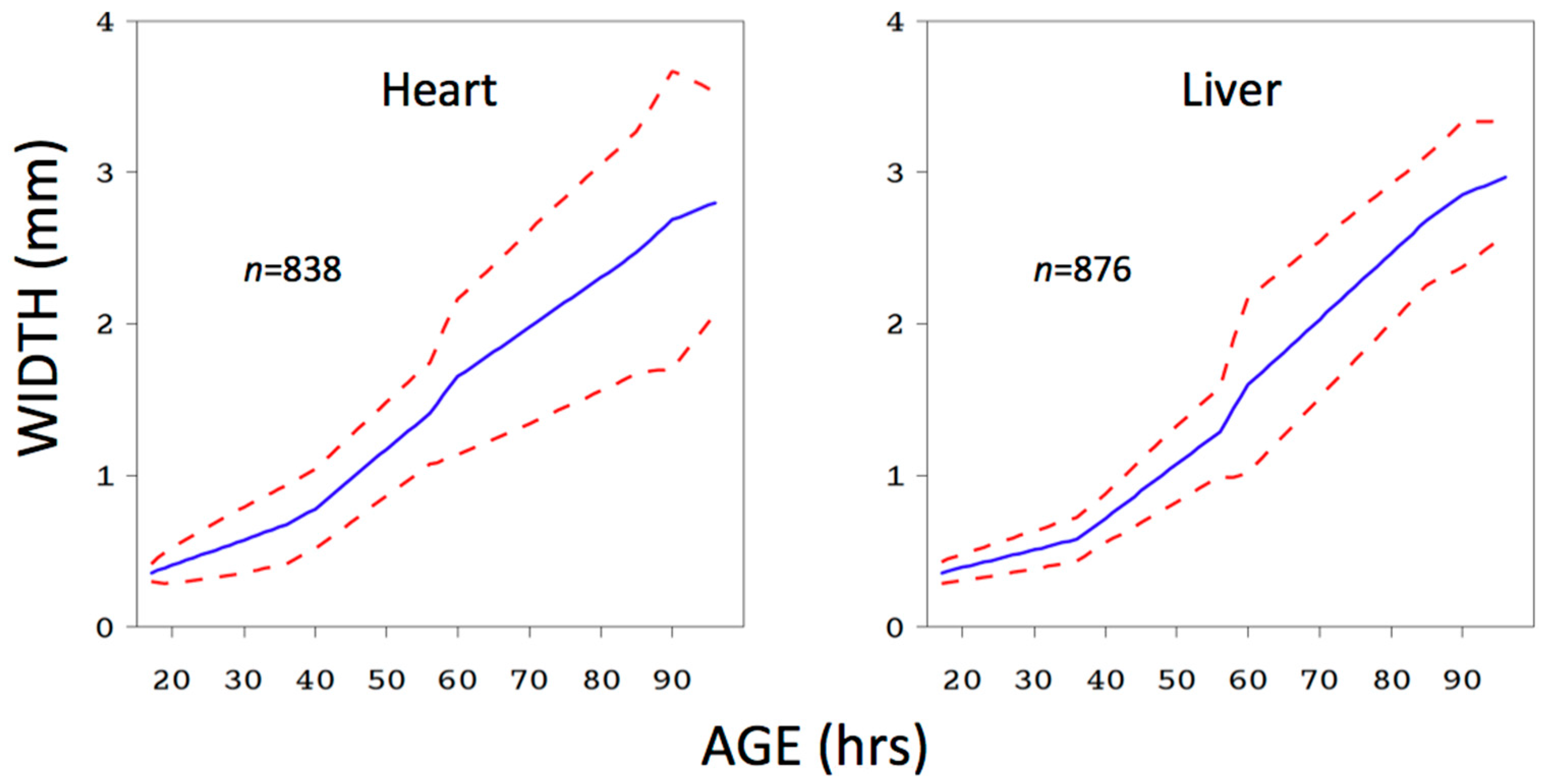
| Reject If ≤ No. TD Matching MS | ||||||
|---|---|---|---|---|---|---|
| No. Response Categories | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 7 | 17 | 28 | 39 | 52 | 64 |
| 3 | 15 | 34 | 55 | 78 | 102 | 128 |
| 4 | 22 | 51 | 83 | 117 | 153 | 191 |
| 8 | 52 | 118 | 192 | 272 | 357 | 444 |
| MODEL | 17 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L | * | * | * | * | * | * | * | * | * | * | * | |||||
| W | * | * | * | * | * | * | * | * | * | * | ||||||
| L, W | * | * | * | * | * | * | * | * | * | * | ||||||
| I | * | * | * | * | * | * | * | * | * | * | * | * | ||||
| L, I | * | * | * | * | * | * | * | * | * | * | * | * | * | |||
| W, I | * | * | * | * | * | * | * | * | * | * | * | * | * | * | ||
| L, W, I | * | * | * | * | * | * | * | * | * | * | * | * | * | * |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wells, J.; LaMotte, L. The Role of a PMI-Prediction Model in Evaluating Forensic Entomology Experimental Design, the Importance of Covariates, and the Utility of Response Variables for Estimating Time Since Death. Insects 2017, 8, 47. https://doi.org/10.3390/insects8020047
Wells J, LaMotte L. The Role of a PMI-Prediction Model in Evaluating Forensic Entomology Experimental Design, the Importance of Covariates, and the Utility of Response Variables for Estimating Time Since Death. Insects. 2017; 8(2):47. https://doi.org/10.3390/insects8020047
Chicago/Turabian StyleWells, Jeffrey, and Lynn LaMotte. 2017. "The Role of a PMI-Prediction Model in Evaluating Forensic Entomology Experimental Design, the Importance of Covariates, and the Utility of Response Variables for Estimating Time Since Death" Insects 8, no. 2: 47. https://doi.org/10.3390/insects8020047
APA StyleWells, J., & LaMotte, L. (2017). The Role of a PMI-Prediction Model in Evaluating Forensic Entomology Experimental Design, the Importance of Covariates, and the Utility of Response Variables for Estimating Time Since Death. Insects, 8(2), 47. https://doi.org/10.3390/insects8020047






