The Morphology of the Outflow in the Grazing Envelope Evolution
Abstract
:1. Introduction
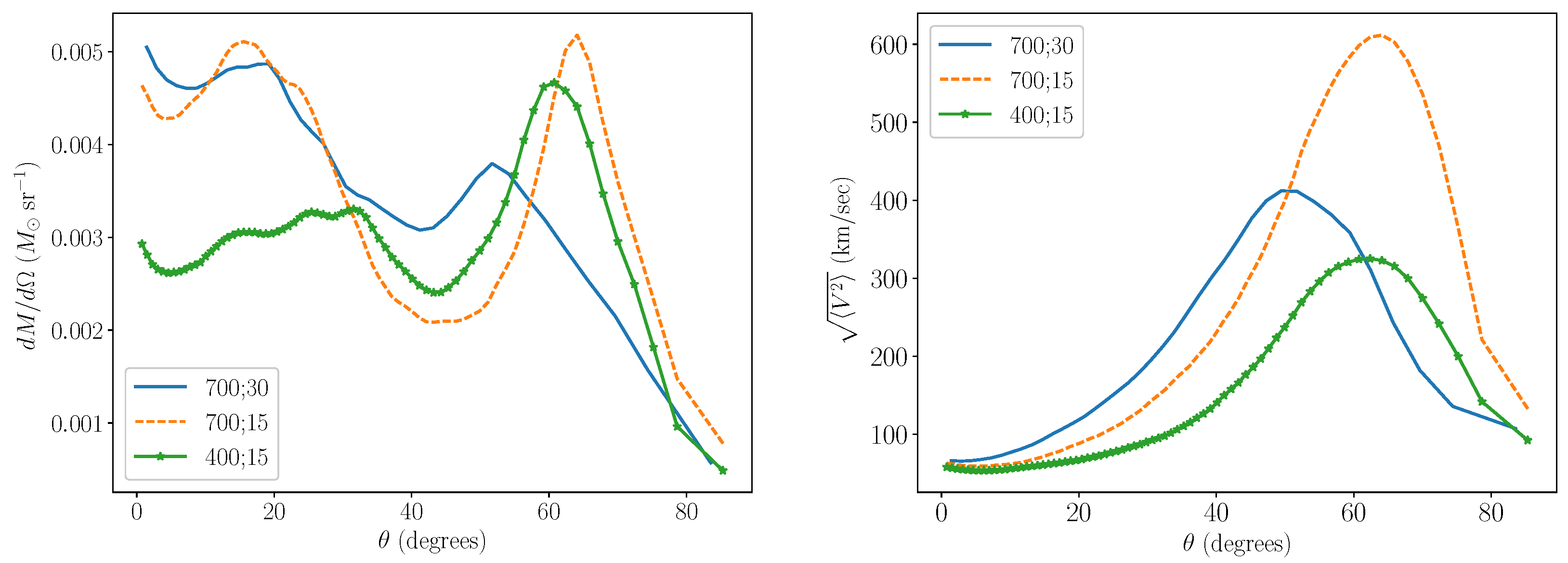
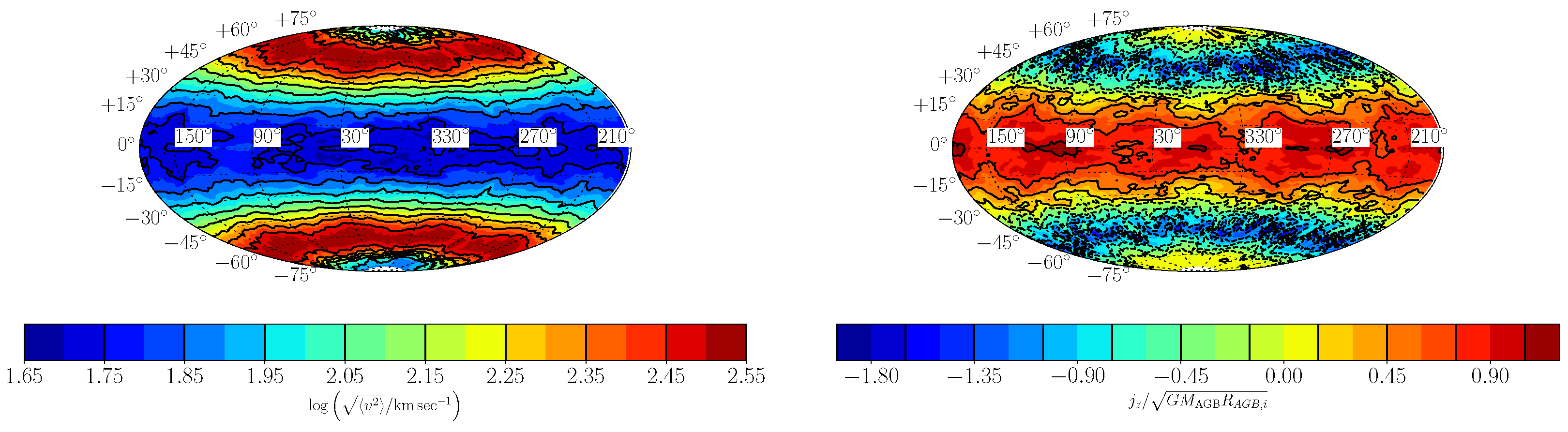
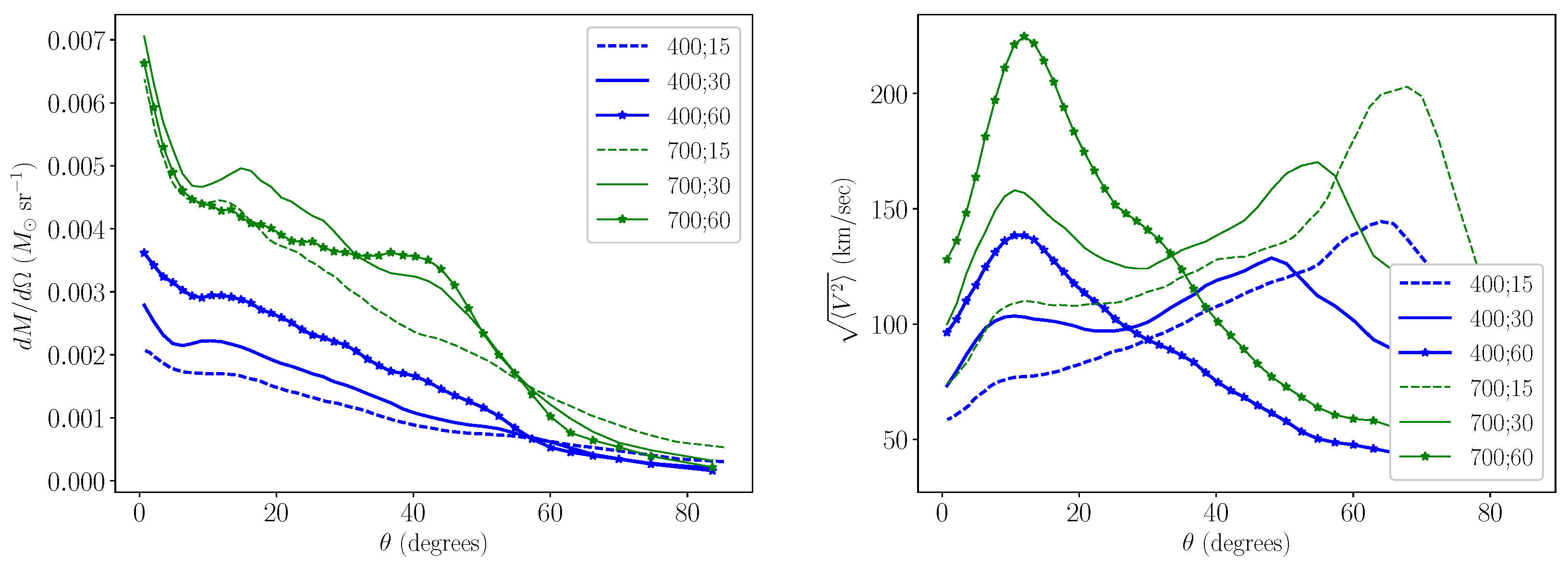
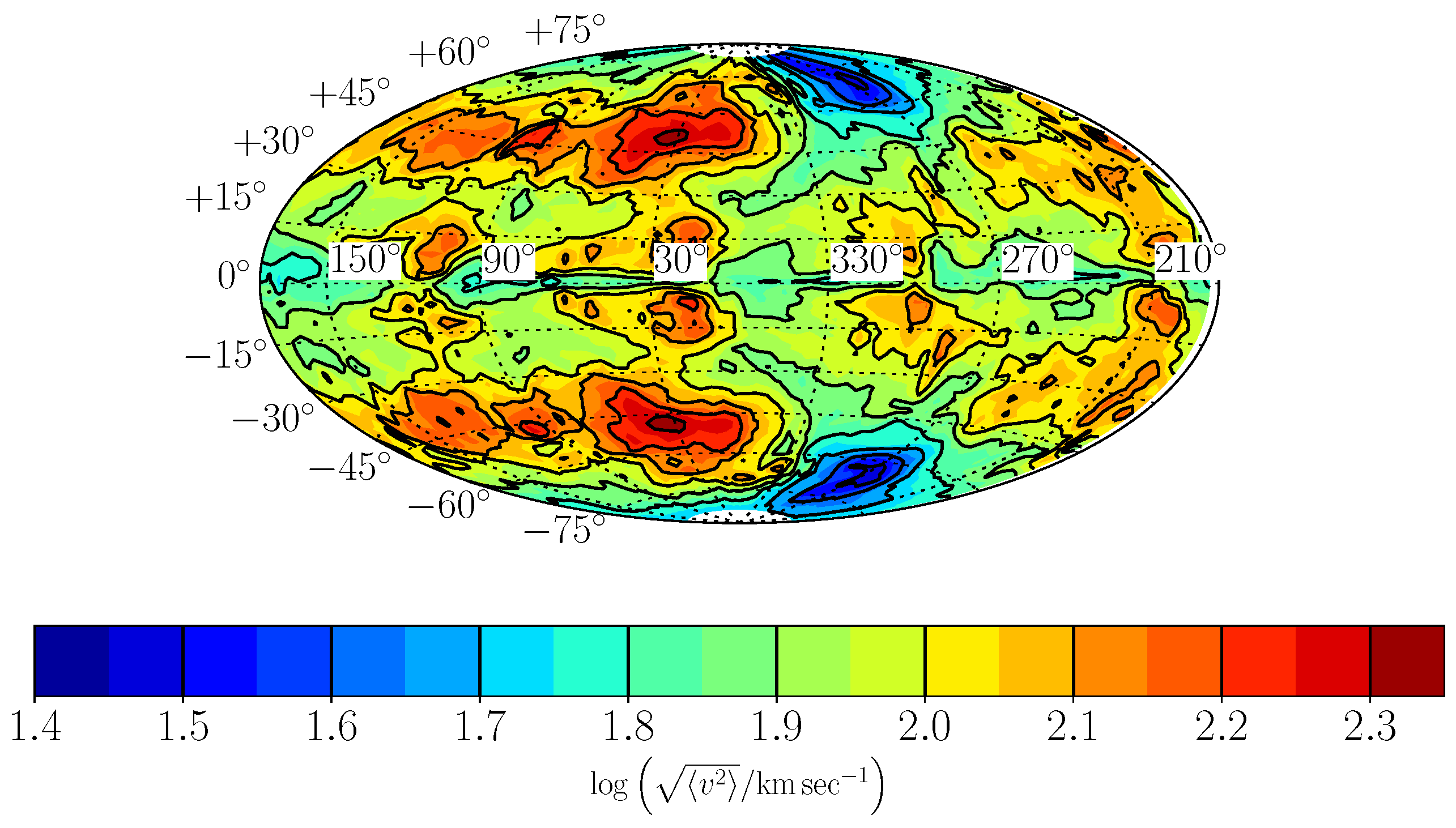
2. Results
2.1. The Onset of the GEE
2.2. GEE with Spiralling-in Orbits
3. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Iaconi, R.; De Marco, O.; Passy, J.-C.; Staff, J. The effect of binding energy and resolution in simulations of the common envelope binary interaction. Mon. Not. R. Astron. Soc. 2018, 477, 2349–2365. [Google Scholar] [CrossRef] [Green Version]
- Livio, M.; Soker, N. The common envelope phase in the evolution of binary stars. Astrophys. J. 1988, 329, 764–779. [Google Scholar] [CrossRef]
- Nandez, J.L.A.; Ivanova, N. Common envelope events with low-mass giants: Understanding the energy budget. Mon. Not. R. Astron. Soc. 2016, 460, 3992–4002. [Google Scholar] [CrossRef]
- Ohlmann, S.T.; Röpke, F.K.; Pakmor, R.; Springel, V. Hydrodynamic Moving-mesh Simulations of the Common Envelope Phase in Binary Stellar Systems. Astrophys. J. Lett. 2016, 816, L9. [Google Scholar] [CrossRef]
- Passy, J.-C.; De Marco, O.; Fryer, C.L.; Herwig, F.; Diehl, S.; Oishi, J.S.; Mac Low, M.-M.; Bryan, G.L.; Rockefeller, G. Simulating the Common Envelope Phase of a Red Giant Using Smoothed-particle Hydrodynamics and Uniform-grid Codes. Astrophys. J. 2012, 744, 52. [Google Scholar] [CrossRef]
- Rasio, F.A.; Livio, M. On the Formation and Evolution of Common Envelope Systems. Astrophys. J. 1996, 471, 366. [Google Scholar] [CrossRef]
- Ricker, P.M.; Taam, R.E. An AMR Study of the Common-envelope Phase of Binary Evolution. Astrophys. J. 2012, 746, 74. [Google Scholar] [CrossRef]
- Sandquist, E.L.; Taam, R.E.; Chen, X.; Bodenheimer, P.; Burkert, A. Double Core Evolution. X. Through the Envelope Ejection Phase. Astrophys. J. 1998, 500, 909. [Google Scholar] [CrossRef]
- De Marco, O.; Izzard, R.G. Dawes Review 6: The Impact of Companions on Stellar Evolution. Publ. Astron. Soc. Aust. 2017, 34, e001. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Chen, X.; De Marco, O.; Fryer, C.L.; Gaburov, E.; Ge, H.; Glebbeek, E.; Han, Z.; Li, X.-D.; et al. Common envelope evolution: Where we stand and how we can move forward. Astron. Astrophys. Rev. 2013, 21, 59. [Google Scholar] [CrossRef] [Green Version]
- Clayton, M.; Podsiadlowski, P.; Ivanova, N.; Justham, S. Episodic mass ejections from common-envelope objects. Mon. Not. R. Astron. Soc. 2017, 470, 1788–1808. [Google Scholar] [CrossRef] [Green Version]
- Grichener, A.; Sabach, E.; Soker, N. The limited role of recombination energy in common envelope removal. Mon. Not. R. Astron. Soc. 2018, 478, 1818–1824. [Google Scholar] [CrossRef]
- Ivanova, N. On the Use of Hydrogen Recombination Energy during Common Envelope Events. Astrophys. J. Lett. 2018, 858, L24. [Google Scholar] [CrossRef] [Green Version]
- Sabach, E.; Hillel, S.; Schreier, R.; Soker, N. Energy transport by convection in the common envelope evolution. Mon. Not. R. Astron. Soc. 2017, 472, 4361–4367. [Google Scholar] [CrossRef]
- Armitage, P.J.; Livio, M. Black Hole Formation via Hypercritical Accretion during Common-Envelope Evolution. Astrophys. J. 2000, 532, 540. [Google Scholar] [CrossRef]
- Chevalier, R.A. Common Envelope Evolution Leading to Supernovae with Dense Interaction. Astrophys. J. 2012, 752, L2. [Google Scholar] [CrossRef]
- López-Cámara, D.; De Colle, F.; Moreno Méndez, E. self-regulating jets during the Common Envelope phase. arXiv, 2018; arXiv:1806.11115. [Google Scholar]
- Moreno Méndez, E.; López-Cámara, D.; De Colle, F. Dynamics of jets during the common-envelope phase. Mon. Not. R. Astron. Soc. 2017, 470, 2929–2937. [Google Scholar] [CrossRef]
- Soker, N. Energy and angular momentum deposition during common envelope evolution. New Astron. 2004, 9, 399. [Google Scholar] [CrossRef]
- Chamandy, L.; Frank, A.; Blackman, E.G.; Carroll-Nellenback, J.; Liu, B.; Tu, Y.; Nordhaus, J.; Chen, Z.; Peng, B. Accretion in common envelope evolution. arXiv, 2018; arXiv:1805.03607. [Google Scholar] [CrossRef]
- Shiber, S.; Schreier, R.; Soker, N. Binary interactions with high accretion rates onto main sequence stars. Res. Astron. Astrophys. 2016, 16, 117. [Google Scholar] [CrossRef]
- Miszalski, B.; Boffin, H.M.J.; Corradi, R.L.M. A carbon dwarf wearing a Necklace: First proof of accretion in a post-common-envelope binary central star of a planetary nebula with jets. Mon. Not. R. Astron. Soc. 2013, 428, L39. [Google Scholar] [CrossRef]
- Jones, D.; Boffin, H.M.J.; Rodríguez-Gil, P.; Wesson, R.; Corradi, R.L.M.; Miszalski, B.; Mohamed, S. The post-common envelope central stars of the planetary nebulae Henize 2-155 and Henize 2-161. Astron. Astrophys. 2015, 580, A19. [Google Scholar] [CrossRef]
- Boffin, H.M.J.; Miszalski, B.; Rauch, T.; Jones, D.; Corradi, R.L.M.; Napiwotzki, R.; Day-Jones, A.C.; Koeppen, J. An Interacting Binary System Powers Precessing Outflows of an Evolved Star. Science 2012, 338, 773–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soker, N. Close Stellar Binary Systems by Grazing Envelope Evolution. Astrophys. J. 2015, 800, 114. [Google Scholar] [CrossRef]
- Shiber, S.; Kashi, A.; Soker, N. Simulating the onset of grazing envelope evolution of binary stars. Mon. Not. R. Astron. Soc. 2017, 465, L54. [Google Scholar] [CrossRef]
- Bondi, H. On spherically symmetrical accretion. Mon. Not. R. Astron. Soc. 1952, 112, 195–204. [Google Scholar] [CrossRef]
- Shiber, S.; Soker, N. Simulating a binary system that experiences the grazing envelope evolution. Mon. Not. R. Astron. Soc. 2018, 477, 2584–2598. [Google Scholar] [CrossRef] [Green Version]
- Frank, A.; Chen, Z.; Reichardt, T.; De Marco, O.; Blackman, E.; Nordhaus, J. Planetary Nebulae Shaped By Common Envelope Evolution. arXiv, 2018; arXiv:1807.05925. [Google Scholar]
- Livio, M.; Soker, N. The “Twin Jet” Planetary Nebula M2-9. Astrophys. J. 2001, 552, 685. [Google Scholar] [CrossRef]
- Burrows, C.J.; Krist, J.; Hester, J.J.; Sahai, R.; Trauger, J.T.; Stapelfeldt, K.R.; Gallagher, J.S., III; Ballester, G.E.; Casertano, S.; Clarke, J.T.; et al. Hubble Space Telescope Observations of the SN 1987A Triple Ring Nebula. Astrophys. J. 1995, 452, 680. [Google Scholar] [CrossRef]
- Manick, R.; Van Winckel, H.; Kamath, D.; Hillen, M.; Escorza, A. Establishing binarity amongst Galactic RV Tauri stars with a disc. Astron. Astrophys. 2017, 597, A129. [Google Scholar] [CrossRef]
- Nie, J.D.; Wood, P.R.; Nicholls, C.P. Predicting the fate of binary red giants using the observed sequence E star population: Binary planetary nebula nuclei and post-RGB stars. Mon. Not. R. Astron. Soc. 2012, 423, 2764–2780. [Google Scholar] [CrossRef]
- Van Winckel, H. Post-AGB binaries as tracers of stellar evolution. In Planetary Nebulae: Multi-Wavelength Probes of Stellar and Galactic Evolution; Cambridge University Press: Cambridge, UK, 2016; Volume 12, pp. 231–234. [Google Scholar]
- Bollen, D.; Van Winckel, H.; Kamath, D. Jet creation in post-AGB binaries: the circum-companion accretion disk around BD+46∘442. Astron. Astrophys. 2017, 607, A60. [Google Scholar] [CrossRef]
- Van Winckel, H. Why is the Red Rectangle Unique? Diffuse Interstellar Bands 2014, 297, 180. [Google Scholar] [CrossRef]
- Abu-Backer, A.; Gilkis, A.; Soker, N. Orbital Radius during the Grazing Envelope Evolution. Astrophys. J. 2018, 861, 136. [Google Scholar] [CrossRef]
| References | |||||||
|---|---|---|---|---|---|---|---|
| 4.3 | 4.4 | 8.6 | 5.9 | 4.2 | 0.43 | 16 | |
| 0.1 | 0.31 | 0.26 | 0.15 | 0.06 | 1 | 0.16 | |
| Grid/SPH | SPH | Grid | Grid | Both | Moving Mesh | SPH | Both |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shiber, S. The Morphology of the Outflow in the Grazing Envelope Evolution. Galaxies 2018, 6, 96. https://doi.org/10.3390/galaxies6030096
Shiber S. The Morphology of the Outflow in the Grazing Envelope Evolution. Galaxies. 2018; 6(3):96. https://doi.org/10.3390/galaxies6030096
Chicago/Turabian StyleShiber, Sagiv. 2018. "The Morphology of the Outflow in the Grazing Envelope Evolution" Galaxies 6, no. 3: 96. https://doi.org/10.3390/galaxies6030096
APA StyleShiber, S. (2018). The Morphology of the Outflow in the Grazing Envelope Evolution. Galaxies, 6(3), 96. https://doi.org/10.3390/galaxies6030096





