Abstract
Automated quantification of galaxy morphology is necessary because the size of upcoming sky surveys will overwhelm human volunteers. Existing classification schemes are inadequate because (a) their uncertainty increases near the boundary of classes and astronomers need more control over these uncertainties; (b) galaxy morphology is continuous rather than discrete; and (c) sometimes we need to know not only the type of an object, but whether a particular image of the object exhibits visible structure. We propose that regression is better suited to these tasks than classification, and focus specifically on determining the extent to which an image of a spiral galaxy exhibits visible spiral structure. We use the human vote distributions from Galaxy Zoo 1 (GZ1) to train a random forest of decision trees to reproduce the fraction of GZ1 humans who vote for the “Spiral” class. We prefer the random forest model over other black box models like neural networks because it allows us to trace post hoc the precise reasoning behind the regression of each image. Finally, we demonstrate that using features from SpArcFiRe—a code designed to isolate and quantify arm structure in spiral galaxies—improves regression results over and above using traditional features alone, across a sample of 470,000 galaxies from the Sloan Digital Sky Survey.
1. Introduction
1.1. Motivation
Galaxies play a crucial role in our understanding of the cosmos at large. On at least three occasions in the past century, they have caused tectonic shifts in our understanding of the Universe. First, until the early 1920s, the Milky Way Galaxy was assumed to constitute the entire known Universe, with the so-called “spiral nebulae” being merely young solar systems—within the Milky Way—in the early stages of their formation. When the “Great Debate” [1] established spiral nebulae as separate “island universes” on par with the Milky Way, the known Universe suddenly expanded in size by many orders of magnitude, relegating humanity to live in just one among millions (now billions) of external galaxies. Several decades later, the high rotation speed of spiral galaxies revealed that they must contain far more mass than is visible in the stars [2,3], leading to the discovery of dark matter—suddenly quadrupling the amount of matter in the known Universe. Finally, in the late 20th century, the expansion rate of the universe, as measured by the motion of distant galaxies, revealed that there was even more “stuff” in the Universe than light and dark matter—which is now called “dark energy” [4]. Today, linking the large-scale structure and evolution of the universe as a whole to the formation and evolution of individual galaxies is one of the Grand Challenges of the 21st century, as illustrated, for example, in the Illustris simulation of a large chunk of the known Universe [5].
Galaxies typically contain billions or trillions of stars, all bound together by their mutual gravitation and that of the dark matter that dominates the mass of all galaxies [6]. More than half of all galaxies in the local universe are spirals, with the remainder being either elliptical or irregular [7]. Spiral galaxies are characterized by a central bulge and two or more “arms” that emanate from and wind around the bulge; some galaxies also contain a central bar (Figure 1). Spiral galaxies are also sometimes called “disk” galaxies since most of the visible stars, and the arms themselves, are confined to a rotating disk.
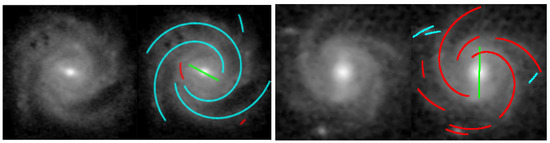
Figure 1.
Two typical spiral galaxies along with SpArcFiRe’s fit to each. These two galaxies have arms that wind in opposite directions as viewed from Earth. The directions are conventionally called S-wise (left) and Z-wise (right), since the arms wind in the same direction as those letters [8]. SpArcFiRe [9] depicts S-wise arm segments as cyan and Z-wise arm segments as red, while bars are depicted in green.
Despite decades of research, the formation of the arms of spiral galaxies is still not well understood [6,10]. At least part of the reason spiral arms defy theoretical description is that comparing any theory to observation requires objective quantification, and until recently there has been no reliable method of objectively quantifying spiral structure in images of spiral galaxies across large databases of galaxy images such as that contained in the Sloan Digital Sky Survey (SDSS, [11]). This changed in 2008 with the introduction of the citizen science project Galaxy Zoo [8,12], which leveraged the Web to co-ordinate the volunteer efforts of hundreds of thousands of people to manually classify almost a million galaxy images from SDSS. While this was an amazing accomplishment, future sky surveys will overwhelm even the plethora of Galaxy Zoo volunteers: the Large Synoptic Survey Telescope (LSST) [13] and James Webb Space Telescope [14] will each produce far more data than the SDSS. As a rough estimate of the amount of upcoming data, the Hubble Ultra Deep Field (HUDF) represents about 1/13,000,000 of the celestial sphere and contains about 10,000 galaxies at least 100 of which have visible structure (by our own estimate), suggesting that the entire sky contains upwards of galaxies with visible structure at the resolution and depth of the HUDF. To quantify the morphology of this number of galaxies will require automated methods.
SpArcFiRe—the SPiral ARC FInder and REporter—is an algorithm designed to automatically extract structural information from the images of spiral galaxies [9,15,16]. It was tested around a sample of 29,250 spiral galaxies from the Sloan Digital Sky Survey (SDSS), as selected by one of the PIs of the Galaxy Zoo project1. In the Galaxy Zoo project, arms are said to wind either S-wise, or Z-wise (cf. Figure 1). The fraction of humans who voted that a galaxy’s arms wind S- or Z-wise are, respectively, and ; note that they do not need to sum to 1 since there were six choices for the humans to select from for each galaxy. We define the spirality of a galaxy as the sum . The selection criterion for our 29,250 test spiral galaxies was: OR AND AND . Our sample also used the same magnitude limit as GZ1—17.7 in the red band.
Even though some galaxy images (e.g., elliptical galaxies or low-resolution spirals) do not have visible arms, we do not know in advance which images exhibit arms. For this reason, we run SpArcFiRe on every galaxy image, and our goal is to figure out when SpArcFiRe’s output is meaningful, preferably using the output of SpArcFiRe itself. SpArcFiRe’s job is to find spiral arms in spiral galaxies; often, it also marks noise as spiral structure. Thus, we wish to recognize when a galaxy image has visible spiral structure. Although ultimately we hope to develop an objective, quantitative, continuous measure of galaxy morphology, for now, we focus on the simple task of reproducing what we call the spirality of a galaxy image: from the GZ1 catalog [8,17], we define the spirality to be , representing the extent to which there is visible spiral structure in the image of the object. We emphasize that spirality is a measure of the image, not the object. We are not trying to classify galaxies; we are trying to discern if a particular image exhibits spiral structure that is unlikely to be caused by noise. For example, although elliptical galaxies should be assigned a spirality of zero, an edge-on disk also should be assigned a spirality of zero because spiral structure is not visible; thus, we wish to detect in both cases that SpArcFiRe’s output should not be interpreted as representing spiral structure.
Since humans introduce certain types of biases into the classification scheme (for example, the chirality bias [17,18,19]), we also wish to “dilute” such biases even though we train our method on human classifications. We do this by carefully choosing which inputs we allow our code to use. For example, we allow SpArcFiRe’s measured pitch angle of spiral arms to be used as input to our regressor, but not the sign of the pitch angle [19], thus reducing chirality discrepancies to about 1 part in 5000 [16,19]. Our work follows up on existing work published in the astronomical literature [20,21,22,23,24,25], and extends it by either (a) using regression over classification; (b) using SpArcFiRe-derived features; or both.
1.2. Related Work
Arguably the most impactful and successful machine learning research published in the astronomical literature for similar tasks is Banerji et al. [22] and Dieleman et al. [24]. The former was one of the first to apply Machine Learning to try and reproduce the human classifications of the GZ1 catalog [8] and the latter focuses specifically on reproducing the vote distribution of the GZ2 catalog [26], a regression problem, exactly like the approach we explore on this paper. The main difference here is that they are not concerned with the bias present in the dataset, so the smaller their Root Mean Squared Error (RMSE) is, “the better” their results are. In the recent Galaxy Zoo dataset releases, there has been an increased effort to eliminate human biases, but Hayes et al. [19] have proven that these datasets, in particular, GZ1, still contain biases so there is a trade-off between lowering the RMSE of a model and avoiding the introduction of such biases on model predictions.
Banerji et al. [22] present good results using neural networks. They classified Sloan galaxies in one of three categories: spiral, elliptical, and point sources/artifacts, using a neural network with inputs listed in Table 1. They found that on the entire sample of about 900,000 Sloan galaxies, they could reproduce the human GZ1 classifications in 92% of cases. Across a sample of brighter galaxies (, they correctly classify about 94% of galaxies. They do even better for a sample called the “Gold sample”, in which galaxies are only included if the humans are themselves more than 80% confident in the classification. We do not believe the Gold sample comparison is meaningful, however, because it is crucial to know how good the machine learning model is when it thinks it is confident but is, in fact, mistaken, and the Gold sample completely disregards this aspect.2

Table 1.
Non-SpArcFiRe input parameters we used, identical to those used in Banerji et al. [22], except for the absolute Magnitudes that also come from Sloan Digital Sky Survey (SDSS).
Other interesting works published recently include Abd Elfattah et al. [27], which uses Neural Networks and Empirical Mode Decomposition to perform galaxy classification but uses a very small test set of 108 objects so it is hard to predict how their models would fare when trying to classify a much larger set of objects, like our test set. Kuminski et al. [23] makes a case for using “high-quality data”, but we believe this will have the same issues as Banerji et al. [22]’s use of a “Gold Sample”. Applebaum and Zhang [28] uses an ensemble of Support Vector Machines to classify GZ2 galaxies achieving good results, and Ferrari et al. [25] uses Linear Discriminant Analysis to classify galaxies from a couple different surveys—but classification is not our goal.
Finally, Kaggle.com—a website devoted to machine learning competitions—offered £10,000 (GBP) to the algorithm which best minimized the RMSE between the automatic regression scheme and the human vote distribution for Galaxy Zoo 2. The winning entry was a Deep Learning algorithm using convolutional Neural Networks [24]. It had an RMSE of about 0.07 relative to the human GZ2 vote distribution. Although this result is closer to the human votes than our result presented on this paper, we are concerned about the professional use of deep learning techniques for several reasons:
- We would prefer a system with parameters that are understood and can be modified by professional astronomers, and decision trees seem better suited to this task.
- Decision trees can be used to measure the quality of features3 used to make a decision and thus are more suitable for our goals in this paper. This is not the case for Deep Neural Networks, which do not yet easily provide a similar measure of feature quality.
- The most damning criticism against neural networks is that they cannot explain their reasoning to us. In particular, the way they make their decisions is not well understood, and research to better understand this issue is still in its infancy [30,31]. In short, we cannot learn from what they have learned, or learn from how they make their decisions, because a neural net is a near-complete “black box”. This is an absolutely critical disadvantage to a scientist who wants to know “why?” The goal of science is to understand, and a black box that cannot explain its rationale cannot provide us with new understanding.
For these reasons, we opt to use Decision Trees, which can be understood, dissected, and whose individual decisions can also be understood and dissected, if necessary. Understanding these decisions can teach us about galaxy characteristics and morphology in ways that “black box” machine learning algorithms cannot.
1.3. Regression, Not Classification, Because Galaxy Morphology Is Continuous, Not Discrete
In the real Universe, galaxy morphology is more continuous than discrete. Adjectives describing galaxies in the literature include: elliptical, spiral, dwarf, regular, irregular, giant, merger, peculiar, and so forth. Even among spiral galaxies, one sees adjectives such as flocculent, grand design, and barred. The range of spiral arm morphologies is enormous: one can quantify the shape, length, width, brightness profiles, color and color gradient, and contrast of individual spiral arms compared to the background disk in which they reside; one can quantify the “forking” structure of arms, how tightly they wind, and how many there are of various shapes and sizes. In addition, from the standpoint of theoretical astrophysics, there are at least three hypothesized mechanisms behind how spiral structure may form [6,7], and these mechanisms may not have clearly distinguishable visible signatures. Mergers or near impacts between galaxies can also form spiral-looking structures, providing still a 4th mechanism behind visible spiral structure. In short, although classification is a good “baby step” towards quantifying galaxy morphology, in reality, it is far too simplistic a view of the essentially continuous distribution of morphologies. As such, regression is the obvious next step in quantifying galaxy morphology.
As we will outline below, our goal is to isolate spiral galaxies and study their morphology. As such, when presented with the image of a random galaxy, our first question—the answer to which we are attempting to quantify in this paper—is simply, “to what extent does this galaxy exhibit spiral structure?” If it displays significant spiral structure, then we are interested in knowing more. If not, we can move on to the next image…but we are also interested in allowing the user to choose a threshold defining the “extent” to which spiral structure is visible. This extent is the spirality, or measure, we are attempting to quantify.
All of the works presented in Section 1.2 provide good accuracies (≥than 90%) but, except for Dieleman et al. [24], they are performing classification rather than regression. There have been tremendous advances in Machine Learning towards improving classifiers, and most of these papers make use of those techniques, but that is not the goal of our work. Whereas in classification one is concerned in finding a line that best separates two or more classes (in this scenario, spiral and non-spiral galaxies), in regression, we seek to learn about the underlying distribution, in this case, how to quantify the extent to which a galaxy image displays spiral structure4, and at present the GZ votes are the best way to do that. Usually more information is gleaned from a continuous distribution than a discrete classification—in particular a user of the output can choose a confidence threshold themselves for classification that is more suitable for a certain task rather than relying on the table creator’s subjective determination of where that threshold should lie. Peng et al. [32], for example, used regression for a task where they needed to analyze how spirality prediction degraded as a function of image quality, a task for which classification gives limited information.
2. Methods
We are mostly concerned with correctly predicting spirality (the extent to which an image of a galaxy displays visible spiral structure) for images of galaxies, in which spiral structure is visible, that have a reasonably high resolution. In particular, since SpArcFiRe is designed to discern spiral structure in disk galaxies, we are most interested in isolating disk galaxies in which spiral structure is visible. By a judicious eyeball study of images at the low end of resolution, we have subjectively determined that spiral structure is invisible in Sloan galaxies if the full major axis of the observable image is less than about 13 pixels, so we ignore any galaxy smaller than this. This is similar to the cutoff of 4.5 arcseconds Petrosian radius used by the GZ1 team for galaxies with visible structure [8]. Also following GZ1, we cut off galaxies dimmer than magnitude 17.7 in the R band. This leaves about 470,000 Sloan galaxies.
We created models using Weka [33] which provides many machine learning algorithms, an easy-to-use interface, and the ability to create sophisticated standalone command-line classifiers and regressors once the model has been trained. Weka provides, among many algorithms, a Neural Network algorithm, and a Random Forest (RF) algorithm. Neural Networks have been used with success in similar tasks like the convolutional model used by Dieleman et al. [24]. These models excel in tasks where the input is spatially or temporal correlated like images or audio, so we briefly used the Neural Network algorithm to roughly reproduce the results of [22], having downloaded the same data they used from the Galaxy Zoo 1 survey [8,17], which was a treated sample of the Sloan Digital Sky Survey Data Release 6 (SDSS DR6) [34]. Since our machine learning algorithm uses the data only after SpArcFiRe has processed it, we found that Weka’s Random Forest model had a lower RMSE, and as described in the previous section, a Random Forest model (described below) makes decisions that are easier for us to dissect and learn from. For the most advanced tasks, we recreated the same random forest models using Julia [35]; the results using Weka and Julia are virtually identical since the underlying mechanisms are the same.
To provide context, we explain the general idea of random forests. The “forest” part refers to a set of decision trees. Each decision tree has a set of input parameters. At each level of the tree, one asks if a particular parameter is in a specific range. For example, one level of the decision tree may ask if the galaxy has an absolute magnitude brighter than 18; another level may ask if it has a color redder than 0. The tree can be very deep, and once we arrive at a leaf node, we have a set of galaxies that satisfy an exact set of characteristics across the parameters that lie along the decision path to that node. The process of optimizing the decision tree is beyond the scope of this paper, but the goal is to optimize the leaf nodes to precisely define whatever output characteristic we are trying to reproduce. In our case, we are trying to reproduce the GZ1 human vote distribution. For example, one leaf may represent all galaxies where the human votes for (elliptical, spiral, other) are close to (0.80, 0.19, 0.01). This helps us determine what characteristics lead a decision tree to its final regression values for each class.
The “random” part of a random forest refers to the fact that each decision tree’s input parameters are chosen randomly from a larger set of input parameters provided by the user. The number of parameters to use for each tree is itself an integer parameter (fixed, in our case), as is the number of trees to use. Each tree effectively constitutes an “expert” in morphology quantification using its chosen set of parameters, and the forest is then a “mixture of experts”, in which a voting mechanism is used to come up with the final output. A mixture of experts generally results in a much better prediction than a single tree trained on all parameters because the signal of each expert reinforces all the others, while the noise of the experts tends to cancel each other out ([36] provides an excellent introduction to this idea).
Figure 2 is a simple example of a two-parameter decision tree. In this example, we will apply it only to galaxies that are clearly either spiral or elliptical. However, rather than a discrete classification, our goal is to provide just one number for each galaxy image: the extent to which it exhibits spiral structure. We use two familiar parameters: color and absolute magnitude. It is well known that elliptical galaxies tend to be both brighter and redder than spirals. Given a training set of galaxies that are truly either spiral or elliptical and given the colors and magnitudes of each, we perform the following set of operations to generate a two-parameter decision tree:
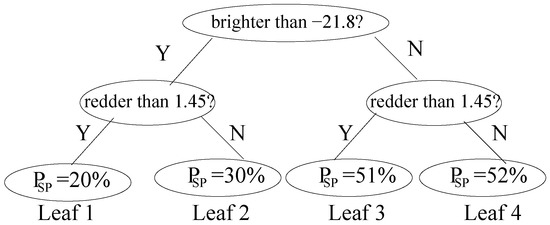
Figure 2.
A simple 2-level, 2-parameter decision tree. The value of in each leaf node is the average extent to which training-set galaxies in that node display spiral structure, as measured by the GZ1 vote fraction for . That value is then used as the predicted for galaxies in the non-training set that land in that node. With proper optimization (beyond the scope of this paper), larger trees with more features can produce more accurate predictions of , etc.
- Compute the mean magnitudes for spirals and ellipticals, respectively.
- Compute the mean colors for spirals and ellipticals, respectively.
- Compute a threshold color intended to separate spirals from ellipticals; we will simply use the midpoint .
- Similarly, compute a threshold magnitude .
- Now, for each galaxy, first ask which side of the threshold its color is on, and then ask which side of the threshold its magnitude is on.
- This bins each galaxy into one of four leaf nodes, as in Figure 2.
As we can see, the results are correlated with the correct answers but not strongly so: dim, blue-ish galaxies only have a slightly greater than 50% chance of being spiral, although it is true that bright, reddish galaxies are correctly measured as unlikely to be spiral.
The advantage of this method over other more opaque methods such as Neural Networks, or SVM, is that once we get to a leaf node of the decision tree, we know exactly why each galaxy is in that node—we can follow the decisions down the tree and build a boolean expression that describes all the galaxies at that node. If we wish, we can then ask ourselves if the decision path makes sense; we can look at the galaxies at that node, and ask if they form an interesting set. This kind of detailed, explicit decision-making analysis is (currently) absent in other machine learning methods although very recent work has begun to study this question [30,31], and is what allows us to be more confident that biases are unlikely to creep into the regression scheme.
3. Results
3.1. Features, Trees, and Forests
Referring again to Figure 2, we see that a 2-feature, 2-level decision tree based only on color and magnitude does a reasonable, though not great, job at separating spiral from non-spiral galaxies. Table 2 quantifies this in more detail, and provides a pair of features that gives better performance, although still only about 75% “correct” in total. In addition to the features listed in Table 1, Table 3 introduces quantities that are output by SpArcFiRe and used as additional input features for our model. Using these features, and in addition allowing the number of trees in the forest to increase, gives better results as summarized in Table 4 and described in more detail below.

Table 2.
Classification results for two-level, two-feature trees like that in Figure 2. Columns represent the average fraction , across galaxies in leaf node i, of GZ1 humans who voted that object to be a spiral galaxy, across the training set. This value is then the assigned for any non-training-set galaxy placed in this leaf node. correctAll: assuming represent a positive spiral classification, the percentage across all galaxies of correct classifications; SPcapture: the fraction of true spirals that are captured by this classification scheme. SPcontam: the fraction of galaxies classified as spiral that are incorrectly classified. Top row: exactly the tree of Figure 2. Second Row: a pair that arguably performs better because it has a higher total correct classification, primarily because it has far less contamination of non-spirals, even though it has a smaller capture fraction. It demonstrates that we can have 75% correct classifications even with just a two-parameter, two-level tree. See Table 1 for the meaning of the input variables.

Table 3.
Outputs from SpArcFiRe that are used as input features for our model, in addition to those from Table 1. See Davis and Hayes [15] for full descriptions of these parameters. Parameters labeled “DCO” are measured only across arcs of “dominant chirality only”—that is, arcs of the “wrong” chirality, which are likely to be noise, are not included. The parameter “arcLenAt50%” means: lay arcs end-to-end sorted longest to shortest, resulting in a line of total length L, and measure the length of the arc that lies at the point L/2 along the line. If the arms are short at L/2, then short arcs tend to suggest the galaxy is either flocculent or non-spiral, whereas a long arc at this point suggests a more grand-design spiral. The “rankAt50%” feature is similar, except this is the integer rank of the arc touching the L/2 point. If the ratio ((diskAxisRatio) / (bulgeAxisRatio)) is close to 1, it is suggestive of an elliptical galaxy, whereas if this ratio is significantly less than one it suggests a spiral galaxy (since the bulge axis ratio tends to be 1 from any vantage point, but not so for the disk).

Table 4.
Illustration of how the results of the classification improve as we allow more complex trees, and larger forests. The lines in which the feature(s) are listed as “various” means that, choosing k features (k from the first column), it is not difficult to find k features that provide a correctness similar to the last column. Of course not every selection of k features will result in that correctness; correctness was enhanced when the feature set included at least some high-quality features (cf. Section 3.3).
We now explore in depth how many total trees should be in the forest, and how many randomly chosen features should be in each tree. Recall that the total number of features is fixed (and is 101 in our case), but that each decision tree chooses some random set of features. We will look at how both of these parameters change the results.
Presumably, the more features a particular tree uses, the better that tree will be, although more care needs to be put into training these models to avoid overfitting. Figure 3 plots the Pearson correlation between the GZ1 human vote proportion for , and our reproduction of that proportion, as a function of how many features are used by each tree. As can be seen, increasing the number of features used by each tree generally results in improvement. However, since each tree chooses a random subset of features, there is a bit of noise in the curve. It becomes less obvious that there is an improvement beyond about 35 features per tree, so we use 35 in our final results below. We also see that the entire curve moves up as the number of trees in the forest increases.
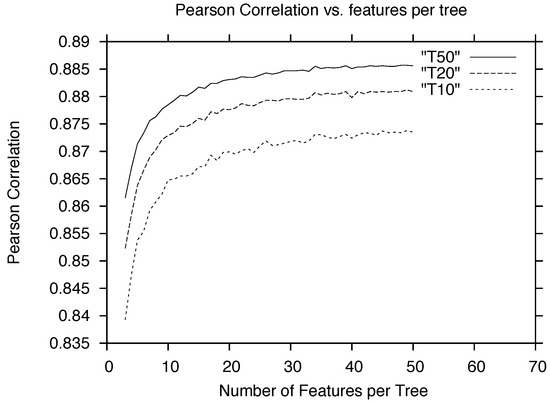
Figure 3.
The Pearson correlation between the fraction of GZ1 humans voting for spiral, and our reproduction of that vote fraction, as a function of the number of features per tree that are chosen at random from the entire feature set. The three curves correspond to the cases where the total number of trees is 10, 20, or 50.
Similarly, we would expect that as the number of trees in the forest is increased, the result would get better. Essentially, as more “experts” weigh into the decision, the better the results should be. Figure 4 demonstrates that this is indeed the case. Furthermore, unlike the case of choosing features, the curve is pretty much monotonically increasing: it seems that more trees are always better [36]. In our results below, we use 150 total trees, each using 35 features out of our total set of 101 combined features from SpArcFiRe and SDSS.
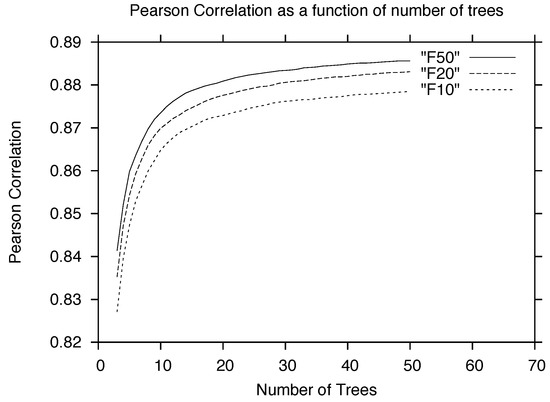
Figure 4.
Similar to Figure 3, the Pearson correlation between the fraction of GZ1 humans voting for spiral, and our reproduction of that fraction, as a function of the number of trees in the forest. The three curves also show how the results change when the number of features per tree is 10, 20, or 50.
3.2. Adding SpArcFiRe Features
As stated before, our goal is to test if adding SpArcFiRe’s features (cf. Table 3) to the set of input features will improve our ability to reproduce the vote distribution of GZ1 for spiral galaxies, so instead of classification, we are using regression to achieve our results. This means that, rather than having a galaxy falling under a class (spiral, elliptical, and other), our output is the extent to which an image of a galaxy displays spiral structure. This value, between 0 and 1, is represented by the percentage of humans that agree that a certain galaxy has visible spiral structure. We represent this idea by making the sum of GZ1 values as our target variable, and this is what we train our machine to reproduce—while simultaneously striving to eliminate the known bias [18,19].
We built three different random forest models using the same hyperparameters (150 total trees, each using 35 features) but with different feature sets. Model 1 uses only SDSS features, Model 2 uses only SpArcFiRe features, and Model 3 used both sets of features (this is the model we discuss throughout the paper). We ran a 10-fold cross validation5 [37,38,39] in each one of those to get a more accurate measure of how those sets performed individually. Model 1 had a mean RMSE of 0.1518, while Model 2 had a mean RMSE of 0.1522, and both had Pearson correlations of about 0.85. Comparing these Pearson correlations using a Student’s t-distribution test [40], we find that they do not differ significantly (both are approximately 170 (sic) standard deviations away from a random distribution)—not surprising since the RMSE’s differ only in the 4th digit. However, by combining the two feature sets, we get Model 3, which had a mean RMSE of 0.1404 and Pearson correlation of about 0.88. This RMSE differs from the other two in the second digit, and, according to the Student’s t-distribution, it differs from a random distribution by approximately 220 standard deviations—50 standard deviations further from random than both Models 1 and 2, meaning the p-value of Model 3’s Pearson correlation is many orders of magnitude more statistically significant than the Pearson correlation of Models 1 and 2. These statistical tests demonstrate that SpArcFiRe features alone are about as good as SDSS features alone at predicting spirality, while the two combined significantly decrease the model error. This is already an indication that there is valuable information in both feature sets. We will explore feature quality in Section 3.3.
The 10-fold cross validation RMSE of Model 3 was 0.1404 but the the best model had an RMSE of 0.1374; this best one is the model we use for the remainder of the paper (note that neither Model 1 nor 2 ever achieved such a low RMSE in any model we tested.). Table 5 shows our results, using both SDSS and SpArcFiRe’s features, for the test set in a 10 × 10 confusion matrix. Each row represents one of 10 bins holding galaxies in which a certain fraction of humans voted for that value of spirality; each column represents one of 10 identical bins containing the predicted spirality from our method. Thus, “correct” predictions (within 10% of the human vote) appear along the diagonal of the matrix. The first off-diagonal elements represent where our prediction was 10%–20% off, etc.; the far corners represent our worst predictions.

Table 5.
Confusion Matrix of the best of our 10-fold cross-validated models. The rows represent the number of objects that have a GZ1 spirality between a specific interval. The columns represent how many of those our Random Forest predicted in the same and different intervals. Notice that these numbers are only for the test set, thus a total of 45,802 objects, which represent a more accurate measure of how our Random Forest would perform in real-world situations. The same data are depicted pictorially in Figure 5.
Notice that our model has high sensitivity and specificity rates, which means that when it predicts that an object is spiral or non-spiral with high confidence, the prediction is very likely correct. For example, let’s look at the case where our model predicts that an object is spiral with more than 90% of confidence, the penultimate column of the Table 5. If we consider a decision for spiral or non-spiral object being made above or below the 0.5 threshold, this gives us a sensitivity rate of more than 98%. The similar case happens for non-spiral predictions with more than 90% confidence (where ≤ 0.1), the second column of the same table, in which, also considering a 0.5 threshold for a decision, our model gets more than 99% specificity rate.
Since we are doing regression, a more global way to visualize our results is to look at the correlation between our results and the GZ1 votes. Figure 5 shows a scatter plot where, for each galaxy, the x-axis represents the human vote fraction and the y-axis is our algorithm’s prediction of the same value, across all 470,000 Sloan galaxies. Each red point represents one galaxy, and its distance from the line depicts our level of agreement. The clustering around the line suggests good agreement with GZ1. It is also notable that more than 98% of the galaxies have and approximately 95% of the objects fall under .
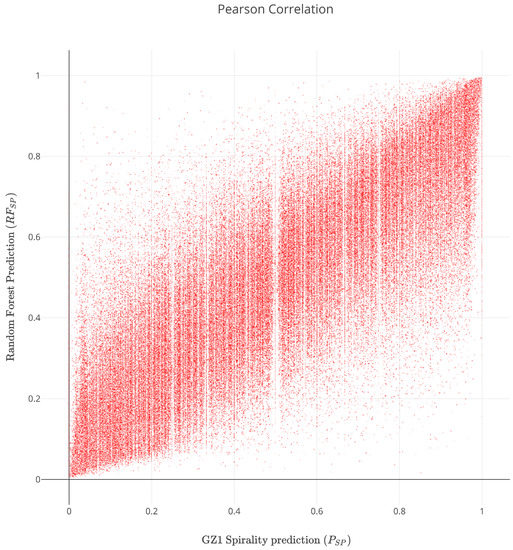
Figure 5.
Scatter plot of both training data and test data depicted in Table 5: our predicted spirality (vertical) vs. the fraction of GZ1 humans voting for spiral (horizontal). The points cluster around the line , depicting good agreement. Additionally, more than 98% of the galaxies have and approximately 95% of the objects fall under . The vertical white lines appear because the fraction of human voters is a ratio of discrete integers.
For the sake of comparison with existing classifiers, we can turn our regressor into a classifier by choosing a boundary for the decision. If we choose that boundary to be 0.5, we will make our decision based on the majority vote, which mimics the choice of the Galaxy Zoo researchers in some releases [8]. That would give our regressor an accuracy of approximately 93% based on the test set presented in Table 5, comparable to existing methods.6
In Figure 6, we show some of our correctly classified objects. Those objects were cases where our model had a high agreement with the classifications provided by GZ1, and looking at the images we understand why. In Figure 6a, we display some of the spiral objects detected, while in Figure 6b we show the non-spiral objects detected, which belong to the other classes of objects in GZ1: Elliptical, Merger, and Artefact, respectively.

Figure 6.
Examples of images that had a high agreement of classification by both, our Random Forest Model and the GZ1 humans. (a) shows images of spirals where AND . Their SDSS IDs are, respectively, 1237654030325973054, 1237662306733916433, and 1237668298219847857; (b) shows images of non-spirals where AND . Their SDSS IDs are, respectively, 1237663529721397476, 1237661465447497940, and 1237661949201154382.
It is important to understand what is going on in the small fraction of objects for which our method performs poorly. These objects are in the opposite corners of the off-diagonal in Table 5: four objects from the bottom left corner and 1 from the top right corner. These are that objects with a high disagreement: . From our total of 45,802 galaxies in the test set, only five fall in this margin, and we show all of them in Figure 7. The top four rows depict the same problem: very faint arms that SpArcFiRe entirely failed to detect during the disk detection phase, so that it zoomed in past the arms, making it impossible for the arm detection code to find anything useful. This is a rare occurrence, and we are aware of this issue and are working on improving this specific step of SpArcFiRe [9]. The object on the bottom row is clearly a merger, and arm-like features are present, so our machine predicts a high spirality. One could argue that this is a correct prediction that the galaxy is not an elliptical galaxy, but the GZ1 humans correctly marked it as a merger and thus not a spiral at all. Since our machine has not been trained to detect mergers, it is unclear whether this should count as a misclassification.7

Figure 7.
Grossly Misclassified Objects. In sets of 3, from left to right column, the images show the Original Input Image, the same image automatically cropped by SpArcFiRe, and the spiral Arcs detected on the image (if any). The SDSS Object IDs, the GZ1 Spirality prediction (), and our Random Forest Prediction () are shown above each trio of images. In all but the last, the problem is low-surface-brightness arms, which we know about and are working on this issue. Despite the disagreement in the 5th object, a merger, spiral structure is indeed present.
3.3. Feature Quality
Blindly adding features to a model does not guarantee that it will get better. Additional features might represent redundant information, which would not translate into more accurate classifiers for certain machine learning models, or worse, they would contribute to the curse of dimensionality [41]. In order to make sure we are adding meaningful information, we further analyzed our feature set—again something that would be difficult to do with any model other than a random forest.
To check which features seem to be the most important overall, we created a feature ranking. As we have depicted in Figure 2, each node in a decision tree is a condition that splits the decision tree in two based upon a threshold in one variable. The measure used to make that decision is called impurity, and it is usually entropy for classification trees and variance for regression trees. It basically encodes how much information a particular feature, upon selection, adds to the decision process. The more outputs a feature can separate, the higher its entropy is going to be, thus decreasing the impurity of the decision tree. Thus, we compute how much each feature decreases the weighted impurity of a tree. In our case, since we are using random forests, the impurity decrease from each feature can be averaged, and the features are ranked according to this measure [42].
Table 6 shows the top 10 features ranked by their importance along with the standard deviations of that score since this is an average over 150 decision trees. We can see that from the top 10 features, five come from SDSS and five from SpArcFiRe, suggesting again that the two feature sets contribute roughly equally to the quality of the results. The five best SpArcFiRe features are all related to the number of arcs greater or equal to a certain number of pixels, which is, not surprisingly, a strong indicator of the presence of spiral structure. Interestingly, in SpArcFiRe’s favor, the best feature overall is the number of dominant-chirality-only arms equal or longer than 120, which is 30% more relevant than the most relevant feature from SDSS—far and away the most relevant feature among all features, way in front of the pack of other features in terms of importance.

Table 6.
Top 10 best features for spirality prediction in decreasing order of importance. The standard deviation is measured across the 150 decision trees.
3.4. Comparison with Other Regression Methods
In Section 2, we argued extensively about why we prefer to use Random Forests over other methods because we want understandable models that perform regression rather than classification. Although we have explained why Random Forests are better than Neural Networks for understandability, here we test whether Random Forests compare favorably against other regression methods. To that end, we trained a Ridge Linear Regressor and a K-Nearest Neighbors (KNN) Regressor using both SDSS and SpArcFiRe features set. Table 7 has a comparison of the results for all the models. As we can see, the Random Forest had by far the best performance out of the three models in all the measurements we used. Although the KNN model presents a comparable RMSE, its Mean Absolute Error (MAE) is over 20% worse than the random forest’s MAE. The random forest also has a Pearson correlation almost 10% better than the next best model.

Table 7.
Measures of error and quality from models trained with both SDSS features and SpArcFiRe features. Note that these three models were each simultaneously trained from scratch on exactly the same data for this comparison, and thus the RMSE and Pearson correlations—which depend upon stochastic parameters—of this particular random forest (RF) model differs from our RF model discussed in the rest of the paper.
To make sure we aren’t overfitting or have introduced different biases to the models, we also show the residual plots for all the models in Figure 8. For visualization purposes, we are using a random sample of 10,000 points from the test set for these plots. A model with no errors would have all the points with a residual value of zero. In a more realistic scenario, the residuals should not be either systematically high or low, meaning that they should be centered on zero throughout the range of predicted values [29]. There’s no apparent shape in any of the plots, other than a higher concentration of points in the range, which is expected since the number of “ellpitical” classifications far outnumbers the spiral classifications in the GZ1 sample. A closer examination of the plots corroborates with the measures of error on Table 7 though. The ridge regression has higher residuals in the range and the KNN model has the same issue in the interval. The random forest plot, on the other hand, has a distribution more symmetrically distributed about the x-axis, especially near the region, indicating that our method produces an unbiased, roughly uniform distribution of predicted spirality when the true spirality is close to 0.5.
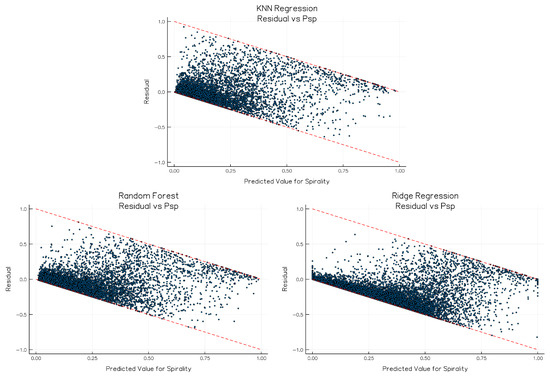
Figure 8.
Residual plots for models trained with both SDSS features and SpArcFiRe features. For visualization purposes we used only 10,000 points from the test set for these plots. The red dashed lines indicate the possible bounds that the values can fall on. Since both the inputs and outputs are constrained to be in the interval [0, 1] (cf. Figure 5), the lower bound is determined by and the upper bound is determined by , for .
4. Conclusions
Our results show that it is possible to have a model that performs well, is in agreement with human votes above 90% of the time, and also deal with the winding bias problem which was addressed in more detail in [19]. In this sense, we “filter” the errors made by humans while still retaining the useful knowledge provided by the Galaxy Zoo. However, it is possible that Random Forests present a compromise at the intersection of understandability and precision, with RFs exceeding in the former while neural networks possibly excelling in the latter—possibly at the expense of reproducing human biases [24] or perhaps even introducing new ones.
What differentiates this from previous work is the addition of SpArcFiRe’s output, which adds more information to the objects we are discriminating and helps to decrease the amount of bias present in the classifications provided in GZ1. These results demonstrate that SpArcFiRe adds valuable (rather than redundant) information; in turn, these new features can be used by other automatic machine learning classifiers and regressors to improve results. We provided some insights on what these models find more descriptive for spiral galaxies demonstrating the most important parameters used by random forests in Table 6.
Author Contributions
Conceptualization, P.S., L.T.C. and W.B.H.; Data curation, P.S. and L.T.C.; Formal analysis, P.S., L.T.C. and W.B.H.; Investigation, P.S. and L.T.C.; Methodology, P.S., L.T.C. and W.B.H.; Project administration, W.B.H.; Resources, W.B.H.; Software, P.S. and L.T.C.; Supervision, W.B.H.; Validation, P.S.; Visualization, P.S., L.T.C. and W.B.H.; Writing—Original Draft, P.S., L.T.C. and W.B.H.; Writing – Review and Editing, P.S. and W.B.H.
Funding
This research received no external funding.
Acknowledgments
This work was supported by CAPES (Coordination for the Improvement of Higher Education Personnel—Brazil) through the Science Without Borders fellowship for Ph.D. Studies awarded to Pedro Silva. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max Planck Institute for Astronomy (MPIA), the Max Planck Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, R.W. The Expanding Universe: Astronomy’s ‘Great Debate’, 1900–1931; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Oort, J.H. Problems of Galactic Structure. Astrophys. J. 1952, 116, 233. [Google Scholar] [CrossRef]
- De Vaucouleurs, G. General physical properties of external galaxies. In Astrophysik IV: Sternsysteme/Astrophysics IV: Stellar Systems; Springer: New York, NY, USA, 1959; pp. 311–372. [Google Scholar]
- Perlmutter, S.; Turner, M.S.; White, M. Constraining dark energy with type Ia supernovae and large-scale structure. Phys. Rev. Lett. 1999, 83, 670. [Google Scholar] [CrossRef]
- Nelson, D.; Pillepich, A.; Genel, S.; Vogelsberger, M.; Springel, V.; Torrey, P.; Rodriguez-Gomez, V.; Sijacki, D.; Snyder, G.F.; Griffen, B.; et al. The illustris simulation: Public data release. Astron. Comput. 2015, 13, 12–37. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics; Princeton Series in Astrophysics; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Mihalas, D.; Binney, J. Galactic Astronomy—Structure and Kinematics; Princeton Series in Astrophysics; W.H. Freeman and Co.: San Francisco, CA, USA, 1981. [Google Scholar]
- Lintott, C.J.; Schawinski, K.; Slosar, A.; Land, K.; Bamford, S.P.; Thomas, D.; Raddick, M.J.; Nichol, R.C.; Szalay, A.; Andreescu, D.; et al. Galaxy Zoo: Morphologies derived from visual inspection of galaxies from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2008, 389, 1179–1189. [Google Scholar] [CrossRef]
- Davis, D.; Hayes, W. Automated quantitative description of spiral galaxy arm-segment structure. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1138–1145. [Google Scholar] [CrossRef]
- Sellwood, J.A. The lifetimes of spiral patterns in disc galaxies. Mon. Not. R. Astron. Soc. 2011, 410, 1637–1646. [Google Scholar] [CrossRef]
- York, D.G.; Adelman, J.; Anderson, J.E., Jr.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bakken, J.A.; Barkhouser, R.; Bastian, S.; Berman, E.; et al. The Sloan Digital Sky Survey: Technical summary. Astron. J. 2000, 120, 1579–1587. [Google Scholar] [CrossRef]
- Lintott, C.; Schawinski, K.; Bamford, S.; Slosar, A.; Land, K.; Thomas, D.; Edmondson, E.; Masters, K.; Nichol, R.C.; Raddick, M.J.; et al. Galaxy Zoo 1: Data release of morphological classifications for nearly 900,000 galaxies. Mon. Not. R. Astron. Soc. 2010, 14, 1–14. [Google Scholar] [CrossRef]
- Kahn, S.; Hall, H.J.; Gilmozzi, R.; Marshall, H.K. Final Design of the Large Synoptic Survey Telescope. Proc. SPIE 2016, 9906, 17. [Google Scholar]
- Kalirai, J. Scientific Discovery with the James Webb Space Telescope. arXiv, 2018; arXiv:1805.06941. [Google Scholar]
- Davis, D.R.; Hayes, W.B. SpArcFiRe: Scalable Automated Detection of Spiral Galaxy Arm Segments. Astrophys. J. 2014, 790, 87. [Google Scholar] [CrossRef]
- Davis, D.R. Fast Approximate Quantification of Arbitrary Arm-Segment Structure in Spiral Galaxies. Ph.D. Thesis, University of California, Irvine, CA, USA, 2014. [Google Scholar]
- Lintott, C.J.; Schawinski, K.; Bamford, S.P.; Slosar, A.; Land, K.; Thomas, D.; Edmondson, E.; Masters, K.; Nichol, R.C.; Raddick, M.J.; et al. Galaxy Zoo 1: Data release of morphological classifications for nearly 900,000 galaxies. Neural Netw. 2011, 410, 166–178. [Google Scholar] [CrossRef]
- Land, K.; Slosar, A.; Lintott, C.J.; Andreescu, D.; Bamford, S.P.; Murray, P.; Nichol, R.; Raddick, M.J.; Schawinski, K.; Szalay, A.; et al. Galaxy Zoo: The large-scale spin statistics of spiral galaxies in the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2008, 388, 1686–1692. [Google Scholar] [CrossRef]
- Hayes, W.B.; Davis, D.R.; Silva, P. On the nature and correction of the spurious S-wise spiral galaxy winding bias in Galaxy Zoo 1. Mon. Not. R. Astron. Soc. 2017, 466, 3928–3936. [Google Scholar] [CrossRef]
- Shamir, L. Automatic morphological classification of galaxy images. Mon. Not. R. Astron. Soc. 2009, 399, 1367–1372. [Google Scholar] [CrossRef] [PubMed]
- Huertas-Company, M.; Aguerri, J.A.L.; Bernardi, M.; Mei, S.; Sánchez Almeida, J. Revisiting the Hubble sequence in the SDSS DR7 spectroscopic sample: A publicly available Bayesian automated classification. Astron. Astrophys. 2010, 525, A157. [Google Scholar] [CrossRef]
- Banerji, M.; Lahav, O.; Lintott, C.J.; Abdalla, F.B.; Schawinski, K.; Bamford, S.P.; Andreescu, D.; Murray, P.; Raddick, M.J.; Slosar, A.; et al. Galaxy Zoo: Reproducing galaxy morphologies via machine learning. Mon. Not. R. Astron. Soc. 2010, 406, 342–353. [Google Scholar] [CrossRef]
- Kuminski, E.; George, J.; Wallin, J.; Shamir, L. Combining Human and Machine Learning for Morphological Analysis of Galaxy Images. Publ. Astrono. Soc. Pac. 2014, 126, 959–967. [Google Scholar] [CrossRef]
- Dieleman, S.; Willett, K.W.; Dambre, J. Rotation-invariant convolutional neural networks for galaxy morphology prediction. Mon. Not. R. Astron. Soc. 2015, 450, 1441–1459. [Google Scholar] [CrossRef]
- Ferrari, F.; de Carvalho, R.R.; Trevisan, M. Morfometryka—A New Way of Establishing Morphological Classification of Galaxies. Astrophys. J. 2015, 814, 55. [Google Scholar] [CrossRef]
- Willett, K.W.; Lintott, C.J.; Bamford, S.P.; Masters, K.L.; Simmons, B.D.; Casteels, K.R.V.; Edmondson, E.M.; Fortson, L.F.; Kaviraj, S.; Keel, W.C.; et al. Galaxy Zoo 2: Detailed morphological classifications for 304 122 galaxies from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2013, 435, 2835–2860. [Google Scholar] [CrossRef]
- Abd Elfattah, M.; Elbendary, N.; Elminir, H.K.; Abu El-Soud, M.A.; Hassanien, A.E. Galaxies image classification using empirical mode decomposition and machine learning techniques. In Proceedings of the 2014 International Conference on Engineering and Technology (ICET), Cairo, Egypt, 19–20 April 2014; pp. 1–5. [Google Scholar]
- Applebaum, K.; Zhang, D. Classifying Galaxy Images through Support Vector Machines. In Proceedings of the 2015 IEEE International Conference on Information Reuse and Integration (IRI), San Francisco, CA, USA, 13–15 August 2015; pp. 357–363. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics), 1st ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 19–17 August 2016; ACM: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Nguyen, A.; Yosinski, J.; Clune, J. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. arXiv, 2015; arXiv:1412.1897. [Google Scholar]
- Peng, T.; English, J.E.; Silva, P.; Davis, D.R.; Hayes, W.B. SpArcFiRe: Morphological selection effects due to reduced visibility of tightly winding arms in distant spiral galaxies. arXiv, 2017; arXiv:1707.02021. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Adelman-McCarthy, J.K.; Agüeros, M.A.; Allam, S.S.; Prieto, C.A.; Anderson, K.S.J.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bailer-Jones, C.A.L.; Baldry, I.K.; et al. The Sixth Data Release of the Sloan Digital Sky Survey. Astrophys. J. Suppl. Ser. 2008, 175, 297–313. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. Soc. Ind. Appl. Math. Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Sibley, C. More Is Always Better: The Power Of Simple Ensembles. 2012. Available online: http://www.overkillanalytics.net/more-is-always-better-the-power-of-simple-ensembles/ (accessed on 1 September 2018).
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross-Validation. In Encyclopedia of Database Systems; Springer: New York, NY, USA, 2016; pp. 1–7. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2014; p. 70. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; p. 184. [Google Scholar]
- Rahman, N. A Course in Theoretical Statistics: For Sixth forms, Technical Colleges, Colleges of Education, Universities; Charles Griffin & Company Limited: London, UK, 1968. [Google Scholar]
- Jensen, R.; Shen, Q. Are More Features Better? A Response to Attributes Reduction Using Fuzzy Rough Sets. IEEE Trans. Fuzzy Syst. 2009, 17, 1456–1458. [Google Scholar] [CrossRef]
- Saabas, A. Selecting Good Features Part III: Random Forests. 2014. Available online: https://blog.datadive.net/selecting-good-features-part-iii-random-forests/ (accessed on 1 September 2018).
| 1 | Stephen Bamford, Personal Communication. |
| 2 | In essence, comparing against the Gold sample says “look how well we do when the humans pre-select the easy ones for us!” More formally, it disregards false positives—galaxies which the prediction is confident but is actually way off. |
| 3 | It is important to clarify that throughout this paper we will be using the term feature(s) to describe an individual measurable property or characteristic of a phenomenon being observed [29] as it is commonly done in the machine learning literature as opposed to features as seen in an image-like globular clusters. |
| 4 | High spirality is a strong indicator of a galaxy being spiral, but it’s not a necessary condition. Galaxies with low spirality may be edge-on spirals, ellipticals, low-resolution spirals, or even disk galaxies without spiral structure, such as the Sombrero Galaxy. |
| 5 | K-Fold cross validation is a method for measuring the quality of a learning algorithm by splitting the data into K buckets, training the algorithm in of these buckets and testing in the holdout bucket. We do this K times, each time holding out a different bucket and we report the average accuracy as the final accuracy of a model in that dataset. Finally, we choose the best out of the K models as our final model, having demonstrated that all the other K-1 models also perform reasonably well. |
| 6 | A higher accuracy can be achieved if we use a boundary below 0.5. Note that, since there were six choices in GZ1, any vote receiving more than 1/6 of the votes can be a winning vote; for example, a vote of 40% could be considered a classification if all the other choices had less than 40% of votes. It is also possible to get better accuracy, using the same features, if we build a classifier rather than a regressor, but that is outside the scope of this paper. |
| 7 | One might argue that perhaps our “spirality” measure is more aptly called “non-ellipticity”. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).