Jsolated Stars of Low Metallicity
Abstract
:1. Introduction
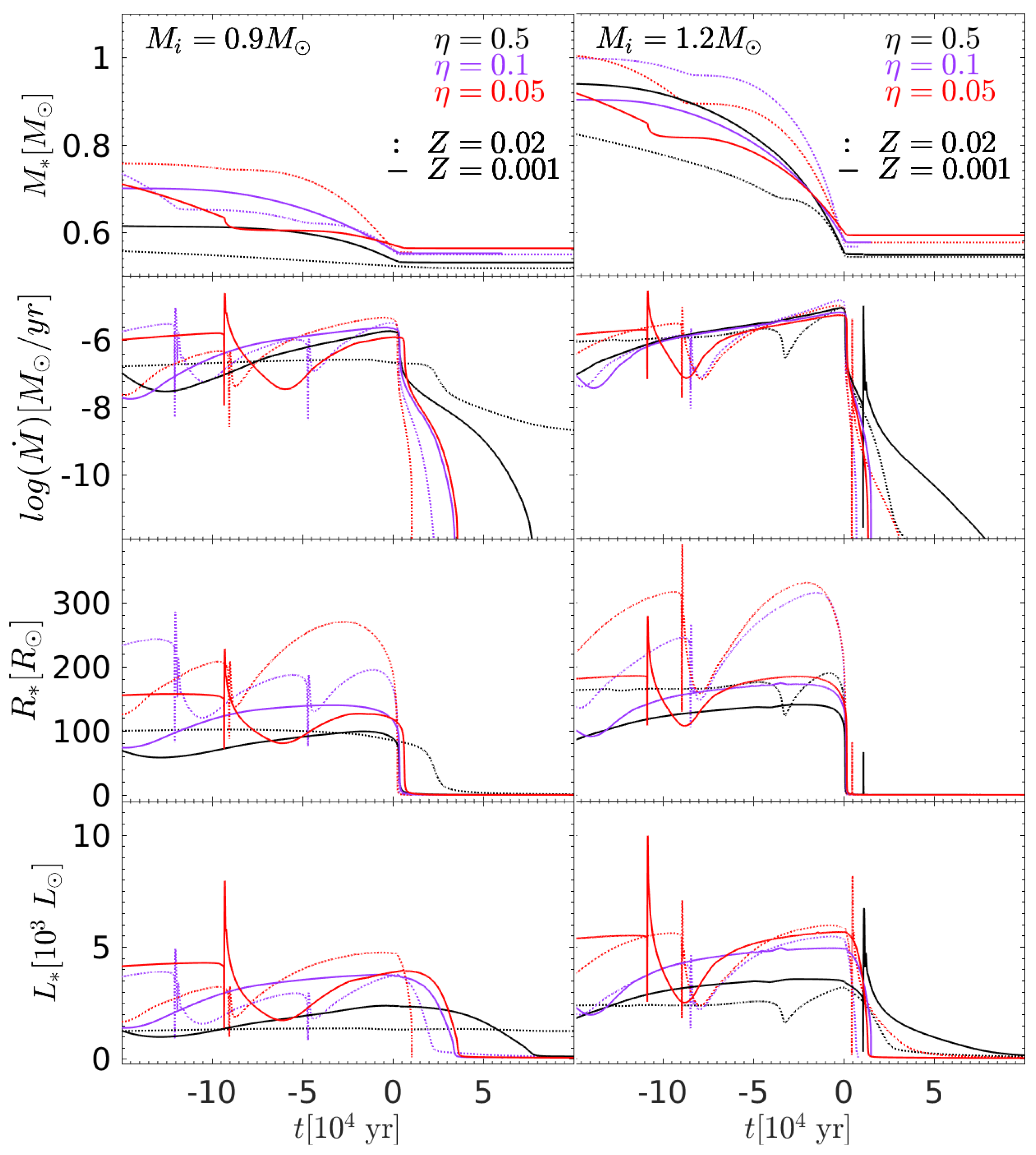
2. Results
3. Discussion
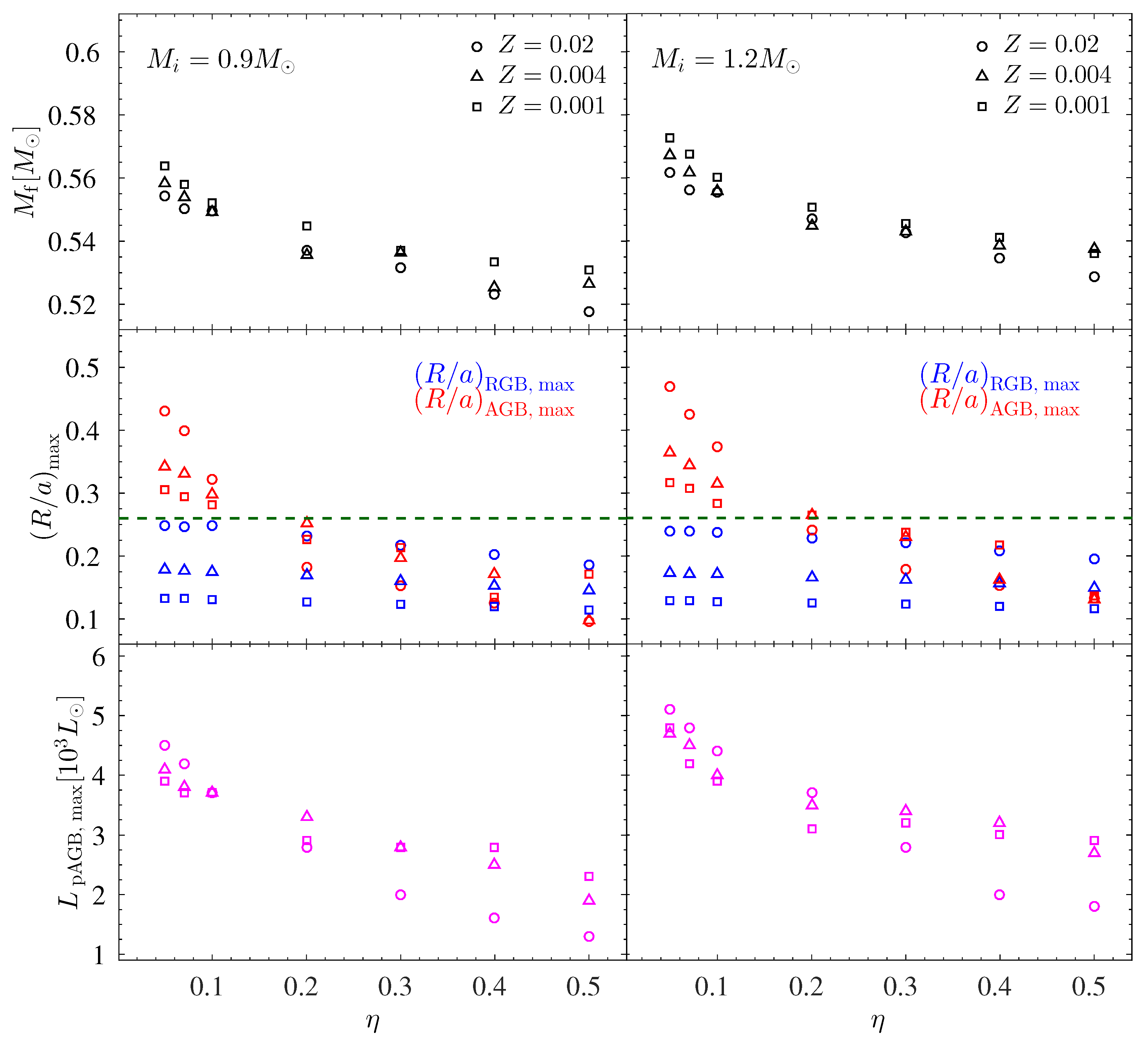
- A higher final mass (higher mass of the central star), , implies a more luminous central star for the ionization of the PN. It can be seen for all metallicities that as the mass-loss rate efficiency parameter decreases the value of increases. There are very small differences between the values of for different metallicities (yet with the same initial mass and the same value of ). Overall, by comparing and there is an increase of 5–8%. On the one hand this increase in might be too small for dynamical effects, but on the other hand it has a large effect on the luminosity, as we shall discuss below, since the luminosity is very sensitive to the central star mass.
- The ratio of the maximum stellar radius and the orbital separation, , clearly increases both with the decrease in and with increasing Z. Moreover, when examining Equation (2) for a planet companion of and at an initial orbital separation of we reach the final conclusions as in [2]: For the RGB phase it is only marginal for the planet to be engulfed in all cases, hence the probability for an early interaction is at most very small. In addition, for the traditional evolution with a high mass-loss rate efficiency parameter of the AGB value of is too small for planet engulfment for the low mass of , and is marginal for the larger mass of . However, when reducing the mass-loss rate efficiency to it is clear from our results that there is a non-negligible range of separations for a planet to exist and be engulfed by the star during the AGB phase. This is because the AGB radius reaches higher values compared to the RGB and compared to the values obtained in “traditional” evolution. In other words, planet engulfment will take place on the AGB of Jsolated stars when the mass-loss rate efficiency parameter is , independent on the metallicity, for the representative cases studied here.
- Though we found that both for solar metallicity and for low metallicities planet engulfment is likely to take place on the AGB of Jsolated stars, it is interesting to note that the value of not only increases with an increasing value of Z, but the increase is also “stronger” as reduces and the metallicity increases.
- Our results have implications on the bright end cut-off of the PNLF in old stellar populations, where luminosities of ≃5000 and higher are needed for the central star to ionize the bright nebula. To examine this possibility of such a bright central star we focus on the post-AGB luminosities reached in our simulations. We find that the post-AGB luminosity also increases with the decrease of the mass-loss rate, reaching the high ≃5000 luminosities needed to explain the brightest PNe in old stellar populations. Interestingly it seems that as the value of decreases the values for different metallicities grow closer together. We point out that the value of has a wide range since it is an approximate value taken at the final AGB phase (the maximum value of the luminosity around in Figure 1), disregarding the sharp rise due to the helium shell flash. Indeed, we have shown that under the Jsolated framework we can explain the bright end cut-off of the PNLF also for low metallicity low mass stars.
Funding
Acknowledgments
Conflicts of Interest
References
- Sabach, E.; Soker, N. The Class of Jsolated Stars and Luminous Planetary Nebulae in old stellar populations. Mon. Not. R. Astron. Soc. 2018, 479, 2249–2255. [Google Scholar] [CrossRef]
- Sabach, E.; Soker, N. Accounting for planet-shaped planetary nebulae. Mon. Not. R. Astron. Soc. 2018, 473, 286–294. [Google Scholar] [CrossRef]
- Soker, N. What Planetary Nebulae Can Tell Us about Planetary Systems. Astrophys. J. Lett. 1996, 460, L53. [Google Scholar] [CrossRef]
- Siess, L.; Livio, M. The accretion of brown dwarfs and planets by giant stars—I. Asymptotic giant branch stars. Mon. Not. R. Astron. Soc. 1999, 304, 925–937. [Google Scholar] [CrossRef]
- Siess, L.; Livio, M. The accretion of brown dwarfs and planets by giant stars—II. Solar-mass stars on the red giant branch. Mon. Not. R. Astron. Soc. 1999, 308, 1133–1149. [Google Scholar] [CrossRef] [Green Version]
- De Marco, O.; Moe, M. Common Envelope Evolution through Planetary Nebula Eyes. In Proceedings of the Planetaty Nebulae as Astronomical Tools: International Conference on Planetaty Nebulae as Astronomical Tools, Gdańsk, Poland, 28 June–2 July 2005; Volume 804, pp. 169–172. [Google Scholar]
- Soker, N.; Subag, E. A Possible Hidden Population of Spherical Planetary Nebulae. Astron. J. 2005, 130, 2717. [Google Scholar] [CrossRef]
- Moe, M.; De Marco, O. Do Most Planetary Nebulae Derive from Binaries? I. Population Synthesis Model of the Galactic Planetary Nebula Population Produced by Single Stars and Binaries. Astrophys. J. 2006, 650, 916. [Google Scholar] [CrossRef]
- Villaver, E.; Livio, M. Can Planets Survive Stellar Evolution? Astrophys. J. 2007, 661, 1192. [Google Scholar] [CrossRef]
- Villaver, E.; Livio, M. The Orbital Evolution of Gas Giant Planets around Giant Stars. Astrophys. J. Lett. 2009, 705, L81. [Google Scholar] [CrossRef]
- Nordhaus, J.; Spiegel, D.S.; Ibgui, L.; Goodman, J.; Burrows, A. Tides and tidal engulfment in post-main-sequence binaries: Period gaps for planets and brown dwarfs around white dwarfs. Mon. Not. R. Astron. Soc. 2010, 408, 631–641. [Google Scholar] [CrossRef]
- De Marco, O.; Soker, N. The Role of Planets in Shaping Planetary Nebulae. Publ. Astron. Soc. Pac. 2011, 123, 402. [Google Scholar] [CrossRef]
- Mustill, A.J.; Veras, D.; Villaver, E. Long-term evolution of three-planet systems to the post-main sequence and beyond. Mon. Not. R. Astron. Soc. 2014, 437, 1404–1419. [Google Scholar] [CrossRef]
- Villaver, E.; Livio, M.; Mustill, A.J.; Siess, L. Hot Jupiters and Cool Stars. Astrophys. J. 2014, 794, 3. [Google Scholar] [CrossRef]
- Meynet, G.; Eggenberger, P.; Privitera, G.; Georgy, C.; Ekström, S.; Alibert, Y.; Lovis, C. Star-planet interactions. IV. Possibility of detecting the orbit-shrinking of a planet around a red giant. Astron. Astrophys. 2017, 602, L7. [Google Scholar] [CrossRef]
- Ciardullo, R.; Jacoby, G.H.; Ford, H.C.; Neill, J.D. Planetary nebulae as standard candles. II—The calibration in M31 and its companions. Astrophys. J. 1989, 339, 53–69. [Google Scholar] [CrossRef]
- Jacoby, G.H. Planetary nebulae as standard candles. I—Evolutionary models. Astrophys. J. 1989, 339, 39–52. [Google Scholar] [CrossRef]
- Ciardullo, R.; Sigurdsson, S.; Feldmeier, J.J.; Jacoby, G.H. Close Binaries as the Progenitors of the Brightest Planetary Nebulae. Astrophys. J. 2005, 629, 499. [Google Scholar] [CrossRef]
- Van de Steene, G.C.; Jacoby, G.H.; Praet, C.; Ciardullo, R.; Dejonghe, H. Distance determination to NGC 55 from the planetary nebula luminosity function. Astron. Astrophys. 2006, 455, 891–896. [Google Scholar] [CrossRef] [Green Version]
- Ciardullo, R. The Planetary Nebula Luminosity Function: Pieces of the Puzzle. Publ. Astron. Soc. Aust. 2010, 27, 149–155. [Google Scholar] [CrossRef] [Green Version]
- Davis, B.D.; Ciardullo, R.; Feldmeier, J.J.; Jacoby, G.H. The Planetary Nebula Luminosity Function (PNLF): Contamination from Supernova Remnants. Res. Notes Am. Astron. Soc. 2018, 2, 32. [Google Scholar] [CrossRef] [Green Version]
- Gesicki, K.; Zijlstra, A.A.; Miller Bertolami, M.M. The mysterious age invariance of the planetary nebula luminosity function bright cut-off. Nat. Astron. 2018, 2, 580. [Google Scholar] [CrossRef]
- Diago, P.D.; Gutiérrez-Soto, J.; Fabregat, J.; Martayan, C. Pulsating B and Be stars in the Small Magellanic Cloud. Astron. Astrophys. 2008, 480, 179–186. [Google Scholar] [CrossRef] [Green Version]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. 2011, 192, 3. [Google Scholar] [CrossRef]
- Badenes, C.; Maoz, D.; Ciardullo, R. Pulsating B and Be stars in the Small Magellanic Cloud. Astrophys. J. 2015, 804, L25. [Google Scholar] [CrossRef]
- Reimers, D. The Progenitors and Lifetimes of Planetary Nebulae. Memoires of the Societe Royale des Sciences de Liege 1975, 8, 369. [Google Scholar]
- Guo, J.; Lin, L.; Bai, C.; Liu, J. The effects of the Reimers η on the solar rotational period when our Sun evolves to the RGB tip. Astrophys. Space Sci. 2017, 362, 15. [Google Scholar] [CrossRef]
- Soker, N. Energy and angular momentum deposition during common envelope evolution. New Astron. 2004, 9, 399–408. [Google Scholar] [CrossRef] [Green Version]
- Giles, H.A.C.; Osborn, H.P.; Blanco-Cuaresma, S.; Lovis, C.; Bayliss, D.; Eggenberger, P.; Cameron, A.C.; Kristiansen, M.H.; Turner, O.; Bouchy, F.; et al. The longest period transiting planet candidate from K2. arXiv, 2018; arXiv:1806.08757. [Google Scholar] [CrossRef]
- Karakas, A.I. Helium enrichment and carbon-star production in metal-rich populations. Mon. Not. R. Astron. Soc. 2014, 445, 347–358. [Google Scholar] [CrossRef] [Green Version]
- Miller Bertolami, M.M. New models for the evolution of post-asymptotic giant branch stars and central stars of planetary nebulae. Astron. Astrophys. 2016, 588, A25. [Google Scholar] [CrossRef]
- Ventura, P.; Karakas, A.; Dell’Agli, F.; García-Hernández, D.A.; Guzman-Ramirez, L. Gas and dust from solar metallicity AGB stars. Mon. Not. R. Astron. Soc. 2018, 475, 2282–2305. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabach, E. Jsolated Stars of Low Metallicity. Galaxies 2018, 6, 89. https://doi.org/10.3390/galaxies6030089
Sabach E. Jsolated Stars of Low Metallicity. Galaxies. 2018; 6(3):89. https://doi.org/10.3390/galaxies6030089
Chicago/Turabian StyleSabach, Efrat. 2018. "Jsolated Stars of Low Metallicity" Galaxies 6, no. 3: 89. https://doi.org/10.3390/galaxies6030089
APA StyleSabach, E. (2018). Jsolated Stars of Low Metallicity. Galaxies, 6(3), 89. https://doi.org/10.3390/galaxies6030089



