Planetary Nebulae Embryo after a Common Envelope Event
Abstract
1. Introduction
2. The Stages of a CE Event, and the Associated Mass Outflows
3. Morphology of the CE Ejecta
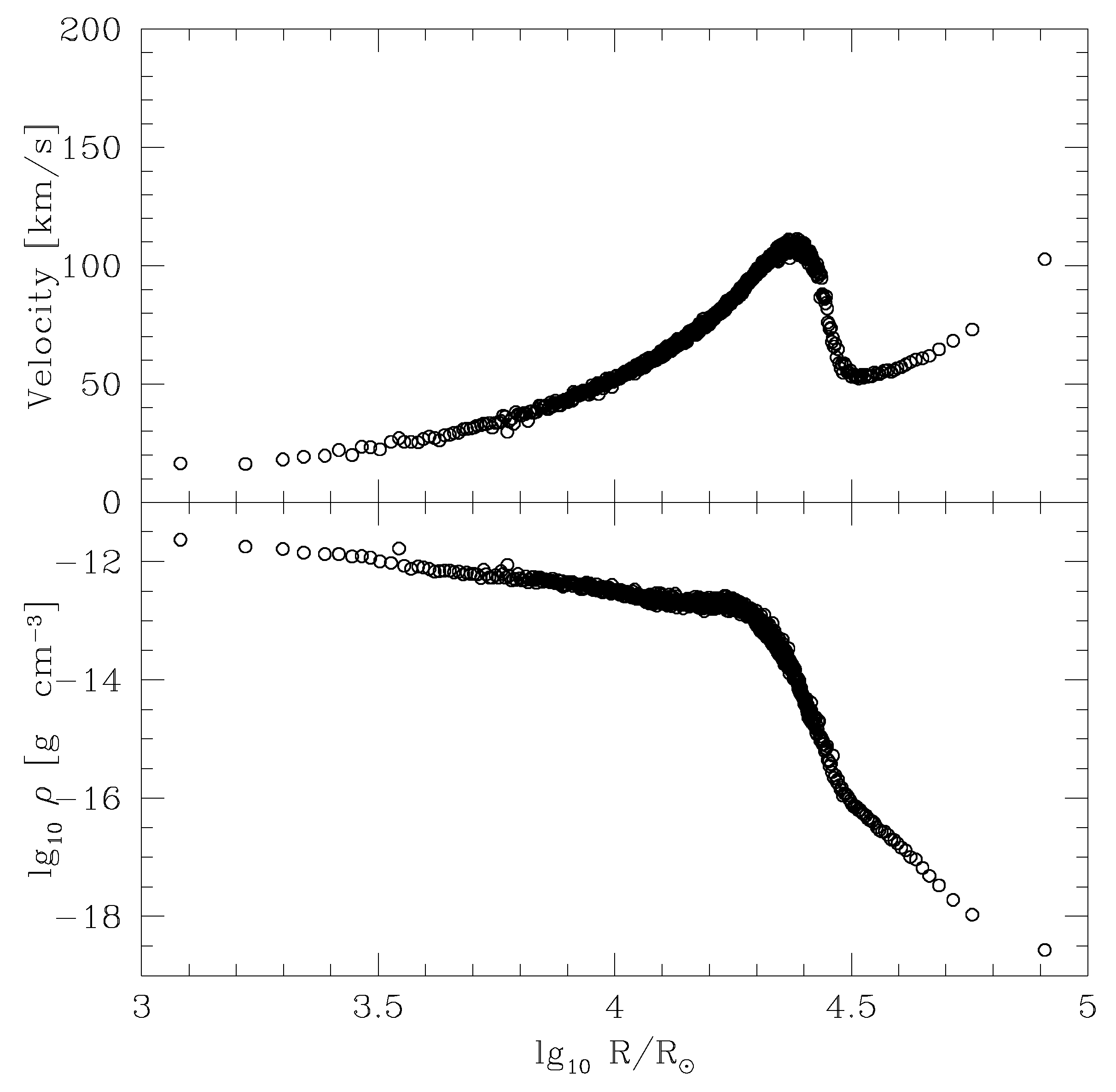
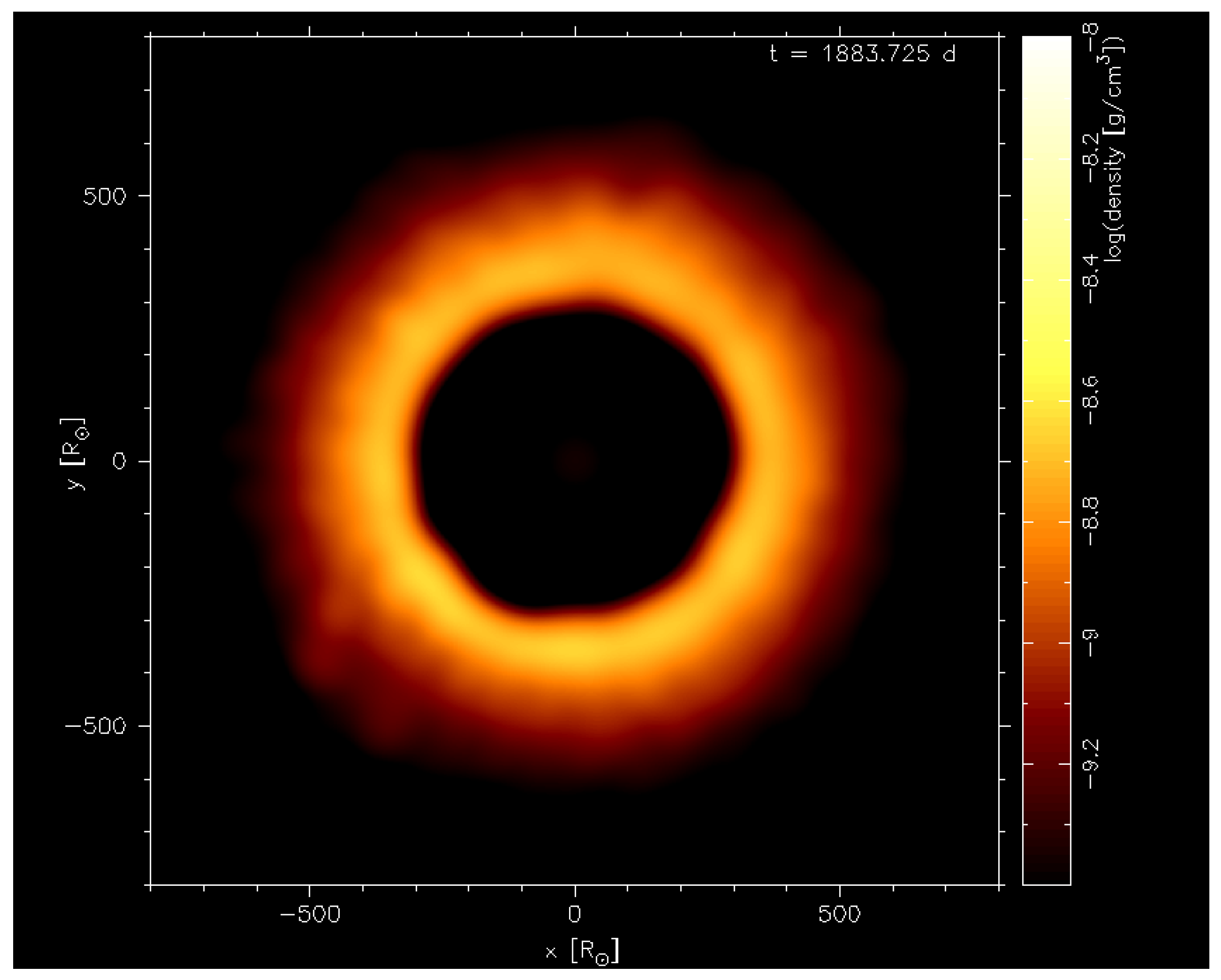
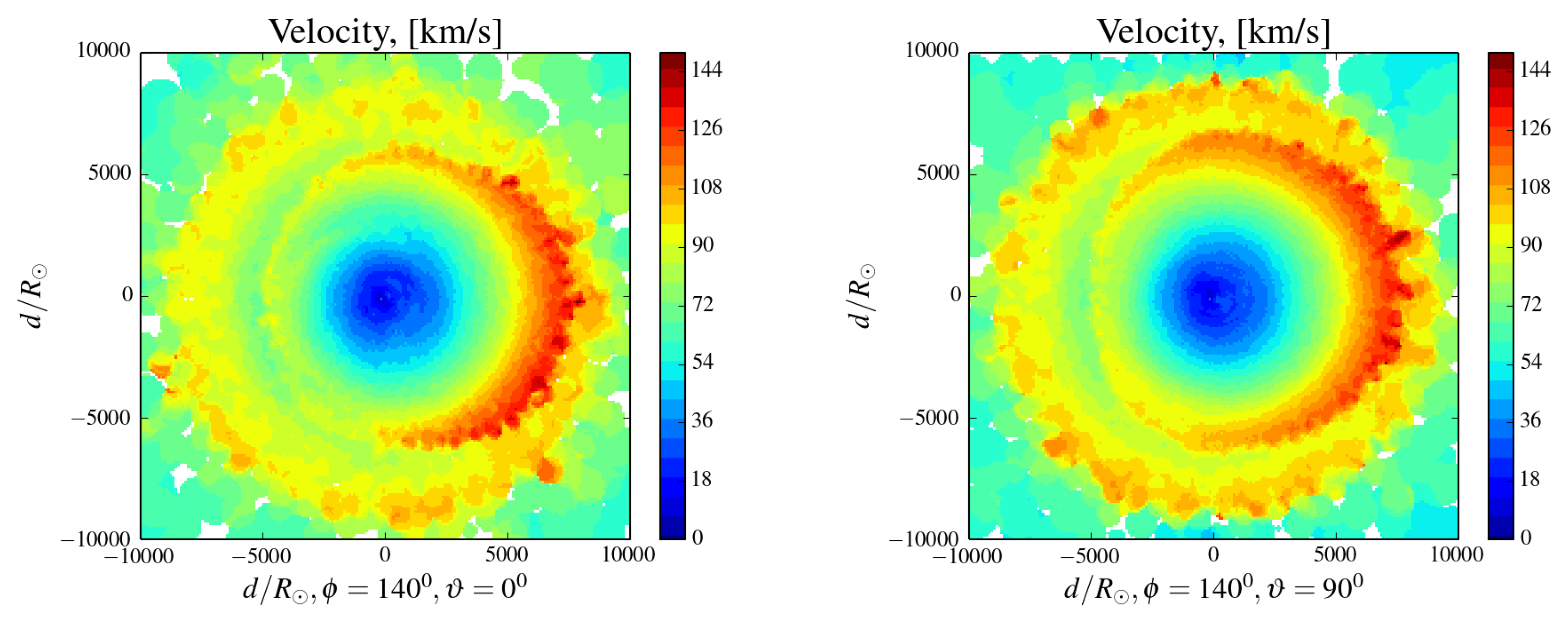
3.1. Typical Shape—Spherical Symmetry
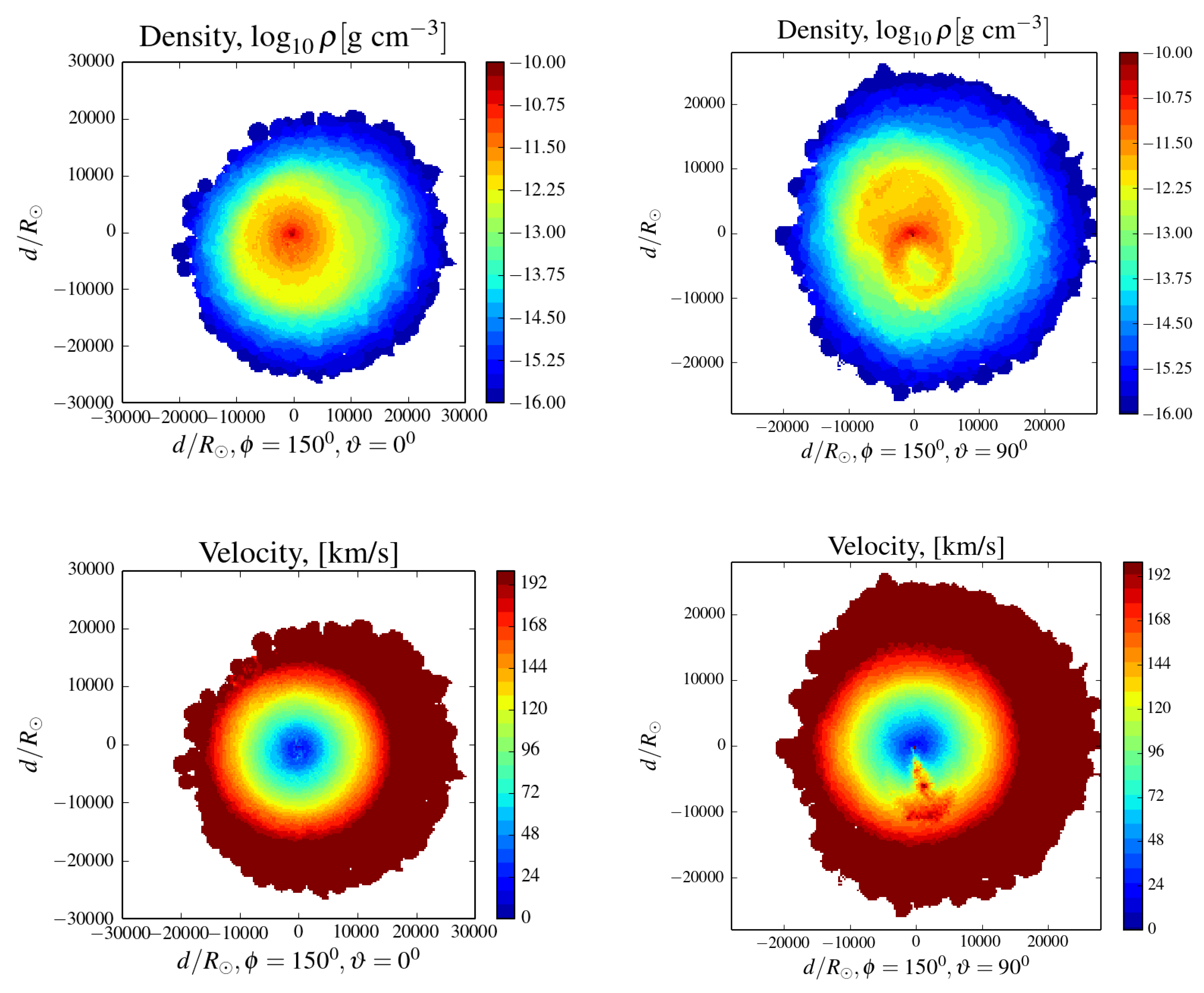
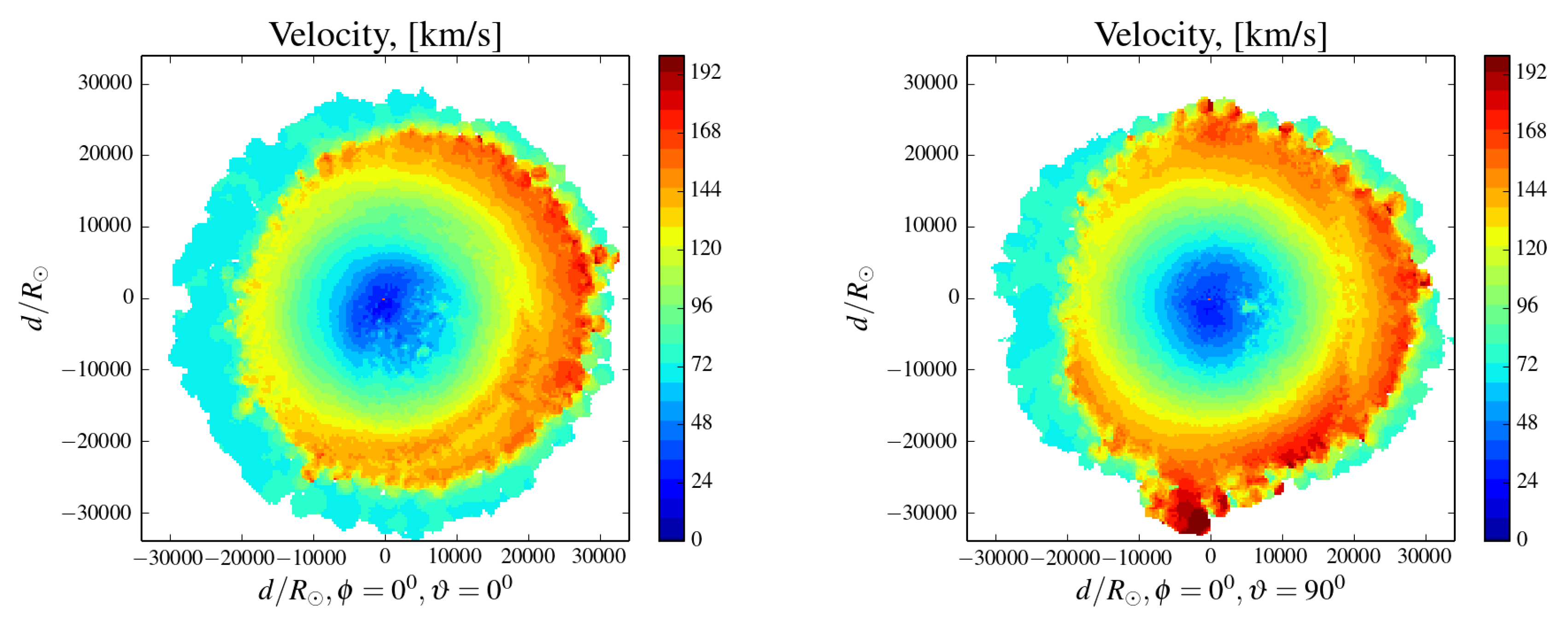
3.2. Deviations from Spherical Symmetry
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Asymptotic Giant Branch |
| PN | planetary nebula |
| CE | common envelope |
References
- De Marco, O.; Reichardt, T.; Iaconi, R.; Hillwig, T.; Jacoby, G.H.; Keller, D.; Izzard, R.G.; Nordhaus, J.; Blackman, E.G. Post-common envelope PN, fundamental or irrelevant? In Planetary Nebulae: Multi-Wavelength Probes of Stellar and Galactic Evolution; Liu, X., Stanghellini, L., Karakas, A., Eds.; International Astronomical Union: Paris, France, 2017; Volume 323, pp. 213–217. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Chen, X.; De Marco, O.; Fryer, C.L.; Gaburov, E.; Ge, H.; Glebbeek, E.; Han, Z.; Li, X.D.; et al. Common envelope evolution: Where we stand and how we can move forward. Astron. Astrophys. Rev. 2013, 21, 59. [Google Scholar] [CrossRef]
- Miszalski, B.; Acker, A.; Moffat, A.F.J.; Parker, Q.A.; Udalski, A. Binary planetary nebulae nuclei towards the Galactic bulge. I. Sample discovery, period distribution, and binary fraction. Astron. Astrophys. 2009, 496, 813–825. [Google Scholar] [CrossRef]
- Miszalski, B.; Acker, A.; Parker, Q.A.; Moffat, A.F.J. Binary planetary nebulae nuclei towards the Galactic bulge. II. A penchant for bipolarity and low-ionisation structures. Astron. Astrophys. 2009, 505, 249–263. [Google Scholar] [CrossRef]
- Barker, H.; Zijlstra, A.; De Marco, O.; Frew, D.J.; Drew, J.E.; Corradi, R.L.M.; Eislöffel, J.; Parker, Q.A. The binary fraction of planetary nebula central stars—III. the promise of VPHAS+. Mon. Not. R. Astron. Soc. 2018, 475, 4504–4523. [Google Scholar] [CrossRef]
- Bear, E.; Soker, N. Planetary Nebulae that Cannot Be Explained by Binary Systems. Astrophys. J. Lett. 2017, 837, L10. [Google Scholar] [CrossRef]
- Sabach, E.; Soker, N. Accounting for planet-shaped planetary nebulae. Mon. Not. R. Astron. Soc. 2018, 473, 286–294. [Google Scholar] [CrossRef]
- García-Segura, G.; Villaver, E.; Langer, N.; Yoon, S.C.; Manchado, A. Single Rotating Stars and the Formation of Bipolar Planetary Nebula. Astrophys. J. 2014, 783, 74. [Google Scholar] [CrossRef]
- García-Segura, G.; Villaver, E.; Manchado, A.; Langer, N.; Yoon, S.C. Rotating Stars and the Formation of Bipolar Planetary Nebulae. II. Tidal Spin-up. Astrophys. J. 2016, 823, 142. [Google Scholar] [CrossRef]
- Garcia-Segura, G.; Ricker, P.M.; Taam, R.E. Common Envelope Shaping of Planetary Nebulae. ArXiv, 2018; arXiv:astro-ph.SR/1804.09309. [Google Scholar]
- Ricker, P.M.; Taam, R.E. An AMR Study of the Common-envelope Phase of Binary Evolution. Astrophys. J. 2012, 746, 74. [Google Scholar] [CrossRef]
- Fryxell, B.; Olson, K.; Ricker, P.; Timmes, F.X.; Zingale, M.; Lamb, D.Q.; MacNeice, P.; Rosner, R.; Truran, J.W.; Tufo, H. FLASH: An Adaptive Mesh Hydrodynamics Code for Modeling Astrophysical Thermonuclear Flashes. Astrophys. J. Suppl. Ser. 2000, 131, 273–334. [Google Scholar] [CrossRef]
- Gaburov, E.; Lombardi, J.C., Jr.; Portegies Zwart, S. On the onset of runaway stellar collisions in dense star clusters—II. Hydrodynamics of three-body interactions. Mon. Not. R. Astron. Soc. Lett. 2010, 402, 105–126. [Google Scholar] [CrossRef]
- Gaburov, E.; Lombardi, J.C., Jr.; Portegies Zwart, S.; Rasio, F.A. StarSmasher: Smoothed Particle Hydrodynamics Code for Smashing Stars and Planets; Astrophysics Source Code Library: Houghton, MI, USA, 2018. [Google Scholar]
- Nandez, J.L.A.; Ivanova, N.; Lombardi, J.C. Recombination energy in double white dwarf formation. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L39–L43. [Google Scholar] [CrossRef]
- Nandez, J.L.A.; Ivanova, N. Common envelope events with low-mass giants: understanding the energy budget. Mon. Not. R. Astron. Soc. 2016, 460, 3992–4002. [Google Scholar] [CrossRef]
- Volk, K.M.; Kwok, S. Evolution of protoplanetary nebulae. Astrophys. J. 1989, 342, 345–363. [Google Scholar] [CrossRef]
- Sahai, R.; Sánchez Contreras, C.; Morris, M. A Starfish Preplanetary Nebula: IRAS 19024+0044. Astrophys. J. 2005, 620, 948–960. [Google Scholar] [CrossRef]
- Webbink, R.F. Double white dwarfs as progenitors of R Coronae Borealis stars and Type I supernovae. Astrophys. J. 1984, 277, 355–360. [Google Scholar] [CrossRef]
- Livio, M.; Soker, N. The common envelope phase in the evolution of binary stars. Astrophys. J. 1988, 329, 764–779. [Google Scholar] [CrossRef]
- Ivanova, N.; Nandez, J.L.A. Common envelope events with low-mass giants: understanding the transition to the slow spiral-in. Mon. Not. R. Astron. Soc. 2016, 462, 362–381. [Google Scholar] [CrossRef]
- Ivanova, N. On the Use of Hydrogen Recombination Energy during Common Envelope Events. Astrophys. J. Lett. 2018, 858, L24. [Google Scholar] [CrossRef]
- Meyer, F.; Meyer-Hofmeister, E. Formation of cataclysmic binaries through common envelope evolution. Astron. Astrophys. 1979, 78, 167–176. [Google Scholar]
- Weinberger, R. A catalogue of expansion velocities of Galactic planetary nebulae. Astron. Astrophys. Suppl. Ser. 1989, 78, 301–324. [Google Scholar]
- Gesicki, K.; Zijlstra, A.A. Expansion velocities and dynamical ages of planetary nebulae. Astron. Astrophys. 2000, 358, 1058–1068. [Google Scholar]
- Arnaboldi, M.; Doherty, M.; Gerhard, O.; Ciardullo, R.; Aguerri, J.A.L.; Feldmeier, J.J.; Freeman, K.C.; Jacoby, G.H. Expansion Velocities and Core Masses of Bright Planetary Nebulae in the Virgo Cluster. Astrophys. J. Lett. 2008, 674, L17. [Google Scholar] [CrossRef]
- Ivanova, N.; Justham, S.; Podsiadlowski, P. On the role of recombination in common-envelope ejections. Mon. Not. R. Astron. Soc. 2015, 447, 2181–2197. [Google Scholar] [CrossRef]
- Clayton, M.; Podsiadlowski, P.; Ivanova, N.; Justham, S. Episodic mass ejections from common-envelope objects. Mon. Not. R. Astron. Soc. 2017, 470, 1788–1808. [Google Scholar] [CrossRef]
- García-Díaz, M.T.; Clark, D.M.; López, J.A.; Steffen, W.; Richer, M.G. The Outflows and Three-Dimensional Structure of NGC 6337: A Planetary Nebula with a Close Binary Nucleus. Astrophys. J. 2009, 699, 1633–1638. [Google Scholar] [CrossRef]
- Hillwig, T.C.; Jones, D.; De Marco, O.; Bond, H.E.; Margheim, S.; Frew, D. Observational Confirmation of a Link Between Common Envelope Binary Interaction and Planetary Nebula Shaping. Astrophys. J. 2016, 832, 125. [Google Scholar] [CrossRef]
- Nandez, J.L.A.; Ivanova, N.; Lombardi, J.C., Jr. V1309 Sco—Understanding a Merger. Astrophys. J. 2014, 786, 39. [Google Scholar] [CrossRef]
- Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: New York, NY, USA, 2015. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanova, N.; Nandez, J.L.A. Planetary Nebulae Embryo after a Common Envelope Event. Galaxies 2018, 6, 75. https://doi.org/10.3390/galaxies6030075
Ivanova N, Nandez JLA. Planetary Nebulae Embryo after a Common Envelope Event. Galaxies. 2018; 6(3):75. https://doi.org/10.3390/galaxies6030075
Chicago/Turabian StyleIvanova, Natalia, and Jose L. A. Nandez. 2018. "Planetary Nebulae Embryo after a Common Envelope Event" Galaxies 6, no. 3: 75. https://doi.org/10.3390/galaxies6030075
APA StyleIvanova, N., & Nandez, J. L. A. (2018). Planetary Nebulae Embryo after a Common Envelope Event. Galaxies, 6(3), 75. https://doi.org/10.3390/galaxies6030075




