The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance
Abstract
1. Introduction
2. Hydrogen
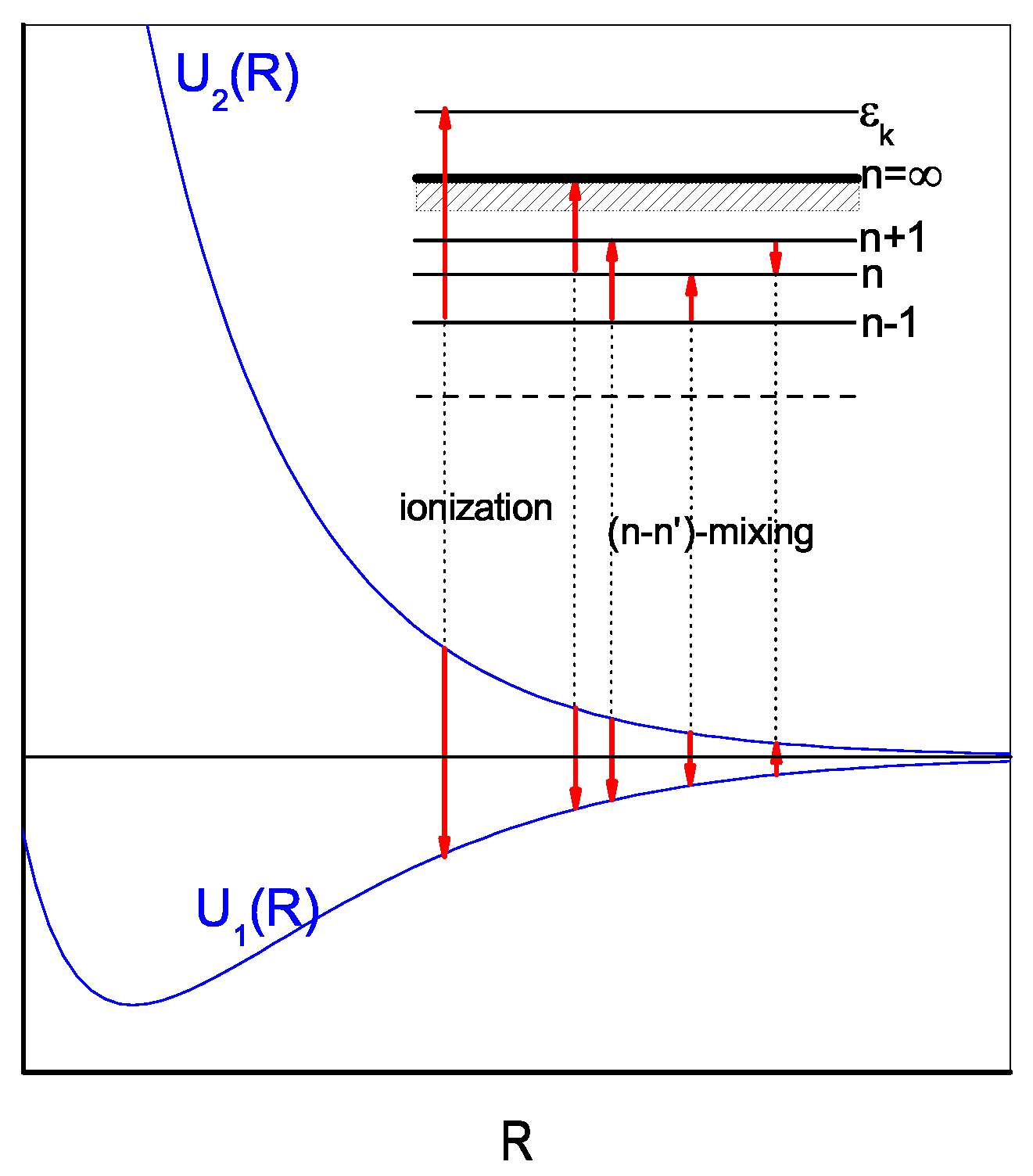
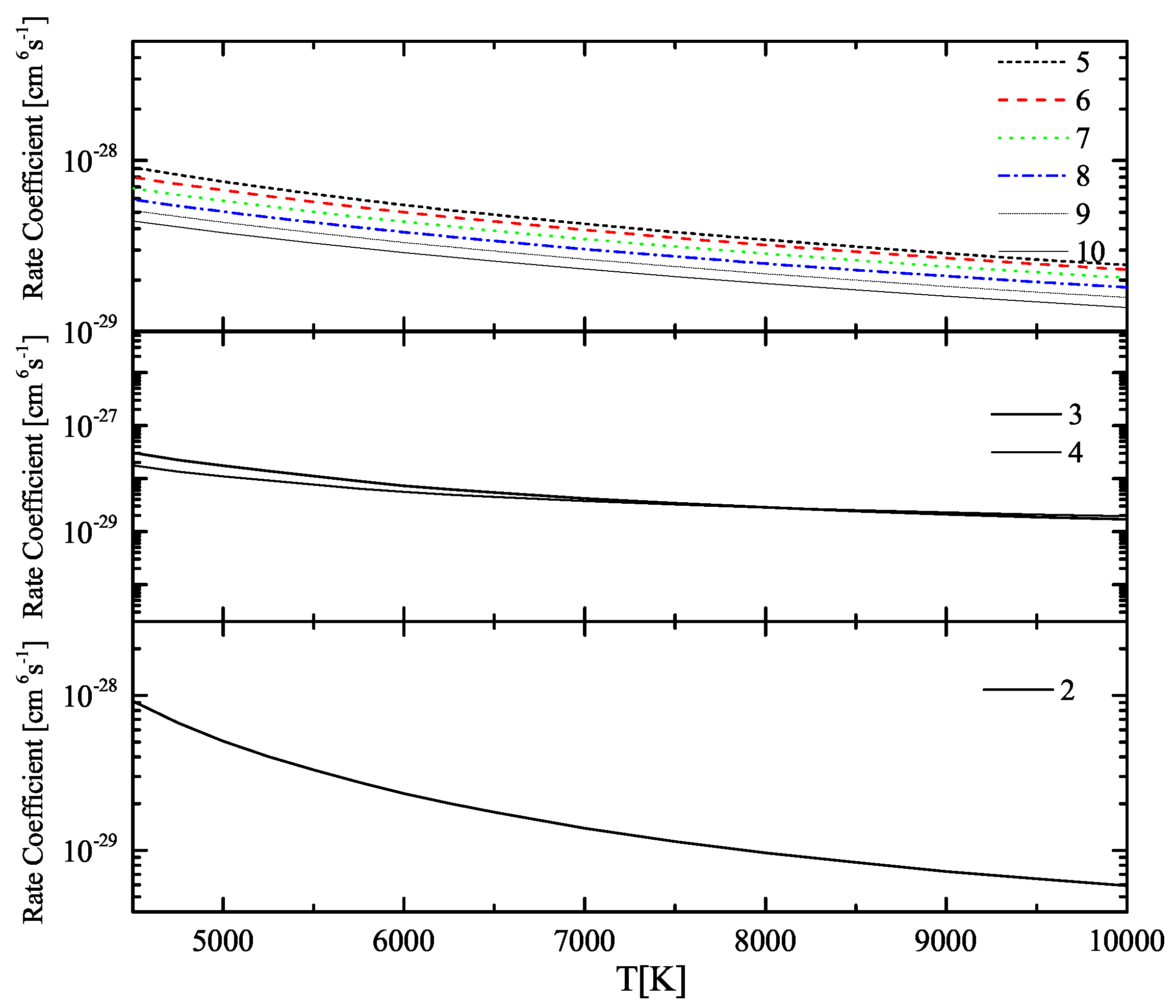
2.1. Collisional Ionization
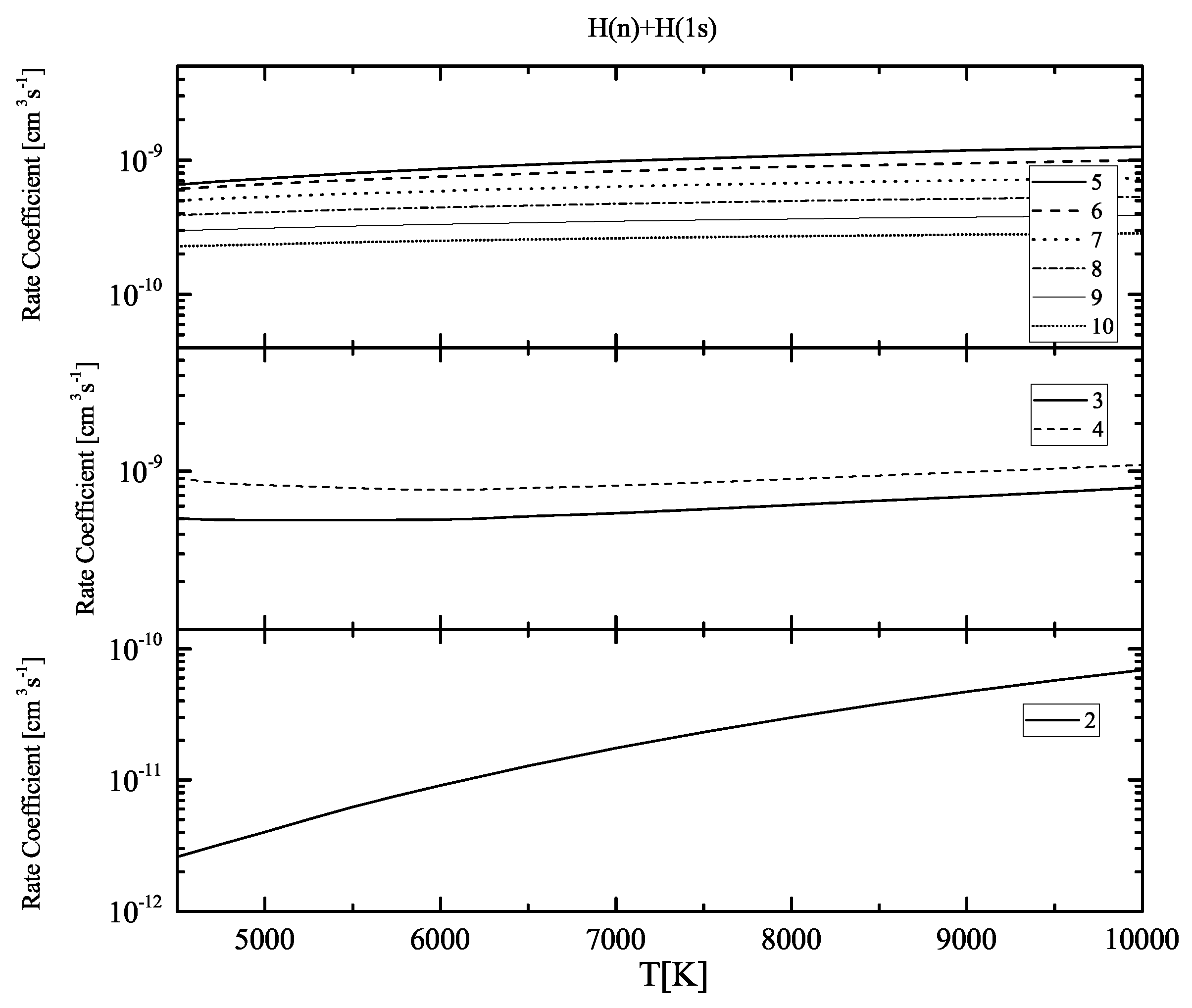
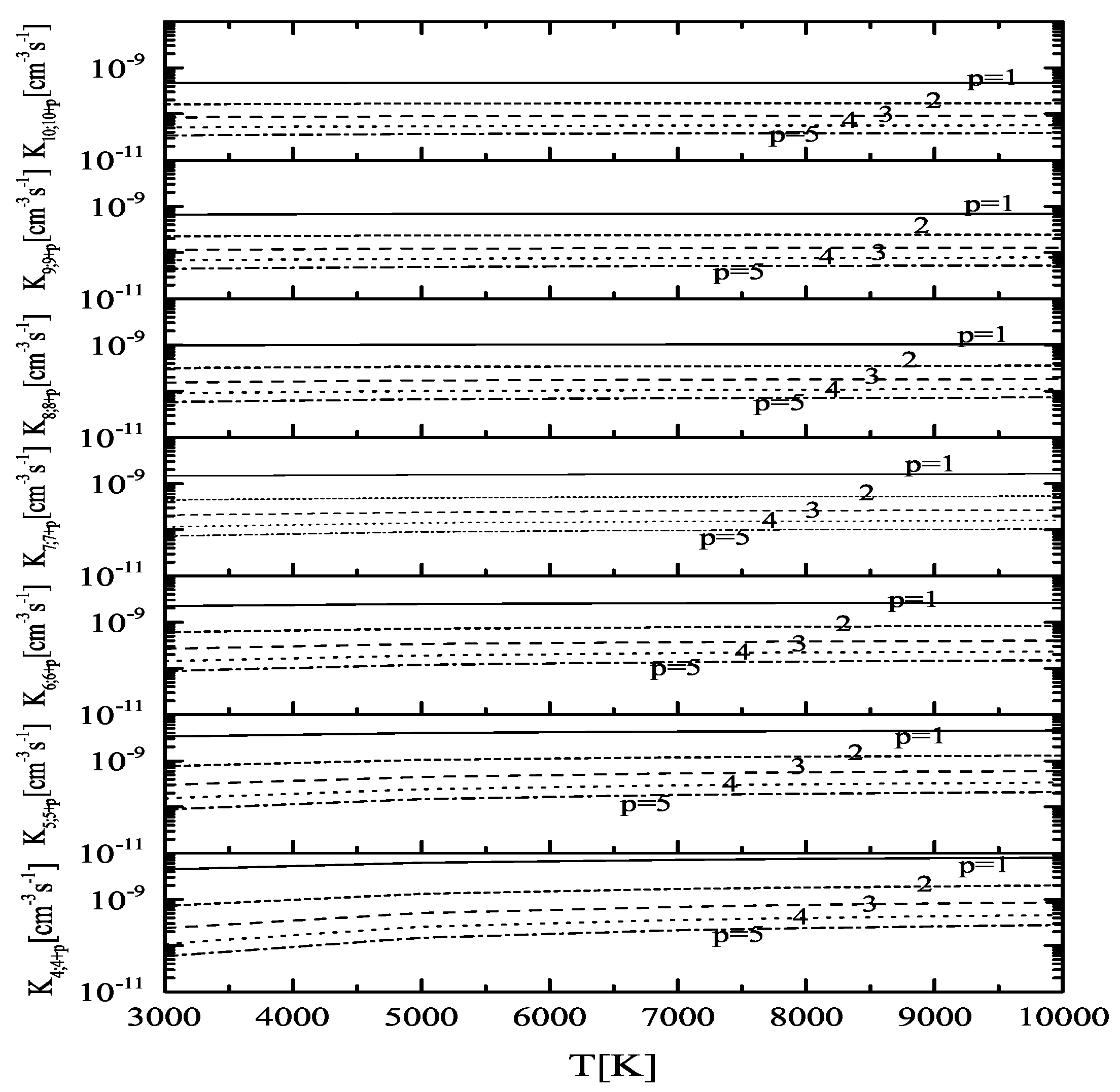
2.2. Collisional Excitation and De-Excitation
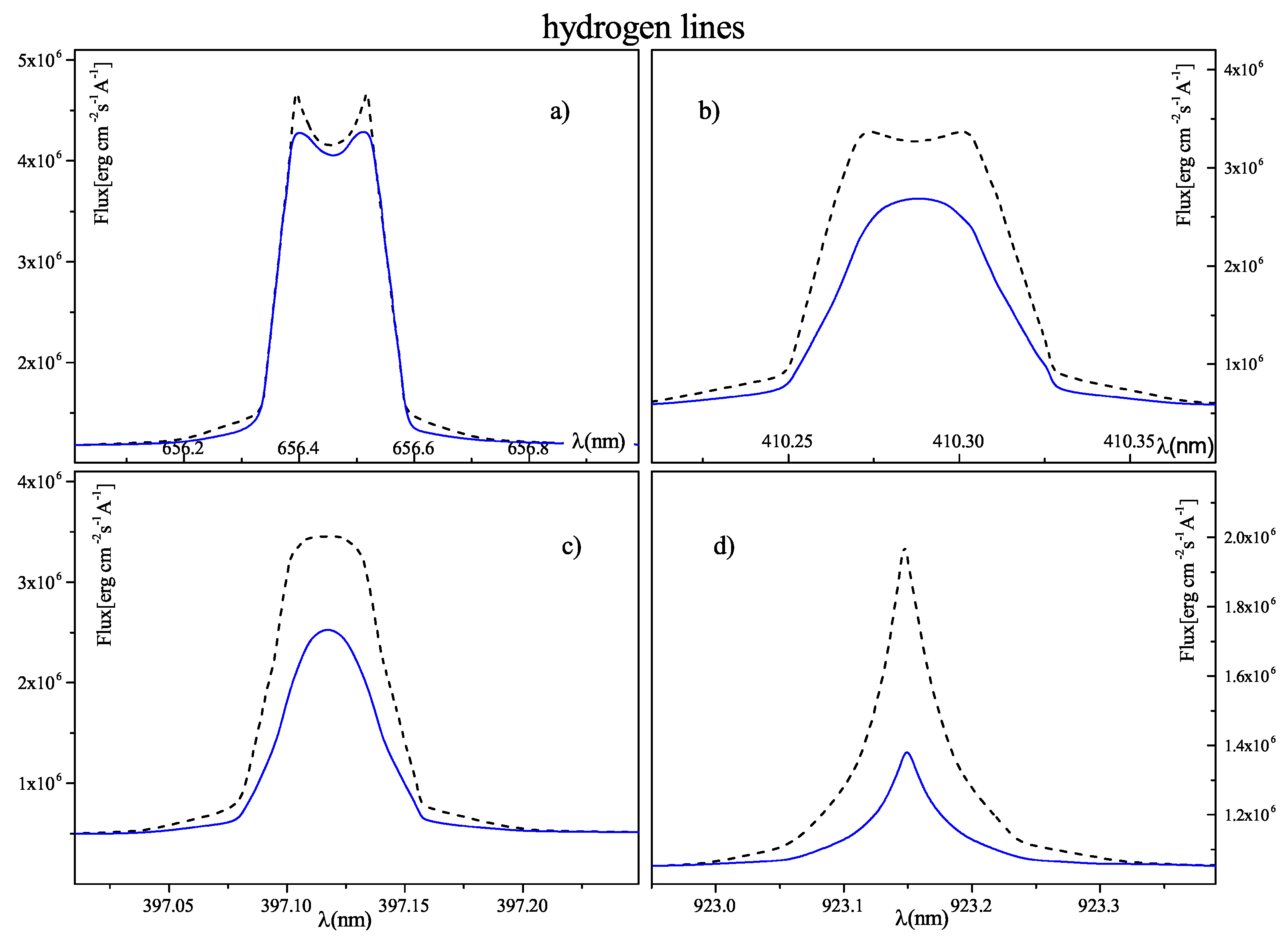
2.3. Astrophysical Targets
3. Helium
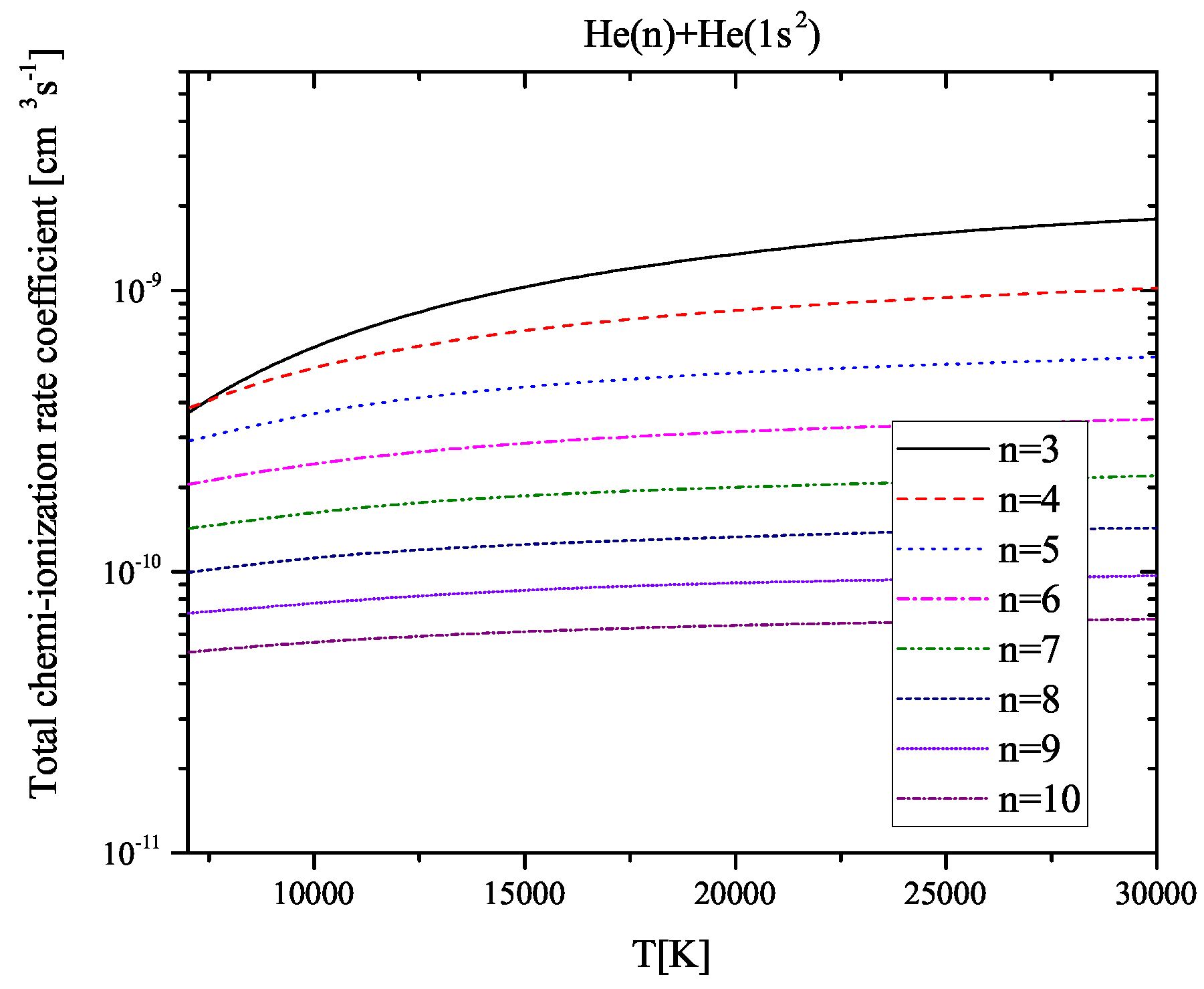
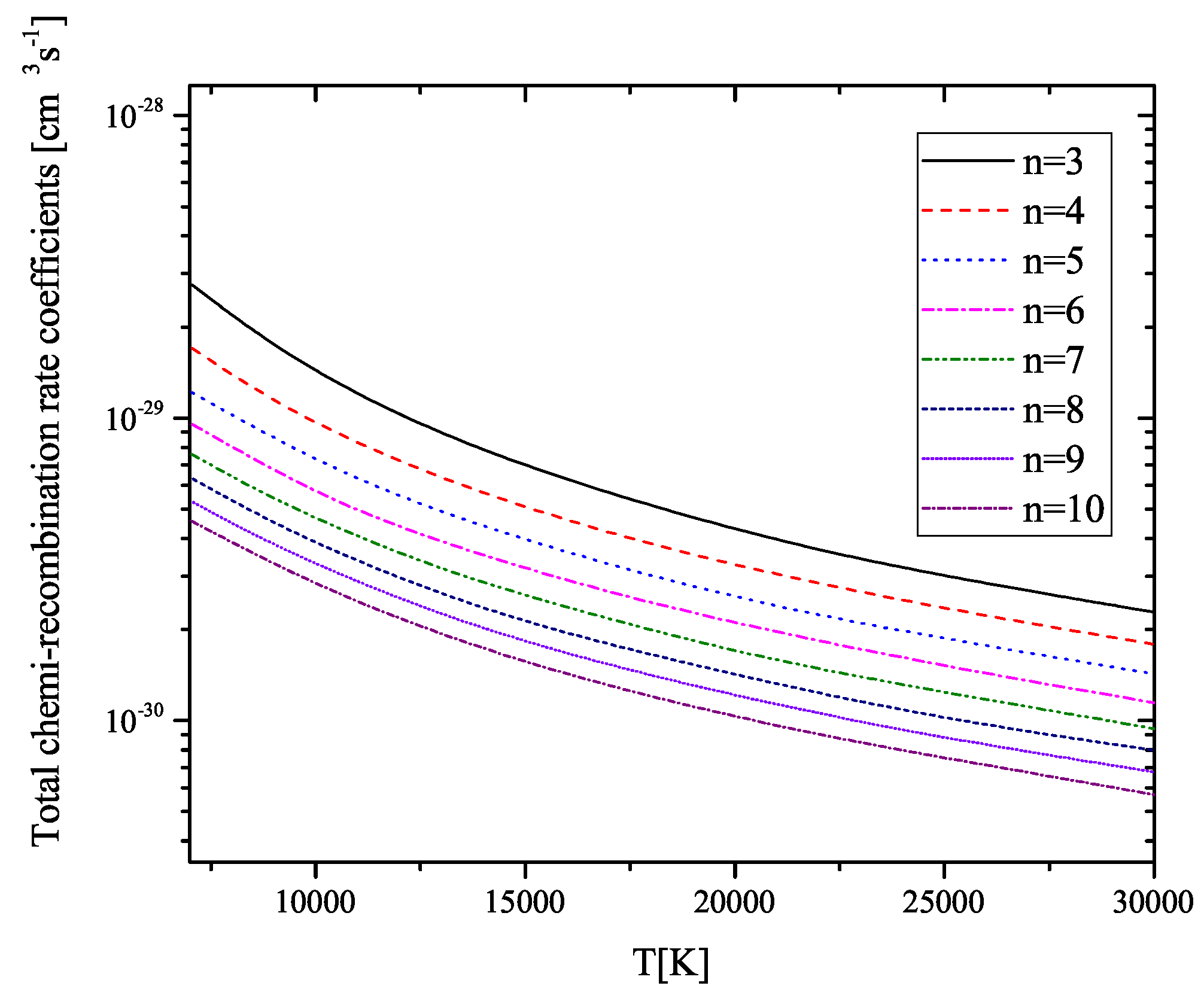
3.1. Collisional Ionization
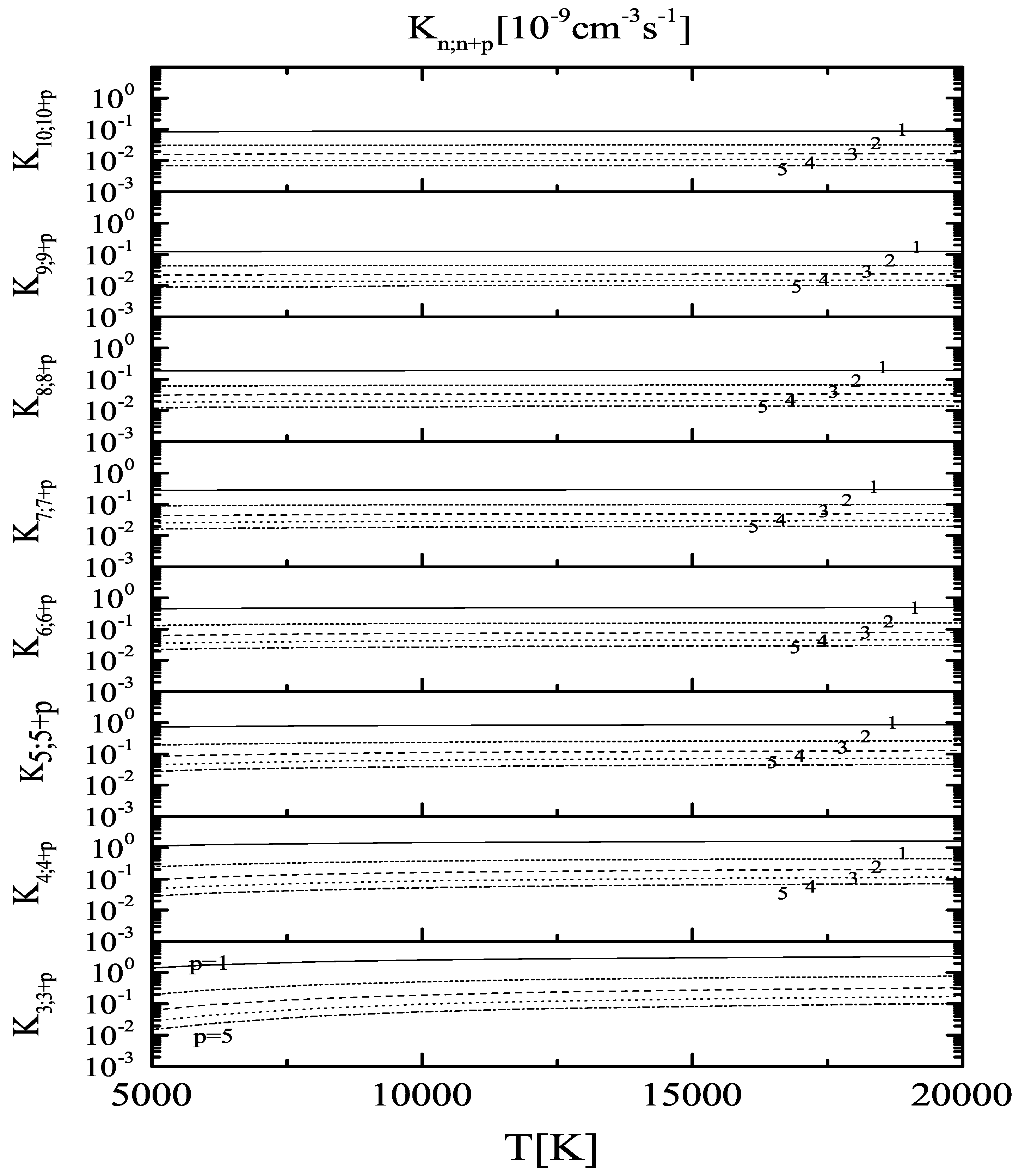
3.2. Collisional Excitation and De-Excitation
3.3. Astrophysical Targets
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fontenla, J.M.; Avrett, E.; Thuillier, G.; Harder, J. Semiempirical Models of the Solar Atmosphere. I. The Quiet- and Active Sun Photosphere at Moderate Resolution. Astrophys. J. 2006, 639, 441–458. [Google Scholar] [CrossRef]
- Koester, D. Model atmospheres for DB white dwarfs. Astron. Astrophys. Suppl. Ser. 1980, 39, 401–409. [Google Scholar]
- Ferland, G.; Chatzikos, M.; Guzmán, F.; Lykins, M.; van Hoof, P.; Williams, R.; Abel, N.; Badnell, N.; Keenan, F.; Porter, R.; et al. The 2017 Release of Cloudy. Rev. Mex. Astron. Astrofis. 2017, 53, 385–438. [Google Scholar]
- Mihajlov, A.A.; Ignjatović, L.M.; Srećković, V.A.; Dimitrijević, M.S.; Metropoulos, A. The non-symmetric ion-atom radiative processes in the stellar atmospheres. Mon. Not. R. Astron. Soc. 2013, 431, 589–599. [Google Scholar] [CrossRef]
- Ignjatović, L.M.; Mihajlov, A.A.; Srećković, V.A.; Dimitrijević, M.S. The ion-atom absorption processes as one of the factors of the influence on the sunspot opacity. Mon. Not. R. Astron. Soc. 2014, 441, 1504–1512. [Google Scholar] [CrossRef]
- Srećković, V.A.; Mihajlov, A.A.; Ignjatović, L.M.; Dimitrijević, M.S. Ion-atom radiative processes in the solar atmosphere: Quiet Sun and sunspots. New Astron. Rev. 2014, 54, 1264–1271. [Google Scholar] [CrossRef]
- Hauschildt, P.; Baron, E. Cool stellar atmospheres with PHOENIX. Memorie della Società Astronomica Italiana Supplement 2005, 7, 140–146. [Google Scholar]
- Hauschildt, P.H.; Baron, E. A 3D radiative transfer framework-VI. PHOENIX/3D example applications. Astron. Astrophys. 2010, 509, 923–936. [Google Scholar] [CrossRef]
- Barklem, P.S. Non-LTE Balmer line formation in late-type spectra: Effects of atomic processes involving hydrogen atoms. Astron. Astrophys. 2007, 466, 327–337. [Google Scholar] [CrossRef]
- Mashonkina, L. Atomic data necessary for the non-LTE analysis of stellar spectra. Phys. Scr. 2009, T134, 014004. [Google Scholar] [CrossRef]
- Przybilla, N.; Butler, K. Non-LTE line formation for hydrogen revisited. Astrophys. J. 2004, 609, 1181–1191. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Srećković, V.A.; Ignjatović, L.M. Chemi-ionization processes in Narrow-Line Seyfert 1 Galaxies. In Proceedings of the Revisiting Narrow-Line Seyfert 1 Galaxies and Their Place in the Universe, Padua, Italy, 9–13 April 2018. Proceeding of Science, NLS1-2018, 049 (1–4). [Google Scholar]
- Mihajlov, A.A.; Srećković, V.A.; Ignjatović, L.M.; Klyucharev, A.N. The Chemi-Ionization Processes in Slow Collisions of Rydberg Atoms with Ground State Atoms: Mechanism and Applications. J. Clust. Sci. 2012, 23, 47–75. [Google Scholar] [CrossRef]
- Mason, N. The status of the database for plasma processing. J. Phys. D 2009, 42, 194003. [Google Scholar] [CrossRef]
- Przybilla, N.; Nieva, M.F.; Butler, K. Testing common classical LTE and NLTE model atmosphere and line-formation codes for quantitative spectroscopy of early-type stars. J. Phys. Conf. Ser. 2011, 328, 012015. [Google Scholar] [CrossRef]
- Vernazza, J.E.; Avrett, E.H.; Loeser, R. Structure of the solar chromosphere. III—Models of the EUV brightness components of the quiet-sun. Astrophys. J. Suppl. Ser. 1981, 45, 635–725. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Ignjatović, L.M.; Srećković, V.A.; Dimitrijević, M.S. Chemi-ionization in Solar Photosphere: Influence on the Hydrogen Atom Excited States Population. Astrophys. J. Suppl. Ser. 2011, 193, 2. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Ignjatovic, L.M.; Djuric, Z.; Ljepojevic, N.N. The rate coefficients for the processes of (n-n′)-mixing in collisions of Rydberg atoms H*(n) with H(1s) atoms. J. Phys. B 2004, 37, 4493–4506. [Google Scholar] [CrossRef]
- Srećković, V.A.; Mihajlov, A.A.; Ignjatović, L.M.; Dimitrijević, M.S. Excitation and deexcitation processes in atom-Rydberg atom collisions in helium-rich white dwarf atmospheres. Astron. Astrophys. 2013, 552, A33. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Ignjatović, L.M.; Srećković, V.A.; Djurić, Z. The influence of (n-n′)-mixing processes in He*(n) + He(1s2) collisions on He*(n) atoms’ populations in weakly ionized helium plasmas. J. Quant. Spectrosc. Radiat. Transf. 2008, 109, 853–862. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Srećković, V.A.; Ignjatović, L.M.; Dimitrijević, M.S. Atom-Rydberg-atom chemi-ionization processes in solar and DB white-dwarf atmospheres in the presence of (n-n′)-mixing channels. Mon. Not. R. Astron. Soc. 2016, 458, 2215–2220. [Google Scholar] [CrossRef]
- Mihajlov, A.; Ignjatović, L.M.; Dimitrijević, M.; Djurić, Z. Symmetrical chemi-ionization and chemi- recombination processes in low-temperature layers of helium-rich DB white dwarf atmospheres. Astrophys. J. Suppl. Ser. 2003, 147, 369. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Jevremović, D.; Hauschildt, P.; Dimitrijević, M.S.; Ignjatović, L.M.; Alard, F. Influence of chemi-ionization and chemi-recombination processes on hydrogen line shapes in M dwarfs. Astron. Astrophys. 2007, 471, 671–673. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Mihajlov, A.A.; Ignjatović, L.M.; Sakan, N.M.; Srećković, V.A.; Zakharov, M.Y.; Bezuglov, N.N.; Klycharev, A.N. Rydberg atoms in astrophysics. New Astr. Rev. 2009, 53, 259–265. [Google Scholar] [CrossRef]
- Djurić, Z.; Mihajlov, A.A. The influence of chemi-recombination and chemi-ionization processes on kinetics of non-equilibrium helium plasma. J. Quant. Spectrosc. Radiat. Transf. 2001, 70, 285–305. [Google Scholar] [CrossRef]
- Rodero, A.; Quintero, M.C.; Álvarez, R.; Sola, À.; Gamero, A.; García, M.C.; Lao, C. The electron temperature determination in a non-equilibrium helium plasma induced by microwave. Czechoslov. J. Phys. Suppl. 2000, 50, 339–342. [Google Scholar] [CrossRef]
- Isakaev, E.K.; Chinnov, V.F.; Sargsyan, M.; Kavyrshin, D.I. Nonequilibrium state of highly ionized helium plasma at atmospheric pressure. High Temp. 2013, 51, 141–146. [Google Scholar] [CrossRef]
- Golding, T.P.; Carlsson, M.; Leenaarts, J. Detailed and simplified nonequilibrium helium ionization in the solar atmosphere. Astrophys. J. 2014, 784, 30. [Google Scholar] [CrossRef]
- Korshunov, O.; Chinnov, V.; Kavyrshin, D.; Ageev, A. Spectral measurements of electron temperature in nonequilibrium highly ionized He plasma. In Proceedings of the XXXI International Conference on Equations of State for Matter (ELBRUS 2016), Elbrus, Russia, 1–6 March 2016. Journal of Physics Conference Series, Volume 774, Article 012199. [Google Scholar]
- Chinnov, V.; Kavyrshin, D.; Ageev, A.; Korshunov, O.; Sargsyan, M.; Efimov, A. Study of spatial distributions of highly ionized nonequilibrium helium plasma at atmospheric pressures. In Proceedings of the XXXI International Conference on Equations of State for Matter (ELBRUS 2016), Elbrus, Russia, 1–6 March 2016. Journal of Physics Conference Series, Volume 774, Article 012200. [Google Scholar]
- Ignjatović, L.M.; Mihajlov, A.A.; Srećković, V.A.; Dimitrijević, M.S. Absorption non-symmetric ion-atom processes in helium-rich white dwarf atmospheres. Mon. Not. R. Astron. Soc. 2014, 439, 2342–2350. [Google Scholar] [CrossRef]
- Przybilla, N.; Butler, K.; Heber, U.; Jeffery, C. Extreme helium stars: non-LTE matters-Helium and hydrogen spectra of the unique objects V652 Her and HD 144941. Astron. Astrophys. 2005, 443, L25–L28. [Google Scholar] [CrossRef]
- Stancil, P. Continuous absorption by He2 (+) and H2 (+) in cool white dwarfs. Astrophys. J. 1994, 430, 360–370. [Google Scholar] [CrossRef]
- Coppola, C.M.; Galli, D.; Palla, F.; Longo, S.; Chluba, J. Non-thermal photons and H2 formation in the early Universe. Mon. Not. R. Astron. Soc. 2013, 434, 114–122. [Google Scholar] [CrossRef]
- Royal, J.; Orel, A. Resonant dissociative excitation and vibrational excitation of He 2+. Phys. Rev. A 2007, 75, 052706. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srećković, V.A.; Dimitrijević, M.S.; Ignjatović, L.M.; Bezuglov, N.N.; Klyucharev, A.N. The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance. Galaxies 2018, 6, 72. https://doi.org/10.3390/galaxies6030072
Srećković VA, Dimitrijević MS, Ignjatović LM, Bezuglov NN, Klyucharev AN. The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance. Galaxies. 2018; 6(3):72. https://doi.org/10.3390/galaxies6030072
Chicago/Turabian StyleSrećković, Vladimir A., Milan S. Dimitrijević, Ljubinko M. Ignjatović, Nikolai N. Bezuglov, and Andrey N. Klyucharev. 2018. "The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance" Galaxies 6, no. 3: 72. https://doi.org/10.3390/galaxies6030072
APA StyleSrećković, V. A., Dimitrijević, M. S., Ignjatović, L. M., Bezuglov, N. N., & Klyucharev, A. N. (2018). The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance. Galaxies, 6(3), 72. https://doi.org/10.3390/galaxies6030072






