A Simple Model for Explaining Galaxy Rotation Curves
Abstract
1. Introduction
2. Proposed Model
- The Modified Newtonian Dynamics (MOND) [22] (see also similar result in [49] and reviews in [19,24,25,38]). It is the most spread modification among astronomers since it is very simple, does not include any exotic ingredients (Dark Matter) and the most important, it is in good agreement with observations. The MOND velocity is given bywhere 1.2 × 10− ms−2 is the critical acceleration. Equation (8) is obtained from the Milgrom’s acceleration formulausing the standard interpolation functionIn the limit , the MOND formalism gives asymptotic constant velocities
- Our previous result [47], coming from Starobinsky model [51] considered in Palatini formalism which is the simplest example of EPS interpretation [52]where we assumed the order of as taken from cosmological considerations [53], is energy density obtained from mass distribution provided by the model and (7), see the details in [47].
3. A Particular Example
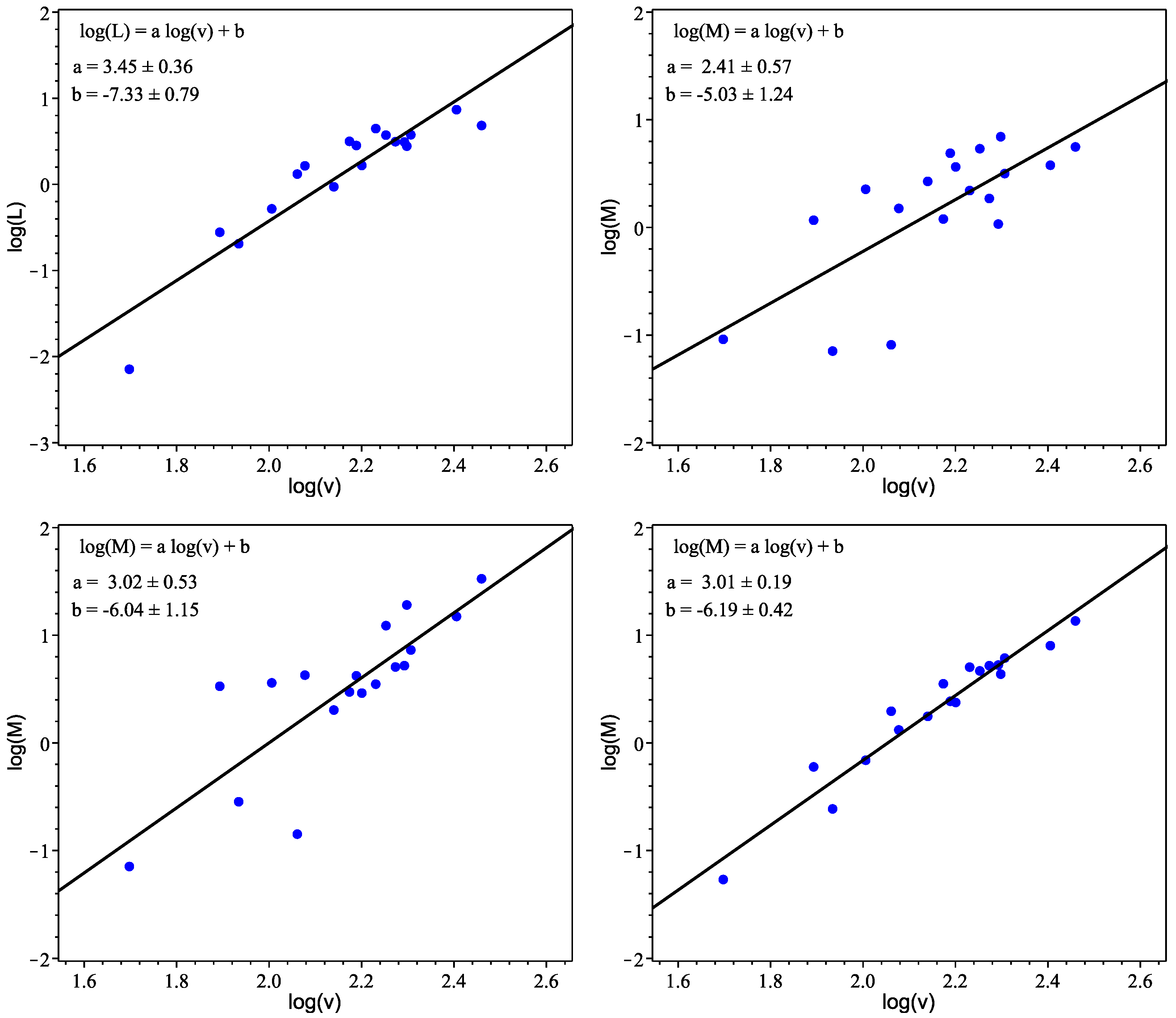
The Tully-Fisher Relation
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ostriker, J.P.; Steinhardt, P.J. The observational case for a low-density Universe with a non-zero cosmological constant. Nature 1995, 377, 600–602. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Tests of cosmological models constrained by inflation. Astrophys. J. 1984, 284, 439–444. [Google Scholar] [CrossRef]
- Joyce, A.; Lombriser, L.; Schmidt, F. Dark Energy Versus Modified Gravity. Ann. Rev. Nucl. Part. Sci. 2016, 66, 95–122. [Google Scholar] [CrossRef]
- Plank 2015 Results. Available online: https://www.cosmos.esa.int/web/planck/publications (accessed on 13 July 2018).
- Sanders, R.H. The Dark Matter Problem: A Historical Perspective; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2010. [Google Scholar]
- Trimble, V. Existence and nature of dark matter in the universe. Annu. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Rubin, V.C.; Kent Ford, W., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Rubin, V.C.; Kent Ford, W., Jr.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R = 4 kpc) to UGC 2885 (R = 122 kpc). Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Karukes, E.V.; Salucci, P. The universal rotation curve of dwarf disc galaxies. Mon. Not. R. Astron. Soc. 2017, 465, 4703–4722. [Google Scholar] [CrossRef]
- Salucci, P.; Lapi, A.; Tonini, C.; Gentile, G.; Yegorova, I.; Kleinet, U. The universal rotation curve of spiral galaxies—II. The dark matter distribution out to the virial radius. Mon. Not. R. Astron. Soc. 2007, 378, 41–47. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation Curves of Spiral Galaxies. Ann. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rep. 2011, 159, 167–321. [Google Scholar] [CrossRef]
- Capozziello, S.; Faraoni, V. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer Science and Business Media: Berlin, Germany, 2010; Volume 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Dark energy, inflation and dark matter from modified F(R) gravity. In Problems of Modern Theoretical Physics : A Volume in Honour of Prof. I.L.Buchbinder in the Occasion of His 60th Birthday; Tomsk State Pedagogical University Press: Tomsk, Russia, 2008. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279–390. [Google Scholar] [CrossRef]
- Davis, M.; Efstathiou, G.; Frenk, C.S.; White, S.D. The evolution of large-scale structure in a universe dominated by cold dark matter. Astrophys. J. 1985, 292, 371–394. [Google Scholar] [CrossRef]
- Refregier, A. Weak Gravitational Lensing by Large-Scale Structure. Annu. Rev. Astron. Astrophys. 2003, 41, 645–668. [Google Scholar] [CrossRef]
- Bekenstein, J.D. The modified Newtonian dynamics—MOND and its implications for new physics. Contemp. Phys. 2006, 47, 387–403. [Google Scholar] [CrossRef]
- McGaugh, S.S.; De Blok, W.J.G. Testing the Hypothesis of Modified Dynamics with Low Surface Brightness Galaxies and Other Evidence. Astrophys. J. 1998, 499, 66. [Google Scholar] [CrossRef]
- McGaugh, S.S. Novel Test of Modified Newtonian Dynamics with Gas Rich Galaxies. Phys. Rev. Lett. 2011, 106, 121303. [Google Scholar] [CrossRef] [PubMed]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics—Implications for galaxies. Astrophys. J. 1983, 270, 371–389. [Google Scholar] [CrossRef]
- Milgrom, M. The MOND paradigm. arXiv, 2008; arXiv:0801.3133. [Google Scholar]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian Dynamics as an Alternative to Dark Matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Relativistic gravitation theory for the modified Newtonian dynamics paradigm. Phys. Rev. D 2004, 70, 083509. [Google Scholar] [CrossRef]
- Moffat, J.W.; Toth, V.T. Rotational velocity curves in the Milky Way as a test of modified gravity. Phys. Rev. D 2015, 91, 043004. [Google Scholar] [CrossRef]
- Cadoni, M.; Casadio, R.; Giusti, A.; Muck, W.; Tuveri, M. Effective fluid description of the dark universe. Phys. Lett. B 2018, 776, 242–248. [Google Scholar] [CrossRef]
- Cadoni, M.; Casadio, R.; Giusti, A.; Tuveri, M. Emergence of a dark force in corpuscular gravity. Phys. Rev. D 2018, 97, 044047. [Google Scholar] [CrossRef]
- Iorio, L.; Ruggiero, M.L. Solar System tests of some models of modified gravity proposed to explain galactic rotation curves without dark matter. Sch. Res. Exchange 2008, 2008, 968393. [Google Scholar] [CrossRef]
- Sebastiani, L.; Vagnozzi, S.; Myrzakulov, R. Static spherically symmetric solutions in mimetic gravity: Rotation curves and wormholes. Class. Quantum Gravity 2016, 33, 125005. [Google Scholar]
- Capozziello, S.; Cardone, V.F.; Trois, A. Dark energy and dark matter as curvature effects? J. Cosmol. Astropart. Phys. 2006, 2006, 001. [Google Scholar] [CrossRef]
- Barrientos, E.; Mendoza, S. A relativistic description of MOND using the Palatini formalism in an extended metric theory of gravity. Eur. Phys. J. Plus 2016, 131, 367. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Dark matter as a ghost free conformal extension of Einstein theory. J. Cosmol. Astropart. Phys. 2014, 2014, 014. [Google Scholar] [CrossRef]
- Bernal, T.; Capozziello, S.; Hidalgo, J.C.; Mendoza, S. Recovering MOND from extended metric theories of gravity. Eur. Phys. J. C 2011, 71, 1794. [Google Scholar] [CrossRef]
- Bruneton, J.P.; Esposito-Farese, G. Field-theoretical formulations of MOND-like gravity. Phys. Rev. D 2007, 76, 124012. [Google Scholar] [CrossRef]
- Esposito-Farese, G. Motion in Alternative Theories of Gravity. Fundam. Theor. Phys. 2011, 162, 461–489. [Google Scholar]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Mannheim, P.D.; O’Brien, J.G. Impact of a Global Quadratic Potential on Galactic Rotation Curves. Phys. Rev. Lett. 2011, 106, 121101. [Google Scholar] [CrossRef] [PubMed]
- Mannheim, P.D.; O’Brien, J.G. Fitting galactic rotation curves with conformal gravity and a global quadratic potential. Phys. Rev. D 2012, 85, 124020. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to dark matter and dark energy. Prog. Part. Nucl. Phys. 2006, 56, 340–445. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Letelier, P.S.; Shapiro, I.L. Galaxy rotation curves from general relativity with renormalization group corrections. J. Cosmol. Astropart. Phys. 2010, 2010, 020. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; de Oliveira, P.L.; Fabris, J.C.; Gentile, G. Modified gravity models and the central cusp of dark matter haloes in galaxies. Mon. Not. R. Astron. Soc. 2014, 445, 3823–3838. [Google Scholar] [CrossRef]
- Rodrigues, D.C.; Mauro, S.; de Almeida, A.O.F. Solar System constraints on renormalization group extended general relativity: The PPN and Laplace-Runge-Lenz analyses with the external potential effect. Phys. Rev. D 2016, 94, 084036. [Google Scholar] [CrossRef]
- Binney, J.; Tremaine, S. Galactic Dynamics, 2nd ed.; Princeton University Press: Princeton, NY, USA, 2008. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 1972. [Google Scholar]
- Sporea, C.A.; Borowiec, A.; Wojnar, A. Galaxy rotation curves via conformal factors. Eur. Phys. J. C 2018, 78, 308. [Google Scholar] [CrossRef] [PubMed]
- Brownstein, J.R.; Moffat, J.W. Galaxy Rotation Curves without Nonbaryonic Dark Matter. Astrophys. J. 2006, 636, 721–741. [Google Scholar] [CrossRef]
- Mendoza, S.; Olmo, G.J. Astrophysical constraints and insights on extended relativistic gravity. Astrophys. Space Sci. 2015, 357, 133. [Google Scholar] [CrossRef]
- Capozziello, S.; Cardone, V.F.; Trois, A. Low surface brightness galaxy rotation curves in the low energy limit of Rn gravity: No need for dark matter? Mon. Not. R. Astron. Soc. 2007, 375, 1423–1440. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Ehlers, J.; Pirani, F.A.E.; Schild, A. The Geometry of Free Fall and Light Propagation, in General Relativity; ORaifeartaigh, L., Ed.; Clarendon: Oxford, UK, 1972. [Google Scholar]
- Stachowski, A.; Szydlowski, M.; Borowiec, A. Starobinsky cosmological model in Palatini formalism. Eur. Phys. J. C 2017, 77, 406. [Google Scholar] [CrossRef]
- De Blok, W.J.G.; Walter, F.; Brinks, E.; Trachternach, C.; Oh, S.H.; Kennicutt, R.C., Jr. High-resolution rotation curves and galaxy mass models from THINGS. Astron. J. 2008, 136, 2648. [Google Scholar] [CrossRef]
- Walter, F.; Brinks, E.; De Blok, W.J.G.; Bigiel, F.; Kennicutt, R.C., Jr.; Thornley, M.D.; Leroy, A. THINGS: The HI Nearby Galaxy Survey. Astrophys. J. 2008, 136, 2563. [Google Scholar] [CrossRef]
- Finzi, A.; Pirani, F.A.E. On the Validity of Newton’s Law at a Long Distance. Mon. Not. R. Astron. Soc. 1963, 127, 21–30. [Google Scholar] [CrossRef]
- Tohline, J.E. Stabilizing a Cold Disk with a l/r Force Law. In Symposium-International Astronomical Union; Cambridge University Press: Cambridge, UK, 1983; Volume 100, pp. 205–206. [Google Scholar]
- Sanders, R.H. Anti-gravity and galaxy rotation curves. Astron. Astrophys. 1984, 136, L21–L23. [Google Scholar]
- Kuhn, J.R.; Kruglyak, L. Non-Newtonian Forces and the Missing Mass Problem. Astrophys. J. 1987, 313, 1–12. [Google Scholar] [CrossRef]
- Minguzzi, E. Possible relation between galactic flat rotational curves and the Pioneers’ anomalous acceleration. New Astron. 2006, 12, 142–145. [Google Scholar] [CrossRef]
- Acedo, L. Modified Newtonian Gravity as an Alternative to the Dark Matter Hypothesis. Galaxies 2017, 5, 74. [Google Scholar] [CrossRef]
- Tully, R.B.; Verheijen, M.A.; Pierce, M.J.; Huang, J.S.; Wainscoat, R.J. The Ursa Major Cluster of Galaxies. I. Cluster Definition and Photometric Data. Astrophys. J. 1996, 112, 2471. [Google Scholar]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Linde, A.D. Hybrid inflation. Phys. Rev. D 1994, 49, 748. [Google Scholar] [CrossRef]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Francaviglia, M.; Mercadante, S. From Dark Energy & Dark Matter to Dark Metric. Found. Phys. 2009, 39, 1161–1176. [Google Scholar]
- Fatibene, L.; Francaviglia, M. Mathematical Equivalence versus Physical Equivalence between Extended Theories of Gravitations. Int. J. Geom. Methods Mod. Phys. 2014, 11, 1450008. [Google Scholar] [CrossRef]
- Bell, E.F.; de Jong, R.S. Stellar Mass-to-Light Ratios and the Tully-Fisher Relation. Astrophys. J. 2001, 550, 212. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Schombert, J.M. Color-Mass-to-Light-Ratio Relations for Disk Galaxies. Astrophys. J. 2014, 148, 77. [Google Scholar] [CrossRef]
- Zibetti, S.; Charlot, S.; Rix, H.-W. Resolved stellar mass maps of galaxies—I. Method and implications for global mass estimates. Mon. Not. R. Astron. Soc. 2009, 400, 1181–1198. [Google Scholar] [CrossRef]
- Bell, E.F.; McIntosh, D.H.; Katz, N.; Weinberg, M.D. The Optical and Near-Infrared Properties of Galaxies. I. Luminosity and Stellar Mass Functions. Astrophys. J. Suppl. Ser. 2003, 149, 289. [Google Scholar] [CrossRef]
- Into, T.; Portinari, L. New colour–mass-to-light relations: The role of the asymptotic giant branch phase and of interstellar dust. Mon. Not. R. Astron. Soc. 2013, 430, 2715–2731. [Google Scholar] [CrossRef]
- Portinari, L.; Sommer-Larsen, J.; Tantalo, R. On the mass-to-light ratio and the initial mass function in disc galaxies. Mon. Not. R. Astron. Soc. 2004, 347, 691–719. [Google Scholar] [CrossRef]
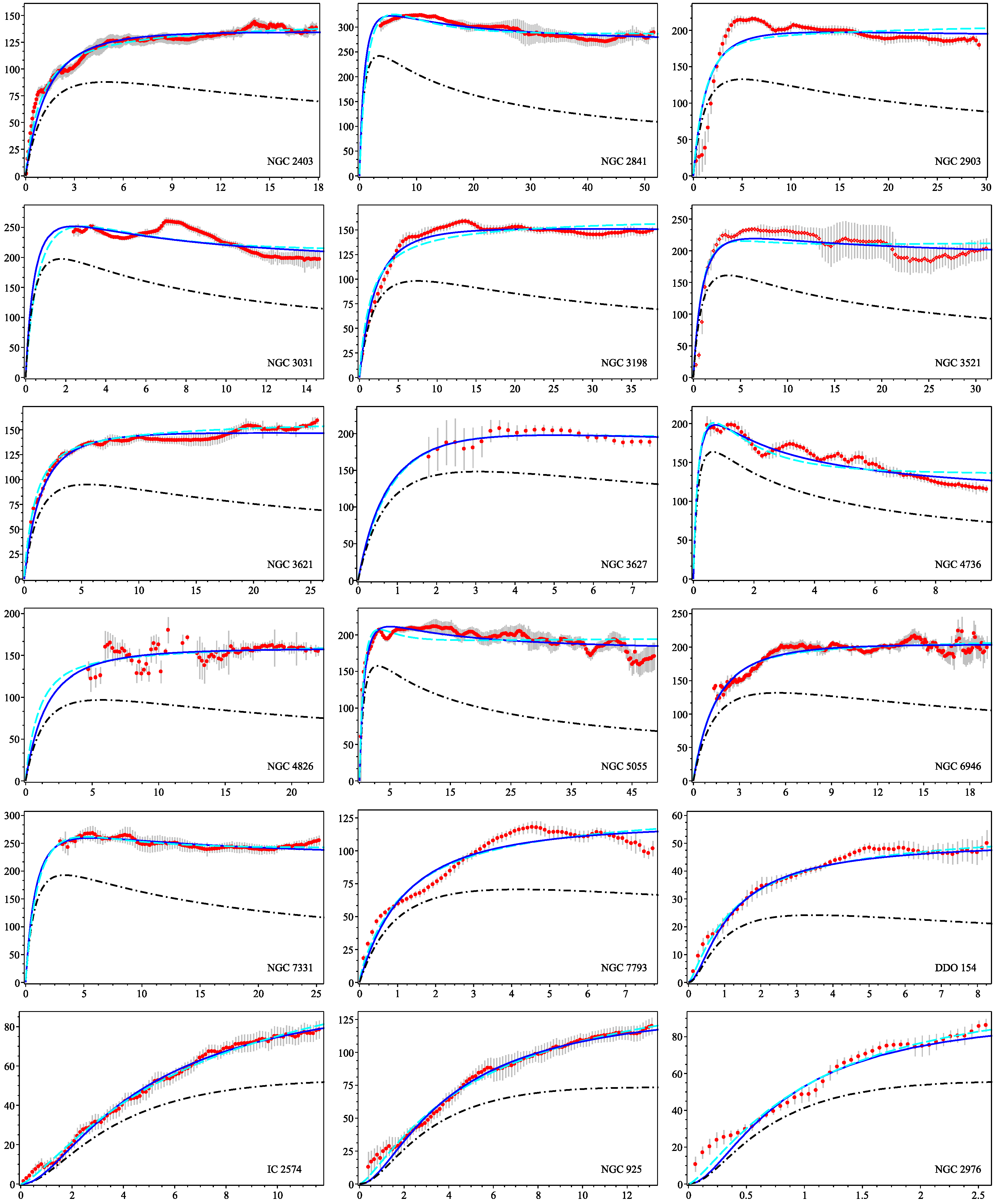
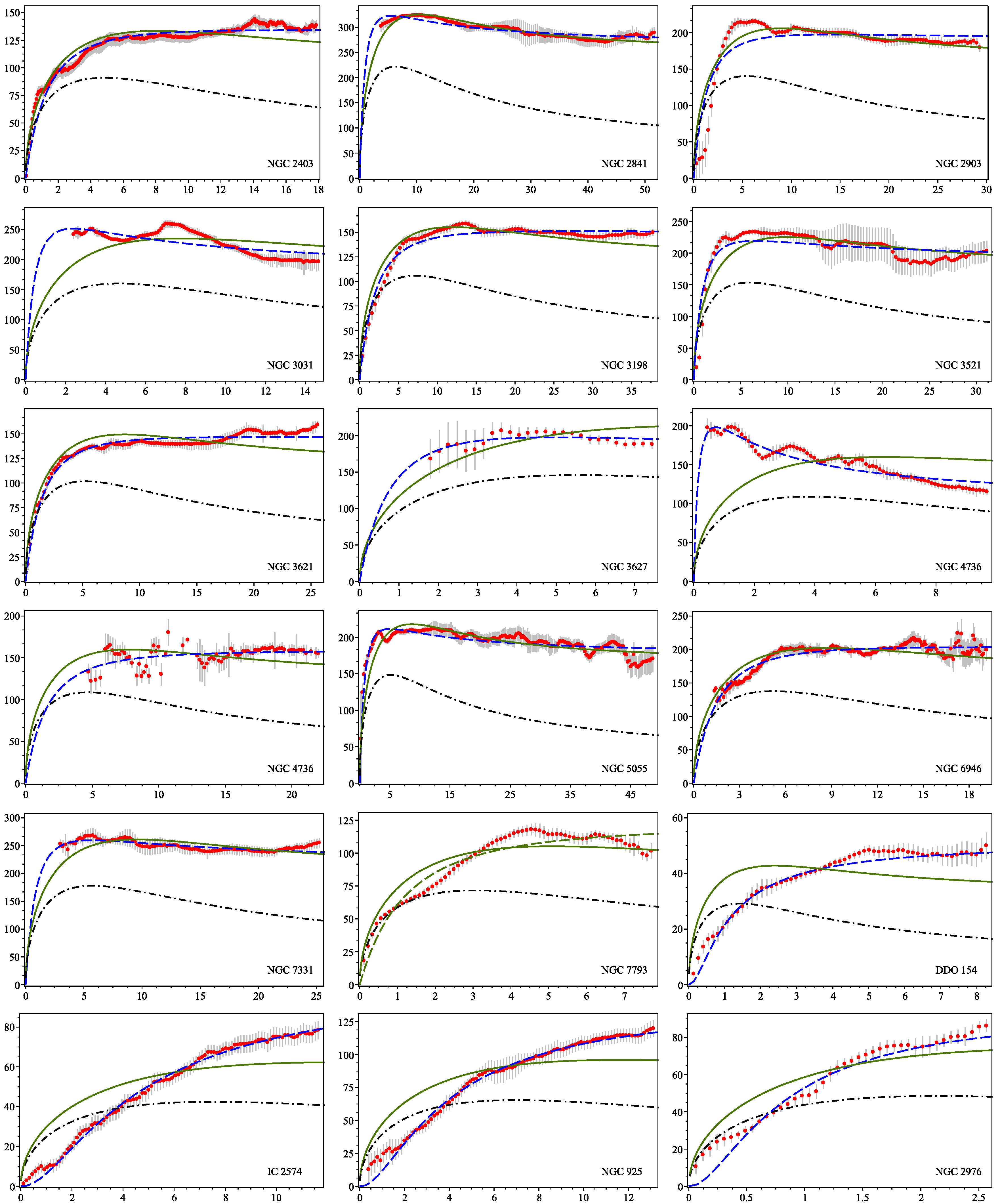
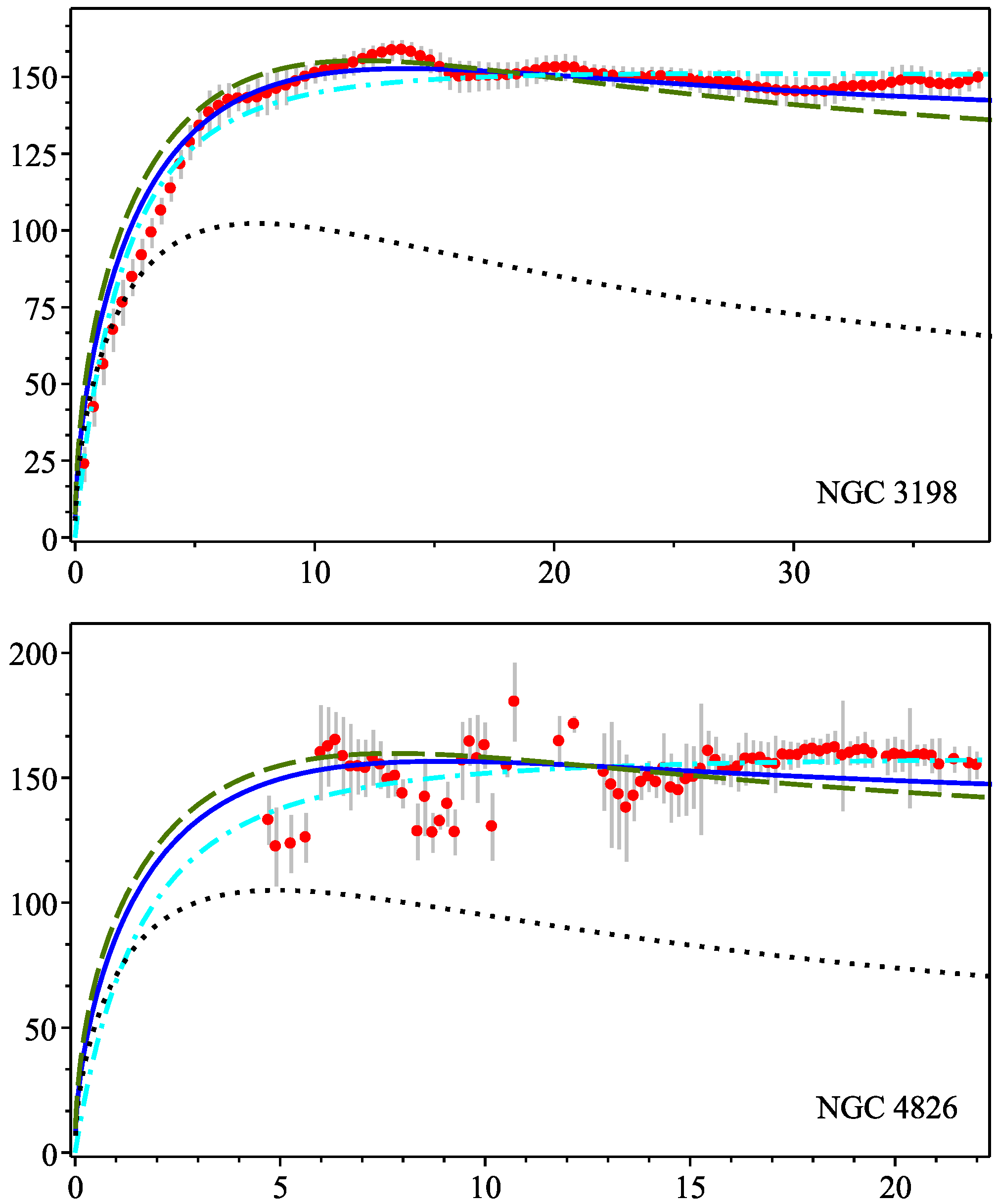
| MOND | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Galaxy | ||||||||||||
| Mpc | kpc | kpc | kpc | |||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) |
| HSB type | ||||||||||||
| NGC 2403 | 3.2 | 2.7 | 9.53 | 0.921 | 10.36 | 2.48 | 1.32 | 2.49 | 10.21 | 2.06 | 0.69 | 1.78 |
| NGC 2841 | 14.1 | 3.5 | 10.06 | 4.742 | 10.64 | 1.73 | 1.11 | 0.92 | 11.50 | 2.81 | 1.71 | 6.71 |
| NGC 2903 | 8.9 | 3.0 | 9.76 | 3.664 | 10.67 | 2.51 | 5.30 | 1.29 | 11.06 | 2.85 | 7.94 | 3.14 |
| NGC 3031 | 3.6 | 2.6 | 9.68 | 3.049 | 9.76 | 0.88 | 5.63 | 0.19 | 10.66 | 1.37 | 6.07 | 1.52 |
| NGC 3198 | 13.8 | 4.0 | 10.13 | 3.106 | 10.58 | 3.76 | 1.61 | 1.23 | 10.19 | 2.96 | 3.99 | 0.50 |
| NGC 3521 | 10.7 | 3.3 | 10.03 | 3.698 | 10.31 | 1.84 | 5.19 | 0.55 | 10.78 | 2.09 | 6.31 | 1.65 |
| NGC 3621 | 6.6 | 2.9 | 9.97 | 1.629 | 10.42 | 2.75 | 1.49 | 1.63 | 10.28 | 2.29 | 0.85 | 1.17 |
| NGC 3627 | 9.3 | 3.1 | 9.04 | 3.076 | 10.23 | 1.53 | 0.83 | 0.56 | 10.68 | 1.87 | 0.91 | 1.59 |
| NGC 4736 | 4.7 | 2.1 | 8.72 | 1.294 | 8.42 | 0.32 | 2.50 | 0.02 | 8.93 | 0.34 | 5.18 | 0.07 |
| NGC 4826 | 7.5 | 2.6 | 8.86 | 2.779 | 10.67 | 2.85 | 1.57 | 1.71 | 10.61 | 2.27 | 1.61 | 1.46 |
| NGC 5055 | 10.1 | 2.9 | 10.08 | 4.365 | 9.98 | 1.50 | 1.24 | 0.22 | 10.35 | 1.47 | 2.54 | 0.51 |
| NGC 6946 | 5.9 | 2.9 | 9.74 | 2.729 | 10.80 | 2.74 | 1.52 | 2.31 | 11.26 | 3.29 | 1.61 | 6.70 |
| NGC 7331 | 14.7 | 3.2 | 10.08 | 7.244 | 10.40 | 1.68 | 0.37 | 0.35 | 11.13 | 2.31 | 0.24 | 1.86 |
| NGC 7793 | 3.9 | 1.7 | 9.07 | 0.511 | 10.32 | 2.09 | 4.65 | 4.13 | 10.53 | 2.29 | 4.23 | 6.73 |
| LSB type | ||||||||||||
| DDO 154 | 4.3 | 0.8 | 8.68 | 0.007 | 8.62 | 0.69 | 1.01 | 6.00 | 8.34 | 0.83 | 0.59 | 3.14 |
| IC 2574 | 4.0 | 4.2 | 9.29 | 0.273 | 9.98 | 3.07 | 0.52 | 3.49 | 10.49 | 4.86 | 0.30 | 11.40 |
| NGC 925 | 9.2 | 3.9 | 9.78 | 1.614 | 9.34 | 2.62 | 0.31 | 0.54 | 10.55 | 3.61 | 0.25 | 2.22 |
| NGC 2976 | 3.6 | 1.2 | 8.27 | 0.201 | 8.71 | 0.58 | 2.19 | 0.26 | 9.41 | 0.75 | 1.37 | 1.30 |
| Galaxy | Type | () | () | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) |
| NGC 2403 | HSB | 10.15 | 3.88 | 1.51 |
| NGC 2841 | HSB | 11.08 | 0.55 | 2.58 |
| NGC 2903 | HSB | 10.60 | 2.10 | 1.09 |
| NGC 3031 | HSB | 10.67 | 15.01 | 1.55 |
| NGC 3198 | HSB | 10.33 | 3.55 | 0.69 |
| NGC 3521 | HSB | 10.69 | 6.18 | 1.34 |
| NGC 3621 | HSB | 10.14 | 10.41 | 0.86 |
| NGC 3627 | HSB | 10.70 | 4.94 | 1.63 |
| NGC 4736 | HSB | 10.27 | - | 1.46 |
| NGC 4826 | HSB | 10.36 | 3.14 | 0.83 |
| NGC 5055 | HSB | 10.57 | 2.99 | 0.86 |
| NGC 6946 | HSB | 10.57 | 2.55 | 1.37 |
| NGC 7331 | HSB | 10.82 | 1.84 | 0.92 |
| NGC 7793 | HSB | 9.75 | 12.47 | 1.09 |
| DDO 154 | LSB | 7.69 | 21.17 | 0.71 |
| IC 2574 | LSB | 9.59 | 18.47 | 1.43 |
| NGC 925 | LSB | 9.83 | 10.98 | 0.42 |
| NGC 2976 | LSB | 9.34 | 12.98 | 1.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wojnar, A.; Sporea, C.A.; Borowiec, A. A Simple Model for Explaining Galaxy Rotation Curves. Galaxies 2018, 6, 70. https://doi.org/10.3390/galaxies6030070
Wojnar A, Sporea CA, Borowiec A. A Simple Model for Explaining Galaxy Rotation Curves. Galaxies. 2018; 6(3):70. https://doi.org/10.3390/galaxies6030070
Chicago/Turabian StyleWojnar, Aneta, Ciprian A. Sporea, and Andrzej Borowiec. 2018. "A Simple Model for Explaining Galaxy Rotation Curves" Galaxies 6, no. 3: 70. https://doi.org/10.3390/galaxies6030070
APA StyleWojnar, A., Sporea, C. A., & Borowiec, A. (2018). A Simple Model for Explaining Galaxy Rotation Curves. Galaxies, 6(3), 70. https://doi.org/10.3390/galaxies6030070





