Bell Inequality and Its Application to Cosmology
Abstract
:1. Introduction
2. Bell Inequalities
2.1. Bell Inequality
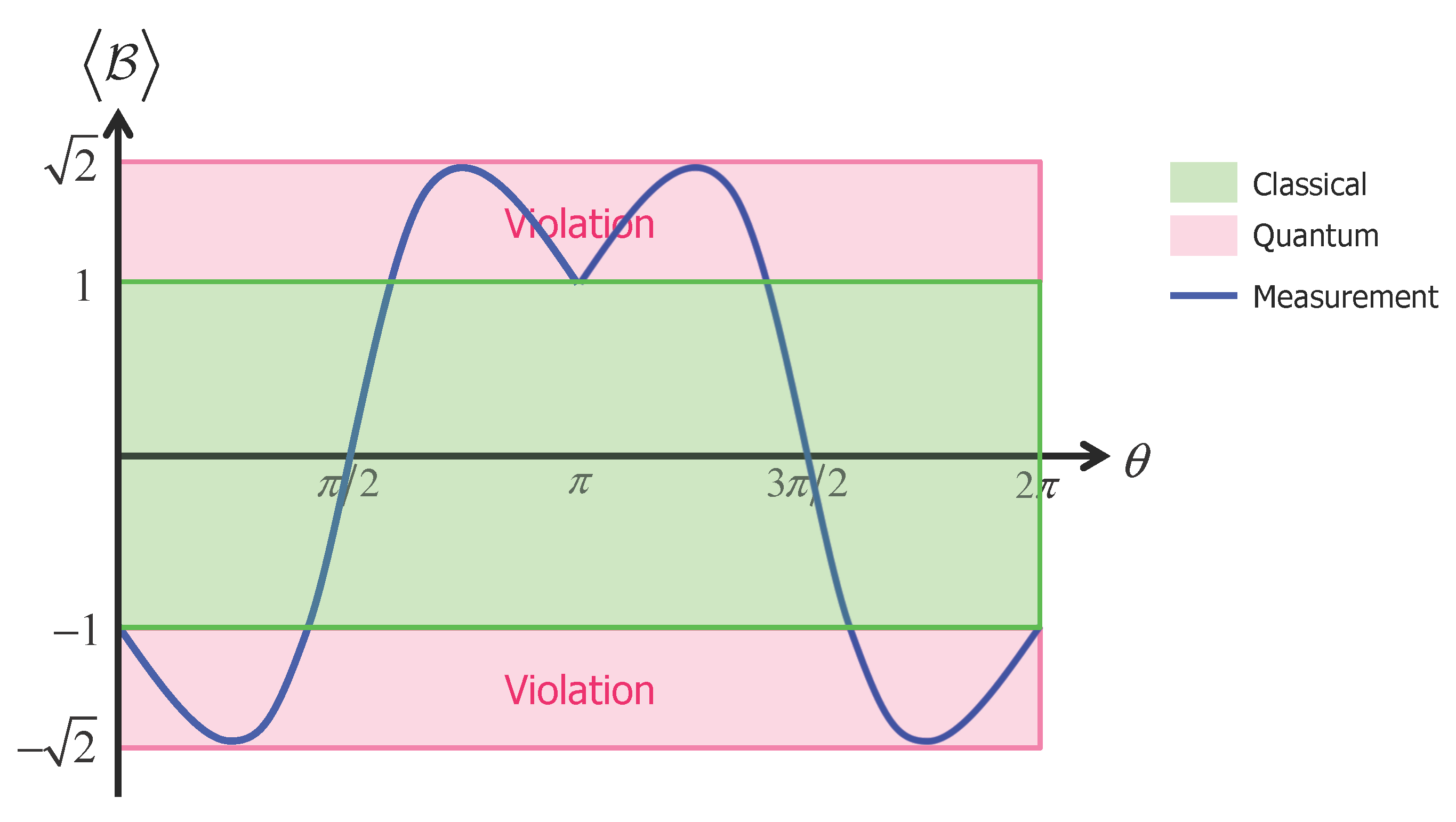
2.2. Mermin–Klyshko Inequalities
3. Cosmological Initial States and Particle Creation
3.1. The Bunch–Davies Vacuum
3.2. A Non-Bunch–Davies Vacuum
3.3. Infinite Violation of Bell Inequalities
4. Results
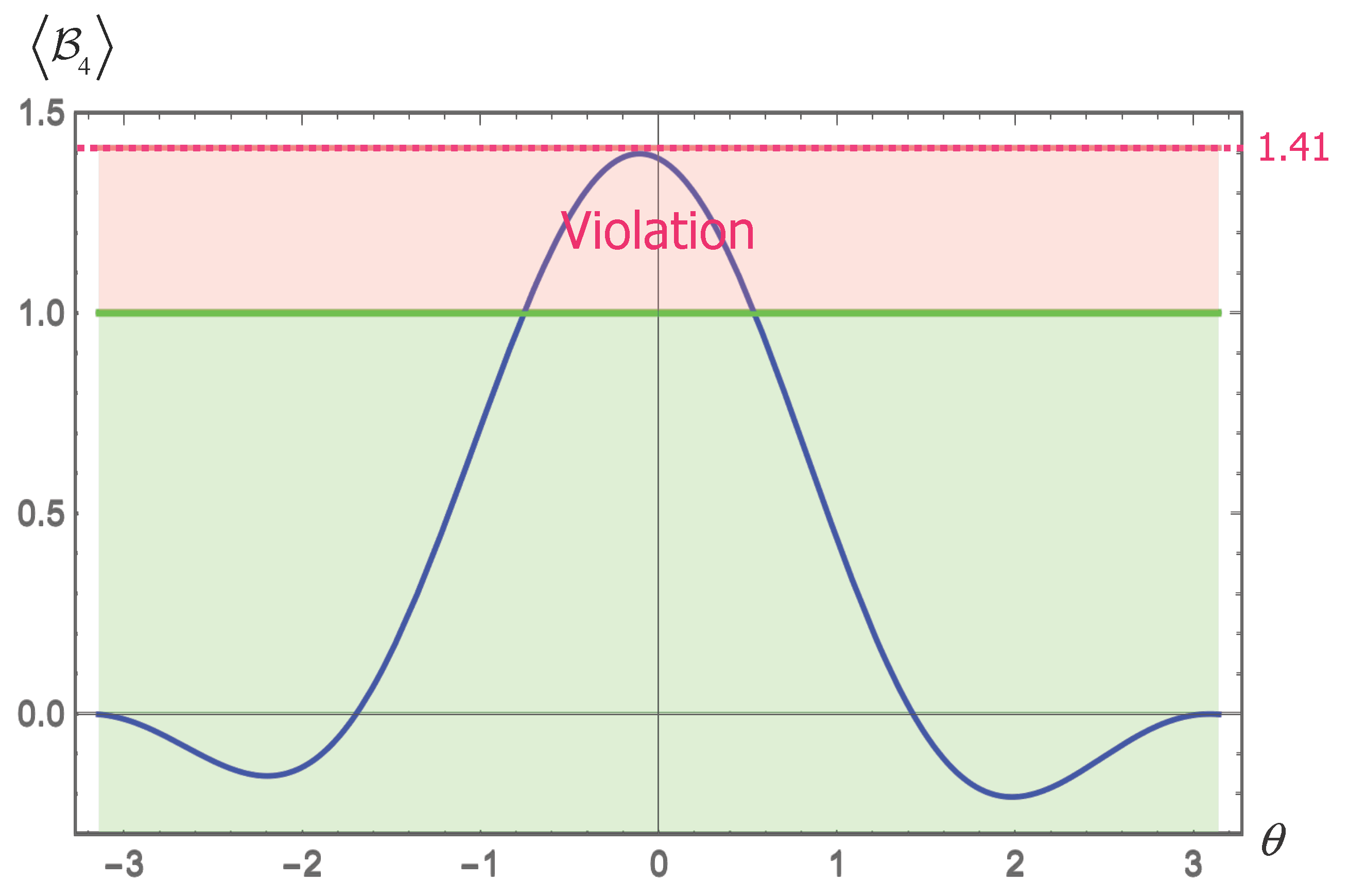
4.1. The Case of the Bunch–Davies (BD) Vacuum
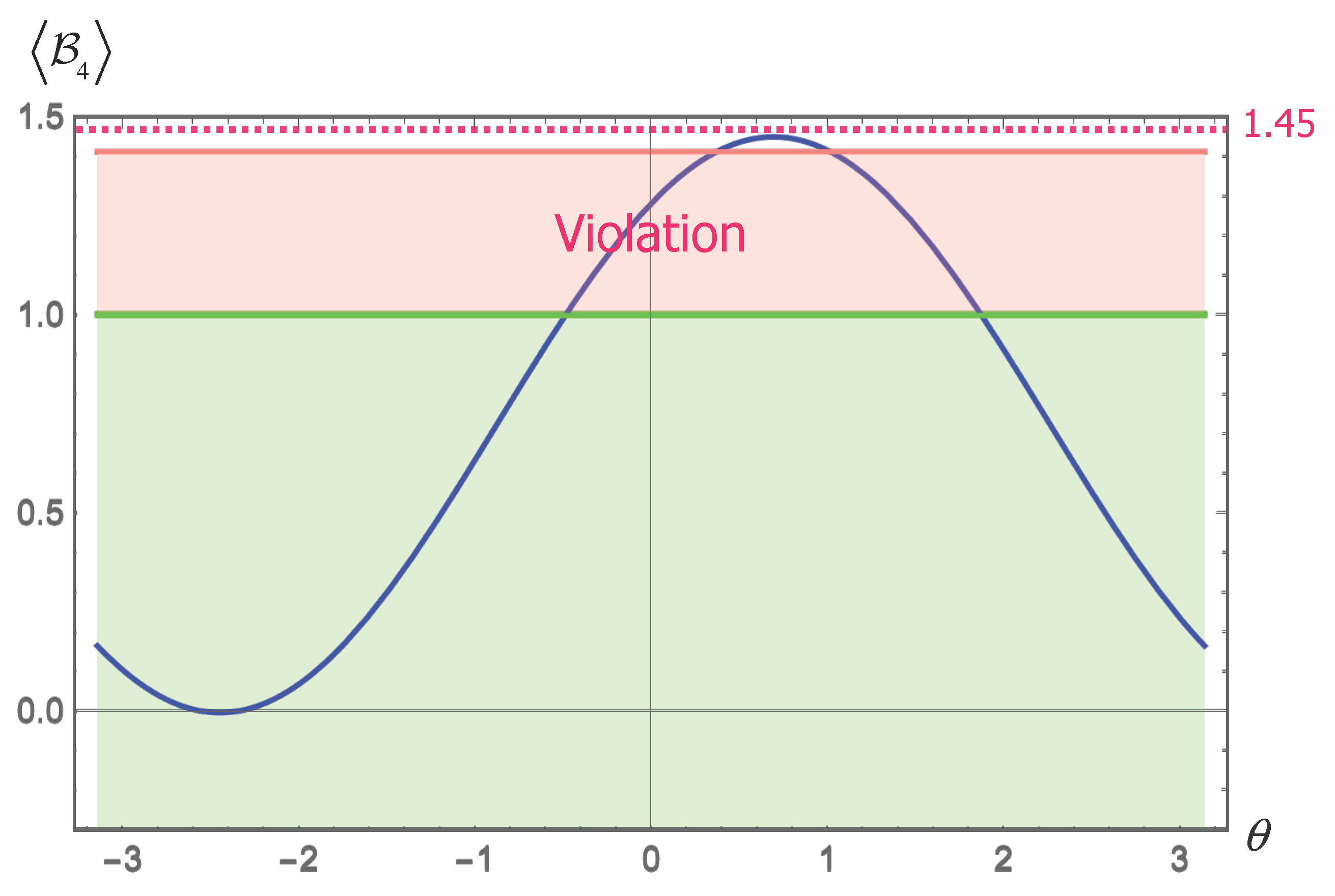
4.2. The Case of a Non-Bunch–Davies Vacuum
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental Tests of Realistic Local Theories via Bell’s Theorem. Phys. Rev. Lett. 1981, 47, 460. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental test of Bell’s inequalities using time varying analyzers. Phys. Rev. Lett. 1982, 49, 1804. [Google Scholar] [CrossRef]
- Maldacena, J. A model with cosmological Bell Inequalities. Fortsch. Phys. 2016, 64, 10. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar]
- Albrecht, A.; Bolis, N.; Holman, R. Cosmological Consequences of Initial State Entanglement. J. High Energy Phys. 2014, 1411, 093. [Google Scholar] [CrossRef]
- Kanno, S. A note on initial state entanglement in inflationary cosmology. Europhys. Lett. 2015, 111, 60007. [Google Scholar] [CrossRef]
- Kanno, S. Cosmological implications of quantum entanglement in the multiverse. Phys. Lett. B 2015, 751, 316. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J. Infinite violation of Bell inequalities in inflation. Phys. Rev. D 2017, 96, 083501. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein-Podolsky-Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Clauser, J.F.; Horne, M.A.; Shimony, A.; Holt, R.A. Proposed experiment to test local hidden variable theories. Phys. Rev. Lett. 1969, 23, 880. [Google Scholar] [CrossRef]
- Mermin, N.D. Extreme quantum entanglement in a superposition of macroscopically distinct states. Phys. Rev. Lett. 1990, 65, 1838. [Google Scholar] [CrossRef] [PubMed]
- Belinski, A.V.; Klyshko, D.N. Interference of light and Bell’s theorem. Phys.-Uspekhi 1993, 36, 653–693. [Google Scholar] [CrossRef]
- Werner, R.F.; Wolf, M.M. Bell’s inequalities for states with positive partial transpose. Phys. Rev. A 2000, 61, 062102. [Google Scholar] [CrossRef]
- Alsina, D.; Cervera, A.; Goyeneche, D.; Latorre, J.I.; Życzkowski, K. Operational approach to Bell inequalities: Application to qutrits. Phys. Rev. A 2016, 94, 032102. [Google Scholar] [CrossRef]
- Cirelson, B.S. Quantum Generalizations of Bell’s Inequality. Lett. Math. Phys. 1980, 4, 93. [Google Scholar] [CrossRef]
- Gisin, N.; Bechmann-Pasquinucci, H. Bell inequality, Bell states and maximally entangled states for n qubits. Phys. Lett. A 1998, 246, 1–6. [Google Scholar] [CrossRef]
- Chen, Z.B.; Pan, J.W.; Hou, G.; Zhang, Y.D. Maximal Violation of Bell’s Inequalities for Continuous Variable Systems. Phys. Rev. Lett. 2002, 88, 040406. [Google Scholar] [CrossRef] [PubMed]
- Nagata, K.; Koashi, M.; Imoto, N. Configuration of Separability and Tests for Multipartite Entanglement in Bell-Type Experiments. Phys. Rev. Lett. 2002, 89, 260401. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Chen, Z.B.; Pan, J.W.; Zhang, Y.D. Classifying N-Qubit Entanglement via Bell’s Inequalities. Phys. Rev. Lett. 2003, 90, 080401. [Google Scholar] [CrossRef] [PubMed]
| 1 | To avoid confusion, the tensor product ⊗ is omitted below for simplicity. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanno, S.; Soda, J. Bell Inequality and Its Application to Cosmology. Galaxies 2017, 5, 99. https://doi.org/10.3390/galaxies5040099
Kanno S, Soda J. Bell Inequality and Its Application to Cosmology. Galaxies. 2017; 5(4):99. https://doi.org/10.3390/galaxies5040099
Chicago/Turabian StyleKanno, Sugumi, and Jiro Soda. 2017. "Bell Inequality and Its Application to Cosmology" Galaxies 5, no. 4: 99. https://doi.org/10.3390/galaxies5040099
APA StyleKanno, S., & Soda, J. (2017). Bell Inequality and Its Application to Cosmology. Galaxies, 5(4), 99. https://doi.org/10.3390/galaxies5040099



