1. Introduction
According to string theory, axions are ubiquitous in the universe, dubbed the string axiverse [
1]. Remarkably, the mass of string axions can take values in the broad range from
to
[
1,
2]. In order to explore the string axiverse, we can use the cosmic microwave background radiations (CMB) [
3], the large scale structure of the universe [
4], pulsar timing arrays [
5,
6,
7], interferometer detectors [
8,
9], the dynamics of binary system [
10], cosmological gravitational waves (GWs) [
11], black hole physics [
12], electromagnetic waves propagating in the axion background [
13,
14], and nuclear spin precession [
15]. On top of these methods, we proposed a novel way to explore the string axions with gravitational waves [
16].
In the presence of the axion, it is natural to consider the Chern–Simons terms both in the gauge sector and in the gravity sector [
17,
18]. Here, we focus on the fact that the gravitational Chern–Simons term induces a coupling between the GWs and the axion. It should be emphasized that the Chern–Simons coupling provides a natural mechanism for parity violation in gravity provided the nontrivial profile of the axion field. Another key ingredient of the axion dark matter is the coherent oscillation of the axion field. Since the axion is coherently oscillating, the occurrence of the parametric resonance of GWs due to the Chern–Simons coupling can be expected.
In this conference report based on the paper [
16], we explain how the resonance phenomena give rise to a new way to explore the string axiverse. It should be noted that the detectable frequency range of GWs with ground based interferometers is from
to
, which corresponds to the axion mass range from
to
. The GWs in this relevant frequency range can undergo the coherent oscillation of the axion in the galaxy. During the journey, the GWs can be enhanced by the resonance. Since the resonance process violates parity, there should be parity-violation in GWs. Thus, if we observe the chiral gravitational waves, we can confirm the existence of the axion dark matter. When we do not observe the chiral gravitational waves, we can constrain the Chern–Simons coupling constant or the abundance of the string axion in the relevant mass range. Hence, it is worth investigating the mechanism in detail.
2. Axion in Chern–Simons Gravity
The model we consider is the dynamical Chern–Simons gravity coupled with the axion. We adopt the natural unit
. We choose the coordinate
with the conformal time
and
. Then, the action is given by
where the Einstein–Hilbert action reads
Here,
is proportional to the inverse of Newton constant,
and
R is a Ricci scalar. The Chern–Simons term
is given by
where
is the axion field,
is a coupling constant, and
is the Pontryagin density defined as
Note that, since the axion field
has the dimensions of the mass, the Chern–Simons coupling constant
has the dimension of length. Hence, it is convenient to express the coupling constant as
where
ℓ has the dimension of the length. The current limit coming from the Solar System test is
[
19]. The future experiment might improve the contraint on
ℓ by a sixth order stronger than the Solar System constraint [
20]. The action
of the axion field
is given by
where
is the potential of the axion field.
From the action, we obtain the equations for the metric field
where
is the Einstein tensor and
is defined as
Here, the parenthesis denotes the symmetrization. The trace of this tensor identically vanishes. The energy momentum tensor
becomes
The equation of motion for the axion field is the modified Klein–Gordon equation given by
where □ is the d’Alembertian operator defined by
.
3. Gravitational Waves in Axion Background
The potential of the axion field is given by
where
m is the mass of the axion. First of all, we must solve the equations of motion in the homogeneous background spacetime
Note that we ignored the scalar gravitational potential induced by the dark matter, which is decoupled with tensor perturbations at the linear order. The axion depends only on the conformal time
, that is,
. Thus, we have the modified Klein–Gordon equation
where the prime denotes the derivative with respect to the conformal time
. These equations can be solved numerically. However, since the time scale of the expansion of the universe is much longer than the oscillation time scale for the mass range
∼
, we can ignore the cosmic expansion in the Klein–Gordon equation. Hence, the scale factor can be put as
. Now, we have the solution as
where
is determined by the energy density of the axion field as
Here, we normalized by the energy density of the dark matter in the halo of the galaxy. Of course, in general, the axions do not need to dominate the dark matter component.
Now, we move on to the analysis of equation of motion for GWs. The GWs can be described by the metric
where the spatial tensor
is transverse and traceless. We work in the Fourier space and consider GWs with the wave number vector
. We can define the unit vector
with
. Then, the transverse condition is rewritten as
in the Fourier space. The perturbed gravitational field can be expressed as
where the circular polarization basis is defined by the plus and cross polarization basis
as
and satisfy the following relation
To derive equation of motion, it is easier to go back to the action rather than to use covariant equations of motion. The quadratic action reads
where the capital latin index represents the each parity state
or
and
is defined by
Thus, the gravitational wave equations can be diagonalized as
where we defined the dimensionless parameter
as
The parameter
characterizes the behavior of the gravitational wave resonance. In the following, we will show that Equation (
23) exhibits the parametric resonance.
4. Resonant Amplification of GWs
Suppose that the GWs from some violent astrophysical events go through our galaxy to reach us. We assume that a lot of clumps whose sizes are about the jeans length exist in the galaxy and the axion is coherently oscillating there. The axion has the interaction with GWs through the Chern–Simons coupling. In addition, the coherent oscillations of the axion induce the parametric resonance of GWs. Thus, GWs are affected by the coherent oscillation of the axion dark matter.
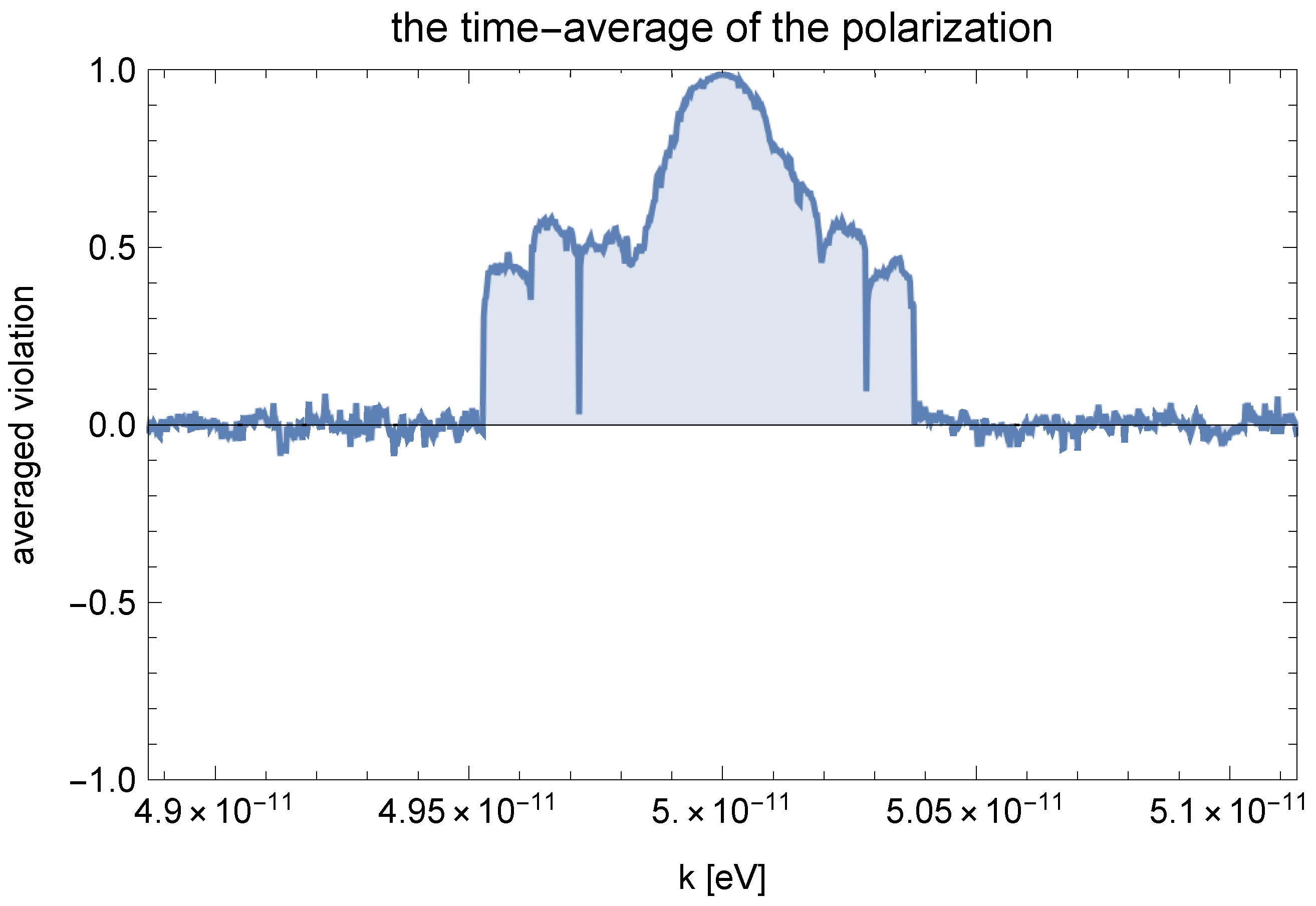
We numerically solved Equation (
23) and found that the parametric resonance of GWs occurs. We also found that the growth rate of amplitudes depends on the chirality, which stems from the parity violation. In
Figure 1, the degree of the circular polarization
is plotted. We can see the parity violation clearly from
Figure 1. Note that the pattern of circular polarization is different from other mechanisms [
21,
22,
23]. Hence, it is easy to distinguish between the parity violation due to the resonance and that due to other mechanisms.
We can also give analytical estimates of the growth rate. From Equation (
23), we find the first resonance frequency
is given by
. This frequency can be converted into
Note that this value lies in the detectable range by the ground based interferometer detectors for GWs. Following the standard analysis of the parametric resonance, we obtain the width of the resonance as
Since
, the resonance peak is very sharp. We can also calculate the growth rate of GWs due to the resonance by the axion oscillation. The maximum growth rate
is given by
Thus, the time
when the amplitude become ten times bigger is estimated as
Note that the time for GWs propagating 1 pc is given by . Hence, the distance traveling during the above time is . For example, if the distance from the source to the earth is , the amplitude of GWs can get enhanced. In that case, since the amplification of one of the chirality modes occurs, the polarization becomes circular. From the fact that we have not observed these phenomena, we can constrain the coupling to be or the density to be . Thus, we have the strongest constraint on the Chern–Simons coupling for the axion dark mater.
When we change the axion mass from up to , we obtain the constraint for each mass. There are two ways to use the results we have obtained. If the current upper limit is assumed, the abundance should be constrained. If we assume the axion is the dominant component of the dark matter, then we obtain a stronger constraint than the current one .
5. Conclusions
We studied the string axiverse and parity violation in the gravity sector by considering propagation of GWs in the axion dark matter with the mass range from to , which corresponds to the detectable frequency range of GWs with ground based interferometers from to . It turned out that the axion coherent oscillation induces the parametric resonance of GWs due to the Chern–Simons term resulting in the circular polarization of GWs. Thus, the observation of GWs can strongly constrain the coupling constant of the Chern–Simons term and/or the abundance of the light axions.
In the core of our galaxy, the dark matter density is higher than that near the sun by about ∼. Therefore, it is possible to have more stringent constraints. If a sizable amount of the light axion exists, the circularly polarized GWs might be observed. If this happens, it would be a great discovery. If not, as the detection events increase, the constraints on the Chern–Simons coupling and/or the abundance of the light axion become tight. In this sense, GWs can explore the string axiverse and parity violation in gravity.