Suborbital Fermi/LAT Analysis of the Brightest Gamma-Ray Flare of Blazar 3C 454.3
Abstract
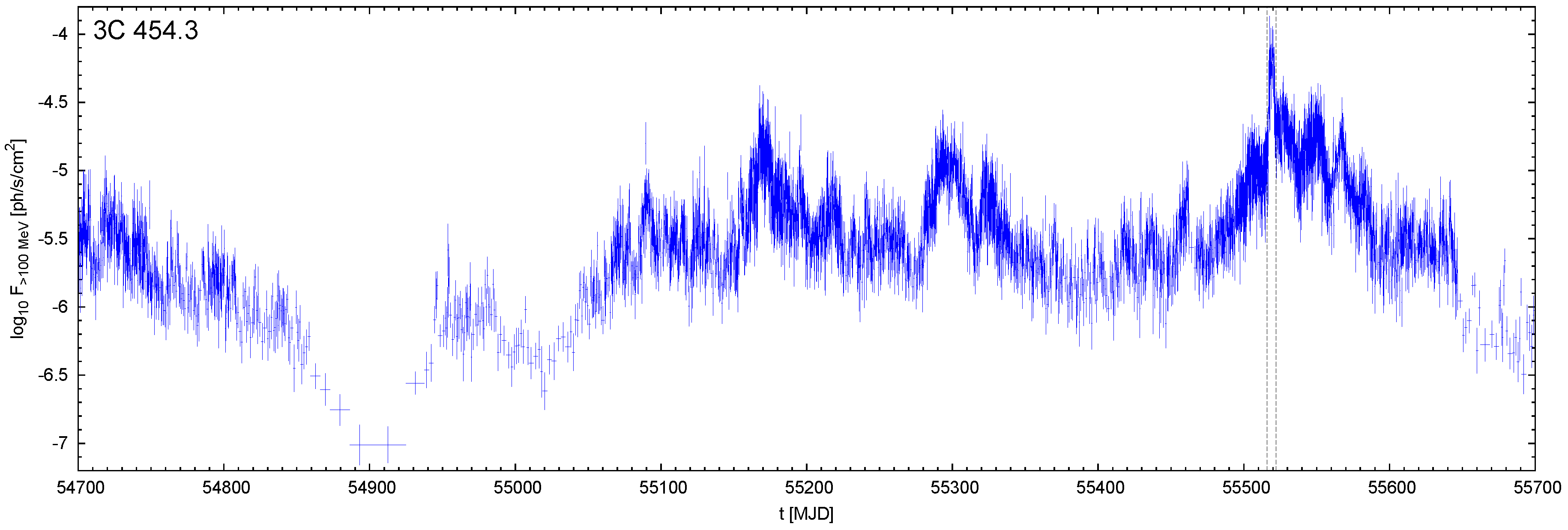
1. Introduction
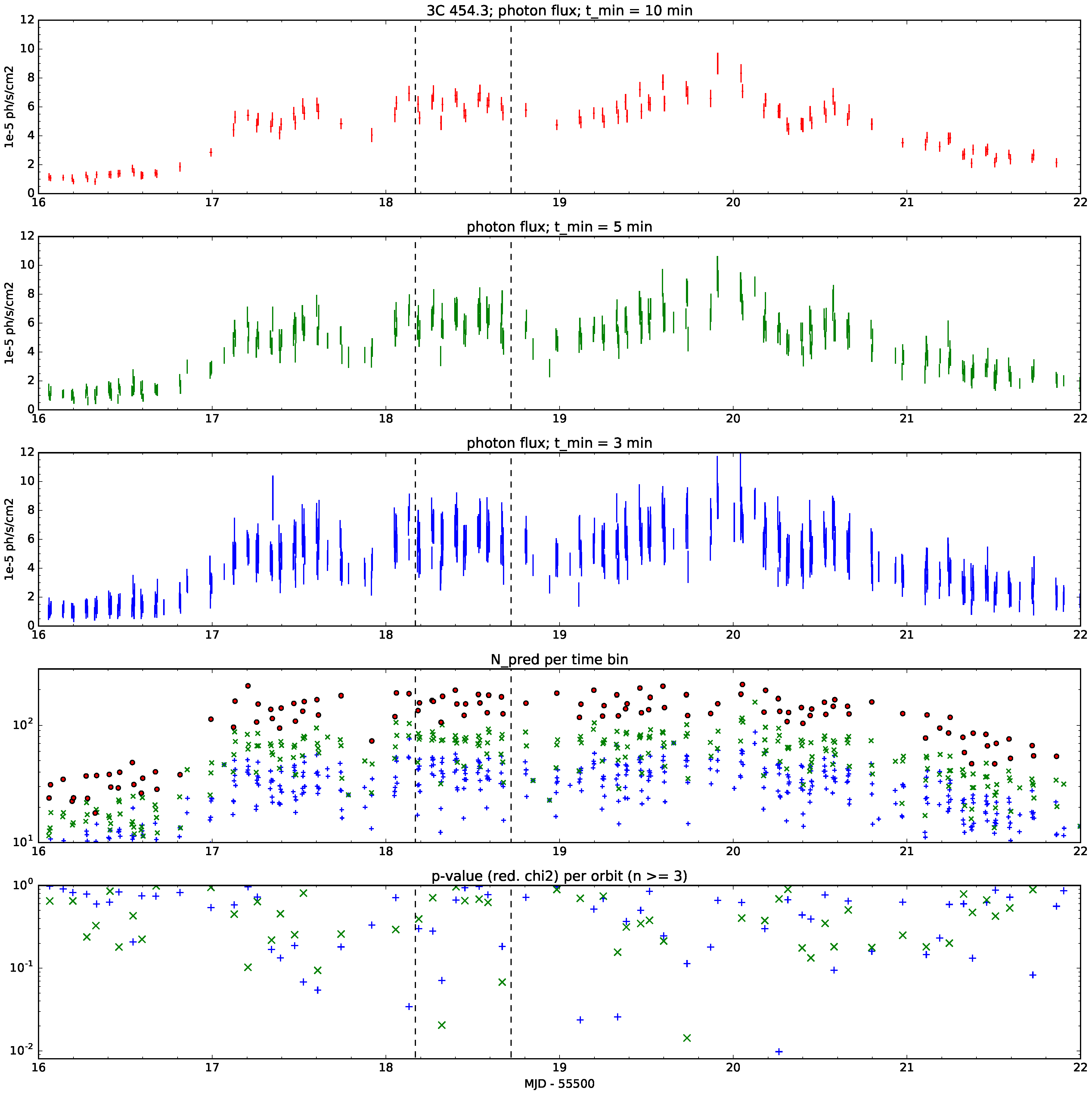
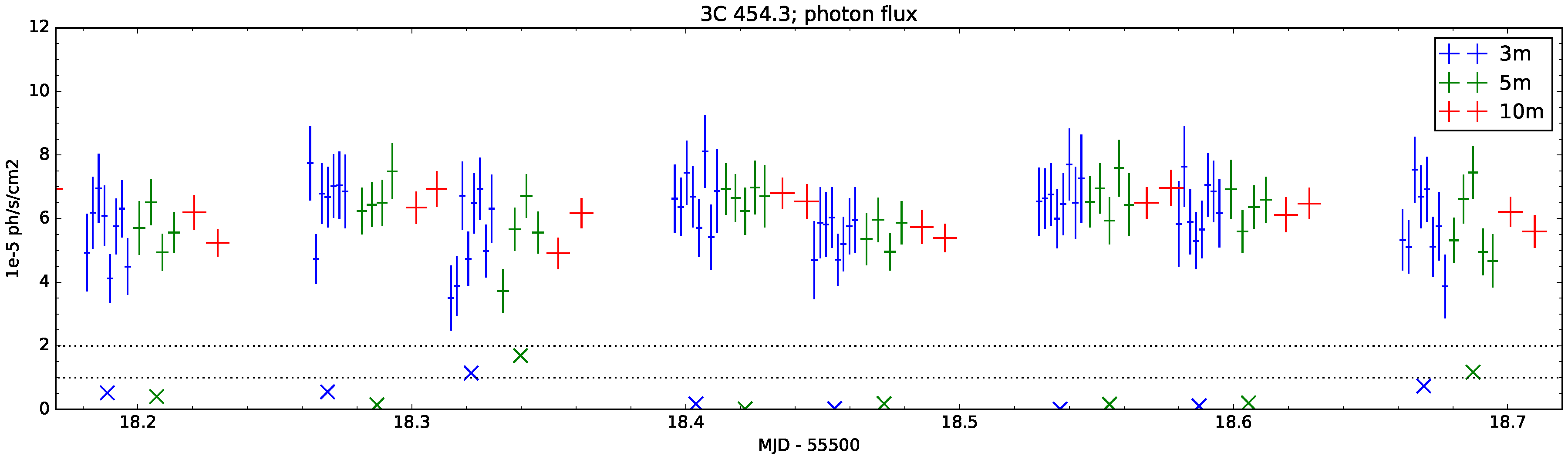
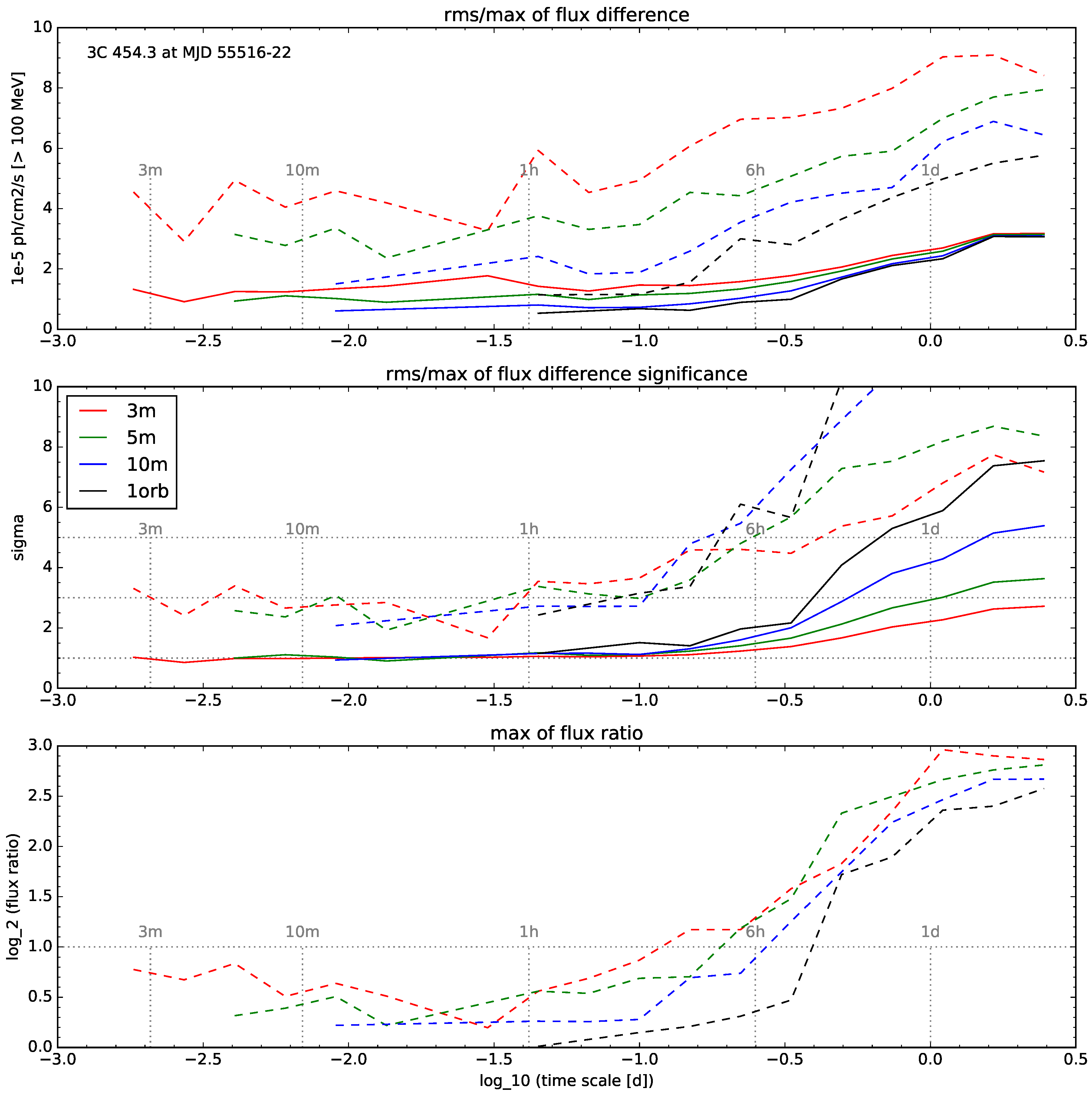
2. Results
3. Discussion
4. Materials and Methods
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Madejski, G.M.; Sikora, M. Gamma-Ray Observations of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2016, 54, 725. [Google Scholar] [CrossRef]
- Atwood, W.B.; Abdo, A.A.; Ackermann, M.; Althouse, W.; Anderson, B.; Axelsson, M.; Baldini, L.; Ballet, J.; Band, D.L.; Barbiellini, G.; et al. The Large Area Telescope on the Fermi Gamma-Ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. An Exceptional Very High Energy Gamma-Ray Flare of PKS 2155-304. Astrophys. J. 2007, 664, L71. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; Becker, J.K.; et al. Variable Very High Energy γ-Ray Emission from Markarian 501. Astrophys. J. 2007, 669, 862. [Google Scholar] [CrossRef]
- Giannios, D.; Uzdensky, D.A.; Begelman, M.C. Fast TeV variability in blazars: Jets in a jet. Mon. Not. Roy. Astron. Soc. 2009, 395, L29. [Google Scholar] [CrossRef]
- Nalewajko, K.; Giannios, D.; Begelman, M.C.; Uzdensky, D.A.; Sikora, M. Radiative properties of reconnection-powered minijets in blazars. Mon. Not. Roy. Astron. Soc. 2011, 413, 333. [Google Scholar] [CrossRef]
- Bodo, G.; Tavecchio, F. Recollimation shocks and radiative losses in extragalactic relativistic jets. arXiv, 2017; arXiv:1710.06713. [Google Scholar]
- Tavecchio, F.; Becerra-Gonzalez, J.; Ghisellini, G.; Stamerra, A.; Bonnoli, G.; Foschini, L.; Maraschi, L. On the origin of the gamma-ray emission from the flaring blazar PKS 1222+216. Astron. Astrophys. 2011, 534, A86. [Google Scholar] [CrossRef]
- Nalewajko, K.; Begelman, M.C.; Cerutti, B.; Uzdensky, D.A.; Sikora, M. Energetic constraints on a rapid gamma-ray flare in PKS 1222+216. Mon. Not. Roy. Astron. Soc. 2012, 425, 2519. [Google Scholar] [CrossRef]
- Begelman, M.C.; Fabian, A.C.; Rees, M.J. Implications of very rapid TeV variability in blazars. Mon. Not. Roy. Astron. Soc. 2008, 384, L19. [Google Scholar] [CrossRef]
- Tavecchio, F.; Roncadelli, M.; Galanti, G.; Bonnoli, G. Evidence for an axion-like particle from PKS 1222+216? Phys. Rev. D 2012, 86, 085036. [Google Scholar] [CrossRef]
- Foschini, L.; Bonnoli, G.; Ghisellini, G.; Tagliaferri, G.; Tavecchio, F.; Stamerra, A. Fermi/LAT detection of extraordinary variability in the gamma-ray emission of the blazar PKS 1510-089. Astron. Astrophys. 2013, 555, A138. [Google Scholar] [CrossRef]
- Nalewajko, K. The brightest gamma-ray flares of blazars. Mon. Not. Roy. Astron. Soc. 2013, 430, 1324. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Berenji, B.; et al. Fermi Gamma-ray Space Telescope Observations of the Gamma-ray Outburst from 3C454.3 in November 2010. Astrophys. J. 2011, 733, L26. [Google Scholar] [CrossRef]
- Foschini, L.; Ghisellini, G.; Tavecchio, F.; Bonnoli, G.; Stamerra, A. Search for the shortest variability at gamma rays in flat-spectrum radio quasars. Astron. Astrophys. 2011, 530, A77. [Google Scholar] [CrossRef]
- Ackermann, M.; Anantua, R.; Asano, K.; Baldini, L.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; et al. Minute-timescale >100 MeV γ-Ray Variability during the Giant Outburst of Quasar 3C 279 Observed by Fermi-LAT in 2015 June. Astrophys. J. 2016, 824, L20. [Google Scholar] [CrossRef]
- Petropoulou, M.; Nalewajko, K.; Hayashida, M.; Mastichiadis, A. A hadronic minute-scale GeV flare from quasar 3C 279? Mon. Not. Roy. Astron. Soc. 2017, 467, L16. [Google Scholar] [CrossRef]
- Vittorini, V.; Tavani, M.; Cavaliere, A. Meeting the Challenge from Bright and Fast Gamma-Ray Flares of 3C 279. Astrophys. J. 2017, 843, L23. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Barkov, M.V.; Khangulyan, D. Scenarios for Ultrafast Gamma-Ray Variability in AGN. Astrophys. J. 2017, 841, 61. [Google Scholar] [CrossRef]
- Dermer, C.D.; Finke, J.D.; Krug, H.; Böttcher, M. Gamma-Ray Studies of Blazars: Synchro-Compton Analysis of Flat Spectrum Radio Quasars. Astrophys. J. 2009, 692, 32–46. [Google Scholar] [CrossRef]
- Sikora, M.; Stawarz, Ł.; Moderski, R.; Nalewajko, K.; Madejski, G.M. Constraining Emission Models of Luminous Blazar Sources. Astrophys. J. 2009, 704, 38. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Foschini, L.; Ghirlanda, G.; Maraschi, L.; Celotti, A. General physical properties of bright Fermi blazars. Mon. Not. Roy. Astron. Soc. 2010, 402, 497. [Google Scholar] [CrossRef]
- Böttcher, M.; Reimer, A.; Sweeney, K.; Prakash, A. Leptonic and Hadronic Modeling of Fermi-Detected Blazars. Astrophys. J. 2013, 768, 54. [Google Scholar] [CrossRef]
- Nalewajko, K.; Begelman, M.C.; Sikora, M. Constraining the Location of Gamma-Ray Flares in Luminous Blazars. Astrophys. J. 2014, 789, 161. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; Berenji, B.; Blandford, R.D.; et al. Fermi Gamma-ray Space Telescope Observations of Gamma-ray Outbursts from 3C 454.3 in 2009 December and 2010 April. Astrophys. J. 2010, 721, 1383. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. 2015, 218, 23. [Google Scholar] [CrossRef]
- Emmanoulopoulos, D.; McHardy, I.M.; Uttley, P. On the use of structure functions to study blazar variability: Caveats and problems. Mon. Not. Roy. Astron. Soc. 2010, 404, 931. [Google Scholar] [CrossRef]
| 1 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nalewajko, K. Suborbital Fermi/LAT Analysis of the Brightest Gamma-Ray Flare of Blazar 3C 454.3. Galaxies 2017, 5, 100. https://doi.org/10.3390/galaxies5040100
Nalewajko K. Suborbital Fermi/LAT Analysis of the Brightest Gamma-Ray Flare of Blazar 3C 454.3. Galaxies. 2017; 5(4):100. https://doi.org/10.3390/galaxies5040100
Chicago/Turabian StyleNalewajko, Krzysztof. 2017. "Suborbital Fermi/LAT Analysis of the Brightest Gamma-Ray Flare of Blazar 3C 454.3" Galaxies 5, no. 4: 100. https://doi.org/10.3390/galaxies5040100
APA StyleNalewajko, K. (2017). Suborbital Fermi/LAT Analysis of the Brightest Gamma-Ray Flare of Blazar 3C 454.3. Galaxies, 5(4), 100. https://doi.org/10.3390/galaxies5040100




