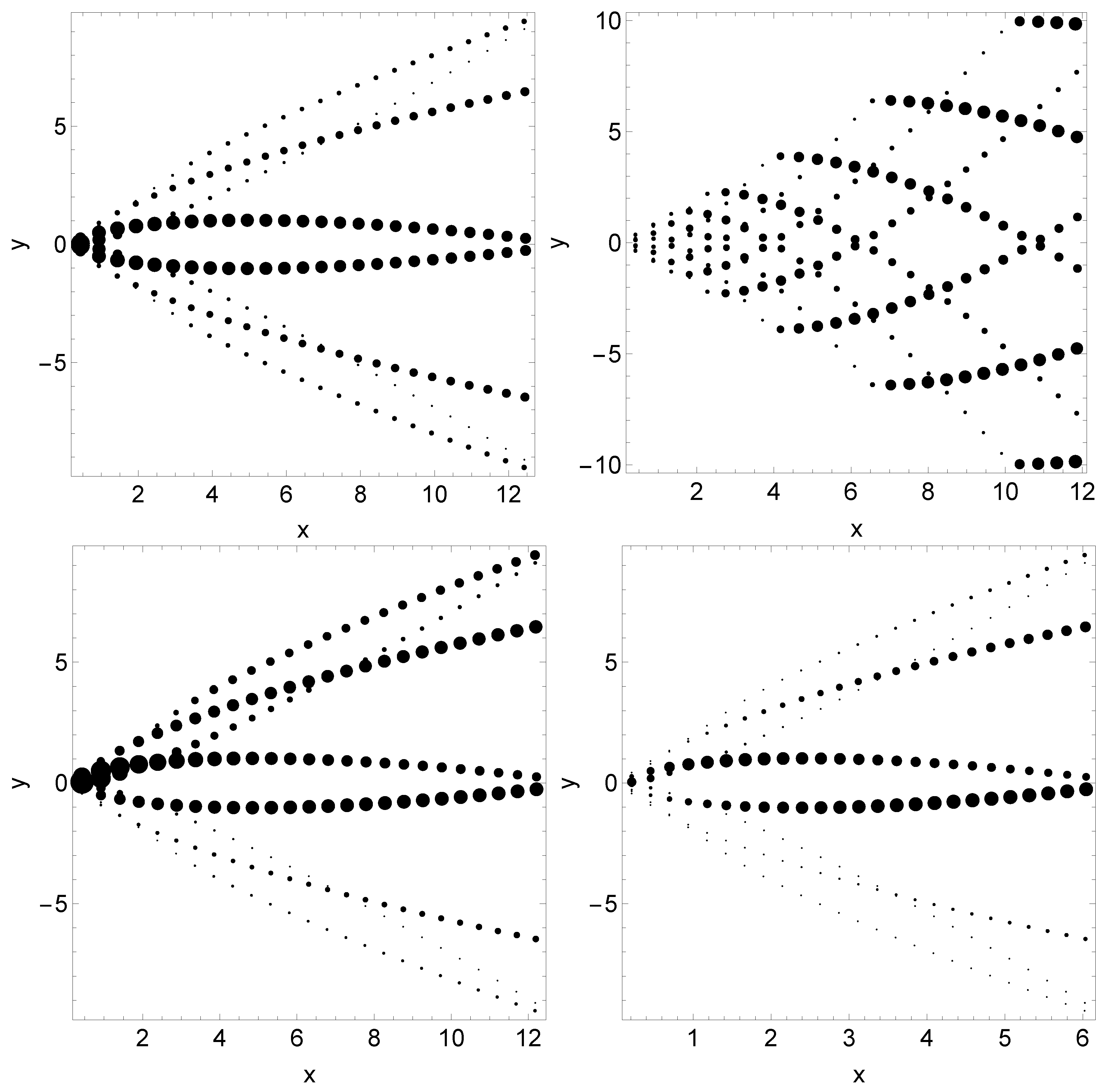Emission Knots and Polarization Swings of Swinging Jets

Abstract

Knots (emission features in jets of active galactic nuclei) often show non-ballistic dynamics and variable emission/polarization properties. We model these features as emission pattern propagating in a jet that carries a helical magnetic field and is launched along a changing direction. The model can reproduce a wide range of phenomena observed in the motion of knots: non-ballistic motion (both smooth and occasional sudden change of direction, and/or oscillatory behavior), variable brightness, and confinement of knots’ motion within an overlaying envelope. The model also reproduces smooth large polarization angle swings, and at the same time allows for the seemingly random behavior of synchrotron fluxes, polarization fraction, and occasional $\pi /2$ polarization jumps.

1. Introduction

Blazars—a sub-class of active galactic nuclei (AGN)—have the orientation of their jets close to the line of sight (LoS). This causes their non-thermal radiation to be highly relativistically beamed. Their linear fractional polarization reaches values up to 50 percent (e.g., [1]), suggesting the presence of highly ordered magnetic fields in their compact regions [2]. Furthermore, the observed behavior of the polarization degree and angle suggest a helical shape of these magnetic fields (e.g., [2,3,4]).

Blazars are observed to show high variability across the electromagnetic spectrum [5,6]. The evolution of the γ-ray, optical, radio, and polarized fluxes often exhibit seemingly random behavior (e.g., [7], and references therein), and in some cases, might be represented by a number of isolated, individual events superimposed on a steady process [8,9]. In contrast, the optical electric vector position angle (EVPA) variations often show smooth swings of linearly polarized radiation, with total rotations up to a few radians. Apparent similarities of optical flux, degree of polarization, and overall EVPA changes during these events—detected in different sources and their different flaring states—suggests that a common mechanism is responsible for such a behavior. The general pattern includes high variability of polarization Π, which drops to zero during the middle of an EVPA swing, and then recovers back to the initial value, smooth and continuous change of polarization angle and peaked behavior of optical flux density.

2. Polarization Swings: Jet With Helical Magnetic Field Propagating along a Variable Direction

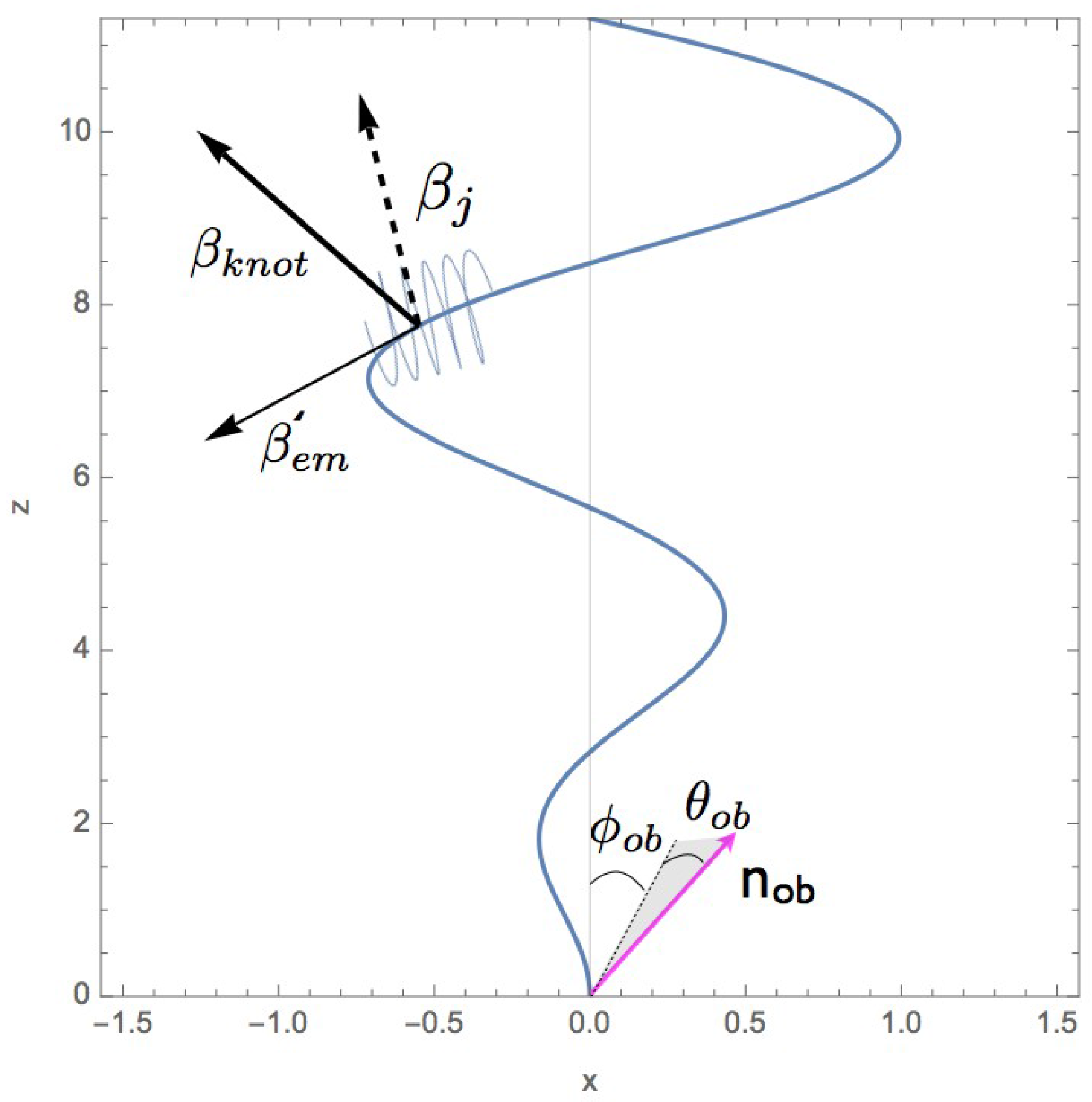
We present a model [10], shown in Figure 1—a jet propagating along a smoothly variable direction carrying a helical magnetic field—which is able to reproduce large smooth variations of the EVPA, yet allow for occasional sudden jumps in EVPA. In addition—and most importantly— the intensity and polarization fraction, though produced by a highly deterministic process, shows large non-monotonic variations that can be mistaken for a random process. Thus, a highly deterministic set-up of the model produces both smooth variation of EVPA and yet allows for some properties of the emission to vary non-monotonically, which can be interpreted as stochastic variation.

We model the emitting element as a jet carrying a helical magnetic field with internal pitch angle ψ, propagating with Lorentz factor ${\gamma }_j$. The jet produces polarized synchrotron emission. We concentrate on the optically thin region, sufficiently far downstream of the core. In terms of physical location, the model is applicable to sub-parsec to parsec scale regions of the jet. In the present paper, we do not make a separation between the different parts of the spectrum (e.g., optical and radio), but outline the general properties of polarized synchrotron emission expected from a jet with variable direction.

Calculations of polarization produced by relativistically moving sources is somewhat complex [2,11,12]. Conventionally (and erroneously for a relativistically moving plasma), the direction of the observed polarization for optically thin regions and the associated magnetic fields are assumed to be in one-to-one correspondence, being orthogonal to each other, so that some observers choose to plot the direction of the electric vector of the wave, while others plot vectors orthogonal to the electric vectors and call them the direction of the magnetic field. This is correct only for non-relativistically moving optically-thin sources, and thus cannot be applied to AGN jets. Since the emission is boosted by the relativistic motion of the jet material, the EVPA rotates parallel to the plane containing the line of sight and the plasma velocity vector, so that the observed electric field of the wave is not, in general, orthogonal to the observed magnetic field [2,12].

In the case of unresolved jets, the average polarization for an axially symmetric jet can only be along or perpendicular to the jet direction. Yet, the same jet can produce the average polarization along or perpendicular depending on its Lorentz factor and the viewing angle.

We consider the synchrotron emission of an unresolved, thin, circular cylindrical shell populated by relativistic electrons with a power law distribution and moving uniformly in the axial direction with constant velocity. The properties of the synchrotron emission are then determined by three parameters: the internal pitch angle of the magnetic field ψ, the Lorentz factor of the shell in the laboratory frame ${\gamma }_j$, and the viewing angle, θ, which the line of sight to the observer makes with the jet axis in the observer reference frame. Thus, even for fixed internal parameters of the jet, the resulting polarization signature strongly depends both on the viewing angle and the jet Lorentz factor.

The polarization direction from an unresolved jet can be either along the projection of the jet onto the plane of the sky, or perpendicular to it. Thus, as a jet’s direction changes with time, the direction of polarization will also change. Most of the time, the EVPA will either be always along or across the jet. In addition, for a fairly narrow range of internal pitch angles and lines of sight, a given jet can show ninety degree EVPA flips.

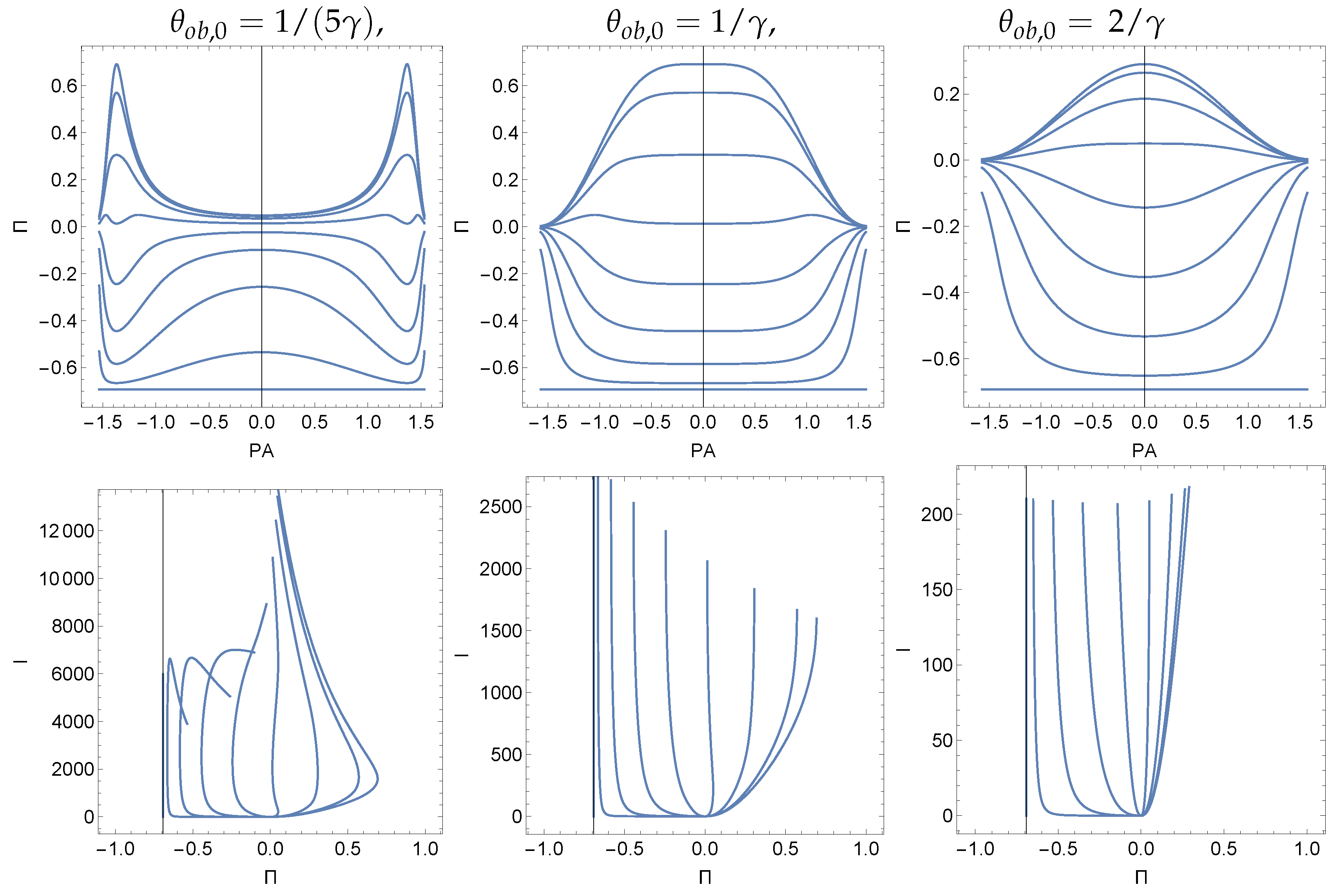
In Figure 2 and Figure 3, we plot the polarization signatures assuming that the motion of the jet is symmetric with respect to the line of sight and that oscillations occur between angles $-\pi /2<{\varphi }_j<\pi /2$ (${\varphi }_j$ is the angle between the instantaneous jet direction and the symmetry axis). We note that for $\Pi >0$, the polarization is along the jet, while the polarization is orthogonal to the jet for $\Pi <0$.

Overall Trends and Special Cases

• Fastest swings of EVPA typically coincide with intensity and polarization extrema (maxima or minima).
• EVPA can experience fast $\pm \pi /2$ jumps near $\Pi =0$. At these points, intensity can be maximal or minimal.
• Swinging jets can produce very fast EVPA swings, up to $\pm \pi$; at the maximum rate of the EVPA swings (second rows in Figure 2), the polarization fraction minima can be maximal or minimal (first rows in Figure 2).
• Intensity depends on the EVPA and the polarization fraction in a complicated way; for accelerating jets, such dependence is not necessarily symmetric.
• Swinging jets can give EVPA rotations in opposite directions within the same source (Figure 2, change in oscillating angle from π/2 back to $-\pi$/2).
• Circularly moving and swinging jets can produce EVPA rotations with amplitude ≤ $\pi /2$, including complex changes if a jet experiences only slight changes in its direction.

We stress that these very complicated, apparently random, and yet correlated variations of intensity, polarization fraction, and EVPA swings come from the assumed highly regular jet motion and very regular jet structure. Most importantly, we assumed constant jet emissivity. We expect that variations in the acceleration/emissivity properties of the jets will further complicate the observed properties. Additionally, more complicated trajectories of a beam can give more complicated profiles.

3. Knots as Emission Patterns in Swinging AGN Jets

Blazar jets often show emission features that move along non-ballistic trajectories [13]. Lyutikov and Kravchenko (in preparation) discuss a kinematic model of the emission features as disturbances propagating along a ballistically moving jet.

Let a jet moving ballistically with velocity ${\beta }_j$ oscillate in the $x-z$ plane. In addition, let an emitting element propagate along the jet with velocity ${\beta }_{em}^{\prime }$ (primes denote quantities measured in the jet frame) with respect to the jet. In the observer frame, the velocity of the element is given by relativistic addition of the radial fluid outflow and velocity along the jet, Figure 1.

We assume that the intrinsic knot emission is constant, so that the observed flux is determined exclusively by the effects of relativistic Doppler boosting; which we assume is $\propto {\delta }^4$, where

$$\delta =\frac{1}{\gamma (1-\beta cos\theta )},$$

(1)

θ is the angle between the knot velocity and the line of sight, and γ is the Lorentz factor of the knot. Selected knot trajectories are pictured in Figure 4.

Properties of Emission Patterns

Motion of the emission feature is the combination of advection with the ballistic jet motion and propagation along the jet. There are two qualitatively different trajectories: advection-dominated and pattern-propagation-modified regimes. In the advection-dominated regime, a given feature is mostly advected with flow, moving along a nearly ballistic trajectory. In the pattern-propagation-modified regime, a feature mostly follows a curved structure of the jet. Figure 1 demonstrates that as the jet propagates further away from the launching site, the direction of the jet becomes more and more perpendicular to the jet motion. Thus, qualitatively, for the pattern speed with respect to the jet on the order of the speed of light, for ${\theta }_{max}{\gamma }_j\ge 1$, a pattern is mostly advected with the flow. On the other hand for ${\theta }_{max}{\gamma }_j\le 1$, a pattern can propagate through a number of different wiggles.

Analyzing Figure 4, we come to the following conclusion:

• The motion of emission knots is non-ballistic.
• The motion of emission knots is confined within a fixed cone; the opening angle of the cone ${\theta }_{open}$ is determined by the amplitude of oscillations and the viewing angle (due to small viewing angle, the opening angle of knots’ motion is generally much larger than the oscillation angle, ${\theta }_{open}$∼${\theta }_{max}/sin{\theta }_{ob}$).
• Knots may experience seemingly sudden changes of direction (top right panel); such sudden changes are usually accompanied by brightness changes.
• Depending on the parameter. ${\theta }_{max}{\gamma }_j$, knots experience smooth curved trajectories that seemingly asymptotically approach straight lines (e.g., top left panel, ${\theta }_{max}{\gamma }_j=1.7$) or oscillatory behavior (e.g., top right panel, ${\theta }_{max}{\gamma }_j=0.36$).
• For cases ${\theta }_{max}{\gamma }_j\ge 1$ typical trajectories “bend-in”—knots are moving toward the symmetry axis (top right); for ${\theta }_{max}{\gamma }_j\le 1$, some trajectories “bend-out”.
• For high Mach numbers, symmetric case (top left panel) blobs propagating along the average jet direction are brighter.
• Blobs may seem to appear not at the core, with seemingly non-ballistic trajectories; knots may also seem to disappear in flux limited observations (top right and bottom left panel).
• At a given projected location, identical knots may have very different brightness (points of intersection of sequences of small and large circles).
• The motion of knots can be asymmetric with respect to the projection of the average direction of motion on the sky: the brightest blobs propagate along a direction which is different from the jet axis (bottom rows).

We stress that these highly variable features come from constant intrinsic knot emissivity.

4. Discussion

We have outlined a model of blazar activity—a jet carrying a helical magnetic field with a regularly changing direction. We demonstrate that this highly deterministic model can produce highly variable polarization, EVPAs, and intensity profiles. At the same time, the model reproduces smoothly varying EVPA changes. Thus, though for any given configuration, the intensity, polarization, and the EVPA are deterministic and thus their behavior is highly correlated, the non-monotonic variations of these values as functions of the jet direction and Lorentz factor produce highly variable overall behavior. We find that for smooth variation of EVPA, (i) Π can be highly variable; (ii) Π∼0 at the moment of fastest EVPA swing; (iii) the intensity is usually maximal at points of fastest EVPA swing, but can have a minimum; (iv) for some special pitch angles, there are large fluctuations of EVPA, but this always occurs at small Π.

Importantly, these features are obtained for the assumed constant intrinsic jet emissivity. Variations in the acceleration/emissivity properties of the jets, more complicated or irregular beam trajectories, as well as existence of multiple emission components within one beam will complicate observed profiles. In addition to the possible presence of a turbulent magnetic field, these features may produce small (<90${}^{\circ }$) seemingly random EVPA variations [7]. Such variations are often observed during the quiescent state of the source, and are not considered in this paper.