The Blazar Sequence 2.0
Abstract
:1. Introduction
2. The Blazar Sequence 1.0
3. The Sample
4. Results
4.1. Accretion and Jets
4.2. Low Black Hole Mass and Low Power FSRQs
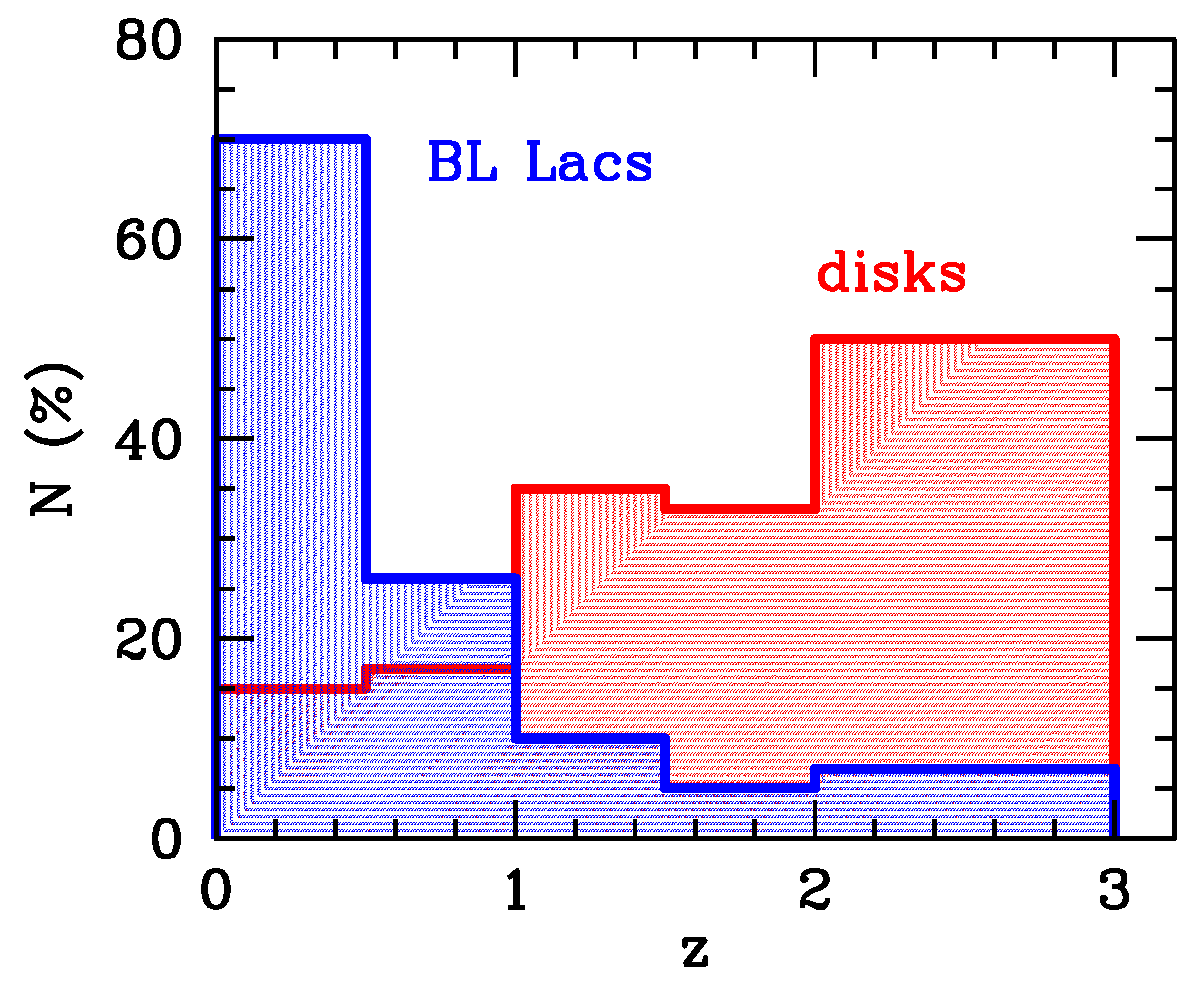
4.3. Host Galaxies of BL Lacs
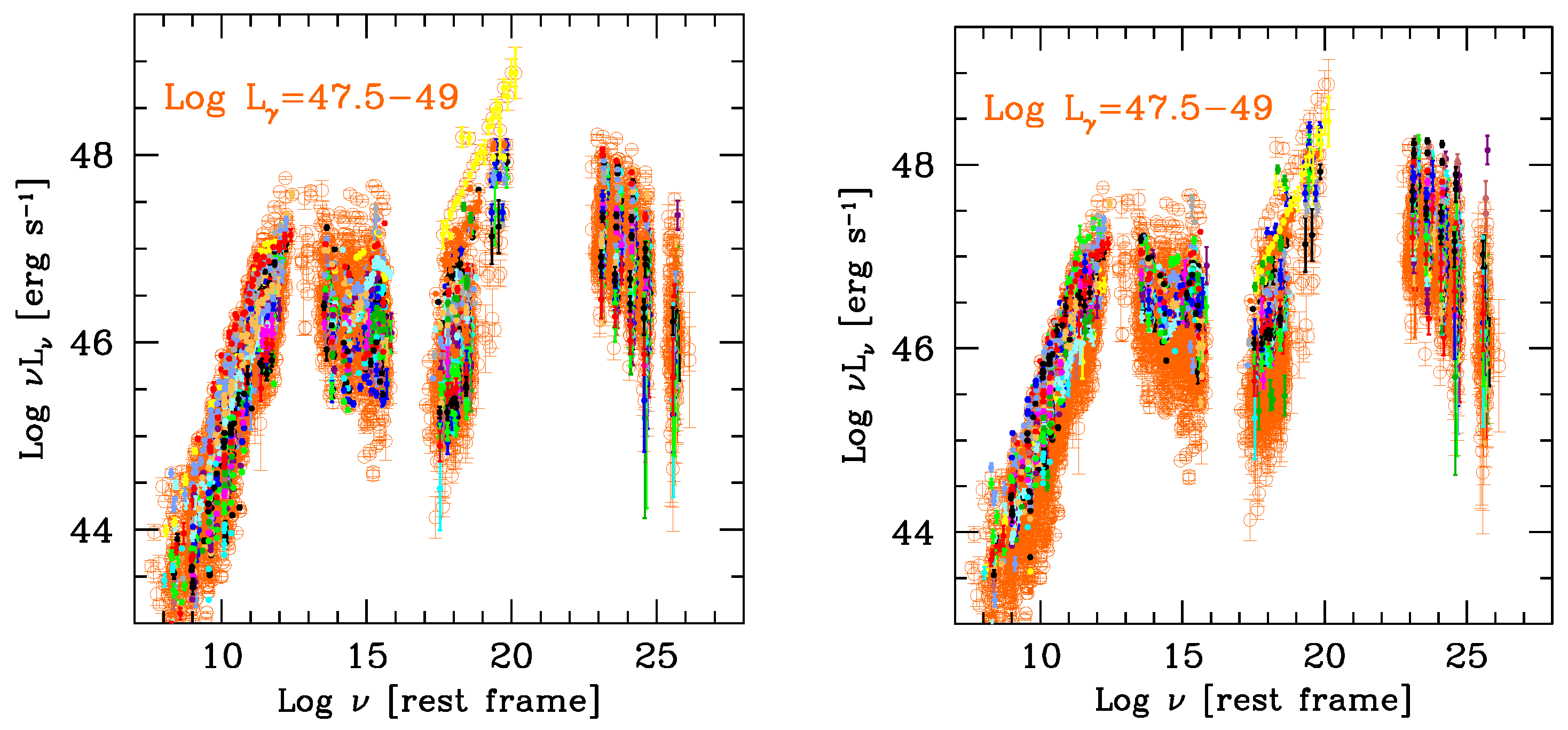
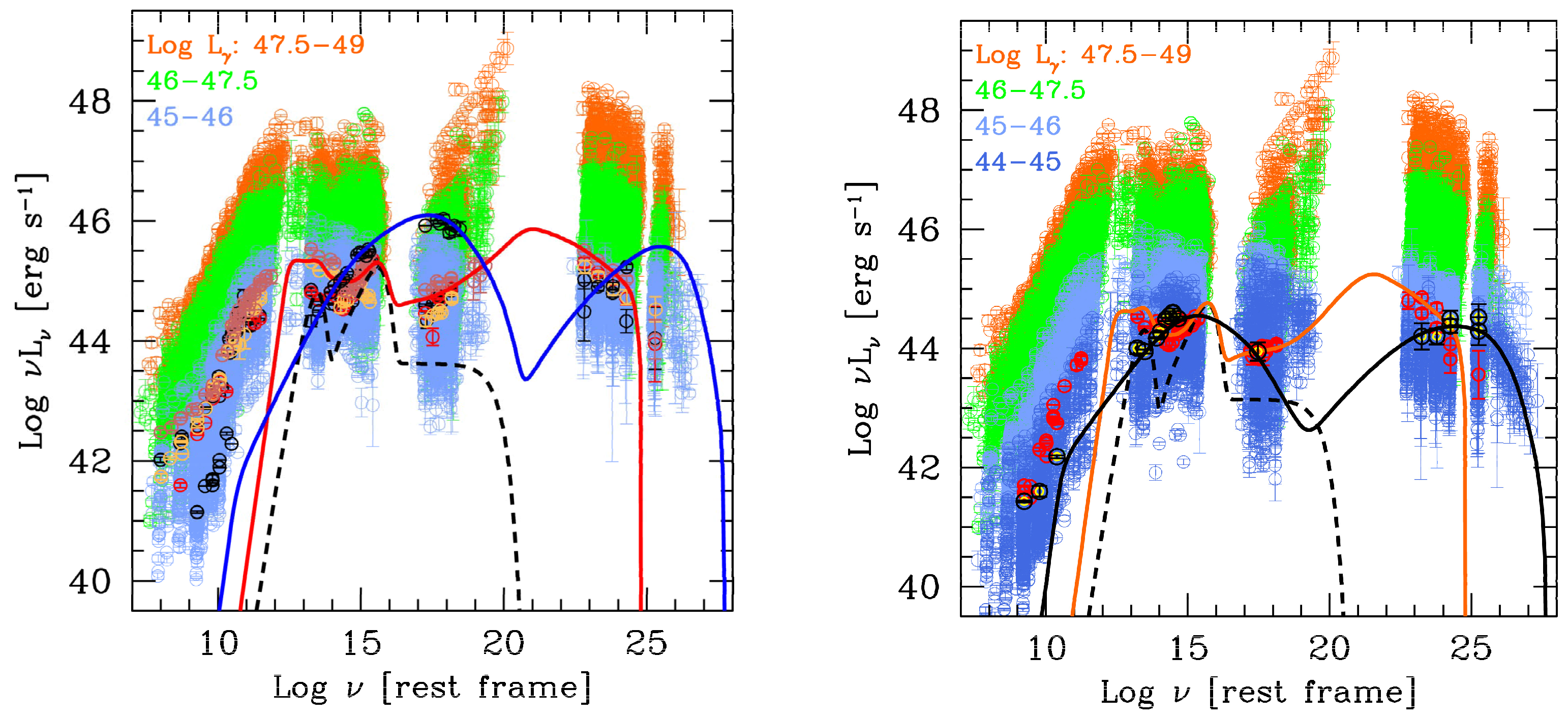
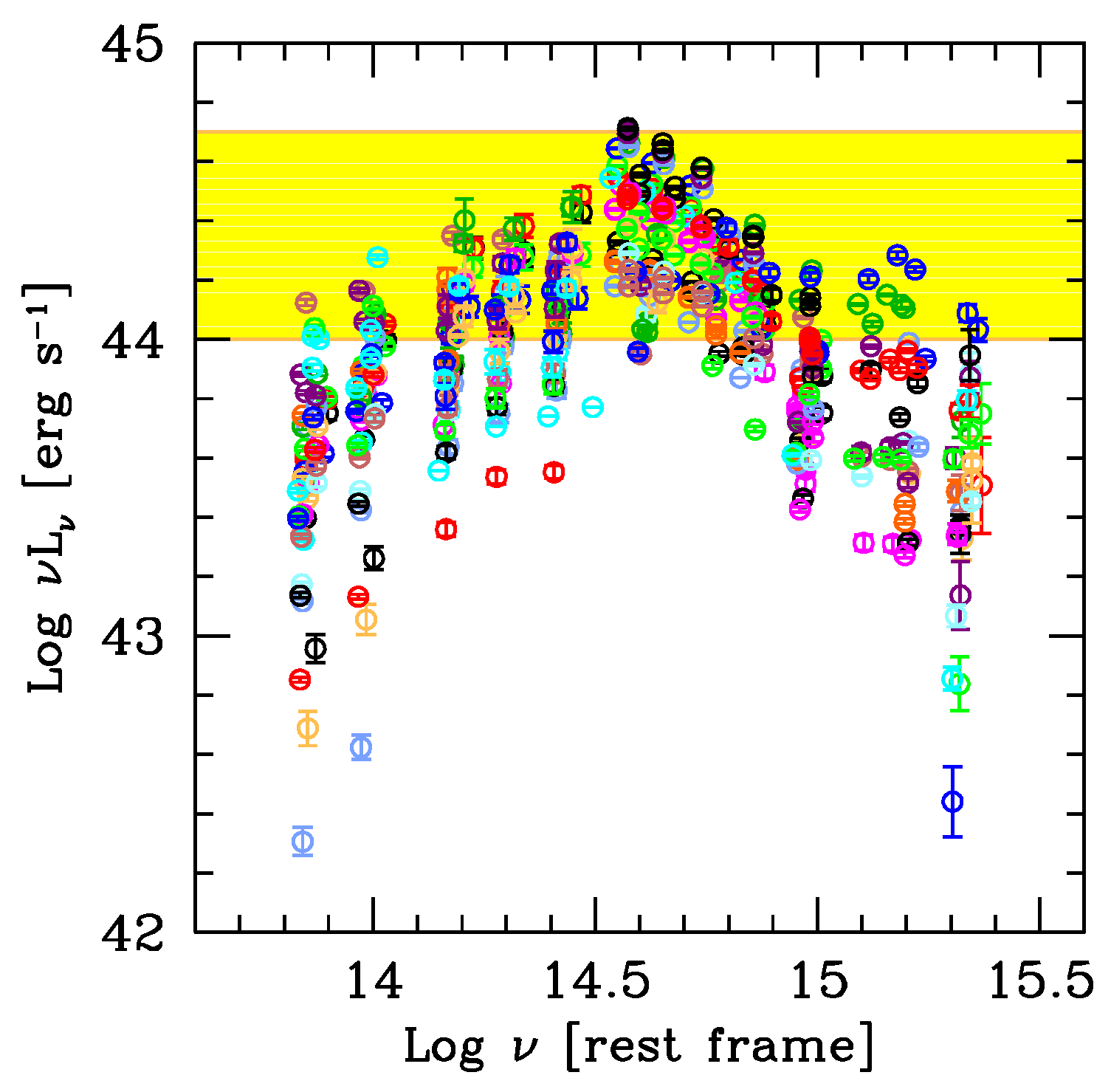
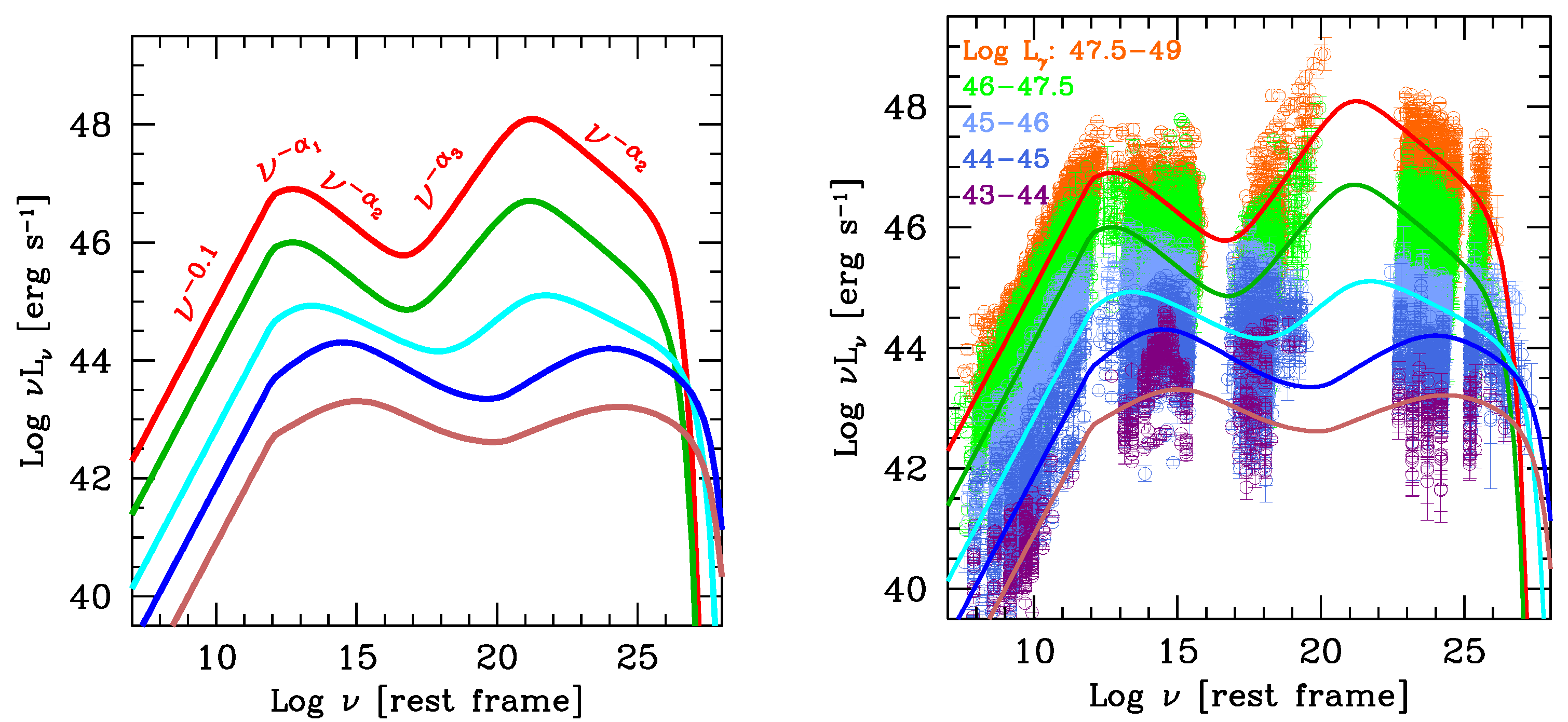
5. Phenomenological SEDs
6. Discussion and Conclusions
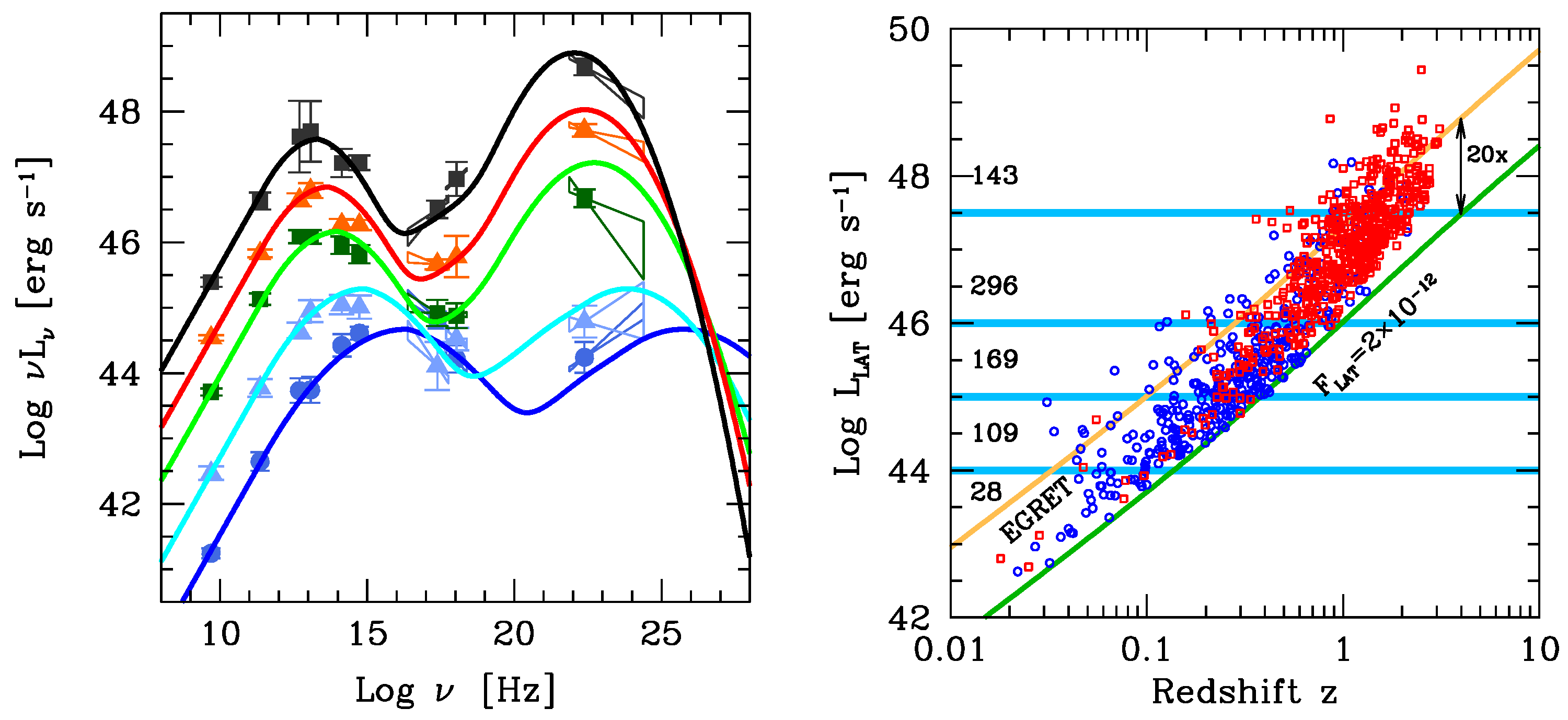
- There still is a blazar sequence, with the same overall properties of the “1.0” version: the SED becomes redder, and the Compton dominance increases as the total luminosity increases.
- In a sizeable fraction of FSRQs, the accretion disk becomes visible through an upturn of the IR–optical spectrum. Pure data show that the accretion luminosity is related to the observed beamed non-thermal luminosity.
- On average, the Compton dominance in powerful blazars is slightly smaller than in [1]. This is the main difference from the old sequence, and it is fully understood: the increased sensitivity of Fermi/LAT allows the exploration of more “normal” blazars, and not only the most luminous. As a consequence, the average γ-ray luminosity is less than in [1]. This explains the puzzling result of [29] when synthesizing the blazar contribution to the γ-ray background. They found that in assuming the blazar radio luminosity function and the same γ-ray-to-radio luminosity ratio as in the original F98 blazar sequence, one overestimates the background, especially at high energies. With the new sequence, the problem is solved (Bonnoli et al. in prep).
- The γ-ray spectrum becomes steeper as the γ–ray luminosity increases. On the other hand, low power BL Lacs do not show, on average, a very hard high energy spectrum (rising in ) in the 0.1–100 GeV band, as was the case in [1] (based on only three sources).
- At intermediate γ-ray luminosities, red FSRQs and blue BL Lacs share the same γ-ray luminosity. This is explained by a difference in black hole masses.
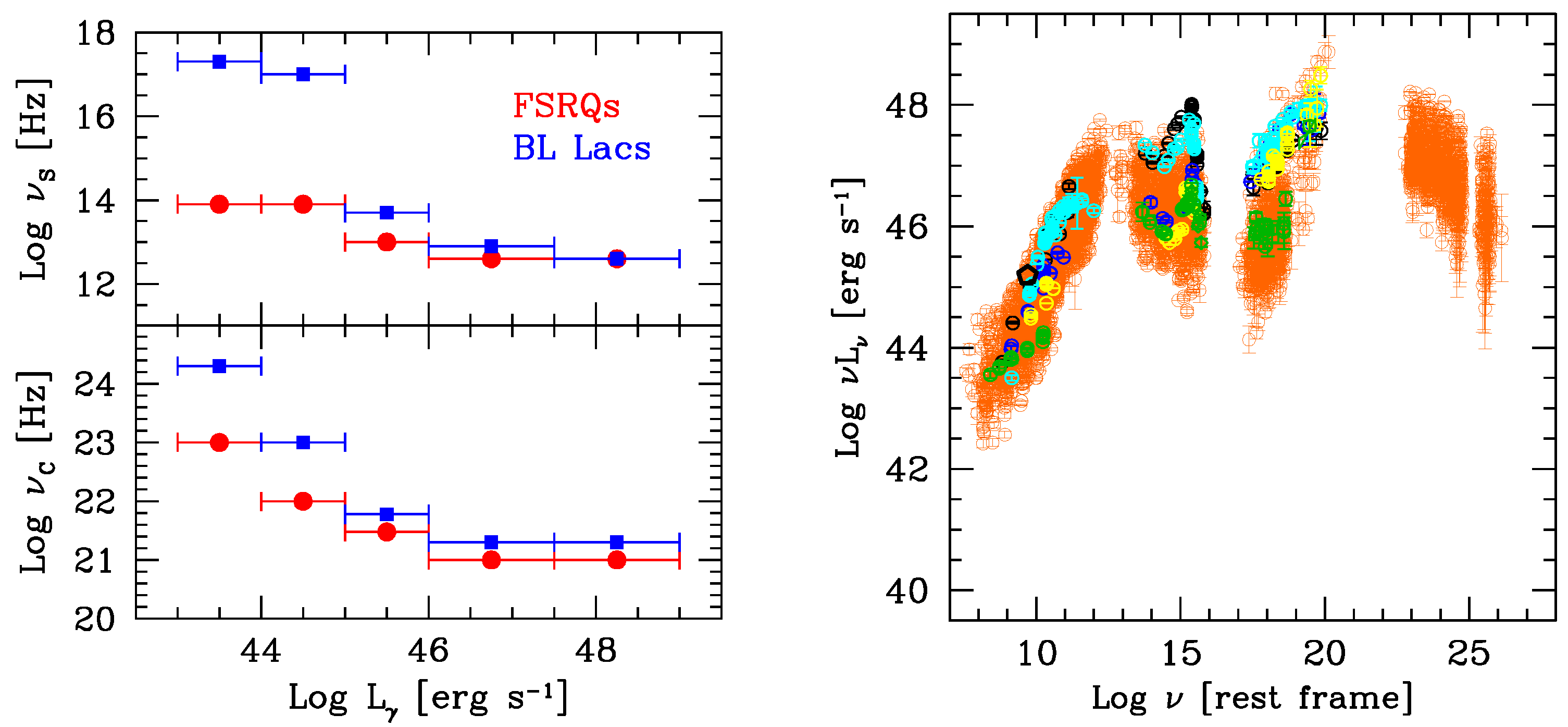
- One can define the average synchrotron () and inverse Compton () peak frequencies for each luminosity bin, but perhaps it is better to define them separately for BL Lacs and FSRQs. This is done in Figure 7 (blue squares: BL Lacs, red circles: FSRQs), showing and as a function of . Both BL Lacs and FSRQs form a sequence, much more pronounced in the BL Lac case.
- The smallest is ∼10 Hz, coincident with of the most compact component. This suggests that there should be even more powerful blazars, with the real synchrotron peak hidden by self-absorption. These blazars should have 1 MeV (i.e., at or below Hz) with a steep spectrum above. In this case, the flux in the 0.1–100 GeV band could become undetectable by Fermi/LAT, and thus be not represented in the new blazar sequence. However, they should be detectable in hard X-rays, and indeed in the Swift/BAT 3 year survey [30] we find ten very powerful blazars with , and five of them are still not detected by Fermi/LAT. These are shown in the right panel of Figure 7.
Conflicts of Interest
References
- Fossati, G.; Maraschi, L.; Celotti, A.; Comastri, A.; Ghisellini, G. A unifying view of the spectral energy distributions of blazars. Mon. Not. R. Astron. Soc. 1998, 299, 433–448. [Google Scholar] [CrossRef]
- Donato, D.; Ghisellini, G.; Tagliaferri, G.; Fossati, G. Hard X-ray properties of blazars. Astron. Astrophys. 2001, 375, 739–751. [Google Scholar] [CrossRef]
- Ghisellini, G.; Celotti, A.; Fossati, G.; Maraschi, L.; Comastri, A. A theoretical unifying scheme for gamma-ray bright blazars. Mon. Not. R. Astron. Soc. 1998, 301, 451–468. [Google Scholar] [CrossRef]
- Bonnoli, G.; Tavecchio, F.; Ghisellini, G.; Sbarrato, T. An emerging population of BL Lacs with extreme properties: Towards a class of EBL and cosmic magnetic field probes? Mon. Not. R. Astron. Soc. 2015, 451, 5130–5140. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Maraschi, L.; Celotti, A.; Sbarrato, T. The power of relativistic jets is larger than the luminosity of their accretion disks. Nature 2014, 515, 376–378. [Google Scholar] [CrossRef] [PubMed]
- Ghisellini, G.; Tavecchio, F. The blazar sequence: A new perspective. Mon. Not. R. Astron. Soc. 2008, 387, 1669–1680. [Google Scholar] [CrossRef]
- Giommi, P.; Menna, M.T.; Padovani, P. The sedentary multifrequency survey—I. Statistical identification and cosmological properties of high-energy peaked BL Lacs. Mon. Not. R. Astron. Soc. 1999, 310, 465–475. [Google Scholar] [CrossRef]
- Perlman, E.S.; Padovani, P.; Landt, H.; Stocke, J.T.; Costamante, L.; Rector, T.; Giommi, P.; Schachter, J.F. Surveys and the Blazar Parameter Space. ASPC 2001, 227, 79–86. [Google Scholar]
- Padovani, P.; Perlman, E.S.; Landt, H.; Giommi, P.; Perri, M. What Types of Jets Does Nature Make? A New Population of Radio Quasars. Astrophys. J. 2003, 588, 128–142. [Google Scholar] [CrossRef]
- Caccianiga, A.; Marcha, M.J.M. The CLASS blazar survey: Testing the blazar sequence. Mon. Not. R. Astron. Soc. 2004, 348, 937–954. [Google Scholar] [CrossRef]
- Antón, S.; Browne, I.W.A. The recognition of blazars and the blazar spectral sequence. Mon. Not. R. Astron. Soc. 2005, 356, 225–231. [Google Scholar] [CrossRef]
- Giommi, P.; Piranomonte, S.; Perri, M.; Padovani, P. The sedentary survey of extreme high energy peaked BL Lacs. Astron. Astrophys. 2005, 434, 385–396. [Google Scholar] [CrossRef]
- Nieppola, E.; Tornikoski, M.; Valtaoja, E. Spectral energy distributions of a large sample of BL Lacertae objects. Astron. Astrophys. 2006, 445, 441–450. [Google Scholar] [CrossRef]
- Raiteri, C.M.; Capetti, A. Testing the blazar sequence with the least luminous BL Lacertae objects. Astron. Astrophys. 2016, 587, A8. [Google Scholar] [CrossRef]
- Padovani, P.; Giommi, P.; Rau, A. The discovery of high-power high synchrotron peak blazars. Mon. Not. R. Astron. Soc. 2012, 422, L48–L52. [Google Scholar] [CrossRef]
- Padovani, P. The blazar sequence: validity and predictions. Astrophys. Space Sci. 2007, 309, 63–71. [Google Scholar] [CrossRef]
- Giommi, P.; Padovani, P.; Polenta, G.; Turriziani, S.; D’Elia, V.; Piranomonte, S. A simplified view of blazars: Clearing the fog around long-standing selection effects. Mon. Not. R. Astron. Soc. 2012, 420, 2899–2911. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Gonzalez, J.B.; Bellazzini, R.; Bissaldi, E.; et al. The third catalog of Active Galactic Nuclei detected by the Fermi Large Area Telescope. Astrophys. J. 2015, 810, 14. [Google Scholar] [CrossRef]
- The 3rd Catalog of AGN Detected by the Fermi LAT (3LAC). Available online: http://www.asdc.asi.it/fermi3lac/ (accessed on 26 September 2016).
- Tavecchio, F.; Ghisellini, G.; Bonnoli, G.; Ghirlanda, G. Constraining the location of the emitting region in Fermi blazars through rapid γ-ray variability. Mon. Not. R. Astron. Soc. 2010, 405, L94–L98. [Google Scholar] [CrossRef]
- Abdo, A.A.; Ackermann, M.; Ajello, M.; Antolini, E.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Gamma-ray Light Curves and Variability of Bright Fermi–detected Blazars. Astrophys. J. 2010, 722, 520–542. [Google Scholar] [CrossRef]
- Rau, A.; Schady, P.; Greiner, J.; Salvato, M.; Ajello, M.; Bottacini, E.; Gehrels, N.; Afonso, P.M.J.; Elliott, J.; Filgas, R.; et al. BL Lacertae objects beyond redshift 1.3—UV-to-NIR photometry and photometric redshift for Fermi/LAT blazars. Astron. Astrophys. 2012, 538, A26. [Google Scholar] [CrossRef]
- Narayan, R.; Garcia, M.R.; McClintock, J.E. Advection-dominated Accretion and Black Hole Event Horizons. Astrophys. J. 1997, 478, L79–L82. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F. Canonical high-power blazars. Mon. Not. R. Astron. Soc. 2009, 397, 985–1002. [Google Scholar] [CrossRef]
- Ghisellini, G.; Maraschi, L.; Tavecchio, F. The Fermi blazars’ divide. Mon. Not. R. Astron. Soc. 2009, 396, L105–L109. [Google Scholar] [CrossRef]
- Sbarufatti, B.; Treves, A.; Falomo, R. Imaging Redshifts of BL Lacertae Objects. Astrophys. J. 2005, 635, 173–179. [Google Scholar] [CrossRef]
- Bentz, M.C.; Peterson, B.M.; Pogge, R.W.; Vestergaard, M. The Black Hole Mass-Bulge Luminosity Relationship for Active Galactic Nuclei From Reverberation Mapping and Hubble Space Telescope Imaging. Astrophys. J. 2009, 694, L166–L170. [Google Scholar] [CrossRef]
- Bettoni, D.; Falomo, R.; Fasano, G.; Govoni, F. The black hole mass of low redshift radiogalaxies. Astron. Astrophys. 2003, 399, 869–878. [Google Scholar] [CrossRef]
- Giommi, P.; Padovani, P. A simplified view of blazars: Contribution to the X-ray and γ-ray extragalactic backgrounds. Mon. Not. R. Astron. Soc. 2015, 450, 2404–2409. [Google Scholar] [CrossRef]
- Ajello, M.; Costamante, L.; Sambruna, R.M.; Gehrels, N.; Chiang, J.; Rau, A.; Escala, A.; Greiner, J.; Tueller, J.; Wall, J.V.; et al. The Evolution of Swift/BAT Blazars and the Origin of the MeV Background. Astrophys. J. 2009, 699, 603–625. [Google Scholar] [CrossRef]
- Ghisellini, G.; Della Ceca, R.; Volonteri, M.; Ghirlanda, G.; Tavecchio, F.; Foschini, L.; Tagliaferri, G.; Haardt, F.; Pareschi, G.; Grindlay, J. Chasing the heaviest black holes of jetted active galactic nuclei. Mon. Not. R. Astron. Soc. 2010, 405, 387–400. [Google Scholar] [CrossRef]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghisellini, G. The Blazar Sequence 2.0. Galaxies 2016, 4, 36. https://doi.org/10.3390/galaxies4040036
Ghisellini G. The Blazar Sequence 2.0. Galaxies. 2016; 4(4):36. https://doi.org/10.3390/galaxies4040036
Chicago/Turabian StyleGhisellini, Gabriele. 2016. "The Blazar Sequence 2.0" Galaxies 4, no. 4: 36. https://doi.org/10.3390/galaxies4040036




