Perspectives on Gravity-Induced Radiative Processes in Astrophysics

Abstract

Single-vertex Feynman diagrams represent the dominant contribution to physical processes, but are frequently forbidden kinematically. This is changed when the particles involved propagate in a gravitational background and acquire an effective mass. Procedures are introduced that allow the calculation of lowest order diagrams, their corresponding transition probabilities, emission powers and spectra to all orders in the metric deviation, for particles of any spin propagating in gravitational fields described by any metric. Physical properties of the “space-time medium” are also discussed. It is shown in particular that a small dissipation term in the particle wave equations can trigger a strong back-reaction that introduces resonances in the radiative process and affects the resulting gravitational background.

1. Introduction

The search for particle processes of astrophysical significance to which gravitation makes a non-negligible contribution is in general difficult, though potentially rewarding. The entire field of gravitational lensing is in fact based on the discovery of one such process in which light interacts with gravity, see e.g. [1]. It is hoped that a number of additional processes will point out new directions of investigation. The search is made more difficult, unfortunately, by the fact that the lowest order Feynman diagrams that represent the dominant contribution to a process are frequently forbidden by kinematics. Consider, for instance, the process in which an incoming massive particle of momentum $p_{\mu }$ and dispersion relation $p_{\mu }{p}^{\mu }=m_1^2$ produces a photon of momentum ${\ell }_{\mu }{\ell }^{\mu }=0$, while the outgoing particle has momentum $p_{\mu }^{\prime }{p}^{\prime \mu }=m^2$. Conservation of energy-momentum requires $p_{\mu }=p_{\mu }^{\prime }+{\ell }_{\mu }$. In the rest frame of p, we have $0=\overrightarrow{p^{\prime }}+\overrightarrow{\ell }$, which gives $\overrightarrow{\ell }=-\overrightarrow{p^{\prime }}$, $p_0=m_1$ and again $m_1=\sqrt{{\ell }^2+m^2}+\ell$. Then, ${(m_1-\ell )}^2={\ell }^2+m^2$ leads to $\ell =(m_1^2-m^2)/2m_1$, which shows that for $m_1=m$, the case considered, we get $\ell =0$, and the process becomes physically meaningless. There are processes, however, in which massive particles emitting a photon are not kinematically forbidden. This is certainly the case when gravitation alters the dispersion relations of at least one of the particles involved [2]. We stress here that even the reduction of a Feynman diagram by a single vertex would result in a cross-section gain of a factor ${(GM/R)}^2$, where M and R are the mass and radius of the gravitational source (units $\text{ℏ}=c=1$).

External gravitational fields have long been known to play the role of a medium, see e.g. [3,4] in the propagation of particles, be these treated classically or according to quantum mechanics. In the latter case, scattering by a Newtonian potential has been the subject of several investigations, [5,6,7], but bremsstrahlung [8,9,10,11], the emission of Cêrenkov radiation [12] and other processes [13] have also been studied in connection with various gravitational sources. As stated above, external gravitational fields do alter the dispersion relations of a particle propagating in a gravitational background at least to the extent that the particle is no longer on shell. It would therefore appear sufficient to somehow solve a wave equation to obtain the desired result. This is done in quantum electrodynamics where the electromagnetic field is however represented by a four-vector, of which only a single component is usually taken into account [14]. The case of gravity, represented by a second rank tensor, is considerably more complicated. Moreover, the theoretical prediction by Mashhoon [15,16,17,18], confirmed by other authors [19,20,21,22], of the existence of a coupling of gravity to spin, requires that the effect of a gravitational field be no longer limited to a single component of the metric. This has become even more pressing since the experimental observation of spin-rotation coupling for photons [23] and neutrons [24] and of other important spin-induced effects at the macroscopic level [25,26,27].

External gravitational fields contribute to the solution of covariant wave equations through a Berry phase [28,29]. This should be expected, because in metric theories of gravitation [30], general relativity in particular, the space parameter of Berry’s theory coincides with space-time. It has been shown that the wave equations for fermions and bosons can be solved exactly to first order in the metric deviation ${\gamma }_{\mu \nu }=g_{\mu \nu }-{\eta }_{\mu \nu }$ for any metric $g_{\mu \nu }$ and that the phases so calculated [20,31,32,33,34] give reliable results in interferometry, gyroscopy [28] and optics [35,36], give the correct Einstein deflection, can be used in the study of neutrino helicity and flavour oscillations [37] and of spin-gravity coupling in general [31,34]. They also reproduce a variety of known effects, as discussed in [32,33,38].

The dispersion relations of a particle propagating in a gravitational background can be derived from the respective covariant wave equations. The gravitational phases mentioned above change, in effect, a particle four-momentum by acting on the wave function of the field-free equations. This result applies equally well to fermions and bosons and can be extended to all orders in ${\gamma }_{\mu \nu }$ [30]. The calculation of even the most elementary Feynman diagrams does require an appropriate treatment when gravitational fields are present. The procedures developed in [2] fill in part of this gap and apply to linearised gravitational, or inertial fields of any type up to intermediate intensities. The present paper focuses on the applications of the procedures outlined in [2] rather than on the individual reactions, though the aim still is to find physical processes capable of leading to potentially observable results. Below, we give examples of processes that can be treated in ways that are similar. Because of the intrinsic resemblance, gravitational bremsstrahlung [39,40,41,42,43] will be added to this category in due time.

Additional interesting possibilities do moreover arise when particles propagate in a gravitational background. In the Conclusions, for instance, we briefly discuss properties of the “space-time medium”, such as dispersion.

2. The Process $\mathbf{P}\to {\mathbf{p}}^{\prime }+\mathbf{\gamma }$

Let us assume, for simplicity, that P in Figure 1 is an incoming fermion and that the photon ℓ and outgoing fermion $p^{\prime }$ are produced on-shell. The solution of the covariant Dirac equation for P, exact to $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$, is [37]:

$$\Psi \left(x\right)=-\frac{1}{2m}\left(-i{\gamma }^{\mu }\left(x\right){\mathcal{D}}_{\mu }-m\right)e^{-i{\Phi }_T}{\Psi }_0\left(x\right)\equiv \widehat{T}{\Psi }_0,$$

(1)

where ${\mathcal{D}}_{\mu }={\nabla }_{\mu }+i{\Gamma }_{\mu }\left(x\right)$, ${\nabla }_{\mu }$ is the covariant derivative, ${\Gamma }_{\mu }\left(x\right)$ the spin connection and the matrices ${\gamma }^{\mu }\left(x\right)$ satisfy the relations $\{{\gamma }^{\mu }\left(x\right),{\gamma }^{\nu }\left(x\right)\}=2g^{\mu \nu }\left(x\right)$. Both ${\Gamma }_{\mu }\left(x\right)$ and ${\gamma }^{\mu }\left(x\right)$ can be obtained from the usual constant Dirac matrices by using the tetrad fields $e_{\widehat{\alpha }}^{\mu }$ and the relations:

$${\gamma }^{\mu }\left(x\right)=e_{\widehat{\alpha }}^{\mu }\left(x\right){\gamma }^{\widehat{\alpha }}=\left({\delta }_{\widehat{\alpha }}^{\mu }+h_{\widehat{\alpha }}^{\mu }\left(x\right)\right){\gamma }^{\widehat{\alpha }},{\Gamma }_{\mu }\left(x\right)=-\frac{1}{4}{\sigma }^{\widehat{\alpha }\widehat{\beta }}{e}_{\widehat{\alpha }}^{\nu }{e}_{\nu \widehat{\beta };\mu },$$

(2)

where ${\sigma }^{\widehat{\alpha }\widehat{\beta }}=\frac{i}{2}[{\gamma }^{\widehat{\alpha }},{\gamma }^{\widehat{\beta }}]$. A semicolon and a comma are also used as alternative ways to indicate covariant and partial derivatives respectively. We use units $\text{ℏ}=c=1$; the signature of ${\eta }_{\mu \nu }$ is $-2,{\Phi }_T={\Phi }_s+{\Phi }_G$,

$${\Phi }_s\left(x\right)=\mathcal{P}{\int }_P^{x}d{z}^{\lambda }{\Gamma }_{\text{λ}}\left(z\right),{\Phi }_G=-\frac{1}{4}{\int }_P^{x}d{z}^{\text{λ}}\left[{\gamma }_{\alpha \text{λ},\beta }\left(z\right)-{\gamma }_{\beta \text{λ},\alpha }\left(z\right)\right]L^{\alpha \beta }\left(z\right)+\frac{1}{2}{\int }_P^{x}d{z}^{\text{λ}}{\gamma }_{\alpha \text{λ}}{k}^{\alpha },$$

(3)

$L^{\alpha \beta }\left(z\right)=(x^{\alpha }-z^{\alpha })k^{\beta }-(x^{\beta }-z^{\beta })k^{\alpha }$ and ${\Psi }_0\left(x\right)$ satisfies the usual, flat space-time Dirac equation. It is convenient to re-write Equation (1) in the form $\Psi \left(x\right)=g\left(x\right)exp(-ipx)u_0\left(\overrightarrow{p}\right)$, where:

$$g\left(x\right)=\frac{1}{2m}\left[\left({\gamma }^{\mu }(p_{\mu }+h_{\mu }^{\widehat{\alpha }}\left(x\right)p_{\widehat{\alpha }}+{\Phi }_{G,\mu }\left(x\right)\right)+m\right]e^{-i{\Phi }_T},$$

(4)

and:

$${\Phi }_{G,\mu }=-\frac{1}{2}{\int }_P^{x}d{z}^{\text{λ}}({\gamma }_{\mu \text{λ},\beta }-{\gamma }_{\beta \text{λ},\mu })p^{\beta }+\frac{1}{2}{\gamma }_{\alpha \mu }{p}^{\alpha }.$$

(5)

We claim that the transition amplitude for the process of Figure 1 can be calculated by introducing the generalized four-momentum:

$$P_{\mu }=p_{\mu }+{\tilde{h}}_{\mu }^{\widehat{\alpha }}{p}_{\widehat{\alpha }}+{\tilde{\Phi }}_{G,\mu }\equiv p_{\mu }+{\tilde{P}}_{\mu },$$

(6)

for the incoming fermion, as Equation (4) itself suggests. The part that contains the gravitational field is indicated by ${\tilde{P}}_{\mu }$. In Equation (6), ${\tilde{h}}_{\mu }^{\widehat{\alpha }}$, ${\tilde{\Phi }}_{G,\mu }$ and ${\tilde{\Phi }}_G$ are quantities that must be calculated, once the metric is known. They are related to the Fourier transforms of the corresponding expressions that appear in Equations (2), (3) and (5). $P_{\mu }$ is not on-shell. In fact:

$$P^{\mu }{P}_{\mu }\equiv m_e^2=m^2+2\left[p^{\mu }{h}_{\mu }^{\widehat{\alpha }}{p}_{\alpha }+p^{\mu }{\Phi }_{G,\mu }\right],$$

(7)

where $p_{\mu }{p}^{\mu }=m^2$, because $p_{\mu }$ is the momentum of the free fermion represented by ${\Psi }_0\left(x\right)$ in Equation (1). The transition amplitude is then:

$$M_{f\to f^{\prime }\gamma }=-iZe{\eta }^{\mu \nu }{\overline{u}}_0\left(\overrightarrow{p^{\prime }}\right){\epsilon }_{\widehat{\mu }\left(\text{λ}\right)}{\gamma }_{\widehat{\nu }}g\left(\right|\overrightarrow{q}\left|\right)u_0\left(\overrightarrow{p}\right),$$

(8)

where $\overrightarrow{q}\equiv \overrightarrow{p}-\overrightarrow{p^{\prime }}-\overrightarrow{\ell }$, ${\epsilon }_{\left(\text{λ}\right)}^{\widehat{\mu }}$ represents the polarization of the photon and $Ze$ is the charge of the fermion. It may be argued that a transition amplitude $M_{f\to f^{\prime }\gamma }^{\prime }$ must be added to Equation (8) at $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$, because the contraction in Equation (8) is, in general, accomplished by means of $g^{\mu \nu }$, and $g\left(x\right)$ contains a part that is independent of ${\gamma }_{\mu \nu }$. The transition amplitude $M^{\prime }$, estimated in [2], is given: by [6]

$$M_{f\to f^{\prime }\gamma }^{\prime }=-iZe{\gamma }^{\mu \nu }\left(\right|\overrightarrow{q}\left|\right){\overline{u}}_0\left(\overrightarrow{p^{\prime }}\right){\epsilon }_{\widehat{\mu }\left(\text{λ}\right)}{\gamma }_{\widehat{\nu }}{u}_0\left(\overrightarrow{p}\right).$$

(9)

However, $M_{f\to f^{\prime }\gamma }^{\prime }$ contains the part $p_{\mu }$ of (6) that comes from ${\Psi }_0$, but not the new part that contains the gravitational contribution due to the propagation of the fermion in the field of the source. To $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$, this process is indistinguishable from bremsstrahlung and is dealt with, more properly, in that context. It will not be discussed further in this work.

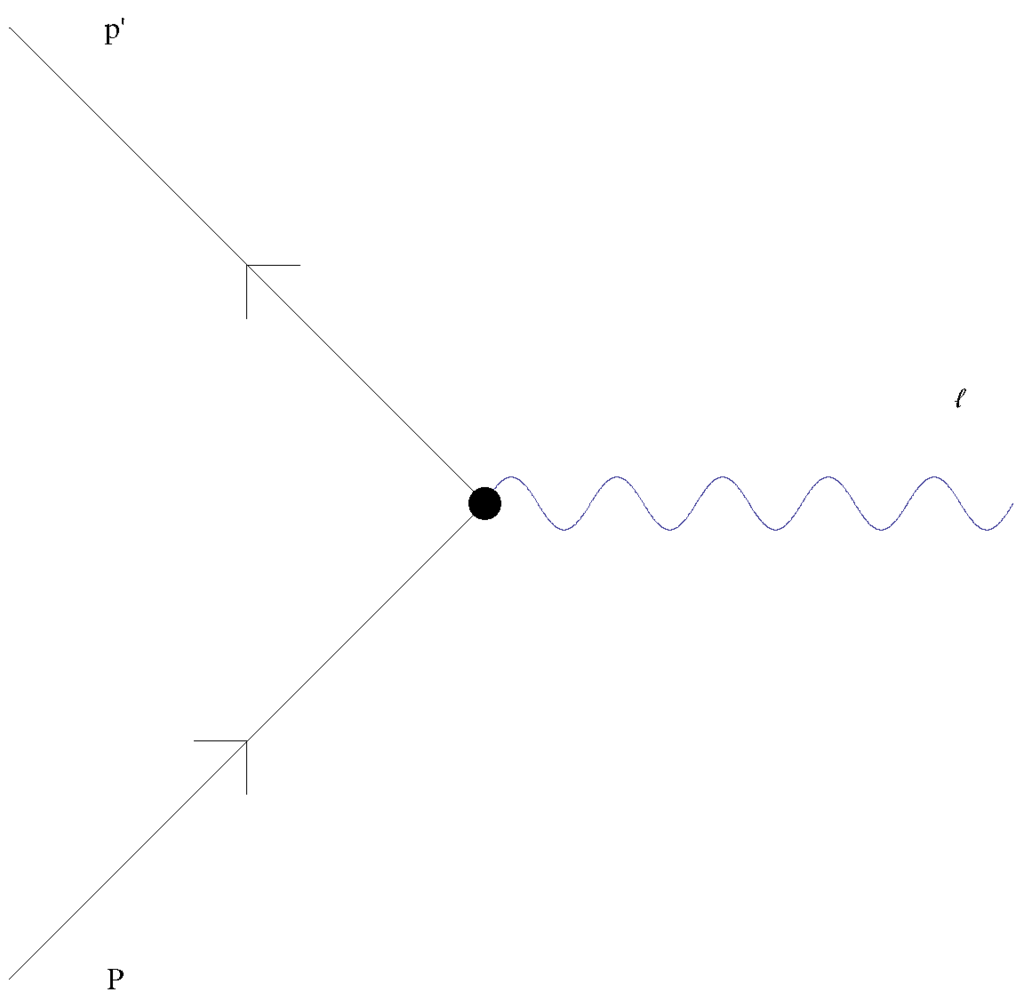
Figure 1. $p^{\prime }$ and ℓ are the outgoing fermion and photon, and P indicates the incoming fermion.

Figure 1. $p^{\prime }$ and ℓ are the outgoing fermion and photon, and P indicates the incoming fermion.

The calculation now requires that a metric be selected.

Let us consider the particular instance of a fermion that is propagating with momentum $p^3\equiv p$, impact parameter $b\ge R$ and $x_2=0$, from $x_3=-\infty$ toward a gravitational source of mass M and radius R placed at the origin and described by the metric ${\gamma }_{00}=2\varphi ,{\gamma }_{ij}=2\varphi {\delta }_{ij}$, where $\varphi =-\frac{GM}{r}$. This metric is frequently used in lensing problems [36,44]. One finds ${\Gamma }_0=-1/2\varphi {,}_j{\sigma }^{0j},{\Gamma }_i=-1/2\varphi {,}_j{\sigma }^{ij}$ and $e_{\widehat{i}}^0=0,e_{\widehat{0}}^0=1-\varphi ,e_{\widehat{k}}^l=\left(1+\varphi \right){\delta }_k^l$. All spin matrices are now expressed in terms of ordinary, constant Dirac matrices. We also assume that the on-shell conditions $p_{\mu }^{\prime }{p}^{\prime \mu }=m^2,{\ell }_{\mu }{\ell }^{\mu }=0$ remain valid. Extension of the calculation to include different particles or higher order gravitational contributions to $p^{\prime },\ell$ and Equation (1) can be derived to all orders in ${\gamma }_{\mu \nu }$ [30]. The Fourier transforms of the quantities that appear in Equation (4) must now be calculated. We obtain:

$$h_0^{\widehat{\alpha }}\left(q\right)p_{\alpha }=8{\pi }^2\delta \left(q_0\right)\delta \left(q_x\right)\delta \left(q_y\right)p_{0}GM{K}_0\left(b{q}_z\right),h_3^{\widehat{\alpha }}\left(q\right)p_{\alpha }=8{\pi }^2\delta \left(q_0\right)\delta \left(q_x\right)\delta \left(q_y\right)pGM{K}_0\left(b{q}_z\right)$$

(10)

$${\Phi }_{G,2}\left(q\right)=0,{\Phi }_{G,3}\left(q\right)=-8{\pi }^2\delta \left(q_0\right)\delta \left(q_x\right)\delta \left(q_y\right)\left(\frac{p_0^2}{p}+p\right)GM{K}_0\left(b{q}_z\right)$$

(11)

Four-momentum conservation to zeroth order only is required because Equations (10) and (11) are already of $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$. Though the gravitational field selected above is stationary, energy conservation must be introduced, because the energy contribution of the field is contained in the generalized momentum of P. We further approximate the Bessel function $K_0\left(b{q}_z\right)\simeq \sqrt{\pi /2b{q}_z}{e}^{-b{q}_z}[1-1/8b{q}_z+\dots ]$, itself a distribution, by $K_0\left(b{q}_z\right)/\pi \simeq 2\pi \delta \left(b{q}_z\right)$ and eliminate ${\delta }^4\left(q\right)$ from Equations (10) and (11). Conservation of energy-momentum will reappear as a factor ${\left(2\pi \right)}^4{\delta }^4\left(q\right)$ in the expression for the radiated power W defined below. By removing ${\left(2\pi \right)}^4{\delta }^4\left(q\right)$ from $h_{\mu }^{\widehat{\alpha }}$ and ${\Phi }_{G,\mu }\left(q\right)$, we obtain ${\tilde{h}}_{\mu }^{\widehat{\alpha }}$ and ${\tilde{\Phi }}_{G,\mu }$ of Equation (6). We find:

$$P_0\simeq p_0+\frac{GM}{b}{p}_0=p_0+{\tilde{P}}_0,P_1\simeq \frac{GM}{b}\left(\frac{p_0^2}{p}+p\right)={\tilde{P}}_1,P_2=0,P^3\equiv P=p-\frac{GM}{b}p=p+\tilde{P}$$

(12)

We calculate the power radiated as photons in the process of Figure 1 according to the formula, see e.g. [45]:

$$W=\frac{1}{8{\left(2\pi \right)}^2}\int {\delta }^4(P-p^{\prime }-\ell )\frac{{\left|M\right|}^2}{P{p}_0^{\prime }}{d}^3{p}^{\prime }{d}^3\ell$$

(13)

There are two ways to calculate $|M_{f\to f^{\prime }\gamma }{|}^2$. In the first one, we replace $p_{\alpha }$ with $P_{\alpha }$ in the field-free (${\gamma }_{\mu \nu }=0$) expression given by ${\Sigma \left|M\right|}^2=Z^2{e}^2[-4m^2\left(p_{\alpha }^{\prime }{p}^{\alpha }\right)+8\left(p_{\alpha }{p}^{\alpha }\right)]$. The gravitational contribution to M then appears in ${\tilde{P}}_{\mu }$ exclusively. We also remove the terms $-32m^2\left(p_{\alpha }^{\prime }{p}^{\alpha }\right)+64m^2$ that do not contain gravitational contributions and therefore refer to the kinematically-forbidden transition. This yields, to $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$, the expression:

$$\Sigma |M_{f\to f^{\prime }\gamma }{|}^2=Z^2{e}^2\left[-4\left(p_{\alpha }^{\prime }{\tilde{P}}^{\alpha }\right)+8\left(p_{\alpha }{\tilde{P}}^{\alpha }\right)\right]$$

(14)

In a second, alternate approach, we calculate ${\left|M\right|}^2$ directly (${\gamma }_{\mu \nu }\ne 0$) from Equation (8). By summing over final spins and averaging over initial spins and polarizations, we obtain:

$$\Sigma |M_{f\to f^{\prime }\gamma }{|}^2=\frac{Z^2{e}^2}{2{\left(2m\right)}^2}Tr\left\{({\mathbf{p}}^{\prime }+m){\gamma }_{\beta }\left[\left(\mathbf{p}+\tilde{\mathbf{P}}+m\right)\left({(\mathbf{p}+m)}^2+(\mathbf{p}+m){\tilde{\mathbf{P}}}^{*}+H(\mathbf{p}+m)\right)\right]{\gamma }^{\beta }\right\}$$

(15)

where $\mathbf{a}\equiv {\gamma }^{\mu }{a}_{\mu }$ and $H=p^0/p^3\varphi ({\gamma }^3{p}^0-{\gamma }^0{p}^3)+(p^0/p^3{\gamma }^1{p}^0-{\gamma }^1{p}^3)4GM{K}_1\left(b{q}_z\right)$. On carrying out the traces of the Dirac matrices, the contribution from H vanishes. By further eliminating from ${\left|M\right|}^2$ the terms that refer to the kinematically-forbidden transition, we again find Equation (14). This supports our claim that the generalized momentum $P_{\mu }$ introduced in Equation (6) leads to the correct value of the transition probability by the substitution of $p_{\mu }$ with $P_{\mu }$ in the field-free expression. The integration over $d^3{p}^{\prime }$ in Equation (13) is performed by means of the identity:

$$\int \frac{d^3{p}^{\prime }}{2p_0^{\prime }}=\int d^4{p}^{\prime }\Theta \left(p_0^{\prime }\right)\delta (p^{\prime 2}-m^2)$$

(16)

while that over θ, the angle between $\overrightarrow{P}$ and $\overrightarrow{\ell }$, can be carried out by writing the on-shell condition for $p^{\prime }$ in the form:

$$\delta \left(2\right|\overrightarrow{P}\left|\right|\overrightarrow{\ell }|cos\theta -P^{\alpha }{P}_{\alpha }+2P_0{\ell }_0+m^2)$$

(17)

We find:

$$W=\frac{Z^2{e}^2}{4\pi }\left(\frac{GM}{b}\right)\frac{p_0^2+p^2}{p^2}{\ell }^2$$

(18)

The radiation spectrum is given by:

$$\frac{dW}{d\ell }=\frac{Z^2{e}^2\ell }{2\pi }\left(\frac{GM}{b}\right)\frac{p_0^2+p^2}{p^2}$$

(19)

Equation (17) and the condition:

$$|cos\theta |\approx \frac{1}{2p\ell \sqrt{1-\frac{2GM}{b}}}\left\{\frac{2GM}{b}\left(p_0^2+p^2\right)-2{\ell }^2{p}_0\left(1+\frac{GM}{b}\right)\right\}\le 1$$

(20)

lead, for $p>m$, to the inequality $p(GM/b)<\ell \le p$. It then follows that the hardest photons are emitted in the backward direction with energy $\ell \sim p$ and power:

$$W_{p>m}\sim \frac{2Z^2{e}^2{p}^2}{8\pi }\left(\frac{GM}{b}\right)$$

(21)

which would obviously take its highest values in the neighbourhood of a very compact source.

For $p<m$, the inequality Equation (20) is satisfied for $\ell (Gm/b)\ge m(1-p/m)$, and we also find:

$$W_{p<m}\sim \frac{Z^2{e}^2}{4\pi }\left(\frac{GM}{b}\right)\frac{m^2{\ell }^2}{p^2}\left(1+\frac{2p^2}{m^2}\right)$$

(22)

which diverges for small values of p. This infrared divergence is well known and arises as a consequence of the finite energy resolution $\Delta ϵ$ of the outgoing fermion. The process, as calculated, is, in fact, indistinguishable from that in which massless particles with energy $\le \Delta ϵ$ are also emitted and from processes in which vertex corrections are present (virtual massless particles emitted and reabsorbed by the external lines of Figure 1). When these additional diagrams are calculated, all infrared divergences disappear [46]. In the particular case at hand, p in Equation (22) can be simply replaced by $GM{p}_0/b$. Below this value, the process is not kinematically allowed.

The process discussed in this section may be considered as the decay of a fermion of effective mass $P_{\alpha }{P}^{\alpha }$ into a photon and a fermion of mass m with a lifetime $\tau =m/W$, which is indeed small. Quantitatively, for electrons with $p\sim 1GeV$, $\ell \sim p$, in the neighbourhood of a canonical neutron star, we find $\tau \sim 3·{10}^{-19}s$.

3. The Process $\mathbf{\gamma }\to \mathbf{f}+\overline{\mathbf{f}}$

Using the replacements $\ell \to -L$ and $P\to -q$ in Figure 1, we can calculate the process by which a photon produces a fermion f of momentum $p^{\prime }$ and an anti-fermion $\overline{f}$ of momentum q after propagating in a gravitational field. In addition $Z^2{e}^2\to -Z^2{e}^2$, because of the presence of the antiparticle. Conservation of energy-momentum now requires that $L_{\mu }=p_{\mu }^{\prime }+q_{\mu }$, while the dispersion relations are $p_{\mu }^{\prime }{p}^{\prime \mu }=m^2,q_{\alpha }{q}^{\alpha }=m^2$ and the generalized photon momentum is $L_{\sigma }={\ell }_{\sigma }+{\Phi }_{G,\sigma }$. In the centre of mass frame of the $(f,\overline{f})$-system, we now have $\overrightarrow{p^{\prime }}+\overrightarrow{q}=\overrightarrow{L}=0$ and also $L_i={\ell }_i+{\Phi }_{G,i}=0$. This and ${\ell }_{\alpha }{\ell }^{\alpha }=0$ again show that if the effect of the gravitational field vanished (${\Phi }_G=0$), we would re-obtain the meaningless result ${\ell }_0=\overrightarrow{\ell }=0$. It is therefore the presence of the gravitational field that enables the process. The effect of the gravitational field on the polarization of the photon is given by $E_{\sigma }={\epsilon }_{\sigma }+\frac{i}{2}({\gamma }_{\alpha \sigma ,\beta }-{\gamma }_{\beta \sigma ,\alpha })S^{\alpha \beta }+\frac{i}{2}{\gamma }_{\alpha \beta ,\sigma }{T}^{\alpha \beta }$, where the matrices $S^{\alpha \beta }$ and $T^{\alpha \beta }$ are given in [36] and act on the matrix $a_{\alpha }$. The contributions of these terms reduce to $\frac{1}{2}(a_1^{+}{a}_2-a_2^{+}{a}_1)({\gamma }_{1\sigma ,2}-{\gamma }_{2\sigma ,1})$. In the approximation $K_0\left(b\kappa \right)/\pi \to \left(2\pi \right)\delta \left(b\kappa \right)$ to be used below, the derivatives of ${\gamma }_{\mu \nu }$ behave as $\left(b\kappa \right)\delta \left(b\kappa \right)=0$, and the whole contribution of $S^{\alpha \beta }$ and $T^{\alpha \beta }$ to the photon polarization can be neglected. We assume that ${\ell }_1={\ell }_2=0,{\ell }_3\equiv \ell$ and use the following result:

$${\Phi }_{G,1}=\frac{1}{2}{\int }_{-\infty }^{z}d{z}^0{\gamma }_{00,1}\ell +\frac{1}{2}{\int }_{-\infty }^{z}d{z}^3{\gamma }_{33,1}\ell =2GM\frac{\ell }{b}(1+\frac{z}{\sqrt{b^2+z^2}})$$

which, for $r\sim b$, becomes ${\Phi }_{G,1}\sim 2GM\ell /b$. Similarly, we find:

$${\Phi }_{G,3}=-\frac{GM\ell }{\sqrt{b^2+z^2}}-GM\ell {\int }_{-\infty }^{z}dz\frac{z}{{(b^2+z^2)}^3/2}=-\frac{2GM\ell }{\sqrt{b^2+z^2}}\sim -\frac{2GM}{b}\ell$$

in the same approximation. Factorizing $\left(2\pi \right)\delta \left(b\kappa \right)$, we find the generalized momenta $L_0=\ell ,L_1\sim 2GM\ell /b,L_2=0,L_3=\ell (1-2GM/b)$. By applying the substitutions indicated above, we can derive the transition amplitude for the process $\gamma \to f+\overline{f}$:

$$\Sigma |M_{\gamma \to f\overline{f}}^2|=Z^2{e}^2\left[4\left(p_{\alpha }^{\prime }{q}^{\alpha }\right)+8\left(q_{\alpha }{q}^{\alpha }\right)\right]$$

(23)

and the rate at which energy is radiated as an anti-fermion:

$$W_1=\frac{1}{8{\left(2\pi \right)}^2}\int \frac{d^3{p}^{\prime }{d}^{3}q}{q_0{p}_0^{\prime }{L}_0}{\delta }^4(q+p^{\prime }-L)\Sigma \left|M_{\gamma \to f\overline{f}}^2\right|q_0$$

(24)

The integration over $d^3{p}^{\prime }$ can be carried out by means of the identity Equation (16), and the on-shell condition for $p^{\prime }$ becomes:

$$\delta \left((L_{\alpha }-q_{\alpha }\right)(L^{\alpha }-q^{\alpha })-m^2)=\delta (L_{\alpha }{L}^{\alpha }-2L_0{q}^0+2|\overrightarrow{L}\left|\right|\overrightarrow{q}|cos{\theta }_1)$$

(25)

Integrating over ${\theta }_1$, the angle between $\overrightarrow{q}$ and $\overrightarrow{L}$, we find:

$$W_1=\frac{Z^2{e}^2}{4\pi }\int dq\frac{q}{L_0\left|\overrightarrow{L}\right|}\left(\frac{1}{2}{L}_{\alpha }{L}^{\alpha }+m^2\right)$$

(26)

We also find $L_{\alpha }{L}^{\alpha }\simeq 2{\ell }^{\alpha }{\Phi }_{G,\alpha }\sim -2GM\ell /b$ after replacing $K_0\left(b\kappa \right)/\pi$ with $\left(2\pi \right)\delta \left(b\kappa \right)$, factorizing $\left(2\pi \right)\delta \left(b\kappa \right)$ and writing $1/|\overrightarrow{L}|\simeq (1+GM/b)/\ell$. We finally obtain:

$$W_1=\frac{Z^2{e}^2}{8\pi }\left(\frac{GM}{b}\right)\frac{m^2{q}^2}{{\ell }^2}\left(1-\frac{{\ell }^2}{m^2}\right)$$

(27)

from which $\frac{d{W}_1}{dq}$ can be immediately obtained. We also have $\Theta (L_0-q_0)=\ell -q_0>0$, while $|cos{\theta }_1|\le 1$ leads to $0\le \frac{4GM\ell }{b}+2q_0$, which is always satisfied in the interval $\pi /2\le {\theta }_1\le \pi$.

4. The Process $\mathbf{f}+\overline{\mathbf{f}}\to \mathbf{\gamma }$

We now consider the process in which a fermion-antifermion couple in the initial state annihilates into a photon. We assume that the fermion that propagates in the gravitational background has generalized momentum P. By conservation of energy-momentum, we then have $P_{\mu }+q_{\mu }={\ell }_{\mu }$, and the generalized momentum is given by $P_0=p_0+p_{0}GM/b\equiv p_0+\widetilde{P_0},P_1=P_2=0,P_3=p_3(1+GM/b)-p_{0}GM/b\equiv p_3+\widetilde{P_3}$. The transition amplitude becomes:

$${\Sigma \left|M\right|}_{f\overline{f}\to \gamma }^2=Z^2{e}^2\left[4\left(q_{\alpha }\widetilde{P^{\alpha }}\right)+8\left(p_{\alpha }\widetilde{P^{\alpha }}\right)\right]$$

(28)

from which all terms referring to the kinematically-forbidden transition have been eliminated. We also find:

$$W_2=\frac{Z^2{e}^2}{{\left(2\pi \right)}^2}\int \frac{d^{3}q{d}^3\ell }{q_0{P}_0}{\delta }^4(P+q-\ell )\left[4\left(q_{\alpha }\widetilde{P^{\alpha }}\right)+8\left(p_{\alpha }\widetilde{P^{\alpha }}\right)\right]$$

(29)

The integration over $d^{3}q$ can be easily performed by using the identity $\int \frac{d^{3}q}{2q_0}=\int d^{4}q\Theta \left(q_0\right)\delta (q^2-m^2)$. We find:

$$W_2={\left(\frac{Ze}{2\pi }\right)}^2\int d^3\ell \Theta (P_0-{\ell }_0)\frac{1}{P_0}\delta \left((P_{\alpha }-{\ell }_{\alpha })(P^{\alpha }-{\ell }^{\alpha })-m^2\right)\left[p_{\alpha }({\ell }^{\alpha }-P^{\alpha })+2\left(p_{\alpha }{P}^{\alpha }\right)\right]$$

(30)

The on-shell condition for q becomes:

$$\delta (q^2-m^2)=\delta \left((P_{\alpha }-{\ell }_{\alpha })(P^{\alpha }-{\ell }^{\alpha })-m^2\right)=\frac{1}{2\ell |\overrightarrow{P}|}\delta \left(cos{\theta }_2+\frac{P_{\alpha }{P}^{\alpha }-2{\ell }_0{P}_0-m^2}{2\ell |\overrightarrow{P}|}\right)$$

(31)

and the integration over ${\theta }_2$ then yields:

$$W_2=\frac{Z^2{e}^2}{4\pi }\frac{GM}{b}\int d\ell \frac{\ell }{P_0\left|\overrightarrow{P}\right|}\left(p_3{p}_0+m^2\right)$$

(32)

In order to carry out the integration over ℓ, we first calculate:

$$\frac{1}{P_0\left|\overrightarrow{P}\right|}\simeq \frac{1}{p_3{p}_0}\left[1-\frac{1}{2}\left(\frac{2GM}{b}-\frac{p_0}{p_3}\frac{GM}{b}\right)\right]$$

(33)

which must be substituted in Equation (32). The integration over ℓ gives:

$$W_2=\frac{Z^2{e}^2}{8\pi }\left(\frac{GM}{b}\right)\left[1-m^2\left(\frac{1}{p_3{p}_0}-\frac{1}{p_3^2}\right)\right]{\ell }^2$$

(34)

from which we obtain the radiation spectrum:

$$\frac{d{W}_2}{d\ell }=\frac{Z^2{e}^2}{4\pi }\left(\frac{GM}{b}\right)\left[1-m^2\left(\frac{1}{p_3{p}_0}-\frac{1}{p_3^2}\right)\right]\ell$$

(35)

The condition $|cos{\theta }_2|\le 1$ then requires that:

$$\frac{(m^2+p_3{p}_0)\frac{GM}{b}}{p_0+p_3+\frac{p_0^2}{p_3}\frac{GM}{b}}\le \ell \le \frac{(m^2+p_3{p}_0)\frac{GM}{b}}{p_0-p_3+\frac{p_0^2}{p_3}\frac{GM}{b}}$$

(36)

Notice that the process calculated in this section is not the time-reverse of $\gamma \to f+\overline{f}$, because in the latter process, gravitation is assumed to act on the incoming photon line and not on the outgoing fermion line.

5. Conclusions

External gravitational fields in radiative processes can be included in the calculation of a transition probability by simply replacing the momentum $p_{\mu }$ of a particle with its generalized version $P_{\mu }$ in the corresponding expression for the zero-field process. The examples given involve spin-$\frac{1}{2}$ and spin-1 particles, but the procedure can be extended to any spin. An essential point here is that the dispersion relations are altered by the external gravitational field and can be calculated if the corresponding wave equations can be solved to $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$ or higher [20,34,35,36,37]. It follows, in particular, that kinematically-forbidden processes similar to that of Figure 1 become physical, and their transition probabilities can be determined. The calculation of the gravitational contributions are greatly simplified and can be extended to higher order in ${\gamma }_{\mu \nu }$. The applications are not confined to fields of a Newtonian type, but extend to any gravitational field. In this respect, the procedure presented goes beyond the results that apply to external electromagnetic potentials [14], not only because the metric has in general ten components rather than just four, but also because time-independence is not a requirement.

The transition amplitudes derived are $\mathcal{O}\left({\gamma }_{\mu \nu }\right)$ to leading order and can therefore be considerably larger than those normally studied in the literature. The examples given are limited to a single type of physically-relevant metric, and we cannot conclude that the resulting spectra are general and can be used to identify the processes. The actual determination of the spectra requires the use of metrics specific to the problems studied. However, the results suggest that particle processes, like bremsstrahlung, Čerenkov radiation, or positron production in the neighbourhood of compact astrophysical objects, or in cosmology, need to be reconsidered.

Space-time has so far been treated as a linear optical medium, though it is by no means clear what its ultimate properties will be as a result of quantum gravity. It is not in particular known whether its index of refraction will remain unaltered in response to high intensity fluxes of particles. There is scope for research on this and other properties of space-time.

Our final considerations regard the back-reaction that physical processes may have on the gravitational background. We show below that the back reaction is not always negligible and provide an example of how a very small disturbance in the wave equation can grow rapidly and alter the background gravitational field.

Equation (1) requires that ${\Psi }_0\left(x\right)$ be a solution of the field-free Dirac equation and, of course, of the equation $({\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }+m^2){\Psi }_0\left(x\right)=0$. The approximation procedure still holds true, however, when ${\Psi }_0\left(x\right)$ satisfies more general equations [28,32]. With the addition of a dissipation term, the equation for ${\Psi }_0$ becomes:

$$\left({\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }+m^2-2m\sigma {\partial }_0\right){\Psi }_0=0$$

(37)

where we take $\sigma =\alpha |\langle {\Psi }_0\left|\widehat{T}\right|{\Psi }_0{\rangle |}^2=\alpha {\left(\frac{m}{p_0}\frac{GM}{2b}\right)}^2$ [37] and α is a dimensionless, arbitrary parameter, $0\le \alpha \le 1$, that reflects the coupling strength of the dissipation term. When we substitute ${\Psi }_0\left(x\right)=exp\left(m\sigma x_0\right){\varphi }_0\left(x\right)$ into Equation (37), we obtain:

$$\left[{\partial }_0^2-{\partial }_z^2+m^2(1-{\sigma }^2)\right]{\varphi }_0\left(x\right)=0$$

(38)

An example of a problem with a similar behaviour is offered by a fluid heated from below. For small temperature gradients, the fluid conducts the heat, but as the gradient increases, conduction is not sufficient to lead the heat away, so the fluid starts to convect. In realistic problems, the exponential growth of ${\Psi }_0$ does not continue indefinitely, but is restricted at times $x_0>\tau \equiv 1/m\sigma$ by nonlinearities or dispersive effects that may have been initially neglected.

The effect of the new solution ${\Psi }_0$ on W can be found as follows. We first neglect the change $m\to m\sqrt{1-{\sigma }^2}$ in W because, in general, $\sigma <1$. Setting $m=1$ for simplicity, the effect of the exponentially increasing term on Equation (13) then amounts to the transformations $\delta (P_0-p_0^{\prime }-{\ell }_0)\to \delta (-2i\sigma +P_0-p_0^{\prime }-{\ell }_0)$ and $\frac{1}{p^2}\to \frac{1}{{\beta }^2{(p_0-2i\sigma )}^2}\simeq \frac{p_0^2}{{\beta }^2[{(p_0^2-4{\sigma }^2)}^2+4p_0^2{\sigma }^2]}$, where we have used the relation $\beta =p/p_0$. W has therefore a resonance at $p_0=2\sigma$ of width $4{\sigma }^2$. Over times $x_0>\tau ={\left(\alpha m\right)}^{-1}{(m/p_0)}^{-2}{(GM/2b)}^{-2}$ GeV${}^{-1}$, $\Psi =\widehat{T}{\Psi }_0$ increases exponentially until the compensating mechanisms mentioned above kick in; for a proton of energy $p_0\sim 10$ GeV in the field of a canonical neutron star $\tau \sim 3.5\times {10}^{-21}{\alpha }^{-1}$ s. Considerably higher values of τ can, of course, be obtained for the lighter fermions. As Ψ grows, so does the energy momentum tensor associated with it and the gravitational field it generates, altering, in the process, the gravitational background.