Mass Distribution in Rotating Thin-Disk Galaxies According to Newtonian Dynamics

Abstract

An accurate computational method is presented for determining the mass distribution in a mature spiral galaxy from a given rotation curve by applying Newtonian dynamics for an axisymmetrically rotating thin disk of finite size with or without a central spherical bulge. The governing integral equation for mass distribution is transformed via a boundary-element method into a linear algebra matrix equation that can be solved numerically for rotation curves with a wide range of shapes. To illustrate the effectiveness of this computational method, mass distributions in several mature spiral galaxies are determined from their measured rotation curves. All the surface mass density profiles predicted by our model exhibit approximately a common exponential law of decay, quantitatively consistent with the observed surface brightness distributions. When a central spherical bulge is present, the mass distribution in the galaxy is altered in such a way that the periphery mass density is reduced, while more mass appears toward the galactic center. By extending the computational domain beyond the galactic edge, we can determine the rotation velocity outside the cut-off radius, which appears to continuously decrease and to gradually approach the Keplerian rotation velocity out over twice the cut-off radius. An examination of circular orbit stability suggests that galaxies with flat or rising rotation velocities are more stable than those with declining rotation velocities especially in the region near the galactic edge. Our results demonstrate the fact that Newtonian dynamics can be adequate for describing the observed rotation behavior of mature spiral galaxies.

1. Introduction

Without direct means for accurate measurement, mass distribution in galaxies—gravitationally bound assemblies of (${10}^5$–${10}^{12}$) stars—can only be inferred from the observable information according to the known physical laws. In astronomy, the observable information is usually carried by electromagnetic radiation—the light—emitted from the visible objects. The light can be analyzed to provide information about the emitting objects, such as their material constituents, surface temperature, distance, moving velocity, etc. Observations have shown that many (mature spiral) galaxies share a common structure, with the visible matter distributed in a flat thin disk, rotating about their center of mass in nearly circular orbits (cf. the book of Binney and Tremaine [1]). The speed of the circular motion of objects in galaxies can be determined from the Doppler shift of light, and its plot against the galactocentric distance is called the rotation curve or circular speed curve. The measured rotation curve has been considered to provide the most reliable information for deriving the mass distribution in thin-disk galaxies [2,3].

Another independent means for estimating mass distribution is based on the luminosity measurements of the galactic surface-brightness profile by assuming a given (usually constant) mass-to-light ratio, the validity of which seems to be rather debatable, especially when it comes to the quantitative calculation of mass distribution. The darker edge against a brighter bulge background often seen from the edge-on view of disk galaxies suggests a varying mass-to-light ratio, inconsistent with the constant mass-to-light ratio assumption. The findings of Herrmann and Ciardullo [4] show that the value of the mass-to-light ratio of the M33 galactic disk can indeed increase by more than a factor of five over a radial distance of six times the disk scale length. Thus, discrepancies often arise between the observed rotation curves and that predicted from the mass distributions following the surface-brightness profile based on Newtonian dynamics, leading to the so-called “galaxy rotation problem” still haunting the astrophysical community to the present day (cf. the book of Freeman and McNamara [5]). Such discrepancies have often been considered as evidence of the luminous disk embedded in a more extensive halo of dark matter [6,7]. With the concept of dark matter, a constant mass-to-light ratio is usually assigned to the luminous disk, and various parameters are determined for an assumed dark matter halo to best fit the observed rotation curve. However, the values of the mass-to-light ratio for the luminous matter are uncertain, and the fitted functional form for the dark matter halo is often chosen arbitrarily [8,9]. On the other hand, Palunas and Williams [10] demonstrated that for many galaxies, the rotation curves observed in the optical disk can be successfully described with the luminous matter having distinct (constant) values of the mass-to-light ratio without including the dark matter halo. Thus, whether a dark matter halo exists or whether it is needed for describing rotating galaxies becomes questionable. The mathematical models involving the dark matter halo have at best been still poorly constrained. Actually, if not being relied on for quantitatively calculating the mass distribution, the typically exponential decaying profile of observed surface brightness in many galaxies [1,11] suggests a likely general structure of decreasing (surface) mass density with the galactocentric distance, which appears qualitatively consistent with that predicted from the measured rotation curves according to Newtonian dynamics for rotating thin-disk galaxies [12].

Given a measured rotation curve, to derive the mass distribution in a thin-disk galaxy requires physical laws that can make the connection between the kinematic behavior and the locations of matter. For galactic dynamics, the best-known, well-established physical laws are Newton’s laws of motion and Newton’s law of gravity [1]. Thus, we focus on the mass distribution in rotating thin-disk galaxies determined from measured rotation curves according to Newtonian dynamics. Although theoretically well-established, the actual computational efforts in applying Newtonian dynamics to thin-disk galaxies appeared to be much more involved than that for a gravitational system with spherical symmetry, such as the solar system. Serious efforts were made for integrating the Poisson equation with mass sources distributed on a disk, as summarized by Binney and Tremaine [1], Bratek, Jalocha and Kutschera [13] and Feng and Gallo [12], among others. The solution directly obtained from such efforts is usually the (Newtonian) gravitational potential, which can yield the gravitational force by taking its gradient. In an axisymmetric disk rotating at steady state, the gravitational force (as the radial gradient of gravitational potential) is expected to equate to the centrifugal force, due to the rotation at every point.

Unlike the spherically symmetric mass distribution that generates the local gravitational force at a given radial position only depending upon the amount of mass within that radius, the gravitational force due to a thin-disk mass distribution can be influenced by matter, both inside and outside that radius. Thus, the mass distribution in a thin-disk galaxy cannot be determined simply by applying Keplerian dynamics, which relates the mass within a radial position to the local rotation speed. In principle, the rotation speed at a radial position is mathematically related to the mass distribution in the entire galactic disk. The fact that the brightness in disk galaxies typically decreases exponentially with radial distance indicates a practical limitation of rotation curve measurements: the detectable signal must terminate at a finite radial position: the so-called “cut-off radius”. All measured rotation curves terminate at their cut-off radii, although sometimes, the cut-off radii may move further out with new signal detection and processing technology development.

Among several possible approaches, using Bessel functions has been the method of choice for many authors [2,11,13,14,15,16,17], probably due to the convenience in theoretical derivations. The mathematical formulations with Bessel functions typically contain integrals extending to infinity, which has become the major practical difficulty when working with rotation curves that always terminate at finite cut-off radii. The part of rotation velocity outside the cut-off radius, although not observable, must be constructed based on various assumptions, to complete the mathematical formulation (as discussed by Nordsieck [14], Bosma [18], Jalocha, Bratek and Kutschera [17], Bratek, Jalocha and Kutschera [13]).

To avoid the need of the fictitious part of the rotation curve outside the cut-off radius, an integral equation for a rotating thin-disk galaxy with its edge coinciding with the cut-off radius of the rotation curve can be formulated according to Newtonian dynamics, consisting of Green’s function in terms of the complete elliptic integrals of the first kind and second kind [12]. With appropriate mathematical treatments, the apparent numerical difficulties associated with singularities in elliptic integrals can be completely removed when carefully evaluating the mathematical limit. To enable dealing with arbitrary forms of rotation curves and mass density distributions, the boundary element method for solving integral equations is adopted here using compactly supported basis functions instead of that extending to infinity, like Bessel functions. Hence, the finite physical problem domain for a disk with the edge ending at a finite radius can be conveniently considered by solving a linear algebra matrix problem. Here, in our treatment, we take the cut-off radius as the galactic disk edge outside of which the mass density becomes negligible. Philosophically, where there is matter, there must be a detectable signal; therefore, no detectable signal must indicate that there is no matter. Thus, by “cut-off radius”, we mean the theoretical cut-off radius, which may not be the same as that currently measured in the rotation curve, due to technological limitations, but it will be approached with the continuous improvement of technology.

Following Feng and Gallo [12], in the present work, we non-dimensionalize the governing equations, such that a dimensionless parameter, which we call the “galactic rotation number”, appears in the force balance (or centrifugal-equilibrium) equation, representing the ratio of centrifugal force and gravitational force. Together with a constraint equation for mass conservation, the value of this galactic rotation number can be determined as part of the numerical solution. The value of the galactic rotation number can be used for calculating the total galactic mass in the disk from the measured galactic (cut-off) radius and characteristic rotation velocity. While Feng and Gallo [12] focused mainly on illustrating the computational method with a few idealized rotation curves, herewith, we apply this method to the in-depth evaluation of the realistic rotation curves available in the open literature (e.g., the Sofue website [19], de Blok et al. [20], etc.) We also extend our method to including the spherical central core and bulge, to further applications, such as for determining rotation velocity beyond the cut-off radius, and so on and so forth.

2. Mathematical Formulation and Solution Method

For the convenience of mathematical treatment, a rotating galaxy is represented by a self-gravitating continuum of axisymmetrically distributed mass in a circular disk with an edge at finite radius $R_g$ (beyond which we expect mass density to diminish precipitously to the inter-galactic level, having inconsequential gravitational effect on the galactic disk dynamics). Without loss of generality, we consider the thin disk having a uniform thickness (h) with a variable mass density (ρ) as a function of radial distance (r) in galactocentric cylindrical polar coordinates. In the situation of the thin disk, the vertical distribution of mass (in the z-direction) is expected to contribute an inconsequential dynamical effect, especially as the disk thickness becomes infinitesimal. In mathematical terms, the meaningful variable here is actually the surface mass density $\sigma (r)\equiv \rho (r)h$. Here, we choose to use the bulk density, $\rho (r)$, for its consistency with the common physical perception of a thin disk with nonzero thickness h.

For steady rotation, there must be a balance between the gravitational force and centrifugal force at every point in the galactic disk. If the force density on a test mass at (r, $\theta =0$) generated by the gravitational attraction due to the summation (or integration) of a distributed mass density, $\rho (\widehat{r})$, at a position described by the variables of integration ($\widehat{r}$, $\widehat{\theta }$) is expressed as an integral over the entire disk, with the distance between (r, $\theta =0$) and ($\widehat{r}$, $\widehat{\theta }$) given by ${({\widehat{r}}^2+r^2-2\widehat{r}rcos\widehat{\theta })}^{1/2}$ and the vector projection given by $(\widehat{r}cos\widehat{\theta }-r)$, the equation of force balance in a rotating thin disk can be written as (according to Newton’s laws):

$$\begin{array}{c}\hfill {\int }_0^1\left[{\int }_0^{2\pi }\frac{(\widehat{r}cos\widehat{\theta }-r)d\widehat{\theta }}{{({\widehat{r}}^2+r^2-2\widehat{r}rcos\widehat{\theta })}^{3/2}}\right]\rho (\widehat{r})h\widehat{r}d\widehat{r}+A\frac{V{(r)}^2}{r}=0\end{array}$$

(1)

where all the variables are made dimensionless by measuring lengths (e.g., r, $\widehat{r}$, h) in units of the outermost galactic radius, $R_g$, the disk mass density (ρ) in units of $M_d/R_g^3$, with $M_d$ denoting the total mass in the galactic disk, and rotation velocities [$V(r)$] in units of the a characteristic galactic rotational velocity, $V_0$ (usually defined according to the rotation curve of interest). The disk thickness, h, is assumed to be constant and small in comparison with $R_g$. The numerical results for surface mass density, $\rho (r)h$, are expected to be insensitive to the exact value of $h/R_g$, as long as it remains small. There is no difference in terms of the physical meaning between the notations $(r,\theta )$ and $(\widehat{r},\widehat{\theta })$; but mathematically, the former denotes the independent variables in the integral Equation (1), whereas the latter, the variables of integration. The gravitational force represented as the summation of a series of concentric rings is described by the first (double integral) term, while the centrifugal force by the second term in Equation (1).

Non-dimensionalizing the force-balance equation yields a dimensionless parameter, which we call the “galactic rotation number”, A, expressed as:

$$A\equiv \frac{V_0^2{R}_g}{M_{d}G}$$

(2)

where G ($=6.67\times {10}^{-11}$ [m${}^3$/(kg·s${}^2$)]) is the gravitational constant. This galactic rotation number, A, simply indicates the relative importance of centrifugal force versus gravitational force.

Equation (1) can either be used to determine the surface mass density, $\rho (r)h$, from a given rotation curve, $V(r)$, or vice versa. However, when both $\rho (r)$ and A are unknown, another independent equation is needed to keep the mathematical problem well-posed. According to the conservation of mass, the total mass of the galaxy disk, $M_d$, should stay as a constant satisfying the constraint:

$$2\pi {\int }_0^1\rho (\widehat{r})h\widehat{r}d\widehat{r}=1$$

(3)

This constraint offers an addition equation for determining the value of galactic rotation number A. With Equations (1)–(3), the mass density distribution, $\rho (r)$, in the disk, the galactic rotation number, A, and the disk galactic mass, $M_d$, can all be determined from the measured values of $V(r)$, $R_g$, $V_0$ and h. On the other hand, if $\rho (r)$ and h (or $\rho (r)h$), as well as A are given, $V(r)$ can, of course, be determined from Equation (1).

The integral with respect to $\widehat{\theta }$ in Equation (1) is known to be equivalent to:

$$\begin{array}{c}\hfill {\int }_0^{2\pi }\frac{(\widehat{r}cos\widehat{\theta }-r)d\widehat{\theta }}{{({\widehat{r}}^2+r^2-2\widehat{r}rcos\widehat{\theta })}^{3/2}}=2\left[\frac{E(m)}{r(\widehat{r}-r)}-\frac{K(m)}{r(\widehat{r}+r)}\right]\end{array}$$

(4)

where $K(m)$ and $E(m)$ denote the complete elliptic integrals of the first kind and second kind, with:

$$m\equiv \frac{4\widehat{r}r}{{(\widehat{r}+r)}^2}$$

(5)

Thus, Equation (1) can be written in a single-integral form:

$${\int }_0^1\left[\frac{E(m)}{\widehat{r}-r}-\frac{K(m)}{\widehat{r}+r}\right]\rho (\widehat{r})h\widehat{r}d\widehat{r}+\frac{1}{2}AV{(r)}^2=0$$

(6)

which is more suitable for the boundary element type of numerical implementation.

Following a standard boundary element approach [21,22], the governing Equations (3) and (6) can be discretized by dividing the one-dimensional problem domain $[0,1]$ into a finite number of line segments called (linear) elements. Each element covers a subdomain confined by two end nodes, e.g., element i corresponds to the subdomain $[r_i,r_{i+1}]$, where $r_i$ and $r_{r+1}$ are nodal values of r at nodes i and $i+1$, respectively. On each element, which is mapped onto a unit line segment $[0,1]$ in the ξ-domain (i.e., the computational domain), ρ is expressed in terms of the linear basis functions as:

$$\rho (\xi )={\rho }_i(1-\xi )+{\rho }_{i+1}\xi ,0\le \xi \le 1$$

(7)

where ${\rho }_i$ and ${\rho }_{i+1}$ are nodal values of ρ at nodes i and $i+1$, respectively. Similarly, the radial coordinate, $\widehat{r}$, on each element is also expressed in terms of the linear basis functions by so-called isoparametric mapping:

$$\widehat{r}(\xi )={\widehat{r}}_i(1-\xi )+{\widehat{r}}_{i+1}\xi ,0\le \xi \le 1$$

(8)

If the rotation curve, $V(r)$, is given (as from measurements), the N nodal values of ${\rho }_i=\rho (r_i)$ are determined by solving N independent residual equations over the $N-1$ element obtained from the collocation procedure, i.e.,

$$\begin{array}{c}\hfill \sum _{n=1}^{N-1}{\int }_0^1\left[\frac{E(m_i)}{\widehat{r}(\xi )-r_i}-\frac{K(m_i)}{\widehat{r}(\xi )+r_i}\right]\rho (\xi )h\widehat{r}(\xi )\frac{d\widehat{r}}{d\xi }d\xi +\frac{1}{2}AV{(r_i)}^2=0,i=1,2,...,N\end{array}$$

(9)

with:

$$m_i(\xi )\equiv \frac{4\widehat{r}(\xi )r_i}{{[\widehat{r}(\xi )+r_i]}^2}$$

(10)

where $\rho (\xi )={\rho }_n(1-\xi )+{\rho }_{n+1}\xi$. The value of A can be solved by the addition of the constraint equation:

$$2\pi \sum _{n=1}^{N-1}{\int }_0^1\rho (\xi )h\widehat{r}(\xi )\frac{d\widehat{r}}{d\xi }d\xi -1=0$$

(11)

Thus, we have $N+1$ independent equations for determining $N+1$ unknowns; the mathematical problem is well-posed. With appropriate mathematical treatments of the singularities arising from the elliptic integrals and boundary conditions at $r=0$ and $r=1$, the set of linear Equations (9) and (11) for $N+1$ unknowns (i.e., N nodal values of ${\rho }_i$ and A) can be put in a matrix form and then solved with a standard matrix solver, such as by Gauss elimination [23].

As in Feng and Gallo [12], the complete elliptic integrals of the first kind and second kind in Equation (9) can be numerically computed with the formulas [24]:

$$K(m)=\sum _{l=0}^4{a}_l{m}_1^l-log(m_1)\sum _{l=0}^4{b}_l{m}_1^l$$

(12)

and:

$$E(m)=1+\sum _{l=1}^4{c}_l{m}_1^l-log(m_1)\sum _{l=1}^4{d}_l{m}_1^l$$

(13)

where:

$$m_1\equiv 1-m={\left(\frac{\widehat{r}-r}{\widehat{r}+r}\right)}^2$$

(14)

Clearly, the terms associated with $K(m_i)$ and $E(m_i)$ in Equation (9) become singular when $\widehat{r}\to r_i$ on the elements with $r_i$ as one of their end points.

The logarithmic singularity can be treated by converting the singular one-dimensional integrals into non-singular two-dimensional integrals by virtue of the identities:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\int }_0^{1}f(\xi )log\xi d\xi =-{\int }_0^1{\int }_0^{1}f(\xi \eta )d\eta d\xi \\ {\int }_0^{1}f(\xi )log(1-\xi )d\xi =-{\int }_0^1{\int }_0^{1}f(1-\xi \eta )d\eta d\xi \end{array}\right.\end{array}$$

(15)

where $f(\xi )$ denotes a well-behaving (non-singular) function of ξ on $0\le \xi \le 1$.

However, a more serious non-integrable singularity, $1/(\widehat{r}-r_i)$, exists, due to the term, $E(m_i)/(\widehat{r}-r_i)$, in Equation (9) as $\widehat{r}\to r_i$. The $1/(\widehat{r}-r_i)$ type of singularity is treated by taking the Cauchy principle value to obtain meaningful evaluation [25], as commonly done with the boundary element method [21,22]. In view of the fact that each $r_i$ is considered to be shared by two adjacent elements covering the intervals $[r_{i-1},r_i]$ and $[r_i,r_{i+1}]$, the Cauchy principle value of the integral over these two elements is given by:

$$\underset{ϵ\to 0}{lim}\left[{\int }_{r_{i-1}}^{r_i-ϵ}\frac{\rho (\widehat{r})\widehat{r}d\widehat{r}}{\widehat{r}-r_i}+{\int }_{r_i+ϵ}^{r_{i+1}}\frac{\rho (\widehat{r})\widehat{r}d\widehat{r}}{\widehat{r}-r_i}\right]$$

(16)

In terms of elemental ξ, Equation (16) is equivalent to:

$$\begin{array}{c}\hfill -\underset{ϵ\to 0}{lim}\left\{{\int }_0^{1-ϵ/(r_i-r_{i-1})}\frac{[{\rho }_{i-1}(1-\xi )+{\rho }_i\xi ][r_{i-1}(1-\xi )+r_i\xi ]d\xi }{1-\xi }\right.\end{array}$$

$$\begin{array}{c}\hfill \left.-{\int }_{ϵ/(r_{i+1}-r_i)}^1\frac{[{\rho }_i(1-\xi )+{\rho }_{i+1}\xi ][r_i(1-\xi )+r_{i+1}\xi ]d\xi }{\xi }\right\}\end{array}$$

(17)

Performing integration by parts on Equation (17) yields:

$$\begin{array}{c}\hfill {\rho }_i{r}_{i}log\left(\frac{r_{i+1}-r_i}{r_i-r_{i-1}}\right)-\left({\int }_0^1\frac{d\left\{[{\rho }_{i-1}(1-\xi )+{\rho }_i\xi ][r_{i-1}(1-\xi )+r_i\xi ]\right\}}{d\xi }log(1-\xi )d\xi \right.\end{array}$$

$$\begin{array}{c}\hfill \left.+{\int }_0^1\frac{d\left\{[{\rho }_i(1-\xi )+{\rho }_{i+1}\xi ][r_i(1-\xi )+r_{i+1}\xi ]\right\}}{d\xi }log\xi d\xi \right)\end{array}$$

where the two terms associated with $logϵ$ cancel out each other; the terms with $ϵlogϵ$ become zero at the limit of $ϵ\to 0$, and the first term becomes nonzero when the nodes are not uniformly distributed (namely, the adjacent elements are not of the same segment size).

At the galaxy center $r_i=0$,

$${\int }_{r_i}^{r_{i+1}}\frac{\rho (\widehat{r})\widehat{r}d\widehat{r}}{\widehat{r}-r_i}={\int }_0^{r_{i+1}}\rho (\widehat{r})d\widehat{r}$$

(18)

Thus, the $1/(\widehat{r}-r_i)$ type of singularity disappears naturally. However, numerical difficulty can still arise if ρ itself becomes singular as $r\to 0$, e.g., $\rho \propto 1/r$ as for the Mestel disk [26]. The singular mass density at $r=0$ corresponds to a mathematical cusp, which usually indicates the need for a finer resolution in the physical space. To avoid the cusp in mass density at the galactic center, we can impose a requirement of continuity of the derivative of ρ at the galaxy center $r=0$. This can be easily implemented at the first node $i=1$ to demand $d\rho /dr=0$ at $r=0$. In discretized form for $r_1=0$, we simply have:

$$\rho (r_1)=\rho (r_2)$$

(19)

When $r_i=1$ (i.e., $i=N$), we are at the end node of the problem domain. Here, we use a numerically relaxing boundary condition by considering an additional element beyond the domain boundary covering the interval $[r_i,r_{i+1}]$, because it is needed to obtain a meaningful Cauchy principle value. In doing so, we can also assume $r_{i+1}-r_i$$=r_i-r_{i-1}$, such that $log[(r_{i+1}-r_i)/(r_i-r_{i-1})]$ becomes zero, to simplify the numerical implementation. Moreover, it is reasonable to assume ${\rho }_{i+1}=0$, because it is located outside the disk edge. With sufficiently fine local discretization, this extra element covers a diminishing physical space, such that its existence becomes numerically inconsequential. Thus, at $r_i=1$, we have:

$$\begin{array}{c}\hfill {\int }_0^1\frac{d\left\{[{\rho }_i(1-\xi )+{\rho }_{i+1}\xi ][r_i(1-\xi )+r_{i+1}\xi ]\right\}}{d\xi }log\xi d\xi \end{array}$$

$$\begin{array}{c}\hfill =({\rho }_{i+1}-{\rho }_i){\int }_0^{1}r(\xi )log\xi d\xi +(r_{i+1}-r_i){\int }_0^1\rho (\xi )log\xi d\xi ={\rho }_i[r_i-\frac{3}{2}(r_i-r_{i-1})]\end{array}$$

Now that only the logarithmic singularities are left, Equation (15) can be used for eliminating all singularities in computing the integrals in Equation (9).

3. Results

To obtain numerical solutions, the value of (constant) disk thickness, h, must be provided; we assume $h=0.01$ out of many possible choices. For computational efficiency, we distribute more nodes in the regions (e.g., near the galactic center and disk edge) where ρ varies more rapidly. Unless the rotation curve has very steep velocity changes that need finer discretization with more elements, the typical number of non-uniformly distributed nodes, N, used in computating most cases is 1001 (corresponding to 1000 linear elements), which we found for most cases to be sufficient for obtaining a smooth curve of ρ versus r and discretization-insensitive values of galactic rotation number A.

The rotation curves available in the open literature (e.g., the Sofue website [19]) are typically provided in a tabular form with data points at radial positions often not coinciding with our nodal positions. We use the cubic spline interpolation method [23] to evaluate our nodal values of $V(r)$ from the rotation curve data, such that the rotation curve used in our computations is guaranteed to smoothly pass through all the original data points.

3.1. NGC 4736

The NGC 4736 galaxy has recently been studied by Jalocha, Bratek and Kutschera [17], for illustrating that the baryonic matter distribution can account for the observed rotation curve. Thus, we believe it deserves our attention to study using our computational method.

There are several different versions of rotation curve data for NGC 4736 in the literature. Here, we consider two of them, one is from the website of Sofue [19] and the other from the H I Nearby Galaxy Survey (THINGS) measurements [20]. Figure 1 shows the two versions of the rotation curves with r measured in units of $R_g=10.35$ (kpc) (where 1 kpc $=3.086\times {10}^{19}$ m), and rotation velocity $V(r)$ in units of $V_0=150$ (km/s).

As shown by Feng and Gallo [12], the value of total galactic mass in the disk can be determined according to Equation (2) with the computed value of A as:

$$M_d=\frac{V_0^2{R}_g}{AG}$$

(20)

Because the computed value of the galactic rotation number, A, is $1.9656$ for the THINGS rotation curve and $1.5908$ for that of Sofue, we obtain $M_d=2.756\times {10}^{10}$$M_{\odot }$ (where one solar-mass $M_{\odot }$$=1.98892\times {10}^{30}$ kg) when the THINGS rotation curve is used and $M_d=3.405\times {10}^{10}$$M_{\odot }$ when the Sofue rotation curve is used. The value of $M_d=3.405\times {10}^{10}$$M_{\odot }$ agrees well with that computed by Jalocha, Bratek and Kutschera [17] (i.e., $3.43\times {10}^{10}$$M_{\odot }$) using the same rotation curve of Sofue.

Figure 1. Profiles of NGC 4736 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of the H I Nearby Galaxy Survey (THINGS) and the thin line for that from Sofue. The computed values of the galactic rotation number, A, are $1.9656$ and $1.5908$ for the cases of THINGS and Sofue, respectively.

Figure 1. Profiles of NGC 4736 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of the H I Nearby Galaxy Survey (THINGS) and the thin line for that from Sofue. The computed values of the galactic rotation number, A, are $1.9656$ and $1.5908$ for the cases of THINGS and Sofue, respectively.

However, Jalocha, Bratek and Kutschera [17] used an iterative spectral method with Bessel functions, which requires the inclusion of a rotation curve beyond the “cut-off” radius extending to infinity. They also considered the mass density due to the neutral atomic hydrogen (H I) outside the cut-off radius. With our method, only the available data for rotation curve within the cut-off radius is needed. Meanwhile, we assume the mass density in the galactic disk diminishes at the same cut-off radius to enable a self-consistent consideration of the mathematical problem on a finite disk domain. The solution of the axisymmetric mass distribution in the galactic disk for a given rotation curve can be computed by one-step Gauss elimination of the linear algebra matrix equation without further successive iterations [12].

If desired, the effect of H I and the “not-yet” measurable rotation curve outside the cut-off radius can be conveniently examined in an a posteriori manner. For example, the surface mass density of H I considered by Jalocha, Bratek and Kutschera [17] at the cut-off radius is $\sim 1$$M_{\odot }/$pc${}^2$, which translates to our non-dimensional $\rho =R_g^2/(M_{d}h)=0.3887$ (or $0.3146$, with $R_g$ in units of pc and $M_d$ in units of $M_{\odot }$) for the THINGS (or Sofue) rotation curve, decreasing one order of magnitude in about 3 (kpc) beyond the cut-off radius at $10.35$ (kpc).

To examine the effect of H I outside the cut-off radius, we modify the mass distribution starting from a radius $r_1<1$, such that the mass density for $r\ge r_1$ is described by:

$$\rho (r)={\rho }_1{e}^{-{[0.2+(r-r_1)/0.3]}^2},r_1\le r<\infty$$

(21)

where $r_1=0.965$ and ${\rho }_1=\rho (r_1)=0.388$. The profile of mass density distribution extending to $r>1$ as described by (21) approximates well to that considered by Jalocha, Bratek and Kutschera [17] while simplifying the analysis. With the given mass distribution extending beyond $r=1$, we can correspondingly extend the integration to $r>1$ in Equations (3) and (6), to calculate rotation velocity beyond the cut-off radius. Figure 2 shows the mass density distribution with (thin line) and without (thick line) the H I outside the (non-dimensional) cut-off radius $r=1$, and the corresponding rotation curves. The integration result of Equation (3) shows that including H I beyond $r=1$ increases the total galactic mass only by $\sim 0.5\%$. Therefore, it is not surprising to notice that the original rotation curve in Figure 2 is barely altered by this mass density modification. In fact, the rotation curves beyond $r=1$ calculated with and without the mass density modification (21) differs so little that they are visually indistinguishable when plotted together in Figure 2.

Figure 2. The distributions of mass density $\rho (r)$ with (thin line) or without (thick line) H I extending beyond the cut-off radius, and the corresponding rotation curves. Only the case based on the THINGS rotation curve is shown here.

Figure 2. The distributions of mass density $\rho (r)$ with (thin line) or without (thick line) H I extending beyond the cut-off radius, and the corresponding rotation curves. Only the case based on the THINGS rotation curve is shown here.

In view of typical uncertainties in rotation curve measurements (as illustrated in Figure 1 for two different versions of the same galaxy), we expect that any matters (such as H I) outside the “cut-off” radius cannot have substantial influence on the disk rotation characteristics, because the amount of mass in comparison to the value of $M_d$ is usually insignificant. Thus, whether including the H I mass outside the “cut-off” radius of NGC 4736 should have inconsequential effect on the Newtonian dynamics relating the measured rotation curve to mass distribution in the galactic disk. As illustrated here, however, the consideration of H I mass beyond $r=1$ can be conveniently implemented as an a posteriori process (without iteratively computing solutions) to evaluate (or, in other words, predict) the rotation velocity beyond the cut-off radius, which could not be obtained from measurements. Then, the needed part of rotation curve beyond the cut-off radius, for using a formulation that requires it (e.g., [13,14,17,18]) to determine the mass distribution from measured rotation curve, can be provided using our method with concrete certainty (namely, without fictitious assumptions).

3.2. Milky Way, NGC 4945

The Milky Way, also called the Galaxy, is the galaxy that contains the Sun and the Earth, which is why it is of particular interest to astronomy and astrophysics. NGC 4945 is a spiral galaxy that appears quite similar to the Milky Way. Therefore, we present results for both of them together here. The rotation curve data provided by Sofue [19] suggest nonzero rotation velocity at $r=0$. According to our continuum treatment of a rotating disk galaxy with a Newtonian dynamics description of force balance (6), nonzero rotation velocity at $r=0$ requires a strongly singular mass density to ensure that:

$${\int }_0^1\rho (\widehat{r})d\widehat{r}\to \infty$$

(22)

This is because the kernel of integral in Equation (6) for any nonzero $\widehat{r}$ has a limit value of zero at $r=0$, i.e.,

$$\underset{r\to 0}{lim}\left[\frac{E(m)}{\widehat{r}-r}-\frac{K(m)}{\widehat{r}+r}\right]=\frac{1}{\widehat{r}}\left[E(0)-K(0)\right]$$

(23)

and $E(0)=K(0)=\pi /2$ [24]. Thus, $V(0)$ must be zero according to Equation (6), unless Equation (22) is true as in Mestel’s disk [26] where $\rho \to 1/r$ as $r\to 0$.

As discussed by Feng and Gallo [12], the computational method used here can reproduce the result of Mestel’s disk [26] for the entire problem domain $(0,1]$ when the rotation velocity in an infinitesimal neighborhood around $r=0$ is modified, such that $V(0)$ becomes zero, which corresponds to replacing $\rho (0)=\infty$ with a finite (large) value of $\rho (0)$. Such a slight modification of rotation curve results in no practical difference in the computed mass density distribution and the value of total galactic mass, $M_d$, while providing great convenience for numerical computation.

Therefore, we take the same approach here to slightly modify the rotation-curve data files of Sofue, such that the first point at $r=0$ has $V(0)=0$, while leaving all the rest of the data points unchanged; the resulting rotation curves are shown in Figure 3 with r measured in units of $R_g=20.55$ and $20.00$ (kpc), rotation velocity $V(r)$ in units of $V_0=220$ and 180 (km/s), respectively for the Milky Way and NGC 4945. Also shown in Figure 3 are the computed mass density distributions. With the computed value of $A=1.6365$, we have $1.4138\times {10}^{11}$$M_{\odot }$ for the Milky Way according to Equation (20). For the Galaxy, one unit of non-dimensional ρ corresponds to the surface mass density of $M_{d}h/R_g^2=3.35$$M_{\odot }/$pc${}^2$. In the solar neighborhood around 8 kpc from the Galactic center, which corresponds to $r=0.3893$, we have $\rho \sim 43$ (from Figure 3), and therefore, the surface mass density around the Sun should be $\sim 144$$M_{\odot }/$pc${}^2$.

Due to the large central peaks in rotation curves near $r=0$, the computed mass density profiles show a sharp increase of ρ toward the galactic center, as is consistent with the previous findings of Feng and Gallo [12] based on a series of idealized rotation curves. Because the rotation curves of the Milky Way and NGC 4945 are generally flat, the mass density profiles show only about a one order of magnitude decrease in the large interval $(0.1,0.9)$, unlike that for NGC 4736, with more than a two orders of magnitude decrease, corresponding to a rotation curve of velocity generally decreasing with galactocentric distance.

Figure 3. Profiles of the Milky Way and NGC 4945 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of the Milky Way and the thin line for NGC 4945. The computed values of the galactic rotation number, A, are $1.6365$ and $1.6873$ for the Milky Way and NGC 4945, respectively.

Figure 3. Profiles of the Milky Way and NGC 4945 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of the Milky Way and the thin line for NGC 4945. The computed values of the galactic rotation number, A, are $1.6365$ and $1.6873$ for the Milky Way and NGC 4945, respectively.

3.3. NGC 224, NGC 5055

The NGC 224 and NGC 5055 galaxies were classified as those with rotation curves having “no central peak” [27], in contrast to that of the Milky Way. Their rotation curves (from the Sofue website [19]) and our computed mass density profiles are presented in Figure 4, with r measured in units of $R_g=31.25$ and $39.35$ (kpc), rotation velocity $V(r)$ in units of $V_0=250$ and 190 (km/s), respectively for NGC 224 and NGC 5055. Corresponding to the rotation curves without the central peak, the mass density profiles vary less dramatically as $r\to 0$ than those in Figure 3 with large central peaks.

3.4. NGC 2403, NGC 3198

With their rotation curves being classified as “rigid-body type” [27], NGC 2403 and NGC 3198 have rotation velocities increasing gradually from the galactic center almost like rigid-body rotation for a considerable radial distance before leveling off. Figure 5 shows the rotation curves (from the Sofue website [19]) and the corresponding mass density profiles of NGC 2403 (thick line, which also has the nonzero velocity at $r=0$ replaced with $V(0)=0$) and NGC 3198 (thin line), with r measured in units of $R_g=19.70$ and $31.05$ (kpc) and rotation velocity $V(r)$ in units of $V_0=130$ and 160 (km/s) for NGC 2403 and NGC 3198, respectively. The peak density at $r=0$ in Figure 5 is further reduced from that in Figure 4, due to the less steep change in the rotation velocity around the galactic center.

It is noteworthy that the NGC 3198 rotation curve has a small spike near $r=0$, which results in a sharp turn in the mass density around the same location. Another obvious wiggling spike in the rotation curve is at $r\sim 0.2$, causing a corresponding corner formed in the mass density profile in that neighborhood. Apparently, the effects of some of the fine features in the rotation curve are confined locally in a small nearby neighborhood.

Figure 4. Profiles of NGC 224 and NGC 5055 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of NGC 224 and the thin line for NGC 5055. The computed values of the galactic rotation number, A, are $1.6450$ and $1.6888$ for NGC 224 and NGC 5055, respectively.

Figure 4. Profiles of NGC 224 and NGC 5055 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of NGC 224 and the thin line for NGC 5055. The computed values of the galactic rotation number, A, are $1.6450$ and $1.6888$ for NGC 224 and NGC 5055, respectively.

Figure 5. Profiles of NGC 2403 and NGC 3198 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of NGC 2403 and the thin line for NGC 3198. The computed values of the galactic rotation number, A, are $1.4918$ and $1.6022$ for NGC 2403 and NGC 3198, respectively.

Figure 5. Profiles of NGC 2403 and NGC 3198 rotation velocity $V(r)$ and mass density $\rho (r)$, with the thick line for that of NGC 2403 and the thin line for NGC 3198. The computed values of the galactic rotation number, A, are $1.4918$ and $1.6022$ for NGC 2403 and NGC 3198, respectively.

3.5. Tabulated Summary

The values of $R_g$ and $V_0$, and the corresponding A and $M_d$, for various types of galaxies computed in this section are summarized in Table 1 for convenient reference. Here, the value of $R_g$ is well-defined as the cut-off radius from the rotation curve data, such that our non-dimensionalized computational domain is always $[0,1]$, whereas that of the characteristic velocity $V_0$ can be somewhat arbitrary and is chosen to approximately reflect the average rotation velocity outside the region around galactic center, which is often fairly flat. Thus, the value of computed A can vary depending on the chosen value of $V_0$, but the dimensional value of $M_d$ does not change, independent of how $V_0$ is defined.

Table 1. Values of $R_g$ and $V_0$, and the corresponding A and $M_d$, for galaxies computed in this section.

Galaxy	Type	$R_g$ (kpc)	$V_0$ (km/s)	A	$M_d$ ($M_{\odot }$)
NGC 4736 (THINGS)	Sab	10.35	150	1.9656	2.756 $\times {10}^{10}$
NGC 4736 (Sofue)	Sab	10.35	150	1.5908	3.405 $\times {10}^{10}$
Milky Way	Sb	20.55	220	1.6365	1.4138 $\times {10}^{11}$
NGC 4945	Sb	20.00	180	1.6873	8.9337 $\times {10}^{10}$
NGC 224	Sb	31.25	250	1.6450	2.7619 $\times {10}^{11}$
NGC 5055	Sb	39.35	190	1.6888	1.9567 $\times {10}^{11}$
NGC 2403	Sc	19.70	130	1.4918	5.1915 $\times {10}^{10}$
NGC 3198	Sc	31.05	160	1.6022	1.1541 $\times {10}^{11}$

Table 1. Values of $R_g$ and $V_0$, and the corresponding A and $M_d$, for galaxies computed in this section.

Galaxy	Type	$R_g$ (kpc)	$V_0$ (km/s)	A	$M_d$ ($M_{\odot }$)
NGC 4736 (THINGS)	Sab	10.35	150	1.9656	2.756 $\times {10}^{10}$
NGC 4736 (Sofue)	Sab	10.35	150	1.5908	3.405 $\times {10}^{10}$
Milky Way	Sb	20.55	220	1.6365	1.4138 $\times {10}^{11}$
NGC 4945	Sb	20.00	180	1.6873	8.9337 $\times {10}^{10}$
NGC 224	Sb	31.25	250	1.6450	2.7619 $\times {10}^{11}$
NGC 5055	Sb	39.35	190	1.6888	1.9567 $\times {10}^{11}$
NGC 2403	Sc	19.70	130	1.4918	5.1915 $\times {10}^{10}$
NGC 3198	Sc	31.05	160	1.6022	1.1541 $\times {10}^{11}$

4. Discussion

It should be noted that the axisymmetric thin-disk continuum model considered here is at best a simplified approximation of mature spiral galaxies. By “mature”, we mean that the basic galactic structures do not change (or evolve) with time drastically any more, and thus, their dynamic behavior almost approaches the so-called steady state. Realistically, however, even those mature spiral galaxies are not in a perfect axisymmetric steady state, because they typically exhibit spiral arms, tidal streams, bars, etc. [1,28]. Therefore, a hierarchy of models of increasing sophistication exists [29]. However, more sophisticated models usually involve more assumptions, many of which cannot easily be validated by reliable observational measurements (such as the dark matter, dark halo, etc.) and thus become debatable.

On the other hand, we do not think the detailed galactic structures, such as spiral arms, etc., should alter the averaged gross galactic properties in any significant manner. For example, all the mass density profiles predicted by our model in Section 3 exhibit a nearly linear decline (in semi-log plots) if the two abruptly varying ends (around $r=0$ and $r=1$) are trimmed out, indicating that the mass density of most mature galaxies follows approximately a common exponential law of decay as typically observed with luminosity measurements. However, the radial scale length for the surface mass density of many galaxies may not closely match that of the measured brightness distribution [12]. Yet, for some galaxies, such as NGC 4736, our predicted mass distribution (which is basically the same as that by Jalocha, Bratek and Kutschera [17]) has been shown to be quite consistent with the I-band luminosity profile, having a mean mass-to-light ratio $M/L_I$$=1.2$ [17]. Because there are no well-established theoretical constraints for the mass-to-light ratio, quantitative discussion on the discrepancy between our predicted mass distribution and the measured brightness distribution can hardly avoid lack of the desired scientific rigor and, therefore, is not pursued further in the present work. Here, we choose to focus on the axisymmetric thin-disk model with minimum physical assumptions, and apply only the well-established Newtonian dynamics to determine the mass distribution in rotating spiral galaxies based on observed rotation curves. Along with appropriate mathematical treatments, we believe our results provide logically rigorous references for more sophisticated model development. Hence, in this section, we first discuss a few extensions from the strict thin-disk model results presented in the previous section. Other relevant topics, such as the applicability of Keplerian dynamics and circular orbit stability, are also examined.

4.1. Nonzero Rotation Velocity at $r=0$

In Section 3.2, we have treated the rotation curves having nonzero velocity at $r=0$ by replacing the value of $V(0)$ with a zero value in the rotation curve data file. Such a simplistic approach may be a little distasteful to some people with a rigorous mind. Therefore, a more elaborated treatment is provided here.

With the thin-disk model, we have demonstrated with galaxies of various types of realistic rotation curves that the mass density is always highest at the galactic center, and a nonzero rotation velocity at $r=0$ corresponds to an infinite mass density at the galactic center. To enable the numerical treatment of the infinite local mass density, it may not be unreasonable to consider the galaxies with nonzero rotation velocity at $r=0$ to consist of a dense spherical core at the galactic center in addition to a self-gravitating thin disk. In that case, we should modify (6) to include a term due to the dense core with a spherically symmetric gravitational field. Among many choices, we can simply assume a spherical core confined within a small volume, e.g., in $r<R_c$$=0.0001$, having a mass $M(r)=AV{(0)}^{2}r$, where $V(0)$ is nonzero according to the measured rotation curve. This corresponds to a spherically symmetric mass density $\rho (r)=[dM(r)/dr]/(2\pi r^2)$$=AV{(0)}^2/(2\pi r^2)$ in $r<R_c$, becoming infinite as $r\to 0$. As a consequence, the second term in Equation (6), namely $\frac{1}{2}AV{(r)}^2$, can be replaced by $\frac{1}{2}A[V{(r)}^2-V{(0)}^2]$ for $r<R_c$ and by $\frac{1}{2}A[V{(r)}^2-V{(0)}^2{R}_c/r]$ for $r\ge R_c$. Such a modification is actually equivalent to replacing the original rotation curve, $V(r)$, with a modified one that becomes zero at $r=0$ as:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\sqrt{V{(r)}^2-V{(0)}^2},r<R_c\\ \sqrt{V{(r)}^2-V{(0)}^2{R}_c/r},r\ge R_c\end{array}\right.\end{array}$$

(24)

If we apply this approach to the Milky Way, which has $V(0)=0.9282$, with $R_c={10}^{-4}$, we obtain $A=1.6368$ (instead of $1.6365$ in Section 3.2). Thus, the total mass in the Galactic disk is $M_d=1.4135\times {10}^{11}$$M_{\odot }$ (instead of $1.4138\times {10}^{11}$$M_{\odot }$ in Section 3.2). The mass in the spherical core is $AV{(0)}^2{R}_c{M}_d$ $=1.6368\times 0.{9282}^2\times 1.4135\times {10}^7$ $=1.9933\times {10}^7$$M_{\odot }$. The combined mass of the core and disk is then $1.4137\times {10}^{11}$$M_{\odot }$, which is of no practical difference from the value in Section 3.2. With such a small core of $R_c={10}^{-4}$, the modified rotation curve Equation (24) is also of no practical difference from that (thick line) in Figure 3, having <2% change at $r=0.0024$ (the second data point in measured rotation curve), <1% change at $r=0.0049$ (the third data point), ∼0.5% change at $r=0.0073$ (the forth data point), and so on and so forth.

However, if we assume $R_c=0.01$ for a bigger core, the computed value of A for the Milky Way becomes $1.6599$ and the corresponding mass in the galactic disk then is $M_d=1.3939\times {10}^{11}$$M_{\odot }$. Combining with the mass of the core ($AV{(0)}^2{R}_c{M}_d$$=1.9934\times {10}^9$$M_{\odot }$), we have a total galactic mass of $1.4138\times {10}^{11}$$M_{\odot }$, which is basically the same as that in Section 3.2. Hence, the total galactic mass remains unchanged for a substantial range of the spherical core size, $R_c$. However with $R_c=0.01$, the modified Milky Way disk rotation curve according to Equation (24) differs noticeably from the original one provided by Sofue (as shown in Figure 6), especially around the galactic core, where the influence of the gravitational field of the spherical core is more significant. Yet, the computed $\rho (r)$ in the thin disk still appears indistinguishable from that in Figure 3, except that the peak value at $r=0$ is reduced to 3650 from $25,262$ (in Figure 3). This is because in a small core at the galactic center the details of mass distribution, whether axisymmetrically or spherical symmetrically, cannot make much of a difference in the gravitational field some distance away.

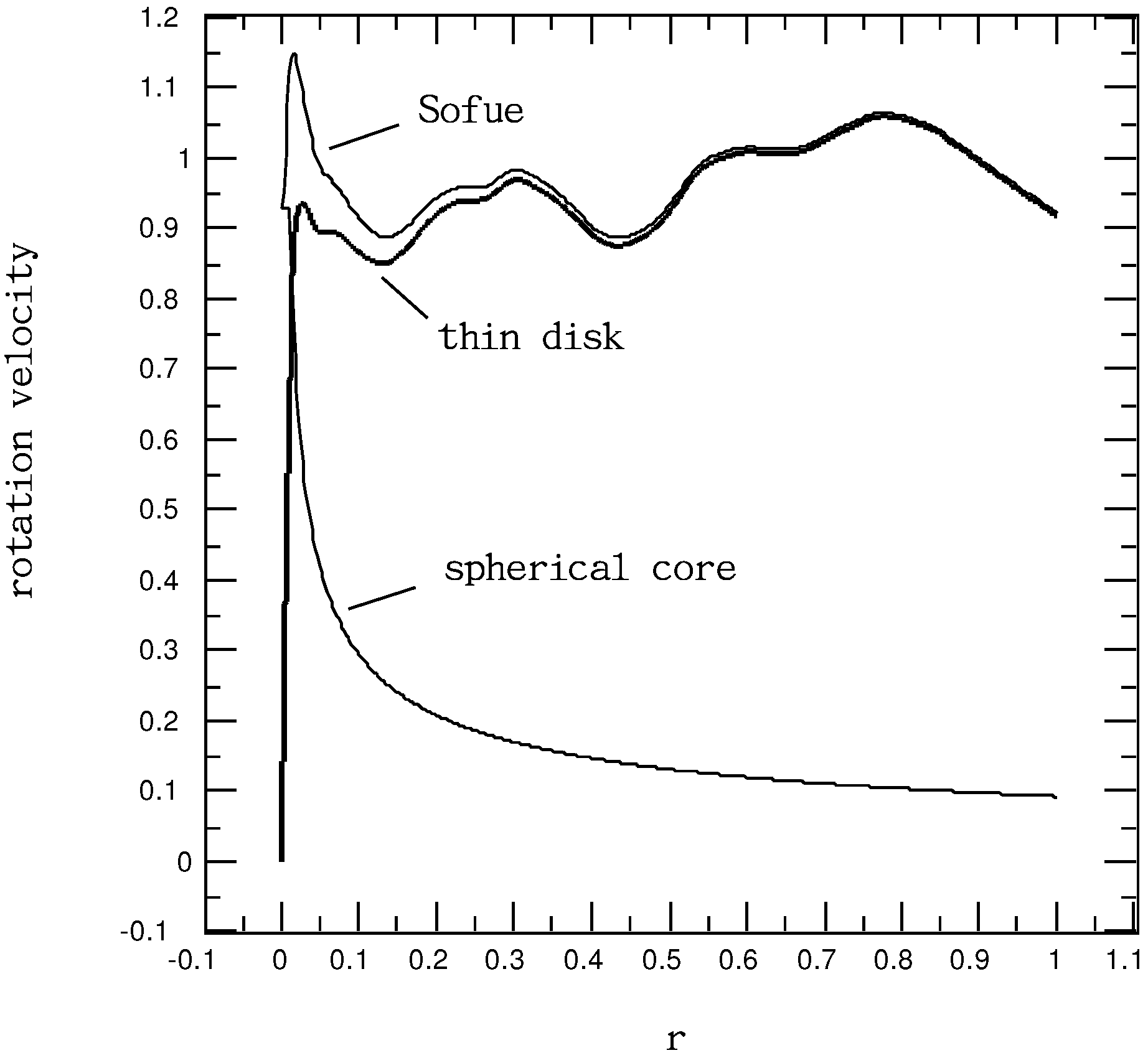
Figure 6. Profiles of the Milky Way rotation curves when decomposed into that corresponding to a spherical core of $R_c=0.01$ and a thin disk. The original rotation curve from Sofue is also shown here as a reference.

Figure 6. Profiles of the Milky Way rotation curves when decomposed into that corresponding to a spherical core of $R_c=0.01$ and a thin disk. The original rotation curve from Sofue is also shown here as a reference.

It seems though that the effort of decomposing the galaxy into a small spherical core and a thin disk only helps treat rotation curves with nonzero velocity at $r=0$ in a mathematically elegant manner, such that the need of explicitly considering the infinite mass density is eliminated. Physically, a nonzero rotation velocity at $r=0$ has unclear meanings and should remain as a debatable subject; so should the implication of the corresponding infinite mass density, because the common wisdom usually indicates that “nature abhors infinities”. Thus, we prefer the straightforward treatment in Section 3.2 to simply bring the rotation velocity to zero at $r=0$, especially when it does not seems to be, at the expense of compromising the general result’s accuracy. The insensitivity of mass distribution in the galactic disk and total galactic mass to detailed descriptions of the structure in a small spherical central core illustrated here is consistent with the findings of previous authors (cf. the discussion of Nordsieck [14] and the citations therein).

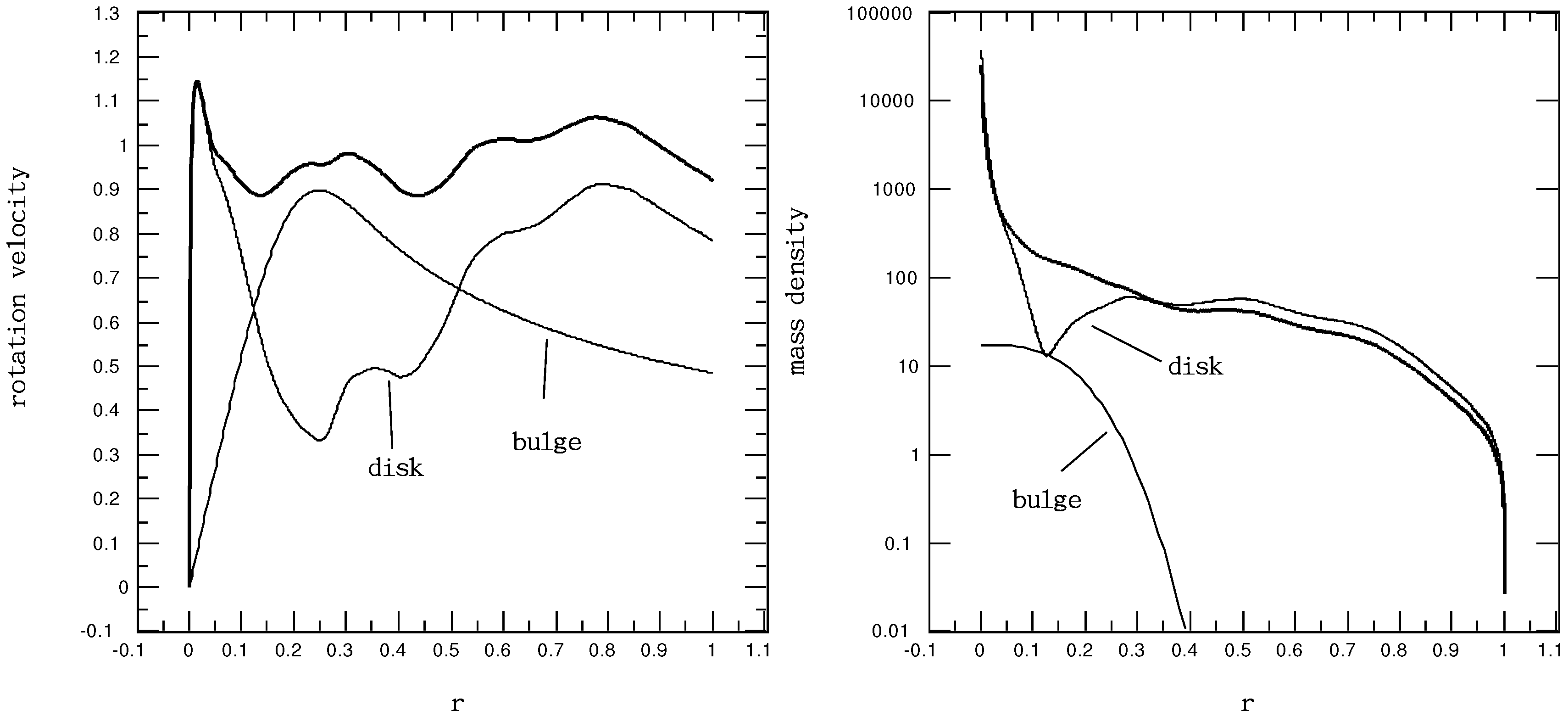
4.2. Central Bulge in Disk Galaxy

Yet, our methodology for treating a central spherical core can be easily extended for analyzing galaxies with a considerably larger central bulge with a priori given spherical mass distributions. As an example, assuming the Milky Way rotation curve in Figure 3 to be a result of the combination of a central bulge with a spherically symmetric mass density:

$${\rho }_b(r)={\rho }_{b0}{e}^{-{(r/R_b)}^3}$$

(25)

and an axisymmetrically distributed mass in a thin-disk, Equation (6), with $V(r)$ in Figure 3 being replaced by:

$$\sqrt{V{(r)}^2-\frac{4\pi {\rho }_{b0}{R}_b^3}{3A}\left[1-e^{-{(r/R_b)}^3}\right]}$$

(26)

For $R_b=0.2$ and ${\rho }_{b0}/A=7$, the disk rotation curve as determined from Equation (26) is shown in Figure 7 together with the computed disk mass density distribution. In the presence of this bulge, the value of A becomes $2.4793$, and the disk mass density exhibits a dip around $r=0.12$. Thus, ${\rho }_{b0}=7\times 2.4793=17.3551$, and the corresponding bulge density profile is also shown in Figure 7. The mass in the disk portion (calculated from Equation (20)) is $M_d=9.3320\times {10}^{10}$$M_{\odot }$ and that in the bulge portion $M_b=4\pi {\rho }_{b0}{R}_b^3{M}_d/3$$=5.4273\times {10}^{10}$$M_{\odot }$. The total galactic mass $M_g=M_d+M_b$ $=1.4759\times {10}^{11}$$M_{\odot }$ (instead of $1.4138\times {10}^{11}$$M_{\odot }$ predicted by a pure disk model in Section 3.2). Because a substantial amount of the mass is concentrated in the central bulge with its portion of spherically symmetric mass density practically diminishing for $r>0.3$, the disk surface mass density in the solar neighborhood around $r=0.3893$ (corresponding to 8 kpc) becomes $\rho (0.3893)M_{d}h/R_g^2$$=108$$M_{\odot }$/pc${}^2$) where $\rho (0.3893)\sim 49$ from the “disk” mass density curve in Figure 7. Even though the presence of our example bulge causes only a few percent of increase in the total galactic mass from that predicted by a pure disk model, the disk surface mass density in the solar neighborhood can decrease by 25%.

Figure 7. Profiles of the Milky Way rotation velocity and mass density for the disk portion and bulge portion (with $R_b=0.2$ and ${\rho }_{b0}/A=7$) as noted along with that in Figure 3 (thick line) as a reference.

Figure 7. Profiles of the Milky Way rotation velocity and mass density for the disk portion and bulge portion (with $R_b=0.2$ and ${\rho }_{b0}/A=7$) as noted along with that in Figure 3 (thick line) as a reference.

If $R_b=0.25$ and ${\rho }_{b0}/A=5$, the value of A will become $3.0223$, and therefore, ${\rho }_{b0}=15.1115$. As a consequence, $M_d=7.6554\times {10}^{10}$$M_{\odot }$, $M_b=7.5716\times {10}^{10}$$M_{\odot }$ and $M_g=1.5227\times {10}^{11}$$M_{\odot }$. The value of $\rho (0.3893)$ is ∼41 corresponding to the disk surface mass density in the solar neighborhood of 74 $M_{\odot }$/pc${}^2$. Thus, for a given rotation curve, the actual value of disk surface mass density in a galaxy can vary significantly when considering a model with a combination of a spherical bulge and an axisymmetric thin disk, depending upon the bulge mass structure. The bulge mass structure described by Equation (25) is only for illustrative purpose with the convenience of mathematical manipulation. The fact that adding a spherical bulge offers a another degree of freedom for adjusting mass distribution in the galactic disk should not depend upon the details in the bulge mass structure. This extra degree of freedom comes at the expense of uncertainty due to the difficulties in determining the bulge mass structure that is governed by much more complicated physical processes than simply balancing the gravitational force and centrifugal force. Hence, we choose to take the bulge mass structure as given a priori in analyzing mass distribution in disk galaxies according to Newtonian dynamics, with our focus kept on the thin-disk portion of galaxies.

Without considering the central bulge, the mass distribution in the galactic disk can be uniquely determined from a given rotation curve. With the central bulge, its mass structure must be known a priori in order to compute a unique disk mass distribution corresponding to the given rotation curve. However, how to reliably determine the bulge mass structure besides using its luminosity information and an assumed mass-to-light ratio seems to be an open question.

Nevertheless, our illustrative analysis presented here demonstrates the general effect of a central bulge to basically shift mass from the periphery toward the center of a galaxy for a given rotation curve. The more massive a central bulge becomes, the less mass is needed in the disk periphery region according to Newtonian dynamics. Yet, the total mass in a galaxy seems to be much less sensitive to the presence or absence of a central bulge.

4.3. Rotation Velocity beyond the Cut-off Radius

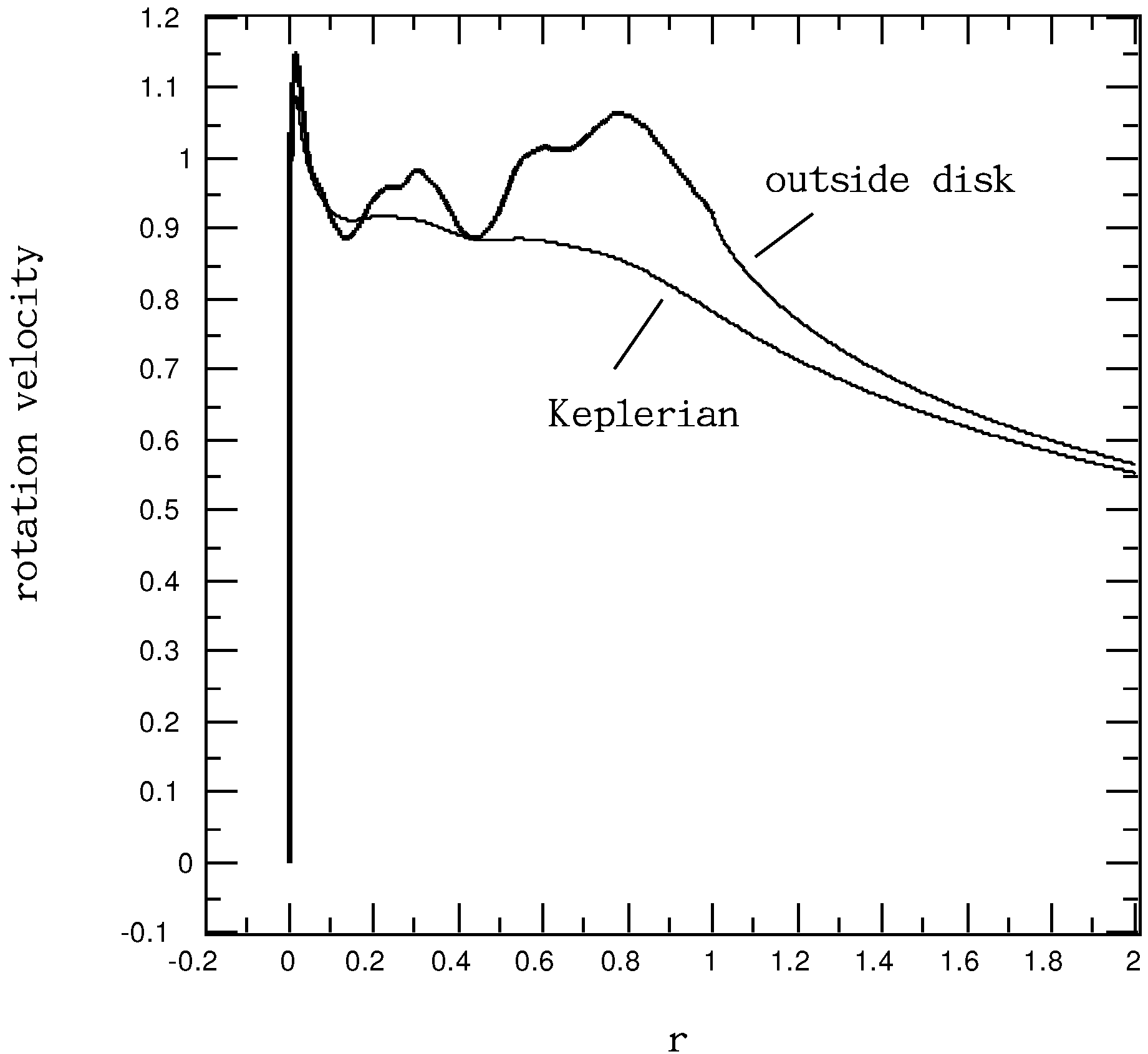
Furthermore, as shown in Section 3.1, our finite-disk galaxy model and the associated computational method can further be used to determine the rotation velocity of matters outside the cut-off radius, which we assume to be the edge of galaxy where the mass density diminishes. Again, taking the Milky Way as an example, Figure 8 shows the computed rotation velocity beyond the galactic edge $r=1$, as a continuation from the measured rotation curve that ends at $r=1$ and gradually approaching the Keplerian rotation curve for $r>2$. Here, the Keplerian rotation curve is generated by applying Keplerian dynamics:

$$V_K(r)=\sqrt{\frac{2\pi }{rA}{\int }_0^r\rho (\widehat{r})h\widehat{r}d\widehat{r}}$$

(27)

with $\rho (\widehat{r})$ and A being obtained through computations in Section 3.2. Because Keplerian dynamics cannot correctly describe the situation of disk galaxies with a non-spherically symmetric gravitational field, the rotation curve predicted by Keplerian dynamics Equation (27) from the disk mass distribution, $\rho (\widehat{r})$, differs noticeably from that of Newtonian dynamics (as depicted with the thick line and its extension in Figure 8). Only at a large distance (e.g., $r>2$) from the galactic disk does the Keplerian rotation curve approach that computed based on Newtonian dynamics, for the effect of the disk structure diminishes at a large distance, where the gravitation field of a finite disk galaxy approaches the spherically symmetric field of a point mass.

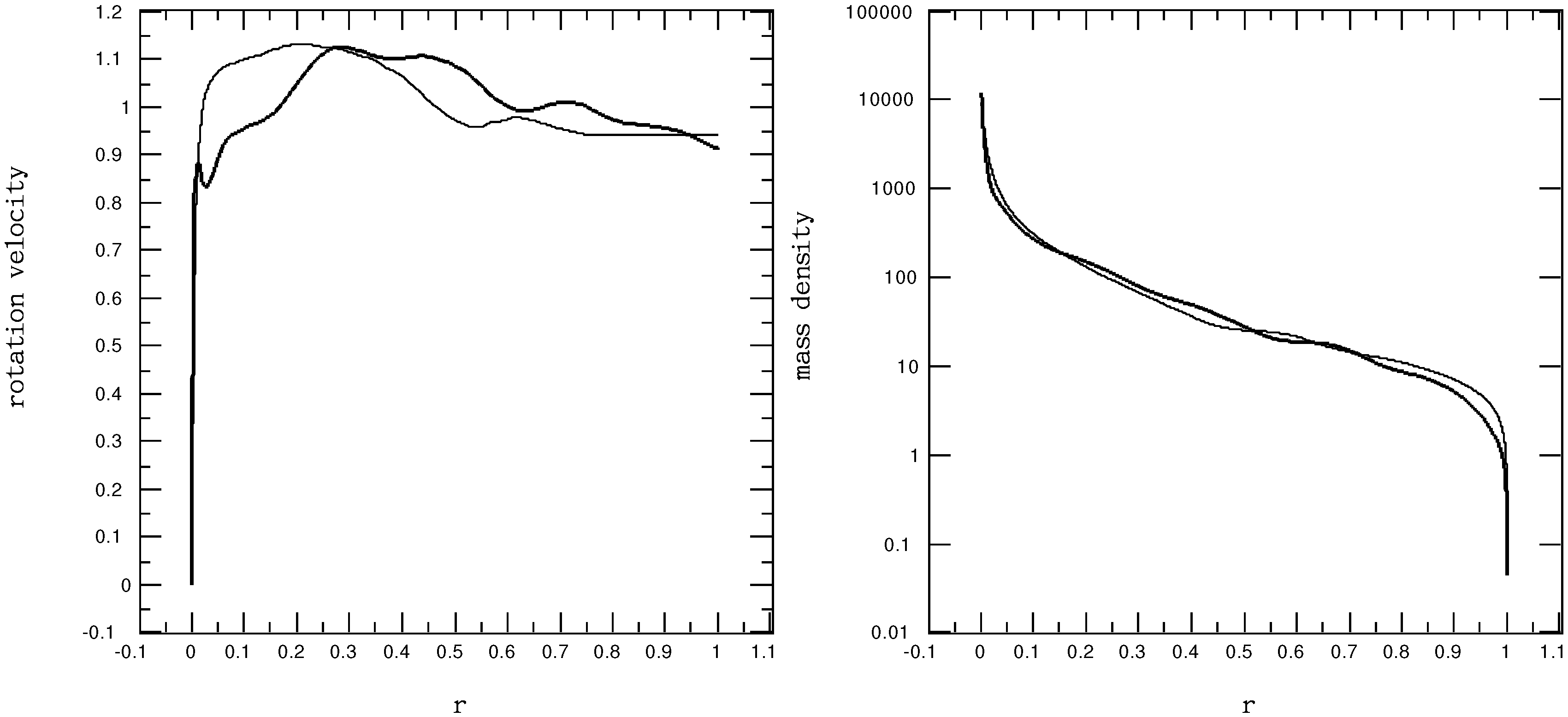
Figure 8. Profiles of the Milky Way rotation curves of the originally measured one (with imposed $V(0)=0$, thick line) and its extension outside the disk edge at $r=1$ (the thin line as labeled), as well as $V_K(r)$ according to Keplerian formula Equation (27) based on the mass density, $\rho (r)$, shown in Figure 3 (the thin line as labeled).

Figure 8. Profiles of the Milky Way rotation curves of the originally measured one (with imposed $V(0)=0$, thick line) and its extension outside the disk edge at $r=1$ (the thin line as labeled), as well as $V_K(r)$ according to Keplerian formula Equation (27) based on the mass density, $\rho (r)$, shown in Figure 3 (the thin line as labeled).

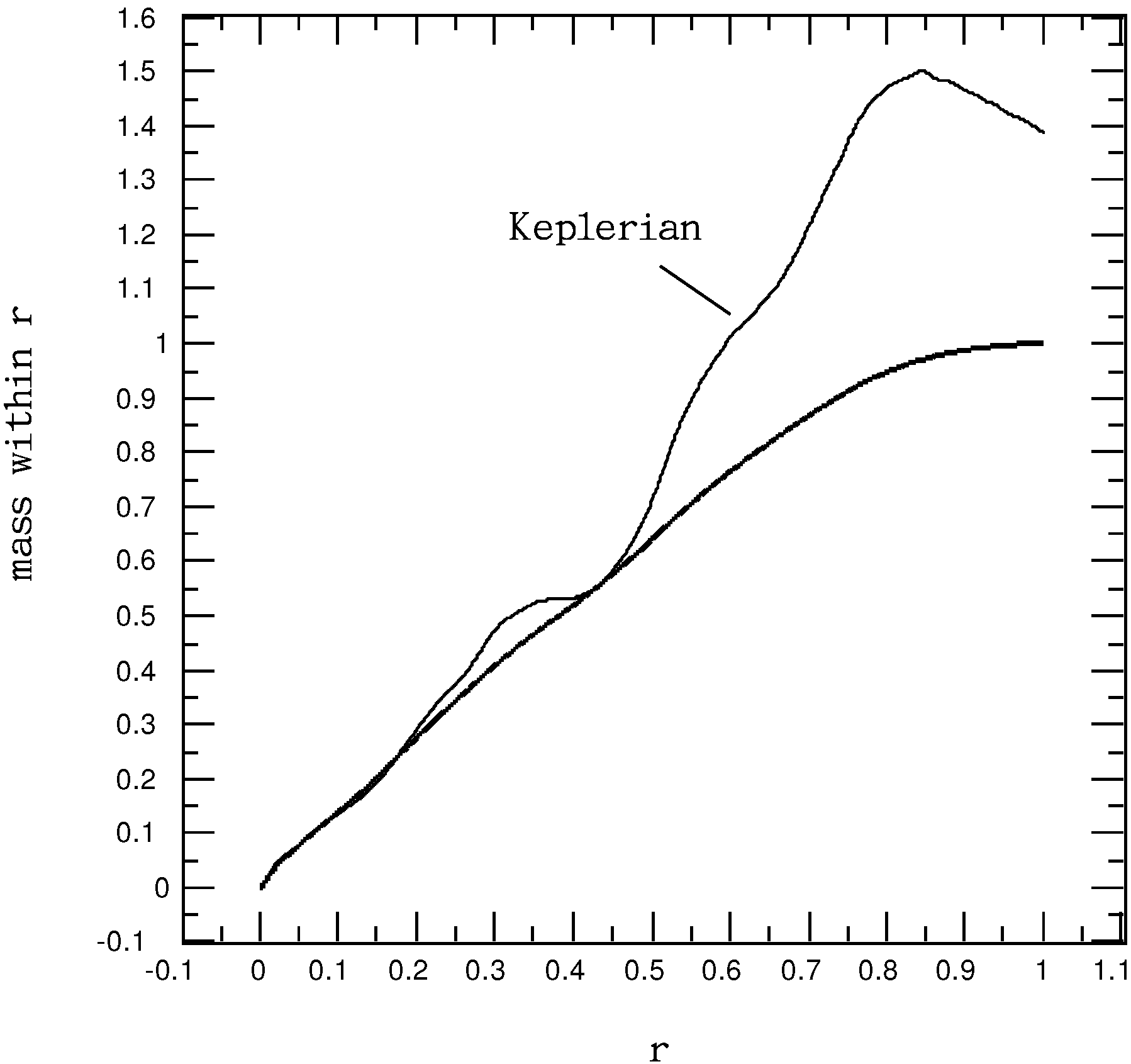
4.4. Applicability of Keplerian Dynamics

If Keplerian dynamics were applied to estimate the amount of mass within the solar radius (8 kpc corresponding to $r=0.3893$) from the measured local rotation velocity (201.0658 km/s corresponding to $V(0.3893)=0.9139$), we would obtain $M_K(r)=ArV{(r)}^2$ $=1.6365\times 0.3893\times 0.{9139}^2$$=0.5321$, which corresponds to $0.5321\times 1.4138\times {10}^{11}$ $=0.7523\times {10}^{11}$$M_{\odot }$. The actual amount of mass within the solar radius calculated using $M(r)=2\pi h{\int }_0^r\rho (\widehat{r})\widehat{r}d\widehat{r}$ at $r=0.3893$ based on the computed $\rho (r)$ in Section 3.2, is $0.5078$, which corresponds to $0.7179\times {10}^{11}$$M_{\odot }$. Although the mass within the solar radius ($r=0.3893$) estimated with Keplerian dynamics ($M_K(0.3893)$$=0.5321$) does not seem too far off the actual value ($M(0.3893)$$=0.5078$), the value of $M_K(r)$ deviates more and more from $M(r)$ with increasing r, as can be seen in Figure 9. The value of $M_K(r)$ may even decrease with r, when calculated according to the measured rotation curve (as clearly shown in Figure 8 for $r>0.85$). Because $M_K(r)$ is expected to monotonically increase with r, for there is no physical evidence of negative mass in the universe, a negative slope of $M_K(r)$ versus r indicates a failure of Keplerian dynamics for correctly predicting the mass distribution corresponding to the measured rotation curve for the Milky Way, even in a qualitative sense; or, in other words, a rotation curve that does not satisfy $d[rV{(r)}^2]/dr\ge 0$, namely:

$$\frac{dV(r)}{dr}\ge -\frac{V(r)}{2r}$$

(28)

is inconsistent with spherically symmetric gravitational potential, and thus, Keplerian dynamics becomes inapplicable in a strict sense.

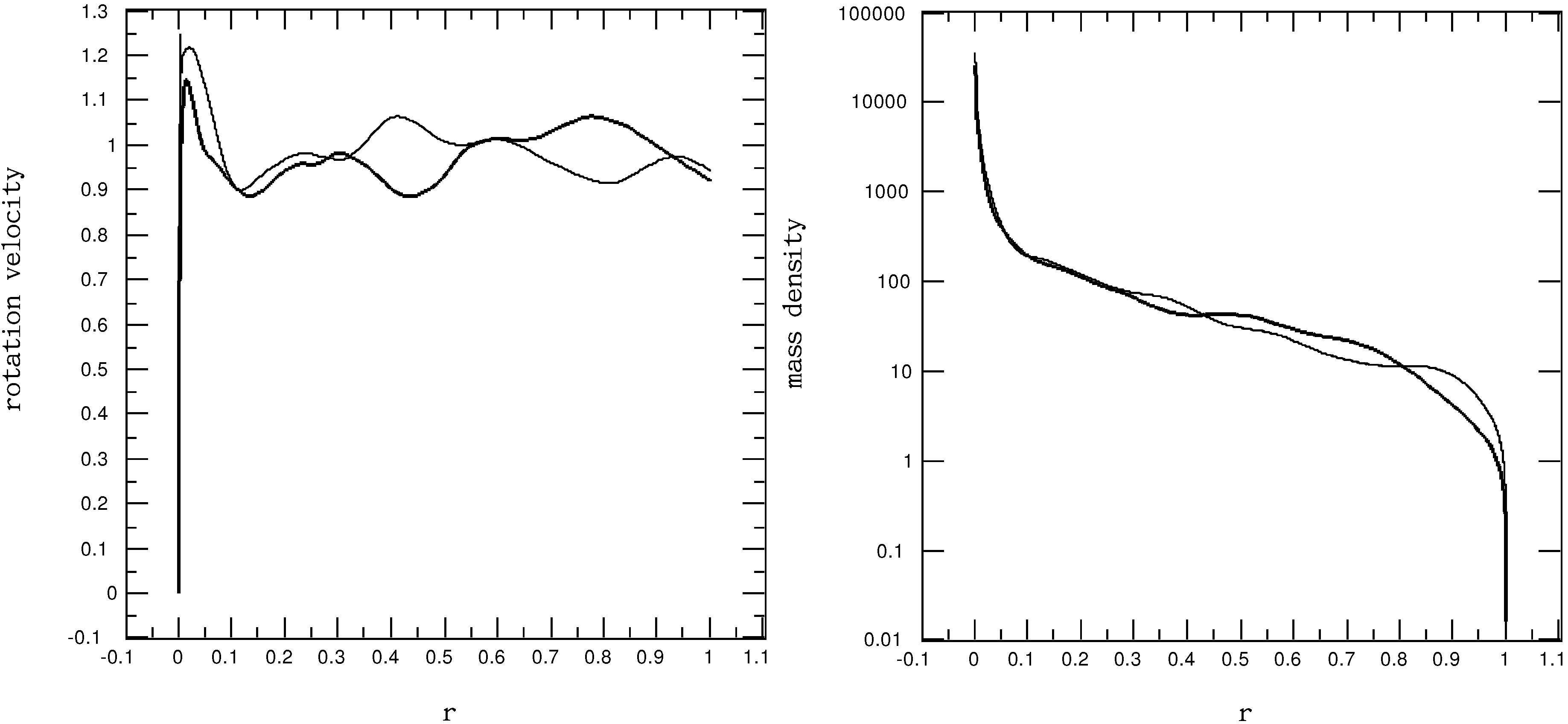
Figure 9. Profiles of the Milky Way mass within radial distance r (thick line), $M(r)=2\pi h{\int }_0^r\rho (\widehat{r})\widehat{r}d\widehat{r}$, and that estimated with Keplerian dynamics (thin line as labeled), $M_K(r)=ArV{(r)}^2$.

Figure 9. Profiles of the Milky Way mass within radial distance r (thick line), $M(r)=2\pi h{\int }_0^r\rho (\widehat{r})\widehat{r}d\widehat{r}$, and that estimated with Keplerian dynamics (thin line as labeled), $M_K(r)=ArV{(r)}^2$.

The same condition of Equation (28) was referred to as the sphericity condition by Jalocha, Bratek and Kutschera [17], Bratek, Jalocha and Kutschera [13] and Jalocha et al. [30] and the violation of which was used as an indication of the disk model being more appropriate for determining the mass distribution and the presence of a massive spherical halo of non-baryonic dark matter being unlikely. Actually, (28) is only a necessary condition for the sphericity of gravitational potential to exist, but not sufficient. A rotation curve satisfying (28) does not guarantee that it must correspond to a spherically symmetric gravitational field. Feng and Gallo [12] showed that a flat rotation curve can be described by both a spherically symmetric and an axisymmetric disk mass distribution. However, using a spherically symmetric mass model, namely Keplerian dynamics, to describe a rotating disk galaxy can lead to erroneous results and conclusions.

4.5. Circular Orbit Stability

It is interesting to note that the mathematical form of the sphericity condition Equation (28) appears quite similar to the necessary condition for circular orbit stability:

$$\frac{dV(r)}{dr}\ge -\frac{V(r)}{r}$$

(29)

which can be derived from the consideration of angular momentum conservation for a rotating object slightly deviating from its original (circular) orbit as follows. An object that is rotating with a velocity, $V(r)$, at radial coordinate r possesses an angular momentum, $rV(r)$. If it deviates from its original orbit at r to $r+\delta r$ (due to some sort of perturbations), its rotation velocity should change from V to $V+\delta V$, such that $(r+\delta r)$$(V+\delta V)$$=rV$ or $\delta V/\delta r=-V/r$ ($\le 0$, i.e., $\delta V<0$ when $\delta r>0$ and $\delta V>0$ when $\delta r<0$), according to the conservation of angular momentum. On the other hand, this object is subjected to a gravitational force at $r+\delta r$ equal to $mV{(r+\delta r)}^2/(r+\delta r)$, where m is its mass and $V(r+\delta r)$ is the rotating velocity of objects at $r+\delta r$ according to the rotation curve. Thus, for this object to be pulled back by gravitational force to its original orbit, namely for its orbit to be centrifugally stable, we must have $V+\delta V<V(r+\delta r)$ for $\delta r>0$ and $V+\delta V>V(r+\delta r)$ for $\delta r<0$. This leads to $\delta V$$<\delta rdV(r)/dr+o(\delta r^2)$ for $\delta r>0$ and $\delta V$$>\delta rdV(r)/dr+o(\delta r^2)$ for $\delta r<0$ as a result of Taylor expansion around $\delta r=0$, namely $\delta V/\delta r=-V/r<dV/dr$ as $\delta r\to 0$.

In the case of the solar system with a point mass at $r=0$, the planets rotate following the Keplerian rotation curve $dV/dr=-V/(2r)$ (taking the equal sign in Equation (28) for the mass, $M_K(r)$, does not change for $r>0$). Because $-1/2>-1$, the Keplerian rotation curve satisfies the circular orbit stability condition Equation (29), as evidenced by the existence of the solar system with many planets circling around the Sun year after year.

Many spiral galaxies exhibit nearly flat rotation curves (cf. the review of Sofue and Rubin [3]), corresponding to $dV/dr\sim 0$, which can easily satisfy Equation (29). Thus, the rotating matter distributed in circular orbits of the galactic disk, as can be computed with the method illustrated in the present work, for flat rotation curves are stable in the sense similar to that of the planets circling around the Sun. However, Equation (29) is only a necessary condition for stability. There have been many other (necessary) conditions proposed in the literature for rotating disk galaxy stability, which often seem controversial, as critically discussed by Jalocha et al. [30]. The circular orbit stability condition Equation (29) derived in the present work is established from a concrete physical principle and can be used to examine the validity of measured rotation curves. Especially for those rotation curves containing decreasing velocity at a large radius, the stability condition Equation (29) with its right side $\propto -1/r$ is likely violated. The portion of a rotation curve not satisfying Equation (29) may point to the issues with too serious deviations from circular orbits and axisymmetry due to the spiral arms. After all, the axisymmetric disk model with rotation velocity depending only on radius is a tremendous simplification of a realistic rotating galaxy; such a simplified description of reality should be regularly checked for consistency.

For the Milky Way rotation curve (cf. Figure 3), the portion of $r>0.8$ has $dV/dr\sim -0.75$, while $0.9<V/r<1.32$. Thus, we have $-0.75>-0.9$, which satisfies the circular orbit stability condition Equation (29), but not the sphericity condition (28), which is consistent with that shown in Figure 9. Thus, the Milky Way appears to be appropriately described with the thin-disk model or with a combination of a central bulge and a thin disk.

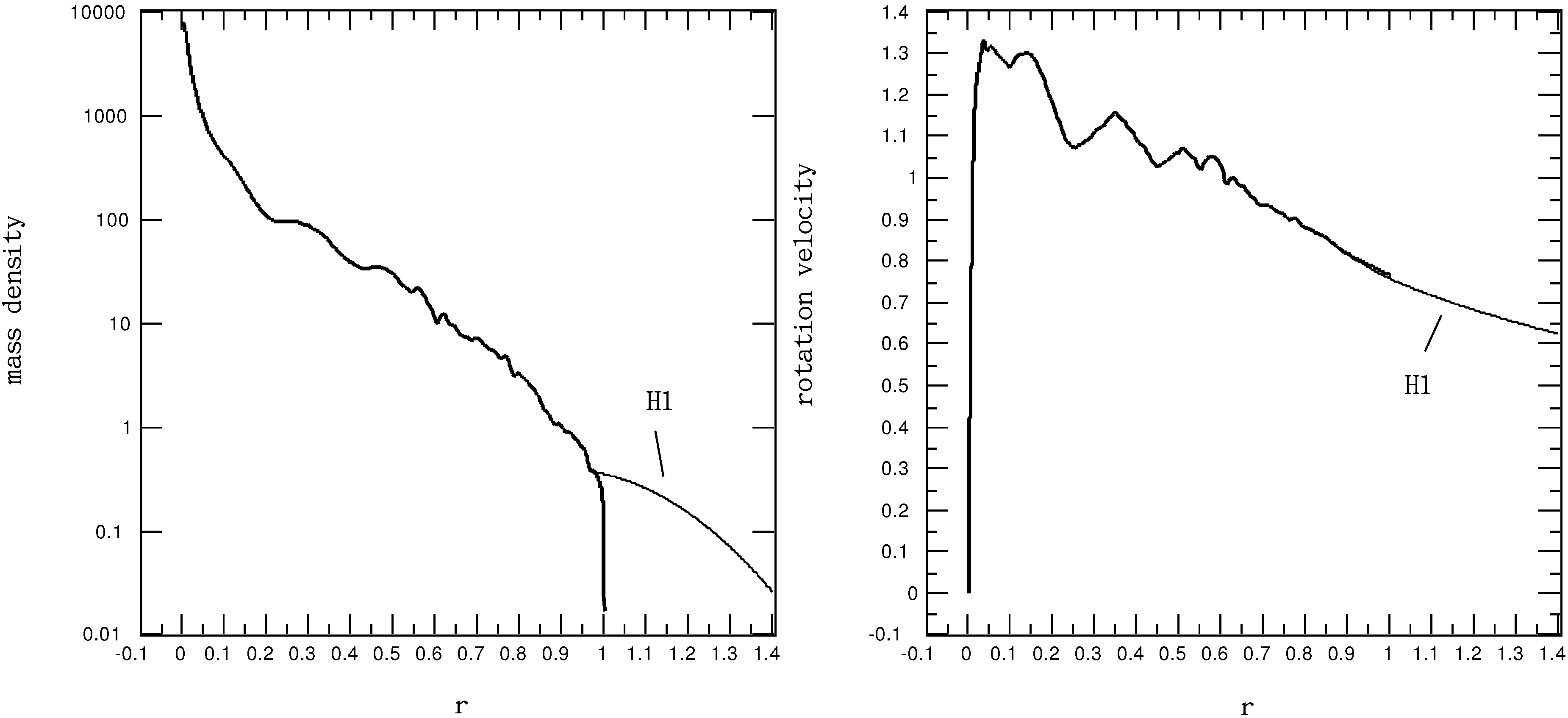
For the NGC 4736 rotation curve of Sofue (cf. Figure 1), the negative slope in the outer region $r>0.6$ is $dV/dr\sim -0.875$, while $0.85<V/r<2$. Thus, circular orbit instability is likely to occur in the outer region of NGC 4736 if the rotating matter indeed follows the rotation curve of Sofue. In a relative sense, the THINGS version of the NGC 4736 rotation curve [20] has a less steep negative slope than that of Sofue, indicating that the THINGS version describes a more stable circular motion of rotating matter.

5. Conclusions

With the computational method presented here, mass distributions in mature spiral galaxies corresponding to various types of measured rotation curves can be accurately determined by solving a linear algebra matrix equation, which clarifies the uniqueness of the solution when it exists. Our formulation for the finite thin-disk model is based solely on Newtonian dynamics without the need of fictitious rotation velocity outside the cut-off radius, with a belief that the cut-off radius in the rotation curve measurement is a consequence of the absence of matter beyond such a galactocentric distance. All the mass density profiles predicted by our model for various galaxies exhibit approximately a common exponential law of decay (if the two abruptly varying ends are trimmed out), qualitatively consistent with typically observed luminosity measurements. Thus, we think Newtonian dynamics can be quite adequate for self-consistently describing the rotation behavior of mature spiral galaxies.

Despite difficulties in clarifying the physical meaning, nonzero rotation velocities at the galactic center ($r=0$) were reported in rotation curve measurements for several galaxies [27]. The nonzero value of rotation velocity at $r=0$ mathematically corresponds to unbounded local mass density in the pure disk model, which is intractable in numerical computations. Such a numerical challenge can be avoided by placing a small spherical core at $r=0$. Thus, the rotation velocity in the galactic disk is modified accordingly by subtracting out the spherical core effect, and the disk mass distribution can be consistently computed from the modified rotation curve. As long as the size of the spherical core is sufficiently small, our computed results show that no noticeable change in the disk mass distribution that can be observed while the nonzero velocity at $r=0$ being elegantly dealt with.

To examine the basic effect of an observed central bulge, we assume a spherically symmetric mass structure for the bulge, whose gravitational effect can be conveniently incorporated in our thin-disk formulation. Our results indicate that the presence of a central bulge tends to shift mass from the periphery toward the galactic center with little change in the total galactic mass.

Extending the computational domain beyond the galactic edge enables us to also compute rotation velocity outside the cut-off radius. Beyond the galactic edge where the mass density should be negligible, the computed rotation velocity does not follow the Keplerian profile until out over $r>2$.

By applying the principle of angular momentum conservation, a necessary condition for circular orbit stability can be derived. It appears that the galaxies with flat or rising rotation velocities are more stable than those with declining rotation velocities. Especially in the region near the galactic edge, those rotation curves having too steep of a negative slope are likely to violate the condition for circular orbit stability, and therefore, their validity for realistically describing galactic rotational characteristics may become questionable.