The I-Love Universal Relation for Polytropic Stars Under Newtonian Gravity
Abstract
1. Introduction
2. I-Love Universal Relations for Polytropic Stars
2.1. Newtonian Gravity
2.2. General Relativity
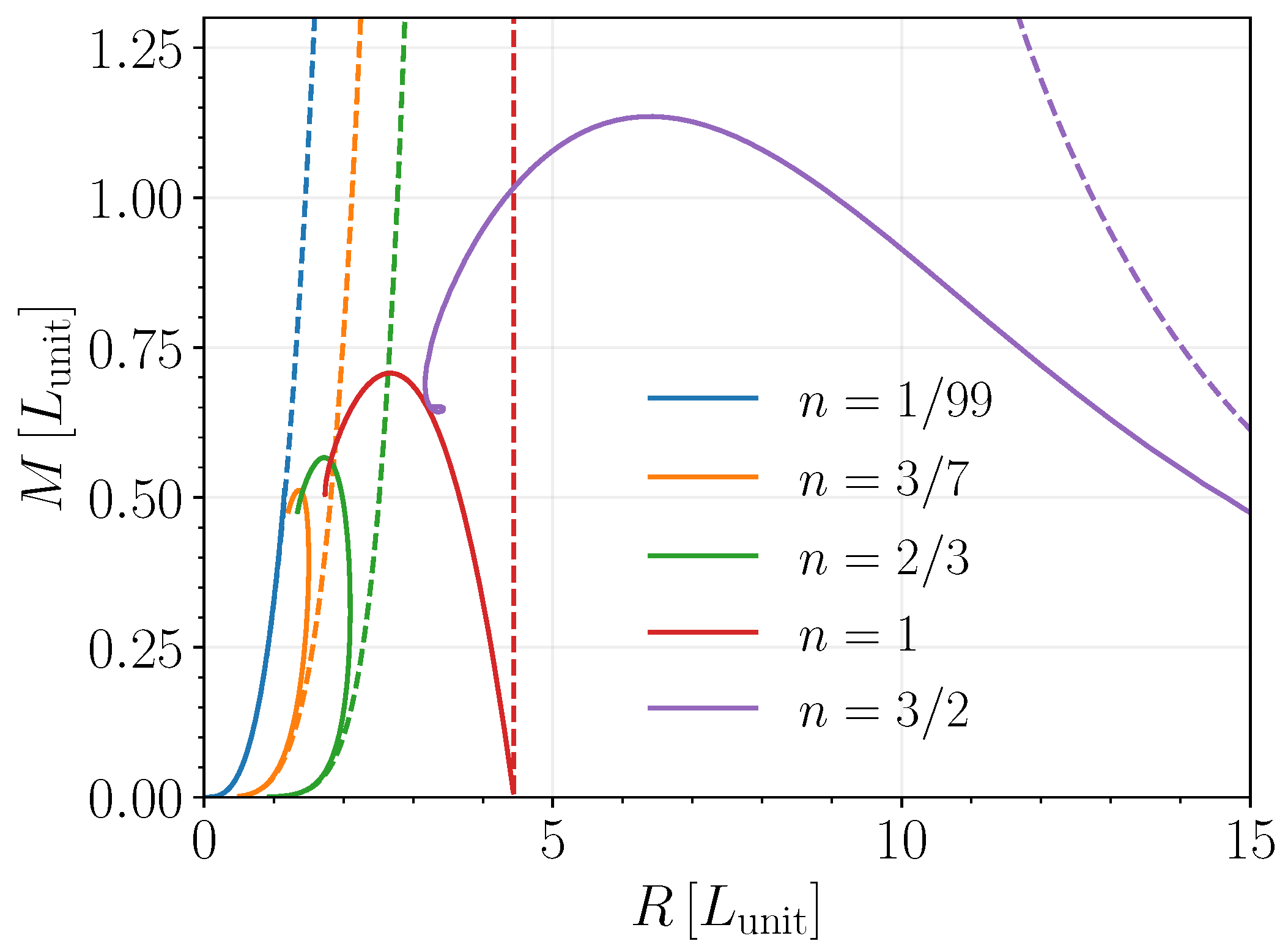
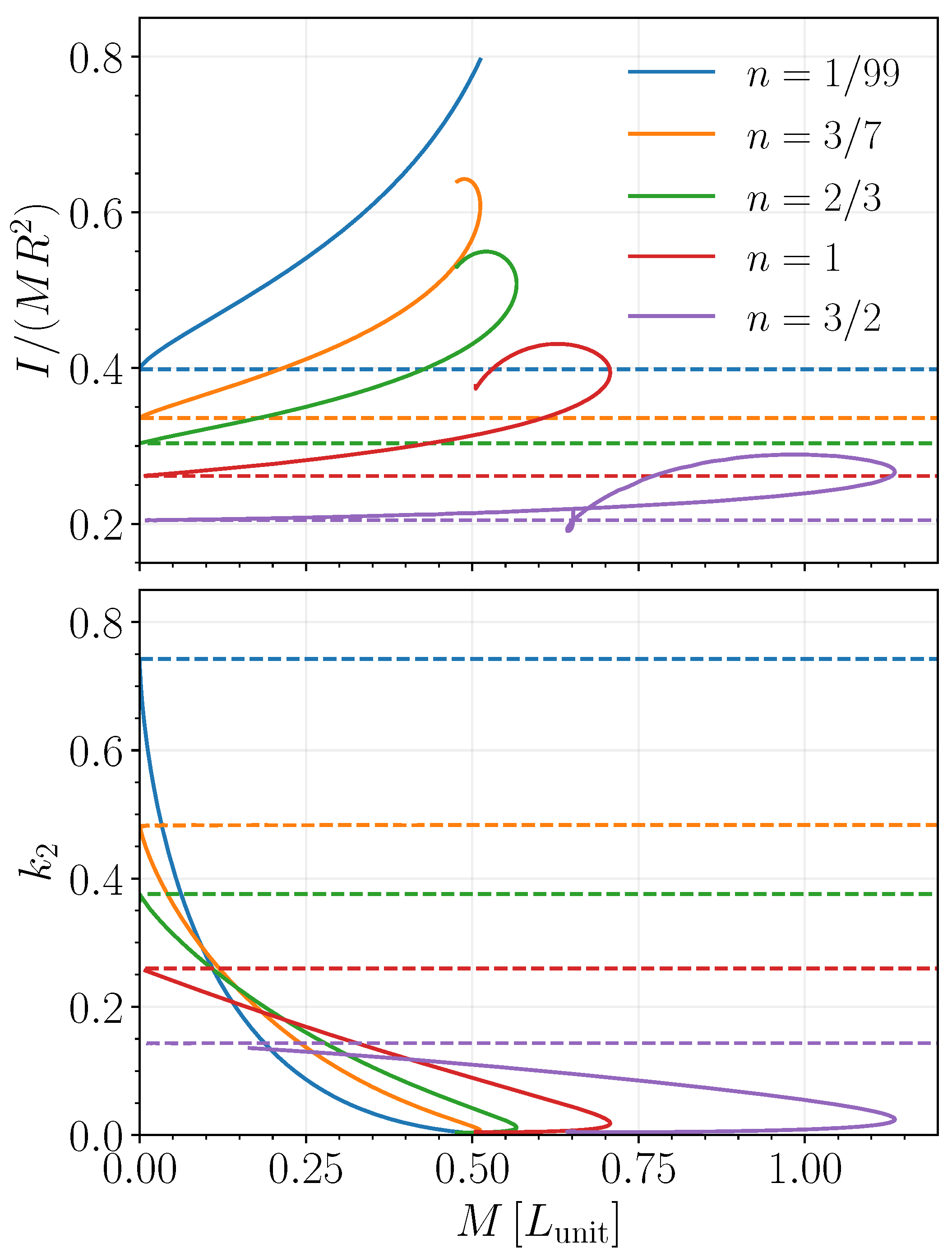
2.3. Numerical Results
2.4. Checking Against the Planets in the Solar System
3. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
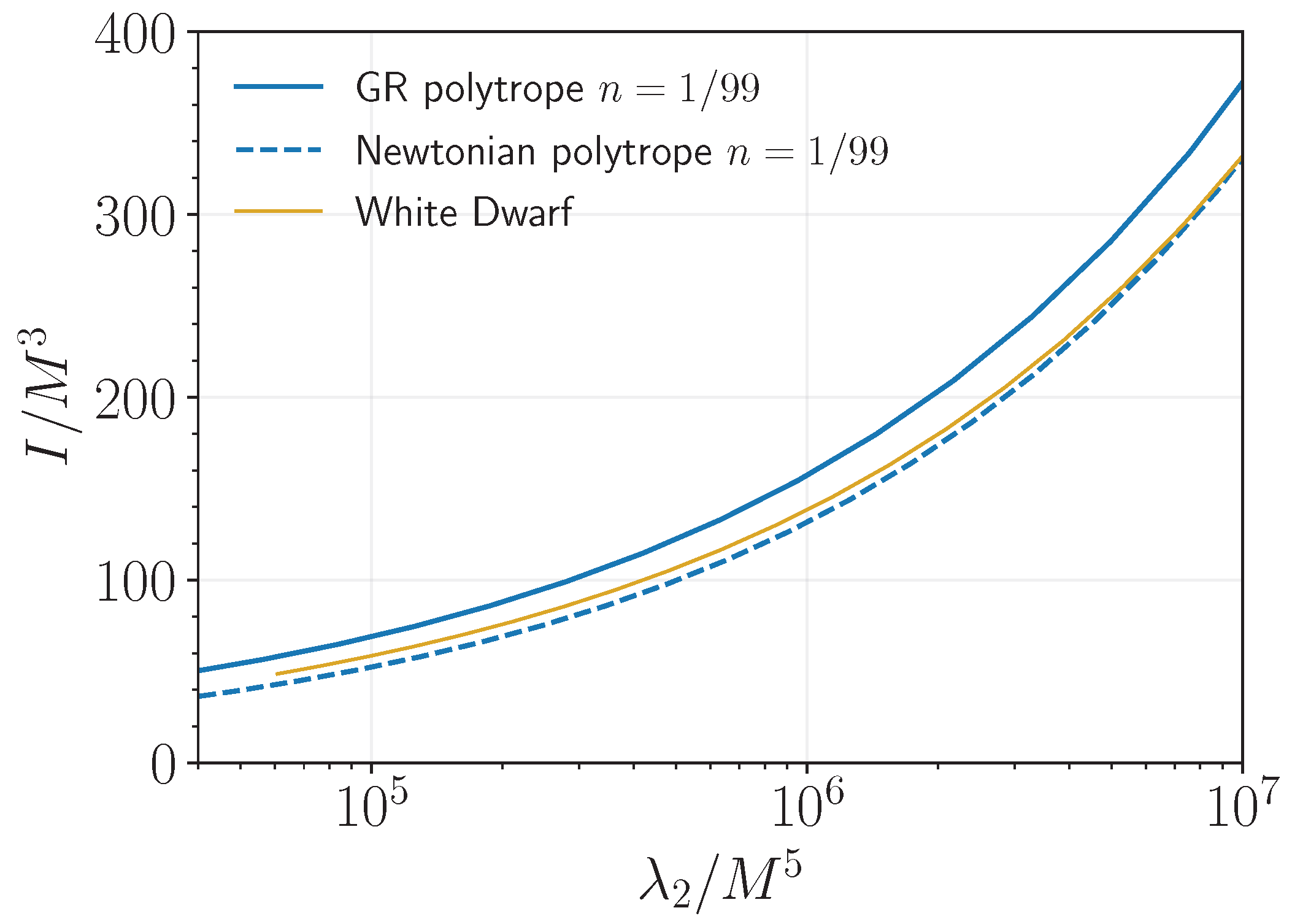
Appendix A. Zero-Temperature White Dwarfs

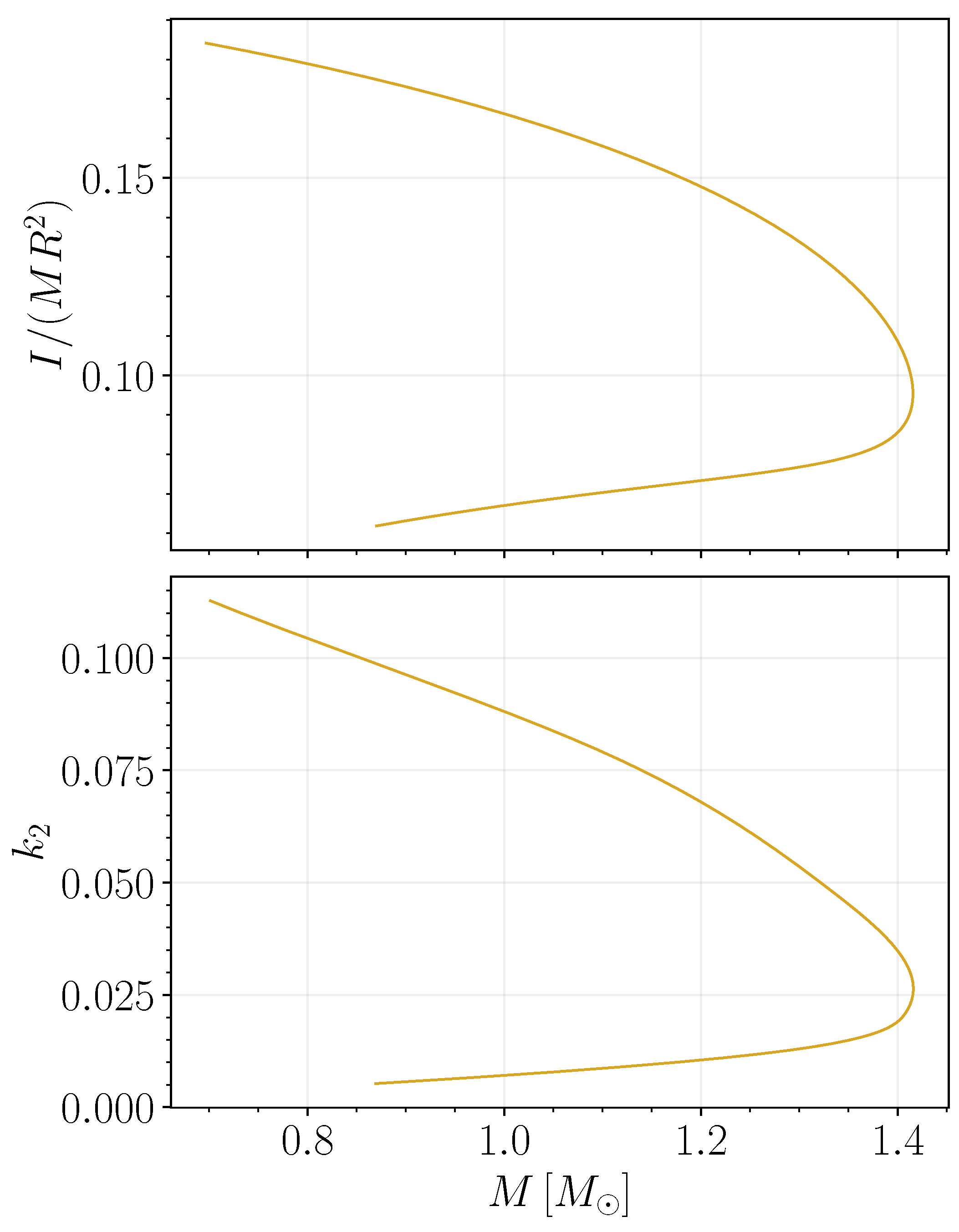
| 1 | We thank the referee for pointing it out. |
References
- Yagi, K.; Yunes, N. I-Love-Q. Science 2013, 341, 365–368. [Google Scholar] [CrossRef] [PubMed]
- Yagi, K.; Yunes, N. I-Love-Q Relations in Neutron Stars and their Applications to Astrophysics, Gravitational Waves and Fundamental Physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Stein, L.C.; Yagi, K.; Yunes, N. Three-Hair Relations for Rotating Stars: Nonrelativistic Limit. Astrophys. J. 2014, 788, 15. [Google Scholar] [CrossRef]
- Yagi, K. Multipole Love Relations. Phys. Rev. D 2014, 89, 043011, Erratum in Phys. Rev. D 2017, 96, 129904; Erratum in Phys. Rev. D 2018, 97, 129901. [Google Scholar] [CrossRef]
- Yagi, K.; Kyutoku, K.; Pappas, G.; Yunes, N.; Apostolatos, T.A. Effective No-Hair Relations for Neutron Stars and Quark Stars: Relativistic Results. Phys. Rev. D 2014, 89, 124013. [Google Scholar] [CrossRef]
- Pani, P.; Gualtieri, L.; Ferrari, V. Tidal Love numbers of a slowly spinning neutron star. Phys. Rev. D 2015, 92, 124003. [Google Scholar] [CrossRef]
- Delsate, T. I-Love relations for irrotational stars. Phys. Rev. D 2015, 92, 124001. [Google Scholar] [CrossRef]
- Bretz, J.; Yagi, K.; Yunes, N. Four-Hair Relations for Differentially Rotating Neutron Stars in the Weak-Field Limit. Phys. Rev. D 2015, 92, 083009. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rept. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Chan, T.K.; Sham, Y.H.; Leung, P.T.; Lin, L.M. Multipolar universal relations between f-mode frequency and tidal deformability of compact stars. Phys. Rev. D 2014, 90, 124023. [Google Scholar] [CrossRef]
- Chirenti, C.; de Souza, G.H.; Kastaun, W. Fundamental oscillation modes of neutron stars: Validity of universal relations. Phys. Rev. D 2015, 91, 044034. [Google Scholar] [CrossRef]
- Doneva, D.D.; Kokkotas, K.D. Asteroseismology of rapidly rotating neutron stars—An alternative approach. Phys. Rev. D 2015, 92, 124004. [Google Scholar] [CrossRef]
- Krüger, C.J.; Kokkotas, K.D. Fast Rotating Relativistic Stars: Spectra and Stability without Approximation. Phys. Rev. Lett. 2020, 125, 111106. [Google Scholar] [CrossRef]
- Pappas, G.; Apostolatos, T.A. Effectively universal behavior of rotating neutron stars in general relativity makes them even simpler than their Newtonian counterparts. Phys. Rev. Lett. 2014, 112, 121101. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Delsate, T.; Gürlebeck, N.; Steinhoff, J. I-Q relation for rapidly rotating neutron stars. Phys. Rev. Lett. 2014, 112, 201102. [Google Scholar] [CrossRef]
- Manoharan, P.; Kokkotas, K.D. Finding universal relations using statistical data analysis. Phys. Rev. D 2024, 109, 103033. [Google Scholar] [CrossRef]
- Maselli, A.; Cardoso, V.; Ferrari, V.; Gualtieri, L.; Pani, P. Equation-of-state-independent relations in neutron stars. Phys. Rev. D 2013, 88, 023007. [Google Scholar] [CrossRef]
- Vretinaris, S.; Stergioulas, N.; Bauswein, A. Empirical relations for gravitational-wave asteroseismology of binary neutron star mergers. Phys. Rev. D 2020, 101, 084039. [Google Scholar] [CrossRef]
- Manoharan, P.; Krüger, C.J.; Kokkotas, K.D. Universal relations for binary neutron star mergers with long-lived remnants. Phys. Rev. D 2021, 104, 023005. [Google Scholar] [CrossRef]
- Guedes, V.; Lau, S.Y.; Chirenti, C.; Yagi, K. Broadening of universal relations at the birth and death of a neutron star. Phys. Rev. D 2024, 109, 083040. [Google Scholar] [CrossRef]
- Yagi, K.; Stein, L.C.; Pappas, G.; Yunes, N.; Apostolatos, T.A. Why I-Love-Q: Explaining why universality emerges in compact objects. Phys. Rev. D 2014, 90, 063010. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Novel ‘‘no-scalar-hair’’ theorem for black holes. Phys. Rev. D 1995, 51, R6608. [Google Scholar] [CrossRef] [PubMed]
- Doneva, D.D.; Yazadjiev, S.S.; Stergioulas, N.; Kokkotas, K.D. Breakdown of I-Love-Q universality in rapidly rotating relativistic stars. Astrophys. J. Lett. 2013, 781, L6. [Google Scholar] [CrossRef]
- Taylor, A.; Yagi, K.; Arras, P.L. I–Love–Q relations for realistic white dwarfs. Mon. Not. Roy. Astron. Soc. 2020, 492, 978–992. [Google Scholar] [CrossRef]
- Chen, K.; Lin, L.M. Fully general relativistic simulations of rapidly rotating quark stars: Oscillation modes and universal relations. Phys. Rev. D 2023, 108, 064007. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.B.; Berti, E.; Crispino, L.C.B. Slowly rotating anisotropic neutron stars in general relativity and scalar–tensor theory. Class. Quant. Grav. 2015, 32, 145008. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q anisotropically: Universal relations for compact stars with scalar pressure anisotropy. Phys. Rev. D 2015, 91, 123008. [Google Scholar] [CrossRef]
- Martinon, G.; Maselli, A.; Gualtieri, L.; Ferrari, V. Rotating protoneutron stars: Spin evolution, maximum mass, and I-Love-Q relations. Phys. Rev. D 2014, 90, 064026. [Google Scholar] [CrossRef]
- Yeung, C.H.; Lin, L.M.; Andersson, N.; Comer, G. The I-Love-Q Relations for Superfluid Neutron Stars. Universe 2021, 7, 111. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Koliogiannis, P.S.; Kanakis-Pegios, A.; Moustakidis, C.C. Universal relations and finite temperature neutron stars. HNPS Adv. Nucl. Phys. 2023, 29, 94–99. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Staykov, K.V.; Kokkotas, K.D. Universal I-Q relations for rapidly rotating neutron and strange stars in scalar-tensor theories. Phys. Rev. D 2014, 90, 104021. [Google Scholar] [CrossRef]
- Doneva, D.D.; Pappas, G. Universal Relations and Alternative Gravity Theories. Astrophys. Space Sci. Libr. 2018, 457, 737–806. [Google Scholar] [CrossRef]
- Gupta, T.; Majumder, B.; Yagi, K.; Yunes, N. I-Love-Q Relations for Neutron Stars in dynamical Chern Simons Gravity. Class. Quant. Grav. 2018, 35, 025009. [Google Scholar] [CrossRef]
- Pappas, G.; Doneva, D.D.; Sotiriou, T.P.; Yazadjiev, S.S.; Kokkotas, K.D. Multipole moments and universal relations for scalarized neutron stars. Phys. Rev. D 2019, 99, 104014. [Google Scholar] [CrossRef]
- Hu, Z.; Gao, Y.; Xu, R.; Shao, L. Scalarized neutron stars in massive scalar-tensor gravity: X-ray pulsars and tidal deformability. Phys. Rev. D 2021, 104, 104014. [Google Scholar] [CrossRef]
- Xu, R.; Gao, Y.; Shao, L. Neutron stars in massive scalar-Gauss-Bonnet gravity: Spherical structure and time-independent perturbations. Phys. Rev. D 2022, 105, 024003. [Google Scholar] [CrossRef]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S. New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef]
- Sham, Y.H.; Chan, T.K.; Lin, L.M.; Leung, P.T. Unveiling the universality of I-Love-Q relations. Astrophys. J. 2015, 798, 121. [Google Scholar] [CrossRef]
- Yip, K.L.S.; Leung, P.T. Tidal Love numbers and moment-Love relations of polytropic stars. Mon. Not. Roy. Astron. Soc. 2017, 472, 4965–4981. [Google Scholar] [CrossRef]
- Poisson, E.; Will, C.M. Gravity: Newtonian, Post-Newtonian, Relativistic; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Thorne, K.S. Multipole Expansions of Gravitational Radiation. Rev. Mod. Phys. 1980, 52, 299–339. [Google Scholar] [CrossRef]
- Hartle, J.B. Slowly rotating relativistic stars. 1. Equations of structure. Astrophys. J. 1967, 150, 1005–1029. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
- Regge, T.; Wheeler, J.A. Stability of a Schwarzschild singularity. Phys. Rev. 1957, 108, 1063–1069. [Google Scholar] [CrossRef]
- Andersson, N.; Comer, G.L. Relativistic fluid dynamics: Physics for many different scales. Living Rev. Rel. 2007, 10, 1. [Google Scholar] [CrossRef]
- Chabanat, E.; Meyer, J.; Bonche, P.; Schaeffer, R.; Haensel, P. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. 2. Nuclei far from stablities. Nucl. Phys. A 1998, 635, 231–256, Erratum in Nucl. Phys. A 1998, 643, 441–441. [Google Scholar] [CrossRef]
- Chan, T.K.; Chan, A.P.O.; Leung, P.T. I-Love relations for incompressible stars and realistic stars. Phys. Rev. D 2015, 91, 044017. [Google Scholar] [CrossRef]
- Chan, T.K.; Chan, A.P.O.; Leung, P.T. Universality and stationarity of the I-Love relation for self-bound stars. Phys. Rev. D 2016, 93, 024033. [Google Scholar] [CrossRef]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S. Moment-of-inertia-compactness universal relations in scalar-tensor theories and R2 gravity. Phys. Rev. D 2016, 93, 084010. [Google Scholar] [CrossRef]
- Genova, A.; Goossens, S.; Mazarico, E.; Lemoine, F.G.; Neumann, G.A.; Kuang, W.; Sabaka, T.J.; Hauck, S.A.; Smith, D.E.; Solomon, S.C.; et al. Geodetic Evidence That Mercury Has A Solid Inner Core. Geophys. Res. Lett. 2019, 46, 3625–3633. [Google Scholar] [CrossRef]
- Wahl, S.M.; Hubbard, W.B.; Militzer, B. Tidal Response of Preliminary Jupiter Model. Astrophys. J. 2016, 831, 14. [Google Scholar] [CrossRef]
- Fortney, J.J.; Helled, R.; Nettelmann, N.; Stevenson, D.J.; Marley, M.S.; Hubbard, W.B.; Iess, L. The Interior of Saturn. In Saturn in the 21st Century; Baines, K.H., Flasar, F.M., Krupp, N., Stallard, T., Eds.; Cambridge University Press: Cambridge, UK, 2018; pp. 44–68. [Google Scholar] [CrossRef]
- Stixrude, L.; Baroni, S.; Grasselli, F. Thermal and Tidal Evolution of Uranus with a Growing Frozen Core. Planet. Sci. J. 2021, 2, 222. [Google Scholar] [CrossRef]
- James, D.A.; Stixrude, L. Thermal and Tidal Evolution of Ice Giants with Growing Frozen Cores: The Case of Neptune. Space Sci. Rev. 2024, 220, 21. [Google Scholar] [CrossRef]
- McCord, T.B.; Sotin, C. Ceres: Evolution and current state. J. Geophys. Res. (Planets) 2005, 110, E05009. [Google Scholar] [CrossRef]
- Mao, X.; McKinnon, W.B. Faster paleospin and deep-seated uncompensated mass as possible explanations for Ceres’ present-day shape and gravity. Icarus 2018, 299, 430–442. [Google Scholar] [CrossRef]
- Zharkov, V.N.; Gudkova, T.V. Models, figures and gravitational moments of Jupiter’s satellite Io: Effects of the second order approximation. Planet. Space Sci. 2010, 58, 1381–1390. [Google Scholar] [CrossRef]
- Kervazo, M.; Tobie, G.; Choblet, G.; Dumoulin, C.; Běhounková, M. Inferring Io’s interior from tidal monitoring. Icarus 2022, 373, 114737. [Google Scholar] [CrossRef]
- Schubert, G.; Anderson, J.D.; Spohn, T.; McKinnon, W.B. Interior composition, structure and dynamics of the Galilean satellites. In Jupiter. The Planet, Satellites and Magnetosphere; Bagenal, F., Dowling, T.E., McKinnon, W.B., Eds.; Cambridge University Press: Cambridge, UK, 2004; Volume 1, pp. 281–306. [Google Scholar]
- Petricca, F.; Tharimena, S.; Melini, D.; Spada, G.; Bagheri, A.; Styczinski, M.J.; Vance, S.D. Exploring the tidal responses of ocean worlds with PyALMA3. Icarus 2024, 417, 116120. [Google Scholar] [CrossRef]
- Van Hoolst, T.; Tobie, G.; Vallat, C.; Altobelli, N.; Bruzzone, L.; Cao, H.; Dirkx, D.; Genova, A.; Hussmann, H.; Iess, L.; et al. Geophysical Characterization of the Interiors of Ganymede, Callisto and Europa by ESA’s JUpiter ICy moons Explorer. Space Sci. Rev. 2024, 220, 54. [Google Scholar] [CrossRef]
- Moore, W.B.; Schubert, G. The tidal response of Ganymede and Callisto with and without liquid water oceans. Icarus 2003, 166, 223–226. [Google Scholar] [CrossRef]
- Iess, L.; Jacobson, R.A.; Ducci, M.; Stevenson, D.J.; Lunine, J.I.; Armstrong, J.W.; Asmar, S.W.; Racioppa, P.; Rappaport, N.J.; Tortora, P. The Tides of Titan. Science 2012, 337, 457. [Google Scholar] [CrossRef]
- Durante, D.; Hemingway, D.J.; Racioppa, P.; Iess, L.; Stevenson, D.J. Titan’s gravity field and interior structure after Cassini. Icarus 2019, 326, 123–132. [Google Scholar] [CrossRef]
- Genova, A.; Parisi, M.; Gargiulo, A.M.; Petricca, F.; Andolfo, S.; Torrini, T.; Del Vecchio, E.; Glein, C.R.; Cable, M.L.; Phillips, C.B.; et al. Gravity Investigation to Characterize Enceladus’s Ocean and Interior. Planet. Sci. J. 2024, 5, 40. [Google Scholar] [CrossRef]
- Anderson, J.D.; Schubert, G. Saturn’s satellite Rhea is a homogeneous mix of rock and ice. Geophys. Res. Lett. 2007, 34, L02202. [Google Scholar] [CrossRef]
- Stevenson, D.J. Jupiter’s Interior as Revealed by Juno. Annu. Rev. Earth Planet. Sci. 2020, 48, 465–489. [Google Scholar] [CrossRef]
- Verma, A.K.; Margot, J.L. Mercury’s gravity, tides, and spin from MESSENGER radio science data. J. Geophys. Res. (Planets) 2016, 121, 1627–1640. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Yoder, C.F. Venusian k 2 tidal Love number from Magellan and PVO tracking data. Geophys. Res. Lett. 1996, 23, 1857–1860. [Google Scholar] [CrossRef]
- Margot, J.L.; Campbell, D.B.; Giorgini, J.D.; Jao, J.S.; Snedeker, L.G.; Ghigo, F.D.; Bonsall, A. Spin state and moment of inertia of Venus. Nat. Astron. 2021, 5, 676–683. [Google Scholar] [CrossRef]
- Williams, J.G. Contribution to the Earth’s Obliquity Rate, Precession, and Nutation. Astron. J. 1994, 108, 711. [Google Scholar] [CrossRef]
- Jagoda, M.; Rutkowska, M. Estimation of the Love numbers: K 2, k 3 using SLR data of the LAGEOS1, LAGEOS2, STELLA and STARLETTE satellites. Acta Geod. Et Geophys. 2016, 51, 493–504. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Asmar, S.W.; Folkner, W.M.; Karatekin, Ö.; Nunes, D.C.; Smrekar, S.E.; Yoder, C.F.; Zuber, M.T. Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters. Icarus 2011, 211, 401–428. [Google Scholar] [CrossRef]
- Konopliv, A.S.; Park, R.S.; Rivoldini, A.; Baland, R.M.; Le Maistre, S.; Van Hoolst, T.; Yseboodt, M.; Dehant, V. Detection of the Chandler Wobble of Mars From Orbiting Spacecraft. Geophys. Res. Lett. 2020, 47, e90568. [Google Scholar] [CrossRef]
- Ni, D. Empirical models of Jupiter’s interior from Juno data. Moment of inertia and tidal Love number k2. Astron. Astrophys. 2018, 613, A32. [Google Scholar] [CrossRef]
- Lainey, V.; Dewberry, J.W.; Fuller, J.; Cooper, N.; Rambaux, N.; Zhang, Q. Tidal frequency dependence of the Saturnian k2 Love number. Astron. Astrophys. 2024, 684, L3. [Google Scholar] [CrossRef]
- Yoder, C.F. Astrometric and Geodetic Properties of Earth and the Solar System. In Global Earth Physics: A Handbook of Physical Constants; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; p. 1. [Google Scholar]
- Williams, J.G.; Newhall, X.X.; Dickey, J.O. Lunar moments, tides, orientation, and coordinate frames. Planet. Space Sci. 1996, 44, 1077–1080. [Google Scholar] [CrossRef]
- Williams, J.G.; Konopliv, A.S.; Boggs, D.H.; Park, R.S.; Yuan, D.N.; Lemoine, F.G.; Goossens, S.; Mazarico, E.; Nimmo, F.; Weber, R.C.; et al. Lunar interior properties from the GRAIL mission. J. Geophys. Res. (Planets) 2014, 119, 1546–1578. [Google Scholar] [CrossRef]
- Bourda, G.; Capitaine, N. Precession, nutation, and space geodetic determination of the Earth’s variable gravity field. Astron. Astrophys. 2004, 428, 691–702. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley-VCH: Weinheim, Germany, 1983. [Google Scholar] [CrossRef]
- Chandrasekhar, S. An Introduction to the Study of Stellar Structure; Dover Publications: Mineola, NY, USA, 2010. [Google Scholar]
- Boshkayev, K.; Quevedo, H.; Zhami, B. I -Love- Q relations for white dwarf stars. Mon. Not. Roy. Astron. Soc. 2017, 464, 4349–4359. [Google Scholar] [CrossRef]
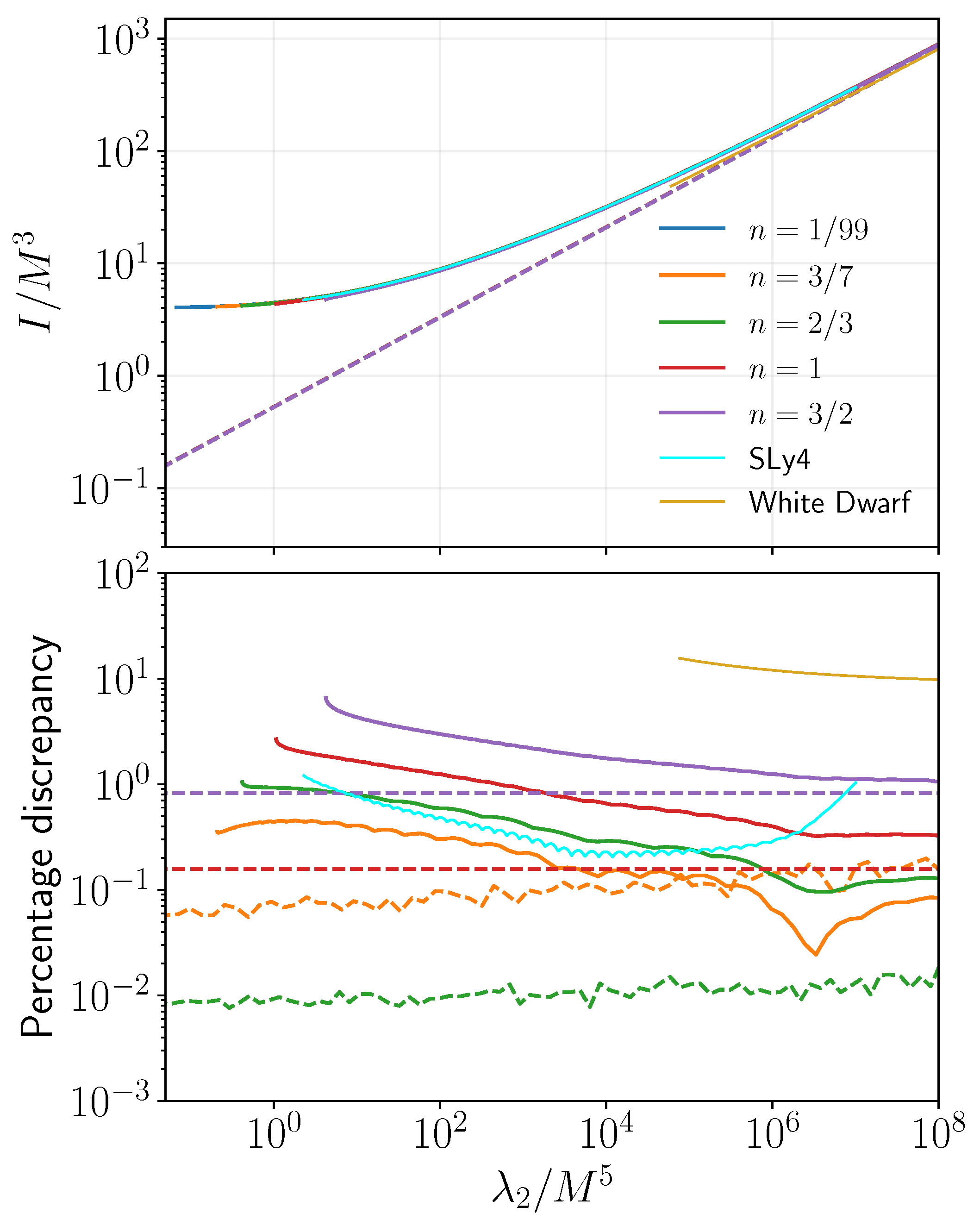

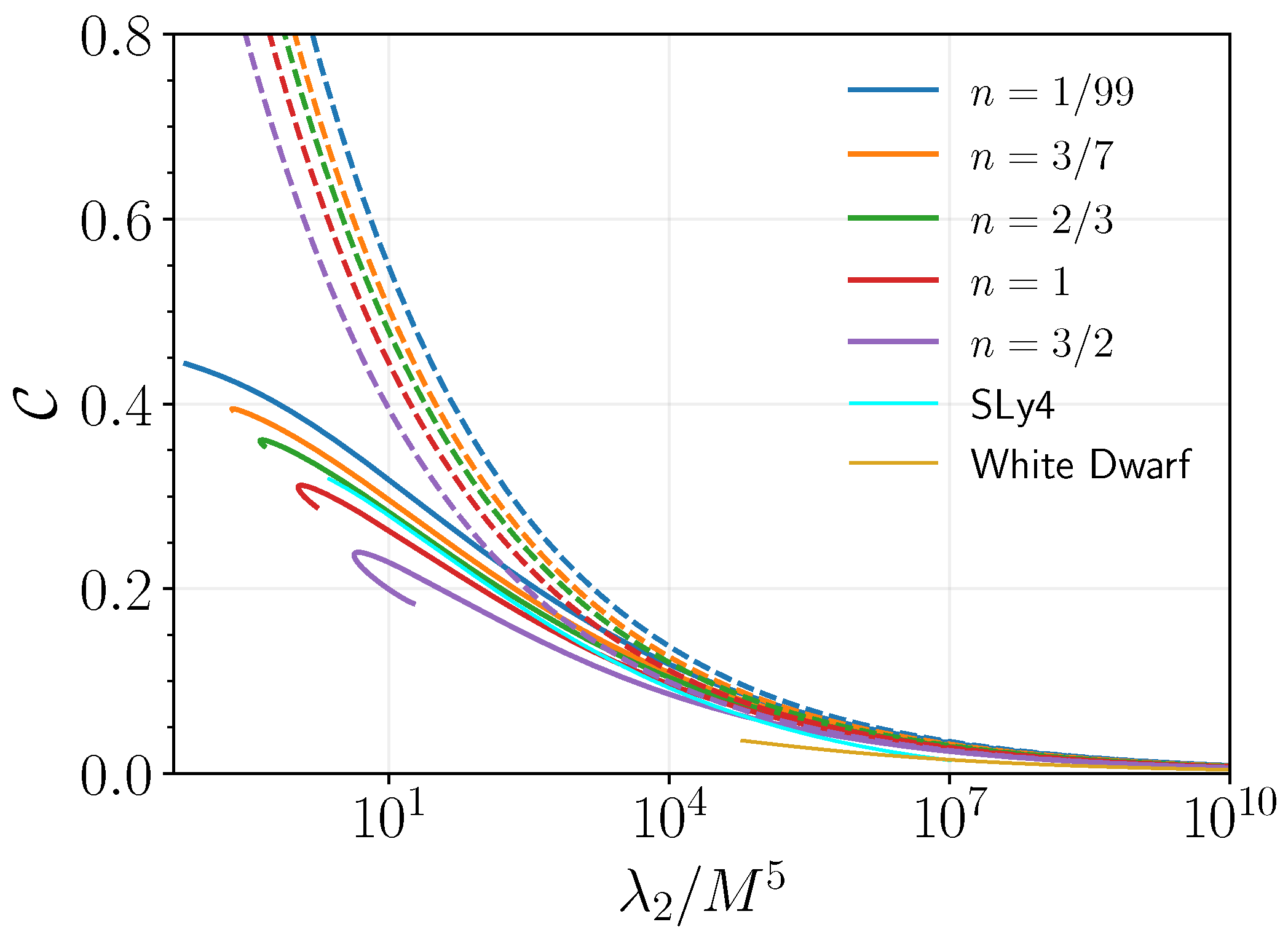
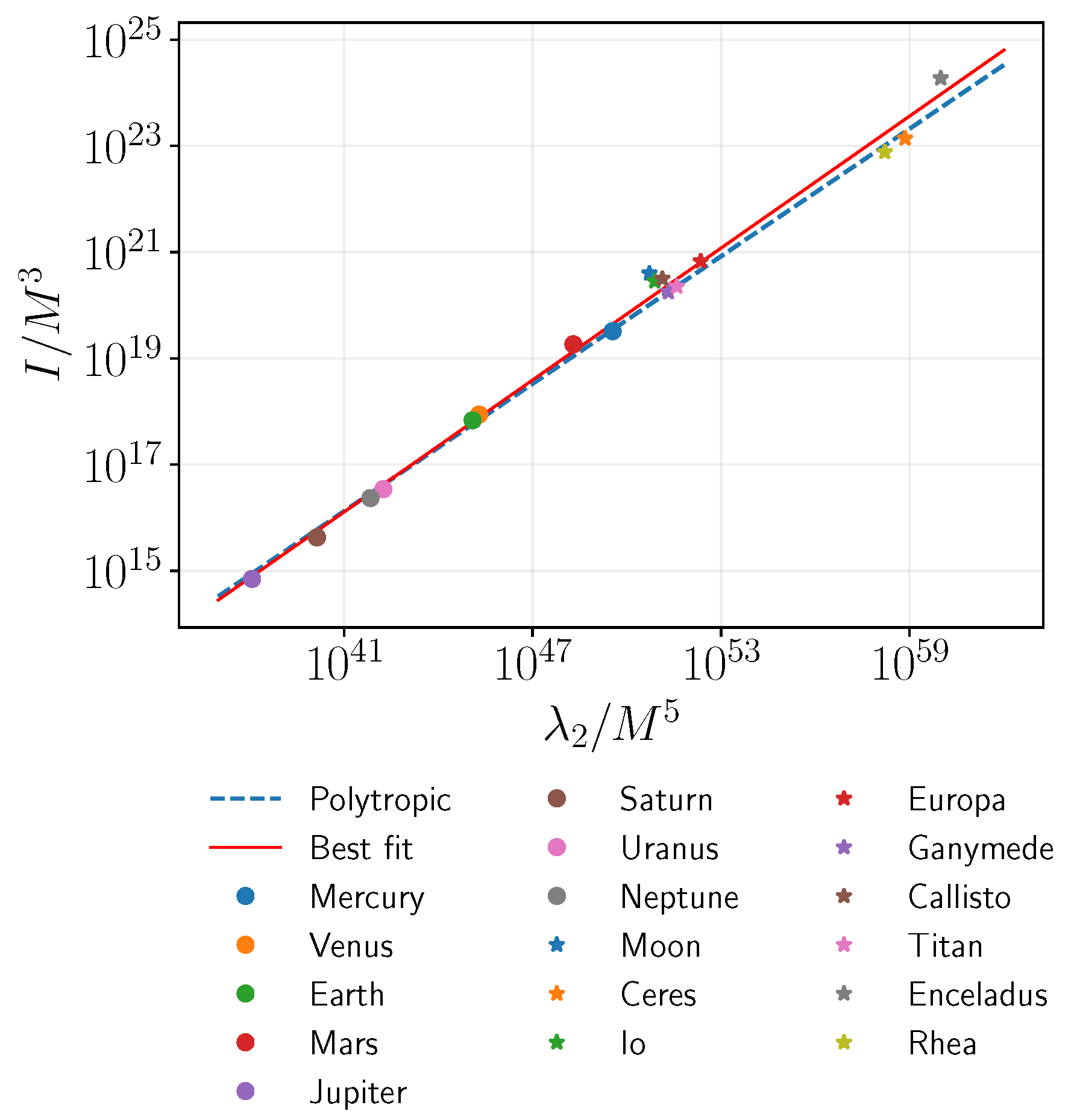
| Object | Ref. | ||||
|---|---|---|---|---|---|
| Mercury | [55,73] | ||||
| Venus | [74,75] | ||||
| Earth | [76,77] | ||||
| Mars | [78,79] | ||||
| Jupiter | * | * | [56,80] | ||
| Saturn | [57,81] | ||||
| Uranus | * | * | [58,82] | ||
| Neptune | * | * | [59,82] | ||
| Moon | [83,84] | ||||
| Ceres | * | * | [60,61] | ||
| Io | * | * | [62,63] | ||
| Europa | * | * | [64,65] | ||
| Ganymede | * | * | [64,66] | ||
| Callisto | * | * | [66,67] | ||
| Titan | * | * | [68,69] | ||
| Enceladus | * | * | [70] | ||
| Rhea | * | * | [71] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, R.; Torres-Orjuela, A.; Amaro Seoane, P. The I-Love Universal Relation for Polytropic Stars Under Newtonian Gravity. Galaxies 2025, 13, 75. https://doi.org/10.3390/galaxies13040075
Xu R, Torres-Orjuela A, Amaro Seoane P. The I-Love Universal Relation for Polytropic Stars Under Newtonian Gravity. Galaxies. 2025; 13(4):75. https://doi.org/10.3390/galaxies13040075
Chicago/Turabian StyleXu, Rui, Alejandro Torres-Orjuela, and Pau Amaro Seoane. 2025. "The I-Love Universal Relation for Polytropic Stars Under Newtonian Gravity" Galaxies 13, no. 4: 75. https://doi.org/10.3390/galaxies13040075
APA StyleXu, R., Torres-Orjuela, A., & Amaro Seoane, P. (2025). The I-Love Universal Relation for Polytropic Stars Under Newtonian Gravity. Galaxies, 13(4), 75. https://doi.org/10.3390/galaxies13040075






