Examination of the Functional Form of the Light and Mass Distribution in Spiral Arms
Abstract
1. Introduction
2. Data and Methods
2.1. Images
2.2. Extraction of the Spiral Arms
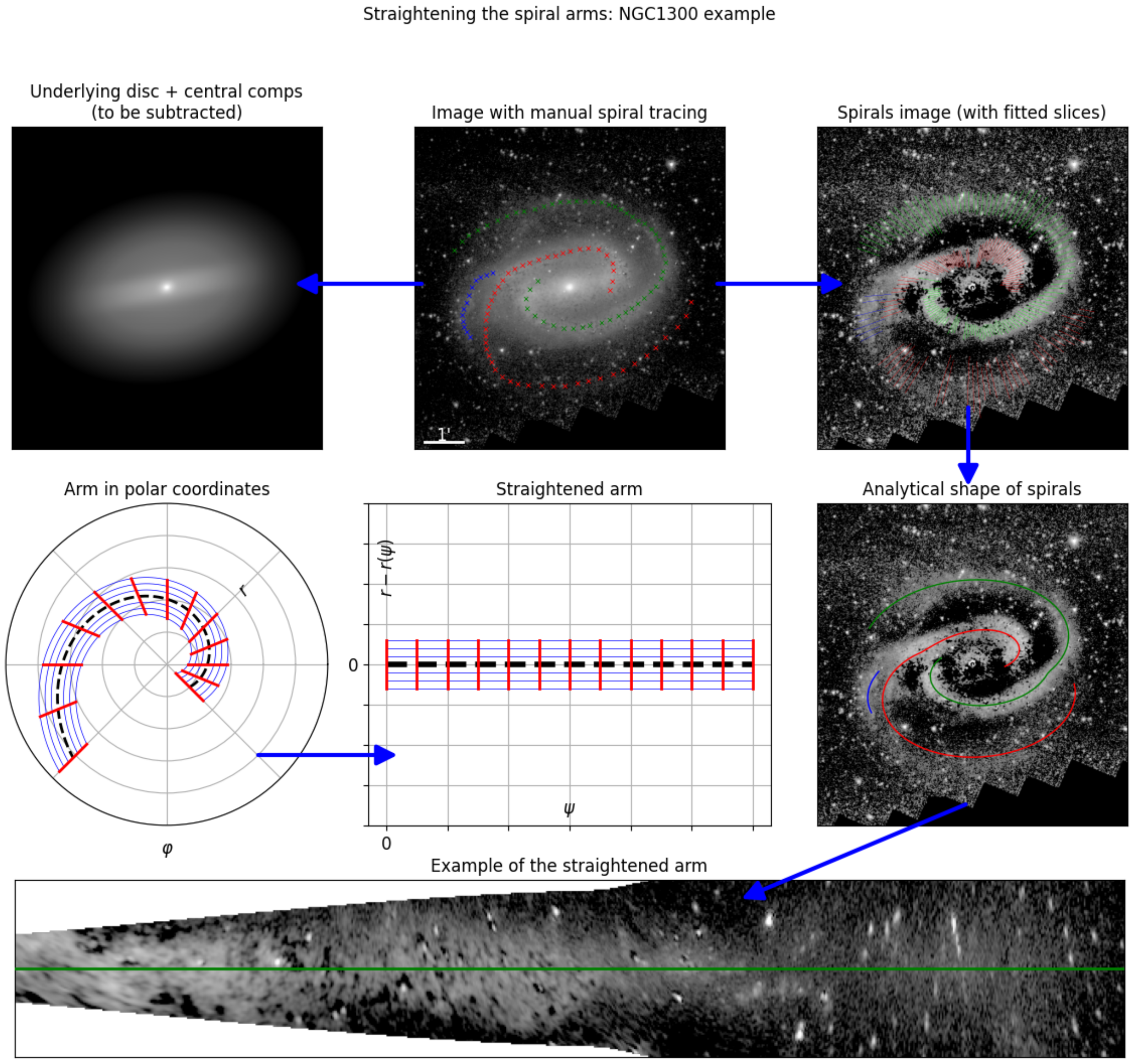
2.3. Straightening of the Spiral Arms
3. Spiral Arm Measurements
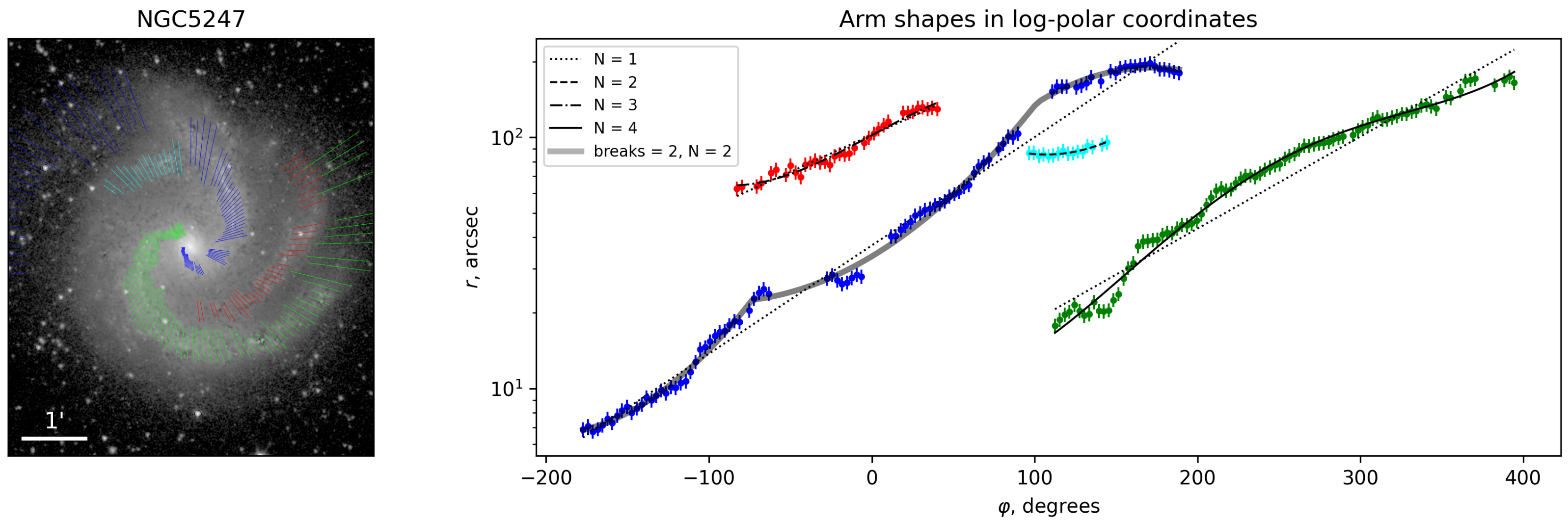
3.1. Shapes of Spiral Arms
3.1.1. Functions Overview
3.1.2. Comparison of the Functions
- For 26 spurs (), 2 or 3 parameters are optimal and do not introduce overfitting in all cases (corresponding to Equation (1) with or ). If the number of parameters is increased to 4, it yields overfitting in more than a half cases.
- For 27 relatively short spiral arms (), 4 parameters (Equation (1) with ) is optimal in most cases; overfitting is present only for 3 spiral arms. Increasing the number of parameters leads to overfitting in more than half the cases.
- For the 12 longest spiral arms (), no overfitting appears at least up to 8 parameters.
- As mentioned above, most spurs are already well-described by logarithmic spirals, but using a polynomial–logarithmic spiral with yields in all cases, without exceptions.
- We observe that spiral arms () are described by the polynomial–logarithmic spiral with much better than by logarithmic spiral. In 73% of cases, they have smaller than the threshold of 0.23 discussed above. Among the short spiral arms (), this fraction is 93%.
- For longer spiral arms (), polynomial–logarithmic spirals with and yield in 70% and 83% of cases, respectively. For the remaining cases, often bendings are the reason why is still larger than this threshold; using the polynomial–logarithmic spiral with or either Equation (2) with and (which does not introduce overfitting for this range of azimuthal lengths), one can achieve in 96% of cases.
- For the longest spiral arms (), polynomial–logarithmic spiral with yields in 67% cases, and again, bendings are playing a role in this. The remaining cases, however, can be fitted with Equation (2) with and , yielding without exceptions.
- Overall, we find 35% of spiral arms exhibit bendings, which was determined after the careful inspection of images, diagrams, and comparison of models that include bendings versus models that do not. In grand-design galaxies, 47% of spiral arms possess bendings, whereas in multi-armed galaxies, 31% of spiral arms are bent. However, according to the two-proportion Z-test, there is not enough evidence to consider this difference to be significant. Bending locations are often associated with bifurcations of spirals or the passages near ends of the bar. In some cases, bendings are weak and a simple polynomial–logarithmic function is enough to fit the spiral arm.
3.1.3. Testing Alternative Functions
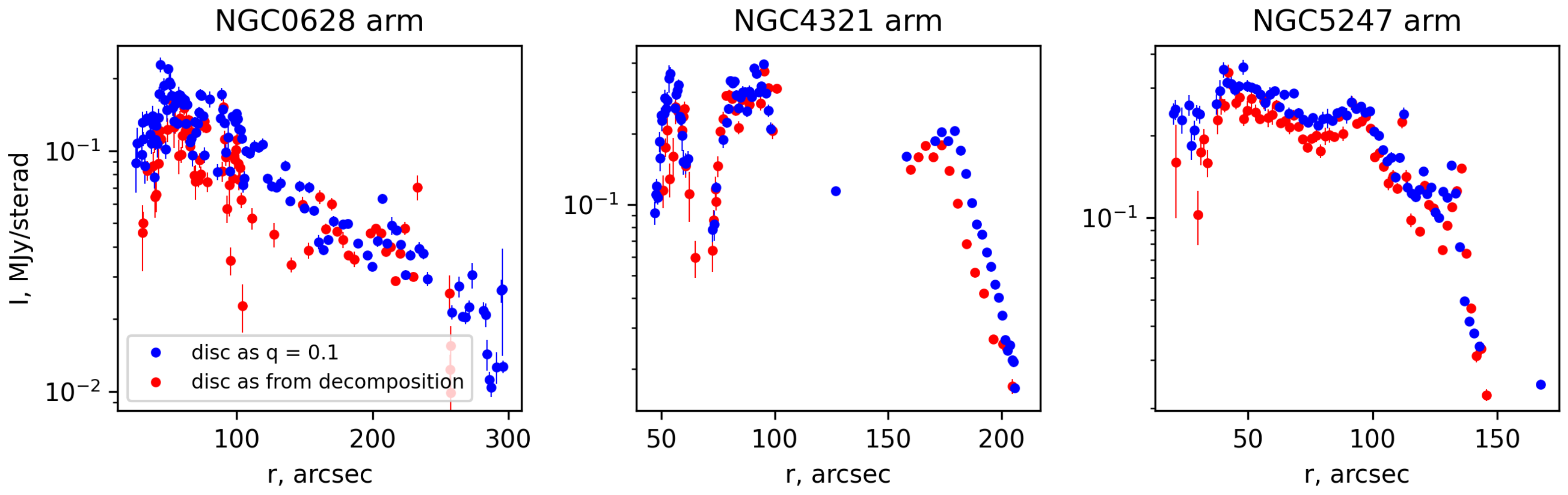
3.2. Distribution of Light Along Spiral Arms
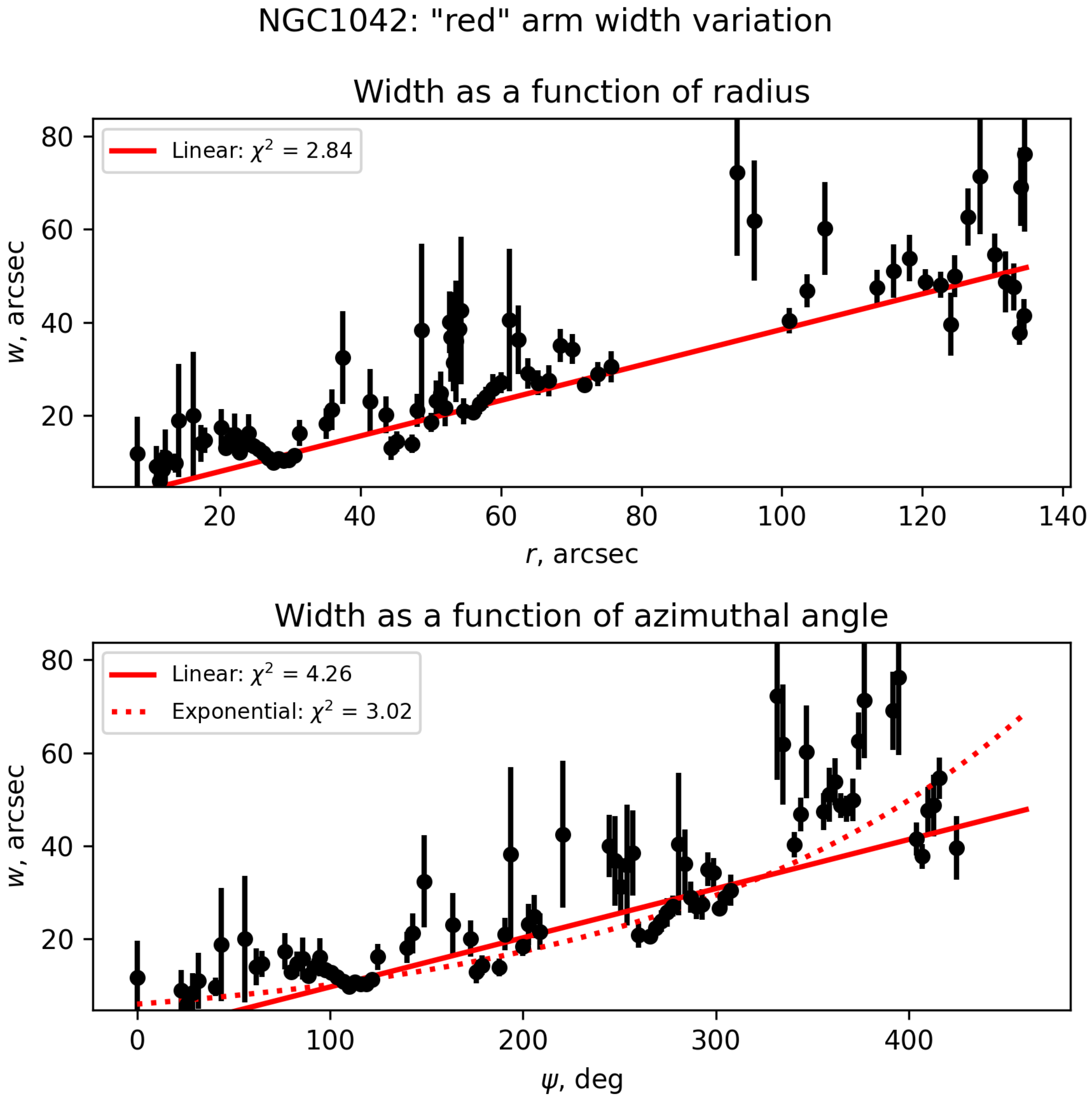
3.3. Widths of Spiral Arms
3.4. Brightness Profiles Across Spiral Arm
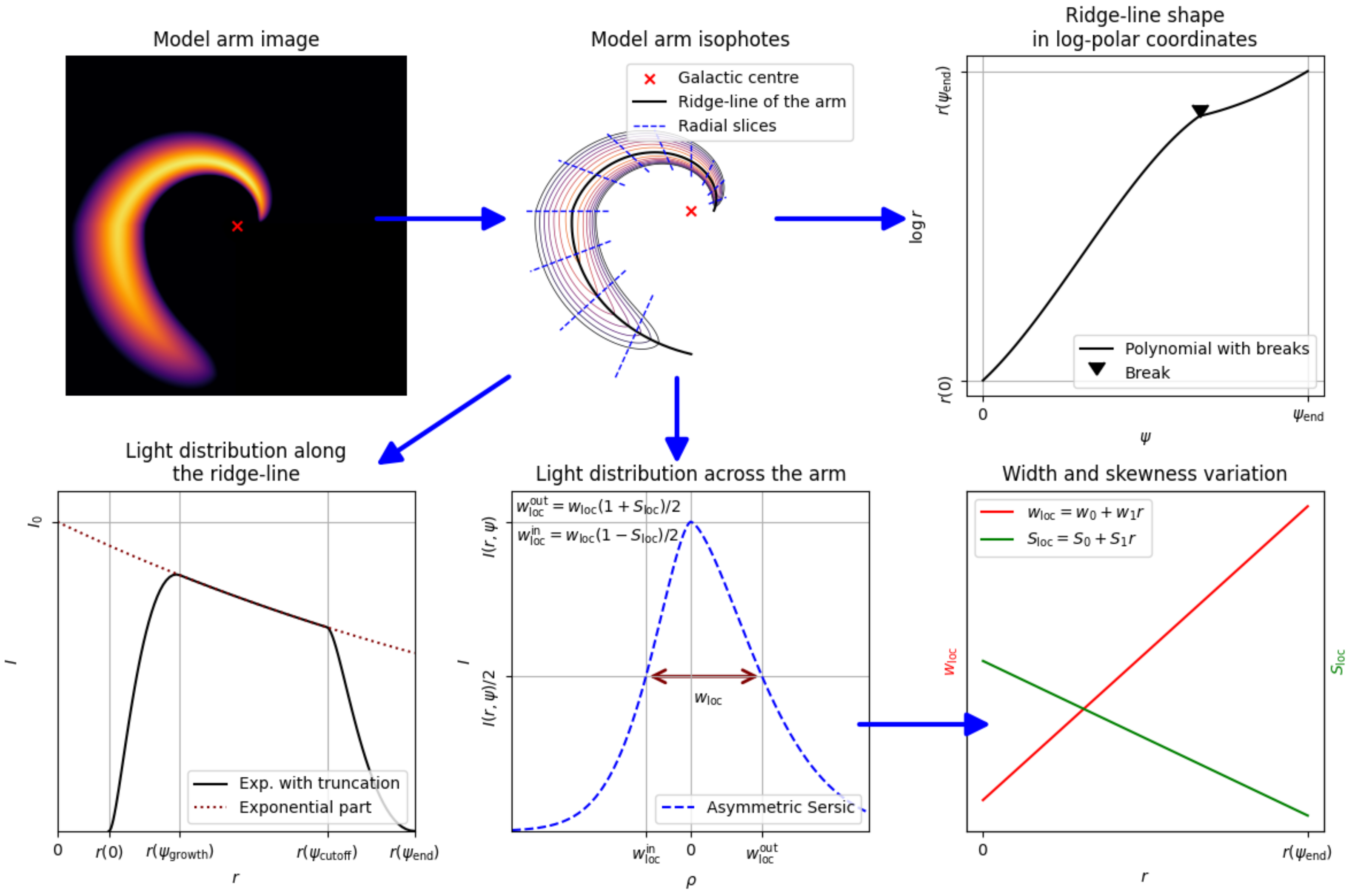
4. Constructing a Photometric Model of a Spiral Arm
4.1. Validation by 2D Fitting
- (1) Function with constant except growth/cutoff parts (effectively, )
- (2) Function with sharp transition of ()
- (3) Function with constant width ()
- (4) Function width proportional to radius ()
- (5) Function with linearly changing skewness (nonzero )
- (6) Function with linearly changing skewness and Sérsic profile (nonzero )
- (7) Function with quadratic and (additional parameters and , see Equation (9))
- (8) Optional, if dips are present: function with 1 or 2 Gaussian brightness dips (Equation (13))
Selecting a Growth and Cutoff Function
4.2. Proposed Photometric Function
5. Connection with the Nature of Spiral Arms
5.1. Observable Features
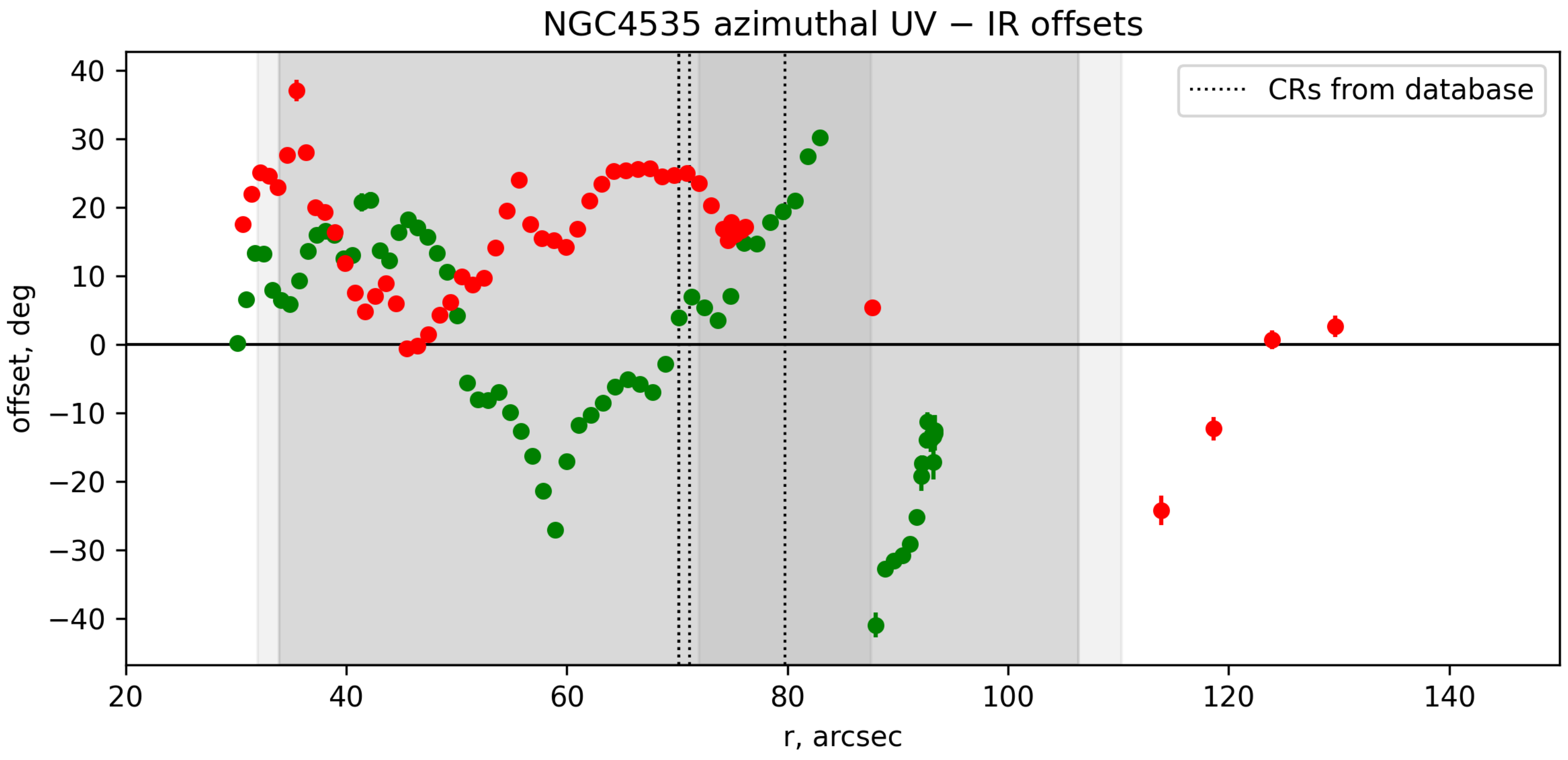
5.1.1. IR–UV Offsets
5.1.2. Width Gradients
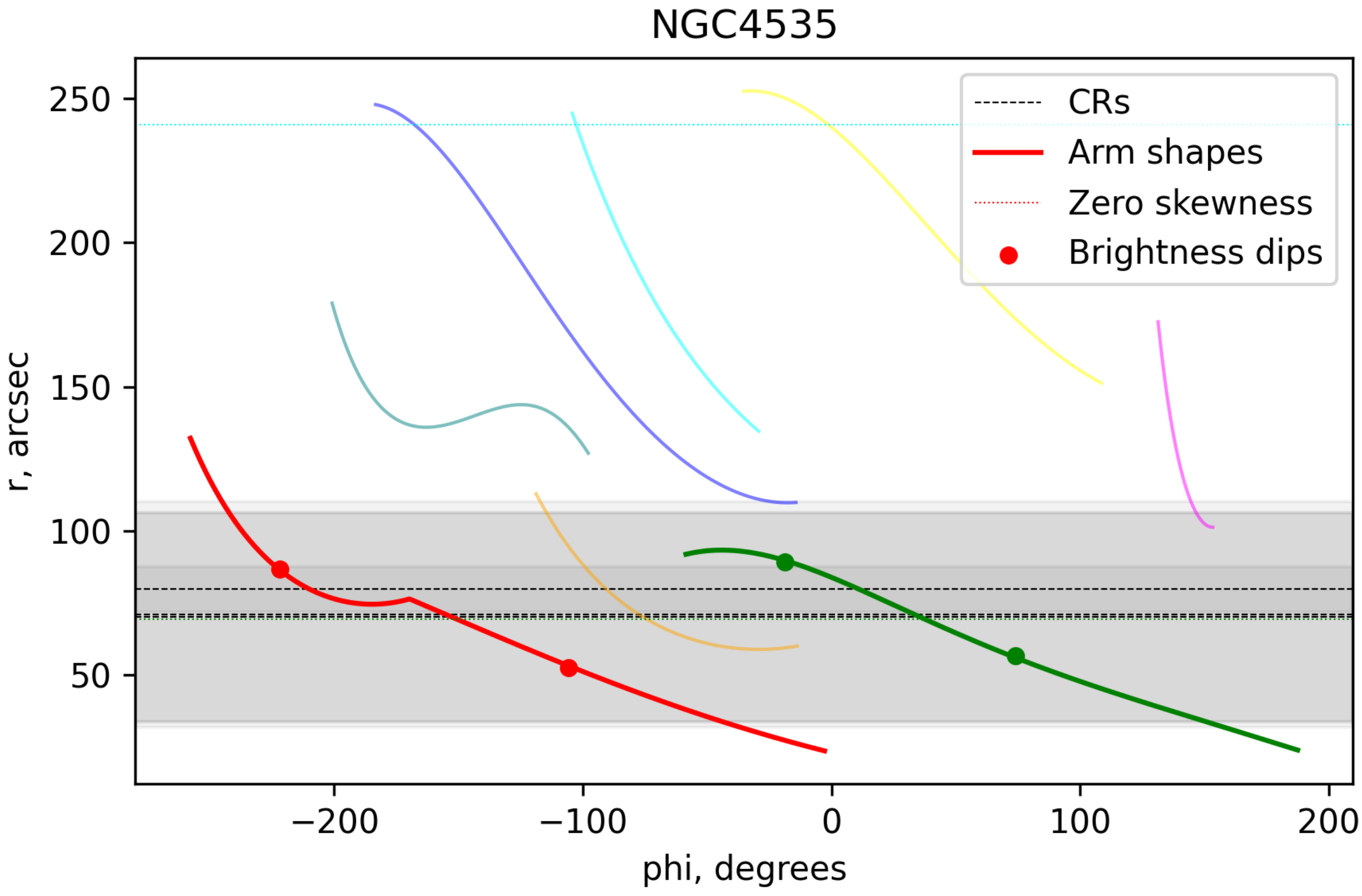
5.1.3. Bendings
5.1.4. Brightness Dips in Arms
5.2. Example of NGC 4535
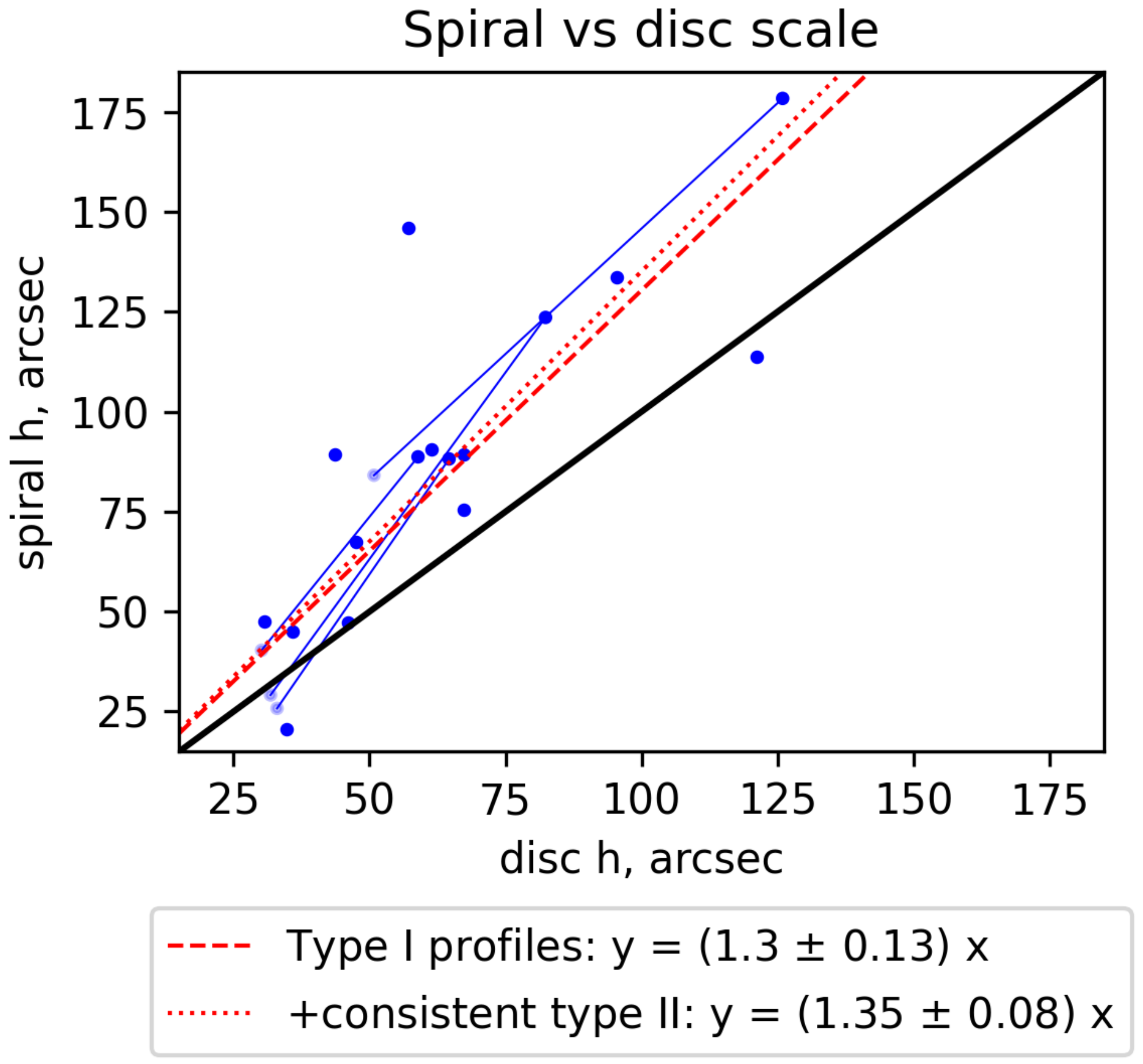
5.3. Exponential Scales of Spiral Arms
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BIC | Bayesian Information Criterion |
| CR | Corotation radius |
| FWHM | Full width at half-maximum |
| HWHM | Half-width at half-maximum |
| IR | Infrared |
| PSF | Point spread function |
| UV | Ultraviolet |
References
- Conselice, C.J. The Fundamental Properties of Galaxies and a New Galaxy Classification System. Mon. Not. R. Astron. Soc. 2006, 373, 1389–1408. [Google Scholar] [CrossRef]
- Dobbs, C.; Baba, J. Dawes Review 4: Spiral Structures in Disc Galaxies. Publ. Astron. Soc. Aust. 2014, 31, e035. [Google Scholar] [CrossRef]
- Breda, I.; van de Ven, G.; Thater, S.; Falcón-Barroso, J.; Jethwa, P.; Gadotti, D.A.; Onodera, M.; Pessa, I.; Schaye, J.; Hensler, G.; et al. Large-Scale Stellar Age-Velocity Spiral Pattern in NGC 4030. Astron. Astrophys. 2024, 692, L10. [Google Scholar] [CrossRef]
- Debattista, V.P.; Khachaturyants, T.; Amarante, J.A.S.; Carr, C.; Beraldo e Silva, L.; Laporte, C.F.P. Azimuthal Metallicity Variations, Spiral Structure, and the Failure of Radial Actions Based on Assuming Axisymmetry. Mon. Not. R. Astron. Soc. 2025, 537, 1620–1645. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ho, L.C.; Wang, J. Spiral Structure Boosts Star Formation in Disk Galaxies. Astrophys. J. 2021, 917, 88. [Google Scholar] [CrossRef]
- Querejeta, M.; Schinnerer, E.; Meidt, S.; Sun, J.; Leroy, A.K.; Emsellem, E.; Klessen, R.S.; Muñoz-Mateos, J.C.; Salo, H.; Laurikainen, E.; et al. Stellar structures, molecular gas, and star formation across the PHANGS sample of nearby galaxies. Astron. Astrophys. 2021, 656, A133. [Google Scholar] [CrossRef]
- Querejeta, M.; Leroy, A.K.; Meidt, S.E.; Schinnerer, E.; Belfiore, F.; Emsellem, E.; Klessen, R.S.; Sun, J.; Sormani, M.; Bešlić, I.; et al. Do spiral arms enhance star formation efficiency? Astron. Astrophys. 2024, 687, A293. [Google Scholar] [CrossRef]
- Sanna, A.; Reid, M.J.; Dame, T.M.; Menten, K.M.; Brunthaler, A. Mapping Spiral Structure on the Far Side of the Milky Way. Science 2017, 358, 227–230. [Google Scholar] [CrossRef]
- Poggio, E.; Drimmel, R.; Cantat-Gaudin, T.; Ramos, P.; Ripepi, V.; Zari, E.; Andrae, R.; Blomme, R.; Chemin, L.; Clementini, G.; et al. Galactic Spiral Structure Revealed by Gaia EDR3. Astron. Astrophys. 2021, 651, A104. [Google Scholar] [CrossRef]
- Hao, C.J.; Xu, Y.; Hou, L.G.; Bian, S.B.; Li, J.J.; Wu, Z.Y.; He, Z.H.; Li, Y.J.; Liu, D.J. Evolution of the Local Spiral Structure of the Milky Way Revealed by Open Clusters. Astron. Astrophys. 2021, 652, A102. [Google Scholar] [CrossRef]
- Griv, E.; Jiang, I.G.; Hou, L.G. The Nearby Spiral Density-Wave Structure of the Galaxy. Mon. Not. R. Astron. Soc. 2017, 468, 3361–3367. [Google Scholar] [CrossRef]
- Shen, J.; Zheng, X.W. The Bar and Spiral Arms in the Milky Way: Structure and Kinematics. Res. Astron. Astrophys. 2020, 20, 159. [Google Scholar] [CrossRef]
- Khrapov, S.; Khoperskov, A.; Korchagin, V. Modeling of Spiral Structure in a Multi-Component Milky Way-like Galaxy. Galaxies 2021, 9, 29. [Google Scholar] [CrossRef]
- Vukcevic, M.; Zekovic, V.; Radeta, M. Spiral Structure of the Galactic Disk and Its Influence on the Rotational Velocity Curve. Astron. Nachrichten 2022, 343, e210108. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. On the Spiral Structure of Disk Galaxies. Astrophys. J. 1964, 140, 646. [Google Scholar] [CrossRef]
- Shu, F.H. Six Decades of Spiral Density Wave Theory. Annu. Rev. Astron. Astrophys. 2016, 54, 667–724. [Google Scholar] [CrossRef]
- Dobbs, C.L.; Pettitt, A.R.; Corbelli, E.; Pringle, J.E. Simulations of the Flocculent Spiral M33: What Drives the Spiral Structure? Mon. Not. R. Astron. Soc. 2018, 478, 3793–3808. [Google Scholar] [CrossRef]
- Kostiuk, V.; Marchuk, A.; Gusev, A.; Chugunov, I.V. A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403. Galaxies 2025, 13, 27. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G. Arm Classifications for Spiral Galaxies. Astrophys. J. 1987, 314, 3. [Google Scholar] [CrossRef]
- Savchenko, S.; Marchuk, A.; Mosenkov, A.; Grishunin, K. A Multiwavelength Study of Spiral Structure in Galaxies. I. General Characteristics in the Optical. Mon. Not. R. Astron. Soc. 2020, 493, 390–409. [Google Scholar] [CrossRef]
- Mosenkov, A.; Savchenko, S.; Marchuk, A. Investigation of the Parameters of Spiral Pattern in Galaxies: The Arm Width. Res. Astron. Astrophys. 2020, 20, 120. [Google Scholar] [CrossRef]
- Mosenkov, A.V.; Panasyuk, A.D.; Turner, S.; Bartier, C.L.; Skryabina, M.N.; Marchuk, A.A.; Savchenko, S.S.; Bergstedt, J.; Reshetnikov, V.P.; Chugunov, I.V. A Multiwavelength Study of Spiral Structure in Galaxies. II. Spiral Arms in Deep Optical Observations. Mon. Not. R. Astron. Soc. 2024, 527, 10615–10631. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Elmegreen, D.M.; Montenegro, L. Optical Tracers of Spiral Wave Resonances in Galaxies. II. Hidden Three-Arm Spirals in a Sample of 18 Galaxies. Astrophys. J. Suppl. Ser. 1992, 79, 37. [Google Scholar] [CrossRef]
- Pan, H. Density Wave Theory with Co-rotation May Have a Critical Problem-[V1]. Preprints.org 2023. [Google Scholar] [CrossRef]
- Abdeen, S.; Kennefick, D.; Kennefick, J.; Miller, R.; Shields, D.W.; Monson, E.B.; Davis, B.L. Determining the Co-Rotation Radii of Spiral Galaxies Using Spiral Arm Pitch Angle Measurements at Multiple Wavelengths. Mon. Not. R. Astron. Soc. 2020, 496, 1610–1619. [Google Scholar] [CrossRef]
- Marchuk, A.A.; Mosenkov, A.V.; Chugunov, I.V.; Kostiuk, V.S.; Skryabina, M.N.; Reshetnikov, V.P. A New, Purely Photometric Method for Determination of Resonance Locations in Spiral Galaxies. Mon. Not. R. Astron. Soc. 2024, 527, L66–L70. [Google Scholar] [CrossRef]
- Kennicutt, R.C., Jr. The Shapes of Spiral Arms along the Hubble Sequence. Astron. J. 1981, 86, 1847–1858. [Google Scholar] [CrossRef]
- Savchenko, S.S.; Reshetnikov, V.P. Pitch Angle Variations in Spiral Galaxies. Mon. Not. R. Astron. Soc. 2013, 436, 1074–1083. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; James, P.A.; Patsis, P.A. Spiral Structure in Barred Galaxies. Observational Constraints to Spiral Arm Formation Mechanisms. Mon. Not. R. Astron. Soc. 2019, 482, 5362–5378. [Google Scholar] [CrossRef]
- Honig, Z.N.; Reid, M.J. Characteristics of Spiral Arms in Late-type Galaxies. Astrophys. J. 2015, 800, 53. [Google Scholar] [CrossRef]
- Díaz-García, S.; Salo, H.; Knapen, J.H.; Herrera-Endoqui, M. The Shapes of Spiral Arms in the S4G Survey and Their Connection with Stellar Bars. Astron. Astrophys. 2019, 631, A94. [Google Scholar] [CrossRef]
- Ringermacher, H.I.; Mead, L.R. A New Formula Describing the Scaffold Structure of Spiral Galaxies. Mon. Not. R. Astron. Soc. 2009, 397, 164–171. [Google Scholar] [CrossRef]
- Peng, C.Y.; Ho, L.C.; Impey, C.D.; Rix, H.W. Detailed Decomposition of Galaxy Images. II. Beyond Axisymmetric Models. Astron. J. 2010, 139, 2097–2129. [Google Scholar] [CrossRef]
- Chugunov, I.V.; Marchuk, A.A.; Mosenkov, A.V.; Savchenko, S.S.; Shishkina, E.V.; Chazov, M.I.; Nazarova, A.E.; Skryabina, M.N.; Smirnova, P.I.; Smirnov, A.A. Galaxies Decomposition with Spiral Arms—I: 29 Galaxies from S4G. Mon. Not. R. Astron. Soc. 2024, 527, 9605–9624. [Google Scholar] [CrossRef]
- Marchuk, A.A.; Chugunov, I.V.; Gontcharov, G.A.; Mosenkov, A.V.; Il’in, V.B.; Savchenko, S.S.; Smirnov, A.A.; Poliakov, D.M.; Seguine, J.; Chazov, M.I. Galaxies Decomposition with Spiral Arms—II. A Multiwavelength Case Study of M 51. Mon. Not. R. Astron. Soc. 2024, 528, 1276–1295. [Google Scholar] [CrossRef]
- Chugunov, I.V.; Marchuk, A.A.; Mosenkov, A.V. Less Wound and More Asymmetric: JWST Confirms the Evolution of Spiral Structure in Galaxies at z ≲ 3. Publ. Astron. Soc. Aust. 2025, 42, e029. [Google Scholar] [CrossRef]
- Griv, E.; Gedalin, M.; Mróz, P.; Liu, D.J.; Jiang, I.G. Spiral Density-Wave Structure Parameters in the Solar Neighbourhood Derived from Longitudinal Velocities of Gaia EDR3 OB Stars: 3D Approach. Mon. Not. R. Astron. Soc. 2022, 509, 463–474. [Google Scholar] [CrossRef]
- Wienen, M.; Brunt, C.M.; Dobbs, C.L.; Colombo, D. Perseus Arm—A New Perspective on Star Formation and Spiral Structure in Our Home Galaxy. Mon. Not. R. Astron. Soc. 2022, 509, 68–84. [Google Scholar] [CrossRef]
- Sheth, K.; Regan, M.; Hinz, J.L.; Gil de Paz, A.; Menéndez-Delmestre, K.; Muñoz-Mateos, J.C.; Seibert, M.; Kim, T.; Laurikainen, E.; Salo, H.; et al. The Spitzer Survey of Stellar Structure in Galaxies (S4G). Publ. Astron. Soc. Pac. 2010, 122, 1397. [Google Scholar] [CrossRef]
- Querejeta, M.; Meidt, S.E.; Schinnerer, E.; Cisternas, M.; Muñoz-Mateos, J.C.; Sheth, K.; Knapen, J.; van de Ven, G.; Norris, M.A.; Peletier, R.; et al. The Spitzer Survey of Stellar Structure in Galaxies (S4G): Precise Stellar Mass Distributions from Automated Dust Correction at 3.6 Mm. Astrophys. J. Suppl. Ser. 2015, 219, 5. [Google Scholar] [CrossRef]
- Buta, R.J.; Sheth, K.; Athanassoula, E.; Bosma, A.; Knapen, J.H.; Laurikainen, E.; Salo, H.; Elmegreen, D.; Ho, L.C.; Zaritsky, D.; et al. A Classical Morphological Analysis of Galaxies in the Spitzer Survey of Stellar Structure in Galaxies (S4G). Astrophys. J. Suppl. Ser. 2015, 217, 32. [Google Scholar] [CrossRef]
- Calzetti, D. Star Formation Rate Indicators; Cambridge University Press: Cambridge, UK, 2013; p. 419. [Google Scholar] [CrossRef]
- Davis, D.R.; Hayes, W.B. SpArcFiRe: Scalable Automated Detection of Spiral Galaxy Arm Segments. Astrophys. J. 2014, 790, 87. [Google Scholar] [CrossRef]
- Forgan, D.H.; Ramón-Fox, F.G.; Bonnell, I.A. Classifying and Modelling Spiral Structures in Hydrodynamic Simulations of Astrophysical Discs. Mon. Not. R. Astron. Soc. 2018, 476, 2384–2395. [Google Scholar] [CrossRef]
- Walmsley, M.; Spindler, A. Deep Learning Segmentation of Spiral Arms and Bars. arXiv 2023, arXiv:2312.02908. [Google Scholar]
- Masters, K.L.; Krawczyk, C.; Shamsi, S.; Todd, A.; Finnegan, D.; Bershady, M.; Bundy, K.; Cherinka, B.; Fraser-McKelvie, A.; Krishnarao, D.; et al. Galaxy Zoo: 3D-Crowdsourced Bar, Spiral, and Foreground Star Masks for MaNGA Target Galaxies. Mon. Not. R. Astron. Soc. 2021, 507, 3923–3935. [Google Scholar] [CrossRef]
- Joye, W.A.; Mandel, E. New Features of SAOImage DS9. In Astronomical Data Analysis Software and Systems XII; Astronomical Society of the Pacific: San Francisco, CA, USA, 2003; Volume 295, p. 489. [Google Scholar]
- Erwin, P. IMFIT: A Fast, Flexible New Program for Astronomical Image Fitting. Astrophys. J. 2015, 799, 226. [Google Scholar] [CrossRef]
- Reshetnikov, V.P.; Marchuk, A.A.; Chugunov, I.V.; Usachev, P.A.; Mosenkov, A.V. Evolution of the Spiral Structure of Galaxies from HST COSMOS Field Data. Astron. Lett. 2022, 48, 644–652. [Google Scholar] [CrossRef]
- Reshetnikov, V.P.; Marchuk, A.A.; Chugunov, I.V.; Usachev, P.A.; Mosenkov, A.V. The Possible Evolution of Pitch Angles of Spiral Galaxies. Astron. Astrophys. 2023, 680, L14. [Google Scholar] [CrossRef]
- Chugunov, I.V.; Marchuk, A.A. Examination of the shape and surface brightness profile of galaxies’ spiral arms. In Proceedings of the 52nd International Student Scientific Conference “Space physics”, Yekaterinburg, Russia, 27–31 January 2025; pp. 393–396. [Google Scholar]
- Kostiuk, V.S.; Marchuk, A.A.; Gusev, A.S. Cross-Method Analysis of Corotation Radii Data Set for Spiral Galaxies. Res. Astron. Astrophys. 2024, 24, 75007. [Google Scholar] [CrossRef]
- Weaver, H.F. Some Characteristics of Interstellar Gas in the Galaxy; Springer: Dordrecht, The Netherlands, 1970; Volume 39, p. 22. [Google Scholar]
- Elmegreen, D.M. Properties of Spurs in Spiral Galaxies. Astrophys. J. 1980, 242, 528–532. [Google Scholar] [CrossRef]
- Pérez-Villegas, A.; Gómez, G.C.; Pichardo, B. The Galactic Branches as a Possible Evidence for Transient Spiral Arms. Mon. Not. R. Astron. Soc. 2015, 451, 2922–2932. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ho, L.C.; Barth, A.J.; Li, Z.Y. The Carnegie-Irvine Galaxy Survey. VI. Quantifying Spiral Structure. Astrophys. J. 2018, 862, 13. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ho, L.C. The Statistical Properties of Spiral Arms in Nearby Disk Galaxies. Astrophys. J. 2020, 900, 150. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; Epinat, B.; Dobbs, C.L.; Querejeta, M. Morphology and Kinematics of the Gas in M51: How Interaction with NGC 5195 Has Molded the Structure of Its Arms. Astrophys. J. 2024, 966, 110. [Google Scholar] [CrossRef]
- Bailer-Jones, C.A.L. Practical Bayesian Inference; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Simard, L.; Mendel, J.T.; Patton, D.R.; Ellison, S.L.; McConnachie, A.W. A Catalog of Bulge+disk Decompositions and Updated Photometry for 1.12 Million Galaxies in the Sloan Digital Sky Survey. Astrophys. J. Suppl. Ser. 2011, 196, 11. [Google Scholar] [CrossRef]
- Head, J.T.C.G.; Lucey, J.R.; Hudson, M.J.; Smith, R.J. Dissecting the red sequence: The bulge and disc colours of early-type galaxies in the Coma cluster. Mon. Not. R. Astron. Soc. 2014, 440, 1690–1711. [Google Scholar] [CrossRef]
- Raftery, A.E. Bayesian Model Selection in Social Research. Sociol. Methodol. 1995, 25, 111–163. [Google Scholar] [CrossRef]
- Sersic, J.L. Atlas de Galaxias Australes; Observatorio Astronomico: Cordoba, Argentina, 1968. [Google Scholar]
- Graham, A.W.; Driver, S.P. A Concise Reference to (Projected) Sérsic R1/n Quantities, Including Concentration, Profile Slopes, Petrosian Indices, and Kron Magnitudes. Publ. Astron. Soc. Aust. 2005, 22, 118–127. [Google Scholar] [CrossRef]
- Lingard, T.K.; Masters, K.L.; Krawczyk, C.; Lintott, C.; Kruk, S.; Simmons, B.; Simpson, R.; Bamford, S.; Nichol, R.C.; Baeten, E. Galaxy Zoo Builder: Four-component Photometric Decomposition of Spiral Galaxies Guided by Citizen Science. Astrophys. J. 2020, 900, 178. [Google Scholar] [CrossRef]
- Marchuk, A.A. Resonance coupling in spiral arms. Patterns for flat rotation curve. Astron. Astrophys. 2024, 686, L14. [Google Scholar] [CrossRef]
- Tamburro, D.; Rix, H.W.; Walter, F.; Brinks, E.; de Blok, W.J.G.; Kennicutt, R.C.; Mac Low, M.M. Geometrically Derived Timescales for Star Formation in Spiral Galaxies. Astron. J. 2008, 136, 2872–2885. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ho, L.C. Dependence of the Spiral Arms Pitch Angle on Wavelength as a Test of the Density Wave Theory. Astrophys. J. 2018, 869, 29. [Google Scholar] [CrossRef]
- Miller, R.; Kennefick, D.; Kennefick, J.; Shameer Abdeen, M.; Monson, E.; Eufrasio, R.T.; Shields, D.W.; Davis, B.L. Investigating the Origins of Spiral Structure in Disk Galaxies through a Multiwavelength Study. Astrophys. J. 2019, 874, 177. [Google Scholar] [CrossRef]
- Kalita, B.S.; Yu, S.Y.; Silverman, J.D.; Daddi, E.; Ho, L.C.; Faisst, A.L.; Dessauges-Zavadsky, M.; Puglisi, A.; Birrer, S.; Kashino, D.; et al. A Multi-Wavelength Investigation of Spiral Structures in z > 1 Galaxies with JWST. arXiv 2025, arXiv:2501.03325. [Google Scholar]
- Scarano, S.; Lépine, J.R.D. Radial Metallicity Distribution Breaks at Corotation Radius in Spiral Galaxies. Mon. Not. R. Astron. Soc. 2013, 428, 625–640. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G. Inner Two-Arm Symmetry in Spiral Galaxies. Astrophys. J. 1995, 445, 591. [Google Scholar] [CrossRef]
- Williams, T.G.; Schinnerer, E.; Emsellem, E.; Meidt, S.; Querejeta, M.; Belfiore, F.; Bešlić, I.; Bigiel, F.; Chevance, M.; Dale, D.A.; et al. Applying the Tremaine-Weinberg Method to Nearby Galaxies: Stellar-mass-based Pattern Speeds and Comparisons with ISM Kinematics. Astron. J. 2021, 161, 185. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; Epinat, B.; Fathi, K.; Gutiérrez, L.; Hernandez, O. Resonant Structure in the Disks of Spiral Galaxies, Using Phase Reversals in Streaming Motions from Two-dimensional Hα Fabry-Perot Spectroscopy. Astrophys. J. 2011, 741, L14. [Google Scholar] [CrossRef]
- Laudage, S.; Eibensteiner, C.; Bigiel, F.; Leroy, A.K.; Meidt, S.; Schinnerer, E.; de Blok, W.J.G.; Querejeta, M.; Stuber, S.; Colombo, D.; et al. Neutral Atomic and Molecular Gas Dynamics in the Nearby Spiral Galaxies NGC 1512, NGC 4535, and NGC 7496. Astron. Astrophys. 2024, 690, A169. [Google Scholar] [CrossRef]
- Ponomareva, A.A.; Verheijen, M.A.W.; Bosma, A. Detailed H I kinematics of Tully-Fisher calibrator galaxies. Mon. Not. R. Astron. Soc. 2016, 463, 4052–4067. [Google Scholar] [CrossRef]
- Pohlen, M.; Erwin, P.; Trujillo, I.; Beckman, J.E. Three Types of Galaxy Disks. ASP Conf. Ser. 2008, 390, 247. [Google Scholar] [CrossRef]
- Fiteni, K.; De Rijcke, S.; Debattista, V.P.; Caruana, J. The Role of Density Breaks in Driving Spiral Structure in Disc Galaxies. Mon. Not. R. Astron. Soc. 2024, 529, 4879–4895. [Google Scholar] [CrossRef]
- Kendall, S.; Clarke, C.; Kennicutt, R.C. Spiral Structure in Nearby Galaxies—II. Comparative Analysis and Conclusions. Mon. Not. R. Astron. Soc. 2015, 446, 4155–4167. [Google Scholar] [CrossRef]
- Kregel, M.; van der Kruit, P.C. Radial Truncations in Stellar Discs in Galaxies. Mon. Not. R. Astron. Soc. 2004, 355, 143–146. [Google Scholar] [CrossRef][Green Version]
- Gao, H.; Ho, L.C. An Optimal Strategy for Accurate Bulge-to-disk Decomposition of Disk Galaxies. Astrophys. J. 2017, 845, 114. [Google Scholar] [CrossRef]
- Kalita, B.S.; Suzuki, T.L.; Kashino, D.; Silverman, J.D.; Daddi, E.; Ho, L.C.; Ding, X.; Mercier, W.; Faisst, A.L.; Sheth, K.; et al. Clumps as Multiscale Structures in Cosmic Noon Galaxies. Mon. Not. R. Astron. Soc. 2025, 536, 3090–3111. [Google Scholar] [CrossRef]
- Marchuk, A.A.; Chugunov, I.V.; Galliano, F.; Mosenkov, A.V.; Strekalova, P.V.; Kostiuk, V.S.; Gontcharov, G.A.; Il’in, V.B.; Savchenko, S.S.; Smirnov, A.A.; et al. Accurate Decomposition of Galaxies with Spiral Arms: Dust Properties and Distribution. Galaxies 2025, 13, 39. [Google Scholar] [CrossRef]






| Galaxy | R25.5 (arcmin) | log M* | D (Mpc) | AC | Galaxy | R25.5 (arcmin) | log M* | D (Mpc) | AC |
|---|---|---|---|---|---|---|---|---|---|
| NGC0613 | 3.28 | 11.1 | 25.1 | M | NGC0628 | 5.77 | 10.3 | 9.1 | M |
| NGC0986 | 2.29 | 10.4 | 17.2 | G | NGC1042 | 2.66 | 9.6 | 9.4 | M |
| NGC1073 | 2.53 | 10.0 | 15.2 | M | NGC1232 | 3.79 | 10.7 | 18.7 | M |
| NGC1300 | 3.42 | 10.6 | 18.0 | G | NGC1566 | 4.39 | 10.6 | 12.2 | G |
| NGC1672 | 3.92 | 10.7 | 14.5 | G | NGC3184 | 4.11 | 10.4 | 12.0 | M |
| NGC4123 | 2.12 | 10.3 | 21.9 | M | NGC4254 | 3.20 | 10.7 | 15.4 | M |
| NGC4303 | 3.78 | 10.9 | 16.5 | M | NGC4321 | 5.21 | 10.9 | 16.0 | G |
| NGC4535 | 4.01 | 10.7 | 17.0 | M | NGC5085 | 2.33 | 10.8 | 28.9 | M |
| NGC5236 | 9.48 | 11.0 | 7.0 | M | NGC5247 | 3.57 | 10.8 | 22.2 | G |
| NGC7412 | 2.11 | 9.8 | 12.5 | M |
Add. par. | Baseline Function 10 | (1) −1 | (2) −2 | (3) −1 | (4) −1 | (5) +2 | (6) +3 | (7) +2 | (8) +3/+6 |
|---|---|---|---|---|---|---|---|---|---|
| disc | |||||||||
| All | 1 | 1.017 | 1.196 | 1.120 | 1.018 | 0.991 | 0.983 | 0.972 | 0.817 |
| 1 | 1.012 | 1.195 | 1.086 | 1.021 | 0.990 | 0.985 | 0.961 | 0.817 | |
| , decomposition disc | |||||||||
| All | 1 | 1.021 | 1.137 | 1.043 | 1.008 | 0.987 | 0.982 | 0.960 | 0.829 |
| 1 | 1.034 | 1.118 | 1.024 | 1.010 | 0.987 | 0.979 | 0.959 | 0.829 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chugunov, I.V.; Marchuk, A.A.; Savchenko, S.S. Examination of the Functional Form of the Light and Mass Distribution in Spiral Arms. Galaxies 2025, 13, 44. https://doi.org/10.3390/galaxies13020044
Chugunov IV, Marchuk AA, Savchenko SS. Examination of the Functional Form of the Light and Mass Distribution in Spiral Arms. Galaxies. 2025; 13(2):44. https://doi.org/10.3390/galaxies13020044
Chicago/Turabian StyleChugunov, Ilia V., Alexander A. Marchuk, and Sergey S. Savchenko. 2025. "Examination of the Functional Form of the Light and Mass Distribution in Spiral Arms" Galaxies 13, no. 2: 44. https://doi.org/10.3390/galaxies13020044
APA StyleChugunov, I. V., Marchuk, A. A., & Savchenko, S. S. (2025). Examination of the Functional Form of the Light and Mass Distribution in Spiral Arms. Galaxies, 13(2), 44. https://doi.org/10.3390/galaxies13020044






