Nonlinear Stability of the Bardeen–De Sitter Wormhole in f(R) Gravity
Abstract
1. Introduction
2. Bardeen–De Sitter Formalism
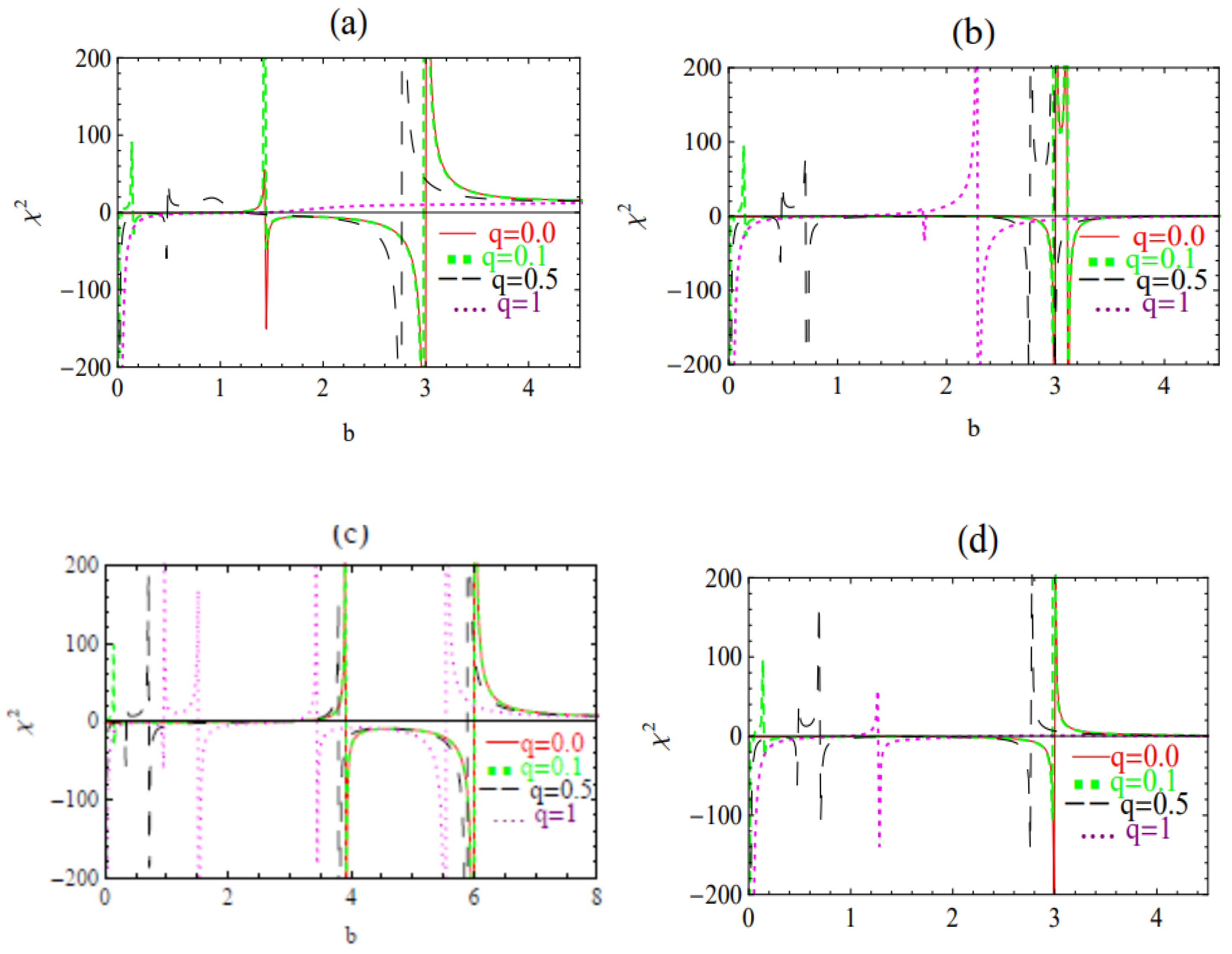
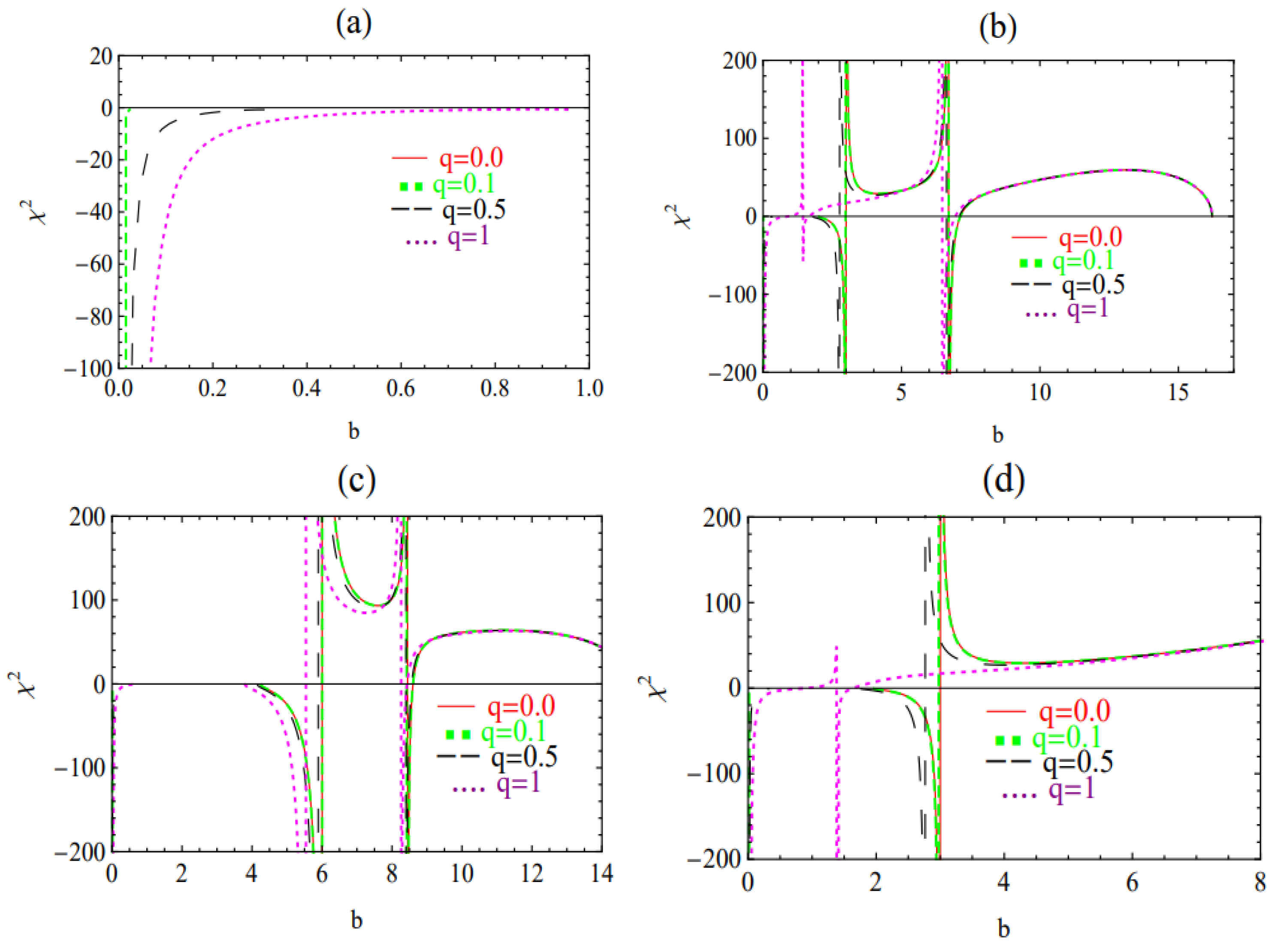
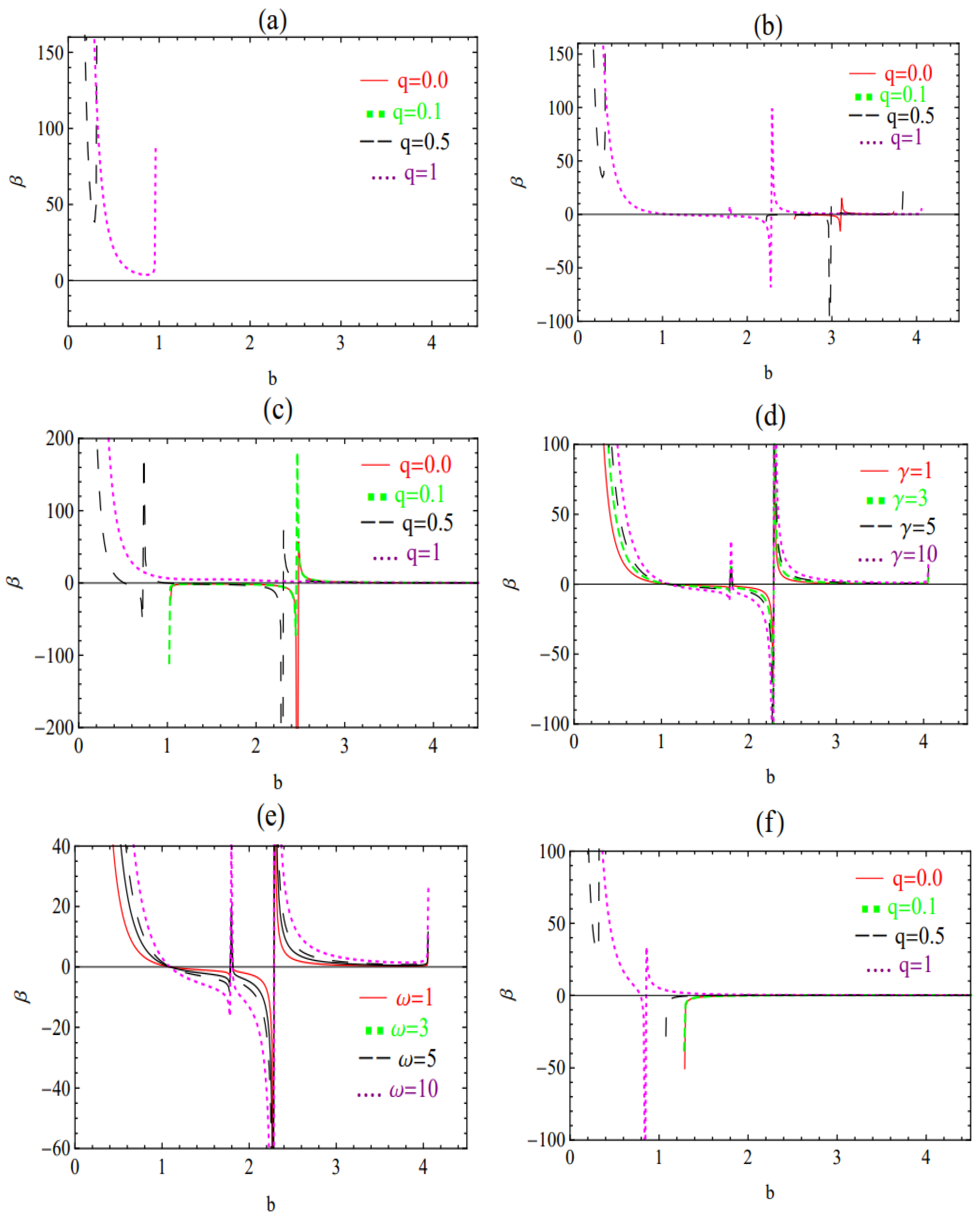
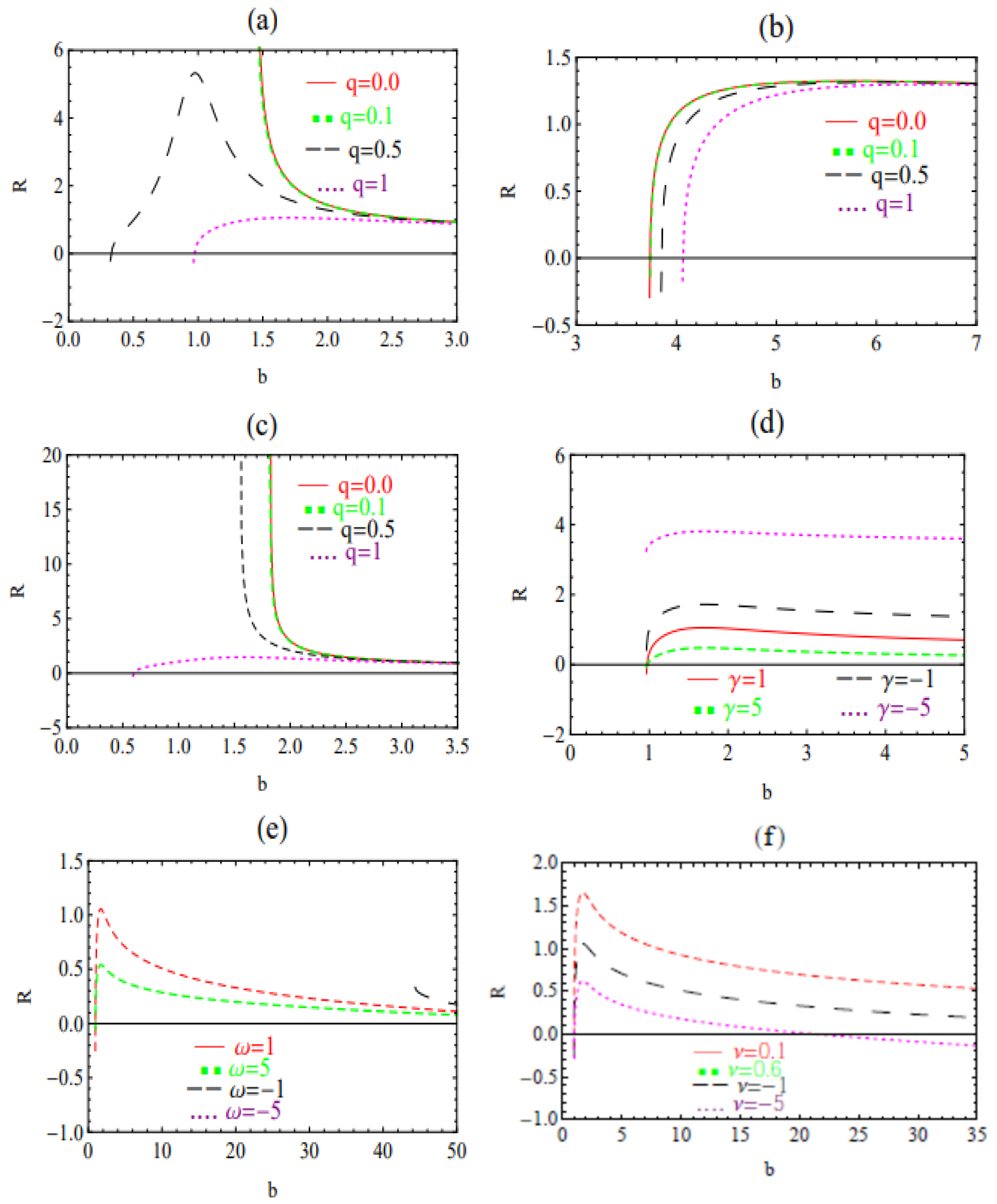
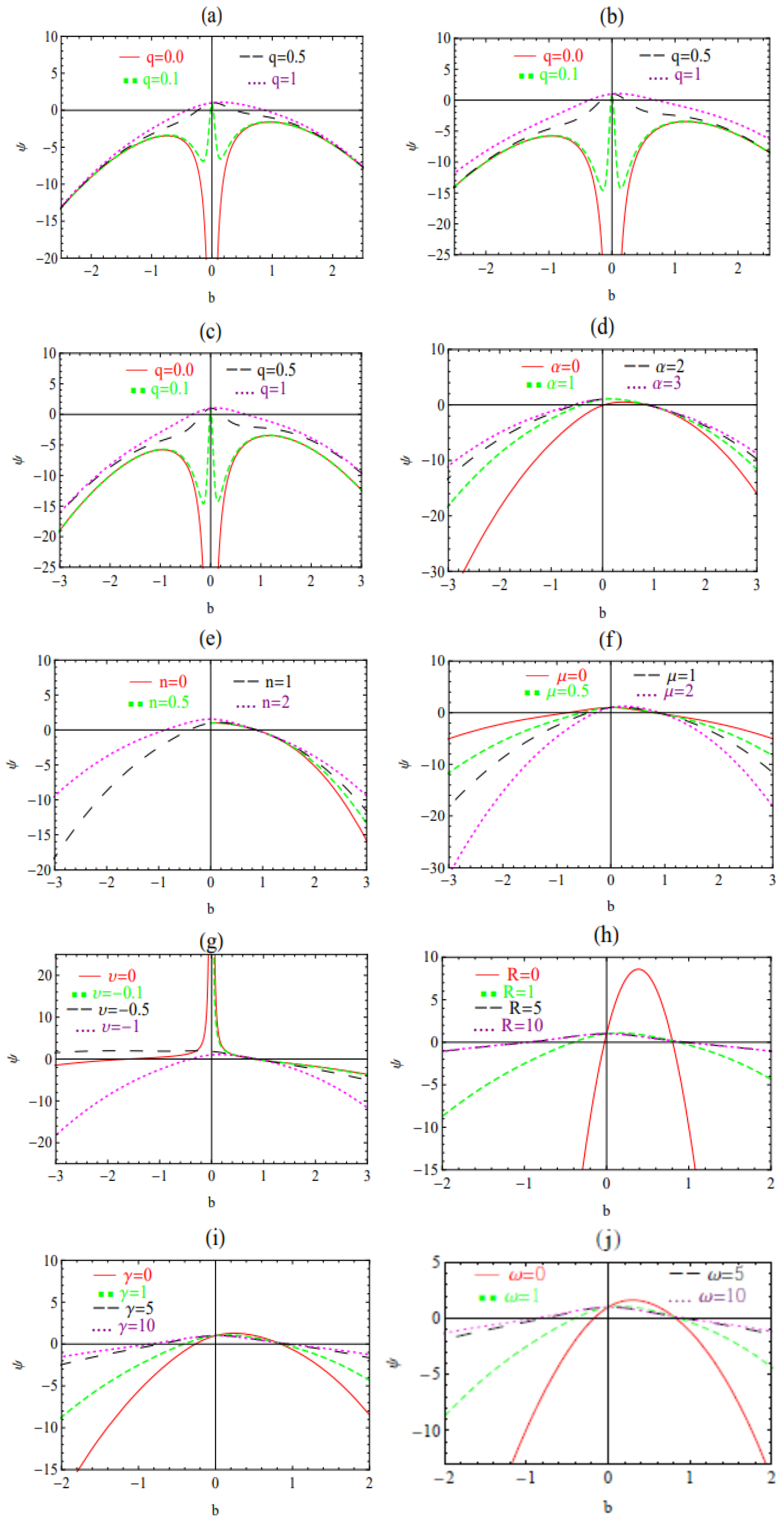
3. Stability Analysis
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395. [Google Scholar]
- Visser, M. Traversable wormholes from surgically modified Schwarzschild spacetimes. Nucl. Phys. B 1989, 328, 203. [Google Scholar] [CrossRef]
- Visser, M. Traversable wormholes: Some simple examples. Phys. Rev. D 1989, 39, 3182. [Google Scholar]
- Varela, V. Note on linearized stability of Schwarzschild thin-shell wormholes with variable equations of State. Phys. Rev. D 2015, 92, 044002. [Google Scholar]
- Li, A.-C.; Xu, W.-L.; Zeng, D.-F. Linear stability analysis of evolving thin shell wormholes. J. Cosmol. Astropart. Phys. 2019, 3, 16. [Google Scholar]
- Javed, F.; Fatima, G.; Mustafa, G.; Övgün, A. Effects of variable equations of state on the stability of nonlinear electrodynamics thin-shell wormholes. Int. J. Geom. Meth. Mod. Phys. 2023, 20, 2350010. [Google Scholar]
- Bardeen, J.M. Non-singular general-relativistic gravitational collapse. In Proceedings of the 5th International Conference on Gravitation and the Theory of Relativity, Tbilisi, Georgia, 9–16 September 1968; p. 174. [Google Scholar]
- Ayon–Beato, E.; Garcia, A. The Bardeen model as a nonlinear magnetic monopole. Phys. Lett. B 2000, 493, 149. [Google Scholar]
- Shamir, M.F. Massive compact Bardeen stars with conformal motion. Phys. Lett. B 2020, 811, 135927. [Google Scholar]
- Sharif, M.; Javed, F. On the stability of bardeen thin-shell wormholes. Gen. Relativ. Gravit. 2016, 48, 158. [Google Scholar]
- Sharif, M.; Javed, F. Linearized stability of Bardeen anti-de Sitter wormholes. Astrophys. Space Sci. 2019, 364, 179. [Google Scholar]
- Hayward, S.A. Formation and evaporation of nonsingular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, F.; Rahman, K.A.; Rakib, S.A.; Kuhfittig, P.K.F. Thin-shell wormholes from regular charged black Holes. Int. J. Theor. Phys. 2010, 49, 2364. [Google Scholar] [CrossRef]
- Eid, A. Dynamics and stability of Bardeen-de Sitter TSWs. New Astron. 2023, 98, 101934. [Google Scholar] [CrossRef]
- Fernando, S. Bardeen–de Sitter black holes. Int. J. Mod. Phys. D 2017, 26, 1750071. [Google Scholar] [CrossRef]
- Li, C.; Fang, C.; He, M.; Ding, J.; Li, P.; Deng, J. Thermodynamics of the Bardeen black hole in anti-de Sitter space. Mod. Phys. Lett. A 2019, 34, 1950336. [Google Scholar] [CrossRef]
- Alshal, H. Linearized stability of Bardeen de-Sitter thin-shell wormholes. Europhys. Lett. 2019, 128, 60007. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar]
- Martin, J.; Ringeval, C.; Vennin, V. How well can future CMB missions constrain cosmic inflation. J. Cosmol. Astropart. Phys. 2014, 10, 38. [Google Scholar] [CrossRef]
- Buchdahl, H.A. Non-linear lagrangians and cosmological theory. Mon. Not. R. Astron. Soc. 1970, 150, 1–8. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef]
- Capozziell, S.; Faraoni, V. Beyond Einstein Gravity; Springer: New York, NY, USA, 2010. [Google Scholar]
- Capozziello, S.; De Laurentis, M. Extended theories of gravity. Phys. Rep. 2011, 509, 167. [Google Scholar]
- Shamir, M.F.; Fayyaz, I. Traversable wormhole solutions in f(R) gravity via Karmarkar condition. Eur. Phys. J. C 2020, 80, 1102. [Google Scholar]
- Godani, N. Linear and nonlinear stability of charged thin-shell wormholes in f(R) gravity. Eur. Phys. J. Plus 2022, 137, 883. [Google Scholar]
- Godani, N. Thin-shell wormholes in non-linear f(R) gravity with variable scalar curvature. New Astron. 2022, 96, 101835. [Google Scholar]
- Samanta, G.C.; Godani, N. Physical Parameters for stable f(R) models. Ind. J. Phys. 2020, 94, 1303. [Google Scholar]
- Shamir, M.F.; Malik, A. Bardeen compact stars in modified f (R) gravity. Chin. J. Phys. 2021, 69, 312. [Google Scholar]
- Eid, A. The stability of TSW in f(R) theory of gravity. Phys. Dark Universe 2020, 30, 100705. [Google Scholar]
- Godani, N. Stability of Heyward wormhole in f(R) gravity. New Astro. 2023, 100, 101994. [Google Scholar]
- Godani, N. Linear stability of Bardeen anti-de Sitter thin-shell wormhole in f(R) gravity. Inter. J. Geom. Meth. Mod. Phys. 2022, 19, 2250208. [Google Scholar]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Il Nuovo C. B 1966, 44, 1–14. [Google Scholar]
- Sharif, M.; Kausar, H.R. Gravitational perfect fluid collapse in f(R) gravity. Astrophys. Space Sci. 2011, 331, 281. [Google Scholar]
- Senovilla, J.M.M. Junction conditions for F(R) gravity and their consequences. Phys. Rev. D 2013, 88, 064015. [Google Scholar]
- Yilmaz, A.O.; Gudekli, E. Dynamical system analysis of FLRW models with Modified Chaplygin Gas. Sci. Rep. 2021, 11, 2750. [Google Scholar]
- Debnath, U.; Banerjee, A.; Chakraborty, S. Role of Modified Chaplygin Gas in Accelerated Universe. Class. Quantum Gravity 2004, 21, 5609–5618. [Google Scholar]
- Shamir, M.F.; Malik, A. Investigating cosmology with equation of state. Can. J. Phys. 2019, 97, 752. [Google Scholar]
- Malik, A.; Shamir, M.F. Dynamics of some cosmological solutions in modified f(R) gravity. New Astron. 2020, 82, 101460. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99. [Google Scholar]
- Astashenok, A.; Capozziello, S.; Odintsov, S. Nonperturbative models of quark stars in f(R) gravity. Phys. Lett. B 2015, 742, 160–166. [Google Scholar]
- Sharif, M.; Yousaf, Z. Cylindrical Thin-shell Wormholes in f(R) gravity. Astrophys. Space Sci. 2014, 351, 351. [Google Scholar]
- Godani, N.; Samanta, G.C. Non-violation of energy conditions in wormholes modelling. Mod. Phys. Lett. A 2019, 34, 1950226. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eid, A. Nonlinear Stability of the Bardeen–De Sitter Wormhole in f(R) Gravity. Galaxies 2025, 13, 30. https://doi.org/10.3390/galaxies13020030
Eid A. Nonlinear Stability of the Bardeen–De Sitter Wormhole in f(R) Gravity. Galaxies. 2025; 13(2):30. https://doi.org/10.3390/galaxies13020030
Chicago/Turabian StyleEid, A. 2025. "Nonlinear Stability of the Bardeen–De Sitter Wormhole in f(R) Gravity" Galaxies 13, no. 2: 30. https://doi.org/10.3390/galaxies13020030
APA StyleEid, A. (2025). Nonlinear Stability of the Bardeen–De Sitter Wormhole in f(R) Gravity. Galaxies, 13(2), 30. https://doi.org/10.3390/galaxies13020030





