A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403
Abstract
:1. Introduction
2. Objects Under Investigation
2.1. NGC 3686
2.2. NGC 4321 (M 100)
2.3. NGC 2403
3. Applications of Methods
3.1. Font-Beckman Method
3.2. Stellar Age Gradient
3.3. Metallicity Gradient
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Velocity Maps

Appendix B. Decomposition with Spiral Arms


| 1 | https://github.com/ValerieKostiuk/CRs_dataset (accessed on 1 March 2024). |
References
- Elmegreen, D.M.; Elmegreen, B.G. Flocculent and grand design spiral structure in field, binary and group galaxies. Mon. Not. R. Astron. Soc. 1982, 201, 1021–1034. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G. Arm Classifications for Spiral Galaxies. Astrophys. J. 1987, 314, 3. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G.; Yau, A.; Athanassoula, E.; Bosma, A.; Buta, R.J.; Helou, G.; Ho, L.C.; Gadotti, D.A.; Knapen, J.H.; et al. Grand Design and Flocculent Spirals in the Spitzer Survey of Stellar Structure in Galaxies (S4G). Astrophys. J. 2011, 737, 32. [Google Scholar] [CrossRef]
- Buta, R.J.; Sheth, K.; Athanassoula, E.; Bosma, A.; Knapen, J.H.; Laurikainen, E.; Salo, H.; Elmegreen, D.; Ho, L.C.; Zaritsky, D.; et al. A Classical Morphological Analysis of Galaxies in the Spitzer Survey of Stellar Structure in Galaxies (S4G). Astrophys. J. Suppl. Ser. 2015, 217, 32. [Google Scholar] [CrossRef]
- Hart, R.E.; Bamford, S.P.; Willett, K.W.; Masters, K.L.; Cardamone, C.; Lintott, C.J.; Mackay, R.J.; Nichol, R.C.; Rosslowe, C.K.; Simmons, B.D.; et al. Galaxy Zoo: Comparing the demographics of spiral arm number and a new method for correcting redshift bias. Mon. Not. R. Astron. Soc. 2016, 461, 3663–3682. [Google Scholar] [CrossRef]
- Freeman, K.C. On the Disks of Spiral and S0 Galaxies. Astrophys. J. 1970, 160, 811. [Google Scholar] [CrossRef]
- Davis, B.L.; Kennefick, D.; Kennefick, J.; Westfall, K.B.; Shields, D.W.; Flatman, R.; Hartley, M.T.; Berrier, J.C.; Martinsson, T.P.K.; Swaters, R.A. A Fundamental Plane of Spiral Structure in Disk Galaxies. Astrophys. J. Lett. 2015, 802, L13. [Google Scholar] [CrossRef]
- Yu, S.Y.; Yuo, L.C. On the Connection between Spiral Arm Pitch Angle and Galaxy Properties. Astrophys. J. 2019, 871, 194. [Google Scholar] [CrossRef]
- Seigar, M.S.; Kennefick, D.; Kennefick, J.; Lacy, C.H.S. Discovery of a Relationship between Spiral Arm Morphology and Supermassive Black Hole Mass in Disk Galaxies. Astrophys. J. Lett. 2008, 678, L93. [Google Scholar] [CrossRef]
- Kendall, S.; Clarke, C.; Kennicutt, R.C. Spiral structure in nearby galaxies—II. Comparative analysis and conclusions. Mon. Not. R. Astron. Soc. 2015, 446, 4155–4167. [Google Scholar] [CrossRef]
- Sarkar, S.; Narayanan, G.; Banerjee, A.; Prakash, P. Identification of Grand-design and Flocculent spirals from SDSS using deep convolutional neural network. Mon. Not. R. Astron. Soc. 2023, 518, 1022–1040. [Google Scholar] [CrossRef]
- Masters, K.L.; Lintott, C.J.; Hart, R.E.; Kruk, S.J.; Smethurst, R.J.; Casteels, K.V.; Keel, W.C.; Simmons, B.D.; Stanescu, D.O.; Tate, J.; et al. Galaxy Zoo: Unwinding the winding problem—Observations of spiral bulge prominence and arm pitch angles suggest local spiral galaxies are winding. Mon. Not. R. Astron. Soc. 2019, 487, 1808–1820. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. On the Spiral Structure of Disk Galaxies. Astrophys. J. 1964, 140, 646. [Google Scholar] [CrossRef]
- Lin, C.C.; Shu, F.H. Density waves in disk galaxies. In Proceedings of the Radio Astronomy and the Galactic System, Noordwijk, The Netherlands, 25 August–1 September 1966; van Woerden, H., Ed.; International Astronomical Union: Paris, France, 1967; Volume 31, IAU Symposium. p. 313. [Google Scholar]
- Roberts, W.W. Large-Scale Shock Formation in Spiral Galaxies and its Implications on Star Formation. Astrophys. J. 1969, 158, 123. [Google Scholar] [CrossRef]
- Bertin, G.; Lin, C.C.; Lowe, S.A.; Thurstans, R.P. Modal Approach to the Morphology of Spiral Galaxies. II. Dynamical Mechanisms. Astrophys. J. 1989, 338, 104. [Google Scholar] [CrossRef]
- Julian, W.H.; Toomre, A. Non-Axisymmetric Responses of Differentially Rotating Disks of Stars. Astrophys. J. 1966, 146, 810. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Carlberg, R.G. Spiral instabilities provoked by accretion and star formation. Astrophys. J. 1984, 282, 61–74. [Google Scholar] [CrossRef]
- Sellwood, J.A. The lifetimes of spiral patterns in disc galaxies. Mon. Not. R. Astron. Soc. 2011, 410, 1637–1646. [Google Scholar] [CrossRef]
- Thomasson, M.; Elmegreen, B.G.; Donner, K.J.; Sundelius, B. A Computer-generated Galaxy Model with Long-lived Two-armed Spiral Structure. Astrophys. J. Lett. 1990, 356, L9. [Google Scholar] [CrossRef]
- Toomre, A. Group Velocity of Spiral Waves in Galactic Disks. Astrophys. J. 1969, 158, 899. [Google Scholar] [CrossRef]
- Donner, K.J.; Thomasson, M. Structure and evolution of long-lived spiral patterns in galaxies. Astron. Astrophys. 1994, 290, 785–795. [Google Scholar]
- D’Onghia, E.; Vogelsberger, M.; Hernquist, L. Self-perpetuating Spiral Arms in Disk Galaxies. Astrophys. J. 2013, 766, 34. [Google Scholar] [CrossRef]
- Sanders, R.H.; Huntley, J.M. Gas response to oval distortions in disk galaxies. Astrophys. J. 1976, 209, 53–65. [Google Scholar] [CrossRef]
- Sellwood, J.A.; Sparke, L.S. Pattern speeds in barred spiral galaxies. Mon. Not. R. Astron. Soc. 1988, 231, 25P–31. [Google Scholar] [CrossRef]
- Kormendy, J.; Norman, C.A. Observational constraints on driving mechanisms for spiral density waves. Astrophys. J. 1979, 233, 539–552. [Google Scholar] [CrossRef]
- Byrd, G.G.; Howard, S. Tidal Arms are Ubiquitous in Spiral Galaxies. Astron. J. 1992, 103, 1089. [Google Scholar] [CrossRef]
- Rautiainen, P.; Salo, H. Multiple pattern speeds in barred galaxies. I. Two-dimensional models. Astron. Astrophys. 1999, 348, 737–754. [Google Scholar]
- Oh, S.H.; Kim, W.T.; Lee, H.M.; Kim, J. Physical Properties of Tidal Features in Interacting Disk Galaxies. Astrophys. J. 2008, 683, 94–113. [Google Scholar] [CrossRef]
- Kumar, A.; Ghosh, S.; Kataria, S.K.; Das, M.; Debattista, V.P. Excitation of vertical breathing motion in disc galaxies by tidally-induced spirals in fly-by interactions. Mon. Not. R. Astron. Soc. 2022, 516, 1114–1126. [Google Scholar] [CrossRef]
- Struck, C.; Dobbs, C.L.; Hwang, J.S. Slowly breaking waves: The longevity of tidally induced spiral structure. Mon. Not. R. Astron. Soc. 2011, 414, 2498–2510. [Google Scholar] [CrossRef]
- Dobbs, C.L.; Pringle, J.E. Age distributions of star clusters in spiral and barred galaxies as a test for theories of spiral structure. Mon. Not. R. Astron. Soc. 2010, 409, 396–404. [Google Scholar] [CrossRef]
- Semczuk, M.; Łokas, E.L.; del Pino, A. Tidal Origin of Spiral Arms in Galaxies Orbiting a Cluster. Astrophys. J. 2017, 834, 7. [Google Scholar] [CrossRef]
- Sygnet, J.F.; Tagger, M.; Athanassoula, E.; Pellat, R. Non-linear coupling of spiral modes in disc galaxies. Mon. Not. R. Astron. Soc. 1988, 232, 733–752. [Google Scholar] [CrossRef]
- Masset, F.; Tagger, M. Non-linear coupling of spiral waves in disk galaxies: A numerical study. Astron. Astrophys. 1997, 322, 442–454. [Google Scholar] [CrossRef]
- Buta, R.J.; Zhang, X. Pattern Corotation Radii from Potential-Density Phase-Shifts for 153 OSUBGS Sample Galaxies. Astrophys. J. Suppl. Ser. 2009, 182, 559–583. [Google Scholar] [CrossRef]
- Meidt, S.E.; Rand, R.J.; Merrifield, M.R. Uncovering the Origins of Spiral Structure by Measuring Radial Variation in Pattern Speeds. Astrophys. J. 2009, 702, 277–290. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; Querejeta, M.; Epinat, B.; James, P.A.; Blasco-herrera, J.; Erroz-Ferrer, S.; Pérez, I. Interlocking Resonance Patterns in Galaxy Disks. Astrophys. J. Suppl. Ser. 2014, 210, 2. [Google Scholar] [CrossRef]
- Marchuk, A.A. Resonance coupling in spiral arms. Patterns for flat rotation curve. Astron. Astrophys. 2024, 686, L14. [Google Scholar] [CrossRef]
- Kostiuk, V.S.; Marchuk, A.A.; Gusev, A.S. Cross-method Analysis of Corotation Radii Data Set for Spiral Galaxies. Res. Astron. Astrophys. 2024, 24, 075007. [Google Scholar] [CrossRef]
- Tremaine, S.; Weinberg, M.D. A kinematic method for measuring the pattern speed of barred galaxies. Astrophys. J. Lett. 1984, 282, L5–L7. [Google Scholar] [CrossRef]
- Merrifield, M.R.; Rand, R.J.; Meidt, S.E. The lifetime of grand design. Mon. Not. R. Astron. Soc. 2006, 366, L17–L21. [Google Scholar] [CrossRef]
- Vallée, J.P. Statistics on 24 spiral galaxies having different observed arm locations using different arm tracers. New Astron. 2020, 76, 101337. [Google Scholar] [CrossRef]
- Oey, M.S.; Parker, J.S.; Mikles, V.J.; Zhang, X. H II Regions in Spiral Galaxies: Size Distribution, Luminosity Function, and New Isochrone Diagnostics of Density-Wave Kinematics. Astron. J. 2003, 126, 2317–2329. [Google Scholar] [CrossRef]
- Tamburro, D.; Rix, H.W.; Walter, F.; Brinks, E.; de Blok, W.J.G.; Kennicutt, R.C.; Mac Low, M.M. Geometrically Derived Timescales for Star Formation in Spiral Galaxies. Astron. J. 2008, 136, 2872–2885. [Google Scholar] [CrossRef]
- Shabani, F.; Grebel, E.K.; Pasquali, A.; D’Onghia, E.; Gallagher, J.S.; Adamo, A.; Messa, M.; Elmegreen, B.G.; Dobbs, C.; Gouliermis, D.A.; et al. Search for star cluster age gradients across spiral arms of three LEGUS disc galaxies. Mon. Not. R. Astron. Soc. 2018, 478, 3590–3604. [Google Scholar] [CrossRef]
- Abdeen, S.; Kennefick, D.; Kennefick, J.; Miller, R.; Shields, D.W.; Monson, E.B.; Davis, B.L. Determining the co-rotation radii of spiral galaxies using spiral arm pitch angle measurements at multiple wavelengths. Mon. Not. R. Astron. Soc. 2020, 496, 1610–1619. [Google Scholar] [CrossRef]
- Abdeen, S.; Davis, B.L.; Eufrasio, R.; Kennefick, D.; Kennefick, J.; Miller, R.; Shields, D.; Monson, E.B.; Bassett, C.; O’Mara, H. Evidence in favour of density wave theory through age gradients observed in star formation history maps and spatially resolved stellar clusters. Mon. Not. R. Astron. Soc. 2022, 512, 366–377. [Google Scholar] [CrossRef]
- Rand, R.J.; Wallin, J.F. Pattern Speeds of BIMA SONG Galaxies with Molecule-dominated Interstellar Mediums Using the Tremaine-Weinberg Method. Astrophys. J. 2004, 614, 142–157. [Google Scholar] [CrossRef]
- Hernandez, O.; Wozniak, H.; Carignan, C.; Amram, P.; Chemin, L.; Daigle, O. On the Relevance of the Tremaine-Weinberg Method Applied to an Hα Velocity Field: Pattern Speed Determination in M100 (NGC 4321). Astrophys. J. 2005, 632, 253–265. [Google Scholar] [CrossRef]
- Beckman, J.E.; Font, J.; Borlaff, A.; García-Lorenzo, B. Precision Determination of Corotation Radii in Galaxy Disks: Tremaine-Weinberg versus Font-Beckman for NGC 3433. Astrophys. J. 2018, 854, 182. [Google Scholar] [CrossRef]
- Williams, T.G.; Schinnerer, E.; Emsellem, E.; Meidt, S.; Querejeta, M.; Belfiore, F.; Bešlić, I.; Bigiel, F.; Chevance, M.; Dale, D.A.; et al. Applying the Tremaine-Weinberg Method to Nearby Galaxies: Stellar-mass-based Pattern Speeds and Comparisons with ISM Kinematics. Astron. J. 2021, 161, 185. [Google Scholar] [CrossRef]
- Garcia-Burillo, S.; Sempere, M.J.; Combes, F.; Neri, R. Molecular gas in the barred spiral M 100. II. 12 CO(1-0) interferometer observations and numerical simulations. Astron. Astrophys. 1998, 333, 864–876. [Google Scholar] [CrossRef]
- Rautiainen, P.; Salo, H.; Laurikainen, E. Model-based pattern speed estimates for 38 barred galaxies. Mon. Not. R. Astron. Soc. 2008, 388, 1803–1818. [Google Scholar] [CrossRef]
- Elmegreen, D.M.; Elmegreen, B.G. Inner Two-Arm Symmetry in Spiral Galaxies. Astrophys. J. 1995, 445, 591. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; Epinat, B.; Fathi, K.; Gutiérrez, L.; Hernandez, O. Resonant Structure in the Disks of Spiral Galaxies, Using Phase Reversals in Streaming Motions from Two-dimensional Hα Fabry-Perot Spectroscopy. Astrophys. J. Lett. 2011, 741, L14. [Google Scholar] [CrossRef]
- McCall, M.L. The Chemistry of Galaxies. Ph.D. Thesis, University of Texas, Austin, TX, USA, 1982. [Google Scholar]
- Scarano, S.; Lépine, J.R.D. Radial metallicity distribution breaks at corotation radius in spiral galaxies. Mon. Not. R. Astron. Soc. 2013, 428, 625–640. [Google Scholar] [CrossRef]
- Marchuk, A.A.; Mosenkov, A.V.; Chugunov, I.V.; Kostiuk, V.S.; Skryabina, M.N.; Reshetnikov, V.P. A new, purely photometric method for determination of resonance locations in spiral galaxies. Mon. Not. R. Astron. Soc. 2024, 527, L66–L70. [Google Scholar] [CrossRef]
- Marino, A.; Plana, H.; Rampazzo, R.; Bianchi, L.; Rosado, M.; Bettoni, D.; Galletta, G.; Mazzei, P.; Buson, L.; Ambrocio-Cruz, P.; et al. Galaxy evolution in nearby loose groups—II. Photometric and kinematic characterization of USGC U268 and USGC U376 group members in the Leo cloud. Mon. Not. R. Astron. Soc. 2013, 428, 476–501. [Google Scholar] [CrossRef]
- Knapen, J.H.; Cepa, J.; Beckman, J.E.; Soledad del Rio, M.; Pedlar, A. Star Formation in the Spiral Arms of NGC 4321. II. H i Distribution and Kinematics. Astrophys. J. 1993, 416, 563. [Google Scholar] [CrossRef]
- Font, J.; Beckman, J.E.; Zaragoza-Cardiel, J.; Fathi, K.; Epinat, B.; Amram, P. The ratio of pattern speeds in double-barred galaxies. Mon. Not. R. Astron. Soc. 2014, 444, L85–L89. [Google Scholar] [CrossRef]
- Elmegreen, B.G.; Elmegreen, D.M.; Montenegro, L. Optical Tracers of Spiral Wave Resonances in Galaxies. II. Hidden Three-Arm Spirals in a Sample of 18 Galaxies. Astrophys. J. Suppl. Ser. 1992, 79, 37. [Google Scholar] [CrossRef]
- Carlin, J.L.; Garling, C.T.; Peter, A.H.G.; Crnojević, D.; Forbes, D.A.; Hargis, J.R.; Mutlu-Pakdil, B.; Pucha, R.; Romanowsky, A.J.; Sand, D.J.; et al. Tidal Destruction in a Low-mass Galaxy Environment: The Discovery of Tidal Tails around DDO 44. Astrophys. J. 2019, 886, 109. [Google Scholar] [CrossRef]
- Veronese, S.; de Blok, W.J.G.; Walter, F. Extended neutral hydrogen filamentary network in NGC 2403. Astron. Astrophys. 2023, 672, A55. [Google Scholar] [CrossRef]
- Roberts, W.W., Jr.; Roberts, M.S.; Shu, F.H. Density wave theory and the classification of spiral galaxies. Astrophys. J. 1975, 196, 381–405. [Google Scholar] [CrossRef]
- Fathi, K.; Beckman, J.E.; Piñol-Ferrer, N.; Hernandez, O.; Martínez-Valpuesta, I.; Carignan, C. Pattern Speeds of Bars and Spiral Arms from Hα Velocity Fields. Astrophys. J. 2009, 704, 1657–1675. [Google Scholar] [CrossRef]
- Kalnajs, A.J. A Confrontation of Density Wave Theories with Observations. In Proceedings of the Structure and Properties of Nearby Galaxies, Bad Münstereifel, Germany, 22–26 August 1977; Berkhuijsen, E.M., Wielebinski, R., Eds.; International Astronomical Union: Paris, France, 1978; Volume 77, p. 113. [Google Scholar]
- Sakhibov, F.K.; Smirnov, M.A. Noncircular Gas Motion in the Spiral Galaxies NGC3031 NGC2903 and NGC925. Sov. Astron. 1989, 33, 476. [Google Scholar]
- Canzian, B. A New Way to Locate Corotation Resonances in Spiral Galaxies. Astrophys. J. 1993, 414, 487. [Google Scholar] [CrossRef]
- Sempere, M.J.; Garcia-Burillo, S.; Combes, F.; Knapen, J.H. Determination of the pattern speed in the grand design spiral galaxy NGC 4321. Astron. Astrophys. 1995, 296, 45. [Google Scholar]
- Lyakhovich, V.V.; Fridman, A.M.; Khoruzhii, O.V.; Pavlov, A.I. A method for reconstructing the full vector velocity field in the gaseous disks of spiral galaxies. Astron. Rep. 1997, 41, 447–471. [Google Scholar]
- Chemin, L.; Balkowski, C.; Cayatte, V.; Carignan, C.; Amram, P.; Garrido, O.; Hernandez, O.; Marcelin, M.; Adami, C.; Boselli, A.; et al. A Virgo high-resolution Hα kinematical survey - II. The Atlas. Mon. Not. R. Astron. Soc. 2006, 366, 812–857. [Google Scholar] [CrossRef]
- Daigle, O.; Carignan, C.; Amram, P.; Hernandez, O.; Chemin, L.; Balkowski, C.; Kennicutt, R. Hαkinematics of the SINGS nearby galaxies survey—I*. Mon. Not. R. Astron. Soc. 2006, 367, 469–512. [Google Scholar] [CrossRef]
- Di Teodoro, E.M.; Fraternali, F. 3DBAROLO: A new 3D algorithm to derive rotation curves of galaxies. Mon. Not. R. Astron. Soc. 2015, 451, 3021–3033. [Google Scholar] [CrossRef]
- Nersesian, A.; Xilouris, E.M.; Bianchi, S.; Galliano, F.; Jones, A.P.; Baes, M.; Casasola, V.; Cassarà, L.P.; Clark, C.J.R.; Davies, J.I.; et al. Old and young stellar populations in DustPedia galaxies and their role in dust heating. Astron. Astrophys. 2019, 624, A80. [Google Scholar] [CrossRef]
- Ashby, M.L.N.; Mahajan, S.; Smith, H.A.; Willner, S.P.; Fazio, G.G.; Raychaudhury, S.; Zezas, A.; Barmby, P.; Bonfini, P.; Cao, C.; et al. The Star Formation Reference Survey. I. Survey Description and Basic Data. Publ. Astron. Soc. Pac. 2011, 123, 1011. [Google Scholar] [CrossRef]
- Sorai, K.; Kuno, N.; Muraoka, K.; Miyamoto, Y.; Kaneko, H.; Nakanishi, H.; Nakai, N.; Yanagitani, K.; Tanaka, T.; Sato, Y.; et al. CO multi-line imaging of nearby galaxies (COMING). IV. Overview of the project. Publ. Astron. Soc. Jpn. 2019, 71, S14. [Google Scholar] [CrossRef]
- Sheth, K.; Regan, M.; Hinz, J.L.; Gil de Paz, A.; Menéndez-Delmestre, K.; Muñoz-Mateos, J.C.; Seibert, M.; Kim, T.; Laurikainen, E.; Salo, H.; et al. The Spitzer Survey of Stellar Structure in Galaxies (S4G). Publ. Astron. Soc. Pac. 2010, 122, 1397. [Google Scholar] [CrossRef]
- Makarov, D.; Prugniel, P.; Terekhova, N.; Courtois, H.; Vauglin, I. HyperLEDA. III. The catalogue of extragalactic distances. Astron. Astrophys. 2014, 570, A13. [Google Scholar] [CrossRef]
- Miller, R.; Kennefick, D.; Kennefick, J.; Shameer Abdeen, M.; Monson, E.; Eufrasio, R.T.; Shields, D.W.; Davis, B.L. Investigating the Origins of Spiral Structure in Disk Galaxies through a Multiwavelength Study. Astrophys. J. 2019, 874, 177. [Google Scholar] [CrossRef]
- Martínez-García, E.E.; González-Lópezlira, R.A. Signatures of Long-lived Spiral Patterns. Astrophys. J. 2013, 765, 105. [Google Scholar] [CrossRef]
- Martínez-García, E.E.; González-Lópezlira, R.A.; Puerari, I. Colour jumps across the spiral arms of Hubble Ultra Deep Field galaxies. Mon. Not. R. Astron. Soc. 2023, 524, 18–31. [Google Scholar] [CrossRef]
- Pettitt, A.R.; Tasker, E.J.; Wadsley, J.W.; Keller, B.W.; Benincasa, S.M. Star formation and ISM morphology in tidally induced spiral structures. Mon. Not. R. Astron. Soc. 2017, 468, 4189–4204. [Google Scholar] [CrossRef]
- Egusa, F.; Kohno, K.; Sofue, Y.; Nakanishi, H.; Komugi, S. Determining Star Formation Timescale and Pattern Speed in Nearby Spiral Galaxies. Astrophys. J. 2009, 697, 1870–1891. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ho, L.C. Dependence of the Spiral Arms Pitch Angle on Wavelength as a Test of the Density Wave Theory. Astrophys. J. 2018, 869, 29. [Google Scholar] [CrossRef]
- Foyle, K.; Rix, H.W.; Dobbs, C.L.; Leroy, A.K.; Walter, F. Observational Evidence Against Long-lived Spiral Arms in Galaxies. Astrophys. J. 2011, 735, 101. [Google Scholar] [CrossRef]
- Choi, Y.; Dalcanton, J.J.; Williams, B.F.; Weisz, D.R.; Skillman, E.D.; Fouesneau, M.; Dolphin, A.E. Testing Density Wave Theory with Resolved Stellar Populations around Spiral Arms in M81. Astrophys. J. 2015, 810, 9. [Google Scholar] [CrossRef]
- Ferreras, I.; Cropper, M.; Kawata, D.; Page, M.; Hoversten, E.A. The Swift/UVOT catalogue of NGC 4321 star-forming sources: A case against density wave theory. Mon. Not. R. Astron. Soc. 2012, 424, 1636–1646. [Google Scholar] [CrossRef]
- Louie, M.; Koda, J.; Egusa, F. Geometric Offsets across Spiral Arms in M51: Nature of Gas and Star Formation Tracers. Astrophys. J. 2013, 763, 94. [Google Scholar] [CrossRef]
- Egusa, F.; Mentuch Cooper, E.; Koda, J.; Baba, J. Gas and stellar spiral arms and their offsets in the grand-design spiral galaxy M51. Mon. Not. R. Astron. Soc. 2017, 465, 460–471. [Google Scholar] [CrossRef]
- Sakhibov, F.; Gusev, A.S.; Hemmerich, C. Azimuthal propagation of star formation in nearby spiral galaxies: NGC 628, NGC 3726, and NGC 6946. Mon. Not. R. Astron. Soc. 2021, 508, 912–925. [Google Scholar] [CrossRef]
- Marchuk, A.A.; Chugunov, I.V.; Gontcharov, G.A.; Mosenkov, A.V.; Il’in, V.B.; Savchenko, S.S.; Smirnov, A.A.; Poliakov, D.M.; Seguine, J.; Chazov, M.I. Galaxies Decomposition with Spiral Arms—II. A Multiwavelength Case Study of M 51. Mon. Not. R. Astron. Soc. 2024, 528, 1276–1295. [Google Scholar] [CrossRef]
- Chugunov, I.V.; Marchuk, A.A.; Mosenkov, A.V.; Savchenko, S.S.; Shishkina, E.V.; Chazov, M.I.; Nazarova, A.E.; Skryabina, M.N.; Smirnova, P.I.; Smirnov, A.A. Galaxies decomposition with spiral arms—I: 29 galaxies from S4G. Mon. Not. R. Astron. Soc. 2024, 527, 9605–9624. [Google Scholar] [CrossRef]
- Davis, B.L.; Berrier, J.C.; Shields, D.W.; Kennefick, J.; Kennefick, D.; Seigar, M.S.; Lacy, C.H.S.; Puerari, I. Measurement of Galactic Logarithmic Spiral Arm Pitch Angle Using Two-dimensional Fast Fourier Transform Decomposition. Astrophys. J. Suppl. Ser. 2012, 199, 33. [Google Scholar] [CrossRef]
- Pour-Imani, H.; Kennefick, D.; Kennefick, J.; Davis, B.L.; Shields, D.W.; Shameer Abdeen, M. Strong Evidence for the Density-wave Theory of Spiral Structure in Disk Galaxies. Astrophys. J. Lett. 2016, 827, L2. [Google Scholar] [CrossRef]
- Twarog, B.A.; Ashman, K.M.; Anthony-Twarog, B.J. Some Revised Observational Constraints on the Formation and Evolution of the Galactic Disk. Astron. J. 1997, 114, 2556. [Google Scholar] [CrossRef]
- Lépine, J.R.D.; Roman-Lopes, A.; Abraham, Z.; Junqueira, T.C.; Mishurov, Y.N. The spiral structure of the Galaxy revealed by CS sources and evidence for the 4:1 resonance. Mon. Not. R. Astron. Soc. 2011, 414, 1607–1616. [Google Scholar] [CrossRef]
- Vila-Costas, M.B.; Edmunds, M.G. The relation between abundance gradients and the physical properties of spiral galaxies. Mon. Not. R. Astron. Soc. 1992, 259, 121–145. [Google Scholar] [CrossRef]
- Martin, P.; Roy, J.R. The Oxygen Distribution in NGC 3359 or a Disk Galaxy in the Early Phase of Bar Formation. Astrophys. J. 1995, 445, 161. [Google Scholar] [CrossRef]
- Belfiore, F.; Maiolino, R.; Tremonti, C.; Sánchez, S.F.; Bundy, K.; Bershady, M.; Westfall, K.; Lin, L.; Drory, N.; Boquien, M.; et al. SDSS IV MaNGA—Metallicity and nitrogen abundance gradients in local galaxies. Mon. Not. R. Astron. Soc. 2017, 469, 151–170. [Google Scholar] [CrossRef]
- Sánchez-Menguiano, L.; Sánchez, S.F.; Pérez, I.; Ruiz-Lara, T.; Galbany, L.; Anderson, J.P.; Krühler, T.; Kuncarayakti, H.; Lyman, J.D. The shape of oxygen abundance profiles explored with MUSE: Evidence for widespread deviations from single gradients. Astron. Astrophys. 2018, 609, A119. [Google Scholar] [CrossRef]
- Chen, Q.H.; Grasha, K.; Battisti, A.J.; Kewley, L.J.; Madore, B.F.; Seibert, M.; Rich, J.A.; Beaton, R.L. Metallicity gradient of barred galaxies with TYPHOON. Mon. Not. R. Astron. Soc. 2023, 519, 4801–4817. [Google Scholar] [CrossRef]
- Lépine, J.R.D.; Mishurov, Y.N.; Dedikov, S.Y. A New Model for the Spiral Structure of the Galaxy: Superposition of 2- and 4-armed Patterns. Astrophys. J. 2001, 546, 234–247. [Google Scholar] [CrossRef]
- Garcia, A.M.; Torrey, P.; Hemler, Z.S.; Hernquist, L.; Kewley, L.J.; Nelson, E.J.; Grasha, K.; Zovaro, H.R.M.; Chen, Q.H. Gas-phase metallicity break radii of star-forming galaxies in IllustrisTNG. Mon. Not. R. Astron. Soc. 2023, 519, 4716–4734. [Google Scholar] [CrossRef]
- Hemler, Z.S.; Torrey, P.; Qi, J.; Hernquist, L.; Vogelsberger, M.; Ma, X.; Kewley, L.J.; Nelson, D.; Pillepich, A.; Pakmor, R.; et al. Gas-phase metallicity gradients of TNG50 star-forming galaxies. Mon. Not. R. Astron. Soc. 2021, 506, 3024–3048. [Google Scholar] [CrossRef]
- Acharyya, A.; Peeples, M.S.; Tumlinson, J.; Shea, B.W.O.; Lochhaas, C.; Wright, A.C.; Simons, R.C.; Augustin, R.; Smith, B.D.; Hyeonmin Lee, E. Figuring Out Gas & Galaxies In Enzo (FOGGIE) VIII: Complex and Stochastic Metallicity Gradients at z > 2. arXiv 2024, arXiv:2404.06613. [Google Scholar] [CrossRef]
- Minchev, I.; Famaey, B.; Combes, F.; Di Matteo, P.; Mouhcine, M.; Wozniak, H. Radial migration in galactic disks caused by resonance overlap of multiple patterns: Self-consistent simulations. Astron. Astrophys. 2011, 527, A147. [Google Scholar] [CrossRef]
- Spitoni, E.; Cescutti, G.; Minchev, I.; Matteucci, F.; Silva Aguirre, V.; Martig, M.; Bono, G.; Chiappini, C. 2D chemical evolution model: The impact of Galactic disc asymmetries on azimuthal chemical abundance variations. Astron. Astrophys. 2019, 628, A38. [Google Scholar] [CrossRef]
- Spitoni, E.; Cescutti, G.; Recio-Blanco, A.; Minchev, I.; Poggio, E.; Palicio, P.A.; Matteucci, F.; Peirani, S.; Barbillon, M.; Vasini, A. 2D chemical evolution models. II. Effects of multiple spiral arm patterns on O, Eu, Fe, and Ba abundance gradients. Astron. Astrophys. 2023, 680, A85. [Google Scholar] [CrossRef]
- Friedli, D.; Benz, W.; Kennicutt, R. On the Influence of Bars and Star Formation on Galactic Abundance Gradients. Astrophys. J. Lett. 1994, 430, L105. [Google Scholar] [CrossRef]
- Roy, J.R.; Walsh, J.R. The abundance gradient of NGC 1365: Evidence for a recently formed bar in an archetypal barred spiral galaxy? Mon. Not. R. Astron. Soc. 1997, 288, 715–725. [Google Scholar] [CrossRef]
- Friedli, D. Birth, Aging, and Death of Galactic Bars. In Proceedings of the The Evolution of Galaxies on Cosmological Timescales, Tenerife, Spain, 30 November–5 December 1998; Beckman, J.E., Mahoney, T.J., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1999; Volume 187, Astronomical Society of the Pacific Conference Series. pp. 88–99. [Google Scholar] [CrossRef]
- Belfiore, F.; Maiolino, R.; Bundy, K.; Masters, K.; Bershady, M.; Oyarzún, G.A.; Lin, L.; Cano-Diaz, M.; Wake, D.; Spindler, A.; et al. SDSS IV MaNGA—sSFR profiles and the slow quenching of discs in green valley galaxies. Mon. Not. R. Astron. Soc. 2018, 477, 3014–3029. [Google Scholar] [CrossRef]
- Simons, R.C.; Papovich, C.; Momcheva, I.; Trump, J.R.; Brammer, G.; Estrada-Carpenter, V.; Backhaus, B.E.; Cleri, N.J.; Finkelstein, S.L.; Giavalisco, M.; et al. CLEAR: The Gas-phase Metallicity Gradients of Star-forming Galaxies at 0.6 < z < 2.6. Astrophys. J. 2021, 923, 203. [Google Scholar] [CrossRef]
- Kewley, L.J.; Rupke, D.; Zahid, H.J.; Geller, M.J.; Barton, E.J. Metallicity Gradients and Gas Flows in Galaxy Pairs. Astrophys. J. Lett. 2010, 721, L48–L52. [Google Scholar] [CrossRef]
- Miralles-Caballero, D.; Díaz, A.I.; Rosales-Ortega, F.F.; Pérez-Montero, E.; Sánchez, S.F. Ionizing stellar population in the disc of NGC 3310—I. The impact of a minor merger on galaxy evolution. Mon. Not. R. Astron. Soc. 2014, 440, 2265–2289. [Google Scholar] [CrossRef]
- Gusev, A.S.; Dodin, A.V. Peculiarities of the chemical abundance distribution in galaxies NGC 3963 and NGC 7292. Mon. Not. R. Astron. Soc. 2021, 505, 2009–2019. [Google Scholar] [CrossRef]
- Carton, D.; Brinchmann, J.; Shirazi, M.; Contini, T.; Epinat, B.; Erroz-Ferrer, S.; Marino, R.A.; Martinsson, T.P.K.; Richard, J.; Patrício, V. Inferring gas-phase metallicity gradients of galaxies at the seeing limit: A forward modelling approach. Mon. Not. R. Astron. Soc. 2017, 468, 2140–2163. [Google Scholar] [CrossRef]
- Acharyya, A.; Krumholz, M.R.; Federrath, C.; Kewley, L.J.; Goldbaum, N.J.; Sharp, R. Quantifying the effects of spatial resolution and noise on galaxy metallicity gradients. Mon. Not. R. Astron. Soc. 2020, 495, 3819–3838. [Google Scholar] [CrossRef]
- Berg, D.A.; Skillman, E.D.; Garnett, D.R.; Croxall, K.V.; Marble, A.R.; Smith, J.D.; Gordon, K.; Kennicutt, R.C. New Radial Abundance Gradients for NGC 628 and NGC 2403. Astrophys. J. 2013, 775, 128. [Google Scholar] [CrossRef]
- Bresolin, F.; Kudritzki, R.P.; Urbaneja, M.A. The Metallicity and Distance of NGC 2403 from Blue Supergiants. Astrophys. J. 2022, 940, 32. [Google Scholar] [CrossRef]
- Rogers, N.S.J.; Skillman, E.D.; Pogge, R.W.; Berg, D.A.; Moustakas, J.; Croxall, K.V.; Sun, J. CHAOS. VI. Direct Abundances in NGC 2403. Astrophys. J. 2021, 915, 21. [Google Scholar] [CrossRef]
- Moustakas, J.; Kennicutt, R.C.; Tremonti, C.A.; Dale, D.A.; Smith, J.D.T.; Calzetti, D. Optical Spectroscopy and Nebular Oxygen Abundances of the Spitzer/SINGS Galaxies. Astrophys. J. Suppl. Ser. 2010, 190, 233–266. [Google Scholar] [CrossRef]
- Pilyugin, L.S.; Grebel, E.K.; Kniazev, A.Y. The Abundance Properties of Nearby Late-type Galaxies. I. The Data. Astron. J. 2014, 147, 131. [Google Scholar] [CrossRef]
- Zurita, A.; Florido, E.; Bresolin, F.; Pérez-Montero, E.; Pérez, I. Bar effect on gas-phase abundance gradients. I. Data sample and chemical abundances. Mon. Not. R. Astron. Soc. 2021, 500, 2359–2379. [Google Scholar] [CrossRef]
- McCall, M.L.; Rybski, P.M.; Shields, G.A. The chemistry of galaxies. I. The nature of giant extragalactic H II regions. Astrophys. J. Suppl. Ser. 1985, 57, 1–62. [Google Scholar] [CrossRef]
- Shields, G.A.; Skillman, E.D.; Kennicutt, R.C., Jr. High Chemical Abundances in Virgo Spiral Galaxies? Astrophys. J. 1991, 371, 82. [Google Scholar] [CrossRef]
- Goldreich, P.; Tremaine, S. The excitation and evolution of density waves. Astrophys. J. 1978, 222, 850–858. [Google Scholar] [CrossRef]
- Nersesian, A.; Verstocken, S.; Viaene, S.; Baes, M.; Xilouris, E.M.; Bianchi, S.; Casasola, V.; Clark, C.J.R.; Davies, J.I.; De Looze, I.; et al. High-resolution, 3D radiative transfer modelling. III. The DustPedia barred galaxies. Astron. Astrophys. 2020, 637, A25. [Google Scholar] [CrossRef]
- Verstocken, S.; Nersesian, A.; Baes, M.; Viaene, S.; Bianchi, S.; Casasola, V.; Clark, C.J.R.; Davies, J.I.; De Looze, I.; De Vis, P.; et al. High-resolution, 3D radiative transfer modelling. II. The early-type spiral galaxy M 81. Astron. Astrophys. 2020, 637, A24. [Google Scholar] [CrossRef]
- Sánchez-Gil, M.C.; Jones, D.H.; Pérez, E.; Bland-Hawthorn, J.; Alfaro, E.J.; O’Byrne, J. Age patterns in a sample of spiral galaxies. Mon. Not. R. Astron. Soc. 2011, 415, 753–772. [Google Scholar] [CrossRef]
- Ponomareva, A.A.; Verheijen, M.A.W.; Bosma, A. Detailed H I kinematics of Tully-Fisher calibrator galaxies. Mon. Not. R. Astron. Soc. 2016, 463, 4052–4067. [Google Scholar] [CrossRef]
- Smith, B.J.; Giroux, M.L.; Struck, C. The Effect of Environment on Galaxy Spiral Arms, Bars, Concentration, and Quenching. Astron. J. 2022, 164, 146. [Google Scholar] [CrossRef]
- Savchenko, S.; Marchuk, A.; Mosenkov, A.; Grishunin, K. A multiwavelength study of spiral structure in galaxies. I. General characteristics in the optical. Mon. Not. R. Astron. Soc. 2020, 493, 390–409. [Google Scholar] [CrossRef]
- Chen, Q.H.; Grasha, K.; Battisti, A.J.; Wisnioski, E.; Mendel, T.; Sharda, P.; Santucci, G.; Li, Z.; Foster, C.; Mun, M.; et al. The MAGPI survey: Effects of spiral arms on different tracers of the interstellar medium and stellar populations at z 0.3. Mon. Not. R. Astron. Soc. 2024, 527, 2991–3005. [Google Scholar] [CrossRef]
- Peterken, T.G.; Merrifield, M.R.; Aragón-Salamanca, A.; Drory, N.; Krawczyk, C.M.; Masters, K.L.; Weijmans, A.M.; Westfall, K.B. A direct test of density wave theory in a grand-design spiral galaxy. Nat. Astron. 2019, 3, 178–182. [Google Scholar] [CrossRef]
- Kendall, S.; Kennicutt, R.C.; Clarke, C. Spiral structure in nearby galaxies—I. Sample, data analysis and overview of results. Mon. Not. R. Astron. Soc. 2011, 414, 538–564. [Google Scholar] [CrossRef]
- Meidt, S.E.; Rand, R.J.; Merrifield, M.R.; Shetty, R.; Vogel, S.N. Radial Dependence of the Pattern Speed of M51. Astrophys. J. 2008, 688, 224–236. [Google Scholar] [CrossRef]
- Chugunov, I.V.; Marchuk, A.A.; Mosenkov, A.V. Less Wound and More Asymmetric: JWST Confirms the Evolution of Spiral Structure in Galaxies at z ≲ 3. arXiv 2025, arXiv:2501.11670. [Google Scholar] [CrossRef]
- Erwin, P. IMFIT: A Fast, Flexible New Program for Astronomical Image Fitting. Astrophys. J. 2015, 799, 226. [Google Scholar] [CrossRef]
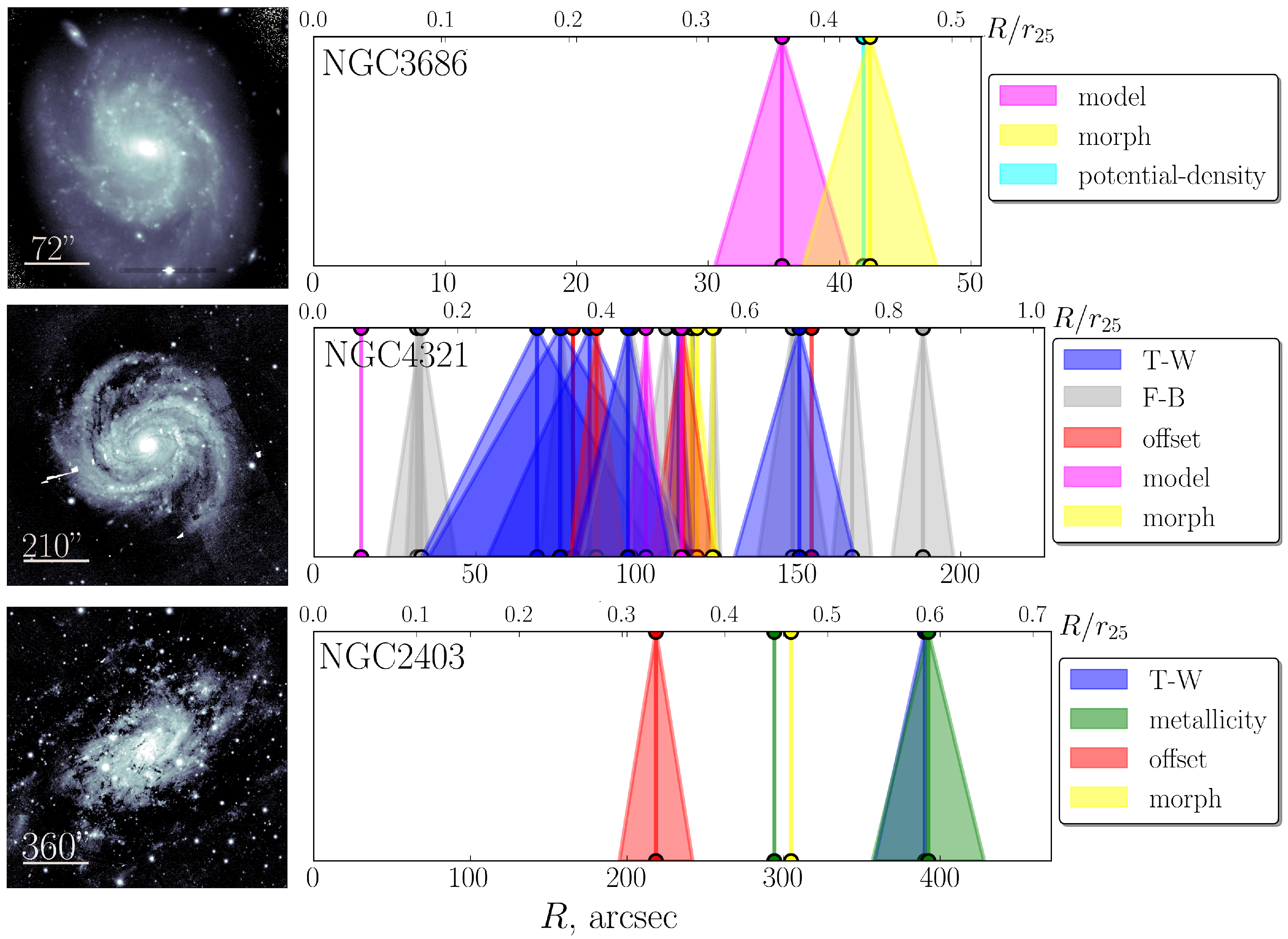

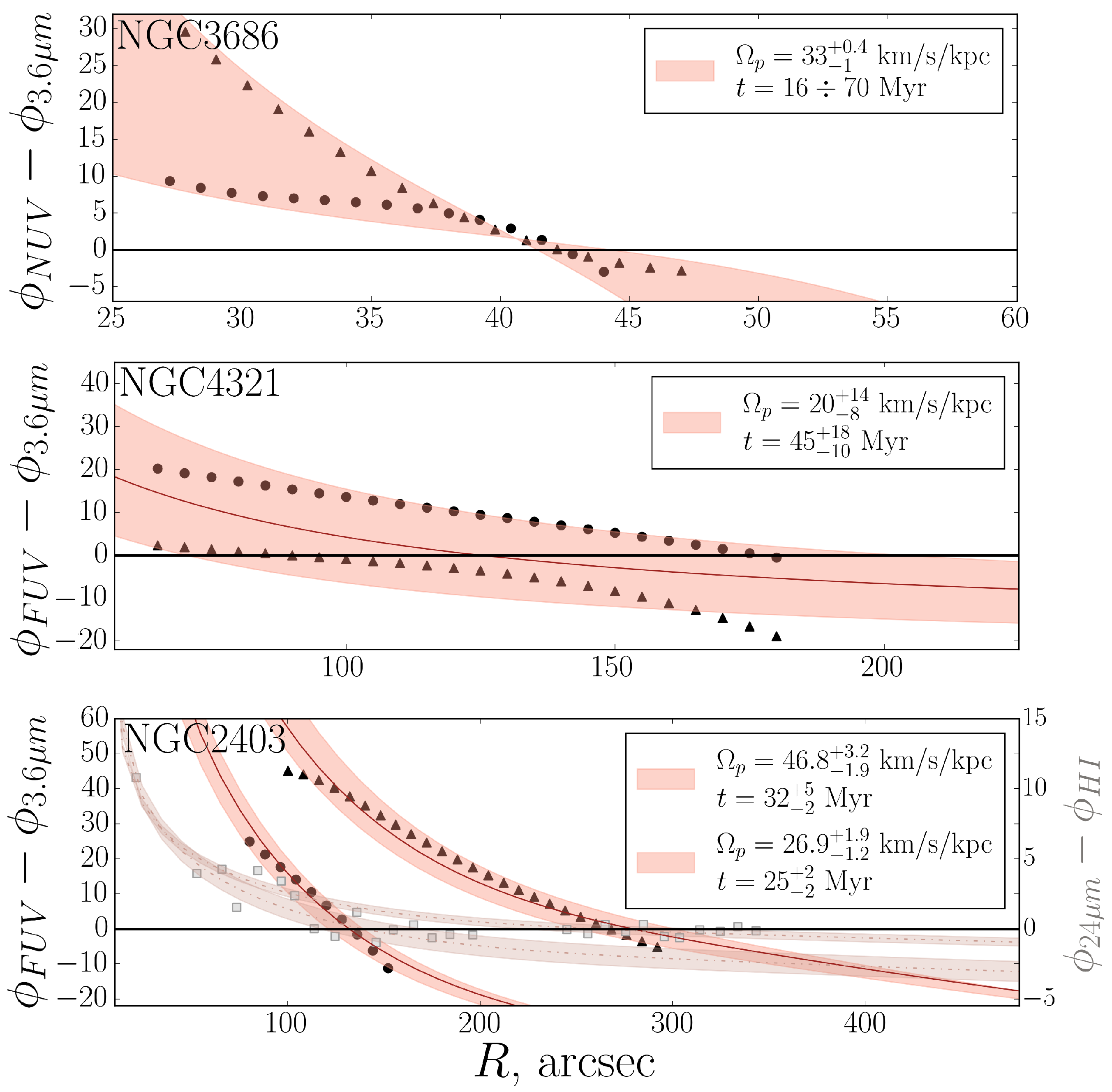
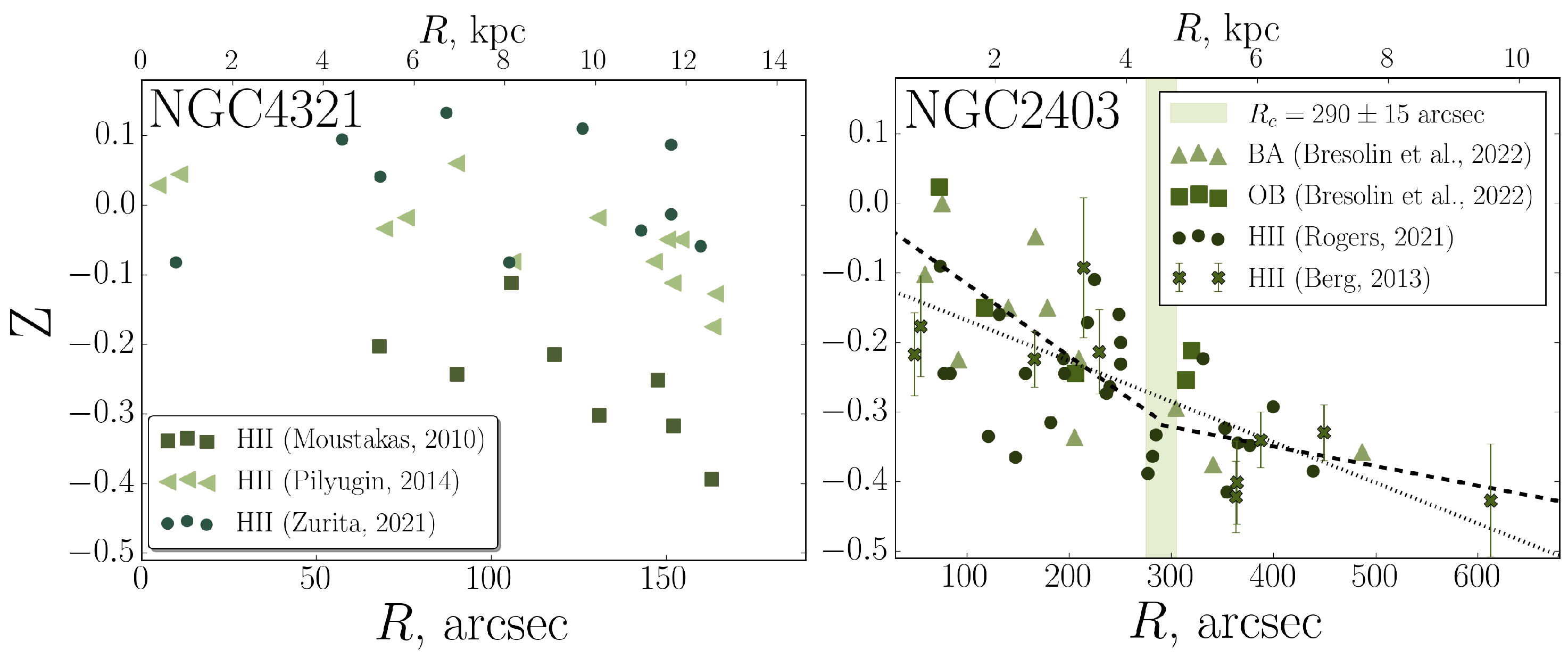

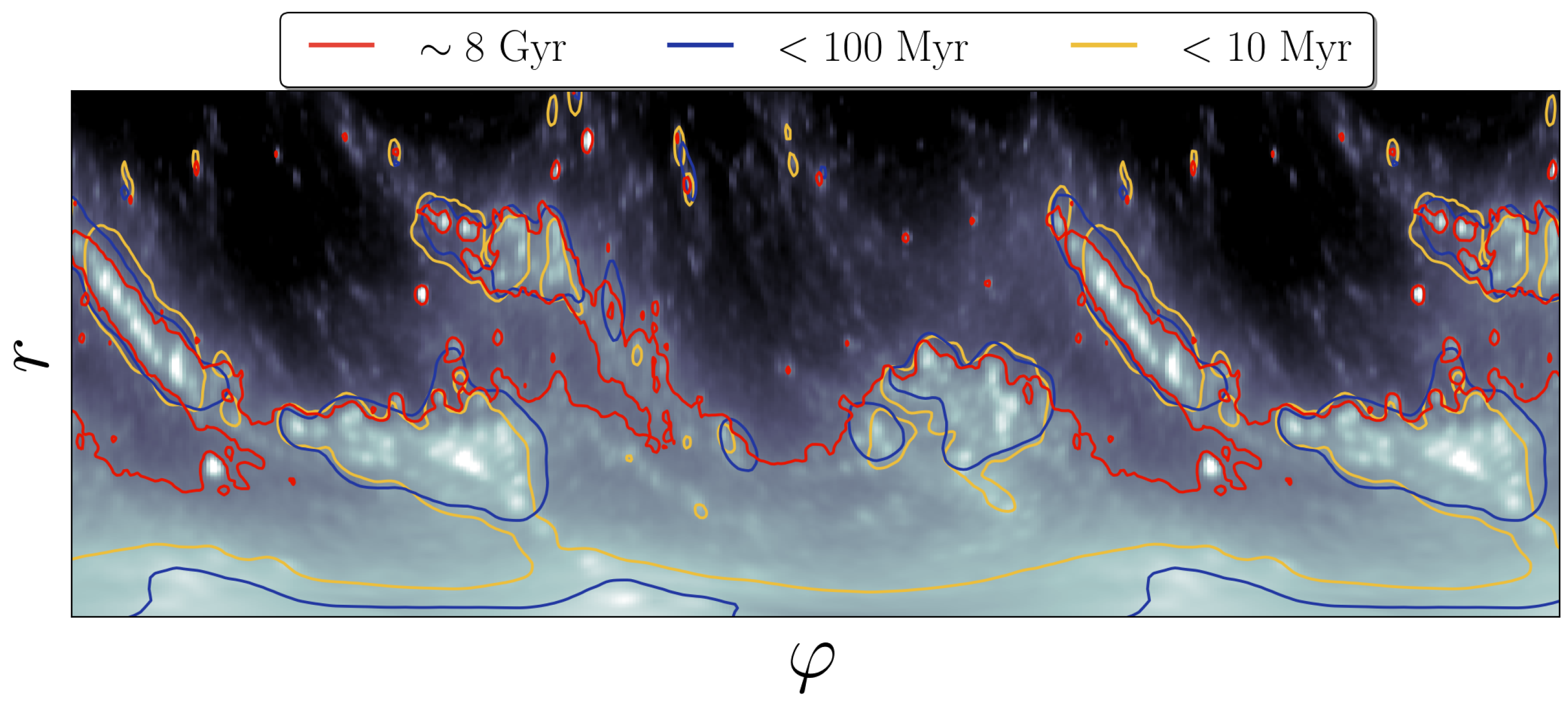

| Object Name | Stellar Mass, M⊙ | Absolute Magnitude, Mag 1 | Distance, Mpc | Positional Angle (PA), Deg | Inclination (i), Deg 2 | Systemic Velocity (Vsys), km/s 3 |
|---|---|---|---|---|---|---|
| NGC 3686 | 8.3 × 109 [76] | −18.7 | 21 [77] | 19 [78] | 35 ± 2 [78] | 1152 ± 1 |
| NGC 4321 | 4.9 × 1010 [76] | −20.5 | 15.9 [79] | 151 [73] | 38 ± 2 [73] | 1561 ± 2 |
| NGC 2403 | 2.9 × 109 [76] | −18.2 | 3.2 [80] | 125 [50] | 60 ± 2 [50] | 144 ± 2 |
| Object Name | Font-Beckman Method | Stellar Age Gradient | Metallicity Gradient |
|---|---|---|---|
| NGC 3686 | arcsec | 43 ± 1 arcsec | |
| NGC 2403 | arcsec | 140 ± 10, 275 ± 25 arcsec | 290 ± 15 arcsec |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kostiuk, V.; Marchuk, A.; Gusev, A.; Chugunov, I.V. A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403. Galaxies 2025, 13, 27. https://doi.org/10.3390/galaxies13020027
Kostiuk V, Marchuk A, Gusev A, Chugunov IV. A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403. Galaxies. 2025; 13(2):27. https://doi.org/10.3390/galaxies13020027
Chicago/Turabian StyleKostiuk, Valeria, Alexander Marchuk, Alexander Gusev, and Ilia V. Chugunov. 2025. "A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403" Galaxies 13, no. 2: 27. https://doi.org/10.3390/galaxies13020027
APA StyleKostiuk, V., Marchuk, A., Gusev, A., & Chugunov, I. V. (2025). A Comprehensive Analysis on the Nature of the Spiral Arms in NGC 3686, NGC 4321, and NGC 2403. Galaxies, 13(2), 27. https://doi.org/10.3390/galaxies13020027






