Abstract
In this paper, we investigate the heliospheric modulation of cosmic rays in interplanetary space, focusing on their propagation times and energy losses over the solar cycle. To perform the calculations, we employed a data-driven model based on the stochastic method. Our model was calibrated using time-resolved and energy-resolved data from several missions including AMS-02, PAMELA, EPHIN/SOHO, BESS, and data from Voyager-1. This approach allows us to calculate probability density functions for the propagation time and energy losses of cosmic protons and antiprotons in the heliosphere. Furthermore, we explore the temporal evolution of these probabilities spanning from 1993 to 2018, covering a full 22-year cycle of magnetic polarity, which includes two solar minima and two magnetic reversals. Our calculations were carried out for cosmic protons and antiprotons, enabling us to investigate the role of charge-sign dependent effects in cosmic ray transport. These findings provide valuable insights into the physical processes of cosmic-ray propagation in the heliosphere and contribute to a deeper understanding of the solar modulation phenomenon.
1. Introduction
Galactic cosmic rays (CRs) are excellent astrophysical messengers for probing the high-energy Universe. When entering the heliosphere, however, they interact with magnetic fields and solar wind disturbances, leading to changes in their intensity and energy spectrum. This phenomenon is known as solar modulation of CRs. Understanding solar modulation is crucial for investigating the origins of cosmic particles and antiparticles [1]. It is also important for evaluating radiation exposure and the risks associated with crewed space missions or orbiting devices [2,3]. Consequently, considerable efforts are being directed towards studying the variations in the CR spectrum, both near Earth and in interplanetary space. An important aspect of solar modulation is its association with the 11-year solar activity cycle. The monthly sunspot number (SSN), a primary indicator of solar activity, exhibits an inverse relationship with long-term CR flux variations [4,5]. At the peak of the SSN cycle, when the Sun releases more energy in the form of solar flares and coronal mass ejections the CR flux is at its minimum. During the solar minimum, the CR flux attains its maximum level. Along with the SSN cycle, the Sun shows a 22-year quasiperiodical cycle of magnetic polarity, with a magnetic field reversal occurring during each solar maximum. This periodicity is of paramount importance for studying particle drifts in the interplanetary magnetic field (IMF).
Observationally, the modulation phenomenon is investigated by time- and energy-dependent measurements of CRs in space. Valuable data have been released recently by the AMS-02 experiment on the International Space Station [6,7,8], and by the PAMELA mission in the Resurs-DK1 satellite [9,10]. Their data add to earlier measurements conducted, in particular, by the EPHIN space instrument onboard SOHO [11] and by several BESS balloon flights [12,13]. Measurements of the local interstellar spectra (LIS) of CRs have been conducted by the Voyager-1 spacecraft outside the heliosphere [14].
From a modeling perspective, an important challenge lies in elucidating the dynamic relationship between the local CR flux and the evolving conditions of the heliospheric plasma. The main physical mechanisms governing this relationship include the diffusion of CRs through small-scale IMF irregularities, convection and adiabatic cooling over the expanding solar wind, and drift motion across the large-scale IMF [1,15]. These mechanisms induce significant modifications in the fluxes of CRs in the heliosphere and may explain most of the observed features. In recent years, many effective models of solar modulation have been developed [16,17,18,19,20,21,22,23,24,25].
The present work focuses on the propagation times and the energy losses of CRs in the heliosphere. By propagation times, here, we refer to the time spent by galactic particles entering the heliosphere to reach the near-Earth environment, i.e., an inner region of heliosphere situated 1 AU from the Sun. The energy losses pertain to the process of adiabatic cooling affecting CRs in their travel through the expanding solar wind. The propagation times and energy losses of CRs have been studied in a number of works. The gross features were established in early studies by analytical calculations [26,27,28]. More recent works rely on sophisticated numerical models [29,30,31,32]. These researchers yielded valuable insights on understanding the timescales of CR transport in the heliosphere under different conditions of IMF polarity and CR energies [31].
In this paper, we explore the temporal evolution of propagation times and energy losses for both CR protons and antiprotons under the real conditions of the past solar cycles. To achieve this, we calculated the associated probability distributions using a data-driven stochastic model of CR modulation. Our model was globally calibrated using large time series of CR proton measurements as a function of kinetic energy and time. The CR data were obtained from space experiments AMS-02, PAMELA, and EPHIN/SOHO, as well as from BESS balloon flights. The temporal extension of these measurements encompasses the tail of solar cycle 22 and include solar cycles 23 and 24. We also utilized IMF plasma data from space probes WIND and ACE, along with the Wilcox Solar Observatory.
The rest of this paper is organized as follows. In Section 2, we provide an overview of the basic CR propagation theory and present our numerical model of solar modulation. In Section 3, we outline the procedure for the data-driven determination of the key model parameters based on measurements of CR protons. In Section 4, we present our results on the CR propagation times and the energy loss fractions; in particular, we present calculations for their probability distributions, how they evolve in different phases of the solar cycle, and how they depend on the CR energies and on their charge-sign. In Section 5, we summarize our results and draw the conclusions.
2. Theoretical Framework
The propagation of high-energy charged particles in the heliospheric plasma is generally described by the Parker equation:
where is the omnidirectional distribution function for a given particle type, t is the time, and is the particle rigidity, i.e., the momentum per charge units. The quantity is the diffusion-drift tensor and is the solar wind velocity. The differential CR flux as a function of rigidity is given by . There are several approaches to numerically solve Equation (1) and obtain the differential intensity for a given CR species and at a given location in the heliosphere [1]. Here, we use the calculation framework presented in detail in Fiandrini et al. [19], Tomassetti et al. [33], which is briefly recapitulated in the following sections. From Equation (1), it can be seen that the distribution function resulting from the propagation of CRs in the heliosphere is time-dependent, and many characteristic parameters of the ambient medium are subjected to temporal variation. However, in order to study the essential features of CR fluxes averaged over Bartels rotation lasting 27 days, or on longer time periods, the steady-state approximation () is often considered a reasonable working assumption. In such a description, the long-term modulation of CRs is described as a continuous series of steady-state solutions, where the effective status of the heliospheric plasma during the CR propagation is defined in a suitable way. Such an approach is usually justified by the different timescales between CR transport in the heliosphere and the changing solar activity, which will be assessed and discussed in this paper. In order to carry out a realistic description of the proton modulation, we need first to clarify the three principal ingredients of this study: (i) The physical characteristic of the modulation region; (ii) The diffusion and drift coefficients that enter the transport equation; (iii) The input LIS for cosmic protons and antiprotons. In the following subsections, we give a brief description of them.
2.1. Key Parameters of the Modulation Domain
In our framework, the modulation region is the entire heliosphere. Its spatial extent is defined by the heliopause and it is modeled as a spherical surface of radius AU. The Earth’s position is located in the equatorial plane at helioradius AU. The solar wind flows out radially from the Sun. During the solar minimum, the wind is fast in the polar region of the heliosphere (7–800 km s−1) and slow in equatorial plane (3–400 km s−1). During the solar maximum, the wind shows no clear latitudinal dependence and its average speed is 4–500 km s−1 at all latitudes [34]. The wind speed remains remarkably constant with the radius, up to the termination shock located at 85 AU. Beyond the termination shock, the wind slows down by a factor , where is the shock compression ratio. All these features are captured by a parametric function of time, and radial and latitudinal coordinates. Like in our past work [19], we assume a factorized form for the wind speed profile:
where we adopt the parametric expression given in Ref. [35]. The termination shock is accounted for in the radial part . The temporal dependence of consists in the changing angular extent of the slow wind region, which we relate to the IMF tilt angle [19]. The normalization is set by the parameter km s−1. To model the large-scale structure of the IMF, we use the modified Parker model:
where is the llocal IMF value at AU, which is continuously measured in situ by spacecraft. The quantity is the so-called winding angle between the IMF and the radial direction , and the function is a high-latitude correction [36]. This description also includes the heliospheric current sheet, the thin layer where IMF polarity changes from north to south. The current sheet is wavy due to the tilt angle between the solar magnetic axis and its rotational axis. The tilt angle is time-dependent, varying from during the solar minimum to during the solar maximum. The IMF polarity, A, is defined by the sign of in proximity of the Sun. Polarity is positive when is directed outwards in its northern hemisphere and inward in the southern hemisphere. Polarity reversals occur during every solar maximum. The CR transport is influenced by changes in polarity, as the drift speed depends on the sign product between charge and polarity.
2.2. CR Diffusion and Drift
Diffusion and drift processes are captured by the tensor appearing in the third term of Equation (1).
where and are the symmetric and antisymmetric parts of the tensor, respectively, describing diffusion and drift. The symmetric part includes the coefficient , associated with parallel diffusion along the field direction, and the perpendicular coefficients and describe transverse radial and transverse polar diffusion, respectively. All coefficients can also be expressed in terms of the mean free path , by means of relations such as , where . Like in [19], and following earlier works [35,37], we model the spatial and rigidity dependence of the CR parallel diffusion with the following formula:
where is of the order cm2s−1 and to set the rigidity units. The rigidity dependence is a broken power-law function describing the two diffusion regimes [38]. The spectral indices a and b set the log-slopes below and above the characteristic rigidity . The latter represents the scale rigidity value where the GCR gyroradius matches the correlation length of the IMF power spectrum. The parameter determines the smoothness of the transition. The perpendicular coefficients are determined by the scaling assumptions with [39]. The overall spatial dependence of CR diffusion is determined by the IMF model via B. Its temporal dependence is, therefore, captured by the free parameters , a and b, which are determined by CR data. The antisymmetric part of the tensor is specified by the drift coefficient:
where is the rigidity below which the drift is reduced due to scattering. The normalization factor is set to unity by default. In other works, low values are often used to reduce drift during the reversal phase. In our model, however, the flux during reversal is modeled as a superposition of fluxes with opposite polarities [19,40], and, thus, we do not need to suppress manually. From Equation (6), the average drift velocity is given by .
2.3. Local Interstellar Spectra
The LIS of CRs beyond the heliopause is an important factor for solar modulation models. In this study, we focus on CR protons and antiprotons. To determine their LIS, a dedicated modeling effort is required. Here, we employ the results of a two-halo model of CR propagation in the Galaxy [41,42,43]. In this model, protons and other primary nuclei accelerated in the shocks of supernova remnants and then were injected in the interstellar space. The primary acceleration spectrum of CRs is described by a source term of the type , with index 2.28 ± 0.12 for and index 2.35 ± 0.13 for all nuclei. The production of secondary nuclei is then calculated by a source term . This term describes the fragmentation of h-type species of density into s-type nuclei at rate , where n is the gas density and is the cross sections for the process. The calculations depends on many cross sections that were estimated in earlier works [44,45]. For the production of secondary nuclei, it is assumed that the kinetic energy per nucleon is maintained (i.e., ), while for antiprotons, this is not the case. The source term is of the type:
where the production rate depends on the differential cross section [41]. Both CR acceleration and secondary production occur in the galactic disk, where sources and matter are located. Away from the disk, CR propagation is described by a two-halo diffusion model. The CR diffusion coefficient is , where we assume two diffusion regimes: a shallow diffusion for the near-disk region with index , occurring within distance from the disk (inner halo), and a faster diffusion in the extended halo with index (outer halo). Other processes such as ionization losses, destruction processes are also accounted for. Based on previous works, we found 0.18 ± 0.05 and 0.01 ± 0.002 kpc/Myr, ± 0.11, and ± 0.03.
The key model parameters are constrained using LIS data from Voyager-1 [14], high-energy measurements on primary nuclei (H-He-C-O), and secondary to primary ratios from AMS-02 [6]. The calculations are described in detail in earlier works [41,42,44]. The resulting LIS fluxes of CR protons and antiprotons are evaluated at near-Earth position, in galactic cylindrical coordinates 0 of height and 8.3 kpc. The resulting LIS fluxes as a function of kinetic energy are is shown in Figure 1 in comparison with the data.
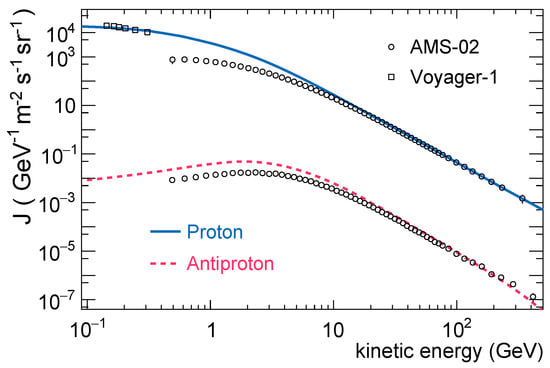
Figure 1.
Local interstellar spectra of CR protons and antiprotons used as input boundary condition for the modulation along with the estimated uncertainty band. The data are from Voyager-1 in interstellar space and from AMS-02 in low Earth orbit [6,14].
3. Methodology
3.1. The Stochastic Method
Our calculations are based on the so-called stochastic differential equation (SDE) method. It consists in transforming the Parker equation into a set of SDEs that can be integrated using Monte-Carlo techniques. The solution of Equation (1) is then obtained by sampling. The SDE method is implemented in several solar modulation codes and, in the recent years, with the increase of computing power and resources, it has become very popular [17,46,47,48,49,50,51]. A nice review on this subject is provided in Strauss & Effenberger [52]. For a stochastic process, the stochastic equation can be recast in the form:
where is the total velocity of the particle, is a matrix such that , and is a multidimensional Wiener process related to a normalized Gaussian distribution. The corresponding change of kinetic energy E in time for a CR proton with mass is given by:
The SDE method returns the normalized transition function between an initial energy at the boundary and a final energy E at the Earth’s position. The near-Earth phase space density is, therefore, given by:
where is the space density corresponding to the LIS flux .
The integration of the equations, in practice, requires the simulation of a large number of pseudo-trajectories. An example of two typical trajectories is illustrated in Figure 2 where the radial and colatitudinal coordinates are represented in a polar diagram. The figure shows the Brownian motion of 1 GeV protons traveling from the heliopause (placed at AU) to the Earth’s vicinity ( AU). Our IMF model is azimuthally symmetric. The two trajectories are related to opposite situations of IMF polarity that will be discussed in Section 4.
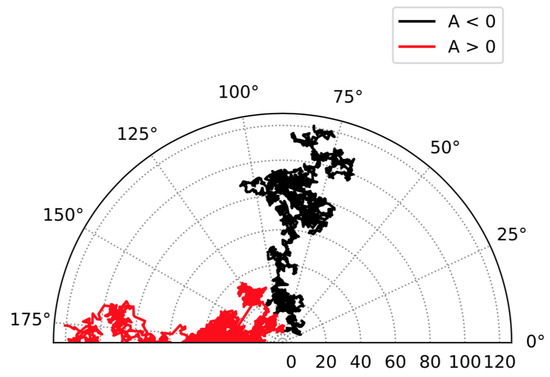
Figure 2.
Two simulated trajectories for a 1 GeV proton in polarity phase (black) and (red) represented in a polar diagram of the radial and colatitudinal coordinates.
To efficiently sample the steady-state solution in the Earth’s vicinity, the SDE generated trajectories were propagated backward in time, starting from Earth and until they reached the heliospheric boundary [46,48,50]. For each pseudo-particle k, the method utilizes a time-step incremental scheme, , and we can determine the total duration of the trajectory as . Such a trajectory duration, calculated from the particle source to the observational point, is simply called the propagation time. With a large number N of simulated trajectories, the expectation value of the propagation time can be calculated as:
where is the number of pseudo-particles for which the trajectory time falls in a bin around . In some papers, propagation time or its expectation value is called the residence time of CRs in the heliosphere. It is important to note, however, that the quantity is calculated specifically for those CR trajectories that reach Earth’s position. The kinetic energy loss associated to a trajectory can be computed in a similar way, together with its expectation value . Since energy changes account only for adiabatic cooling, the simulated CR particles always end with a net energy loss: . It should also be noted, however, that the backward propagation scheme leads to an increase in the pseudo-particle energy during the simulation. This is simply due to the time-reversed adiabatic processes. In the following, we will refer to the energy loss fraction and its expectation value . For a given pseudo-proton trajectory, the loss fraction is calculated relative to the proton initial energy . The SDE method is well suited to calculating and . Its applicability has been known since its first formulations [50,51]. As we will discuss in Section 4, propagation times and energy losses of CRs depend on several factors related to the conditions of the background plasma and to the particle properties.
3.2. Modeling the Time Dependence
In our framework, near-Earth CR fluxes are calculated in terms of a time series of steady-state solutions of Equation (1), with a resulting proton flux associated with a time series of input parameters . The input parameters can be divided in two classes. On one side, the heliospheric parameters that characterize the variable conditions of the Sun and the surrounding plasma, i.e., the background medium where the CR propagation takes place. On the other side, the transport parameters that describe the physical processes of CR propagation through the heliosphere. In our model, we identified a basic set of six time-dependent parameters that best capture the CR modulation phenomenon [19]. The heliospheric parameters are as follows: the tilt angle of the heliospheric current sheet , the intensity of the local IMF , and its polarity . The transport parameters are as follows: the normalization coefficient of the parallel diffusion tensor , and the two spectral indices and , describing the rigidity dependence of CR diffusion below and above the break , as seen in Equation (5). For convenience, all parameters are expressed here as continuous functions of time t. In practice, their value has been evaluated from observations and eventually interpolated in a defined time-grid of epochs.
3.3. Determination of the Heliospheric Parameters
The temporal dependence of the heliospheric parameters is determined from observations. Time series of tilt angle and polarity are continuously provided by the Wilcox Solar Observatory on a 10-day or 27-day basis, respectively. Measurements of the local IMF are performed in situ on a daily basis by the spacecraft WIND and ACE on an orbit [53]. From these data, we built smoothed and continuous functions of time , and by following the procedure of Fiandrini et al. [19], but with a wider time coverage. The method is based on the calculation of the backward moving average over a moving interval . The extent of the interval ranges between 8 and 16 months, depending on the angular profile of at a given epoch. For the tilt angle , a 16-month interval was used, because the current sheet lies entirely within the slow wind region, while for , it depends on the latitudinal profile of the wind speed at a given epoch. The results are shown in Figure 3 between 1993 and 2018. In the figure, the backward moving average functions are shown as tick solid lines, along with the measurements. We note that the considered time range spans over two solar cycles. It includes the magnetic reversal of cycle 23, when polarity changed from to , and the latest reversal of cycle 24, where polarity changed from to . Note that, from the figure, the polarity A is given by the sign of the N/S averaged and polar field, i.e., the pink line of panel (iii).
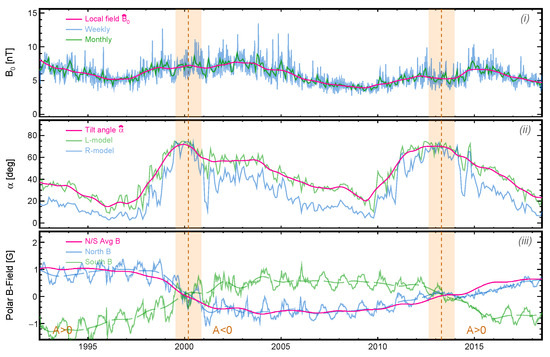
Figure 3.
Reconstruction of the heliospheric parameters as a function of time: (i) Local IMF value measured on daily (blue) and weekly basis (green), along with its smoothed reconstruction (pink thick line); (ii) tilt angle of the heliospheric current sheet reconstructed on 27-day basis within L-model (green) and the R-model (blue); (iii) outward component of the polar magnetic field of the Sun in the north (blue) and south (green) hemisphere, measured on 10-day basis, along with their yearly smoothed values (long dashed lines) and their N/S average (pink solid line). The sign of the N/S average sets the magnetic polarity A. The data are from the space probes WIND and ACE and from the Wilcox Solar Observatory [53,54,55].
3.4. Determination of the Transport Parameters
The time-dependent diffusion parameters of the model , , and have been determined from CR proton measurements by a standard procedure of statistical inference. While the method is similar to that of our previous paper [19], here we used a richer sets of data covering the period between 1993 and 2018. We used monthly resolved data on the CR proton flux collected by the AMS-02 experiment in the International Space Station in 2011–2018, consisting of a set of 79 Bartels-averaged fluxes measured between 2011 and 2018 [8] in the kinetic energy range from 0.4 GeV to 60 GeV. We also included the 47 + 36 Bartels-averaged proton fluxes measured by the PAMELA experiment onboard Resurs-DK1 from 2006 to 2014 at kinetic energies from 80 MeV to 50 GeV [9,10]. For past epochs, we used 20 yearly averaged fluxes from the EPHIN/SOHO probe observed between 1995 to 2015 at kinetic energies from 0.29 GeV to 1.6 GeV, and nine measurements of the proton flux made by the BESS balloon flights between 1993 and 2005 at kinetic energies from 0.2 GeV to 20 GeV. The whole sample corresponds to a total of about 15,000 data points collected over a time span of nearly 25 years. To sample the six dimensional parameter space, a discrete grid of the vector = {, , A, , a, b} was built. For all the 938,400 nodes of the grid, calculations of the CR proton flux were carried out and evaluated over 120 values of kinetic energy, ranging from 20 MeV to 200 GeV with log-uniform step. Then, for each set of measurements , representing time series of energy-binned fluxes, the following estimator was evaluated:
Using a 5-dimensional multilinear interpolation technique, the estimator is built such to be a continuous function of the parameters , except for the dichotomous variable A. From the function, the best-fit transport parameters and their corresponding uncertainties were determined at any epoch by standard minimization techniques. In this procedure, the minimization involves only three free parameters out of six. The remaining heliospheric parameters were considered as fixed inputs, as they are determined by the epoch t with reconstruction presented in Section 3.3.
Our results for the transport parameters are summarized in Figure 4, showing their best-fit values and uncertainties obtained for the various datasets. The corresponding SSN cycle is also shown in the bottom panel. In the figure, the vertical dashed lines and the shaded bands around them represent the reversal phases. It can be seen that the parameter shows a distinct temporal dependence, in anti-correlation with the SSN cycle. CRs are subjected to a slower diffusion during epochs of solar minimum, and faster during the solar maximum. The temporal dependence of the a and b parameters is less pronounced, although some variability can be observed for these parameters, in connection with the solar cycle. This may be suggestive of variability in heliospheric turbulence over the solar cycle [19,56]. In the figure, the solid line represents a simple parametric model that connects smoothly the best-fit results. With these lines, we describe the evolution of , , and as a continuous function of time. This enables us to specify the whole rigidity and time dependence of the CR diffusion coefficients over the two considered solar cycles (and similarly, their associated mean free path ). Once the transport and heliospheric parameters are established, our measurement-validated model can be used for investigating the propagation times and energy losses of CRs in the heliosphere.
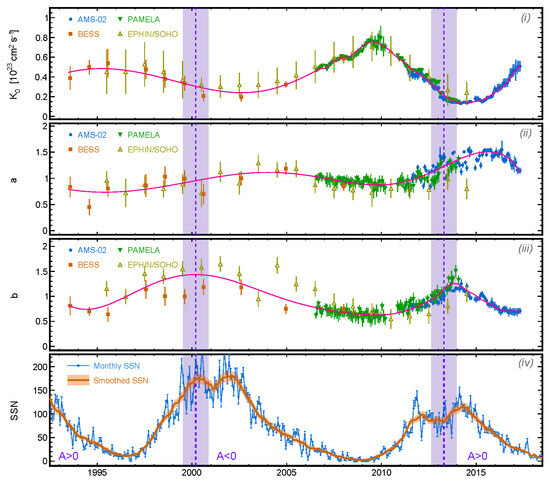
Figure 4.
Best-fit results for the CR propagation parameters , a, and b obtained with proton flux measurements from AMS-02, PAMELA, EPHIN/SOHO, and BESS, from panel (i–iii). The pink solid line is a simple parametric model that smoothly connects the best-fit results. In panel (iv), the monthly SSNs and their 13-month smoothed values. The vertical band indicates the magnetic reversal epochs.
4. Results and Discussions
With the global parametric model of CR transport parameters discussed in Section 3, we can now calculate the flux modulation of CRs during any epoch in the solar cycle. From the best-fit parameters of Figure 4, using Equation (5), the mean free path for parallel diffusion can be readily calculated. The mean free path is shown in Figure 5 (left) as a function of rigidity and time.
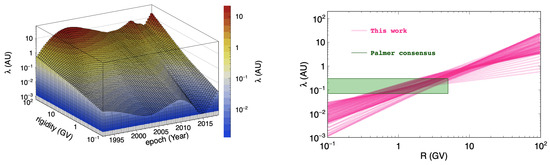
Figure 5.
Left: mean free path of CR parallel scattering obtained from our fits as a function of rigidity and time. Right: envelope of the many -functions inferred from the data (pink shaded band) compared with the “Palmer consensus” (green shaded box) [57].
From the figure, it can be seen that the diffusion mean free path is subjected to changes in both normalization and slope. In the right, the envelope of the many -functions determined from the data (pink shaded band) is compared with the so-called “Palmer consensus” (green shaded box). The latter is based on past observations between 50 MeV and 5 GeV [57].
Since we have adopted a trajectory-based approach, we can compute the distribution of CR propagation times and energy losses associated with the simulated trajectories. As discussed in several prior studies [16,19,40,47,58], the CR modulation is significantly influenced by magnetic reversal, which is a remarkable manifestation of the 22-year solar polarity cycle. Furthermore, CRs are also affected by IMF intensity, its large-scale structure, and its turbulence levels, which are typically captured by heliospheric proxies, such as the SSN, IMF tilt angle, its intensity , or its variations . Based on these considerations, we identified four reference epochs corresponding to distinct phases of the solar polarity cycle: (a) January 2009, corresponding to the solar minimum under negative IMF polarity (across cycles 22 and 23, ); (b) January 2002, corresponding to the solar maximum and negative IMF polarity (cycle 23, following the reversal from to ); (c) March 1996, corresponding to the solar minimum and positive IMF polarity (across cycles 22 and 23, ); (d) March 2014, corresponding to the solar maximum and positive IMF polarity (cycle 24, following the reversal from to ). It should be noted that magnetic reversal occurs during the peak of solar maximum; therefore, epochs (b) and (d) were selected slightly after reversal, when the magnetic polarity can be clearly defined [55]. The results presented in the following sections focus on these reference epochs.
4.1. Propagation Times
In Figure 6, we present the normalized probability distributions of the CR propagation times . For the moment, we focus on cosmic protons with a kinetic energy of E = 1 GeV, as indicated by the blue solid lines. We will discuss cases involving different energies and charge signs later in this discussion. The plots in the figure were generated by sampling, following the method described in Section 3.1, from the simulation of 15,000 pseudo-proton trajectories. Each panel corresponds to a distinct reference epoch in the solar polarity cycle.
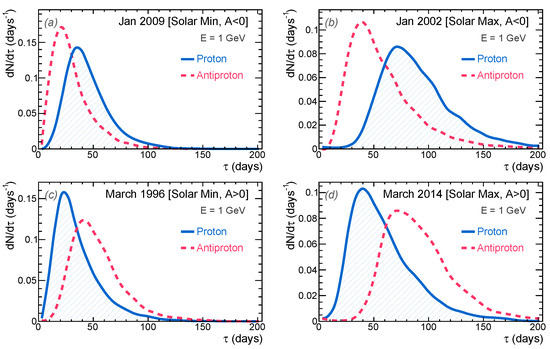
Figure 6.
Distribution of propagation times for galactic CR protons arrived near the Earth at for the (top panels) and (bottom panels) in solar minimum and solar maximum activities (left and right panels, respectively). The average propagation times of cosmic protons (antiprotons) in the four epochs are (a) 45 days (31 days), (b) 89 days (58 days), (c) 36 days (54 days), and (d) 59 days (91 days).
From the figure, it is evident that the distributions exhibit pronounced asymmetric tails towards larger values. The asymmetric nature of these distributions may be attributed, in part, to the effects of drift, as discussed later, and is partially influenced by the fact that trajectory times are bounded by a lower kinematic limit. From these distributions, we can readily calculate the average value and peak values, following Equation (11), for various solar epochs. During the solar minimum (left panels) for , the distribution peaks at 35 days (a), whereas for , it peaks at 22 days (c). During the solar maximum (right panels), the distribution for peaks at 71 days (b), and for , it peaks at 40 days (d). Hence, for 1 GeV protons, the propagation times of CRs during epochs are generally longer compared to epochs. Furthermore, the propagation times during the solar maximum are consistently longer compared to the solar minimum, indicating that the level of solar activity significantly influences CR propagation times. These observations can be explained in terms of drift and diffusion processes. The effects of drift, particularly those arising from the IMF gradient and curvature, drive charged particles along preferential paths, depending on the IMF polarity state [58]. During periods of negative IMF polarity, galactic protons reach the inner heliosphere through equatorial regions (colatitude ). In contrast, during positive polarity epochs, they preferentially pass through the polar regions ( and ). This situation is illustrated in Figure 2, which depicts two typical trajectories of pseudo-protons with a kinetic energy of 1 GeV traveling from the heliopause to the vicinity of Earth. These trajectories represent opposite IMF polarity scenarios. Thus, as a result of drift, CRs probe different regions of the heliosphere characterized by different plasma conditions. Polar regions exhibit faster solar wind speeds and weaker IMF strength, leading to increased convection compared to equatorial regions. However, particles traveling through equatorial regions encounter the heliospheric current sheet, resulting in a substantial increase in the length and duration of their trajectories. The combination of these processes leads to different average values for propagation times and energy losses. As we have found, cosmic protons experience larger propagation times during epochs with polarity. Additionally, the overall change in the diffusion coefficient over the long term also contributes to variations in propagation times, with a generally faster propagation during the solar minimum compared to the solar maximum.
To better understand the situation, it is instructive to examine the relationship between the propagation times of CRs and their energy. In Figure 7, we calculate and plot the average propagation times of protons as a function of their arrival kinetic energy E. The figure presents four sets of calculations for as a function of energy, covering the reference epochs considered and ranging from 50 MeV to 250 GeV. Both Figure 6 and Figure 7 reveal intriguing features reflecting the relationship between the propagation time and CR transport, which can be understood through simple physical considerations. In a diffusion-dominated scenario, the propagation time would exhibit a linear decrease with increasing diffusivity, given by . This relationship depends on the diffusion coefficient K and consequently its energy or rigidity dependence [27]. In particular, as expressed in Equation (5), the rigidity dependence of CR diffusion can be characterized as , where the spectral index takes the value for and for . In practice, based on the reconstruction presented in Figure 4, the indices a and b are similar to each other and their variations are relatively modest. Therefore, for the first approximation, one can consider . Consequently, the diffusion time can be expressed as , with . The temporal dependence of CR diffusion is primarily captured by the parameter [24]. Its relationship with solar activity can be elucidated with the plots of Figure 4i,iv, if we focus on the timescales of several months, where short-term features such as double-peak maxima (in the SSN) or Forbush decreases (in GCRs) can be ignored. In this long-term behavior, the diffusion coefficient appears to be anti-correlated with the SSN cycle. Thus, the diffusion time must be positively correlated with it. During epochs of solar maximum (minimum), CR diffusion is slower (faster), resulting in larger (smaller) propagation times associated with diffusion. At lower rigidities, the effects of convection become increasingly significant. Due to the outward direction of the solar wind, convection reduces the likelihood of Galactic particles reaching Earth. The influence of convection establishes an upper limit on the propagation time, denoted as , which can be approximated as and is in the order of approximately ∼500 days. Conversely, a lower bound of the order of ∼1 day can be obtained as the ballistic limit, given by for rectilinear CR propagation. Based on these considerations, in a diffusion–convection scenario, the resulting propagation time can be derived as a combination of and [31]:
By using typical values such as km s−1, cm s−2, and AU, one would anticipate that the propagation time reaches approximately 6 months in the sub-GeV energy region, where convection dominates. This would be followed by a decrease in the form of in the multi-GeV region, where diffusion becomes the dominant process. These considerations provide an explanation for the general characteristics observed in Figure 7.
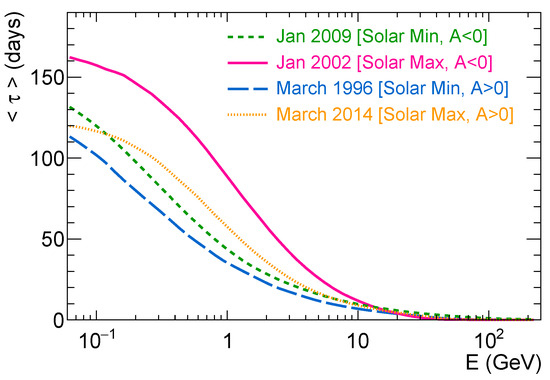
Figure 7.
Propagation times versus the energy of the galactic CR protons arrived near the Earth for the and in solar minimum and solar maximum activities.
To explain the differences between the various curves, it is essential to consider polarity-dependent effects, although drift effects can only be evaluated numerically. In contrast to a diffusion-dominated scenario, the influence of drift is to reduce the propagation time in both polarity states, which may appear counter intuitive. A clear explanation for this effect is provided in Strauss et al. [31]. The action of drift introduces preferential trajectories for CRs reaching Earth while suppressing non-preferential ones. In many instances, this selection process favors straighter trajectories, corresponding to smaller propagation times. This aspect contributes to the observed asymmetric tails in the distributions and helps explain the behavior observed in Figure 7.
An interesting feature that stands out in Figure 7 is the crossing point between curves (d) and (b), occurring at kinetic energies below ∼100 MeV. This crossing point is located between the yellow dotted line (representing the solar maximum, ) and the green short dashed line (representing the solar minimum, ). For high-energy CRs, the most dominant factor affecting the propagation times is the level of solar activity. In this energy regime, the mean propagation times during the solar maximum are consistently larger than those during solar minimum, as observed in Figure 6 for 1 GeV. However, below the crossing energy, the polarity effect becomes dominant, with mean propagation times during negative polarity cycles being consistently larger than those during positive cycles. A possible explanation for this behavior may involve the interplay between diffusion and drift at the different rigidities. However, it is important to note that the two maxima (b) and (d) belong to different solar cycles (23 and 24), which can vary in terms of intensity and turbulence properties. From a look at Figure 4, this is indeed the case. For instance, the maximum of cycle 24 (d) was the smallest recorded in a century of SSN observations and exhibited a double-peak structure. Similarly, the two minima (a) and (c) belong to different solar cycles, with the 2009 minimum across cycles 23/24 (a) being unusually weak and long compared to other minima. As shown in Figure 4, these different minima and maxima of recent solar cycles result in variations in the CR transport parameters, both in terms of normalization and slope.
4.2. Energy Losses
We now turn our attention to the energy losses. In particular, we focus on the loss fraction . In Figure 8, the probability distributions of are shown for cosmic protons (solid blue lines) reaching Earth with a kinetic energy of GeV.
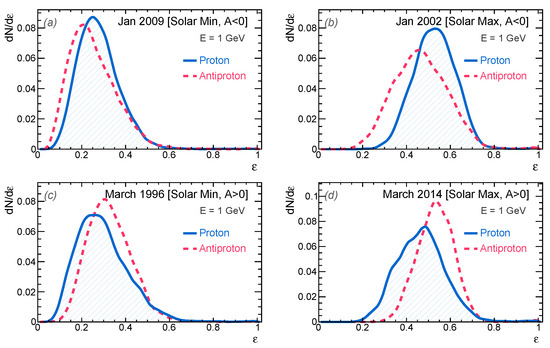
Figure 8.
Distribution of the energy loss fraction for CR protons arriving near the Earth at for the (top panels) and (bottom panels) in solar minimum and solar maximum activities (left and right panels, respectively). The average loss fractions of cosmic protons (antiprotons) in the four epochs are (a) 0.28 (0.25), (b) 0.53 (0.47), (c) 0.30 (0.33), and (d) 0.47 (0.53).
The calculation method employed is similar to that of the propagation times, involving Monte-Carlo sampling through the simulation of 15,000 pseudo-particle trajectories at a fixed epoch, energy, and particle type. The panels in the figure correspond to the same four reference epochs as discussed in the previous section, representing different solar cycle intensities and polarities. In comparison with the distributions, the distributions exhibit less skewness, although asymmetric tails can still be observed in panels (a) and (c), which correspond to the 2009 and 1996 solar minima, respectively. During the solar minimum, the average fraction is 0.3: protons detected near Earth with a kinetic energy of 1 GeV have lost nearly one third of their initial kinetic energy, on average. During the solar maximum, the losses are more significant, reaching values of about 0.4–0.5 in panels (b) and (d). This implies that 1 GeV protons detected during the solar maximum entered the heliosphere with an average initial energy of 2 GeV.
The dependence of the average loss fraction on the near-Earth energy E of the protons is shown in Figure 9. The four curves in the figure correspond to the reference epochs considered in our analysis. The average loss fractions are calculated by constructing profile histograms for the probability distribution as a function of E. It is important to emphasize that, as per the physical mechanisms incorporated in the Parker equation discussed in Section 2, energy changes for cosmic protons consist solely of adiabatic losses. Consequently, the loss fraction is always positive. From Figure 8 and Figure 9, some observations can be made. The loss fraction decreases rapidly with increasing particle energy. However, at low energies, the loss fraction saturates to unity. Here, the dynamics of low-energy particles are primarily governed by convection with the solar wind. These particles are decelerated and then thermalized before reaching the inner heliosphere. In contrast, in the high-energy limit, the loss fraction becomes negligible. Comparing the different epochs, it can be noticed that the curves fall into two distinct groups based on the intensity of solar activity, and they are less sensitive to the polarity states. In particular, the curves associated with solar minima (a) and (c) are nearly indistinguishable. The observed behavior of energy losses at different energies and epochs can be discussed qualitatively in the context of the force-field approximation. In this approximation, energy losses are captured by the modulation potential , which can be expressed as . Hence, a qualitative explanation can be provided in terms of the behavior of the ratio. Notably, from Figure 4a,d, it can be observed that epochs of solar maximum correspond to slower diffusion, implying smaller values of , and vice versa. The solar wind speed , on the other hand, does not exhibit a clear long-term trend over the solar cycle. However, it does display a distinct latitudinal profile, as discussed in Section 2.1. As previously discussed, the action of drift is to guide CR protons along preferential trajectories. During epochs, protons tend to reach Earth predominantly from the polar region through the fast wind region. During epochs, protons tend to travel predominantly through the equatorial region of the heliosphere, in the slow wind region. Based on this observation, one might initially expect higher energy losses during epochs. However, an opposite effect comes into play due to the presence of the heliospheric current sheet. Particles reaching Earth during epochs are more likely to drift across the current sheet, which significantly increases both the total length and duration of their trajectories. The larger trajectory lengths imply higher energy losses for particles during epochs. The interplay between these two competing effects: convection and the heliospheric current sheet, results in a nuanced relationship between energy loss and IMF polarity. From Figure 9, it can be noted that the curves representing opposite polarity states intersect between kinetic energies of 3 and 10 GeV. This crossing feature likely reflects the interplay of these effects.
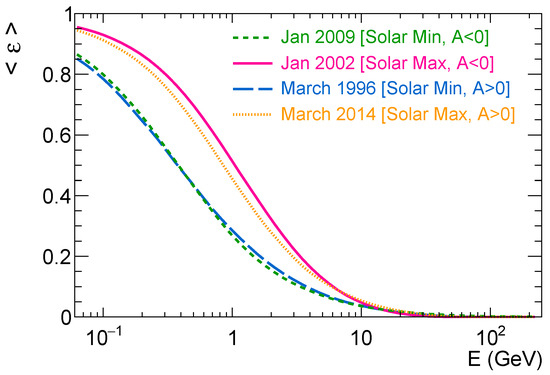
Figure 9.
Energy loss rate as a function of the near-Earth kinetic energy E of CR protons in four reference epochs of the solar cycle.
4.3. Particles and Antiparticles
In the previous paragraphs, the discussion was primarily centered around CR protons. We now analyze the results for antiprotons. For antiprotons, all the relevant calculations were conducted using the same SDE model discussed in Section 2. The key parameters of the model were those determined from CR proton data as described in Section 3.4. Such an approach relies on the assumption that the key parameters governing the transport of protons can describe other nuclear species with different mass, charge, or charge-sign. For diffusion, the CR mean free paths are universally determined by the particles rigidity [23,24]. Moreover, both diffusion or convection are inherently insensitive to the charge-sign of the particles. In fact, from a microscopic point of view, both effects arise from the scattering of charged particles off small-scale irregularities of the IMF, for which there is no distinction between protons and antiprotons. This is not the case for drift processes across the large-scale component of the IMF. The drift speed of particles depends explicitly on the product , where represents the charge sign, and A is the polarity of the IMF.
In our model, the symmetry is rigorously respected. Consequently, a single proton under polarity experiences the same dynamics as an antiproton under polarity, assuming that all other kinematics and plasma conditions are identical. When our description pertains to the differential flux as a function of energy near Earth, however, minor differences may arise between protons and antiprotons due to their different LIS shapes, as illustrated in Figure 1. In fact we note that, even if we have often considered particles at some fixed energy (e.g., GeV), that energy represents the CR final energy, which results from the solar modulation process. This implies a convolution over the initial LIS of kinetic energies . Furthermore, it is crucial to emphasize that, in this work, the calculations were performed for actual solar cycles. When comparing plots associated with and (e.g., January 2009 and March 1996), it is important to recognize that we are not considering the sole effect of a simple polarity switch. Instead, we are examining two distinct solar cycles with opposite polarities, where various other parameters can also differ.
A comparison of proton and antiproton propagation times is provided in Figure 6 for kinetic energies of GeV. In the figure, the distributions of antiprotons are represented by pink dashed lines. Observing panels (a) and (b), it can be seen that during both epochs of negative polarity, the distributions of antiproton propagation times peak at lower values compared to protons. In other words, in epochs, antiprotons propagate faster than protons. Conversely, in panels (c) and (d), the opposite scenario is evident for epochs. During these periods, the antiproton propagation times are significantly larger than those of protons. When comparing the two situations, namely, the top panel with the bottom panels, the symmetry effect becomes evident. The act of polarity reversal seems to effectively exchange the distributions of protons and antiprotons, so that the propagation times depend mainly on the sign product . Explanations for these differences can be attributed to the polarity-dependent action of drift in the trajectories of CRs, as discussed in Section 4.1. In fact, the two typical trajectories illustrated in Figure 2 were calculated in terms of . This means that the trajectory of a proton under positive polarity is identical to that of an antiproton under negative polarity, assuming other kinematics or heliospheric factors remain the same. It is also interesting to compare the evolution of the probability distributions over the entire solar cycle. In Figure 10, the normalized probabilities of CR protons (top) and antiprotons (bottom) at GeV are displayed as a function of the epoch for the considered time interval. In these plots, the probability is represented on the z-axis and is represented by the color palette on the right side. Particularly, the yellow–red serpentine pattern illustrates the temporal evolution of the probability peak. From the figure, it can be noticed that the IMF reversals occurring in 2000 and in 2013 had a significant impact, causing two shifts in the distributions. During the 2000 reversal, when passing from an to polarity, the proton distribution exhibited an increase to larger propagation times, while in the 2013 reversal, the shift was in the opposite direction. On average, the mean propagation time of CR protons under positive polarities is between two and three months, roughly, while during positive polarity it is about one month. For antiprotons, the effect of magnetic reversal on the distributions is also noticeable, leading to similar shifts but in opposite directions. In addition to the effect of magnetic reversal, it is interesting to examine the distributions during a consistent polarity state. For instance, between 2000 and 2013, the distributions of propagation times for CR protons and antiprotons follow a similar evolution over the solar cycle. This suggests that, as long the polarity is well defined and does not change, even when drift processes are at play, the temporal dependence of propagation times is primarily driven by diffusion and convection.
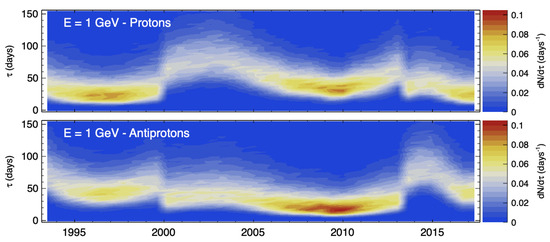
Figure 10.
Temporal evolution of the probability distributions of the propagation time for CR protons (top) and antiprotons (bottom) reaching Earth with GeV of kinetic energy.
Now, we shift our focus to the energy losses. The probability distributions of the loss fraction are shown in Figure 8 for particles with GeV. Once again, the distributions of antiprotons are denoted by pink dashed lines. Again, we observe some differences between antiprotons and protons, including the presence of a -symmetry if we compare the top panels (a, b) with the bottom panels (c, d). However, it is important to note that distinctions in energy losses between protons and antiprotons are not as pronounced as those observed in the case of propagation times. As we explored in Section 4.2, the loss fraction seems to be more responsive to the intensity of solar activity rather than to the IMF polarity. This characteristic is also evident in Figure 11, showing the long-term evolution of the normalized probability distributions of . The figure illustrates that during the two IMF reversals in 2000 and 2013, there is only a modest shift in the distributions. Conversely, a significant evolution over the solar cycle is evident. The yellow–red serpentine pattern seems to follow a nearly continuous trend, resembling a quasi-sinusoidal shape. This overall dependence over the solar cycle can be interpreted in terms of adiabatic losses, as discussed in Section 4.2, since the loss process is charge-sign blind and makes no distinction between protons and antiprotons. Nevertheless, these processes are coupled with drift, which impacts the trajectories of CRs within the large-scale IMF. From one side, the -dependent drift cause CRs of positive (negative) charge to travel preferentially through the fast-wind regions of the heliosphere during () polarity epochs. In the fast-wind regions, particles are subjected to a larger loss rate in comparison to particles of the slow-wind region. On the other hand, particles in the polar (fast-wind) regions make straighter trajectories and with smaller propagation times, in comparison with particles passing across the equatorial (slow-wind) region. In fact, the latter are influenced by the heliospheric current sheet, which causes longer trajectories and larger propagation times, which implies more severe energy losses.
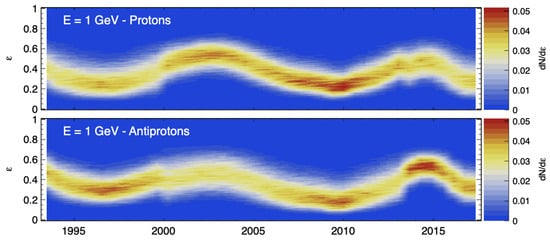
Figure 11.
Temporal evolution of the probability distributions of the loss fraction for CR protons (top) and antiprotons (bottom) reaching Earth with GeV of kinetic energy.
The absence of pronounced shifts in the distributions across the IMF reversal may be attributed to the interplay of two competing effects, as discussed in Section 4.2. On one hand, the -dependent drift leads CRs with positive (negative) charge to preferentially travel through different wind regions where cosmic particles are exposed to different loss rates. On the other hand, particles coming from the polar regions follow shorter trajectories and with smaller losses, in comparison to particles passing through the equatorial regions, due to the presence of the current sheet. As for the mean propagation times and the loss fraction , their energy dependence for CR antiprotons exhibits a qualitative similarity to those of protons, as shown in Figure 7 and Figure 9. These opposing effects contribute to the relatively stable distributions for the loss factors across IMF reversals.
5. Summary and Conclusions
After entering the heliosphere, CRs spend several days traveling the interplanetary plasma before reaching our detectors near Earth. During this journey, CRs are influenced by fundamental physical mechanisms, which include diffusion, drift, convection, and adiabatic cooling. The interplay among these mechanisms depends on the turbulence conditions of the background plasma, which are influenced by the Sun’s magnetic activity. In this paper, we conducted calculations to assess the propagation times energy losses of CRs in the heliosphere. While and are not directly measurable quantities, we devised a data-driven approach to obtain their probability distributions within the framework of a solar modulation model that was globally calibrated through CR proton measurements. To determine the evolution of the model parameters illustrated in Figure 4, we employed a data-driven approach, which relies on conventional techniques of statistical inference [19,33]. The transport parameters were constrained using 25 years of data, consisting of energy- and time-resolved measurements of CR protons from AMS-02, PAMELA, EPHIN/SOHO, BESS, and Voyager-1. Additionally, we incorporated essential inputs in the form of heliospheric parameters, as shown in Figure 3. These parameters are used to capture the varying conditions of the IMF. They were derived from data collected by spacecraft such as WIND and ACE, as well as from the Wilcox Solar Observatory. Using our proton-calibrated model, we computed propagation times and energy losses through trajectory-based sampling. This allowed us to examine the shapes of probability distributions, analyze their dependence on the particle energy, how they are influenced by IMF polarity reversals, and track their evolution throughout the solar activity cycle.
Our solar modulation framework relies on the SDE method. From a computational standpoint, our approach is similar to recent works that also employ the SDE method [30,31,32]. The primary goal of this work, however, was not solely the computation of and distributions. Rather, we focused on investigating their evolution through the actual solar cycles. We can compare our results for the mean propagation time with the work of Moloto et al. [29], which is based on similar calculations but completely different data. Their results appear in good agreement with determination of .
Our results may have implications for understanding the dynamics of the CR modulation phenomenon, particularly concerning the association between CR transport mechanisms and solar variability. Many studies on this subject have explored the time lag between the CR fluxes and solar activity, often attributed to the dynamics of the expanding solar wind [4,5,59]. However, recent studies have reported a 22-year quasi-periodic variation in the lag, following the IMF polarity cycle, and observed a significant dependence on the particle energies [60,61,62]. These works suggested that this feature is due to the energy-dependent propagation times of CRs in the heliosphere, which is well supported by our findings. Specifically, it has been suggested that the CR modulation lag comprises two components: an energy-independent lag of approximately 4–16 months from the expansion of the background plasma, and an energy-dependent lag that reflects CR propagation times [59]. The investigation of the CR propagation times may be of help for advancing the development of 4D time-dependent models of CR modulation. A significant challenge in this respect lies in accurately describing the dynamics of CRs as they traverse a variable medium [15,46,49]. Many effective models, including the framework we employed, rely on a quasi-steady state approximation, where the temporal evolution of CR modulation is represented as a continuous sequence of equilibrium solutions. To rely on this approximation, it is essential to have a comprehensive understanding of the timescales associated with CR propagation in relation to the changing solar activity. Therefore, having estimates of CR propagation times as a function of their energy and for different phases of the solar cycle is crucial.
The study presented here has several limitations that we briefly discuss. One limitation lies in the minimal number of parameters to capture the variable conditions of interplanetary plasma. Expanding the model to incorporate more observations and proxies could provide a more accurate representation of the heliospheric environment. Examples include an account of variations in solar wind speed or changes in the termination shock [20]. Similarly, to constrain CR transport, an account of other time-dependent parameters should be considered. One example is our assumption of the same parameters describing parallel and perpendicular diffusion, while other works observed different dependencies [18]. Another example is the drift parameters or of Equation (6), which we have set to constant values over the solar cycle. However, one may argue that drift may be suppressed at large tilt angles, and in particular, in the reversal phase. The role of drift over the solar cycle can be investigated using the new time-dependent measurements on GCR antiprotons from AMS-02. Regarding energy changes, we assumed that only adiabatic cooling is at work. Nonetheless, at energies lower that those considered in our analysis, reacceleration processes of CRs at the termination shock may influence the evaluation of the loss faction and its probability distribution. Moreover, in the outer region beyond the termination shock, cooling is less effective and the loss fraction may even be affected by regions with adiabatic heating [63]. Moreover, we provide a two-dimensional spatial description of the CR propagation, assuming azimuthal symmetry for the IMF and a spherically shaped structure for the heliopsheric boundaries (i.e., the heliopause and the termination shock). The large values of the propagation times indicate that CRs observed near Earth sample large volumes of the heliosphere, including the heliosheat and the heliotail. While the CR transport in the heliosheat is incorporated into our model, the account for an extended heliotail is missing, as it requires the implementation of a non-spherical model for the heliopause [64]. One may expect that the existence of such an extended modulation region may produce larger tails in the distributions of the GCR propagation times. In fact, the population of GCRs propagating inside the region of the heliotail would spend significant time in that region, before eventually reaching the inner heliosphere or the interstellar space. On the other hand, although past models of the heliosphere broadly assumed an magnetosphere-like shape with an extended heliotail, recent observations from space probes such as Voyager, Cassini, and IBEX have disfavored such a model, suggesting a bubble-like heliosphere [65,66]. Nonetheless, an account of a truly 3D formulation would enable the model to capture effects related to the detailed large-scale structures of the IMF and solar wind. Overcoming all these limitations could enhance the model’s ability to capture the complexity of the problem, possibly leading to a more comprehensive understanding of the solar modulation phenomenon.
Author Contributions
Conceptualization, N.T. and B.B.; Methodology, E.F. and B.K.; Software, N.T., E.F. and B.K.; Validation, E.F. and B.K.; Formal analysis, B.K.; Resources, E.F.; Writing—original draft, N.T.; Writing—review & editing, B.B.; Visualization, N.T.; Supervision, N.T.; Project administration, B.B.; Funding acquisition, B.B. All authors have read and agreed to the published version of the manuscript.
Funding
Funder: Agenzia Spaziale Italiana (ASI). Grant Number: ASI-UniPG 2019-2-HH.0.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We acknowledge the support of Italian Space Agency (ASI) under agreement ASI-UniPG 2019-2-HH.0. B.K. acknowledges support from agreement ASI-INFN 2019-19-HH.0. N.T. acknowledges the project SMILE—Solar ModulatIon of Light Elements in cosmic rays, in the program Fondo Ricerca 2021 of the University of Perugia, Italy. The CR data were retrieved from the ASI-SSDC Cosmic Ray Data Base (https://tools.ssdc.asi.it/CosmicRays/, accessed on 7 November 2024). Spacecraft data were extracted from the OMNIWeb (https://omniweb.gsfc.nasa.gov) service of the NASA Space Physics Data Facility. Solar data were taken from the Wilcox Solar Observatory at Stanford University and from the SILSO (https://www.sidc.be/silso/, accessed on 7 November 2024) SSN database of the Solar Influences Data Analysis Center at the Royal Observatory of Belgium.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Potgieter, M.S. Solar Modulation of Cosmic Rays. Living Rev. Sol. Phys. 2013, 10, 3. [Google Scholar] [CrossRef]
- Cucinotta, F.A.; Alp, M.; Rowedder, B.; Kim, M.Y. Safe days in space with acceptable uncertainty from space radiation exposure. Life Sci. Space Res. 2015, 5, 31–38. [Google Scholar] [CrossRef]
- Norbury, J.W.; Whitman, K.; Lee, K.; Slaba, T.C.; Badavi, F.F. Comparison of space radiation GCR models to recent AMS data. Life Sci. Space Res. 2018, 18, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Hathaway, D.H. The Solar Cycle. Living Rev. Solar Phys. 2015, 12, 4. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Kananen, H.; Mursula, K.; Tanskanen, P.; Kovaltsov, G.A. Correlative study of solar activity and cosmic ray intensity. J. Geophys. Res. Space Phys. 1998, 103, 9567. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, L.; Bartoloni, A.; Basegmez-du Pree, S.; Bates, J.; et al. The Alpha Magnetic Spectrometer (AMS) on the international space station: Part II — Results from the first seven years. Phys. Rep. 2021, 894, 1–116. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Ambrosi, G.; Arruda, L.; Attig, N.; Barao, F.; Barrin, J.; Bartolini, A.; Basegmez-du Pree, S. Periodicities in the Daily Proton Fluxes from 2011 to 2019 Measured by the Alpha Magnetic Spectrometer on the International Space Station from 1 to 100 GV. Phys. Rev. Lett. 2021, 127, 271102. [Google Scholar] [CrossRef]
- Aguilar, M.; Ali Cavasonza, L.; Alpat, B.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A. Observation of Fine Time Structures in the Cosmic Proton and Helium Fluxes with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2018, 121, 051101. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bongi, M.; Bonvinci, V.; Borisov, S.; Bottai, S. Time dependence of the proton flux measured by PAMELA during the 2006 July–2009 December solar minimum. Astrophys. J. 2013, 765, 91. [Google Scholar] [CrossRef]
- Martucci, M.; Munini, R.; Boezio, M.; Di Felice, V.; Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Bongi, M.; Bonvinci, V. Proton Fluxes Measured by the PAMELA Experiment from the Minimum to the Maximum Solar Activity for Solar Cycle 24. Astrophys. J. Lett. 2018, 854, L2. [Google Scholar] [CrossRef]
- Kühl, P.; Gómez-Herrero, R.; Heber, B. Annual Cosmic Ray Spectra from 250 MeV up to 1.6 GeV from 1995–2014 Measured with the Electron Proton Helium Instrument onboard SOHO. Sol. Phys. 2016, 291, 965–974. [Google Scholar] [CrossRef]
- Abe, K.; Fuke, H.; Haino, S.; Hams, T.; Hasegawa, M.; Horikoshi, A.; Itazaki, A.; Kim, C.; Kumazawa, T.; Kusomoto, A. Measurements of cosmic-ray proton and helium spectra from the BESS-Polar long-duration balloon flights over Antartica. Astrophys. J. 2016, 822, 65. [Google Scholar] [CrossRef]
- Shikaze, Y.; Haino, S.; Abe, K.; Fuke, H.; Hams, T.; Kim, K.C.; Makida, Y.; Matsuda, S.; Mitchell, J.W.; Moiseev, A.A.; et al. Measurements of 0.2 20 GeV/n cosmic-ray proton and helium spectra from 1997 through 2002 with the BESS spectrometer. Astropart. Phys. 2007, 28, 154–167. [Google Scholar] [CrossRef]
- Cummings, A.C.; Stone, E.C.; Heikkila, B.C.; Lal, N.; Webber, W.R.; Johannesson, G.; Moskalenko, I.V.; Orlando, E.; Porter, T.A. Galactic cosmic rays in the local interstellar medium: Voyager 1 observations and model results. Astrophys. J. 2016, 831, 18. [Google Scholar] [CrossRef]
- Engelbrecht, N.E.; Effenberger, F.; Florinski, V.; Potgieter, M.S.; Ruffolo, D.; Chhiber, R.; Usmanov, A.V.; Rankin, J.S.; Els, P.L. Theory of Cosmic Ray Transport in the Heliosphere. Space Sci. Rev. 2022, 218, 33. [Google Scholar] [CrossRef]
- Aslam, O.P.M.; Luo, X.; Potgieter, M.S.; Ngobeni, M.D.; Song, X. Unfolding Drift Effects for Cosmic Rays over the Period of the Sun’s Magnetic Field Reversal. Astrophys. J. 2023, 947, 72. [Google Scholar] [CrossRef]
- Boschini, M.J.; Della Torre, S.; Gervasi, M.; La Vacca, G.; Rancoita, P.G. Propagation of cosmic rays in heliosphere: The HELMOD model. Adv. Space Res. 2018, 62, 2859–2879. [Google Scholar] [CrossRef]
- Corti, C.; Potgieter, M.S.; Bindi, V.; Consolandi, C.; Light, C.; Palermo, M.; Popkow, A. Numerical modeling of galactic cosmic ray proton and helium observed by AMS-02 during the solar maximum of Solar Cycle 24. Astrophys. J. 2019, 871, 253. [Google Scholar] [CrossRef]
- Fiandrini, E.; Tomassetti, N.; Bertucci, B.; Donnini, F.; Graziani, M.; Khiali, B. Numerical modeling of cosmic rays in the heliosphere: Analysis of proton data from AMS-02 and PAMELA. Phys. Rev. D 2021, 104, 023012. [Google Scholar] [CrossRef]
- Manuel, R.; Ferreira, S.E.S.; Potgieter, M.S. Time-Dependent Modulation of Cosmic Rays in the Heliosphere. Sol. Phys. 2014, 289, 2207–2231. [Google Scholar] [CrossRef]
- Potgieter, M.S. The global modulation of cosmic rays during a quiet heliosphere: A modeling perspective. Adv. Space Res. 2017, 60, 848–864. [Google Scholar] [CrossRef]
- Song, X.; Luo, X.; Potgieter, M.S.; Liu, X.M.; Geng, Z. A Numerical Study of the Solar Modulation of Galactic Protons and Helium from 2006 to 2017. Astrophys. J. Suppl. Ser. 2021, 257, 48. [Google Scholar] [CrossRef]
- Tomassetti, N.; Barão, F.; Bertucci, B.; Fiandrini, E.; Orcinha, M. Numerical modeling of cosmic-ray transport in the heliosphere and interpretation of the proton-to-helium ratio in Solar Cycle 24. Adv. Space Res. 2019, 64, 2477–2489. [Google Scholar] [CrossRef]
- Tomassetti, N.; Barão, F.; Bertucci, B.; Fiandrini, E.; Figueiredo, J.L.; Lousada, J.B.; Orcinha, M. Testing Diffusion of Cosmic Rays in the Heliosphere with Proton and Helium Data from AMS. Phys. Rev. Lett. 2018, 121, 251104. [Google Scholar] [CrossRef]
- Wang, B.B.; Bi, X.J.; Fang, K.; Lin, S.; Yin, P.F. Solar modulation of cosmic proton and helium with AMS-02. arXiv 2020, arXiv:2011.12531. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Parker, E.N. Energy changes of cosmic rays in the solar system. Planet. Space Sci. 1967, 15, 1375–1386. [Google Scholar] [CrossRef]
- O’Gallagher, J.J. A time-dependent diffusion-convection model for the long-term modulation of cosmic rays. Astrophys. J. 1975, 197, 495–507. Available online: http://adsabs.harvard.edu/full/1975ApJ...197..495O (accessed on 7 November 2024). [CrossRef]
- Parker, E.N. The effect of adiabatic deceleration on the cosmic rayspectrum in the solar system. Planet. Space Sci. 1966, 14, 371–380. [Google Scholar] [CrossRef]
- Moloto, K.D.; Engelbrecht, N.E.; Strauss, R.D.; Diedericks, C. The Southern African neutron monitor program: A regional network to study global cosmic ray modulation. Adv. Space Res. 2023, 72, 830–843. [Google Scholar] [CrossRef]
- Strauss, R.D.; Potgieter, M.S.; Ferreira, S.E.S. Modelling and observing Jovian electron propagation times in the inner heliosphere. Adv. Space. Res. 2013, 51, 339–349. [Google Scholar] [CrossRef]
- Strauss, R.D.; Potgieter, M.S.; Büsching, I.; Kopp, A. On the propagation times and energy losses of cosmic rays in the heliosphere. J. Geophys. Res. 2011, 116, A12105. [Google Scholar] [CrossRef]
- Vogt, A.; Engelbrecht, N.E.; Heber, B.; Kopp, A.; Herbst, K. Numerical and experimental evidence for a new interpretation of residence times in space. Astron. Astrophys. 2022, 657, A39. [Google Scholar] [CrossRef]
- Tomassetti, N.; Bertucci, B.; Donnini, F.; Graziani, M.; Fiandrini, E.; Khiali, B.; Reina Conde, A. Data driven analysis of cosmic rays in the heliosphere: Diffusion of cosmic protons. Rend. Lincei Sci. Fis. Nat. 2023, 34, 333–338. [Google Scholar] [CrossRef]
- Heber, B.; Potgieter, M.S. Cosmic Rays at High Heliolatitudes. Space Sci. Rev. 2006, 127, 117–194. [Google Scholar] [CrossRef]
- Potgieter, M.S.; Vos, E.E.; Boezio, M.; De Simone, N.; Di Felice, V.; Formato, V. Modulation of galactic protons in the heliosphere during the unusual solar minimum of 2006 to 2009. Sol. Phys. 2014, 289, 391. [Google Scholar] [CrossRef]
- Jokipii, J.R.; Kota, J. The polar heliospheric magnetic field. Geophys. Res. Lett. 1989, 16, 1. [Google Scholar] [CrossRef]
- Zank, G.P.; Matthaeus, W.H.; Bieber, J.W.; Moraal, H. The radial and latitudinal dependence of the cosmic ray diffusion tensor in the heliosphere. Grophys. Res. Lett. 1998, 103, 2085. [Google Scholar] [CrossRef]
- Teufel, A.; Schlickeiser, R. Analytic calculation of the parallel mean free path of heliospheric cosmic rays—I. Dynamical magnetic slab turbulence and random sweeping slab turbulence. Astron. Astrophys. 2002, 393, 703–715. [Google Scholar] [CrossRef]
- Giacalone, J.; Jokipii, J.R. The Transport of Cosmic Rays across a Turbulent Magnetic Field. Astrophys. J. 1999, 520, 204. [Google Scholar] [CrossRef]
- Jiang, J.; Lin, S.; Yang, L. A New Scenario of Solar Modulation Model during the Polarity Reversing. arXiv 2023, arXiv:2303.04460. [Google Scholar] [CrossRef]
- Feng, J.; Tomassetti, N.; Oliva, A. Bayesian analysis of spatial-dependent cosmic-ray propagation: Astrophysical background of antiprotons and positrons. Phys. Rev. D 2016, 94, 123007. [Google Scholar] [CrossRef]
- Tomassetti, N. Cosmic-ray protons, nuclei, electrons, and antiparticles under a two-halo scenario of diffusive propagation. Phys. Rev. D 2015, 92, 081301(R). [Google Scholar] [CrossRef]
- Tomassetti, N. Origin of the Cosmic Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Tomassetti, N. Solar and Nuclear Physics Uncertainties in Cosmic Ray Propagation. Phys. Rev. D 2017, 96, 103005. [Google Scholar] [CrossRef]
- Tomassetti, N. Examination of uncertainties in nuclear data for cosmic ray physics with the AMS experiment. Phys. Rev. C 2015, 92, 045808. [Google Scholar] [CrossRef]
- Florinski, V.; Pogorelov, N.V. Four-dimensional transport of galactic cosmic rays in the outer heliosphere and heliosheath. Astrophys. J. 2009, 701, 642. [Google Scholar] [CrossRef]
- Kappl, R. Solarprop: Charge-sign dependent solar modulation for everyone. Comp. Phys. Comm. 2016, 207, 386–399. [Google Scholar] [CrossRef]
- Kopp, A.; Büsching, I.; Strauss, R.D.; Potgieter, M.S. A stochastic differential equation code for multidimensional Fokker–Planck type problems. Comp. Phys. Comm. 2012, 183, 530–542. [Google Scholar] [CrossRef]
- Pei, C.; Bieber, J.W.; Burger, R.A.; Clem, J. A general time-dependent stochastic method for solving Parker’s transport equation in spherical coordinates. Space Phys. 2010, 115, A1412107. [Google Scholar] [CrossRef]
- Yamada, Y.; Yanagita, S.; Yoshida, T. A stochastic view of the solar modulation phenomena of cosmic rays. Geophys. Res. Lett. 1998, 25, 2353–2356. [Google Scholar] [CrossRef]
- Zhang, M. A Markov Stochastic Process Theory of Cosmic-Ray Modulation. Astrophys. J. 1999, 513, 409–420. [Google Scholar] [CrossRef]
- Strauss, R.D.; Effenberger, F. A Hitch-hiker’s Guide to Stochastic Differential Equations. Space Sci. Rev. 2017, 212, 151–192. [Google Scholar] [CrossRef]
- Smith, C.W.; L’Heureux, H.; Ness, N.F.; Acunã, M.H.; Burlaga, L.F.; Scheifele, J. The ACE Magnetic Fields Experiment. Space Sci. Rev. 1998, 86, 613–632. [Google Scholar] [CrossRef]
- Hoeksema, J.T. The Large-Scale Structure of the Heliospheric Current Sheet During the ULYSSES Epoch. Space Sci. Rev. 1995, 72, 137–148. [Google Scholar] [CrossRef]
- Sun, X.; Hoeksema, J.T.; Liu, Y.; Zhao, J. On polar magnetic field reversal and surface flux transport during solar cycle 24. Astrophys. J. 2015, 798, 114. [Google Scholar] [CrossRef]
- Vaisanen, P.; Usoskin, I.; Mursula, K. Long-Term and Solar Cycle Variation of Galactic Cosmic Rays: Evidence for Variable Heliospheric Turbulence. JGR Space Phys. 2019, 124, 804–811. [Google Scholar] [CrossRef]
- Palmer, I.D. Transport coefficients of low-energy cosmic rays in interplanetary space. Rev. Geophys. Space Phys. 1982, 20, 335. [Google Scholar] [CrossRef]
- Potgieter, M.S.; Aslam, O.P.M.; Bisschoff, D.; Ngobeni, M.D. A Perspective on the Solar Modulation of Cosmic Anti-Matter. Physics 2021, 3, 1190–1225. [Google Scholar] [CrossRef]
- Tomassetti, N.; Orcinha, M.; Bertucci, B.; Barão, F. Evidence for a Time Lag in Solar Modulation of Galactic Cosmic Rays. Astrophys. J. Lett. 2017, 849, L32. [Google Scholar] [CrossRef]
- Koldobskiy, S.A.; Kähkönen, R.; Hofer, B.; Krivova, N.A.; Kovaltsov, G.A.; Usoskin, I.G. Time Lag Between Cosmic-Ray and Solar Variability: Sunspot Numbers and Open Solar Magnetic Flux. Sol. Phys. 2022, 297, 38. [Google Scholar] [CrossRef]
- Shen, Z.N.; Qin, G.; Pingbing, Z.; Wei, F.; Xu, X. A Study of Variations of Galactic Cosmic-Ray Intensity Based on a Hybrid Data- processing Method. Astrophys. J. 2020, 900, 143. [Google Scholar] [CrossRef]
- Tomassetti, N.; Bertucci, B.; Fiandrini, F. Temporal evolution and rigidity dependence of the solar modulation lag of Galactic cosmic rays. Phys. Rev. D 2022, 106, 103022. [Google Scholar] [CrossRef]
- Langner, U.W.; Potgieter, M.S.; Fichtner, H.; Borrmann, T. Modulation of anomalous protons: Effects of different solar wind speed profiles in the heliosheath. J. Geophys. Res. 2006, 111, 01106. [Google Scholar] [CrossRef]
- Boschini, M.J.; Della Torre, S.; Gervasi, M.; La Vacca, G.; Rancoita, P.G. The HelMod Model in the Works for Inner and Outer Heliosphere: From AMS to Voyager Probes Observations. Adv. Space Res. 2019, 64, 2459–2476. [Google Scholar] [CrossRef]
- Dialynas, K.; Krimigis, S.M.; Mitchell, D.G.; Decker, R.B.; Roelof, E.C. The bubble-like shape of the heliosphere observed by Voyager and Cassini. Nat. Astron. 2017, 1, 0115. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, K.; Shi, Q.; Tian, A.; Yao, F. The Shape of the Heliosphere Derived from the IBEX Ribbon. Astrophys. J. Lett. 2024, 977, L39. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).