Abstract
We have investigated the Janis–Newman–Winicour spacetime through three fundamental tests of theories of gravity, namely, gravitational lensing, perihelion shift, and redshift due to gravitational force. Focusing initially on the circular motion of a massive particle within the equatorial plane, the analysis disregards external scalar field interactions. The Janis–Newman–Winicour (JNW) spacetime’s unique parameters, mass (M) and the scalar parameter (n), are examined, revealing an intriguing relationship between the innermost stable circular orbit position of the test particle and the scalar field parameter. The study also explores photon motion around a gravitational object in JNW spacetime, revealing the expansion of the photon sphere alongside a diminishing shadow, influenced by the external scalar field. Despite these complexities, gravitational bending of light remains consistent with general relativity predictions. The investigation extends to perihelion precession, where the trajectory of a massive particle in JNW spacetime exhibits eccentricity-dependent shifts, distinguishing it from Schwarzschild spacetime. Finally, oscillatory motion of massive particles in JNW spacetime is explored, providing analytical expressions for epicyclic frequencies using perturbation methods. The study concludes with the application of MCMC analyses to constrain the JNW spacetime parameters based on observational data.
1. Introduction
Einstein’s theory of general relativity has been subjected to numerous tests over the years, and it has withstood these tests with remarkable accuracy. Here are three key tests of general relativity. Gravitational redshift: One of the earliest and most famous tests of general relativity is the measurement of gravitational redshift. According to this theory, light traveling in a gravitational field should be redshifted (its wavelength should increase) as it climbs out of the field. This effect was confirmed in the Pound–Rebka experiment in 1960, where gamma rays were emitted at the bottom of a tower and detected at the top. The observed redshift matched the predictions of general relativity [1]. Gravitational lensing: General relativity predicts that massive objects can bend the path of light that passes near them. In astronomy and cosmology this phenomenon is known as gravitational lensing. The bending of light by massive objects, like galaxies and galaxy clusters, has been observed and confirmed through astronomical observations. One of the most famous examples is the Hubble Space Telescope’s observations of gravitational lensing around galaxy clusters, which have allowed astronomers to study distant galaxies that would otherwise be hidden from view [2]. According to Einstein’s theory of gravity, the deflection angle of the light ray by the massive object of mass M is defined as
where b is the impact parameter of the light ray.
Perihelion precession of Mercury: An important early test of general relativity was the explanation of the anomalous precession of Mercury’s perihelion, which is the point in its orbit closest to the Sun. Classical Newtonian physics could not fully account for this precession, but general relativity provided a precise prediction that matched observations. This test was one of the key pieces of evidence that supported the validity of Einstein’s theory [3]. Perihelion precession refers to the gradual rotation of a planet’s orbit around the Sun, resulting in the slow movement of its closest point of approach, known as perihelion, over time. The observation of this phenomenon was first made for the planet Mercury and became a classic test of Einstein’s general theory of relativity. The formula used to calculate the perihelion precession of a planet due to general relativity is given by
where is the amount of precession, measured in radians per orbit; G is the gravitational constant; is the mass of the sun; and c is the speed of light. Additionally, the semi-major axis of the planet’s orbit is denoted by a, and the eccentricity of the orbit by e. The formula reveals that the perihelion precession is directly proportional to the mass of the sun, but inversely proportional to the square of the speed of light and the semi-major axis of the orbit.
These are just a few of the many tests that have been conducted to confirm the predictions of general relativity. The theory has also been confirmed through experiments involving the bending of starlight during solar eclipses, the behavior of atomic clocks in strong gravitational fields, and the observation of gravitational waves, among others. General relativity has consistently demonstrated its accuracy in describing the behavior of gravity and the structure of the universe.
The formation of a singularity due to the gravitational collapse of a massive object is a common occurrence in spacetime. However, if this singularity is not surrounded by an event horizon, it becomes a hypothetical object known as a naked singularity. Unlike a black hole, which is always hidden from distant observers by an event horizon, a naked singularity would be visible to observers, providing them with the opportunity to study the extreme effects of gravity near the singularity. The concept of naked singularities challenges the cosmic censorship hypothesis, which asserts that singularities must always be hidden from observers by an event horizon. The potential existence of naked singularities raises questions about the predictability and stability of the universe. Therefore, the topic remains a controversial subject in the field of physics. The absence of an event horizon is the main difference between a black hole and a naked singularity. In a black hole, the event horizon surrounds the singularity and prevents anything from escaping. Conversely, in a naked singularity, the singularity is visible to observers since there is no event horizon to obstruct it.
The Janis–Newman–Winicour (JNW) metric is a solution to the Einstein-scalar-field equations that describes a spherically symmetric, static, and non-vacuum solution [4]. This solution is commonly used as a model for naked singularities since it describes a singularity that is not surrounded by an event horizon. Overall, the JNW naked singularity is a theoretical construct in physics that continues to be the subject of debate and research in the scientific community. In this solution, the scalar field is described by a complex scalar function. It is governed by a wave equation in curved spacetime and has properties that are distinct from other matter fields, such as electromagnetic fields or perfect fluids.
One interesting feature of the JNW spacetime is that it can give rise to naked singularities. In general relativity, singularities are regions where the curvature becomes infinitely large, and they are typically hidden within black holes by an event horizon. However, in the JNW spacetime, under certain conditions, the singularity can become visible to external observers, violating the cosmic censorship hypothesis, which suggests that singularities should always be hidden. The study of this spacetime is important for understanding the properties and behavior of black holes, as well as for exploring the interplay between gravity and other fields in extreme conditions.
The recent observations made by the Event Horizon Telescope have unveiled remarkable insights into the mysterious centers of the Messier 87 and Milky Way galaxies. This groundbreaking discovery has illuminated a new avenue in observational astronomy, offering an unprecedented opportunity to investigate the profound realms of gravity and fundamental physics within the strong-field regime in the JNW spacetime [5]. In Ref. [6], the magnetic Penrose process in the rotating JNW spacetime in the presence of an electromagnetic field was studied. It is shown that total energy extraction efficiency within this process can be around for a rotating JNW naked singularity.
Extension of the method of Simpson and Visser of regularization of a black hole spacetime to cases where the initial metric represents a globally naked singularity was analyzed in [7]. Strong lensing by the naked singularity that enters the Fisher/JNW scalar-tensor spacetime was explored in Ref. [8]. The rotating JNW naked singularity spacetime using the Newman–Janis algorithm was obtained in [9]. Analytical formulae for the height, the width, and the periodicities of the steps in visibility as functions of the black hole parameters described by the JNW spacetime have been obtained in [10]. The retrolensing phenomenon in the vicinity of a JNW naked singularity embedded in a scalar field was studied [11]. A study of the ringdown profile of the Janis–Newman–Winicour naked singularity under axial gravitational perturbation was presented in Ref. [12]. The effective dynamics of the loop quantized JNW spacetime was studied in [13].
The orbit equations of particles in naked singularity spacetimes, including Janis–Newman–Winicour geometry, were derived in [14]. Iron line shapes in the reflection spectrum of a putative disk around a JNW singularity were analyzed in [15]. The Janis–Newman–Winicour metric in the framework of conformal gravity was considered in [16]. It was shown that the precession frequency of a test gyroscope at a given radius can be enhanced by almost an order of magnitude in the background of a naked singularity in [17]. The proper Newtonian-like analogous potential corresponding to JNW naked singularity was derived in [18].
A study of the geodesic structure of the JNW spacetime containing a strong curvature naked singularity was presented in [19]. The scalar radiation spectra from a particle in circular orbit, in the background of the JNW naked singularity, was analyzed in [20]. Circular timelike geodesics in the JNW spacetime were analyzed in [21]. The acceleration of particles and high-energy collisions in the JNW spacetime were studied in [22]. Gravitational lensing by a JNW wormhole was discussed in Ref. [23] and gravitational lensing by transparent JNW naked singularities was discussed in [24]. The behavior of a scalar field coupled to gravitons on the JNW background was studied in [25]. The observational signatures of hot spots orbiting a JNW naked singularity, with a focus on discerning them from black holes, were discussed in [26]. A minimal coupling interaction between massive Klein–Gordon quantum scalar free fields and a JNW spherically symmetric static black hole was analyzed in [27]. In Ref. [28], the gravitational lensing effect was investigated in a spherical symmetric solution in the Brans–Dicke solution given in [29,30]. The Schrödinger-type scalar wave equation from JNW naked singularity spacetime was considered in [31]. The motion of timelike test particles in the JNW spacetime was studied in [32]. The gravitational deflection of relativistic massive particles by JNW spacetimes was analyzed in [33]. The energy associated with JNW spacetime was analyzed in [34], and investigation of a timelike particle’s motion around black holes was performed in [35,36,37,38,39,40,41,42,43,44].
In this paper, we study the motion of test particles around the gravitational compact object described by the JNW spacetime which is a solution of the Einstein-scalar-field equations. We use the geodesic equation to find the influence of gravitational and scalar fields on the trajectories and orbital motion of particles. The paper is organized as follows. In Section 2, we study the properties of spacetime formation in the JNW spacetime and the geodesic motion of a test particle in a particularly simple wormhole. Section 3 is devoted to studying the orbital precession of particles in the equatorial plane of a wormhole, while Section 4 is devoted to the epicyclic precession of particles in the same spacetime metric. Section 5 is devoted to application of the fundamental frequencies in evidence of micro-quasars. Finally, in Section 6 we present the concluding remarks.
Throughout the paper, we use a space-like signature and a system of units in which (However, for those expressions with an astrophysical application we have written the speed of light explicitly.) Greek indices are taken to run from 0 to 3 and Latin indices from 1 to 3.
2. Geodesic Motion in JNW Spacetime
In spherical coordinates, , the JNW spacetime is described as [4]
and the associated scalar field is given by
where M is the mass of the object and parameter n arises due to the scalar field. Notice that the spacetime (3) is a non-vacuum solution of the Einstein-scalar-field equations, also known as a naked singularity. The singularity located at can be easily found from the behavior of the curvature scalars of forms
In the case when , the solution (3) reduces to the Schwarzschild spacetime, while for large values of the n parameter (i.e., ) it reduces to the Papapetrou spacetime or the exponential metric [45]
which describes the regular wormhole solution. The Papapetrou spacetime has been tested with massive particle motion and gravitational lensing in [46].
To obtain the equation of motion of a particle in the strong gravitational field of a compact object, one can use the geodesic equation together with normalization of the 4-velocity of the test particle:
where is the 4-velocity of the particle, is the Christoffel symbols, and corresponds to a massless and massive particle, respectively. Due to symmetry, particle motion is associated with two constants, namely, the specific energy and specific angular momentum of a particle measured at infinity. In this case, the specific energy and specific angular momentum read as follows:
For simplicity, we consider the orbital motion of a particle in the equatorial plane, i.e., , and using the normalization of the 4-velocity in (10) and taking into account the expressions for the constants of motion (11), the radial equation reads
2.1. Massive Particle Motion:
We first examine the effect of the scalar field on massive particle motion around the gravitational compact object described by the JNW spacetime. Using the conditions , the critical values of the specific energy and specific angular momentum of the particle can expressed as
where is the orbital angular velocity of the test particle.
The characteristic radii, namely, the innermost stable circular orbit (ISCO) can be found as the stationary points of the specific energy and specific angular momentum of a particle in (13), (14), and can be determined as [46]
It is easy to check that the -metric [47,48] and the JNW spacetime are expressed with the same expression in the equatorial plane. Therefore, the expression for the orbital velocity of a test particle orbiting at the ISCO position around the gravitational compact object described by the JNW spacetime can be determined as [49]
also, the specific energy of a test particle at the ISCO position can be found as [49]
The foregoing analysis reveals that the orbital velocity and specific energy of a particle orbiting in proximity to the ISCO are devoid of any dependence on the mass of the compact object. Instead, their variations are intricately entwined with the n parameter. A discerning examination of the expressions elucidates that, within the Schwarzschild spacetime (characterized by ), a test particle traces orbits at the ISCO position with a velocity equal to half the speed of light, i.e., . Simultaneously, the particle’s energy diminishes to . Conversely, in the Papapetrou spacetime, the corresponding values manifest as follows:
In the context of our discussion on the exponential wormhole metric represented by (3), it is crucial to recognize its unique nature as a specialized instance of the JNW solution. This particular wormhole configuration is intricately linked to the presence of a phantom scalar field, manifesting as an anti-gravitating force that actively diminishes the gravitational field surrounding the compact object under consideration. A notable consequence of this phenomenon is the alteration of characteristic radii within the spacetime. Significantly smaller than those observed in the Schwarzschild space, these radii reflect the distinctive gravitational impact exerted by the phantom scalar field associated with the exponential wormhole metric.
In Figure 1, we illustrate the correlation between characteristic radii in the JNW spacetime and the parameter n. Our initial investigation focuses on examining the ISCO position of a massive particle orbiting within the JNW spacetime. The dynamics of the ISCO can be comprehended by analyzing the intricate interplay between gravitational and centrifugal forces that dictate the geodesic trajectories of test particles. Within the parameter range , gravitational forces exert dominance, while in the interval , centrifugal forces take precedence.
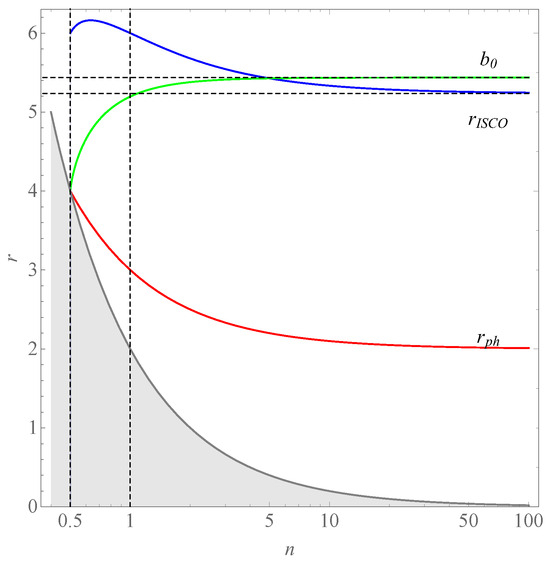
Figure 1.
Dependence of ISCO position , photon sphere , and critical impact parameter on scalar parameter n. The shaved area represents the naked singularity.
Remarkably, an intriguing revelation emerges when exploring the shadows cast by the wormhole and comparing them to those of Schwarzschild black holes. Contrary to expectation based on the diminished characteristic radii, the shadow of the wormhole surpasses that of the Schwarzschild black hole. This peculiarity stands out as one of the most distinguishing features of the Papapetrou spacetime when juxtaposed with the more conventional Schwarzschild spacetime. The underlying dynamics governing this shadow phenomenon present an intriguing avenue for further investigation and analysis within the realm of gravitational physics.
2.2. Massless Particle Motion:
In examining the influence of the scalar field on the motion of photons (assumed to be massless particles, ) around a gravitational compact object characterized by the JNW spacetime, our attention is drawn to the well-established phenomenon wherein a light ray, as it nears the gravitational entity, adheres to geodesic motion. Within the context of the Schwarzschild spacetime, the absence of stable circular orbits is a notable characteristic. The photonsphere radius is distinctly identified as , and the critical impact parameter for photons is established as . This critical impact parameter signifies the minimum distance at which a photon can be captured by the central object. Contrary to the Schwarzschild scenario, the introduction of the scalar field yields the existence of stable circular orbits. The radii of these orbits are explicitly expressed in relation to the scalar parameter n. By imposing the conditions in Equation (12), considering , the determination of the photon sphere radius and the critical impact parameter for photons in the JNW spacetime unfolds as follows:
where the impact parameter of a photon is defined as . In the Schwarzschild spacetime, one obtains and , while in the Papapetrou spacetime, and .
It is also interesting to consider the weak gravitational lensing effect in the JNW spacetime. We focus on weak gravitational lensing by a compact object using the technique presented in Ref. [50]. According to this research, a light ray passes slightly far from the central object, therefore the spacetime metric can be expanded in the power of the Newtonian potential, i.e., , or more correctly, , where is the metric tensor in the Minkowski spacetime while is the small perturbation. We can apply this technique in the JNW spacetime and obtain the following result:
where is the line element in the Minkowski spacetime. The relations between rectangular coordinates and spherical coordinates is , , and ; the perturbations of the components of the metric tensors in the JNW spacetime are
According to Ref. [50], in weak lensing the deflection angle of light is determined as
where b is the impact parameter of the light ray defined as . Hereafter, performing simple algebraic manipulations, we obtain that the deflection angle of the light ray by a compact object is described as
which is also predicted by Einstein’s theory of relativity. It turns out that the deflection angle in the Schwarzschild and JNW spacetimes are calculated by the same expression. Using the lens equation, one can identify the magnification of the main and secondary images of the source. The explicit expressions for the magnification are
3. Orbital Precession
As we mentioned before, another important test of Einstein’s theory of relativity is perihelion precession. Specifically, our focus centers on the orbital precession exhibited by a massive particle navigating the gravitational influence of a compact object, as delineated within the JNW spacetime framework. Recalling the equations of motion, denoted by (11) and (12), we discern the intricate portrayal of the orbital dynamics governing the trajectory of a test particle:
Hereafter, introducing a new radial coordinate and differentiating Equation (31), one can obtain the following expression:
where is a small parameter. As one can see, Equation (32) is the nonlinear differential equation for function and presenting an exact analytical solution is rather difficult. In the absence of the scalar field (i.e., ), it reduces to , which characterizes orbital motion in the Schwarzschild spacetime. In order to obtain the semi-analytical solution of (32), one can expand the solution in the power small parameter and the approximated solution can be found as
where and are the solutions in the zeroth- and first-order approximations. Now, inserting solution (33) into (32), one can obtain
Equation (34) translates the expression into the Newtonian framework and its solution can be easily found as
which can be reduced to in the Newtonian framework (i.e., ), while in the first approximation the solution can be seen as , which satisfies the following condition:
where A, B, and C are unknown constants. Now, comparing the last equation with (35), together with (36), the unknown constants can be found as
Finally, the dimensionless radial coordinate for a massive particle in the JNW spacetime is derived as
From the above expression, one can conclude that, unlike in Einstein’s theory of relativity, the trajectory of a massive body orbiting around a gravitational object described by the JNW metric depends on the energy of the particle and the trajectory is not closed due to the gravity effect. The result is that the orbit of a massive particle is not periodic in anymore and precession must result from the term . Perihelion first occurs at ; however, the second perihelion occurs when the term in (42) generating the precession has gone through a full . So, one can obtain the relation for the preccesion angle, which means that
It is easy to check that in the case of general relativity (i.e., ), the expression for the periastron precession reduces to which is shown in Equation (2), while in the Papapetrou spacetime, i.e., , it takes the form
In Figure 2, we show the trajectory of the test particle orbiting around the compact object described the JNW spacetime. We draw the contour plot of the expression in (43) in the plane for the different values of the scalar parameter n, for particular values of the particle energy , eccentricity e, and expansion parameter . As one can see, the perihelion becomes larger when increasing the scalar parameter n.
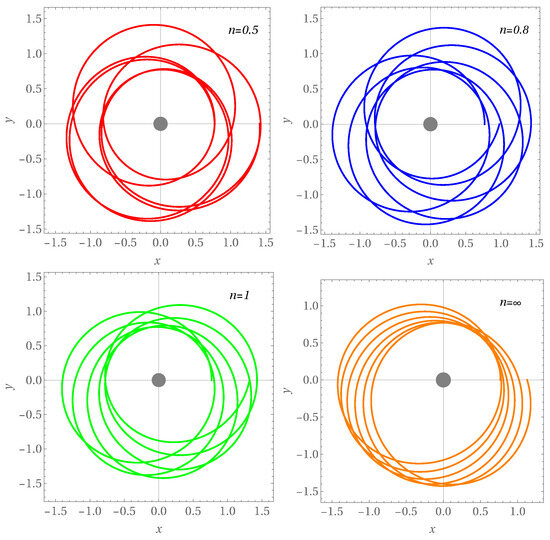
Figure 2.
The perihelion shift of a point particle for different values of n with particular values of the particle’s energy and eccentricity.
4. Epicyclic Precession
Here, we discuss the orbital as well as epicyclic motion of a massive particle near a stable circular orbit in the JNW spacetime. We have derived the exact analytic expression of the fundamental frequencies in the following form [51]:
where is the Keplerian frequency. It is easy to see that in the case when , expressions (45) and (46) reduce to the frequencies reproduced in the Schwarzschild space and . Furthermore, we convert the epicyclic frequencies into units of Hz for the analysis:
where G and c are the gravitational constant and speed of light, respectively. These frequencies can be used directly to analyze the observed data set. Note that the fundamental frequencies depend on n and M.
To have an idea about the order of magnitude of these frequencies, the orbital frequency of a particle orbiting a Schwarzschild black hole can be estimated as
High-frequency QPOs at 40–450 Hz are thus of the right magnitude to be associated with the orbital frequencies near the ISCO radius of stellar-mass black holes. Interestingly, we also have evidence of high-frequency QPOs in supermassive black holes (<1 ) [52] and intermediate-mass black holes (∼1 ) [53]. After restoring the unit, we present radial dependence of of fundamental frequencies in Figure 3 for different values of the scalar parameter n.
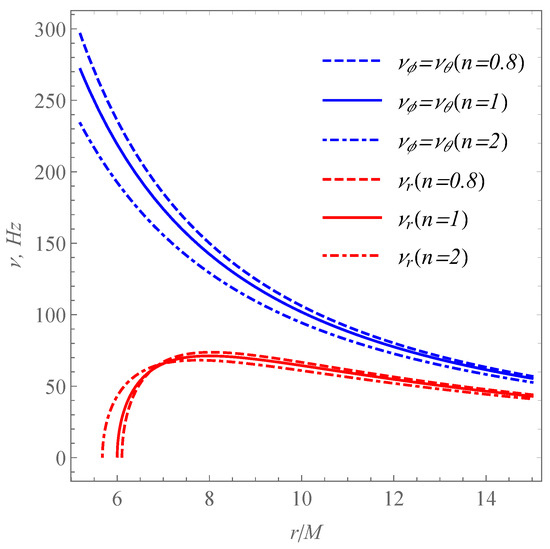
Figure 3.
The radial dependence of the fundamental frequencies governed by test particle’s motion around a black hole for , , and 1.
5. Constraining Mass and Range of ‘’ from Twin-Peak QPOs
In this section, we select twin-peak QPOs from a stellar mass BH (sMBH), super-massive BH (SMBH), and an intermediate mass BH (IMBH), i.e., GRO 1655-40, Sgr-A* and M82-X1, with well-reported observational results, as presented in Table 1. We use these results to investigate the above-mentioned three systems to constrain the parameters associated with the static JNW spacetime.

Table 1.
Frequencies of twin-peak QPOs in microquasars and galactic center.
5.1. A Detailed Analysis of Monte Carlo Markov Chain (MCMC)
The MCMC analysis is performed using the well-resourced library emcee analysis [55] to determine constraints on the parameters of the JNW spacetime in the presence of a test particle. We incorporate the relativistic precision (RP) method to accomplish our analysis.
The posterior distribution can be defined following the standard definition [55,56]
where is chosen as a Gaussian prior within suitable boundaries (see Table 2), i.e., , . In this work, the parameters are and is their corresponding standard deviations. We take up the orbital, periastron precession frequencies from Section 4, and employ it in our MCMC analysis. Eventually, the likelihood function can be expressed as
where denotes the likelihood of the orbital frequencies,
and represents the likelihood of the periastron precession frequency ().
Here, and are explicit observational results of the orbital/Keplerian frequencies () and periastron precession frequencies for the sources of our interest. On the other hand, and are the respective model predictions.

Table 2.
The Gaussian prior of the JNW spacetime from QPOs for the sMBH, SMBH, and IMBH sources.
With all this information, we perform an MCMC simulation to constrain the parameters {M, n, } for the JNW spacetime. Overall, we sample points for each parameter according to the Gaussian prior distribution. This enables us to explore the physically possible parameter space while staying within set boundaries and obtain the parameter values that best fit the data.
5.2. Results of MCMC Simulation
Based on the setup described in the previous subsections, we conducted an exploration of the three-dimensional parameter space using MCMC to analyze a test particle in the JNW spacetime. As part of this process, we accurately constrained the mass of compact objects and the range of the variable “n” for a wide range of black hole masses, starting from stellar to intermediate to supermassive.
Here, we present the results of the MCMC analysis of all parameters of the JNW for the three twin-peak QPO events in Figure 4. The contour plots in these figures highlight the 1 (), 2 (), and 3 () confidence levels (CLs) of the posterior probability distributions for the entire set of parameters. The shaded regions on the contour plots represent these confidence levels. For more information on the best-fit values of these three parameters, please refer to Table 3.
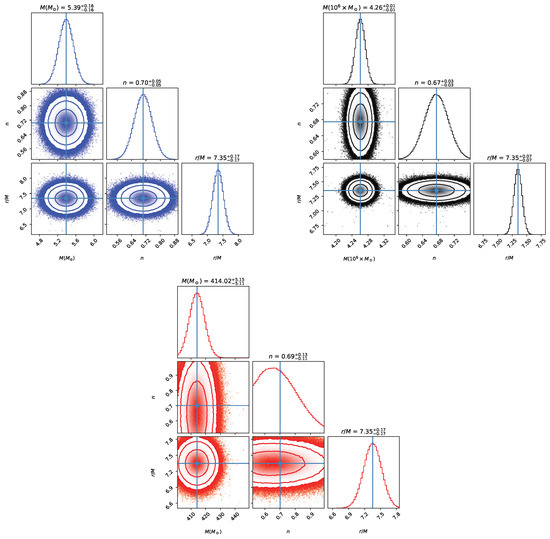
Figure 4.
Three -dimensional parameter constraints for the JNW spacetime with GRO J1655-40 (blue contours), Sgr-A* (black contours), and M82-X1 (red contours) from current observations of QPOs within the relativistic precession model.

Table 3.
The best-fit values of the JNW spacetime from QPOs for the sMBH, IMBH, and SMBH sources.
6. Conclusions
We have investigated the JNW spacetime with the three well-known tests of general theory of relativity, namely, gravitational lensing, perihelion shift of massive objects, and redshift due to gravitational force. Our findings are summarized as follows:
- In the initial stages of our investigation, we focused on the circular motion of a massive particle in the JNW spacetime. To streamline our analysis, we initially disregarded the potential interaction between the massive particle and an external scalar field. It is noteworthy that the JNW spacetime is characterized by two key parameters, namely, the mass, represented by M, and the scalar parameter, denoted as n. Our examination specifically concentrated on the motion of the particle within the equatorial plane, and determined how the ISCO position depends on those two parameters. Intriguingly, our investigation shows that the ISCO position of the test particle increases up to a specific value of the scalar field parameter initially. There is an ascent in this position as it attains a specific value; however, beyond this critical threshold, a subsequent decline occurs for larger values of the scalar field parameter. This is one of main differences of the JNW spacetime from the Schwarzschild one.
- Using a null geodesic equation, we consider photon motion orbiting the gravitational compact object described by the JNW metric. We have derived the analytical expressions for the radii of the photon sphere and shadow of the object in terms of the scalar field parameter. In the JNW spacetime, an intriguing phenomenon unfolds as the photon sphere undergoes expansion, even as the shadow it casts diminishes in size. This captivating occurrence can be attributed to the influence of the external scalar field, adding an additional layer of complexity to the interplay of forces within this unique spacetime framework. We have demonstrated that the gravitational bending of light rays around a compact object, as characterized by the JNW spacetime, remains unaffected by variations in the scalar field parameter. Remarkably, the expression for the deflection angle of light remains consistent with predictions made by general relativity.
- The perihelion precession for a massive particle orbiting around a gravitational object has been extensively investigated. The explicit formulation describing the trajectory of a test particle orbiting a central object within the context of JNW spacetime has been derived. An in-depth analysis of the relationship between the shape of the trajectory of a massive particle and its eccentricity has been explicitly conducted. It has been revealed that as the eccentricity increases, the perihelion of the particle approaches the central object. This study establishes that the particle follows an elliptic trajectory around the gravitational object, yet uniquely experiences a perihelion shift with each orbit, a phenomenon initially predicted by the general theory of relativity. Furthermore, it is demonstrated that the perihelion shift of the massive particle can be expressed in terms of the specific energy of the particle in the JNW spacetime unlike in the Schwarzschild spacetime. However, this mathematical representation does not provide insights into the perihelion shift of a particle orbiting a gravitational object.
- Finally, we have studied the oscillatory motion of a massive particle in the JNW spacetime; in particular, we have derived an equation for the orbital and epicyclic motion of the test particle. Using the perturbation method, we obtained a linear oscillator equation for the radial and angular displacement near the stable orbit. We have derived the exact analytical expressions for the epicyclic frequencies of the oscillations along the radial and vertical directions. In order to constrain the parameters in the JNW spacetime with observations, we used a promising statistical method, the so-called MCMC analysis.
Author Contributions
Conceptualization, B.T. and K.K.; methodology, B.T., K.K. and S.M.; software, B.T., K.K. and S.M.; validation, B.T., K.K. and S.M.; formal analysis, A.A. and S.K.; investigation, B.T., K.K. and S.M.; data curation, S.M.; writing—original draft preparation, B.T., K.K., A.A. and S.M.; writing—review and editing, B.T. and S.K.; visualization, K.K. and S.M.; supervision, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No data are associated within this paper.
Acknowledgments
This research was supported by the Grants F-FA-2021-510 from the Uzbekistan Ministry for Innovative Development.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pound, R.V.; Snider, J.L. Effect of Gravity on Nuclear Resonance. Phys. Rev. Lett. 1964, 13, 539–540. [Google Scholar] [CrossRef]
- Einstein, A. Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field. Science 1936, 84, 506–507. [Google Scholar] [CrossRef] [PubMed]
- Clemence, G.M. The Relativity Effect in Planetary Motions. Rev. Mod. Phys. 1947, 19, 361–364. [Google Scholar] [CrossRef]
- Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild Singularity. Phys. Rev. Lett. 1968, 20, 878–880. [Google Scholar] [CrossRef]
- Pal, K.; Pal, K.; Shaikh, R.; Sarkar, T. A rotating modified JNW spacetime as a Kerr black hole mimicker. arXiv 2023, arXiv:2305.07518. [Google Scholar] [CrossRef]
- Patel, V.; Acharya, K.; Bambhaniya, P.; Joshi, P.S. Energy extraction from Janis-Newman-Winicour naked singularity. Phys. Rev. D 2023, 107, 064036. [Google Scholar] [CrossRef]
- Pal, K.; Pal, K.; Roy, P.; Sarkar, T. Regularizing the JNW and JMN naked singularities. Eur. Phys. J. C 2023, 83, 397. [Google Scholar] [CrossRef]
- Chauvineau, B. Lensing by a Fisher-Janis-Newman-Winicour naked singularity: Observational issues related to the existence of caustic bending in the strongly scalarized case. Phys. Rev. D 2022, 105, 024071, Erratum in Phys. Rev. D 2022, 106, 129901. [Google Scholar] [CrossRef]
- Solanki, D.N.; Bambhaniya, P.; Dey, D.; Joshi, P.S.; Pathak, K.N. Shadows and precession of orbits in rotating Janis–Newman–Winicour spacetime. Eur. Phys. J. C 2022, 82, 77. [Google Scholar] [CrossRef]
- Aratore, F.; Bozza, V. Decoding a black hole metric from the interferometric pattern of the relativistic images of a compact source. J. Cosmol. Astropart. Phys. 2021, 10, 054. [Google Scholar] [CrossRef]
- Babar, G.Z.; Atamurotov, F.; Babar, A.Z.; Lim, Y.K. Retrolensing by a spherically symmetric naked singularity. arXiv 2021, arXiv:2104.01340. [Google Scholar]
- Chowdhury, A.; Banerjee, N. Echoes from a singularity. Phys. Rev. D 2020, 102, 124051. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, X. Quantum geometry and effective dynamics of Janis-Newman-Winicour singularities. Phys. Rev. D 2020, 101, 086002. [Google Scholar] [CrossRef]
- Joshi, A.B.; Bambhaniya, P.; Dey, D.; Joshi, P.S. Timelike Geodesics in Naked Singularity and Black Hole Spacetimes II. arXiv 2019, arXiv:1909.08873. [Google Scholar]
- Liu, H.; Zhou, M.; Bambi, C. Distinguishing black holes and naked singularities with iron line spectroscopy. J. Cosmol. Astropart. Phys. 2018, 2018, 044. [Google Scholar] [CrossRef]
- Chakrabarty, H.; Benavides-Gallego, C.A.; Bambi, C.; Modesto, L. Unattainable extended spacetime regions in conformal gravity. J. High Energy Phys. 2018, 2018, 13. [Google Scholar] [CrossRef]
- Karmakar, T.; Sarkar, T. Distinguishing between Kerr and rotating JNW space-times via frame dragging and tidal effects. Gen. Rel. Grav. 2018, 50, 85. [Google Scholar] [CrossRef]
- Ghosh, S.; Sarkar, T.; Bhadra, A. Newtonian analogue of static general relativistic spacetimes: An extension to naked singularities. Phys. Rev. D 2015, 92, 083010. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, R.; Chen, J.; Wang, Y. Geodesic Structure of Janis-Newman-Winicour Space-time. Int. J. Theor. Phys. 2015, 54, 2905–2920. [Google Scholar] [CrossRef]
- Dey, A.; Roy, P.; Sarkar, T. Scalar Radiation in the Background of a Naked Singularity. arXiv 2013, arXiv:1303.6824. [Google Scholar]
- Chowdhury, A.N.; Patil, M.; Malafarina, D.; Joshi, P.S. Circular geodesics and accretion disks in Janis-Newman-Winicour and Gamma metric. Phys. Rev. D 2012, 85, 104031. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S. Acceleration of particles in Janis-Newman-Winicour singularities. Phys. Rev. D 2012, 85, 104014. [Google Scholar] [CrossRef]
- Dey, T.K.; Sen, S. Gravitational lensing by wormholes. Mod. Phys. Lett. A 2008, 23, 953–962. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Y.; Wang, P.; Wu, T.; Wu, H. Gravitational lensing by transparent Janis–Newman–Winicour naked singularities. Eur. Phys. J. C 2024, 84, 584. [Google Scholar] [CrossRef]
- Alvarez, E.; Anero, J. Quantum gravity in JNW spacetime. arXiv 2023, arXiv:2309.14750. [Google Scholar]
- Chen, Y.; Wang, P.; Yang, H. Observations of Orbiting Hot Spots around Naked Singularities. arXiv 2023, arXiv:2309.04157. [Google Scholar] [CrossRef]
- Ghaffarnejad, H.; Faghani, H.R. Particles creation from JNW quantum perturbed black holes by minimally coupled Klein Gordon scalar free fields. J. Cosmol. Astropart. Phys. 2023, 11, 10. [Google Scholar] [CrossRef]
- Izmailov, R.N.; Karimov, R.K.; Potapov, A.A.; Nandi, K.K. Vacuum Brans-Dicke theory in the Jordan and Einstein frames: Can they be distinguished by lensing? Mod. Phys. Lett. A 2020, 35, 2050308. [Google Scholar] [CrossRef]
- Nandi, K.K.; Bhattacharjee, B.; Alam, S.M.K.; Evans, J. Brans-Dicke wormholes in the Jordan and Einstein frames. Phys. Rev. D 1998, 57, 823–828. [Google Scholar] [CrossRef]
- Nandi, K.K.; Zhang, Y.Z. Traversable Lorentzian wormholes in the vacuum low energy effective string theory in Einstein and Jordan frames. Phys. Rev. D 2004, 70, 044040. [Google Scholar] [CrossRef]
- Liao, P.; Chen, J.; Huang, H.; Wang, Y. Absorption and scattering of scalar wave by naked singularity. Gen. Rel. Grav. 2014, 46, 1752. [Google Scholar] [CrossRef]
- Babar, G.Z.; Babar, A.Z.; Lim, Y.K. Periodic orbits around a spherically symmetric naked singularity. Phys. Rev. D 2017, 96, 084052. [Google Scholar] [CrossRef]
- Jusufi, K.; Banerjee, A.; Gyulchev, G.; Amir, M. Distinguishing rotating naked singularities from Kerr-like wormholes by their deflection angles of massive particles. Eur. Phys. J. C 2019, 79, 28. [Google Scholar] [CrossRef]
- Virbhadra, K.S. Janis-Newman-Winicour and Wyman solutions are the same. Int. J. Mod. Phys. A 1997, 12, 4831–4836. [Google Scholar] [CrossRef]
- Deng, X.M. Periodic orbits around brane-world black holes. Eur. Phys. J. C 2020, 80, 489. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Rational orbits around 4 Einstein–Lovelock black holes. Phys. Dark Universe 2021, 31, 100745. [Google Scholar] [CrossRef]
- Gao, B.; Deng, X.M. Dynamics of charged test particles around quantum-corrected Schwarzschild black holes. Eur. Phys. J. C 2021, 81, 983. [Google Scholar] [CrossRef]
- Gao, B.; Deng, X.M. Bound orbits around modified Hayward black holes. Mod. Phys. Lett. A 2021, 36, 2150237. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Precessing and periodic orbits around Lee–Wick black holes. Eur. Phys. J. Plus 2022, 137, 176. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Bound Orbits and Epicyclic Motions around Renormalization Group Improved Schwarzschild Black Holes. Universe 2022, 8, 278. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Precessing and periodic orbits around hairy black holes in Horndeski’s Theory. Eur. Phys. J. C 2023, 83, 311. [Google Scholar] [CrossRef]
- Lin, H.Y.; Deng, X.M. Dynamics of test particles around hairy black holes in Horndeski’s theory. Ann. Phys. 2023, 455, 169360. [Google Scholar] [CrossRef]
- Huang, L.; Deng, X.M. Can a particle’s motion distinguish scale-dependent Planck stars from renormalization group improved Schwarzschild black holes? Phys. Rev. D 2024, 109, 124005. [Google Scholar] [CrossRef]
- Huang, L.; Deng, X.M. On the (un)testability of the general free scalar–tensor gravity for the Solar System tests. Eur. Phys. J. C 2024, 84, 615. [Google Scholar] [CrossRef]
- Papapetrou, A. Eine Theorie des Gravitationsfeldes mit einer Feldfunktion. Z. Phys. 1954, 139, 518–532. [Google Scholar] [CrossRef]
- Turimov, B.; Turaev, Y.; Ahmedov, B.; Stuchlík, Z. Circular motion of test particles around wormhole represented by exponential metric. Phys. Dark Universe 2022, 35, 100946. [Google Scholar] [CrossRef]
- Zipoy, D.M. Topology of Some Spheroidal Metrics. J. Math. Phys. 1966, 7, 1137–1143. [Google Scholar] [CrossRef]
- Voorhees, B.H. Static Axially Symmetric Gravitational Fields. Phys. Rev. D 1970, 2, 2119–2122. [Google Scholar] [CrossRef]
- Turimov, B.; Ahmedov, B. Observable Properties of Thin Accretion Disk in the γ Spacetime. Symmetry 2023, 15, 1858. [Google Scholar] [CrossRef]
- Bisnovatyi-Kogan, G.S.; Tsupko, O.Y. Gravitational lensing in a non-uniform plasma. Mon. Not. R. Astron. Soc. 2010, 404, 1790–1800. [Google Scholar] [CrossRef]
- Turimov, B.; Rahimov, O. The Orbital and Epicyclic Frequencies in Axially Symmetric and Stationary Spacetime. Universe 2022, 8, 507. [Google Scholar] [CrossRef]
- Ghez, A.M.; Salim, S.; Weinberg, N.N.; Lu, J.R.; Do, T.; Dunn, J.K.; Matthews, K.; Morris, M.R.; Yelda, S.; Becklin, E.E.; et al. Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits. Astrophys. J. 2008, 689, 1044–1062. [Google Scholar] [CrossRef]
- Stuchlík, Z.; Kološ, M. Mass of intermediate black hole in the source M82 X-1 restricted by models of twin high-frequency quasi-periodic oscillations. Mon. Not. R. Astron. Soc. 2015, 451, 2575–2588. [Google Scholar] [CrossRef]
- Strohmayer, T.E. Discovery of a 450 HZ Quasi-periodic Oscillation from the Microquasar GRO J1655-40 with the Rossi X-Ray Timing Explorer. Astrophys. J. 2001, 552, L49–L53. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306. [Google Scholar] [CrossRef]
- Mitra, S.; Vrba, J.; Rayimbaev, J.; Stuchlik, Z.; Ahmedov, B. Charged particles and quasiperiodic oscillations in Black–bounce–Reissner–Nordström geometry in braneworlds. Phys. Dark Universe 2024, 46, 101561. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).