A Lepton–Hadron Model for the Multi-Wavelength Emission from Extreme High-Frequency Peaked BL Lacertae 1ES 1218+304
Abstract
1. Introduction
2. The Model
2.1. SSC Component
2.2. Hadronic Component
3. Application of the Model to 1ES 1218+304
4. Discussion and Conclusions
4.1. Power-Law Proton Distribution
4.2. p →
4.3. The Free-Path of the Photomeson Process
4.4. The Contribution to the Total Spectrum
4.5. Luminosity Estimates
4.6. The Selection of Seed Photons
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Urry, C.M.; Padovani, P. Unified Schemes for Radio-Loud Active Galactic Nuclei. Publ. Astron. Soc. Pac. 1995, 107, 803. [Google Scholar] [CrossRef]
- Scarpa, R.; Falomo, R. Are high polarization quasars and BL Lacertae objects really different? A study of the optical spectral properties. Astron. Astrophys. 1997, 325, 109–123. [Google Scholar]
- Costamante, L.; Ghisellini, G.; Giommi, P.; Tagliaferri, G.; Celotti, A.; Chiaberge, M.; Fossati, G.; Maraschi, L.; Tavecchio, F.; Treves, A.; et al. Extreme synchrotron BL Lac objects. Stretching the blazar sequence. Astron. Astrophys. 2001, 371, 512–526. [Google Scholar] [CrossRef]
- Urry, C.M. Multiwavelength properties of blazars. Adv. Space Res. 1998, 21, 89–100. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R. Model for the High-Energy Emission from Blazars. Astrophys. J. 1993, 416, 458. [Google Scholar] [CrossRef]
- Maraschi, L.; Ghisellini, G.; Celotti, A. A Jet Model for the Gamma-Ray–emitting Blazar 3C 279. Astrophys. J. 1992, 397, L5. [Google Scholar] [CrossRef]
- Bloom, S.D.; Marscher, A.P. An Analysis of the Synchrotron Self-Compton Model for the Multi–Wave Band Spectra of Blazars. Astrophys. J. 1996, 461, 657. [Google Scholar] [CrossRef]
- Mastichiadis, A.; Kirk, J.G. Variability in the synchrotron self-Compton model of blazar emission. Astron. Astrophys. 1997, 320, 19–25. [Google Scholar] [CrossRef]
- Dermer, C.D.; Cerruti, M.; Lott, B.; Boisson, C.; Zech, A. Equipartition Gamma-Ray Blazars and the Location of the Gamma-Ray Emission Site in 3C 279. Astrophys. J. 2014, 782, 82. [Google Scholar] [CrossRef]
- Ghisellini, G.; Madau, P. On the origin of the gamma-ray emission in blazars. Mon. Not. R. Astron. Soc. 1996, 280, 67–76. [Google Scholar] [CrossRef]
- Dermer, C.D.; Schlickeiser, R.; Mastichiadis, A. High-energy gamma radiation from extragalactic radio sources. Astron. Astrophys. 1992, 256, L27–L30. [Google Scholar]
- Sikora, M.; Begelman, M.C.; Rees, M.J. Comptonization of Diffuse Ambient Radiation by a Relativistic Jet: The Source of Gamma Rays from Blazars? Astrophys. J. 1994, 421, 153. [Google Scholar] [CrossRef]
- Błażejowski, M.; Sikora, M.; Moderski, R.; Madejski, G.M. Comptonization of Infrared Radiation from Hot Dust by Relativistic Jets in Quasars. Astrophys. J. 2000, 545, 107–116. [Google Scholar] [CrossRef]
- Aharonian, F.A. TeV gamma rays from BL Lac objects due to synchrotron radiation of extremely high energy protons. New Astron. 2000, 5, 377–395. [Google Scholar] [CrossRef]
- Mücke, A.; Protheroe, R.J. A proton synchrotron blazar model for flaring in Markarian 501. Astropart. Phys. 2001, 15, 121–136. [Google Scholar] [CrossRef]
- Mannheim, K.; Biermann, P.L. Gamma-ray flaring of 3C 279: A proton-initiated cascade in the jet? Astron. Astrophys. 1992, 253, L21–L24. [Google Scholar]
- Mannheim, K. The proton blazar. Astron. Astrophys. 1993, 269, 67–76. [Google Scholar] [CrossRef]
- Mariotti, M. MAGIC discovers VHE gamma-ray emission from the blazar 1ES 1727+502. Astron. Telegr. 2011, 3774, 1. [Google Scholar]
- Foffano, L.; Prandini, E.; Franceschini, A.; Paiano, S. A new hard X-ray-selected sample of extreme high-energy peaked BL Lac objects and their TeV gamma-ray properties. Mon. Not. R. Astron. Soc. 2019, 486, 1741–1762. [Google Scholar] [CrossRef]
- Tavecchio, F.; Ghisellini, G.; Ghirlanda, G.; Costamante, L.; Franceschini, A. The hard TeV spectrum of 1ES 0229+200: New clues from Swift. Mon. Not. R. Astron. Soc. 2009, 399, L59–L63. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Observations of selected AGN with HESS. Astron. Astrophys. 2005, 441, 465–472. [Google Scholar] [CrossRef]
- Wagner, R.M. Synoptic studies of 17 blazars detected in very high-energy γ-rays. Mon. Not. R. Astron. Soc. 2008, 385, 119–135. [Google Scholar] [CrossRef]
- Gould, R.J.; Schréder, G. Opacity of the Universe to High-Energy Photons. Phys. Rev. Lett. 1966, 16, 252–254. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Fast Variability of Tera-Electron Volt γ Rays from the Radio Galaxy M87. Science 2006, 314, 1424–1427. [Google Scholar] [CrossRef] [PubMed]
- Acciari, V.A.; Aliu, E.; Arlen, T.; Beilicke, M.; Benbow, W.; Böttcher, M.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; Butt, Y.; et al. Veritas Observations of a Very High Energy γ-Ray Flare From the Blazar 3C 66A. Astrophys. J. 2009, 693, L104–L108. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Bazer-Bachi, A.R.; Beilicke, M.; Benbow, W.; Berge, D.; Bernlöhr, K.; Boisson, C.; Bolz, O.; Borrel, V.; et al. Detection of VHE gamma-ray emission from the distant blazar 1ES 1101-232 with HESS and broadband characterisation. Astron. Astrophys. 2007, 470, 475–489. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. New constraints on the mid-IR EBL from the HESS discovery of VHE γ-rays from 1ES 0229+200. Astron. Astrophys. 2007, 475, L9–L13. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.G.; Barres de Almeida, U.; Bazer-Bachi, A.R.; Behera, B.; Beilicke, M.; Benbow, W.; Bernlöhr, K.; Boisson, C.; Bolz, O.; et al. Discovery of VHE γ-rays from the distant BL Lacertae 1ES 0347-121. Astron. Astrophys. 2007, 473, L25–L28. [Google Scholar] [CrossRef]
- Neronov, A.; Semikoz, D.; Taylor, A.M. Very hard gamma-ray emission from a flare of Mrk 501. Astron. Astrophys. 2012, 541, A31. [Google Scholar] [CrossRef]
- Cologna, G.; Mohamed, M.; Wagner, S.; Wierzcholska, A.; Romoli, C.; Kurtanidze, O. Long term lightcurve of the BL Lac object 1ES 0229+200 at TeV energies. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), Hague, The Netherlands, 30 July–6 August 2015; International Cosmic Ray Conference. Volume 34, p. 762. [Google Scholar] [CrossRef][Green Version]
- Cerruti, M.; Zech, A.; Boisson, C.; Inoue, S. A hadronic origin for ultra-high-frequency-peaked BL Lac objects. Mon. Not. R. Astron. Soc. 2015, 448, 910–927. [Google Scholar] [CrossRef]
- Tavecchio, F.; Maraschi, L.; Ghisellini, G. Constraints on the Physical Parameters of TeV Blazars. Astrophys. J. 1998, 509, 608–619. [Google Scholar] [CrossRef]
- Murase, K.; Dermer, C.D.; Takami, H.; Migliori, G. Blazars as Ultra-high-energy Cosmic-ray Sources: Implications for TeV Gamma-Ray Observations. Astrophys. J. 2012, 749, 63. [Google Scholar] [CrossRef]
- Lefa, E.; Rieger, F.M.; Aharonian, F. Formation of Very Hard Gamma-Ray Spectra of Blazars in Leptonic Models. Astrophys. J. 2011, 740, 64. [Google Scholar] [CrossRef]
- Simet, M.; Hooper, D.; Serpico, P.D. Milky Way as a kiloparsec-scale axionscope. Phys. Rev. D 2008, 77, 063001. [Google Scholar] [CrossRef]
- Protheroe, R.J.; Meyer, H. An infrared background-TeV gamma-ray crisis? Phys. Lett. B 2000, 493, 1–6. [Google Scholar] [CrossRef]
- Essey, W.; Kusenko, A. A new interpretation of the gamma-ray observations of distant active galactic nuclei. Astropart. Phys. 2010, 33, 81–85. [Google Scholar] [CrossRef]
- Essey, W.; Kalashev, O.E.; Kusenko, A.; Beacom, J.F. Secondary Photons and Neutrinos from Cosmic Rays Produced by Distant Blazars. Phys. Rev. Lett. 2010, 104, 141102. [Google Scholar] [CrossRef]
- Essey, W.; Kalashev, O.; Kusenko, A.; Beacom, J.F. Role of Line-of-sight Cosmic-ray Interactions in Forming the Spectra of Distant Blazars in TeV Gamma Rays and High-energy Neutrinos. Astrophys. J. 2011, 731, 51. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Kang, T. Evidence for Secondary Emission as the Origin of Hard Spectra in TeV Blazars. Astrophys. J. 2013, 764, 113. [Google Scholar] [CrossRef]
- Dong, Q.; Zheng, Y.G.; Yang, C.Y. Two components model for TeV γ -ray emission from extreme high-energy BL Lac objects. Astrophys. Space Sci. 2021, 366, 36. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Yang, C.Y.; Kang, S.J. Bethe-Heitler cascades as a plausible origin of hard spectra in distant TeV blazars. Astron. Astrophys. 2016, 585, A8. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A. Energy spectra of gamma rays, electrons, and neutrinos produced at interactions of relativistic protons with low energy radiation. Phys. Rev. D 2008, 78, 034013. [Google Scholar] [CrossRef]
- Katarzyński, K.; Sol, H.; Kus, A. The multifrequency emission of Mrk 501. From radio to TeV gamma-rays. Astron. Astrophys. 2001, 367, 809–825. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Zhang, L. Rapid TeV Flaring in Markarian 501. Astrophys. J. 2011, 728, 105. [Google Scholar] [CrossRef]
- Mandolesi, N. Book Review: The galactic and extragalactic background radiation (IAU symposium 139)/Kluwer, 1990. Space Sci. Rev. 1992, 61, 426. [Google Scholar]
- Ackermann, M.; Ajello, M.; Allafort, A.; Schady, P.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Blandford, R.D.; et al. The Imprint of the Extragalactic Background Light in the Gamma-Ray Spectra of Blazars. Science 2012, 338, 1190. [Google Scholar] [CrossRef] [PubMed]
- H. E. S. S. Collaboration; Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Balenderan, S.; Balzer, A.; Barnacka, A.; Becherini, Y.; et al. Measurement of the extragalactic background light imprint on the spectra of the brightest blazars observed with H.E.S.S. Astron. Astrophys. 2013, 550, A4. [Google Scholar] [CrossRef]
- Dwek, E.; Krennrich, F. The extragalactic background light and the gamma-ray opacity of the universe. Astropart. Phys. 2013, 43, 112–133. [Google Scholar] [CrossRef]
- Sanchez, D.A.; Fegan, S.; Giebels, B. Evidence for a cosmological effect in γ-ray spectra of BL Lacertae. Astron. Astrophys. 2013, 554, A75. [Google Scholar] [CrossRef]
- Dwek, E.; Krennrich, F. Simultaneous Constraints on the Spectrum of the Extragalactic Background Light and the Intrinsic TeV Spectra of Markarian 421, Markarian 501, and H1426+428. Astrophys. J. 2005, 618, 657–674. [Google Scholar] [CrossRef]
- Mücke, A.; Engel, R.; Rachen, J.P.; Protheroe, R.J.; Stanev, T. Monte Carlo simulations of photohadronic processes in astrophysics. Comput. Phys. Commun. 2000, 124, 290–314. [Google Scholar] [CrossRef]
- Bade, N.; Beckmann, V.; Douglas, N.G.; Barthel, P.D.; Engels, D.; Cordis, L.; Nass, P.; Voges, W. On the evolutionary behaviour of BL Lac objects. Astron. Astrophys. 1998, 334, 459–472. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antoranz, P.; Armada, A.; Asensio, M.; Baixeras, C.; Barrio, J.A.; Bartel, M.; Bartko, H.; et al. MAGIC Observations of Very High Energy γ-Rays from HESS J1813-178. Astrophys. J. 2006, 637, L41–L44. [Google Scholar] [CrossRef]
- Acciari, V.A.; Aliu, E.; Arlen, T.; Beilicke, M.; Benbow, W.; Bradbury, S.M.; Buckley, J.H.; Bugaev, V.; Butt, Y.; Byrum, K.L.; et al. VERITAS Observations of the BL Lac Object 1ES 1218+304. Astrophys. J. 2009, 695, 1370–1375. [Google Scholar] [CrossRef]
- Nolan, P.L.; Abdo, A.A.; Ackermann, M.; Ajello, M.; Allafort, A.; Antolini, E.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; et al. Fermi Large Area Telescope Second Source Catalog. Astrophys. J. Suppl. Ser. 2012, 199, 31. [Google Scholar] [CrossRef]
- Acero, F.; Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; et al. Fermi Large Area Telescope Third Source Catalog. Astrophys. J. Suppl. Ser. 2015, 218, 23. [Google Scholar] [CrossRef]
- Ajello, M.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bellazzini, R.; Bissaldi, E.; Blandford, R.D.; Bloom, E.D.; et al. 3FHL: The Third Catalog of Hard Fermi-LAT Sources. Astrophys. J. Suppl. Ser. 2017, 232, 18. [Google Scholar] [CrossRef]
- Sahakyan, N. Broad-band study of high-synchrotron-peaked BL Lac object 1ES 1218+304. Mon. Not. R. Astron. Soc. 2020, 496, 5518–5527. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. Astron. J. 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Giommi, P.; Polenta, G.; Lähteenmäki, A.; Thompson, D.J.; Capalbi, M.; Cutini, S.; Gasparrini, D.; González-Nuevo, J.; León-Tavares, J.; López-Caniego, M.; et al. Simultaneous Planck, Swift, and Fermi observations of X-ray and γ-ray selected blazars. Astron. Astrophys. 2012, 541, A160. [Google Scholar] [CrossRef]
- D’Elia, V.; Perri, M.; Puccetti, S.; Capalbi, M.; Giommi, P.; Burrows, D.N.; Campana, S.; Tagliaferri, G.; Cusumano, G.; Evans, P.; et al. VizieR Online Data Catalog: 7 year Swift-XRT point source catalog (1SWXRT) (D’Elia+, 2013). Vizier Online Data Cat. 2013, J/A+A/551/A142. [Google Scholar] [CrossRef]
- Oh, K.; Koss, M.; Markwardt, C.B.; Schawinski, K.; Baumgartner, W.H.; Barthelmy, S.D.; Cenko, S.B.; Gehrels, N.; Mushotzky, R.; Petulante, A.; et al. The 105-Month Swift-BAT All-sky Hard X-Ray Survey. Astrophys. J. Suppl. Ser. 2018, 235, 4. [Google Scholar] [CrossRef]
- Liodakis, I.; Hovatta, T.; Huppenkothen, D.; Kiehlmann, S.; Max-Moerbeck, W.; Readhead, A.C.S. Constraining the Limiting Brightness Temperature and Doppler Factors for the Largest Sample of Radio-bright Blazars. Astrophys. J. 2018, 866, 137. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Long, G.B.; Yang, C.Y.; Bai, J.M. Verification of the diffusive shock acceleration in Mrk 501. Mon. Not. R. Astron. Soc. 2018, 478, 3855–3861. [Google Scholar] [CrossRef]
- Zheng, Y.G.; Long, G.B.; Yang, C.Y.; Bai, J.M. Formation of the Electronic Spectrum in Relativistic Jets of Gamma-Ray Blazars. Publ. Astron. Soc. Pac. 2018, 130, 083001. [Google Scholar] [CrossRef]
- Kirk, J.G.; Dendy, R.O. Shock acceleration of cosmic rays - a critical review. J. Phys. G Nucl. Phys. 2001, 27, 1589–1595. [Google Scholar] [CrossRef][Green Version]
- Romero, G.E.; Torres, D.F.; Kaufman Bernadó, M.M.; Mirabel, I.F. Hadronic gamma-ray emission from windy microquasars. Astron. Astrophys. 2003, 410, L1–L4. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Allafort, A.; Baldini, L.; Ballet, J.; Barbiellini, G.; Baring, M.G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. Detection of the Characteristic Pion-Decay Signature in Supernova Remnants. Science 2013, 339, 807–811. [Google Scholar] [CrossRef]
- Padovani, P.; Resconi, E. Are both BL Lacs and pulsar wind nebulae the astrophysical counterparts of IceCube neutrino events? Mon. Not. R. Astron. Soc. 2014, 443, 474–484. [Google Scholar] [CrossRef]
- Begelman, M.C.; Rudak, B.; Sikora, M. Consequences of Relativistic Proton Injection in Active Galactic Nuclei. Astrophys. J. 1990, 362, 38. [Google Scholar] [CrossRef]
- Petropoulou, M.; Mastichiadis, A. Bethe-Heitler emission in BL Lacs: Filling the gap between X-rays and γ-rays. Mon. Not. R. Astron. Soc. 2015, 447, 36–48. [Google Scholar] [CrossRef]
- Stecker, F.W. Effect of Photomeson Production by the Universal Radiation Field on High-Energy Cosmic Rays. Phys. Rev. Lett. 1968, 21, 1016–1018. [Google Scholar] [CrossRef]
- Mücke, A.; Rachen, J.P.; Engel, R.; Protheroe, R.J.; Stanev, T. Photohadronic Processes in Astrophysical Environments. Publ. Astron. Soc. Aust. 1999, 16, 160–166. [Google Scholar] [CrossRef]
- Sikora, M.; Stawarz, Ł.; Moderski, R.; Nalewajko, K.; Madejski, G.M. Constraining Emission Models of Luminous Blazar Sources. Astrophys. J. 2009, 704, 38–50. [Google Scholar] [CrossRef]
- Singh, K.K.; Bisschoff, B.; van Soelen, B.; Tolamatti, A.; Marais, J.P.; Meintjes, P.J. Long-term multiwavelength view of the blazar 1ES 1218+304. Mon. Not. R. Astron. Soc. 2019, 489, 5076–5086. [Google Scholar] [CrossRef]
- Celotti, A.; Ghisellini, G. The power of blazar jets. Mon. Not. R. Astron. Soc. 2008, 385, 283–300. [Google Scholar] [CrossRef]
- Ghisellini, G.; Tavecchio, F.; Foschini, L.; Ghirlanda, G.; Maraschi, L.; Celotti, A. General physical properties of bright Fermi blazars. Mon. Not. R. Astron. Soc. 2010, 402, 497–518. [Google Scholar] [CrossRef]
- Zhang, J.; Liang, E.W.; Zhang, S.N.; Bai, J.M. Radiation Mechanisms and Physical Properties of GeV-TeV BL Lac Objects. Astrophys. J. 2012, 752, 157. [Google Scholar] [CrossRef]
- Yan, D.; Zeng, H.; Zhang, L. The physical properties of Fermi BL Lac objects jets. Mon. Not. R. Astron. Soc. 2014, 439, 2933–2942. [Google Scholar] [CrossRef]
- Ding, N.; Zhang, X.; Xiong, D.R.; Zhang, H.J. The physical properties of Fermi TeV BL Lac objects’ jets. Mon. Not. R. Astron. Soc. 2017, 464, 599–612. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Q.; Fan, J.; Yu, X.; Zhong, X.; Liu, H.; Ding, N.; Xiong, D.; Guo, X. General Physical Properties of Fermi Blazars. Astrophys. J. Suppl. Ser. 2023, 268, 6. [Google Scholar] [CrossRef]
- Diwan, R.; Prince, R.; Agarwal, A.; Bose, D.; Majumdar, P.; Özdönmez, A.; Chandra, S.; Khatoon, R.; Ege, E. Multiwavelength study of TeV blazar 1ES 1218+304 using gamma-ray, X-ray and optical observations. Mon. Not. R. Astron. Soc. 2023, 524, 4333–4345. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G. The extragalactic background light revisited and the cosmic photon-photon opacity. Astron. Astrophys. 2017, 603, A34. [Google Scholar] [CrossRef]
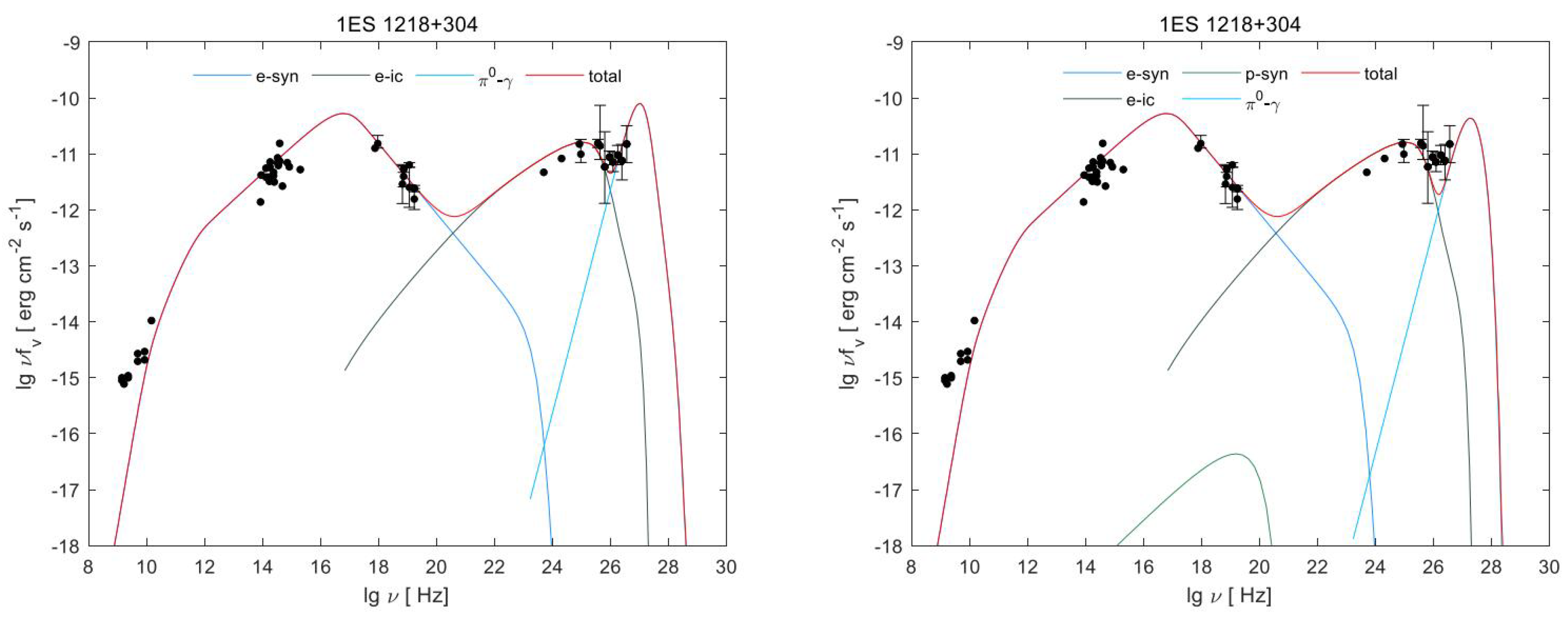
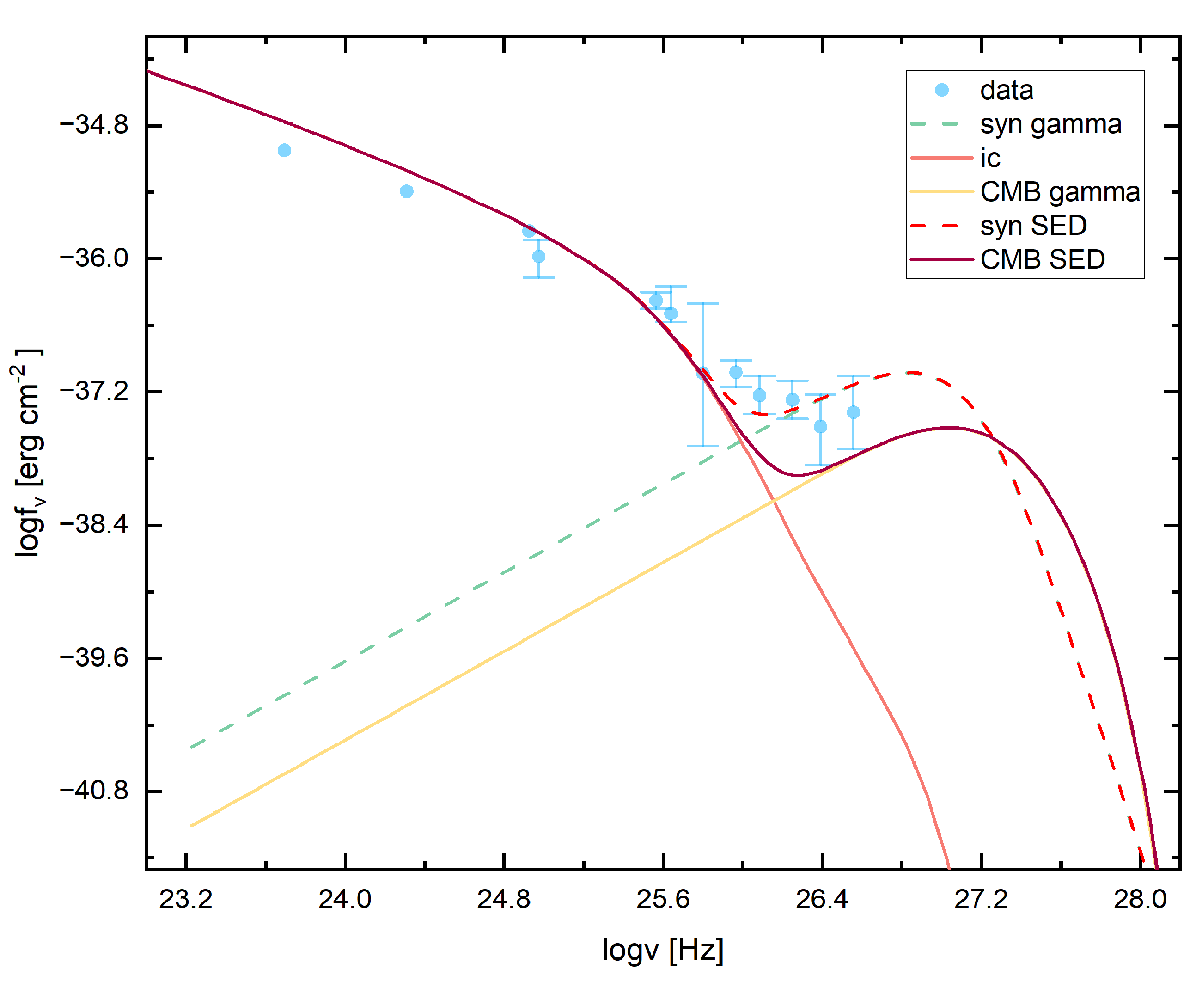
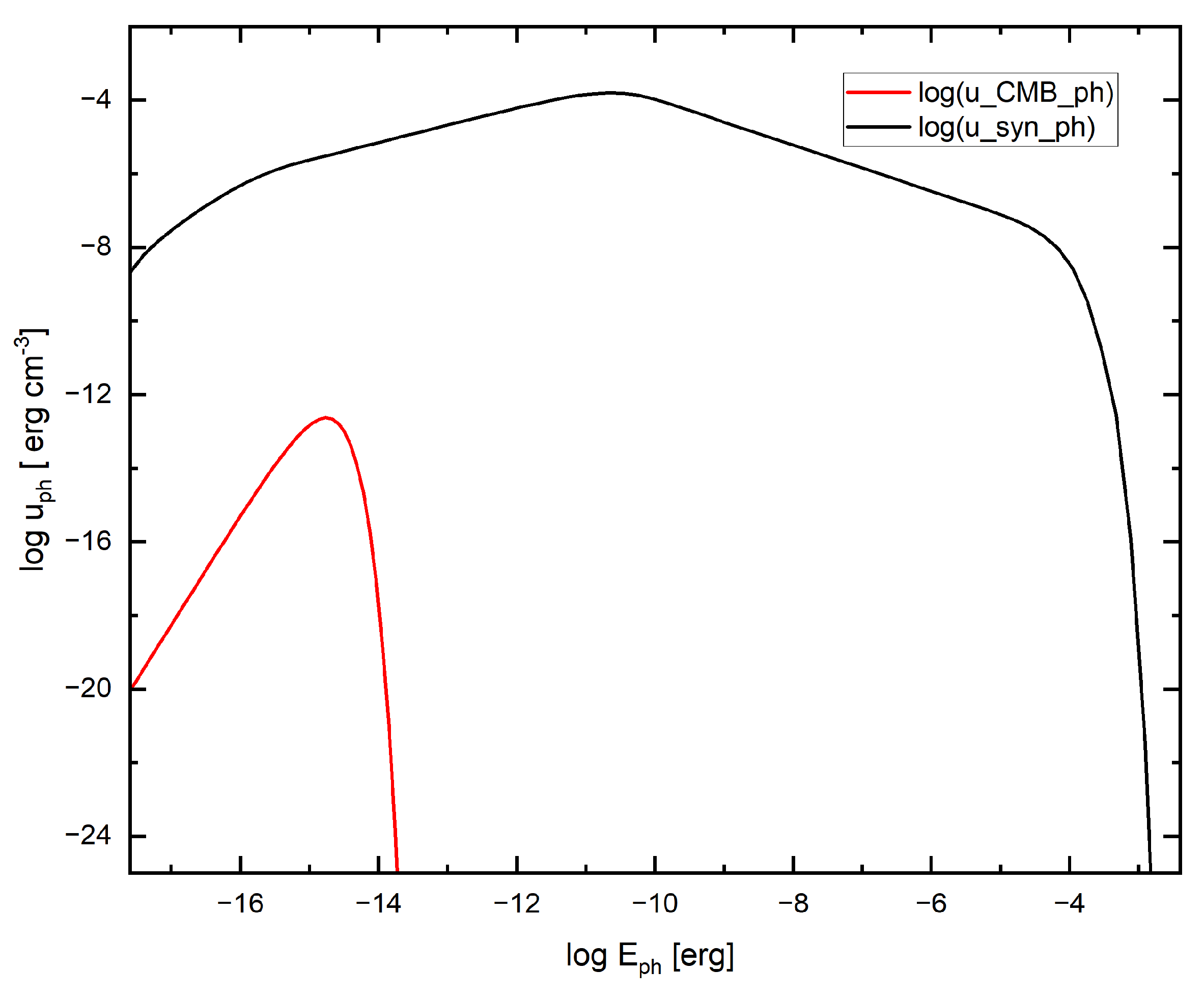
| Parameter | Synchrotron Radiation Soft Photons | CMB Photons |
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, W.; Dong, Q.; Zheng, Y. A Lepton–Hadron Model for the Multi-Wavelength Emission from Extreme High-Frequency Peaked BL Lacertae 1ES 1218+304. Galaxies 2024, 12, 2. https://doi.org/10.3390/galaxies12010002
Dong W, Dong Q, Zheng Y. A Lepton–Hadron Model for the Multi-Wavelength Emission from Extreme High-Frequency Peaked BL Lacertae 1ES 1218+304. Galaxies. 2024; 12(1):2. https://doi.org/10.3390/galaxies12010002
Chicago/Turabian StyleDong, Wenjing, Qian Dong, and Yonggang Zheng. 2024. "A Lepton–Hadron Model for the Multi-Wavelength Emission from Extreme High-Frequency Peaked BL Lacertae 1ES 1218+304" Galaxies 12, no. 1: 2. https://doi.org/10.3390/galaxies12010002
APA StyleDong, W., Dong, Q., & Zheng, Y. (2024). A Lepton–Hadron Model for the Multi-Wavelength Emission from Extreme High-Frequency Peaked BL Lacertae 1ES 1218+304. Galaxies, 12(1), 2. https://doi.org/10.3390/galaxies12010002






