Three Dimensional Natures of Massive Star Envelopes
Abstract
1. Introduction
2. 1D Stellar Evolution Models
2.1. Convective Flux Based on Mixing Length Theory
2.2. Convective Velocities
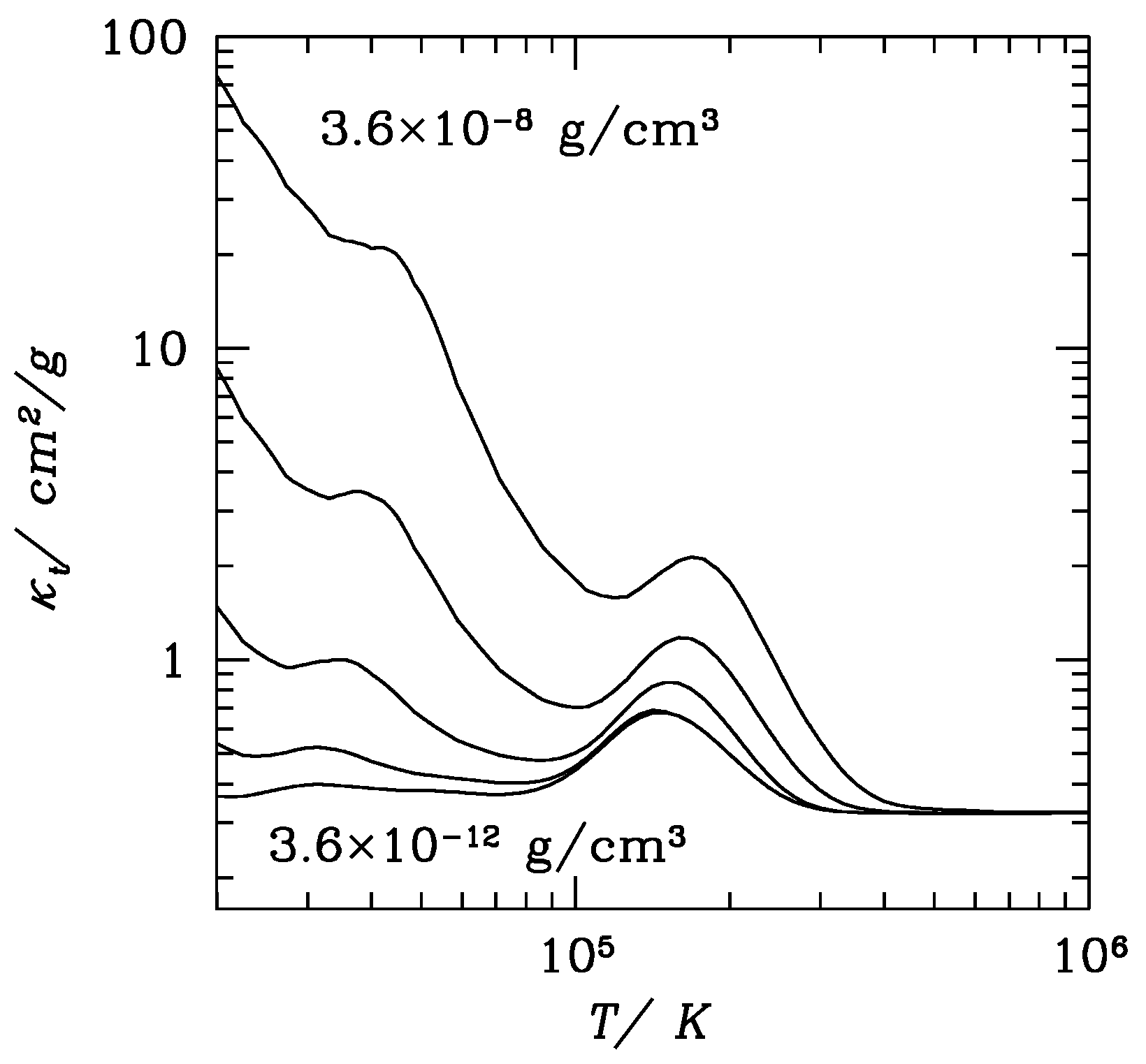
2.3. Typical 1D Models of Massive Star Envelopes
3. Structures of Massive Star Envelopes in 3D
3.1. Numerical Methods
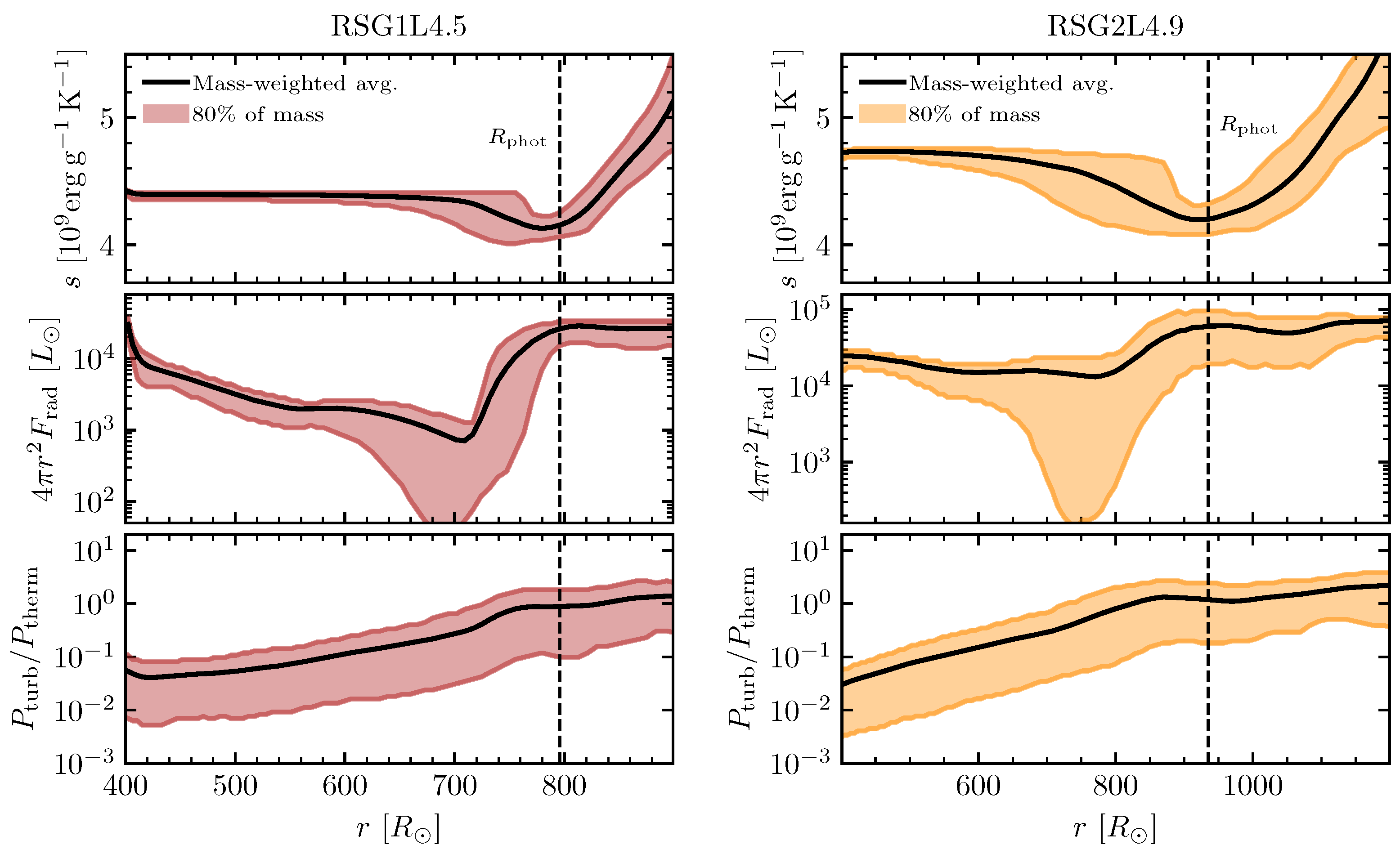
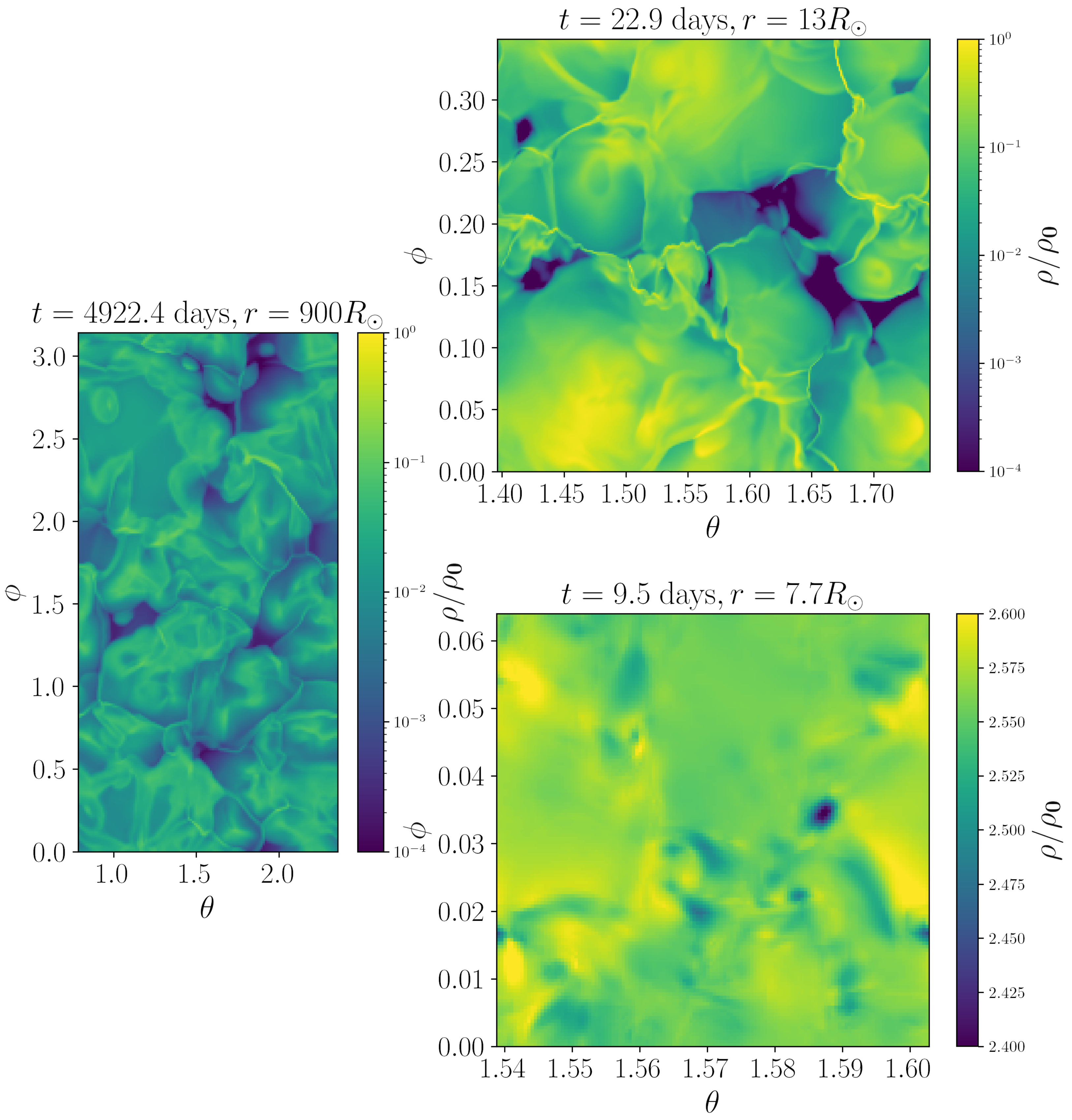
3.2. Convection in 3D
3.3. Turbulent Pressure Support
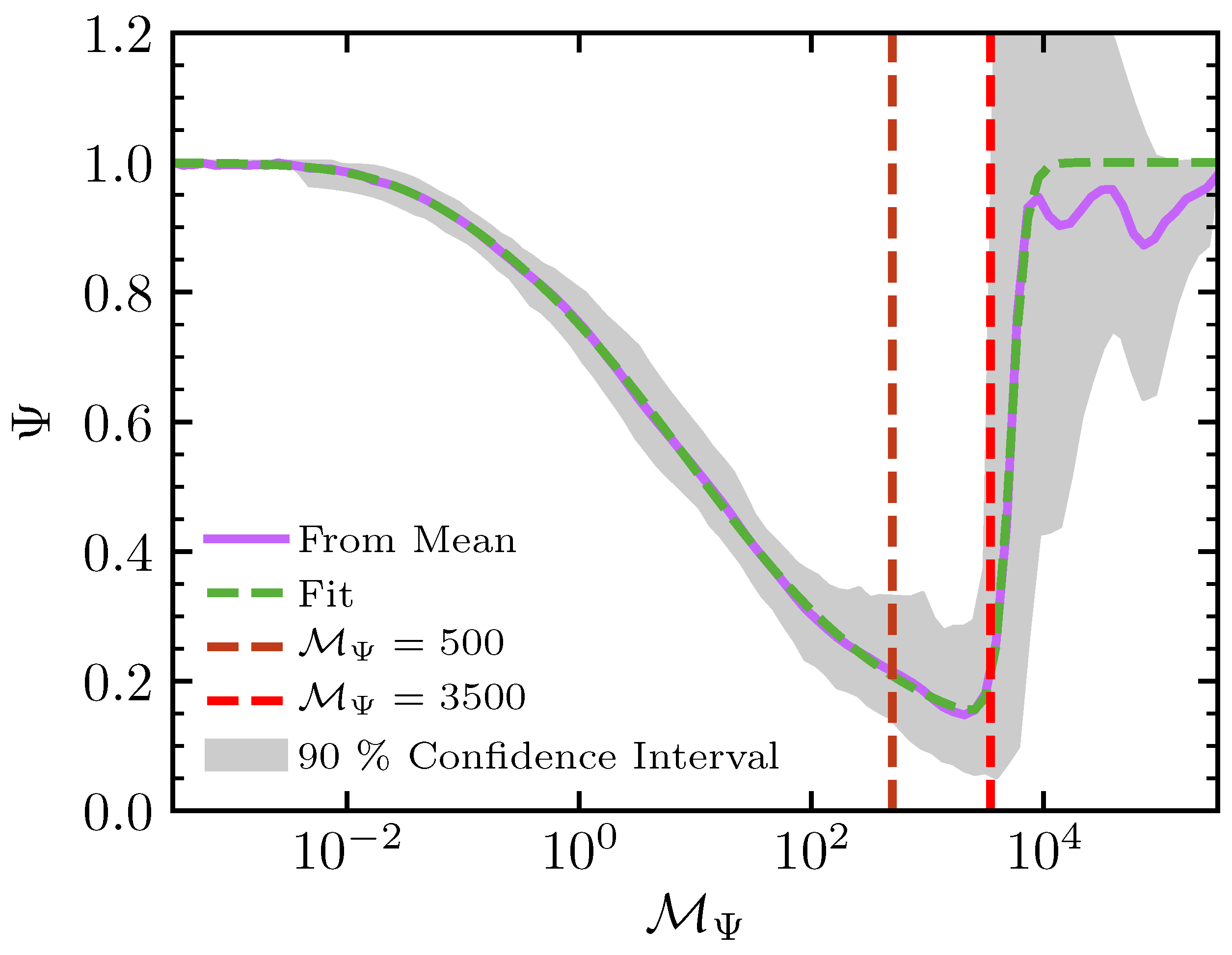
3.4. Porosity
4. Observational Consequences
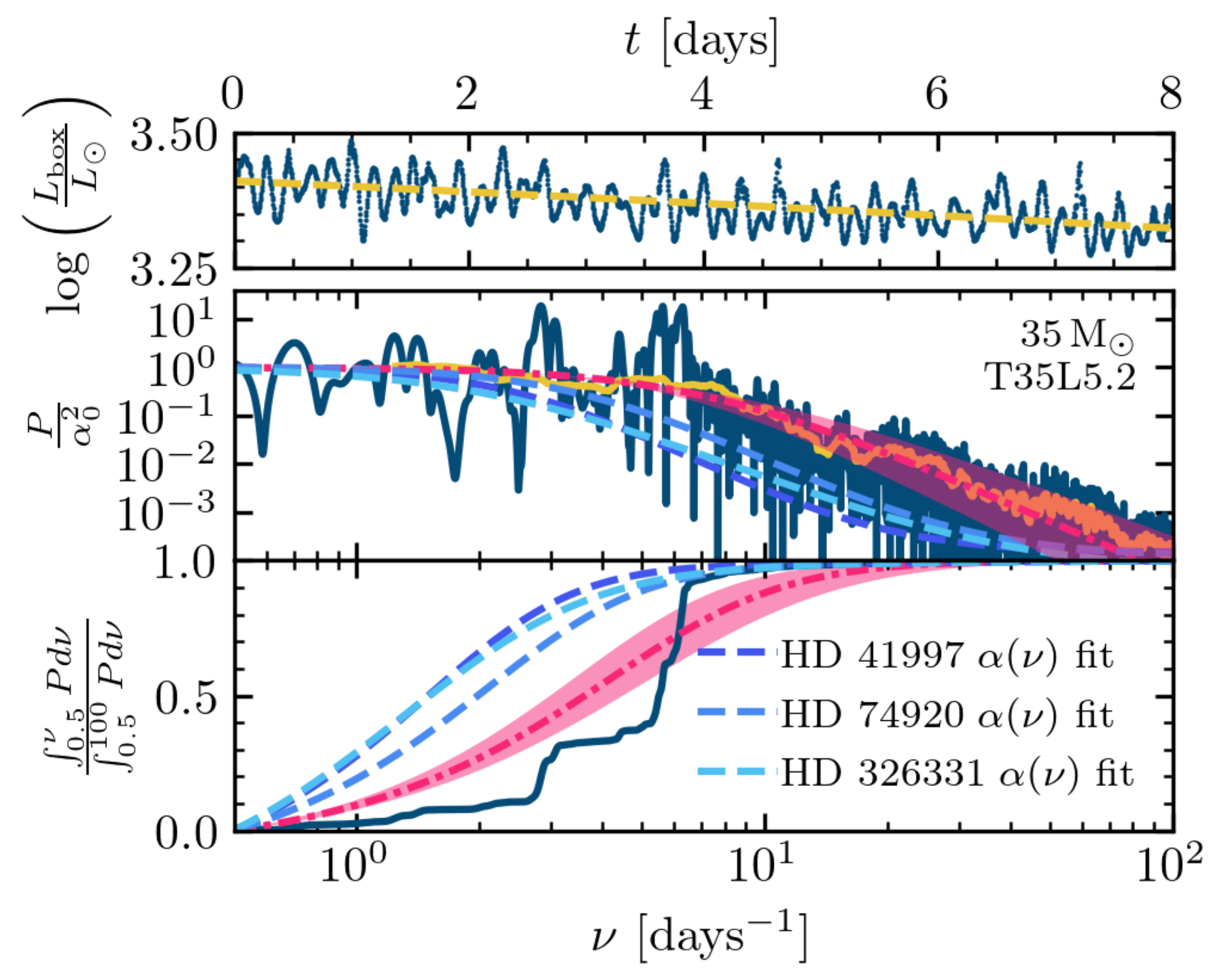
4.1. Impact on Photometric and Spectroscopic Variability
4.2. Impact on Spectroscopic Fitting of Massive Stars
5. Future Directions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schaller, G.; Schaerer, D.; Meynet, G.; Maeder, A. New Grids of Stellar Models from 0.8-SOLAR-MASS to 120-SOLAR-MASSES at Z = 0.020 and Z = 0.001. Astron. Astrophys. Suppl. 1992, 96, 269. [Google Scholar]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. 2011, 192, 3. [Google Scholar] [CrossRef]
- Ekström, S.; Georgy, C.; Eggenberger, P.; Meynet, G.; Mowlavi, N.; Wyttenbach, A.; Granada, A.; Decressin, T.; Hirschi, R.; Frischknecht, U.; et al. Grids of stellar models with rotation. I. Models from 0.8 to 120 M⊙ at solar metallicity (Z = 0.014). Astron. Astrophys. 2012, 537, A146. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. 2013, 208, 4. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. 2015, 220, 15. [Google Scholar] [CrossRef]
- Choi, J.; Dotter, A.; Conroy, C.; Cantiello, M.; Paxton, B.; Johnson, B.D. Mesa Isochrones and Stellar Tracks (MIST). I. Solar-scaled Models. Astrophys. J. 2016, 823, 102. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. 2018, 234, 34. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. 2019, 243, 10. [Google Scholar] [CrossRef]
- Jermyn, A.S.; Bauer, E.B.; Schwab, J.; Farmer, R.; Ball, W.H.; Bellinger, E.P.; Dotter, A.; Joyce, M.; Marchant, P.; Mombarg, J.S.G.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Time-dependent Convection, Energy Conservation, Automatic Differentiation, and Infrastructure. Astrophys. J. Suppl. 2023, 265, 15. [Google Scholar] [CrossRef]
- Yusof, N.; Hirschi, R.; Meynet, G.; Crowther, P.A.; Ekström, S.; Frischknecht, U.; Georgy, C.; Abu Kassim, H.; Schnurr, O. Evolution and fate of very massive stars. Mon. Not. R. Astron. Soc. 2013, 433, 1114–1132. [Google Scholar] [CrossRef]
- Köhler, K.; Langer, N.; de Koter, A.; de Mink, S.E.; Crowther, P.A.; Evans, C.J.; Gräfener, G.; Sana, H.; Sanyal, D.; Schneider, F.R.N.; et al. The evolution of rotating very massive stars with LMC composition. Astron. Astrophys. 2015, 573, A71. [Google Scholar] [CrossRef]
- Agrawal, P.; Szécsi, D.; Stevenson, S.; Eldridge, J.J.; Hurley, J. Explaining the differences in massive star models from various simulations. Mon. Not. R. Astron. Soc. 2022, 512, 5717–5725. [Google Scholar] [CrossRef]
- Agrawal, P.; Stevenson, S.; Szécsi, D.; Hurley, J. A systematic study of super-Eddington layers in the envelopes of massive stars. Astron. Astrophys. 2022, 668, A90. [Google Scholar] [CrossRef]
- Cantiello, M.; Langer, N.; Brott, I.; de Koter, A.; Shore, S.N.; Vink, J.S.; Voegler, A.; Lennon, D.J.; Yoon, S.C. Sub-surface convection zones in hot massive stars and their observable consequences. Astron. Astrophys. 2009, 499, 279–290. [Google Scholar] [CrossRef]
- Böhm-Vitense, E. Über die Wasserstoffkonvektionszone in Sternen verschiedener Effektivtemperaturen und Leuchtkräfte. Mit 5 Textabbildungen. Z. Fuer Astrophys. 1958, 46, 108. [Google Scholar]
- Joyce, M.; Tayar, J. A Review of the Mixing Length Theory of Convection in 1D Stellar Modeling. Galaxies 2023, 11, 75. [Google Scholar] [CrossRef]
- Henyey, L.; Vardya, M.S.; Bodenheimer, P. Studies in Stellar Evolution. III. The Calculation of Model Envelopes. Astrophys. J. 1965, 142, 841–854. [Google Scholar] [CrossRef]
- Kiriakidis, M.; Fricke, K.J.; Glatzel, W. The Stability of Massive Stars and its Dependence on Metallicity and Opacity. Mon. Not. R. Astron. Soc. 1993, 264, 50–62. [Google Scholar] [CrossRef][Green Version]
- Blaes, O.; Socrates, A. Local Radiative Hydrodynamic and Magnetohydrodynamic Instabilities in Optically Thick Media. Astrophys. J. 2003, 596, 509–537. [Google Scholar] [CrossRef]
- Glatzel, W.; Kiriakidis, M. Stability of Massive Stars and the Humphreys/Davidson Limit. Mon. Not. R. Astron. Soc. 1993, 263, 375–384. [Google Scholar] [CrossRef]
- Owocki, S.P. Instabilities in the Envelopes and Winds of Very Massive Stars. In Very Massive Stars in the Local Universe; Vink, J.S., Ed.; Astrophysics and Space Science Library; Springer: Cham, Switzerland, 2015; Volume 412, p. 113. [Google Scholar] [CrossRef]
- Sobolev, V.V. Moving Envelopes of Stars; Harvard University Press: Cambridge, MA, USA, 1960. [Google Scholar] [CrossRef]
- Vink, J.S. Theory and Diagnostics of Hot Star Mass Loss. Annu. Rev. Astron Astrophys. 2022, 60, 203–246. [Google Scholar] [CrossRef]
- Davidson, K. Radiation-Driven Stellar Eruptions. Galaxies 2020, 8, 10. [Google Scholar] [CrossRef]
- Freytag, B.; Höfner, S. Three-dimensional simulations of the atmosphere of an AGB star. Astron. Astrophys. 2008, 483, 571–583. [Google Scholar] [CrossRef]
- Chiavassa, A.; Collet, R.; Casagrande, L.; Asplund, M. Three-dimensional hydrodynamical simulations of red giant stars: Semi-global models for interpreting interferometric observations. Astron. Astrophys. 2010, 524, A93. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Cantiello, M.; Bildsten, L.; Quataert, E.; Blaes, O. Local Radiation Hydrodynamic Simulations of Massive Star Envelopes at the Iron Opacity Peak. Astrophys. J. 2015, 813, 74. [Google Scholar] [CrossRef]
- Freytag, B.; Liljegren, S.; Höfner, S. Global 3D radiation-hydrodynamics models of AGB stars. Effects of convection and radial pulsations on atmospheric structures. Astron. Astrophys. 2017, 600, A137. [Google Scholar] [CrossRef]
- Chiavassa, A.; Casagrande, L.; Collet, R.; Magic, Z.; Bigot, L.; Thévenin, F.; Asplund, M. The STAGGER-grid: A grid of 3D stellar atmosphere models. V. Synthetic stellar spectra and broad-band photometry. Astron. Astrophys. 2018, 611, A11. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Cantiello, M.; Bildsten, L.; Quataert, E.; Blaes, O. The Effects of Magnetic Fields on the Dynamics of Radiation Pressure-dominated Massive Star Envelopes. Astrophys. J. 2017, 843, 68. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Cantiello, M.; Bildsten, L.; Quataert, E.; Blaes, O.; Stone, J. Outbursts of luminous blue variable stars from variations in the helium opacity. Nature 2018, 561, 498–501. [Google Scholar] [CrossRef]
- Sundqvist, J.O.; Owocki, S.P.; Puls, J. 2D wind clumping in hot, massive stars from hydrodynamical line-driven instability simulations using a pseudo-planar approach. Astron. Astrophys. 2018, 611, A17. [Google Scholar] [CrossRef]
- Schultz, W.C.; Bildsten, L.; Jiang, Y.F. Convectively Driven 3D Turbulence in Massive Star Envelopes. I. A 1D Implementation of Diffusive Radiative Transport. Astrophys. J. 2020, 902, 67. [Google Scholar] [CrossRef]
- Moens, N.; Sundqvist, J.O.; El Mellah, I.; Poniatowski, L.; Teunissen, J.; Keppens, R. Radiation-hydrodynamics with MPI-AMRVAC. Flux-limited diffusion. Astron. Astrophys. 2022, 657, A81. [Google Scholar] [CrossRef]
- Moens, N.; Poniatowski, L.G.; Hennicker, L.; Sundqvist, J.O.; El Mellah, I.; Kee, N.D. First 3D radiation-hydrodynamic simulations of Wolf-Rayet winds. Astron. Astrophys. 2022, 665, A42. [Google Scholar] [CrossRef]
- Goldberg, J.A.; Jiang, Y.F.; Bildsten, L. Numerical Simulations of Convective Three-dimensional Red Supergiant Envelopes. Astrophys. J. 2022, 929, 156. [Google Scholar] [CrossRef]
- Schultz, W.C.; Bildsten, L.; Jiang, Y.F. Turbulence-supported Massive Star Envelopes. Astrophys. J. Lett. 2023, 951, L42. [Google Scholar] [CrossRef]
- Shaviv, N.J. The Eddington Luminosity Limit for Multiphased Media. Astrophys. J. Lett. 1998, 494, L193–L197. [Google Scholar] [CrossRef]
- Shaviv, N.J. The Porous Atmosphere of η Carinae. Astrophys. J. Lett. 2000, 532, L137–L140. [Google Scholar] [CrossRef]
- Owocki, S.P.; Gayley, K.G.; Shaviv, N.J. A Porosity-Length Formalism for Photon-Tiring-limited Mass Loss from Stars above the Eddington Limit. Astrophys. J. 2004, 616, 525–541. [Google Scholar] [CrossRef]
- Owocki, S.P.; Sundqvist, J.O. Characterizing the turbulent porosity of stellar wind structure generated by the line-deshadowing instability. Mon. Not. R. Astron. Soc. 2018, 475, 814–821. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Stone, J.M.; Davis, S.W. A Godunov Method for Multidimensional Radiation Magnetohydrodynamics Based on a Variable Eddington Tensor. Astrophys. J. Suppl. 2012, 199, 14. [Google Scholar] [CrossRef]
- Davis, S.W.; Stone, J.M.; Jiang, Y.F. A Radiation Transfer Solver for Athena Using Short Characteristics. Astrophys. J. Suppl. 2012, 199, 9. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Stone, J.M.; Davis, S.W. An Algorithm for Radiation Magnetohydrodynamics Based on Solving the Time-dependent Transfer Equation. Astrophys. J. Suppl. 2014, 213, 7. [Google Scholar] [CrossRef]
- Tsang, B.T.H.; Milosavljević, M. Radiation pressure driving of a dusty atmosphere. Mon. Not. R. Astron. Soc. 2015, 453, 1108–1120. [Google Scholar] [CrossRef]
- Jiang, Y.F. An Implicit Finite Volume Scheme to Solve the Time-dependent Radiation Transport Equation Based on Discrete Ordinates. Astrophys. J. Suppl. 2021, 253, 49. [Google Scholar] [CrossRef]
- Jiang, Y.F. Multigroup Radiation Magnetohydrodynamics Based on Discrete Ordinates including Compton Scattering. Astrophys. J. Suppl. 2022, 263, 4. [Google Scholar] [CrossRef]
- Menon, S.H.; Federrath, C.; Krumholz, M.R.; Kuiper, R.; Wibking, B.D.; Jung, M. VETTAM: A scheme for radiation hydrodynamics with adaptive mesh refinement using the variable Eddington tensor method. Mon. Not. R. Astron. Soc. 2022, 512, 401–423. [Google Scholar] [CrossRef]
- Sander, A.A.C.; Vink, J.S.; Hamann, W.R. Driving classical Wolf-Rayet winds: A Γ- and Z-dependent mass-loss. Mon. Not. R. Astron. Soc. 2020, 491, 4406–4425. [Google Scholar] [CrossRef]
- Cox, J.P.; Giuli, R.T. Principles of Stellar Structure; Gordon and Breach: New York, USA, 1968. [Google Scholar]
- Cantiello, M.; Lecoanet, D.; Jermyn, A.S.; Grassitelli, L. On the Origin of Stochastic, Low-Frequency Photometric Variability in Massive Stars. Astrophys. J. 2021, 915, 112. [Google Scholar] [CrossRef]
- Joss, P.C.; Salpeter, E.E.; Ostriker, J.P. On the “Critical Luminosity” in Stellar Interiors and Stellar Surface Boundary Conditions. Astrophys. J. 1973, 181, 429–438. [Google Scholar] [CrossRef]
- Alongi, M.; Bertelli, G.; Bressan, A.; Chiosi, C.; Fagotto, F.; Greggio, L.; Nasi, E. Evolutionary sequences of stellar models with semiconvection and convective overshoot. I. Z = 0.008. Astron. Astrophys. Suppl. 1993, 97, 851–871. [Google Scholar]
- Chen, Y.; Bressan, A.; Girardi, L.; Marigo, P.; Kong, X.; Lanza, A. PARSEC evolutionary tracks of massive stars up to 350 M⊙ at metallicities 0.0001 ≤ Z ≤ 0.04. Mon. Not. R. Astron. Soc. 2015, 452, 1068–1080. [Google Scholar] [CrossRef]
- Szécsi, D.; Agrawal, P.; Wünsch, R.; Langer, N. Bonn Optimized Stellar Tracks (BoOST). Simulated populations of massive and very massive stars for astrophysical applications. Astron. Astrophys. 2022, 658, A125. [Google Scholar] [CrossRef]
- Sanyal, D.; Grassitelli, L.; Langer, N.; Bestenlehner, J.M. Massive main-sequence stars evolving at the Eddington limit. Astron. Astrophys. 2015, 580, A20. [Google Scholar] [CrossRef]
- Gräfener, G.; Owocki, S.P.; Vink, J.S. Stellar envelope inflation near the Eddington limit. Implications for the radii of Wolf-Rayet stars and luminous blue variables. Astron. Astrophys. 2012, 538, A40. [Google Scholar] [CrossRef]
- Mihalas, D.; Klein, R.I. On the solution of the time-dependent inertial-frame equation of radiative transfer in moving media to O(v/c). J. Comput. Phys. 1982, 46, 97–137. [Google Scholar] [CrossRef]
- Lowrie, R.B.; Morel, J.E.; Hittinger, J.A. The Coupling of Radiation and Hydrodynamics. Astrophys. J. 1999, 521, 432–450. [Google Scholar] [CrossRef]
- Hillier, D.J.; Miller, D.L. The Treatment of Non-LTE Line Blanketing in Spherically Expanding Outflows. Astrophys. J. 1998, 496, 407–427. [Google Scholar] [CrossRef]
- Puls, J.; Najarro, F.; Sundqvist, J.O.; Sen, K. Atmospheric NLTE models for the spectroscopic analysis of blue stars with winds. V. Complete comoving frame transfer, and updated modeling of X-ray emission. Astron. Astrophys. 2020, 642, A172. [Google Scholar] [CrossRef]
- Chiavassa, A.; Freytag, B.; Masseron, T.; Plez, B. Radiative hydrodynamics simulations of red supergiant stars. IV. Gray versus non-gray opacities. Astron. Astrophys. 2011, 535, A22. [Google Scholar] [CrossRef]
- Stein, R.F.; Nordlund, Å. Simulations of Solar Granulation. I. General Properties. Astrophys. J. 1998, 499, 914–933. [Google Scholar] [CrossRef]
- Freytag, B.; Ludwig, H.G.; Steffen, M. Hydrodynamical models of stellar convection. The role of overshoot in DA white dwarfs, A-type stars, and the Sun. Astron. Astrophys. 1996, 313, 497–516. [Google Scholar]
- Steffen, M.; Freytag, B.; Ludwig, H.G. 3D simulation of convection and spectral line formation in A-type stars. In Proceedings of the 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, Hamburg, Germany, 5–9 July 2004; Favata, F., Hussain, G.A.J., Battrick, B., Eds.; ESA Special Publication: Hamburg, Germany, 2005; Volume 560, p. 985. [Google Scholar] [CrossRef]
- Trampedach, R.; Stein, R.F.; Christensen-Dalsgaard, J.; Nordlund, Å.; Asplund, M. Improvements to stellar structure models, based on a grid of 3D convection simulations - II. Calibrating the mixing-length formulation. Mon. Not. R. Astron. Soc. 2014, 445, 4366–4384. [Google Scholar] [CrossRef]
- De Jager, C. The Brightest Stars; D. Reidel Publishing Company: Moscow, Russia, 1984. [Google Scholar]
- Schultz, W.C.; Bildsten, L.; Jiang, Y.F. Stochastic Low-frequency Variability in Three-dimensional Radiation Hydrodynamical Models of Massive Star Envelopes. Astrophys. J. Lett. 2022, 924, L11. [Google Scholar] [CrossRef]
- Grassitelli, L.; Langer, N.; Mackey, J.; Gräfener, G.; Grin, N.J.; Sander, A.A.C.; Vink, J.S. Wind-envelope interaction as the origin of the slow cyclic brightness variations of luminous blue variables. Astron. Astrophys. 2021, 647, A99. [Google Scholar] [CrossRef]
- Oskinova, L.M.; Feldmeier, A.; Hamann, W.R. X-ray emission lines from inhomogeneous stellar winds. Astron. Astrophys. 2004, 422, 675–691. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Latham, D.W.; Bakos, G.Á.; Bean, J.L.; Berta-Thompson, Z.K.; Brown, T.M.; Buchhave, L.; Butler, N.R.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Bowman, D.M.; Burssens, S.; Simón-Díaz, S.; Edelmann, P.V.F.; Rogers, T.M.; Horst, L.; Röpke, F.K.; Aerts, C. Photometric detection of internal gravity waves in upper main-sequence stars. II. Combined TESS photometry and high-resolution spectroscopy. Astron. Astrophys. 2020, 640, A36. [Google Scholar] [CrossRef]
- Bowman, D.M.; Burssens, S.; Pedersen, M.G.; Johnston, C.; Aerts, C.; Buysschaert, B.; Michielsen, M.; Tkachenko, A.; Rogers, T.M.; Edelmann, P.V.F.; et al. Low-frequency gravity waves in blue supergiants revealed by high-precision space photometry. Nat. Astron. 2019, 3, 760–765. [Google Scholar] [CrossRef]
- Bowman, D.M. Asteroseismology of high-mass stars: New insights of stellar interiors with space telescopes. Front. Astron. Space Sci. 2020, 7, 70. [Google Scholar] [CrossRef]
- Aerts, C.; Rogers, T.M. Observational Signatures of Convectively Driven Waves in Massive Stars. Astrophys. J. Lett. 2015, 806, L33. [Google Scholar] [CrossRef]
- Bowman, D.M.; Aerts, C.; Johnston, C.; Pedersen, M.G.; Rogers, T.M.; Edelmann, P.V.F.; Simón-Díaz, S.; Van Reeth, T.; Buysschaert, B.; Tkachenko, A.; et al. Photometric detection of internal gravity waves in upper main-sequence stars. I. Methodology and application to CoRoT targets. Astron. Astrophys. 2019, 621, A135. [Google Scholar] [CrossRef]
- Edelmann, P.V.F.; Ratnasingam, R.P.; Pedersen, M.G.; Bowman, D.M.; Prat, V.; Rogers, T.M. Three-dimensional Simulations of Massive Stars. I. Wave Generation and Propagation. Astrophys. J. 2019, 876, 4. [Google Scholar] [CrossRef]
- Lecoanet, D.; Cantiello, M.; Quataert, E.; Couston, L.A.; Burns, K.J.; Pope, B.J.S.; Jermyn, A.S.; Favier, B.; Le Bars, M. Low-frequency Variability in Massive Stars: Core Generation or Surface Phenomenon? Astrophys. J. Lett. 2019, 886, L15. [Google Scholar] [CrossRef]
- Anders, E.H.; Lecoanet, D.; Cantiello, M.; Burns, K.J.; Hyatt, B.A.; Kaufman, E.; Townsend, R.H.D.; Brown, B.P.; Vasil, G.M.; Oishi, J.S.; et al. The photometric variability of massive stars due to gravity waves excited by core convection. arXiv 2023, arXiv:2306.08023. [Google Scholar] [CrossRef]
- David-Uraz, A.; Owocki, S.P.; Wade, G.A.; Sundqvist, J.O.; Kee, N.D. Investigating the origin of cyclical wind variability in hot massive stars—II. Hydrodynamical simulations of corotating interaction regions using realistic spot parameters for the O giant ξ Persei. Mon. Not. R. Astron. Soc. 2017, 470, 3672–3684. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Aerts, C.; Urbaneja, M.A.; Camacho, I.; Antoci, V.; Fredslund Andersen, M.; Grundahl, F.; Pallé, P.L. Low-frequency photospheric and wind variability in the early-B supergiant HD 2905. Astron. Astrophys. 2018, 612, A40. [Google Scholar] [CrossRef]
- Krtička, J.; Feldmeier, A. Light variations due to the line-driven wind instability and wind blanketing in O stars. Astron. Astrophys. 2018, 617, A121. [Google Scholar] [CrossRef]
- Krtička, J.; Feldmeier, A. Stochastic light variations in hot stars from wind instability: Finding photometric signatures and testing against the TESS data. Astron. Astrophys. 2021, 648, A79. [Google Scholar] [CrossRef]
- Gray, D.F. The Observation and Analysis of Stellar Photospheres; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Slettebak, A. Line Broadening in the Spectra of o- and Early B-Type Stars. Astrophys. J. 1956, 124, 173. [Google Scholar] [CrossRef]
- Conti, P.S.; Ebbets, D. Spectroscopic studies of O-type stars. VII. Rotational velocities V sin i and evidence for macroturbulent motions. Astrophys. J. 1977, 213, 438–447. [Google Scholar] [CrossRef]
- Howarth, I.D.; Siebert, K.W.; Hussain, G.A.J.; Prinja, R.K. Cross-correlation characteristics of OB stars from IUE spectroscopy. Mon. Not. R. Astron. Soc. 1997, 284, 265–285. [Google Scholar] [CrossRef]
- Ryans, R.S.I.; Dufton, P.L.; Rolleston, W.R.J.; Lennon, D.J.; Keenan, F.P.; Smoker, J.V.; Lambert, D.L. Macroturbulent and rotational broadening in the spectra of B-type supergiants. Mon. Not. R. Astron. Soc. 2002, 336, 577–586. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Herrero, A.; Uytterhoeven, K.; Castro, N.; Aerts, C.; Puls, J. Observational Evidence for a Correlation Between Macroturbulent Broadening and Line-profile Variations in OB Supergiants. Astrophys. J. Lett. 2010, 720, L174–L178. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Herrero, A.; Sabín-Sanjulián, C.; Najarro, F.; Garcia, M.; Puls, J.; Castro, N.; Evans, C.J. The IACOB project. II. On the scatter of O-dwarf spectral type—Effective temperature calibrations. Astron. Astrophys. 2014, 570, L6. [Google Scholar] [CrossRef]
- Simón-Díaz, S.; Godart, M.; Castro, N.; Herrero, A.; Aerts, C.; Puls, J.; Telting, J.; Grassitelli, L. The IACOB project. III. New observational clues to understand macroturbulent broadening in massive O- and B-type stars. Astron. Astrophys. 2017, 597, A22. [Google Scholar] [CrossRef]
- Holgado, G.; Simón-Díaz, S.; Herrero, A.; Barbá, R.H. The IACOB project. VII. The rotational properties of Galactic massive O-type stars revisited. Astron. Astrophys. 2022, 665, A150. [Google Scholar] [CrossRef]
- Schultz, W.C.; Tsang, B.T.H.; Bildsten, L.; Jiang, Y.F. Synthesizing Spectra from 3D Radiation Hydrodynamic Models of Massive Stars Using Monte Carlo Radiation Transport. Astrophys. J. 2023, 945, 58. [Google Scholar] [CrossRef]
- Kasen, D.; Thomas, R.C.; Nugent, P. Time-dependent Monte Carlo Radiative Transfer Calculations for Three-dimensional Supernova Spectra, Light Curves, and Polarization. Astrophys. J. 2006, 651, 366–380. [Google Scholar] [CrossRef]
- Castor, J.I.; Abbott, D.C.; Klein, R.I. Radiation-driven winds in Of stars. Astrophys. J. 1975, 195, 157–174. [Google Scholar] [CrossRef]
- Davis, S.W.; Jiang, Y.F.; Stone, J.M.; Murray, N. Radiation Feedback in ULIRGs: Are Photons Movers and Shakers? Astrophys. J. 2014, 796, 107. [Google Scholar] [CrossRef]
- Sana, H.; de Mink, S.E.; de Koter, A.; Langer, N.; Evans, C.J.; Gieles, M.; Gosset, E.; Izzard, R.G.; Le Bouquin, J.B.; Schneider, F.R.N. Binary Interaction Dominates the Evolution of Massive Stars. Science 2012, 337, 444–446. [Google Scholar] [CrossRef] [PubMed]
- Sana, H.; de Koter, A.; de Mink, S.E.; Dunstall, P.R.; Evans, C.J.; Hénault-Brunet, V.; Maíz Apellániz, J.; Ramírez-Agudelo, O.H.; Taylor, W.D.; Walborn, N.R.; et al. The VLT-FLAMES Tarantula Survey. VIII. Multiplicity properties of the O-type star population. Astron. Astrophys. 2013, 550, A107. [Google Scholar] [CrossRef]
- Offner, S.S.R.; Moe, M.; Kratter, K.M.; Sadavoy, S.I.; Jensen, E.L.N.; Tobin, J.J. The Origin and Evolution of Multiple Star Systems. arXiv 2022, arXiv:2203.10066. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.-F. Three Dimensional Natures of Massive Star Envelopes. Galaxies 2023, 11, 105. https://doi.org/10.3390/galaxies11050105
Jiang Y-F. Three Dimensional Natures of Massive Star Envelopes. Galaxies. 2023; 11(5):105. https://doi.org/10.3390/galaxies11050105
Chicago/Turabian StyleJiang, Yan-Fei. 2023. "Three Dimensional Natures of Massive Star Envelopes" Galaxies 11, no. 5: 105. https://doi.org/10.3390/galaxies11050105
APA StyleJiang, Y.-F. (2023). Three Dimensional Natures of Massive Star Envelopes. Galaxies, 11(5), 105. https://doi.org/10.3390/galaxies11050105





