Abstract
We investigate some properties of exotic spherical configurations made of dark matter and dark energy. For the former, we adopt a polytropic equation-of-state, while for the latter, we adopt the extended Chaplygin gas equation-of-state. Solving the Tolman–Oppenheimer–Volkoff equations, within the two-fluid formalism, we compute the factor of compactness, the mass-to-radius relationships, as well as the tidal Love numbers and dimensionless deformabilities. A comparison between single-fluid objects and two-fluid configurations is made as well.
1. Introduction
According to the CDM cosmological model, the Universe is not only composed of ordinary matter, but also of a strange substance known as dark matter (DM) [1]. The CDM model, based on cold dark matter and a positive cosmological constant, has been very successful as it is in excellent agreement with observational data. If we study massive stellar objects, such as galaxies or clusters of galaxies, it can be inferred that there is more matter than the visible one. The existence of dark matter was speculated for the first time when Fritz Zwicky studied the Coma cluster of galaxies, and determined that its mean density was 400 times greater than that derived from observations of light matter [2]. Later on, Rubin and Ford obtained the rotation curve of the Andromeda galaxy, and they observed that the speed along all the arms of the galaxy remained almost constant, which suggested the presence of matter in the halo that we cannot see [3]. For a discussion on current evidence for dark matter or galaxy rotation curves, see for instance [4,5,6,7].
Dark and ordinary matter are not the only components that exist in the Universe according to the CDM model [8], since it proposes the existence of an energy that currently accelerates the expansion of the Universe, and that represents around 70% of the energy content of the Universe (∼25% dark matter and ∼5% ordinary matter), known as dark energy (DE). For some more recent cosmological constraints coming from supernova data, see, e.g., [9,10,11,12], and also see [13,14] for historical research.
Compact objects [15], such as neutron stars [16] and strange quark stars [17,18,19,20,21,22] (provided that the latter exist in Nature), are the final fate of sufficiently massive stars, since less massive stars lead to white dwarfs, which are considerably less relativistic. Those objects are characterized by ultra-high matter densities and strong gravitational fields. As matter becomes relativistic under those extreme conditions, the Newtonian description is inadequate, and therefore a relativistic description is more appropriate. In addition to that, there are studies of less conventional or even exotic stars. It has been proposed that stars made entirely of self-interacting dark matter may exist, called boson stars [23,24,25,26,27,28] (see, e.g., [29,30] for recent progress in the numerical simulations of boson star binaries). See [31] for a classic review of boson stars and [32] for a very recent one.
The properties of compact stars made of ordinary matter admixed with condensed dark matter or fermionic dark matter were also extensively studied, as can be seen, for instance, in [33,34,35,36,37,38,39,40,41,42,43]. Similarly, there are a few works where the authors contemplate the possibility that exotic objects made of dark energy might exist as well [44,45,46,47].
Despite the success of the CDM model at large (cosmological) scales (see, however, [48,49] for challenges), one may go beyond the concordance model for several reasons. First, as far as DM is concerned, beyond the collisionless dark matter paradigm, the self-interacting DM [50] has been proposed as an attractive solution to the dark matter crisis at short (galactic) scales, for reviews see, e.g., [51,52]. Similarly, given that current cosmic acceleration calls for dark energy, in some recent works, the authors proposed to study non-rotating dark energy stars [44,45,46,47] assuming an extended equation-of-state (EoS) of the form [53,54], with A, B and being constant parameters, where are the pressure and the density of the fluid, respectively. A simplified version of this, namely , with , known as generalized Chaplygin gas equation-of-state, was introduced in cosmology a long time ago to unify the description of non-relativistic matter and the cosmological constant [55,56].
In a binary system, one of the stars is subject to the gravitational field produced by its companion. Due to the gravitational interaction, tidal forces are generated. The theory for tidal deformability was introduced by Love [57,58] more than 110 years ago to study the deformability of the Earth due to the tides produced by the Moon. Love introduced dimensionless numbers, the tidal love numbers, such as k, which describes the relative deformation of the gravitational potential. Those numbers can also be used for the studies of relativistic stars in binary systems [59,60,61,62,63,64]. In the case of two compact objects, each star produces deformabilities, or tides on its surface, towards the other, due to the mutual gravitational attraction. Those deformabilities may be quantified introducing , which is a dimensionless number that can be calculated in terms of the tidal Love number k, as can be seen in the discussion below.
Through observations from gravitational waves (GWs) from mergers of binaries containing neutron stars and/or black holes, it has been possible to obtain information about the nature of the colliding bodies, thanks to the GW detectors LIGO and Virgo [65,66,67], see [68] for their latest catalogue paper. KAGRA [69] and LIGO-India [70] will also contribute to such future observations, and future ground-based GW detectors (Einstein Telescope [71] and Cosmic Explorer [72]) are planned for the future. Low-frequency space-based GW detectors, such as LISA [73,74], have also been planned, although space-based detectors are not expected to constrain the neutron star EoS, and LISA will not be able to probe the tidal deformability of objects with the masses we are considering here. For constraints on the nuclear equation-of-state that may be obtained from GW observations, see, for instance, [75,76,77,78], and for constraints on boson stars from putative binary black hole signals, see, e.g., [79,80].
In this article, we propose to investigate some properties of spherical configurations made of both dark matter and dark energy. To be more precise, the goal here is two-fold, namely generate the mass-to-radius profiles of isolated objects, as well as compute the tidal Love numbers and deformabilities in binaries. It would be interesting to see what can be expected if those objects do exist in Nature, and also to know how their properties differ as compared to other classes of compact objects.
Our work is organized as follows: after this introduction, we present the structure equations governing hydrostatic equilibrium as well as the tidal Love numbers in Section 2. The equations-of-state employed here and our numerical results are shown and discussed in Section 3. Finally, we summarize and conclude our work in Section 4. We adopt the mostly positive metric signature (−,+,+,+), and we work in natural geometrical units setting c = 1 = G.
2. Theoretical Framework: Notation and Setup
2.1. Hydrostatic Equilibrium
We work with relativistic configurations, in four dimensions, with a vanishing cosmological constant, and assuming that the objects are electrically neutral and non-rotating.
The metric for static, spherically symmetric space-times in Schwarzschild-like coordinates, (t, r, , ), is given by
for interior solutions, , where R is the radius of the star, while for the discussion to follow, it is more convenient to work with the mass function, , defined by
To obtain interior solutions describing the hydrostatic equilibrium of dark stars, one needs to integrate the Tolman–Oppenheimer–Volkoff equations [81,82], for a two-fluid spherical configuration, i.e., made of both dark matter and dark energy, given by the equations in the two-fluid formalism [83,84]
where a prime denotes differentiation with respect to r, and where and are the pressure and the energy density for dark matter, respectively, while and are the corresponding quantities for dark energy, respectively. The total pressure and density are, respectively,
The function may be computed by
with M being the mass of the star. The Equations (3)–(5) are to be integrated, imposing at the center of the star appropriate conditions
where is the central pressure for dark matter and for dark energy. In addition, the following matching conditions must be satisfied at the surface of the object
taking into account that the exterior vacuum solution is given by the Schwarzschild geometry.
2.2. Tidal Love Numbers
In a binary system, each star is subjected to the gravitational field produced by its companion. This interaction produces tides on the surface of stars.
For a spherical body, we used a dimensionless number, k, that describes the relative deformation of the gravitational potential. The tidal Love number, k, was originally introduced by Love [57,58], while the relativistic theory of tidal Love numbers was formulated in [59,60,61,62,63,64]. In the latter case, k is computed by
where is the factor of compactness of the star, and
is a fifth-order polynomial given by
While the function satisfies a Riccati differential Equation [64]:
supplemented by the initial condition at the center, , where
and with being the speed of sound. The speed of sound for each fluid component may be computed using either the solution , with , or the definition since the EoS is known. However, for the total pressure and energy density, as there is no EoS for those, the speed of sound is computed once the solution is obtained.
It has been pointed out in [61,63,64] that, when phase transitions or density discontinuities are present, it is necessary to slightly modify the expressions above. Since, in the present work, the energy density takes a non-vanishing surface value, , we incorporated the following correction in our analysis:
where is the density discontinuity, and
is the mean energy density throughout the object.
In terms of the tidal Love number, we may determine the deformabilities of the star produced by the gravitational field of its companion. These are determined by
where is the tidal deformability and is the dimensionless deformability, derived from the relationship between the induced quadrupole moment Q and the applied tidal field
The interested reader may consult [59,60,61,62,63,64] for more details.
The Riccati Equations (19) and (20) correspond to a single-fluid object. In the two-fluid formalism, the correct equation is obtained, making the substitution [85]
However, in our work, we numerically verified that Equations (20) and (25) lead to the same results for the tidal Love numbers and deformabilities. This is no surprise, since using the structure equations and the definition of the sound speed, both sides of the above equation give .
Finally, it is worth mentioning that, due to the overall factor in the expression for k, clearly the tidal Love number for black holes is precisely zero as , or at least for the Schwarzschild black hole of general relativity [62]. On the contrary, for any other relativistic object (neutron stars, quark stars or dark stars) and . Moreover, since the dark sector does not directly interact with light, one expects only gravity waves emitted from dark binaries without the electromagnetic counterpart, similarly to black hole binaries. Those properties may allow us to differentiate between different classes of objects.
3. Equation-of-State and Numerical Results
3.1. Equations-of-State
To integrate the TOV equations, we must specify the equation-of-state of the matter content. In the two-fluid formalism, since there is no direct interaction between the two fluid components, each fluid is characterized by its own EoS.
Recently, there has been a reinterpretation of DM as a Bose–Einstein Condensate [86,87,88] as it solves the cusp/core problem [89]. The single wave-function describing the Bose–Einstein condensation [90,91,92] satisfies the Gross–Pitaevskii Equation [93,94], also known as non-linear Schrödinger equation, as can be seen in, e.g., [95,96,97,98] (see also [99,100,101,102,103] for the cosmological implications of ultra-light bosons). The presence of the non-linear term, interpreted as enthalpy, gives rise to a polytropic EoS of the form [95,96,97]
where the constant of proportionality, K, is computed to be [35,95,96]
with m being the mass of the dark matter particle, and l being the scattering length that determines the cross-section of 2 by 2 elastic scattering processes, [35,95,96]. Assuming numerical values for the free parameters of the model, , as follows: and [104], then the constant K is found to be .
Then, the EoS for dark energy is assumed to be the extended Chaplygin gas equation-of-state [53,54]
where A and B are positive constants, out of which A is dimensionless, while B has dimensions of energy density and pressure. Also, note that Chaplygin’s EoS is given by [55], while the additional barotropic term corresponds to , also leading to a good DE model [105]. The numerical values of A and B considered here are shown in Table 1.

Table 1.
Numerical values of A and B for the three different DE models [46,47].
The choice of the numerical values of the parameters has been made with two criteria in mind: first, to obtain realistic, well behaved solutions, and in addition to that, to model objects with properties similar to the ones of neutron stars, namely radii of the order of 10 km as well as stellar masses of the order of solar mass. We should mention, however, that according to our numerical results, the highest masses we obtained here are notably lower than the masses of the most massive pulsars, as can be seen in the discussion below in Section 3.2. It must be taken into account that, given the form of the EoS, the pressure and density cannot become zero at the same time. Therefore, a vanishing pressure at the surface of the star implies a non-vanishing value for the energy density, which is found to be .
Furthermore, regarding the conditions at the center of the objects, for the numerical analysis, it turns out that it is convenient to introduce a new dimensionless factor defined as
and, in the following, we shall consider three different values, namely .
3.2. Discussion of the Results
Our numerical results are displayed in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 below, where we vary both the factor f and the pair of constants related to the dark energy model (Table 1). The factor of compactness, C, the tidal Love number, k, as well as the deformability, , are dimensionless quantities, whereas the stellar mass, M, as well as the stellar radius, R, are dimensional quantities, the former in solar masses and the latter in km.
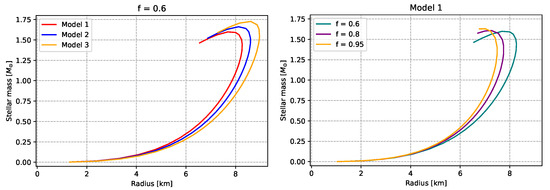
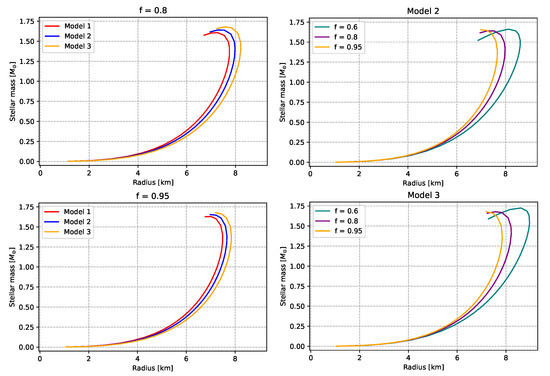
Figure 1.
Mass-to-radius relationships (mass in solar masses and radius in km) for the exotic configurations considered in this work. In the first column, we vary the DE model for a given value of the factor f, while, in the second column we vary f for a given DE model. See text for more details.
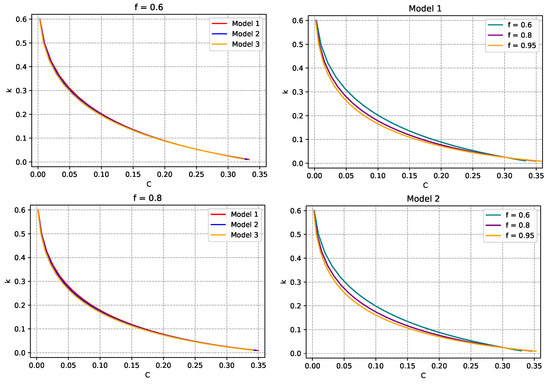
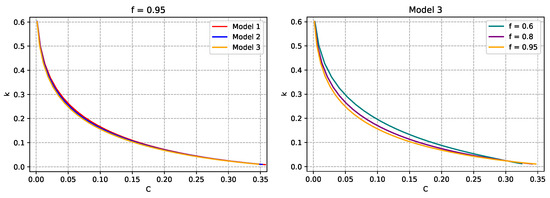
Figure 2.
Tidal Love number, k, as a function of the factor of compactness, . As in the previous figure, in the first column, we vary the DE model for a given value of the factor f, while in the second column, we vary f for a given DE model. See text for more details.
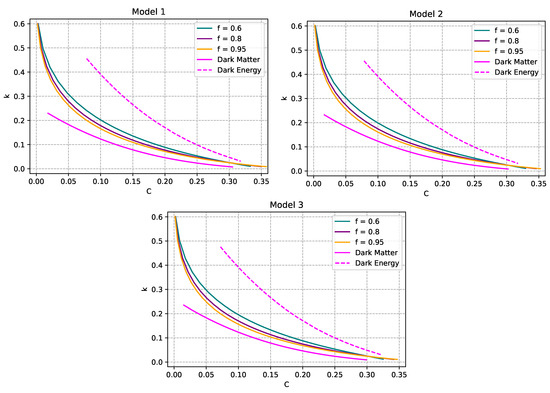
Figure 3.
Tidal Love number, k, as a function of the factor of compactness, . We fix the DE model (model 1), and we vary the factor . For comparison reasons, the predictions corresponding to the single-fluid objects (made of dark matter only or dark energy only) are shown as well. Notice that the dashed curves do not extend to zero compactness, the only reason being that it was difficult to generate it. The omitted portions, however, are not vital to the conclusions of this work.
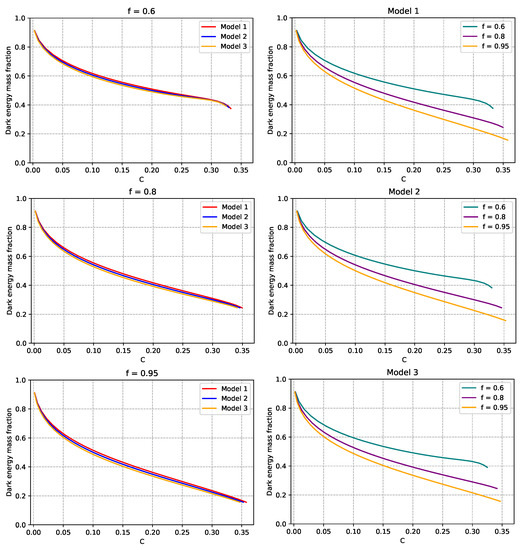
Figure 4.
Dark energy mass fraction as a function of the factor of compactness. As in the first two figures, in the first column, we vary the DE model for a given value of the factor f, while in the second column, we vary f for a given DE model. See text for more details.
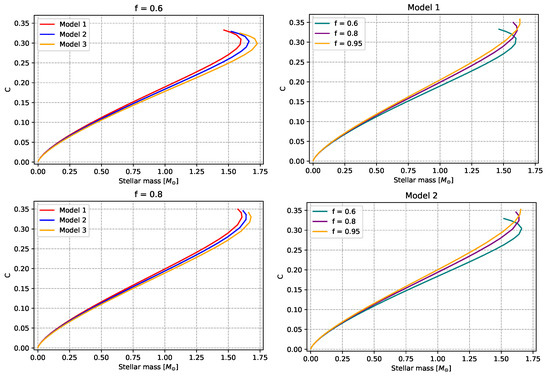
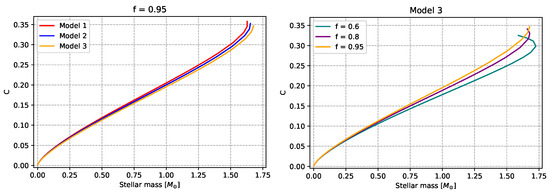
Figure 5.
Factor of compactness vs. stellar mass (in solar masses). As in the previous figure, in the first column, we vary the DE model for a given value of the factor f, while in the second column, we vary f for a given DE model. See text for more details.
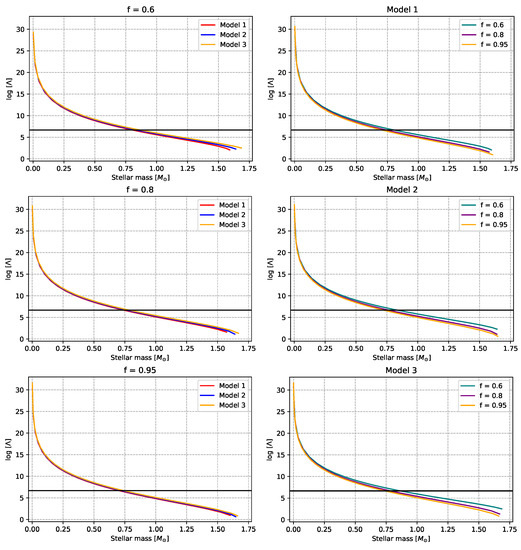
Figure 6.
Natural logarithm (base e) of dimensionless deformability as a function of stellar mass (in solar masses). The horizontal line indicates the bound from the GW170817 [67] . As in the previous figure, in the first column, we vary the DE model for a given value of the factor f, while in the second column, we vary f for a given DE model. See text for more details.
In Figure 1, the M-R profiles are shown. In all six cases, the stellar radius reaches a maximum value first, and then the stellar mass also reaches its own highest value. We can notice that, for the same central pressure ratio, the most massive stars are those of model 3, while the least massive are those of model 1. Within the same models, the masses are similar, but in model 1, we can notice that they are more massive for f = 0.95, while in model 3, they are for f = 0.6. For a given value of f (column on the left), the difference between different DE models is more important for lower values of f, whereas, as , the profiles lie one very close to another. On the contrary, for a given DE model (column on the right), there is always a considerable difference from one value of f to another. Although the models considered in this work are not proposed to explain any observations of pulsars, we remark in passing that the maximum masses found here are notably lower than the largest measured pulsar masses (such as J1614-2230, mass at solar masses), see for instance [106].
In Figure 2, we display k versus C fixing the f factor (column on the left) or fixing the DE model (column on the right). In all six cases, the curves qualitatively exhibit the same behavior. Namely, they monotonically decrease tending to zero as , which is the black hole limit as already mentioned previously. For a given f and varying the DE model, we observe no significant difference from one case to another. Contrary to that, the difference from one case to another is comparable to all three cases when we fix the DE model and vary f. Moreover, the curves are shifted downwards as we increase f. To compare with previous results on neutron stars or quark stars, it was found in [64] that the figures k versus C for quark stars are quite different in comparison to hadronic EoSs. To be more precise, in the case of NSs, the curves exhibit a pronounced maximum, as can be seen, for instance, in Figure 4 of [61] or Figure 7 of [64], and the maximum value lies between 0.1 and 0.14. On the contrary, in the case of quark stars, the tidal Love number may be as high as 0.8. Our results show that with a tidal Love number as high as 0.6, and without a pronounced maximum, the configurations studied here look more like quark stars than NSs.
In Figure 3a, the comparison is made between single-fluid objects, made of dark matter only or dark energy only, and two-fluid objects made of both dark components investigated here. The curve corresponding to pure DM objects (polytrope with ) is the one shown in Figure 1 of [61,62]. The two-fluid case lies in between and approaches the pure DM curve as we increase f. The tidal Love number corresponding to the pure dark matter case is the lowest for a given compactness, whereas the curves corresponding to the two-fluid case are qualitatively similar to the curves corresponding to pure dark energy case. The curves corresponding to pure DE (dashed magenta) do not extend to zero compactness, the only reason being that it was difficult to generate it. The omitted portions, however, are not vital to the conclusions of this work, since a very low factor of compactness implies a non-relativistic object, whereas here we are mostly interested in compact configurations.
Next, in Figure 4, we show the DE mass fraction, , as a function of the factor of compactness. As in previous figures, we vary the model fixing f in the column on the left, and we vary the f factor for a given model in the column on the right. In all six cases, we observe that the DE mass fraction monotonically decreases with C, and that the factor of compactness always remains lower than in agreement with the Buchdahl limit [107]. The objects are less compact when they are DE-dominated, and more compact when they are dark matter dominated. Furthermore, for a given f, there is no significant difference from one model to another, whereas within the same DE model, the DE mass fraction decreases with f for a given value of C.
The factor of compactness versus the stellar mass is displayed in Figure 5. In all six cases, the curves exhibit the same behavior qualitatively, where C increases with M. The highest value of the mass and the maximum value of the compactness are the same as the ones shown in Figure 1 and Figure 4, respectively.
Finally, the dimensionless deformability versus stellar mass (semilogarithmic plot) is shown in Figure 6. decreases with M monotonically. In all six panels, the three curves lie very close to another, and some difference is observed for stellar masses at around 0.75 solar masses. The difference from one model to another for a given f (column on the right) is somewhat more significant compared to the panels in the column on the left, where we fix the f factor and we vary the DE model. In all six cases, the dimensionless deformability is in agreement with the bound coming from GW170817 [67].
4. Summary and Conclusions
To summarize our work, in the present article, we studied exotic, electrically neutral, spherical configurations made of both dark energy and self-interacting dark matter. We employed the two-fluid formalism within Einstein’s general relativity without a cosmological constant. We have adopted the extended Chaplygin gas for dark energy, and a polytopic EoS for condensed dark matter. The numerical values of the parameters of the models correspond to realistic, well behaved solutions describing objects with masses and radii similar to those of neutron stars and quark stars. We numerically integrated the structure (TOV) equations describing hydrostatic equilibrium to compute the mass, the radius, and the factor of compactness of the exotic configurations. Moreover, we numerically integrated the Riccati equation for metric perturbations in binaries to compute the tidal Love numbers as well as the dimensionless deformabilities. Our main results are displayed in the six figures of six panels each, where we vary both the dark energy model (models 1, 2, and 3) and the dimensionless factor f, as can be seen in the text for more details. Finally, we made a direct comparison between the two-fluid objects versus single-fluid spherical configurations made of dark matter only or dark energy only. For some works that consider distinguishing between different binaries, see, e.g., [108,109,110,111].
Author Contributions
Conceptualization: G.P., Methodology: G.P., Formal analysis: G.P., Investigation: C.S. and G.P., Writing original draft preparation: C.S., Software: C.S., Writing—review and editing: C.S. and G.P., Visualization: C.S. and G.P., Supervision: G.P. All authors have read and agreed to the published version of the manuscript.
Funding
The author C. S. acknowledges financial support from Universidad de la Frontera.
Data Availability Statement
This is a theoretical work and so no data have been reported here.
Acknowledgments
We are grateful to the reviewers for useful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Freedman, W.L.; Turner, M.S. Measuring and understanding the universe. Rev. Mod. Phys. 2003, 75, 1433–1447. [Google Scholar] [CrossRef]
- Zwicky, F. The redshift of extragalactic nebulae. Helv. Phys. Acta 2009, 6, 110–127. [Google Scholar]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions. Astrophys. J. 1970, 159, 379–403. [Google Scholar] [CrossRef]
- Paolo, C.D.; Salucci, P.; Erkurt, A. The universal rotation curve of low surface brightness galaxies—IV. The interrelation between dark and luminous matter. Mon. Not. R. Astron. Soc. 2019, 490, 5451–5477. [Google Scholar]
- Shen, T.W.; Abidin, Z.Z.; Hashim, N. A comprehensive analysis using 9 dark matter halo models on the spiral galaxy NGC 4321. Indian J. Phys. 2022, 96, 671–687. [Google Scholar]
- Salucci, P.; Paolo, C.D. Fundamental Properties of the Dark and the Luminous Matter from the Low Surface Brightness Discs. Universe 2021, 7, 344. [Google Scholar] [CrossRef]
- de Martino, I.; Chakrabarty, S.S.; Cesare, V.; Gallo, A.; Ostorero, L.; Diaferio, A. Dark matters on the scale of galaxies. Universe 2020, 6, 107. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck]. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar]
- Abbott, T.M.C. et al. [DES]. First Cosmology Results using Type Ia Supernovae from the Dark Energy Survey: Constraints on Cosmological Parameters. Astrophys. J. Lett. 2019, 872, L30. [Google Scholar] [CrossRef]
- Wang, B.; Qi, J.Z.; Zhang, J.F.; Zhang, X. Cosmological Model-independent Constraints on Spatial Curvature from Strong Gravitational Lensing and SN Ia Observations. Astrophys. J. 2020, 898, 100. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A.G.; Zuntz, J.; Kessler, R.; Carr, A.; Davis, T.M.; Hinton, S.; Jones, D.; et al. The Pantheon+ Analysis: Cosmological Constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Diao, J.W.; Pan, Y.; Xu, W. Testing the Coincidence Problem with Strong Gravitational Lens, Type Ia Supernovae and Hubble Parameter Observational Data. Res. Astron. Astrophys. 2022, 22, 115019. [Google Scholar] [CrossRef]
- Riess, A.G. et al. [Supernova Search Team]. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Perlmutter, S. et al. [Supernova Cosmology Project]. Measurements of Ω and Λ from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects; Wiley: New York, NY, USA, 1983; p. 645. [Google Scholar]
- Lattimer, J.M.; Prakash, M. Neutron Star Observations: Prognosis for Equation of State Constraints. Phys. Rept. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Weber, F. Strange quark matter and compact stars. Prog. Part. Nucl. Phys. 2005, 54, 193–288. [Google Scholar] [CrossRef]
- Alcock, C.; Farhi, E.; Olinto, A. Strange stars. Astrophys. J. 1986, 310, 261–272. [Google Scholar] [CrossRef]
- Alcock, C.; Olinto, A. Exotic Phases of Hadronic Matter and their Astrophysical Application. Ann. Rev. Nucl. Part. Sci. 1988, 38, 161–184. [Google Scholar] [CrossRef]
- Madsen, J. Physics and astrophysics of strange quark matter. Lect. Notes Phys. 1999, 516, 162–203. [Google Scholar]
- Yue, Y.L.; Cui, X.H.; Xu, R.X. Is psr b0943+10 a low-mass quark star? Astrophys. J. Lett. 2006, 649, L95–L98. [Google Scholar] [CrossRef]
- Leahy, D.; Ouyed, R. Supernova SN2006gy as a first ever Quark Nova? Mon. Not. R. Astron. Soc. 2008, 387, 1193. [Google Scholar] [CrossRef]
- Kaup, D.J. Klein-Gordon Geon. Phys. Rev. 1968, 172, 1331–1342. [Google Scholar] [CrossRef]
- Ruffini, R.; Bonazzola, S. Systems of selfgravitating particles in general relativity and the concept of an equation of state. Phys. Rev. 1969, 187, 1767–1783. [Google Scholar] [CrossRef]
- Colpi, M.; Shapiro, S.L.; Wasserman, I. Boson Stars: Gravitational Equilibria of Selfinteracting Scalar Fields. Phys. Rev. Lett. 1986, 57, 2485–2488. [Google Scholar] [CrossRef] [PubMed]
- Kusmartsev, F.V.; Mielke, E.W.; Schunck, F.E. Gravitational stability of boson stars. Phys. Rev. D 1991, 43, 3895–3901. [Google Scholar] [CrossRef]
- Eby, J.; Kouvaris, C.; Nielsen, N.G.; Wijewardhana, L.C.R. Boson Stars from Self-Interacting Dark Matter. JHEP 2016, 2, 28. [Google Scholar] [CrossRef]
- Croon, D.; Fan, J.; Sun, C. Boson Star from Repulsive Light Scalars and Gravitational Waves. JCAP 2019, 4, 8. [Google Scholar] [CrossRef]
- Evstafyeva, T.; Sperhake, U.; Helfer, T.; Croft, R.; Radia, M.; Ge, B.X.; Lim, E.A. Unequal-mass boson-star binaries: Initial data and merger dynamics. Class. Quant. Grav. 2023, 40, 085009. [Google Scholar] [CrossRef]
- Siemonsen, N.; East, W.E. Generic initial data for binary boson stars. arXiv 2023, arXiv:2306.17265. [Google Scholar]
- Schunck, F.E.; Mielke, E.W. General relativistic boson stars. Class. Quant. Grav. 2003, 20, R301–R356. [Google Scholar] [CrossRef]
- Liebling, S.L.; Palenzuela, C. Dynamical boson stars. Living Rev. Rel. 2023, 26, 1. [Google Scholar] [CrossRef]
- Leung, S.C.; Chu, M.C.; Lin, L.M. Dark-matter admixed neutron stars. Phys. Rev. D 2011, 84, 107301. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.; Schaffner-Bielich, J. Quark stars admixed with dark matter. Phys. Rev. D 2016, 93, 083009. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with condensed dark matter. Phys. Rev. D 2017, 96, 083013. [Google Scholar] [CrossRef]
- Lopes, I.; Panotopoulos, G. Dark matter admixed strange quark stars in the Starobinsky model. Phys. Rev. D 2018, 97, 024030. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Millisecond pulsars modeled as strange quark stars admixed with condensed dark matter. Int. J. Mod. Phys. D 2018, 27, 1850093. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Radial oscillations of strange quark stars admixed with fermionic dark matter. Phys. Rev. D 2018, 98, 083001. [Google Scholar] [CrossRef]
- Rahman, N.; Molla, S.; Kalam, M. Possible existence of dark matter admixed pulsar. Eur. Phys. J. Plus 2020, 135, 637. [Google Scholar] [CrossRef]
- Das, A.; Malik, T.; Nayak, A.C. Dark matter admixed neutron star properties in light of gravitational wave observations: A two fluid approach. Phys. Rev. D 2022, 105, 123034. [Google Scholar] [CrossRef]
- Emma, M.; Schianchi, F.; Pannarale, F.; Sagun, V.; Dietrich, T. Numerical Simulations of Dark Matter Admixed Neutron Star Binaries. Particles 2022, 5, 273–286. [Google Scholar] [CrossRef]
- Routaray, P.; Das, H.C.; Sen, S.; Kumar, B.; Panotopoulos, G.; Zhao, T. Radial oscillations of dark matter admixed neutron stars. Phys. Rev. D 2023, 107, 103039. [Google Scholar] [CrossRef]
- Lopes, L.L.; Das, H.C. Strange stars within bosonic and fermionic admixed dark matter. JCAP 2023, 5, 34. [Google Scholar] [CrossRef]
- Singh, K.N.; Ali, A.; Rahaman, F.; Nasri, S. Compact stars with exotic matter. Phys. Dark Univ. 2020, 29, 100575. [Google Scholar] [CrossRef]
- Tello-Ortiz, F.; Malaver, M.; Rincón, X.; Gomez-Leyton, Y. Relativistic anisotropic fluid spheres satisfying a non-linear equation of state. Eur. Phys. J. C 2020, 80, 371. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, x.; Lopes, I. Radial oscillations and tidal Love numbers of dark energy stars. Eur. Phys. J. Plus 2020, 135, 856. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, x.; Lopes, I. Slowly rotating dark energy stars. Phys. Dark Univ. 2021, 34, 100885. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Anomalies in physical cosmology. Annals Phys. 2022, 447, 169159. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational evidence for selfinteracting cold dark matter. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef]
- Suárez, A.; Robles, V.H.; Matos, T. A Review on the Scalar Field/Bose–Einstein Condensate Dark Matter Model. Astrophys. Space Sci. Proc. 2014, 38, 107–142. [Google Scholar]
- Li, B.; Rindler-Daller, T.; Shapiro, P.R. Cosmological Constraints on Bose–Einstein–Condensed Scalar Field Dark Matter. Phys. Rev. D 2014, 89, 083536. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. Extended Chaplygin gas model. Results Phys. 2014, 4, 101–102. [Google Scholar] [CrossRef]
- Pourhassan, B.; Kahya, E.O. FRW cosmology with the extended Chaplygin gas. Adv. High Energy Phys. 2014, 2014, 231452. [Google Scholar] [CrossRef]
- Kamenshchik, A.Y.; Moschella, U.; Pasquier, V. An Alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion and dark energy matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Love, A.E.H. The yielding of the Earth to disturbing forces. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1909, 82, 73–88. [Google Scholar] [CrossRef]
- Love, A.E.H. Some problems of geodynamics. Nature 1912, 89, 471. [Google Scholar]
- Flanagan, E.E.; Hinderer, T. Constraining neutron star tidal Love numbers with gravitational wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love Numbers of Neutron and Self-Bound Quark Stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef]
- Acernese, F. et al. [VIRGO]. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Aasi, J. et al. [LIGO Scientific]. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific and Virgo]. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific, VIRGO and KAGRA]. GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Aso, Y. et al. [KAGRA]. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Saleem, M.; Rana, J.; Gayathri, V.; Vijaykumar, A.; Goyal, S.; Sachdev, S.; Suresh, J.; Sudhagar, S.; Mukherjee, A.; Gaur, G.; et al. The science case for LIGO-India. Class. Quant. Grav. 2022, 39, 025004. [Google Scholar] [CrossRef]
- Punturo, M.; Abernathy, M.; Acernese, F.; Allen, B.; Andersson, N.; Arun, K.; Barone, F.; Barr, B.; Barsuglia, M.; Beker, M.; et al. The Einstein Telescope: A third-generation gravitational wave observatory. Class. Quant. Grav. 2010, 27, 194002. [Google Scholar] [CrossRef]
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar]
- Amaro-Seoane, P. et al. [LISA]. Laser Interferometer Space Antenna. arXiv 2021, arXiv:1702.00786. [Google Scholar]
- Barausse, E.; Berti, E.; Hertog, T.; Hughes, S.A.; Jetzer, P.; Pani, P.; Sotiriou, T.P.; Tamanini, N.; Witek, H.; Yagi, K.; et al. Prospects for Fundamental Physics with LISA. Gen. Rel. Grav. 2020, 52, 81. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific and Virgo]. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Landry, P.; Essick, R.; Chatziioannou, K. Nonparametric constraints on neutron star matter with existing and upcoming gravitational wave and pulsar observations. Phys. Rev. D 2020, 101, 123007. [Google Scholar] [CrossRef]
- Gupta, P.K.; Puecher, A.; Pang, P.T.H.; Janquart, J.; Koekoek, G.; Den, C.B.V. Determining the equation of state of neutron stars with Einstein Telescope using tidal effects and r-mode excitations from a population of binary inspirals. arXiv 2022, arXiv:2205.01182. [Google Scholar]
- Coupechoux, J.F.; Chierici, R.; Hansen, H.; Margueron, J.; Somasundaram, R.; Sordini, V. Impact of O4 future detections on the determination of the dense matter equations of state. Phys. Rev. D 2023, 107, 124006. [Google Scholar] [CrossRef]
- Narikawa, T.; Uchikata, N.; Tanaka, T. Gravitational-wave constraints on the GWTC-2 events by measuring the tidal deformability and the spin-induced quadrupole moment. Phys. Rev. D 2021, 104, 084056. [Google Scholar] [CrossRef]
- Vaglio, M.; Pacilio, C.; Maselli, A.; Pani, P. Bayesian parameter estimation on boson-star binary signals with a coherent inspiral template and spin-dependent quadrupolar corrections. Phys. Rev. D 2023, 108, 023021. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Sandin, F.; Ciarcelluti, P. Effects of mirror dark matter on neutron stars. Astropart. Phys. 2009, 32, 278–284. [Google Scholar] [CrossRef]
- Ciarcelluti, P.; Sandin, F. Have neutron stars a dark matter core? Phys. Lett. B 2011, 695, 19–21. [Google Scholar] [CrossRef]
- Leung, K.L.; Chu, M.c.; Lin, L.M. Tidal deformability of dark matter admixed neutron stars. Phys. Rev. D 2022, 105, 123010. [Google Scholar] [CrossRef]
- Boehmer, C.G.; Harko, T. Can dark matter be a Bose–Einstein condensate? JCAP 2007, 6, 25. [Google Scholar] [CrossRef]
- Pires, M.O.C.; de Souza, J.C.C. Galactic cold dark matter as a Bose–Einstein condensate of WISPs. JCAP 2012, 11, 24, Erratum in JCAP 2013, 11, E01. [Google Scholar]
- Souza, J.C.C.; Ujevic, M. Constraining condensate dark matter in galaxy clusters. Gen. Rel. Grav. 2015, 47, 100. [Google Scholar] [CrossRef]
- Harko, T. Bose–Einstein condensation of dark matter solves the core/cusp problem. JCAP 2011, 5, 22. [Google Scholar] [CrossRef]
- Bose, S. Plancks gesetz und lichtquantenhypothese. Z. Phys. 1924, 26, 178. [Google Scholar] [CrossRef]
- Einstein, A. Sitzungsber. Kgl. Preuss. Akad. Wiss. 261, 1924.
- Einstein, A. Sitzungsber. Kgl. Preuss. Akad. Wiss. 3, 1925.
- Dalfovo, F.; Giorgini, S.; Pitaevskii, L.P.; Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 1999, 71, 463–512. [Google Scholar] [CrossRef]
- Pethick, C.J.; Smith, H. Bose–Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Li, X.Y.; Harko, T.; Cheng, K.S. Condensate dark matter stars. JCAP 2012, 6, 1. [Google Scholar] [CrossRef]
- Chavanis, P.H. Phase transitions between dilute and dense axion stars. Phys. Rev. D 2018, 98, 023009. [Google Scholar] [CrossRef]
- Fan, J. Ultralight Repulsive Dark Matter and BEC. Phys. Dark Univ. 2016, 14, 84–94. [Google Scholar] [CrossRef]
- Lopes, I.; Panotopoulos, G. Radial oscillations of boson stars made of ultralight repulsive dark matter. Nucl. Phys. B 2020, 961, 115266. [Google Scholar] [CrossRef]
- Ji, S.U.; Sin, S.J. Late time phase transition and the galactic halo as a bose liquid: 2. The Effect of visible matter. Phys. Rev. D 1994, 50, 3655–3659. [Google Scholar] [CrossRef] [PubMed]
- Schive, H.Y.; Chiueh, T.; Broadhurst, T. Cosmic Structure as the Quantum Interference of a Coherent Dark Wave. Nature Phys. 2014, 10, 496–499. [Google Scholar] [CrossRef]
- Hui, L.; Ostriker, J.P.; Tremaine, S.; Witten, E. Ultralight scalars as cosmological dark matter. Phys. Rev. D 2017, 95, 043541. [Google Scholar] [CrossRef]
- Bernal, T.; Fernández-Hernxaxndez, L.M.; Matos, T.; Rodríguez-Meza, M.A. Rotation curves of high-resolution LSB and SPARC galaxies with fuzzy and multistate (ultralight boson) scalar field dark matter. Mon. Not. R. Astron. Soc. 2018, 475, 1447–1468. [Google Scholar] [CrossRef]
- Meinert, J.; Hofmann, R. Axial Anomaly in Galaxies and the Dark Universe. Universe 2021, 7, 198. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I. Dark stars in Starobinsky’s model. Phys. Rev. D 2018, 97, 024025. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Lopes, I.; Rincón, X. Lagrangian formulation for an extended cosmological equation-of-state. Phys. Dark Univ. 2021, 31, 100751. [Google Scholar] [CrossRef]
- Arzoumanian, Z. et al. [NANOGrav]. The NANOGrav 11-year Data Set: High-precision timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. 2018, 235, 37. [Google Scholar] [CrossRef]
- Buchdahl, H.A. General Relativistic Fluid Spheres. Phys. Rev. 1959, 116, 1027. [Google Scholar] [CrossRef]
- Chen, H.Y.; Chatziioannou, K. Distinguishing Binary Neutron Star from Neutron Star–Black Hole Mergers with Gravitational Waves. Astrophys. J. Lett. 2020, 893, L41. [Google Scholar] [CrossRef]
- Chen, A.; Johnson-McDaniel, N.K.; Dietrich, T.; Dudi, R. Distinguishing high-mass binary neutron stars from binary black holes with second- and third-generation gravitational wave observatories. Phys. Rev. D 2020, 101, 103008. [Google Scholar] [CrossRef]
- Fasano, M.; Wong, K.W.K.; Maselli, A.; Berti, E.; Ferrari, V.; Sathyaprakash, B.S. Distinguishing double neutron star from neutron star-black hole binary populations with gravitational wave observations. Phys. Rev. D 2020, 102, 023025. [Google Scholar] [CrossRef]
- Coupechoux, J.F.; Arbey, A.; Chierici, R.; Hansen, H.; Margueron, J.; Sordini, V. Discriminating same-mass neutron stars and black holes gravitational waveforms. Phys. Rev. D 2022, 105, 064063. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).