Eclipsing Binaries in Dynamically Interacting Close, Multiple Systems
Abstract
1. Introduction
- The short-term perturbations (with characteristic periods of the same order as the period of the outer orbit) in a hierarchical system are driven by the same physical and dynamical quantities which determine the long-term dynamical evolution through secular perturbations (Harrington [29]; Naoz [30]). Thus, proper analysis of the short-term photodynamical properties and behaviour of compact multiple systems allows all key stellar and orbital parameters, as well as the dynamical evolution of the orbits, to be determined with high accuracy;
- The formation of young, unevolved, and close binary stars with short periods (of a few days or less) cannot be explained without the assumption of some effective orbit-shrinking mechanism. Different mechanisms have been suggested in the literature (see below for details); however, most of them require an initial gravitational interaction with additional bodies (being either bound or unbound companion stars);
- Stars in close binaries evolve in markedly different ways than their single counterparts. In multiple systems, the evolutionary scenarios may be even more different and variegated (Toonen et al. [31,32,33]). For example, it is hypothesized that a significant fraction of the common envelope binaries (the supposed progenitors of cataclysmic variables), type Ia supernovae (Maoz et al. [34]), and contact binaries (of the W UMa type) might be formed through some interactions with a third body (Eggleton [35]; Paczyński et al. [36]; Csizmadia et al. [37]);
- The existence of some subgroups of close binary and multiple systems containing one or more compact objects (neutron stars, black holes), the progenitors of which went through supernova explosion, is hardly understandable without the initial multiplicity of such systems. For example, Podsiadlowski et al. [38] have pointed out that, in contrast to their more massive counterparts, black hole X-ray binaries with low-mass donor stars cannot form through a previous common envelope phase of the binary star. Therefore, the question of their origin remained open for a long time, while Naoz et al. [39] have shown that black-hole low-mass X-ray binaries can form through dynamical interactions with a third body. Similarly, some peculiar binary pulsars have been discovered during the last few decades (see, e.g., Champion et al. [40]) which probably have a triple system origin (see Freire et al. [41]; Portegies Zwart et al. [42]; Pijloo et al. [43]). Moreover, the discovery of the triply degenerate hierarchical triple system PSR J0337+1715, a millisecond pulsar with two orbiting white dwarfs, naturally requires the consideration of triple-star evolutionary scenarios in order to understand its formation process (Tauris & van den Heuvel [44]);
- Connected to the previous item, hierarchical triples may play an important role in the formation and also in the merger of black hole binaries. For example, Rodriguez & Antonini [45] have shown that the Lidov–Kozai mechanism (see later in Section 2.2) may explain the frequency of some special classes of the observed black hole mergers. We note, also, that, recently, Deme et al. [46] found that, in some special cases, third-body interactions amongst intermediate and supermassive black holes would also be detectable with the future space-borne gravitational wave observatory LISA 3 (see Amaro-Seoane et al. [47]). Naturally, on the other hand, these triple systems are very far from the category of CHTs and, therefore, in what follows we do not deal with them;
- Last but not least, we refer to circumbinary planets which, from a dynamical point of view, should also be considered as hierarchical triple systems. The existence of such systems challenges our planetary formation theories. It is unclear how these planets form and evolve; it is also not clear where they form and how they migrate to their present position (e.g., Pierens & Nelson [48]; Marzari et al. [49]; Meschiari [50]; Lines et al. [51,52,53]). The role of dynamical interactions in such systems, as well as their stability, have been studied intensively over the past few years (see the review of Marzari & Thebault [54], and further references therein). Moreover, we note that, in addition to these theoretical difficulties, that there are only limited observational clues to understanding the circumbinary planet populations because the observations suffer from many selection effects as well as the observational window function which prevents us from detecting more circumbinary planets and from understanding the observational biases (see Klagyivik et al. [55]);
2. Dynamics of CHTs
- Short-period perturbations, for which the typical period is on the order of , and the amplitude is related to ;
- Long-period perturbations, with a characteristic period of and an amplitude of ;
- Apse-node terms, having a period of about and an amplitude that may reach unity.
2.1. Long-Period Perturbations
2.2. Apse-Node Type Perturbations
3. Detection Methods of CHTs
3.1. Radial Velocity Measurements
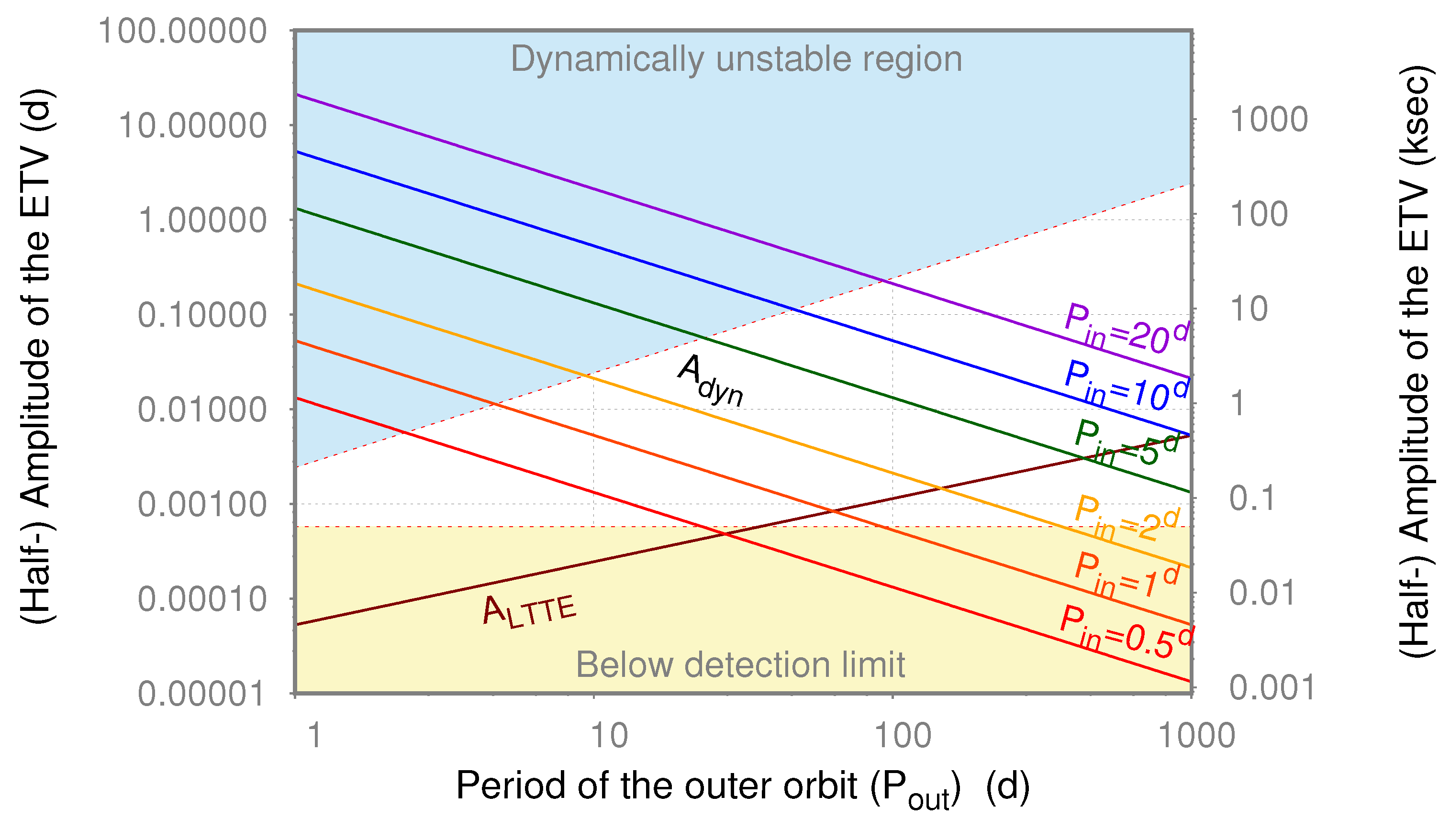
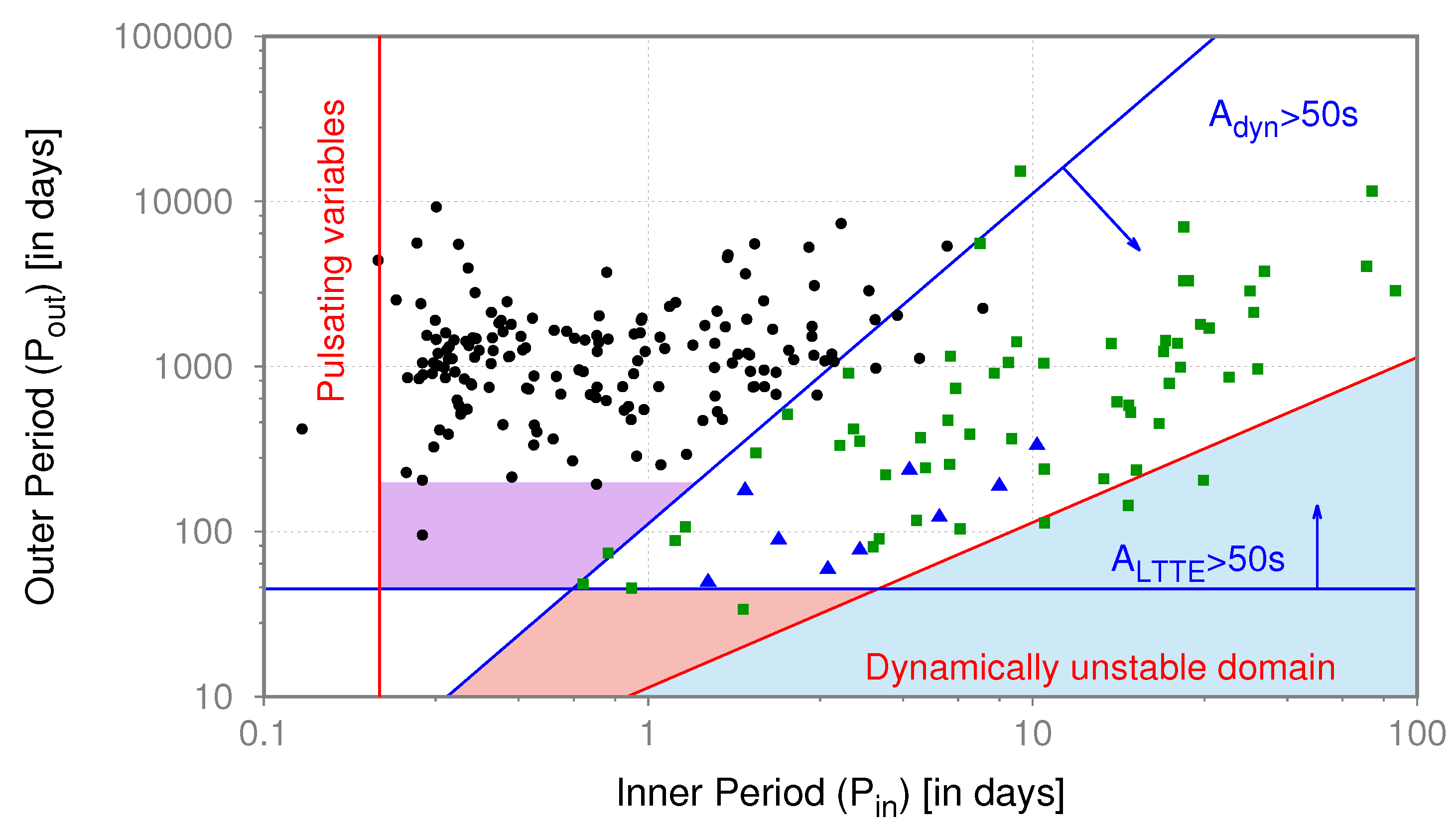
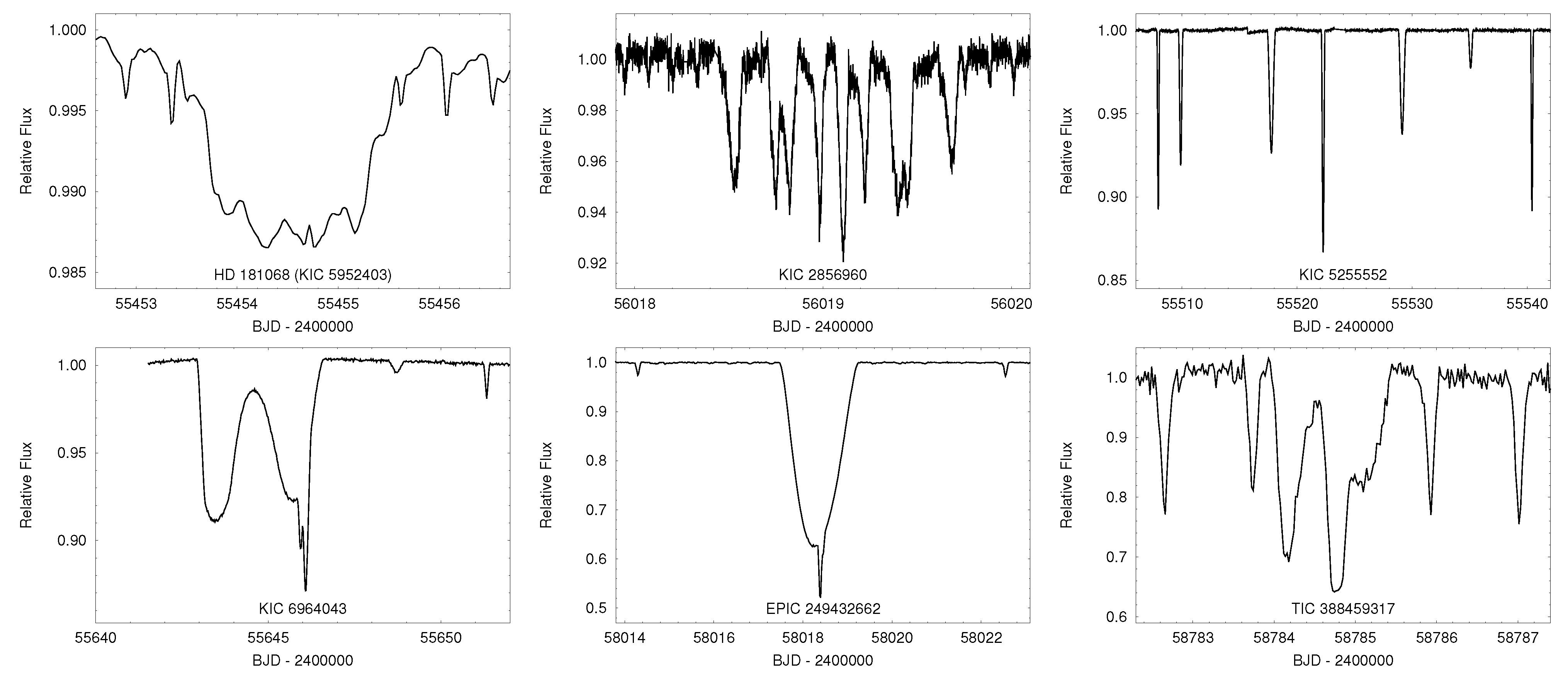
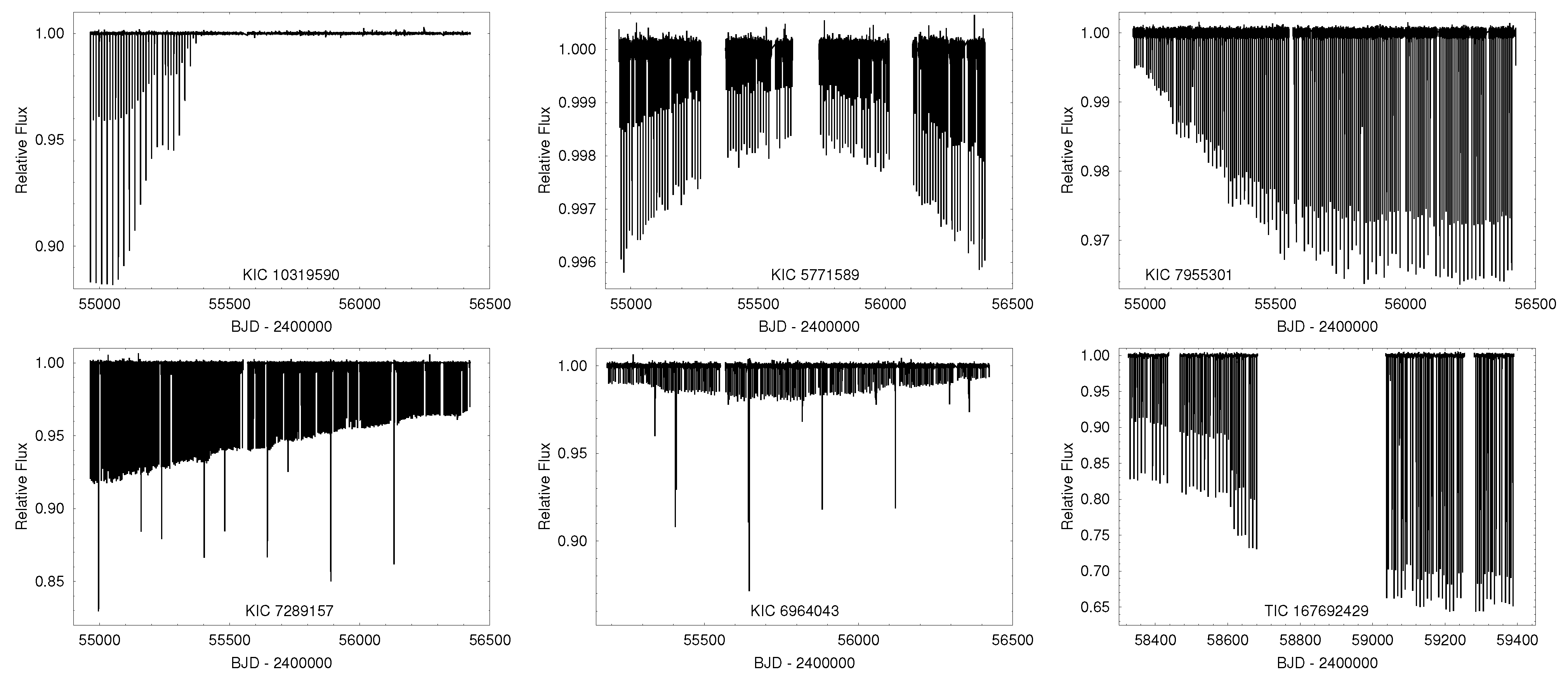
3.2. Eclipse Timing Variations
3.3. Extra Eclipses
3.3.1. Third-Body Eclipses
3.3.2. Double (Multiple) EBs
3.4. Eclipse Depth Variations—Disappearing Eclipses
3.5. Astrometry/Interferometry
4. Discussion and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | While the probability of the eclipses (being either total or grazing ones) in an ordinary binary depends on the sum of the fractional radii of the two stars, calculating the same quantity for third-body eclipses, one may use the half of the ratio of the inner to outer semi-major axes as an effective fractional radius of the inner binary (see e.g., Appendix A of Borkovits et al. [23]). |
| 2 | To be clear we are defining CHT’s as triples with d, i.e., short outer periods amenable to easy detection and follow-up studies, whereas ‘tight’ indicates a small ratio of , i.e., small enough for significant third-body perturbations. Of course, most ideal is the situation where a ‘compact’ system is also ‘tight’. |
| 3 | https://lisa.nasa.gov/ (accessed on 5 January 2022). |
| 4 | Note, higher order multiple stars can be built up from triple subsystems. |
| 5 | As we will discuss shortly below, for the tightest ECHTs, the apse-node perturbations also significantly influence the eclipse times. |
| 6 | An exact equivalence occurs in the case of the asymptotic solution, i.e., when the orbital angular momentum is stored exclusively in a circular outer orbit |
| 7 | Note, however, that one can find specific solutions even for nearly perpendicular configurations, where the inner eccentricity remains (essentially) constant and the major axis of the orbit freezes into a specific direction. |
| 8 | Note also the former pioneering work of Mazeh & Shaham [80] which also addressed the connection between the third-body forced eccentricity cycles and tidal dissipation. This study, however, was restricted to only the low mutual inclination regime and, therefore was less general than that of the work of Kiseleva et al. [79]. |
| 9 | https://cdsarc.cds.unistra.fr/viz-bin/cat/J/ApJS/235/6 (accessed on 25 November 2021). |
| 10 | For comparison, we note that the former compilation of Fekel [94] counted only eight CHTs. |
| 11 | Formerly, before the advent of extensive investigations of transiting exoplanets, any kind of timing variations in the binary star community were referred to almost exclusively as studies. This terminology stems from the use of Observed minus Calculated diagrams in which one plots the observed times of eclipse minima (or, in the case of pulsating variables, maxima) minus the times calculated with the assumption of a constant period (see Sterken [115] for details). While terms such as ‘ diagram’, ‘ analysis,’ etc. continue to be in wide-spread use, in this review we apply the newest, and somewhat more accurate, terminology of ‘ETV’. |
| 12 | In this regard we feel it necessity to make the following important cautionary note. In order to make his graphical solution simpler, Irwin [15] shifted the reference plane of the light-time orbit from the CM of the triple, i.e., the focal point of the outer ellipse to the geometric center of the orbit and thereby introduced an extra term of in his Equation (2) (compare his Equations (1) and (2)). This extra term has been also used in many of the recent papers dealing with LTTE. Besides the fact that there are no reasons to use this form in the era of numerical fitting procedures, an additional caveat is also warranted. In particular, this step can be justified only insofar as the orbital elements of the light-time orbit remain constant. If the situation is in fact different (which may well occur in tight CHT-s, where the third-body perturbations can cause variations of the orbital elements), this extra term would no longer remain constant and would lead to an error. Therefore, we recommend omitting the use of this additional term in all future studies. We made the same cautionary note in Borkovits et al. [83], but, unfortunately, we have found the same treatment in several newer papers as well. |
| 13 | http://www.as.up.krakow.pl/o-c/ (accessed on 5 January 2022). |
| 14 | http://keplerebs.villanova.edu/ (accessed on 5 January 2022). |
| 15 | A second peak in was also found, around , which coincides with the predictions of the numerical simulations of Fabrycky & Tremaine [81] based on the KCTF mechanism (Section 2.2). However, the distribution of the inner periods does not follow the parallel prediction of the same model and, therefore, the mentioned agreement is most probably incidental. |
| 16 | |
| 17 | Note also, for wider systems where astrometric measurements for both the inner and outer orbits are achievable, another problem arises, namely, insufficient coverage of the very long-period outer orbits. Consequently, the number of wider multiples with robustly determined mutual inclinations is also modest (see, e.g., Tokovinin & Latham [254]). |
| 18 | For a very conscise summary see e.g., Southworth [256] and references therein. |
References
- Chandler, S.C. On the period of Algol. Astron. J. 1888, 7, 165–168. [Google Scholar] [CrossRef]
- Chandler, S.C. Contributions to the knowledge of the variable stars, VI. Astron. J. 1892, 11, 121–126. [Google Scholar] [CrossRef]
- Chandler, S.C. Contributions to the knowledge of the variable stars, VII. Astron. J. 1893, 13, 45–47. [Google Scholar] [CrossRef]
- Chandler, S.C. The period of Algol. Astron. J. 1901, 22, 39–42. [Google Scholar] [CrossRef]
- Argelander, F.W.A. On the variable star Algol. Astron. J. 1855, 4, 57–59. [Google Scholar] [CrossRef]
- Rovithis-Livaniou, H. Study of Eclipsing Binaries: Light Curves & O-C Diagrams Interpretation. Gal 2020, 8, 78–92. [Google Scholar]
- Tisserand, F. Les Variations de Lumiére de L’étoile Algol. Bull. Soc. Astron. Fr. Rev. Mens. D’Astronomie Meteorol. Phys. Globe 1895, 9, 73–77. [Google Scholar]
- Cowling, T.G. On the motion of the apsidal line in close binary systems. Mon. Not. R. Astron. Soc. 1938, 98, 734. [Google Scholar] [CrossRef]
- Sterne, T.E. Apsidal motion in binary stars. Mon. Not. R. Astron. Soc. 1939, 99, 451–462. [Google Scholar] [CrossRef]
- Shakura, N.I. On the Apsidal Motion in Binary Stars. Sov. Astron. Lett. 1985, 11, 224–226. [Google Scholar]
- Hegedüs, T.; Nuspl, J. On the apsidal motion and its photometric observation in certain close binary systems. Acta Astron. 1986, 36, 381–393. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Borkovits, T.; Forgács-Dajka, E.; Regály, Z. Tidal and rotational effects in the perturbations of hierarchical triple stellar systems. II. Eccentric systems—The case of AS Camelopardalis. Astron. Astrophys. 2007, 473, 191–206. [Google Scholar] [CrossRef]
- Borkovits, T.; Forgács-Dajka, E.; Rappaport, S.A. Third-body perturbed apsidal motion in eclipsing binaries. EAS Publ. Ser. 2019, 82, 99–106. [Google Scholar] [CrossRef]
- Irwin, J.B. The Determination of a Light-Time Orbit. Astrophys. J. 1952, 116, 211–217. [Google Scholar] [CrossRef]
- Irwin, J.B. Standard light-time curves. Astron. J. 1959, 64, 149–155. [Google Scholar] [CrossRef]
- Borkovits, T.; Rappaport, S.; Hajdu, T.; Sztakovics, J. Eclipse timing variation analyses of eccentric binaries with close tertiaries in the Kepler field. Mon. Not. R. Astron. Soc. 2015, 448, 946–993. [Google Scholar] [CrossRef]
- Belopolski, A. Pulkova Mitt. 1906; 1, 101.
- Belopolski, A. Pulkova Mitt. 1911; 4, 171.
- Curtiss, R.H. On the Orbital Elements of Algol. Astrophys. J. 1908, 28, 150–161. [Google Scholar] [CrossRef]
- Tokovinin, A. Architecture of Hierarchical Stellar Systems and Their Formation. Universe 2021, 7, 352. [Google Scholar] [CrossRef]
- Tokovinin, A. From Binaries to Multiples. II. Hierarchical Multiplicity of F and G Dwarfs. Astron J. 2014, 147, 87. [Google Scholar] [CrossRef]
- Borkovits, T.; Derekas, A.; Kiss, L.L.; Király, A.; Forgács-Dajka, E.; Bíró, I.B.; Bedding, T.R.; Bryson, S.T.; Huber, D.; Szabó, R. Dynamical masses, absolute radii and 3D orbits of the triply eclipsing star HD 181068 from Kepler photometry. Mon. Not. R. Astron. Soc. 2013, 428, 1656–1672. [Google Scholar] [CrossRef]
- Borkovits, T.; Rappaport, S.A.; Tan, T.G.; Gagliano, R.; Jacobs, T.; Huang, X.; Mitnyan, T.; Hambsch, F.-J.; Kaye, T.; Maxted, P.F.L.; et al. The compact triply eclipsing triple star TIC 209409435 discovered with TESS. Mon. Not. R. Astron. Soc. 2020, 496, 4624–4636. [Google Scholar] [CrossRef]
- Xia, F.; Fu, Y.; Wang, X. The nearby very low mass triple star LHS 1070. Astrophys. J. 2019, 882, 147. [Google Scholar] [CrossRef]
- Mardling, R.A.; Aarseth, S.J. Tidal interactions in star cluster simulations. Mon. Not. R. Astron. Soc. 2001, 321, 398–420. [Google Scholar] [CrossRef]
- Orosz, J.A. Triple Stars Observed by Kepler. In Living Together: Planets, Host Stars and Binaries; Astronomical Society of the Pacific Conference Series; Rucinski, S.M., Torres, G., Zejda, M., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2015; Volume 496, pp. 55–70. [Google Scholar]
- Ebbighausen, E.G.; Struve, O. The Triple System Lambda Tauri. Astrophys. J. 1956, 124, 507–521. [Google Scholar] [CrossRef]
- Harrington, R.S. Dynamical Evolution of Triple Stars. Astron. J. 1968, 73, 190–194. [Google Scholar] [CrossRef]
- Naoz, S. The Eccentric Kozai-Lidov Effect and Its Applications. Ann. Rev. Astron. Astrophys. 2016, 54, 441–489. [Google Scholar] [CrossRef]
- Toonen, S.; Hamers, A.; Portegies Zwart, S. The evolution of hierarchical triple star-systems. Comput. Astrophys. 2016, 3, 6. [Google Scholar] [CrossRef]
- Toonen, S.; Portegies Zwart, S.; Hamers, A.S.; Bandopadhyay, D. The evolution of stellar triples. The most common evolutionary pathways. Astron. Astrophys. 2020, 640, A16. [Google Scholar] [CrossRef]
- Toonen, S.; Boekholt, T.C.N.; Portegies Zwart, S. Stellar triples on the edge; Comprehensive overview of the evolution of destabilised triples leading to stellar and binary exotica. arXiv 2021, arXiv:2108.04272. [Google Scholar]
- Maoz, D.; Mannucci, F.; Nelemans, G. Observational Clues to the Progenitors of Type Ia Supernovae. Ann. Rev. Astron. Astrophys. 2014, 52, 107–170. [Google Scholar] [CrossRef]
- Eggleton, P. Evolutionary Processes in Binary and Multiple Stars, 1st ed.; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Paczyński, B.; Szczygieł, D.M.; Pilecki, B.; Pojmański, G. Eclipsing binaries in the All Sky Automated Survey catalogue. Mon. Not. R. Astron. Soc. 2006, 368, 1311–1318. [Google Scholar] [CrossRef]
- Csizmadia, S.; Marton, G.; Klagyivik, P.; Spindler, S. Updated catalogue of the light curve solutions of contact binary stars. Astron. Nachr. 2007, 328, 821. [Google Scholar] [CrossRef]
- Podsiadlowski, P.; Rappaport, S.; Han, Z. On the formation and evolution of black hole binaries. Mon. Not. R. Astron. Soc. 2003, 341, 385–404. [Google Scholar] [CrossRef]
- Naoz, S.; Fragos, T.; Geller, A.; Stephan, A.P.; Rasio, F.A. Formation of Black Hole Low-mass X-ray Binaries in Hierarchical Triple Systems. Astrophys. J. 2016, 822, L24. [Google Scholar] [CrossRef]
- Champion, D.J.; Ransom, S.M.; Lazarus, P.; Camilo, F.; Bassa, C.; Kaspi, V.M.; Nice, D.J.; Freire, P.C.; Stairs, I.H.; Van Leeuwen, J.; et al. An Eccentric Binary Millisecond Pulsar in the Galactic Plane. Science 2008, 320, 1309. [Google Scholar] [CrossRef] [PubMed]
- Freire, P.C.C.; Bassa, C.G.; Wex, N.; Stairs, I.H.; Champion, D.J.; Ransom, S.M.; Lazarus, P.; Kaspi, V.M.; Hessels, J.W.T.; Kramer, M.; et al. On the nature and evolution of the unique binary pulsar J1903+0327. Mon. Not. R. Astron. Soc. 2011, 412, 2763–2780. [Google Scholar] [CrossRef]
- Portegies Zwart, S.; van den Heuvel, E.P.J.; van Leeuwen, J.; Nelemans, G. The Formation of the Eccentric-orbit Millisecond Pulsar J1903+0327 and the Origin of Single Millisecond Pulsars. Astrophys. J. 2011, 734, 55. [Google Scholar] [CrossRef]
- Pijloo, J.T.; Caputo, D.P.; Portegies Zwart, S.F. Asymmetric supernova in hierarchical multiple star systems and application to J1903+0327. Mon. Not. R. Astron. Soc. 2012, 424, 2914–2925. [Google Scholar] [CrossRef]
- Tauris, T.M.; van den Heuvel, E.P.J. Formation of the Galactic Millisecond Pulsar Triple System PSR J0337+1715014A Neutron Star with Two Orbiting White Dwarfs. Astrophys. J. 2014, 781, L13. [Google Scholar] [CrossRef][Green Version]
- Rodriguez, C.L.; Antonini, F. A Triple Origin for the Heavy and Low-spin Binary Black Holes Detected by LIGO/VIRGO. Astrophys. J. 2018, 863, 7. [Google Scholar] [CrossRef]
- Deme, B.; Hoang, B.-M.; Naoz, S.; Kocsis, B. Detecting Kozai-Lidov Imprints on the Gravitational Waves of Intermediate-mass Black Holes in Galactic Nuclei. Astrophys. J. 2020, 901, 125. [Google Scholar] [CrossRef]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Pierens, A.; Nelson, R.P. Migration and gas accretion scenarios for the Kepler 16, 34, and 35 circumbinary planets. Astron. Astrophys. 2013, 556, A134. [Google Scholar] [CrossRef]
- Marzari, F.; Thebault, P.; Scholl, H.; Picogna, G.; Baruteau, C. Influence of the circumbinary disk gravity on planetesimal accumulation in the Kepler-16 system. Astron. Astrophys. 2013, 553, A71. [Google Scholar] [CrossRef][Green Version]
- Meschiari, S. Circumbinary Planet Formation in the Kepler-16 System. I. N-body Simulations. Astrophys. J. 2012, 752, 71. [Google Scholar] [CrossRef]
- Lines, S.; Leinhardt, Z.M.; Paardekooper, S.; Baruteau, C.; Thebault, P. Forming Circumbinary Planets: N-body Simulations of Kepler-34. Astrophys. J. 2014, 782, L11. [Google Scholar] [CrossRef]
- Lines, S.; Leinhardt, Z.M.; Baruteau, C.; Paardekooper, S.-J.; Carter, P.J. Modelling circumbinary protoplanetary disks. I. Fluid simulations of the Kepler-16 and 34 systems. Astron. Astrophys. 2015, 582, A5. [Google Scholar] [CrossRef][Green Version]
- Lines, S.; Leinhardt, Z.M.; Baruteau, C.; Paardekooper, S.-J.; Carter, P.J. Modelling circumbinary protoplanetary disks. II. Gas disk feedback on planetesimal dynamical and collisional evolution in the circumbinary systems Kepler-16 and 34. Astron. Astrophys. 2016, 590, A62. [Google Scholar] [CrossRef]
- Marzari, F.; Thebault, P. Planets in Binaries: Formation and Dynamical Evolution. Galaxies 2019, 7, 84. [Google Scholar] [CrossRef]
- Klagyivik, P.; Deeg, H.J.; Cabrera, J.; Csizmadia, S.; Almenara, J.M. Limits to the presence of transiting circumbinary planets in CoRoT Data. Astron. Astrophys. 2017, 602, A117. [Google Scholar] [CrossRef]
- Slavenas, P. The Stellar Case of the Problem of Three Bodies. Transactions of the Astronomical observatory of Yale University; The Observatory: New Haven, CT, USA, 1927; Volume 6, p. 33. [Google Scholar]
- Slavenas, P. A Note on the Triple System, λ Tauri. Proc. Nat. Acad. Sci. USA 1927, 13, 833–837. [Google Scholar] [CrossRef]
- Brown, E.W. The stellar problem of three bodies. I. Application of satellite theory. Mon. Not. R. Astron. Soc. 1936, 97, 56–61. [Google Scholar] [CrossRef]
- Brown, E.W. The stellar problem of three bodies. II. The equations of motion with a simplified solution. Mon. Not. R. Astron. Soc. 1936, 97, 62–65. [Google Scholar] [CrossRef]
- Brown, E.W. The stellar problem of three bodies. III. The motions of the apse and node with applications to the Moon. Mon. Not. R. Astron. Soc. 1936, 97, 116–126. [Google Scholar] [CrossRef]
- Harrington, R.S. The Stellar Three-Body Problem. Celest. Mech. 1969, 1, 200–209. [Google Scholar] [CrossRef]
- Von Zeipel, H. Recherches sur le mouvement des petites planétes. Premiére partie. Ark. Mat. Astron. Fys. 1916, 11, 1–58. [Google Scholar]
- Von Zeipel, H. Recherches sur le mouvement des petites planétes. Deuxiéme partie. Ark. Mat. Astron. Fys. 1916, 11, 1–62. [Google Scholar]
- Von Zeipel, H. Recherches sur le mouvement des petites planétes. Troisiéme partie. Ark. Mat. Astron. Fys. 1917, 12, 1–89. [Google Scholar]
- Von Zeipel, H. Recherches sur le mouvement des petites planétes. Quatriéme partie. Ark. Mat. Astron. Fys. 1917, 13, 1–93. [Google Scholar]
- Söderhjelm, S. The three-body problem and eclipsing binaries. Application to Algol and lambda Tauri. Astron. Astrophys. 1975, 42, 229–236. [Google Scholar]
- Söderhjelm, S. Studies of the stellar three-body problem. Astron. Astrophys. 1982, 107, 54–60. [Google Scholar]
- Söderhjelm, S. Third-order and tidal effects in the stellar three-body problem. Astron. Astrophys. 1984, 141, 232–240. [Google Scholar]
- Mayer, P. Eclipsing Binaries with Light-time Effect. Bull. Astr. Inst. Czech. 1990, 41, 231–236. [Google Scholar]
- Borkovits, T.; Érdi, B.; Forgács-Dajka, E.; Kovács, T. On the detectability of long period perturbations in close hierarchical triple stellar systems. Astron. Astrophys. 2003, 398, 1091–1102. [Google Scholar] [CrossRef]
- Borkovits, T.; Csizmadia, S.; Forgács-Dajka, E.; Hegedüs, T. Transit timing variations in eccentric hierarchical triple exoplanetary systems. I. Perturbations on the time scale of the orbital period of the perturber. Astron. Astrophys. 2011, 528, A35. [Google Scholar] [CrossRef]
- Von Zeipel, H. Sur l’application des séries de M. Lindstedt à l’étude du mouvement des comètes périodiques. Astron. Nachr. 1910, 183, 345. [Google Scholar] [CrossRef]
- Lidov, M.L. The evolution of orbits of artificial satellites of planets under the action of gravitational perturbations of external bodies. Planet. Space Sci. 1962, 9, 719–759. [Google Scholar] [CrossRef]
- Kozai, Y. Secular perturbations of asteroids with high inclination and eccentricity. Astron. J. 1962, 67, 591–598. [Google Scholar] [CrossRef]
- Ford, E.B.; Kozinsky, B.; Rasio, F.A. Secular Evolution of Hierarchical Triple Star Systems. Astrophys. J. 2000, 535, 385–401. [Google Scholar] [CrossRef]
- Naoz, S.; Farr, W.M.; Lithwick, Y.; Rasio, F.A.; Teyssandier, J. Secular dynamics in hierarchical three-body systems. Mon. Not. R. Astron. Soc. 2013, 431, 2155–2171. [Google Scholar] [CrossRef]
- Ito, T.; Ohtsuka, K. The Lidov-Kozai Oscillation and Hugo von Zeipel. Monogr. Environ. Earth Planets 2019, 7, 1–113. [Google Scholar] [CrossRef]
- Zavala, R.T.; Hummel, C.A.; Boboltz, D.A.; Ojha, R.; Shaffer, D.B.; Tycner, C.; Richards, M.T.; Hutter, D.J. The Algol Triple System Spatially Resolved at Optical Wavelengths. Astrophys. J. 2010, 715, L44–L48. [Google Scholar] [CrossRef]
- Kiseleva, L.G.; Eggleton, P.P.; Mikkola, S. Tidal friction in triple stars. Mon. Not. R. Astron. Soc. 1998, 300, 292–302. [Google Scholar] [CrossRef]
- Mazeh, T.; Shaham, J. The orbital evolution of close triple systems: The binary eccentricity. Astron. Astrophys. 1979, 77, 145–151. [Google Scholar]
- Fabrycky, D.; Tremaine, S. Shrinking Binary and Planetary Orbits by Kozai Cycles with Tidal Friction. Astrophys. J. 2007, 669, 1298–1315. [Google Scholar] [CrossRef]
- Naoz, S.; Fabrycky, D. Mergers and Obliquities in Stellar Triples. Astrophys. J. 2014, 793, 137. [Google Scholar] [CrossRef]
- Borkovits, T.; Hajdu, T.; Sztakovics, J.; Rappaport, S.; Levine, A.; Bíró, I.B.; Klagyivik, P. A comprehensive study of the Kepler triples via eclipse timing. Mon. Not. R. Astron. Soc. 2016, 455, 4136–4165. [Google Scholar] [CrossRef]
- Moe, M.; Kratter, K.M. Dynamical Formation of Close Binaries during the Pre-main-sequence Phase. Astrophys. J. 2018, 854, 44. [Google Scholar] [CrossRef]
- Tokovinin, A.; Moe, M. Formation of close binaries by disc fragmentation and migration, and its statistical modelling. Mon. Not. R. Astron. Soc. 2020, 491, 5158–5171. [Google Scholar] [CrossRef]
- Yenawine, M.E.; Welsh, W.F.; Orosz, J.A.; Bieryla, A.; Cochran, W.D.; Endl, M.; Latham, D.W.; Quinn, S.N.; Short, D.R.; Windmiller, G. Photodynamical Modeling of the Fascinating Eclipses in the Triple-Star System KOI-126. arXiv 2021, arXiv:2110.09661. [Google Scholar]
- Khaliullin, K.F.; Khodykin, S.A.; Zakharov, A.I. On the Nature of the Anomalously Slow Apsidal Motion of DI Herculis. Astrophys. J. 1991, 375, 314–320. [Google Scholar] [CrossRef]
- Khodykin, S.A.; Vedeneyev, V.G. On the Third-Body Hypothesis of the Eclipsing Binary AS Camelopardalis. Astrophys. J. 1997, 475, 798–802. [Google Scholar] [CrossRef]
- Khodykin, S.A.; Zakharov, A.I.; Andersen, W.L. Stability of Triple Star Systems with Highly Inclined Orbits. Astrophys. J. 2004, 615, 506–511. [Google Scholar] [CrossRef]
- Albrecht, S.; Reffert, S.; Snellen, I.A.G.; Winn, J.N. Misaligned spin and orbital axes cause the anomalous precession of DI Herculis. Nature 2009, 461, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Pavlovski, K.; Southworth, J.; Kolbas, V. Apsidal Motion of the Eclipsing Binary AS Camelopardalis: Discrepancy Resolved. Astrophys. J. 2011, 734, L29. [Google Scholar] [CrossRef]
- Söderhjelm, S. Geometry and dynamics of the Algol system. Astron. Astrophys. 1980, 89, 100–112. [Google Scholar]
- Tokovinin, A. The Updated Multiple Star Catalog. Astrophys. J. 2018, 235, 6. [Google Scholar] [CrossRef]
- Fekel, F.C., Jr. The properties of close multiple stars. Astrophys. J. 1981, 246, 879–898. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.; Brown, T.; Caldwell, D.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Kepler Planet-Detection Mission: Introduction and First Results. Science 2010, 327, 977. [Google Scholar] [CrossRef] [PubMed]
- Auvergne, M.; Bodin, P.; Boisnard, L.; Buey, J.T.; Chaintreuil, S.; Epstein, G.; Jouret, M.; Lam-Trong, T.; Levacher, P.; Magnan, A.; et al. The CoRoT satellite in flight: Description and performance. Astron. Astrophys. 2009, 506, 411–424. [Google Scholar] [CrossRef]
- Howell, S.B.; Sobeck, C.; Haas, M.; Still, M.; Barclay, T.; Mullally, F.; Troeltzsch, J.; Aigrain, S.; Bryson, S.T.; Caldwell, D.; et al. The K2 Mission: Characterization and Early Results. Publ. Astron. Soc. Pac. 2014, 126, 398–408. [Google Scholar] [CrossRef]
- Ricker, G.R.; Winn, J.N.; Vanderspek, R.; Ennico, K.A.; Bakos, G.; Brown, T.M.; Burgasser, A.J.; Charbonneau, D.; Clampin, M.; Deming, L.D.; et al. Transiting Exoplanet Survey Satellite (TESS). J. Astron. Telesc. Instrum. Syst. 2015, 1, 014003. [Google Scholar] [CrossRef]
- Tokovinin, A. From Binaries to Multiples. I. Data on F and G Dwarfs within 67 pc of the Sun. Astron. J. 2014, 147, 86. [Google Scholar] [CrossRef]
- Schlesinger, F. Spectrographic observations of λ Tauri, indicating the presence of a third body in the system. In Publications of the Allegheny Observatory of the University of Pittsburgh; University of Pittsburgh: Pittsburgh, PA, USA, 1916; Volume 3, pp. 167–178. [Google Scholar]
- Pribulla, T.; Rucinski, S.M.; Lu, W.; Mochnacki, S.W.; Conidis, G.; Blake, R.M.; De Bond, H.; Thomson, J.R.; Pych, W.; Ogłoza, W.; et al. Radial Velocity Studies of Close Binary Stars. XI. Astron. J. 2006, 132, 769–780. [Google Scholar] [CrossRef]
- Borkovits, T.; Sperauskas, J.; Tokovinin, A.; Latham, D.W.; Csányi, I.; Hajdu, T.; Molnár, L. The compact multiple system HIP 41431. Mon. Not. R. Astron. Soc. 2019, 487, 4631–4647. [Google Scholar] [CrossRef]
- Guillout, P.; Klutsch, A.; Frasca, A.; Freire Ferrero, R.; Marilli, E.; Mignemi, G.; Biazzo, K.; Bouvier, J.; Monier, R.; Motch, C.; et al. A spectroscopic survey of the youngest field stars in the solar neighbourhood. I. The optically bright sample. Astron. Astrophys. 2009, 504, 829–843. [Google Scholar] [CrossRef]
- Derekas, A.; Kiss, L.L.; Borkovits, T.; Huber, D.; Lehmann, H.; Southworth, J.; Bedding, T.R.; Balam, D.; Hartmann, M.; Hrudkova, M.; et al. HD 181068: A Red Giant in a Triply Eclipsing Compact Hierarchical Triple System. Science 2011, 332, 216. [Google Scholar] [CrossRef] [PubMed]
- Tokovinin, A. Orbits of Subsystems in Four Hierarchical Multiple Stars. Astron. J. 2016, 152, 10. [Google Scholar] [CrossRef]
- Tokovinin, A. Orbits of Four Young Triple-Lined Multiple Systems. Astron. J. 2016, 152, 11. [Google Scholar] [CrossRef]
- Tokovinin, A. Spectroscopic Orbits of Subsystems in Multiple Stars. III. Astron. J. 2018, 156, 48. [Google Scholar] [CrossRef]
- Tokovinin, A. Spectroscopic Orbits of Subsystems in Multiple Stars. IV. Double-lined Pairs. Astron. J. 2018, 156, 194. [Google Scholar] [CrossRef]
- Tokovinin, A. Spectroscopic Orbits of Subsystems in Multiple Stars. V. Astron. J. 2019, 157, 91. [Google Scholar] [CrossRef]
- Tokovinin, A. Spectroscopic Orbits of Subsystems in Multiple Stars. VI. Astron. J. 2019, 158, 222. [Google Scholar] [CrossRef]
- Tokovinin, A. Spectroscopic Orbits of Subsystems in Multiple Stars. VII. Astron. J. 2020, 160, 69. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Ukita, N.; Kambe, E.; Kozłowski, S.K.; Sybilski, P.; Ratajczak, M.; Maehara, H.; Konacki, M. HIDES spectroscopy of bright detached eclipsing binaries from the Kepler field—I. Single-lined objects. Mon. Not. R. Astron. Soc. 2016, 461, 2896–2913. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Ukita, N.; Kambe, E.; Kozłowski, S.K.; Sybilski, P.; Maehara, H.; Ratajczak, M.; Konacki, M.; Pawłaszek, R.K. HIDES spectroscopy of bright detached eclipsing binaries from the Kepler field—II. Double- and triple-lined objects. Mon. Not. R. Astron. Soc. 2017, 468, 1726–1746. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Konacki, M.; Maehara, H.; Kambe, E.; Ukita, N.; Ratajczak, M.; Pigulski, A.; Kozłowski, S.K. HIDES spectroscopy of bright detached eclipsing binaries from the Kepler field—III. Spectral analysis, updated parameters and new systems. Mon. Not. R. Astron. Soc. 2019, 484, 451–475. [Google Scholar] [CrossRef]
- Sterken, C. The O-C Diagram: Basic Procedures. In The Light-Time Effect in Astrophysics: Causes and Cures of the O-C Diagram; Astronomical Society of the Pacific Conference Series; Sterken, C., Ed.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2005; Volume 335, pp. 3–23. [Google Scholar]
- Hertzsprung, E. On the possibility of determining the parallax of certain eclipsing variables and spectroscopic binaries. Bull. Astron. Inst. Neth. 1922, 1, 87. [Google Scholar]
- Woltjer, J., Jr. On a special case of orbit determination in the theory of eclipsing variables. Bull. Astron. Inst. Neth. 1922, 1, 93–94. [Google Scholar]
- Frieboes-Conde, H.; Herczeg, T. Period variations of fourteen eclipsing binaries with possible light-time effect. Astron. Astrophys. Suppl. Ser. 1973, 12, 1–78. [Google Scholar]
- Frieboes-Conde, H.; Herczeg, T.; Høg, E. The multiple system of Algol. Astron. Astrophys. 1970, 4, 78–88. [Google Scholar]
- Rappaport, S.; Deck, K.; Levine, A.; Borkovits, T.; Carter, J.; El Mellah, I.; Sanchis-Ojeda, R.; Kalomeni, B. Triple-star Candidates among the Kepler Binaries. Astrophys. J. 2013, 768, 33. [Google Scholar] [CrossRef]
- Kreiner, J.M.; Kim, C.-H.; Nha, I.-S. An Atlas of O-C Diagrams of Eclipsing Binary Stars; Wydawnictwo Naukowe AP: Krakow, Poland, 2001. [Google Scholar]
- Hall, D.S. The Relation Between Rs CVn and Algol. Space Sci. Rev. 1989, 50, 219–233. [Google Scholar] [CrossRef]
- Applegate, J.H. A Mechanism for Orbital Period Modulation in Close Binaries. Astrophys. J. 1992, 385, 621–629. [Google Scholar] [CrossRef]
- Lanza, A.F.; Rodonò, M. Gravitational quadrupole-moment variations in active binaries. Astron. Nachr. 2002, 323, 424–431. [Google Scholar] [CrossRef]
- Kalimeris, A.; Rovithis-Livaniou, H.; Rovithis, P. Starspots and photometric noise on observed minus calculated (O-C) diagrams. Astron. Astrophys. 2002, 387, 969–976. [Google Scholar] [CrossRef]
- Tran, K.; Levine, A.; Rappaport, S.; Borkovits, T.; Csizmadia, S.; Kalomeni, B. The Anticorrelated Nature of the Primary and Secondary Eclipse Timing Variations for the Kepler Contact Binaries. Astrophys. J. 2013, 774, 81. [Google Scholar] [CrossRef]
- Balaji, B.; Croll, B.; Levine, A.M.; Rappaport, S. Tracking the stellar longitudes of starspots in short-period Kepler binaries. Mon. Not. R. Astron. Soc. 2015, 448, 429–444. [Google Scholar] [CrossRef]
- Borkovits, T.; Derekas, A.; Fuller, J.; Szabó, G.M.; Pavlovski, K.; Csák, B.; Dózsa, Á.; Kovács, J.; Szabó, R.; Hambleton, K.M.; et al. HD 183648: A Kepler eclipsing binary with anomalous ellipsoidal variations and a pulsating component. Mon. Not. R. Astron. Soc. 2014, 443, 3068–3081. [Google Scholar] [CrossRef]
- Borkovits, T.; Hegedüs, T. On the invisible components of some eclipsing binaries. Astron. Astrophys. Suppl. Ser. 1996, 120, 63–75. [Google Scholar] [CrossRef]
- Moffat, A.F.J.; Vogt, N.; Vaz, L.P.R.; Gronbech, B. The early B-type eclipsing binary FZ CMA (HD 52942): A massive triple system. Astron. Astrophys. 1983, 120, 278–286. [Google Scholar]
- Bartolini, C.; Zoffoli, M. Light-time effect in IM Aurigae. Astron. Astrophys. 1986, 168, 377–379. [Google Scholar]
- Chambliss, C.R. Eclipsing Binaries in Multiple Star Systems. Publ. Astron. Soc. Pac. 1992, 104, 663–677. [Google Scholar] [CrossRef]
- Mayer, P. Eclipsing variable IU Aurigae. Bull. Astron. Inst. Czech. 1971, 22, 168–187. [Google Scholar]
- Mayer, P. Photometric Monitoring of IU Aurigae. Bull. Astron. Inst. Czech. 1983, 34, 335–340. [Google Scholar]
- Van Hamme, W.; Wilson, R.E. Third-Body Parameters from Whole Light and Velocity Curves. Astrophys. J. 2007, 661, 1129–1151. [Google Scholar] [CrossRef]
- Pribulla, T.; Baluďanský, D.; Dubovský, P.; Kudzej, I.; Parimucha, Š.; Siwak, M.; Vaňko, M. VW LMi: Tightest quadruple system known. Light-time effect and possible secular changes of orbits. Mon. Not. R. Astron. Soc. 2008, 390, 798–806. [Google Scholar] [CrossRef]
- Gies, D.R.; Williams, S.J.; Matson, R.A.; Guo, Z.; Thomas, S.M.; Orosz, J.A.; Peters, G.J. A Search for Hierarchical Triples using Kepler Eclipse Timing. Astron. J. 2012, 143, 137. [Google Scholar] [CrossRef]
- Conroy, K.E.; Prša, A.; Stassun, K.G.; Orosz, J.A.; Fabrycky, D.C.; Welsh, W.F. Kepler Eclipsing Binary Stars. IV. Precise Eclipse Times for Close Binaries and Identification of Candidate Three-body Systems. Astron. J. 2014, 147, 45. [Google Scholar] [CrossRef]
- Zasche, P.; Wolf, M.; Kučáková, H.; Vraštil, J.; Juryšek, J.; Mašek, M.; Jelínek, M. Ten Kepler Eclipsing Binaries Containing the Third Components. Astron. J. 2015, 149, 197. [Google Scholar] [CrossRef]
- Derekas, A.; Kiss, L.L.; Bedding, T.R. Eclipsing Binaries in the MACHO Database: New Periods and Classifications for 3031 Systems in the Large Magellanic Cloud. Astrophys. J. 2007, 663, 249–257. [Google Scholar] [CrossRef]
- Faccioli, L.; Alcock, C.; Cook, K.; Prochter, G.E.; Protopapas, P.; Syphers, D. Eclipsing Binary Stars in the Large and Small Magellanic Clouds from the MACHO Project: The Sample. Astron. J. 2007, 134, 1963–1993. [Google Scholar] [CrossRef]
- Wyrzykowski, L.; Udalski, A.; Kubiak, M.; Szymanski, M.K.; Zebrun, K.; Soszynski, I.; Wozniak, P.R.; Pietrzynski, G.; Szewczyk, O. The Optical Gravitational Lensing Experiment. Eclipsing Binary Stars in the Small Magellanic Cloud. Acta Astron. 2004, 54, 1–17. [Google Scholar]
- Pawlak, M.; Graczyk, D.; Soszyński, I.; Pietrukowicz, P.; Poleski, R.; Udalski, A.; Szymański, M.K.; Kubiak, M.; Pietrzyński, G.; Wyrzykowski, Ł.; et al. Eclipsing Binary Stars in the OGLE-III Fields of the Small Magellanic Cloud. Acta Astron. 2013, 63, 323–338. [Google Scholar]
- Pawlak, M.; Soszyński, I.; Udalski, A.; Szymański, M.K.; Wyrzykowski, Ł.; Ulaczyk, K.; Poleski, R.; Pietrukowicz, P.; Kozłowski, S.; Skowron, D.M.; et al. The OGLE Collection of Variable Stars. Eclipsing Binaries in the Magellanic System. Acta Astron. 2016, 66, 421–432. [Google Scholar]
- Zasche, P.; Wolf, M.; Vraštil, J.; Pilarčík, L.; Juryšek, J. The first study of the light-travel time effect in massive LMC eclipsing binaries. Astron. Astrophys. 2016, 590, A85. [Google Scholar] [CrossRef][Green Version]
- Zasche, P.; Wolf, M.; Vraštil, J. The first study of the light-traveltime effect in bright eclipsing binaries in the Small Magellanic Cloud. Mon. Not. R. Astron. Soc. 2017, 472, 2241–2248. [Google Scholar] [CrossRef]
- Hajdu, T.; Borkovits, T.; Forgács-Dajka, E.; Sztakovics, J.; Marschalkó, G.; Kutrovátz, G. Eclipse timing variation analysis of OGLE-IV eclipsing binaries towards the Galactic Bulge - I. Hierarchical triple system candidates. Mon. Not. R. Astron. Soc. 2019, 485, 2562–2572. [Google Scholar] [CrossRef]
- Hajdu, T.; Borkovits, T.; Forgács-Dajka, E.; Sztakovics, J.; Bódi, A. Eclipse timing variation analysis of OGLE-IV eclipsing binaries towards the Galactic Bulge - II. Short periodic triple stellar systems. Mon. Not. R. Astron. Soc. 2022, 509, 246–260. [Google Scholar] [CrossRef]
- Soszyński, I.; Pawlak, M.; Pietrukowicz, P.; Udalski, A.; Szymański, M.K.; Wyrzykowski, Ł.; Ulaczyk, K.; Poleski, R.; Kozłowski, S.; Skowron, D.M.; et al. The OGLE Collection of Variable Stars. Over 450 000 Eclipsing and Ellipsoidal Binary Systems Toward the Galactic Bulge. Acta Astron. 2016, 66, 405–420. [Google Scholar]
- Li, M.C.A.; Rattenbury, N.J.; Bond, I.A.; Sumi, T.; Bennett, D.P.; Koshimoto, N.; Abe, F.; Asakura, Y.; Barry, R.; Bhattacharya, A.; et al. The first eclipsing binary catalogue from the MOA-II data base. Mon. Not. R. Astron. Soc. 2017, 470, 539–550. [Google Scholar] [CrossRef]
- Li, M.C.A.; Rattenbury, N.J.; Bond, I.A.; Sumi, T.; Bennett, D.P.; Koshimoto, N.; Abe, F.; Asakura, Y.; Barry, R.; Bhattacharya, A.; et al. A study of the light travel time effect in short-period MOA eclipsing binaries via eclipse timing. Mon. Not. R. Astron. Soc. 2018, 480, 4557–4577. [Google Scholar] [CrossRef]
- Wolf, M.; Zasche, P.; Kučáková, H.; Vraštil, J.; Hornoch, K.; Šmelcer, L.; Bílek, F.; Pilarčík, L.; Chrastina, M. Substellar companions in low-mass eclipsing binaries. NSVS 01286630, NSVS 02502726, and NSVS 07453183. Astron. Astrophys. 2016, 587, A82. [Google Scholar] [CrossRef]
- Agol, E.; Steffen, J.; Sari, R.; Clarkson, W. On detecting terrestrial planets with timing of giant planet transits. Mon. Not. R. Astron. Soc. 2005, 359, 567–579. [Google Scholar] [CrossRef]
- Mitnyan, T.; Borkovits, T.; Rappaport, S.A.; Pál, A.; Maxted, P.F.L. TIC 278825952: A triply eclipsing hierarchical triple system with the most intrinsically circular outer orbit. Mon. Not. R. Astron. Soc. 2020, 498, 6034–6043. [Google Scholar] [CrossRef]
- Borkovits, T.; Mitnyan, T.; Rappaport, S.A.; Pribulla, T.; Powell, B.P.; Kostov, V.B.; Bíró, I.B.; Csányi, I.; Garai, Z.; Gary, B.L.; et al. Triply eclipsing triple stars in the northern TESS fields: TICs 193993801, 388459317 and 52041148. Mon. Not. R. Astron. Soc. 2022, 510, 1352–1374. [Google Scholar] [CrossRef]
- Özdemir, S.; Mayer, P.; Drechsel, H.; Demircan, O.; Ak, H. Refinement of third body parameters and new photometric results for the early-type multiple system IU Aurigae. Astron. Astrophys. 2003, 403, 675–681. [Google Scholar] [CrossRef]
- Steffen, J.H.; Quinn, S.N.; Borucki, W.J.; Brugamyer, E.; Bryson, S.T.; Buchhave, L.A.; Cochran, W.D.; Endl, M.; Fabrycky, D.C.; Ford, E.B.; et al. The architecture of the hierarchical triple star KOI 928 from eclipse timing variations seen in Kepler photometry. Mon. Not. R. Astron. Soc. 2011, 417, L31–L35. [Google Scholar] [CrossRef]
- Prša, A.; Batalha, N.; Slawson, R.W.; Doyle, L.R.; Welsh, W.F.; Orosz, J.A.; Seager, S.; Rucker, M.; Mjaseth, K.; Engle, S.G.; et al. Kepler Eclipsing Binary Stars. I. Catalog and Principal Characterization of 1879 Eclipsing Binaries in the First Data Release. Astron. J. 2011, 141, 83. [Google Scholar] [CrossRef]
- Slawson, R.W.; Prša, A.; Welsh, W.F.; Orosz, J.A.; Rucker, M.; Batalha, N.; Doyle, L.R.; Engle, S.G.; Conroy, K.; Coughlin, J.; et al. Kepler Eclipsing Binary Stars. II. 2165 Eclipsing Binaries in the Second Data Release. Astron. J. 2011, 142, 160. [Google Scholar] [CrossRef]
- Matijevič, G.; Prša, A.; Orosz, J.A.; Welsh, W.F.; Bloemen, S.; Barclay, T. Kepler Eclipsing Binary Stars. III. Classification of Kepler Eclipsing Binary Light Curves with Locally Linear Embedding. Astron. J. 2012, 143, 123. [Google Scholar] [CrossRef]
- Hajdu, T.; Borkovits, T.; Forgács-Dajka, E.; Sztakovics, J.; Marschalkó, G.; Benko, J.M.; Klagyivik, P.; Sallai, M.J. A search for tight hierarchical triple systems amongst the eclipsing binaries in the CoRoT fields. Mon. Not. R. Astron. Soc. 2017, 471, 1230–1245. [Google Scholar] [CrossRef]
- Borkovits, T.; Rappaport, S.A.; Hajdu, T.; Maxted, P.F.L.; Pál, A.; Forgács-Dajka, E.; Klagyivik, P.; Mitnyan, T. TICs 167692429 and 220397947: The first compact hierarchical triple stars discovered with TESS. Mon. Not. R. Astron. Soc. 2020, 493, 5005–5023. [Google Scholar] [CrossRef]
- Carter, J.A.; Fabrycky, D.C.; Ragozzine, D.; Holman, M.J.; Quinn, S.N.; Latham, D.W.; Buchhave, L.A.; Van Cleve, J.; Cochran, W.D.; Cote, M.T.; et al. KOI-126: A Triply Eclipsing Hierarchical Triple with Two Low-Mass Stars. Science 2011, 331, 562. [Google Scholar] [CrossRef]
- Marsh, T.R.; Armstrong, D.J.; Carter, P.J. KIC 2856960: The impossible triple star. Mon. Not. R. Astron. Soc. 2014, 445, 309–319. [Google Scholar] [CrossRef][Green Version]
- Masuda, K.; Uehara, S.; Kawahara, H. Absolute Dimensions of a Flat Hierarchical Triple System KIC 6543674 from the Kepler Photometry. Astrophys. J. 2015, 806, L37. [Google Scholar] [CrossRef]
- Nemravová, J.A.; Harmanec, P.; Brož, M.; Vokrouhlický, D.; Mourard, D.; Hummel, C.A.; Cameron, C.; Matthews, J.M.; Bolton, C.T.; Božić, H.; et al. ξ Tauri: A unique laboratory to study the dynamic interaction in a compact hierarchical quadruple system. Astron. Astrophys. 2016, 594, A55. [Google Scholar] [CrossRef]
- Armstrong, D.; Pollacco, D.; Watson, C.A.; Faedi, F.; Gómez Maqueo Chew, Y.; Cegla, H.M.; McDaid, P.; Burton, J.; McCormac, J.; Skillen, I. A transiting companion to the eclipsing binary KIC002856960. Astron. Astrophys. 2012, 545, L4. [Google Scholar] [CrossRef]
- Getley, A.K.; Carter, B.; King, R.; O’Toole, S. Stability of planetary, single M dwarf, and binary star companions to Kepler detached eclipsing binaries and a possible five-body system. Mon. Not. R. Astron. Soc. 2020, 498, 4356–4364. [Google Scholar] [CrossRef]
- Shibahashi, H.; Kurtz, D.W. FM stars: A Fourier view of pulsating binary stars, a new technique for measuring radial velocities photometrically. Mon. Not. R. Astron. Soc. 2012, 422, 738–752. [Google Scholar] [CrossRef]
- Hełminiak, K.G.; Ukita, N.; Kambe, E.; Kozłowski, S.K.; Pawłaszek, R.; Maehara, H.; Baranec, C.; Konacki, M. KIC 4150611: A rare multi-eclipsing quintuple with a hybrid pulsator. Astron. Astrophys. 2017, 602, A30. [Google Scholar] [CrossRef]
- Conroy, K.E.; Prša, A.; Stassun, K.G. A Triple Eclipsing System as a Test Case for Close Binary Formation through Kozai Cycles. In Living Together: Planets, Host Stars and Binaries; Astronomical Society of the Pacific Conference Series; Rucinski, S.M., Torres, G., Zejda, M., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2015; Volume 496, pp. 99–103. [Google Scholar]
- Alonso, R.; Deeg, H.J.; Hoyer, S.; Lodieu, N.; Palle, E.; Sanchis-Ojeda, R. HD 144548: A young triply eclipsing system in the Upper Scorpius OB association. Astron. Astrophys. 2015, 584, L8. [Google Scholar] [CrossRef][Green Version]
- Borkovits, T.; Rappaport, S.; Kaye, T.; Isaacson, H.; Vanderburg, A.; Howard, A.W.; Kristiansen, M.H.; Omohundro, M.R.; Schwengeler, H.M.; Terentev, I.A.; et al. Photodynamical analysis of the triply eclipsing hierarchical triple system EPIC 249432662. Mon. Not. R. Astron. Soc. 2019, 483, 1934–1951. [Google Scholar] [CrossRef]
- Pollacco, D.L.; Skillen, I.; Cameron, A.C.; Christian, D.J.; Hellier, C.; Irwin, J.; Lister, T.A.; Street, R.A.; West, R.G.; Anderson, D.; et al. The WASP Project and the SuperWASP Cameras. Publ. Astron. Soc. Pac. 2006, 118, 1407–1418. [Google Scholar] [CrossRef]
- Kochanek, C.S.; Shappee, B.J.; Stanek, K.Z.; Holoien, T.W.-S.; Thompson, T.A.; Prieto, J.L.; Dong, S.; Shields, J.V.; Will, D.; Britt, C.; et al. The All-Sky Automated Survey for Supernovae (ASAS-SN) Light Curve Server v1. 0 Publ. Astron. Soc. Pac. 2017, 129, 104502. [Google Scholar] [CrossRef]
- Heinze, A.N.; Tonry, J.L.; Denneau, L.; Flewelling, H.; Stalder, B.; Rest, A.; Smith, K.W.; Smartt, S.J.; Weiland, H. A First Catalog of Variable Stars Measured by the Asteroid Terrestrial-impact Last Alert System (ATLAS). Astron. J. 2018, 156, 241. [Google Scholar] [CrossRef]
- Pepper, J.; Pogge, R.W.; DePoy, D.L.; Marshall, J.L.; Stanek, K.Z.; Stutz, A.M.; Poindexter, S.; Siverd, R.; O’Brien, T.P.; Trueblood, M.; et al. The Kilodegree Extremely Little Telescope (KELT): A Small Robotic Telescope for Large-Area Synoptic Surveys. Publ. Astron. Soc. Pac. 2007, 119, 923–935. [Google Scholar] [CrossRef]
- Hill, G.; Aikman, G.C.L.; Cowley, A.P.; Bolton, C.T.; Thomas, J.C. The radio-flaring triple system b Persei. Astrophys. J. 1976, 208, 152–164. [Google Scholar] [CrossRef]
- Armstrong, J.T.; Mozurkewich, D.; Rickard, L.J.; Hutter, D.J.; Benson, J.A.; Bowers, P.F.; Elias, N.M., II; Hummel, C.A.; Johnston, K.J.; Buscher, D.F.; et al. The Navy Prototype Optical Interferometer. Astrophys. J. 1998, 496, 550–571. [Google Scholar] [CrossRef]
- Hummel, C.A.; Zavala, R.T.; Sanborn, J. Binary Studies with the Navy Precision Optical Interferometer. Cent. Eur. Astrophys. Bull. 2013, 37, 127–135. [Google Scholar]
- Hegedüs, T.; Bíró, I.B.; Borkovits, T.; Paragi, Z. Photoelectric Minima of 30 Eclipsing Binary Systems; Information Bulletin on Variable Stars No. 4340; Konkoly Observatory: Budapest, Hungary, 1996. [Google Scholar]
- Collins, D.F.; Sanborn, J.; Zavala, R.T. Modern V Photometry of the Eclipsing Triple System b Persei. In Proceedings of the Society for Astronomical Sciences Annual Symposium, Ontario, CA, USA, 12–14 June 2014; Volume 33, pp. 205–211. [Google Scholar]
- Collins, D.F. Time Series Observations of the 2015 Eclipse of b Persei (not beta Persei). J. AAVSO 2016, 44, 82. [Google Scholar]
- Doyle, L.R.; Carter, J.A.; Fabrycky, D.C.; Slawson, R.W.; Howell, S.B.; Winn, J.N.; Orosz, J.A.; Prša, A.; Welsh, W.F.; Quinn, S.N.; et al. Kepler-16: A Transiting Circumbinary Planet. Science 2011, 333, 1602. [Google Scholar] [CrossRef]
- Orosz, J.A.; Welsh, W.F.; Carter, J.A.; Fabrycky, D.C.; Cochran, W.D.; Endl, M.; Ford, E.B.; Haghighipour, N.; MacQueen, P.J.; Mazeh, T.; et al. Kepler-47: A Transiting Circumbinary Multiplanet System. Science 2012, 337, 1511. [Google Scholar] [CrossRef] [PubMed]
- Kostov, V.B.; Orosz, J.A.; Feinstein, A.D.; Welsh, W.F.; Cukier, W.; Haghighipour, N.; Quarles, B.; Martin, D.V.; Montet, B.T.; Torres, G.; et al. TOI-1338: TESS’ First Transiting Circumbinary Planet. Astron. J. 2020, 159, 253. [Google Scholar] [CrossRef]
- Kostov, V.B.; Powell, B.P.; Orosz, J.A.; Welsh, W.F.; Cochran, W.; Collins, K.A.; Endl, M.; Hellier, C.; Latham, D.W.; MacQueen, P.; et al. TIC 172900988: A Transiting Circumbinary Planet Detected in One Sector of TESS Data. Astron. J. 2021, 162, 234. [Google Scholar] [CrossRef]
- Powell, B.P.; Kostov, V.B.; Rappaport, S.A.; Borkovits, T.; Zasche, P.; Tokovinin, A.; Kruse, E.; Latham, D.W.; Montet, B.T.; Jensen, E.L.; et al. TIC 168789840: A Sextuply Eclipsing Sextuple Star System. Astron. J. 2021, 161, 162. [Google Scholar] [CrossRef]
- Lee, C.-U.; Kim, S.-L.; Lee, J.W.; Kim, C.-H.; Jeon, Y.-B.; Kim, H.-I.; Yoon, J.-N.; Humphrey, A. V994 Herculis: The multiple system with a quadruple-lined spectrum and a double eclipsing feature. Mon. Not. R. Astron. Soc. 2008, 389, 1630–1636. [Google Scholar] [CrossRef]
- Zasche, P.; Uhlař, R. Ole Rømer’s method still on the stage: The study of two bound eclipsing binaries in quintuple system V994 Her. Mon. Not. R. Astron. Soc. 2013, 429, 3472–3476. [Google Scholar] [CrossRef]
- Zasche, P.; Uhlař, R. Updated study of the quintuple system V994 Herculis. Astron. Astrophys. 2016, 588, A121. [Google Scholar] [CrossRef][Green Version]
- Rappaport, S.; Vanderburg, A.; Borkovits, T.; Kalomeni, B.; Halpern, J.P.; Ngo, H.; Mace, G.N.; Fulton, B.J.; Howard, A.W.; Isaacson, H.; et al. EPIC 220204960: A Quadruple Star System Containing Two Strongly Interacting Eclipsing Binaries. Mon. Not. R. Astron. Soc. 2017, 467, 2160–2179. [Google Scholar] [CrossRef]
- Kostov, V.B.; Powell, B.P.; Torres, G.; Borkovits, T.; Rappaport, S.A.; Tokovinin, A.; Zasche, P.; Anderson, D.; Barclay, T.; Berlind, P.; et al. TIC 454140642: A Compact, Coplanar, Quadruple-lined Quadruple Star System Consisting of Two Eclipsing Binaries. Astrophys. J. 2021, 917, 93. [Google Scholar] [CrossRef]
- Borkovits, T.; Rappaport, S.A.; Maxted, P.F.L.; Terentev, I.; Omohundro, M.; Gagliano, R.; Jacobs, T.; Kristiansen, M.H.; LaCourse, D.; Schwengeler, H.M.; et al. BG Ind: The nearest doubly eclipsing, compact hierarchical quadruple system. Mon. Not. R. Astron. Soc. 2021, 503, 3759–3774. [Google Scholar] [CrossRef]
- Rowden, P.; Borkovits, T.; Jenkins, J.M.; Stassun, K.G.; Twicken, J.D.; Newton, E.R.; Ziegler, C.; Hellier, C.; Soto, A.G.; Matthews, E.C.; et al. TIC 278956474: Two Close Binaries in One Young Quadruple System Identified by TESS. Astron. J. 2020, 160, 76. [Google Scholar] [CrossRef]
- Volkov, I.M.; Kravtsova, A.S.; Chochol, D. BU CMi as a Quadruple Doubly Eclipsing System. Astron. Rep. 2021, 65, 826–838. [Google Scholar] [CrossRef]
- Jayaraman, R.; Rappaport, S.; Borkovits, T.; Pribulla, T.; Komžik, R.; Mitnyan, T.; Zasche, P.; Tokovinin, A.; Rodriguez, J.E.; Terentev, I.; et al. BU Canis Minoris: The Tightest-Known Flat Quadruple System. In Proceedings of the Posters from the TESS Science Conference II (TSC2), Virtual Conference. 2–6 August 2021; p. 14. [Google Scholar]
- Drechsel, H.; Haas, S.; Lorenz, R.; Mayer, P. New photometric and spectroscopic results for IU Aurigae—An early-type eclipsing binary in a multiple system. Astron. Astrophys. 1994, 284, 853–864. [Google Scholar]
- Marcadon, F.; Hełminiak, K.G.; Marques, J.P.; Pawłaszek, R.; Sybilski, P.; Kozłowski, S.K.; Ratajczak, M.; Konacki, M. Analysis of eclipsing binaries in multiple stellar systems: The case of V1200 Centauri. Mon. Not. R. Astron. Soc. 2020, 499, 3019–3033. [Google Scholar] [CrossRef]
- Hong, K.; Koo, J.-R.; Lee, J.W.; Kim, S.-L.; Lee, C.-U.; Park, J.-H.; Kim, H.-W.; Lee, D.-J.; Kim, D.-J.; Han, C. KMTNet Time-series Photometry of the Doubly Eclipsing Binary Stars Located in the Large Magellanic Cloud. Publ. Astron. Soc. Pac. 2018, 130, 054204. [Google Scholar] [CrossRef]
- Hall, D.S. A gross secular expansion of the primary of RW Per. In Mass Loss from Stars, Proceedings of the Second Trieste Colloquium on Astrophysics, 12–17 September 1968; Hack, M., Ed.; Astrophysics and Space Science Library; Springer: Berlin/Heidelberg, Germany, 1969; Volume 13, pp. 171–183. [Google Scholar]
- Schaefer, B.E.; Fried, R.E. RW Per: Nodal Motion Changes its Amplitude by 1.4 Mag. Astron. J. 1991, 101, 208–213. [Google Scholar] [CrossRef]
- Olson, E.C.; Schaefer, B.E.; Lines, R.; Lines, H.; Fried, R.E. A New Investigation of Photometric Changes in RW Persei. Astron. J. 1992, 103, 256–262. [Google Scholar] [CrossRef]
- Söderhjelm, S. AY Mus: A Triple System? Information Bulletin on Variable Stars No. 885; Konkoly Observatory: Budapest, Hungary, 1974. [Google Scholar]
- Zakirov, M.M.; Azimov, A.A. The Disappearance of Minima of Eclipsing Binary SS Lac in Open Cluster NGC 7209; Information Bulletin on Variable Stars No. 3487; Konkoly Observatory: Budapest, Hungary, 1990. [Google Scholar]
- Lehmann, T. The Unusual Eclipsing Variable SS Lacertae. Information Bulletin on Variable Stars No. 3610; Konkoly Observatory: Budapest, Hungary, 1991. [Google Scholar]
- Mossakovskaya, L.V. On disappearance of eclipses in the eclipsing variable star SS Lacertae. Astron. Lett. 1993, 19, 35. [Google Scholar]
- Schiller, S.J.; Milone, E.F. Binaries in Clusters: Exploring Binary and Cluster Evolution. In The Origins, Evolution, and Destinies of Binary Stars in Clusters; Astronomical Society of the Pacific Conference Series; Milone., E.F., Mermilliod, J.-C., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 1996; Volume 90, pp. 120–130. [Google Scholar]
- Milone, E.F.; Schiller, S.J.; Munari, U.; Kallrath, J. Analyses of the Currently Noneclipsing Binary SS Lacertae or SS Lacertae’s Eclipses. Astron. J. 2000, 119, 1405–1423. [Google Scholar] [CrossRef]
- Torres, G.; Stefanik, R.P. The Cessation of Eclipses in SS Lacertae: The Mystery Solved. Astron. J. 2000, 119, 1914–1929. [Google Scholar] [CrossRef]
- Torres, G. The Change in the Inclination Angle of the Noneclipsing Binary SS Lacertae: Future Eclipses. Astron. J. 2001, 121, 2227–2238. [Google Scholar] [CrossRef]
- Lacy, C.H.S.; Helt, B.E.; Vaz, L.P.R. V907 Scorpii: A remarkable binary star whose eclipses turn on and off and on and off. Astron. J. 1999, 117, 541–547. [Google Scholar] [CrossRef]
- Zasche, P.; Paschke, A. HS Hydrae about to turn off its eclipses. Astron. Astrophys. 2012, 542, L23. [Google Scholar] [CrossRef][Green Version]
- Davenport, J.R.A.; Windemuth, D.; Warmbein, K.; Howard, E.L.; Klein, C.; Birky, J. The Rise and Fall of the Eclipsing Binary HS Hydrae. Astron. J. 2021, 162, 189. [Google Scholar] [CrossRef]
- Guinan, E.; Bonaro, M.; Engle, S.; Prsa, A. Eclipsing Binaries That Don’t Eclipse Anymore: The Strange Case of the Once (and Future?) Eclipsing Binary QX Cassiopeiae. J. AAVSO 2012, 40, 417. [Google Scholar]
- Mayer, P.; Pribulla, T.; Chochol, D. Variable Depths of Minima of the Eclipsing Binary V685 Cen. Inf. Bull. Var. Stars 2004, 5563. [Google Scholar]
- Drechsel, H.; Lorenz, R.; Mayer, P. Solution of light curves with third light contribution: The eclipsing binaries LY Aurigae and AH Cephei reconsidered. Astron. Astrophys. 1989, 221, 49–61. [Google Scholar]
- Azimov, A.A.; Zakirov, M.M. An Enigmatic Close Binary V699 Cygni; Information Bulletin on Variable Stars No. 3667; Konkoly Observatory: Budapest, Hungary, 1991. [Google Scholar]
- Guilbault, P.R.; Lloyd, C.; Paschke, A. A Study of the Non-Eclipsing Binary SV Geminorum; Information Bulletin on Variable Stars No. 5090; Konkoly Observatory: Budapest, Hungary, 2001. [Google Scholar]
- Southworth, J.; Bowman, D.M.; Pavlovski, K. A β Cephei pulsator and a changing orbital inclination in the high-mass eclipsing binary system VV Orionis. Mon. Not. R. Astron. Soc. Lett. 2021, 501, L65–L70. [Google Scholar] [CrossRef]
- Gaulme, P.; McKeever, J.; Rawls, M.L.; Jackiewicz, J.; Mosser, B.; Guzik, J.A. Red Giants in Eclipsing Binary and Multiple-star Systems: Modeling and Asteroseismic Analysis of 70 Candidates from Kepler Data. Astrophys. J. 2013, 767, 82. [Google Scholar] [CrossRef]
- Gaulme, P. A comprehensive analysis of KIC 7955301. 2022; under preparation. [Google Scholar]
- Chambliss, C.R.; Leung, K.-C. Multicolor photometry of the eclipsing binary system VV Orionis. Astrophys. J. Suppl. Ser. 1982, 49, 531–544. [Google Scholar] [CrossRef]
- Daniel, Z. The orbit and spectrum of VV Orionis. InPublications of the Allegheny Observatory of the University of Pittsburgh; University of Pittsburgh: Pittsburgh, PA, USA, 1915; Volume 3, pp. 179–188. [Google Scholar]
- Chambliss, C.R. A Re-Analysis of the Eclipsing Binary System VV Orionis. Astrophys. Space Sci. 1983, 89, 15–32. [Google Scholar] [CrossRef]
- Terrell, D.; Munari, U.; Siviero, A. Observational studies of early-type binary stars: VV Orionis. Mon. Not. R. Astron. Soc. 2007, 374, 530–534. [Google Scholar] [CrossRef]
- Graczyk, D.; Soszyński, I.; Poleski, R.; Pietrzyński, G.; Udalski, A.; Szymański, M.K.; Kubiak, M.; Wyrzykowski, Ł.; Ulaczyk, K. The Optical Gravitational Lensing Experiment. The OGLE-III Catalog of Variable Stars. XII. Eclipsing Binary Stars in the Large Magellanic Cloud. Acta Astron. 2011, 61, 103–122. [Google Scholar]
- Zasche, P.; Wolf, M. The first analysis of extragalactic binary-orbit precession. Astron. Astrophys. 2013, 559, A41. [Google Scholar] [CrossRef]
- Juryšek, J.; Zasche, P.; Wolf, M.; Vraštil, J.; Vokrouhlický, D.; Skarka, M.; Liška, J.; Janík, J.; Zejda, M.; Kurfürst, P.; et al. New inclination changing eclipsing binaries in the Magellanic Clouds. Astron. Astrophys. 2018, 609, A46. [Google Scholar] [CrossRef]
- Bachmann, P.J.; Hershey, J.L. Orbital analysis of Algol AB, C from combined astrometric photometric and radial velocity data. Astron. J. 1975, 80, 836–843. [Google Scholar] [CrossRef]
- Labeyrie, A.; Bonneau, D.; Stachnik, R.V.; Gezari, D.Y. Speckle Interferometry. III. High-Resolution Measurements of Twelve Close Binary Systems. Astrophys. J. 1974, 194, L147–L151. [Google Scholar] [CrossRef]
- Bonneau, D. Orbital inclination and masses newly determined from the triple system Algol. Astron. Astrophys. 1979, 80, L11–L12. [Google Scholar]
- Pan, X.; Shao, M.; Colavita, M.M. High Angular Resolution Measurements of Algol. Astrophys. J. 1993, 413, L129–L131. [Google Scholar] [CrossRef]
- Lestrade, J.-F.; Phillips, R.B.; Hodges, M.W.; Preston, R.A. VLBI Astrometric Identification of the Radio-emitting Region in Algol and Determination of the Orientation of the Close Binary. Astrophys. J. 1993, 410, 808–814. [Google Scholar] [CrossRef]
- Rudy, R.J. Polarimetric determination of the directions of revolution and spatial orientations of close binary systems. Mon. Not. R. Astron. Soc. 1979, 186, 473–477. [Google Scholar] [CrossRef][Green Version]
- Kemp, J.C.; Barbour, M.S.; McBirney, R.E.; Rudy, R.J. Algol: A further study of the optical polarization. Astrophys. J. 1981, 243, 557–566. [Google Scholar] [CrossRef]
- Kemp, J.C.; Henson, G.D.; Barbour, M.S.; Kraus, D.J.; Collins, G.W., II. Discovery of eclipse polarization in Algol. Astrophys. J. 1983, 273, L85–L88. [Google Scholar] [CrossRef]
- Hummel, C.A.; Benson, J.A.; Hutter, D.J.; Johnston, K.J.; Mozurkewich, D.; Armstrong, J.T.; Hindsley, R.B.; Gilbreath, G.C.; Rickard, L.J.; White, N.M. First Observations with a Co-phased Six-Station Optical Long-Baseline Array: Application to the Triple Star η Virginis. Astron. J. 2003, 125, 2630–2644. [Google Scholar] [CrossRef]
- Colavita, M.M.; Wallace, J.K.; Hines, B.E.; Gursel, Y.; Malbet, F.; Palmer, D.L.; Pan, X.P.; Shao, M.; Yu, J.W.; Boden, A.F.; et al. The Palomar Testbed Interferometer. Astrophys. J. 1999, 510, 505–521. [Google Scholar] [CrossRef]
- Lane, B.F.; Muterspaugh, M.W. Differential Astrometry of Subarcsecond Scale Binaries at the Palomar Testbed Interferometer. Astrophys. J. 2004, 601, 1129–1135. [Google Scholar] [CrossRef]
- Muterspaugh, M.W.; Lane, B.F.; Konacki, M.; Burke, B.F.; Colavita, M.M.; Kulkarni, S.R.; Shao, M. PHASES differential astrometry and the mutual inclination of the V819 Herculis triple star system. Astron. Astrophys. 2006, 446, 723–732. [Google Scholar] [CrossRef]
- Muterspaugh, M.W.; Lane, B.F.; Konacki, M.; Wiktorowicz, S.; Burke, B.F.; Colavita, M.M.; Kulkarni, S.R.; Shao, M. PHASES Differential Astrometry and Iodine Cell Radial Velocities of the κ Pegasi Triple Star System. Astrophys. J. 2006, 636, 1020–1032. [Google Scholar] [CrossRef]
- Borkovits, T.; Forgács-Dajka, E.; Regály, Z. Tidal and rotational effects in the perturbations of hierarchical triple stellar systems. I. Numerical model and a test application for Algol. Astron. Astrophys. 2004, 426, 951–961. [Google Scholar] [CrossRef][Green Version]
- Csizmadia, S.; Borkovits, T.; Paragi, Z.; Ábrahám, P.; Szabados, L.; Mosoni, L.; Sturmann, L.; Sturmann, J.; Farrington, C.; McAlister, H.A.; et al. Interferometric Observations of the Hierarchical Triple System Algol. Astrophys. J. 2009, 705, 436–445. [Google Scholar] [CrossRef]
- Ten Brummelaar, T.A.; McAlister, H.A.; Ridgway, S.T.; Bagnuolo, W.G., Jr.; Turner, N.H.; Sturmann, L.; Sturmann, J.; Berger, D.H.; Ogden, C.E.; Cadman, R.; et al. First Results from the CHARA Array. II. A Description of the Instrument. Astrophys. J. 2005, 628, 453–465. [Google Scholar] [CrossRef]
- Perryman, M.A.C.; Lindegren, L.; Kovalevsky, J.; Hoeg, E.; Bastian, U.; Bernacca, P.; Crézé, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The HIPPARCOS catalogue. Astron. Astrophys. 1997, 323, L49–L52. [Google Scholar]
- Gaia Collaboration; Prusti, T.; de Bruijne, J.H.J.; Brown, A.G.; Vallenari, A.; Babusiaux, C.; Bailer-Jones, C.A.L.; Bastian, U.; Biermann, M.; Evans, D.W.; et al. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar]
- Kervella, P.; Arenou, F.; Mignard, F.; Thévenin, F. Stellar and substellar companions of nearby stars from Gaia DR2. Binarity from proper motion anomaly. Astron. Astrophys. 2019, 623, A72. [Google Scholar] [CrossRef]
- Kervella, P.; Arenou, F.; Thévenin, F. Stellar and substellar companions from Gaia EDR3—Proper motion anomaly and resolved common proper motion pairs. arXiv 2022, arXiv:2109.10912. [Google Scholar]
- Brandt, T.D. The Hipparcos-Gaia Catalog of Accelerations. Astrophys. J. Suppl. Ser. 2018, 239, 31. [Google Scholar] [CrossRef]
- Brandt, T.D. The Hipparcos-Gaia Catalog of Accelerations: Gaia EDR3 Edition. Astrophys. J. Suppl. Ser. 2021, 254, 42. [Google Scholar] [CrossRef]
- Tokovinin, A.A. Relative orientation of angular momenta in multiple star systems. Astron. Lett. 1993, 19, 383–388. [Google Scholar]
- Sterzik, M.F.; Tokovinin, A.A. Relative orientation of orbits in triple stars. Astron. Astrophys. 2002, 384, 1030–1037. [Google Scholar] [CrossRef]
- Tokovinin, A.; Latham, D.W. Relative Orbit Orientation in Several Resolved Multiple Systems. Astrophys. J. 2017, 838, 54. [Google Scholar] [CrossRef]
- Batten, A.H. Digging Foundations for the ‘Royal Road’. Astrophys. Space Sci. 2005, 296, 3–15. [Google Scholar] [CrossRef]
- Southworth, J. Rediscussion of eclipsing binaries. Paper 1: The totally-eclipsing B-type system zeta Phoenicis. Observatory 2020, 140, 247–262. [Google Scholar]
- Maxted, P.F.L.; Gaulme, P.; Graczyk, D.; Hełminiak, K.G.; Johnston, C.; Orosz, J.A.; Prša, A.; Southworth, J.; Torres, G.; Davies, G.R.; et al. The TESS light curve of AI Phoenicis. Mon. Not. R. Astron. Soc. 2020, 498, 332–343. [Google Scholar] [CrossRef]
- Southworth, J. Rediscussion of edlipsing binaries. Paper 2: The eccentric solar-type system KX Cancri. Observatory 2021, 141, 22–31. [Google Scholar]
- Southworth, J. Rediscussion of edlipsing binaries. Paper 5: The triple system V455 Aurigae. Observatory 2021, 141, 190–203. [Google Scholar]
- Southworth, J. DEBCat: A Catalog of Detached Eclipsing Binary Stars. In Living Together: Planets, Host Stars and Binaries; Astronomical Society of the Pacific Conference Series; Rucinski, S.M., Torres, G., Zejda, M., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2015; Volume 496, pp. 164–165. [Google Scholar]
- Garrido, H.E.; Cruz, P.; Diaz, M.P.; Aguilar, J.F. The radius inflation problem in short-period low-mass binaries: A large sample analysis. Mon. Not. R. Astron. Soc. 2019, 482, 5379–5388. [Google Scholar] [CrossRef]
- Ragozzine, D.; Holman, M.J. The Value of Systems with Multiple Transiting Planets. arXiv 2010, arXiv:1006.3727. [Google Scholar]
- Pál, A. Light-curve modelling for mutual transits. Mon. Not. R. Astron. Soc. 2012, 420, 1630–1635. [Google Scholar] [CrossRef]
- Brož, M. An Advanced N-body Model for Interacting Multiple Stellar Systems. Astrophys. J. Suppl. Ser. 2017, 230, 19. [Google Scholar] [CrossRef]
- Short, D.R.; Orosz, J.A.; Windmiller, G.; Welsh, W.F. Accurate Computation of Light Curves and the Rossiter-McLaughlin Effect in Multibody Eclipsing Systems. Astron. J. 2018, 156, 297. [Google Scholar] [CrossRef]
- Miller, N.J.; Maxted, P.F.L.; Smalley, B. Fundamental effective temperature measurements for eclipsing binary stars—I. Development of the method and application to AI Phoenicis. Mon. Not. R. Astron. Soc. 2020, 497, 2899–2909. [Google Scholar] [CrossRef]
- Csizmadia, S. The Transit and Light Curve Modeller. Mon. Not. R. Astron. Soc. 2020, 496, 4442–4467. [Google Scholar] [CrossRef]
- Csizmadia, S.; Pasternacki, T.; Dreyer, C.; Cabrera, J.; Erikson, A.; Rauer, H. The effect of stellar limb darkening values on the accuracy of the planet radii derived from photometric transit observations. Astron. Astrophys. 2013, 549, A9. [Google Scholar] [CrossRef]

| Identifier | References | ||
|---|---|---|---|
| KOI-126 | 1.77 | 33.92 | [163] |
| HD 144548 | 1.63 | 33.95 | [172] |
| HD 181068 | 0.91 | 45.47 | [104] |
| TIC 193993801 | 1.43 | 49.28 | [155] |
| TIC 388459317 | 2.18 | 88.86 | [155] |
| CoRoT 104079133 | 2.76 | 90(?) | [161] |
| KIC 4150611 | 1.52 | 94.2 | [169,170] |
| OGLE-BLG-ECL-126114 | 6.65 | 105.3 | [148] |
| TIC 209409435 | 5.72 | 121.9 | [24] |
| TIC 52041148 | 1.79 | 177.1 | [155] |
| EPIC 249432662 | 8.19 | 188.4 | [173] |
| KIC 2856960 | 0.26 | 204.8 | [164,167] |
| KIC 7668648 | 27.83 | 204.8 | [17,27] |
| TIC 278825952 | 4.78 | 235.5 | [154] |
| KIC 6964043 | 10.73 | 239.1 | [17] |
| KIC 7289157 | 5.27 | 243.4 | [17,27] |
| OGLE-BLG-ECL-187370 | 11.96 | 280.5 | [148] |
| KIC 9007918 | 1.39 | 470.9 | [83] |
| b Persei | 1.52 | 704.5 | [182] |
| KIC 2835289 | 0.86 | 755 | [138] |
| KIC 5255552 | 32.47 | 862.1 | [17] |
| KIC 6543674 | 2.39 | 1101.4 | [17,165] |
| System | [day] | [day] | [yr] | Current Status | References |
|---|---|---|---|---|---|
| IU Aur | 1.8115 | 293.3 | 330 | d | [156] |
| QX Cas | 6.0047 | ? | ? | n | [215] |
| V685 Cen | 1.1910 | ? | ? | d? | [216] |
| AH Cep | 1.7747 | ? | ? | i | [217] |
| V699 Cyg | 3.1031 | ? | ? | n | [218] |
| SV Gem | 4.0061 | ? | ? | n | [219] |
| HS Hya | 1.5680 | 190 | 631 | n | [213] |
| SS Lac | 14.4162 | 679 | 600 | n | [211] |
| AY Mus | 3.2055 | ? | ? | n | [204] |
| RW Per | 13.1989 | ? | ? | d | [203] |
| V907 Sco | 3.7763 | 99.3 | 68? | i | [212] |
| KIC 4769799 | 21.9286 | 1231 | 826 | n | [17] |
| KIC 5003117 | 37.6094 | 2128 | 1484 | n | [17] |
| KIC 5255552 | 32.4486 | 883 | 140 | i | [17] |
| KIC 5653126 | 38.4923 | 968 | 157 | i | [17] |
| KIC 5731312 | 7.9464 | 911 | 1013 | d | [17] |
| KIC 5771589 | 10.7382 | 113 | 7.5 | i | [17] |
| KIC 5897826 | 1.7671 | 33.92 | 2.7 | ? | [86,163] |
| KIC 6964043 | 10.7255 | 239.1 | 26 | n | [17] |
| KIC 7289157 | 5.2665 | 243.4 | 80 | n | [17] |
| KIC 7668648 | 27.8256 | 204.8 | 25 | i | [17] |
| KIC 7670617 | 24.7032 | 3304 | 1678 | n | [17] |
| KIC 7955301 | 15.3278 | 209.1 | 19.2 | n | [17] |
| KIC 8023317 | 16.5791 | 607 | 633 | c | [17] |
| KIC 8143170 | 28.7868 | 1710 | 890 | c | [17] |
| KIC 8938628 | 6.8622 | 388.6 | 170 | n | [17] |
| KIC 9715925 | 6.3083 | 736 | 1163 | i | [17] |
| KIC 9963009 | 40.0716 | 3770 | 2703 | c? | [17] |
| KIC 10268809 | 24.7084 | 7000 | 3333 | n? | [17] |
| KIC 10319590 | 21.3212 | 452 | 110 | n | [17,27] |
| KIC 10666242 | 81.2455 | ? | ? | ? | [83] |
| HIP 41431 | 2.9329 | 58.9 | 11 | d | [102] |
| TIC 167692429 | 10.2648 | 331.5 | 70 | d | [162] |
| VV Ori | 1.4854 | ? | ? | d | [220] |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| or | ✓ | ✓ | |||||||||
| , , | ✓ | ✓ | ✓ | ✓ | |||||||
| , , , , , d | (✓) | ✓ | ✓ | ✓ | |||||||
| , , | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| ✓ | ✓ | ✓ | ✓ | ||||||||
| (✓) | (✓) | (✓) | (✓) | (✓) | (✓) | ||||||
| , , , , , , , | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
| ✓ | ? | ? | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
| (✓) | (✓) | (✓) | (✓) | ✓ | ✓ | ✓ | |||||
| ✓ | ✓ | ✓ | |||||||||
| ✓ | ✓ | ✓ | ✓ | ||||||||
| (✓) | (✓) | ||||||||||
| ✓ | ✓ | ✓ | |||||||||
| ✓ | (✓) | ||||||||||
| , , | (✓) | (✓) | (✓) | (✓) | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| , , | ✓ | (✓) | ✓ | ✓ | |||||||
| , | ✓ | ✓ | ✓ | ||||||||
| , | (✓) | ✓ | ✓ | ✓ | |||||||
| , , , , , , , | ✓ | ✓ | |||||||||
| , , , , , , , , | ✓ | ||||||||||
| , , d | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borkovits, T. Eclipsing Binaries in Dynamically Interacting Close, Multiple Systems. Galaxies 2022, 10, 9. https://doi.org/10.3390/galaxies10010009
Borkovits T. Eclipsing Binaries in Dynamically Interacting Close, Multiple Systems. Galaxies. 2022; 10(1):9. https://doi.org/10.3390/galaxies10010009
Chicago/Turabian StyleBorkovits, Tamás. 2022. "Eclipsing Binaries in Dynamically Interacting Close, Multiple Systems" Galaxies 10, no. 1: 9. https://doi.org/10.3390/galaxies10010009
APA StyleBorkovits, T. (2022). Eclipsing Binaries in Dynamically Interacting Close, Multiple Systems. Galaxies, 10(1), 9. https://doi.org/10.3390/galaxies10010009






