Comparing CT and MR Properties of Artificial Thrombi According to Their Composition
Abstract
1. Introduction
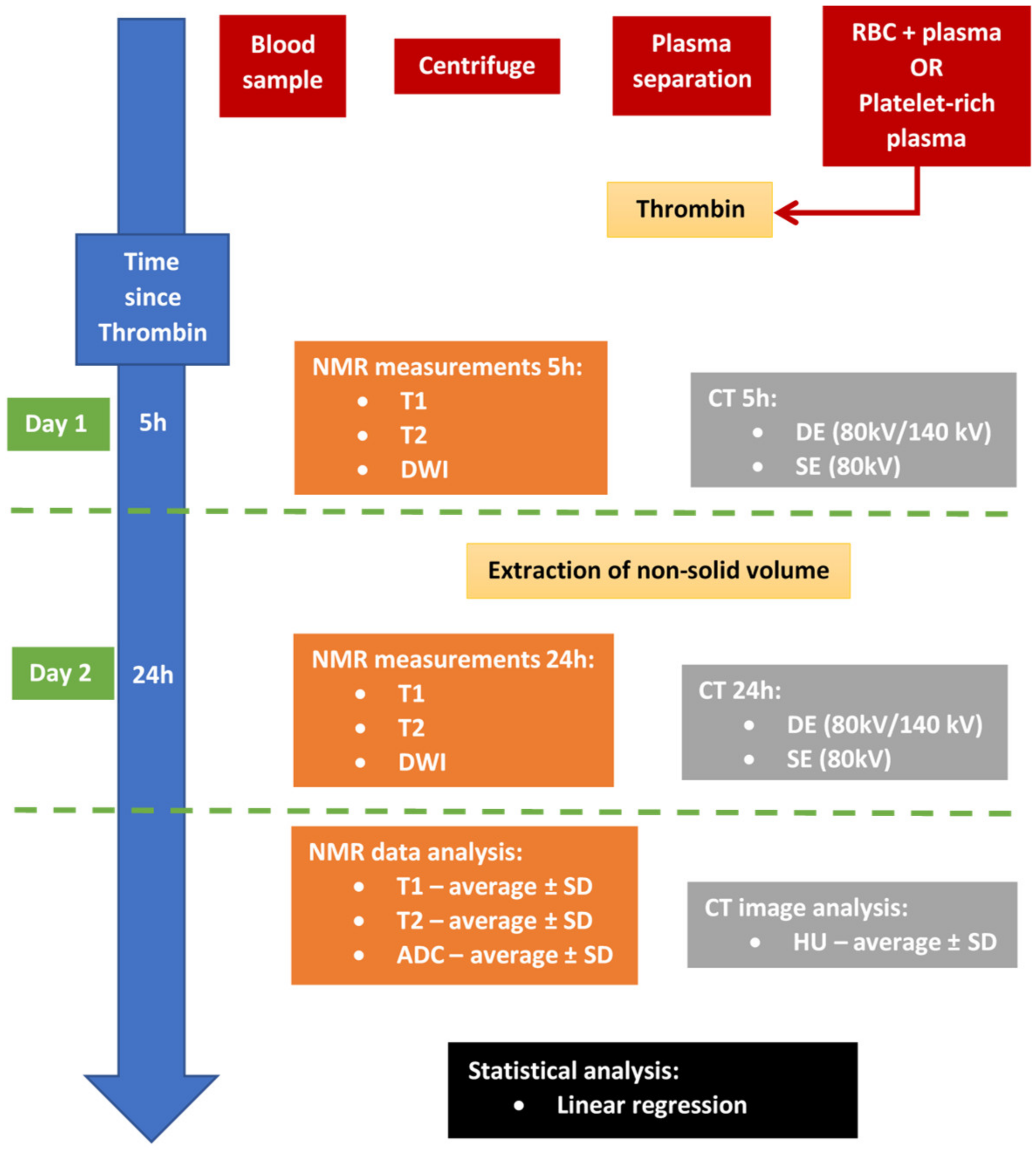
2. Materials and Methods
2.1. Artificial Thrombi
2.2. Nuclear Magnetic Resonance Measurements and Analysis
2.3. Computer Tomography Imaging and Analysis
2.4. Statistical Analysis
3. Results
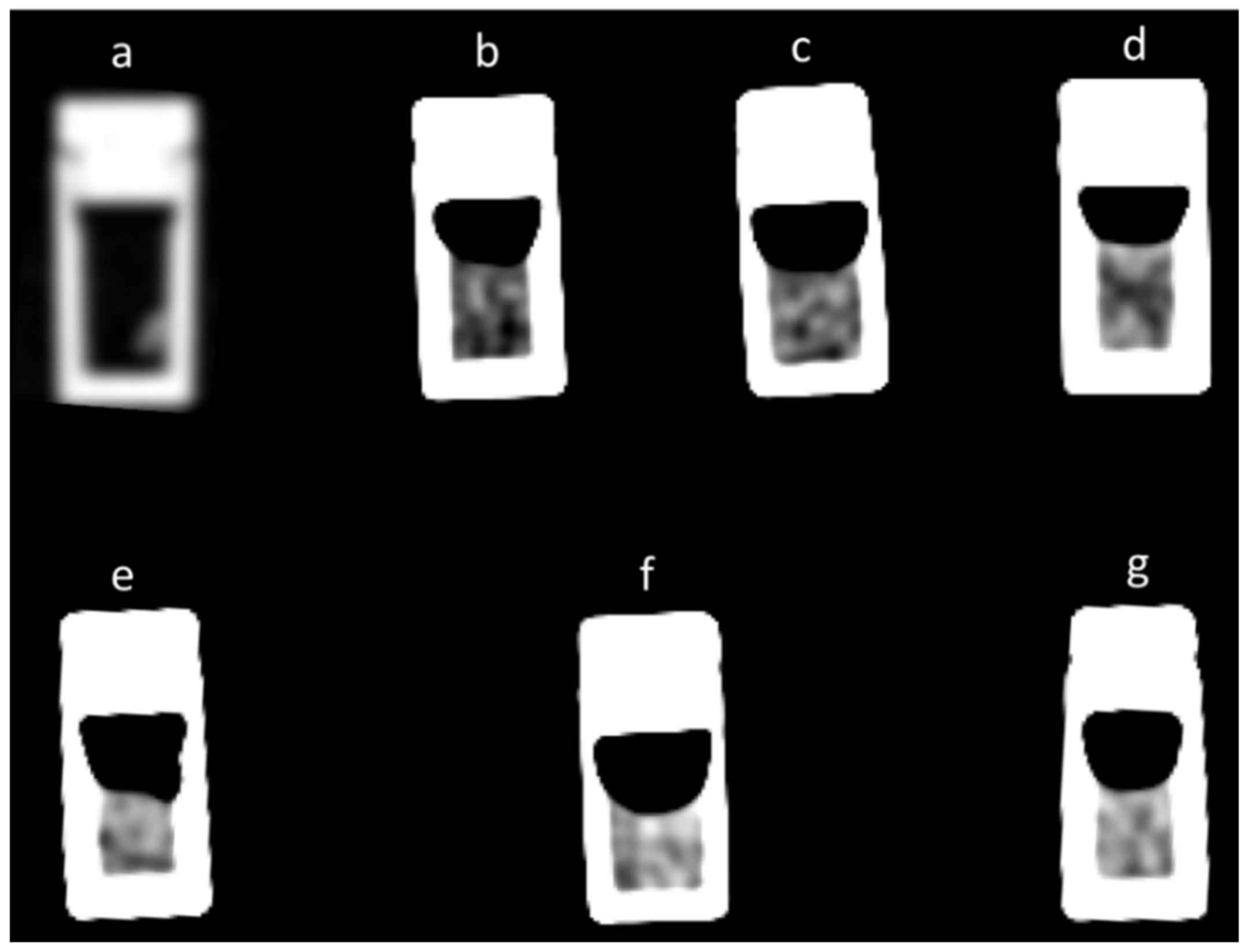
3.1. Extruded Serum and RBC Fraction
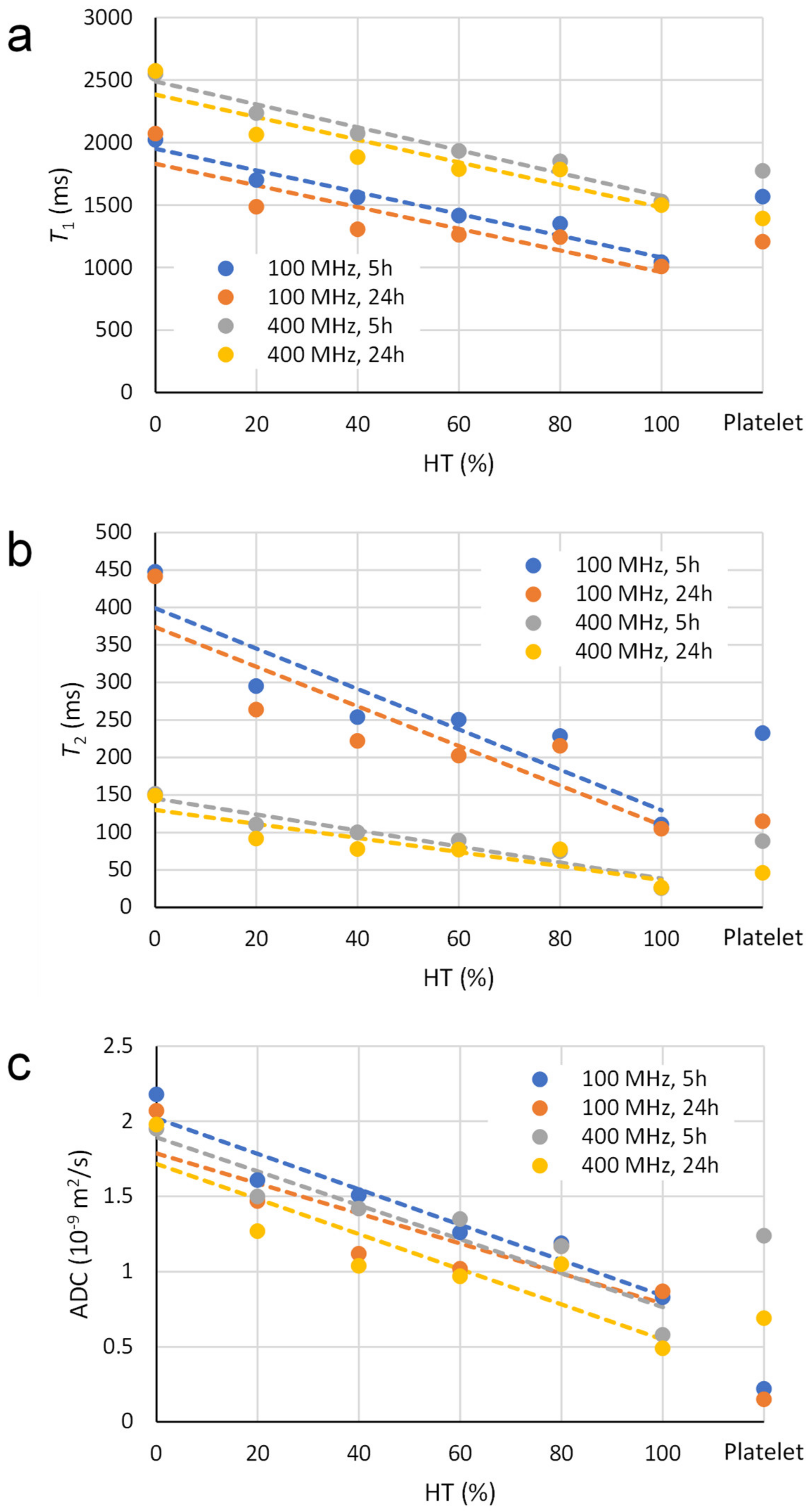
3.2. NMR Measurements
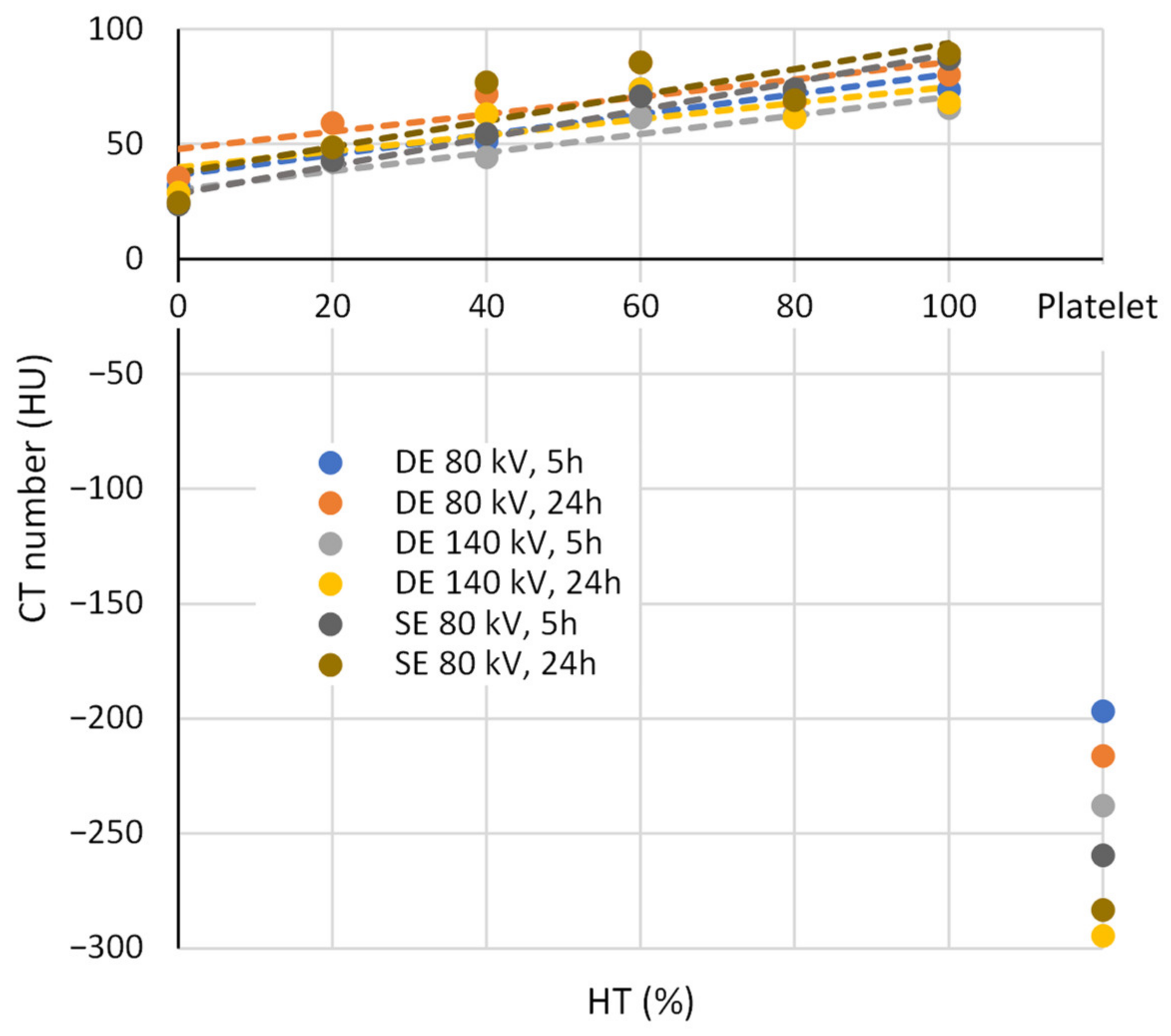
3.3. CT Measurements
3.4. Regression and Statistical Analyses of NMR and CT Measurements
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mackman, N. Triggers, targets and treatments for thrombosis. Nature 2008, 451, 914. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.; Coull, B.M. Thrombosis. In Primer on Cerebrovascular Diseases, 2nd ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 108–113. [Google Scholar] [CrossRef]
- Vidmar, J.; Serša, I.; Kralj, E.; Tratar, G.; Blinc, A. Discrimination between red blood cell and platelet components of blood clots by MR microscopy. Eur. Biophys. J. 2008, 37, 1235–1240. [Google Scholar] [CrossRef] [PubMed]
- Polanczyk, A.; Piechota-Polanczyk, A.; Huk, I.; Neumayer, C.; Balcer, J.; Strzelecki, M. Computational Fluid Dynamic Technique for Assessment of How Changing Character of Blood Flow and Different Value of Hct Influence Blood Hemodynamic in Dissected Aorta. Diagnostics 2021, 11, 1866. [Google Scholar] [CrossRef] [PubMed]
- Bajd, F.; Vidmar, J.; Fabjan, A.; Blinc, A.; Kralj, E.; Bizjak, N.; Sersa, I. Impact of altered venous hemodynamic conditions on the formation of platelet layers in thromboemboli. Thromb. Res. 2012, 129, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Gunning, G.M.; McArdle, K.; Mirza, M.; Duffy, S.; Gilvarry, M.; Brouwer, P.A. Clot friction variation with fibrin content; implications for resistance to thrombectomy. J. Neurointerv. Surg. 2018, 10, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Yuki, I.; Kan, I.; Vinters, H.V.; Kim, R.H.; Golshan, A.; Vinuela, F.A.; Sayre, J.W.; Murayama, Y.; Vinuela, F. The impact of thromboemboli histology on the performance of a mechanical thrombectomy device. AJNR Am. J. Neuroradiol. 2012, 33, 643–648. [Google Scholar] [CrossRef]
- Alkarithi, G.; Duval, C.; Shi, Y.; Macrae, F.L.; Ariëns, R.A.S. Thrombus Structural Composition in Cardiovascular Disease. Arterioscler. Thromb. Vasc. Biol. 2021, 41, 2370–2383. [Google Scholar] [CrossRef]
- Litvinov, R.I.; Weisel, J.W. What Is the Biological and Clinical Relevance of Fibrin? Semin. Thromb. Hemost. 2016, 42, 333. [Google Scholar] [CrossRef]
- Fereidoonnezhad, B.; Dwivedi, A.; Johnson, S.; McCarthy, R.; McGarry, P. Blood clot fracture properties are dependent on red blood cell and fibrin content. Acta Biomater. 2021, 127, 213–228. [Google Scholar] [CrossRef]
- Ye, G.; Cao, R.; Lu, J.; Qi, P.; Chen, J.; Wang, D. CT-based Higher Thrombus Density is associated with Secondary Embolism during Mechanical Thrombectomy: A Preliminary Observation. J. Stroke Cerebrovasc. Dis. 2019, 28, 104311. [Google Scholar] [CrossRef]
- Brinjikji, W.; Duffy, S.; Burrows, A.; Hacke, W.; Liebeskind, D.; Majoie, C.B.L.M.; Dippel, D.W.J.; Siddiqui, A.H.; Khatri, P.; Baxter, B.; et al. Correlation of imaging and histopathology of thrombi in acute ischemic stroke with etiology and outcome: A systematic review. J. Neurointerv. Surg. 2017, 9, 529–534. [Google Scholar] [CrossRef] [PubMed]
- Kozak, M.; Mikac, U.; Blinc, A.; Serša, I. Lysability of arterial thrombi assessed by magnetic resonance imaging. VASA Z. Gefasskrankh. 2005, 34, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Kozak, M.; Blinc, A.; Sers, A.I.; Mikac, U.A.; Urlan, M.S. Magnetic resonance imaging of arterial thrombi and its possible correlation to fibrinolytic treament. Cell. Mol. Biol. Lett. 2002, 7, 82–86. [Google Scholar] [PubMed]
- Francis, C.W.; Totterman, S. Magnetic resonance imaging of deep vein thrombi correlates with response to thrombolytic therapy. Thromb. Haemost. 1995, 73, 386–391. [Google Scholar] [CrossRef] [PubMed]
- Yew, K.S.; Cheng, E. Acute Stroke Diagnosis. Am. Fam. Physician 2009, 80, 33. [Google Scholar] [PubMed]
- Provost, C.; Soudant, M.; Legrand, L.; Ben Hassen, W.; Xie, Y.; Soize, S.; Bourcier, R.; Benzakoun, J.; Edjlali, M.; Boulouis, G.; et al. Magnetic resonance imaging or computed tomography before treatment in acute ischemic stroke: Effect on workflow and functional outcome. Stroke 2019, 50, 659–664. [Google Scholar] [CrossRef]
- Tucker, K.L.; Sage, T.; Gibbins, J.M. Clot retraction. In Platelets and Megakaryocytes; Methods in Molecular Biology; Springer: New York, NY, USA, 2012; Volume 788, pp. 101–107. [Google Scholar] [CrossRef]
- Keeler, J. Understanding NMR Spectroscopy, 2nd ed.; Wiley: Hoboken, NJ, USA, 2010; p. 528. [Google Scholar]
- Carr, H.Y.; Purcell, E.M. Effects of Diffusion on Free Precession in Nuclear Magnetic Resonance Experiments. Phys. Rev. Lett. 1954, 94, 630–638. [Google Scholar] [CrossRef]
- Stejskal, E.O.; Tanner, J.E. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time-Dependent Field Gradient. J. Chem. Phys. 1965, 42, 288–292. [Google Scholar] [CrossRef]
- Kattula, S.; Byrnes, J.R.; Wolberg, A.S. Fibrinogen and fibrin in hemostasis and thrombosis. Arterioscler. Thromb. Vasc. Biol. 2017, 37, 13. [Google Scholar] [CrossRef]
- Zborowski, M.; Ostera, G.R.; Moore, L.R.; Milliron, S.; Chalmers, J.J.; Schechter, A.N. Red Blood Cell Magnetophoresis. Biophys. J. 2003, 84, 2638. [Google Scholar] [CrossRef] [PubMed]
- Bushberg, J.T.; Siebert, J.A.; Leidholdt, E.M.; Boone, J.M. The Essential Physics of Medical Imaging, 2nd ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2002. [Google Scholar]
- Crooks, L.E.; Arakawa, M.; Hoenninger, J.; McCarten, B.; Watts, J.; Kaufman, L. Magnetic resonance imaging: Effects of magnetic field strength. Radiology 1984, 151, 127–133. [Google Scholar] [CrossRef] [PubMed]
- Brownstein, K.R.; Tarr, C.E. Spin-Lattice Relaxation in a System Governed by Diffusion. J. Magn. Reson. 1977, 26, 17–24. [Google Scholar] [CrossRef]
- Ogura, A.; Tamura, T.; Ozaki, M.; Doi, T.; Fujimoto, K.; Miyati, T.; Ito, Y.; Maeda, F.; Tarewaki, H.; Takahashi, M. Apparent Diffusion Coefficient Value Is Not Dependent on Magnetic Resonance Systems and Field Strength under Fixed Imaging Parameters in Brain. J. Comput. Assist. Tomogr. 2015, 39, 760–765. [Google Scholar] [CrossRef] [PubMed]
- Sersa, I. Sequential Diffusion Spectra as a Tool for Studying Time-Dependent Translational Molecular Dynamics: A Cement Hydration Study. Molecules 2019, 25, 68. [Google Scholar] [CrossRef]
- Pisani, L. Simple Expression for the Tortuosity of Porous Media. Transp. Porous Media 2011, 88, 193–203. [Google Scholar] [CrossRef]
- Hu, H.H.; Nayak, K.S. Change in the Proton T1 of Fat and Water in Mixture. Magn. Reson. Med. Off. J. Soc. Magn. Reson. Med./Soc. Magn. Reson. Med. 2010, 63, 494. [Google Scholar] [CrossRef]
- Chougule, V.N.; Mulay, A.; Ahuja, B.B. Clinical Case Study: Spine Modeling for Minimum Invasive Spine Surgeries (MISS) using Rapid Prototyping. Bone 2018, 226, 3071. [Google Scholar]
- Vidmar, J.; Blinc, A.; Sersa, I. A comparison of the ADC and T-2 mapping in an assessment of blood-clot lysability. NMR Biomed. 2010, 23, 34–40. [Google Scholar] [CrossRef]
- Schmidt, B.; Flohr, T. Principles and applications of dual source CT. Phys. Med. 2020, 79, 36–46. [Google Scholar] [CrossRef]
- Cines, D.B.; Lebedeva, T.; Nagaswami, C.; Hayes, V.; Massefski, W.; Litvinov, R.I.; Rauova, L.; Lowery, T.J.; Weisel, J.W. Clot contraction: Compression of erythrocytes into tightly packed polyhedra and redistribution of platelets and fibrin. Blood 2014, 123, 1596–1603. [Google Scholar] [CrossRef] [PubMed]

| MR System and Measurement Time | |||||
|---|---|---|---|---|---|
| 100 MHz | 400 MHz | ||||
| HT (%) | 5 h | 24 h | 5 h | 24 h | |
| T1 (ms) | 0 | 2020 ± 100 | 2070 ± 80 | 2550 ± 70 | 2570 ± 100 |
| 20 | 1700 ± 180 | 1490 ± 110 | 2240 ± 200 | 2060 ± 80 | |
| 40 | 1560 ± 180 | 1310 ± 110 | 2070 ± 140 | 1880 ± 110 | |
| 60 | 1420 ± 130 | 1260 ± 190 | 1930 ± 170 | 1790 ± 180 | |
| 80 | 1350 ± 80 | 1250 ± 60 | 1850 ± 100 | 1780 ± 70 | |
| 100 | 1040 ± 70 | 1010 ± 60 | 1530 ± 110 | 1500 ± 140 | |
| Platelet | 1570 ± 230 | 1210 ± 150 | 1780 ± 390 | 1390 ± 460 | |
| T2 (ms) | 0 | 447 ± 31 | 442 ± 28 | 152 ± 8 | 149 ± 16 |
| 20 | 295 ± 58 | 264 ± 47 | 111 ± 32 | 92 ± 18 | |
| 40 | 254 ± 42 | 222 ± 43 | 100 ± 22 | 78 ± 18 | |
| 60 | 250 ± 29 | 202 ± 75 | 90 ± 15 | 77 ± 40 | |
| 80 | 229 ± 63 | 216 ± 67 | 75 ± 15 | 78 ± 34 | |
| 100 | 111 ± 13 | 105 ± 25 | 26 ± 5 | 27 ± 9 | |
| Platelet | 232 ± 91 | 115 ± 38 | 89 ± 24 | 47 ± 16 | |
| ADC (10−9 m2/s) | 0 | 2.18 ± 0.32 | 2.07 ± 0.07 | 1.95 ± 0.04 | 1.98 ± 0.07 |
| 20 | 1.61 ± 0.24 | 1.47 ± 0.18 | 1.5 ± 0.21 | 1.27 ± 0.16 | |
| 40 | 1.51 ± 0.21 | 1.12 ± 0.21 | 1.42 ± 0.13 | 1.04 ± 0.2 | |
| 60 | 1.26 ± 0.11 | 1.02 ± 0.29 | 1.35 ± 0.11 | 0.97 ± 0.34 | |
| 80 | 1.19 ± 0.1 | 1.17 ± 0.25 | 1.17 ± 0.19 | 1.05 ± 0.17 | |
| 100 | 0.83 ± 0.13 | 0.87 ± 0.24 | 0.58 ± 0.1 | 0.49 ± 0.11 | |
| Platelet | 0.22 ± 0.05 | 0.15 ± 0.04 | 1.24 ± 0.37 | 0.69 ± 0.4 | |
| NMR | CT | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | ADC | DE | SE | ||||||
| 100 MHz | 400 MHz | 100 MHz | 400 MHz | 100 MHz | 400 MHz | 80 kV | 140 kV | 80 kV | ||
| 5 h | Slope (k) | −8.7 | −9.2 | −2.7 | −1.1 | −0.012 | −0.011 | 0.44 | 0.40 | 0.61 |
| Intercept (n) | 1950 ms | 2490 ms | 400 ms | 145 ms | 2.0 | 1.9 | 37 HU | 30 HU | 28 HU | |
| R2 | 0.96 | 0.96 | 0.85 | 0.92 | 0.93 | 0.89 | 0.86 | 0.90 | 0.97 | |
| χ2 | 2.7 | 2.2 | 2.3 | 8.4 | 6.8 | 7.5 | 2.8 | 1.6 | 1.6 | |
| 100k/(50k + n) | −58% | −45% | −83% | −85% | −101% | −116% | 75% | 80% | 103% | |
| 24 h | Slope (k) | −8.7 | −9.0 | −2.6 | −0.94 | −0.010 | −0.012 | 0.38 | 0.35 | 0.56 |
| Intercept (n) | 1830 ms | 2380 ms | 375 ms | 130 ms | 1.8 | 1.7 | 48 HU | 40 HU | 37 HU | |
| R2 | 0.80 | 0.86 | 0.79 | 0.79 | 0.75 | 0.80 | 0.62 | 0.65 | 0.72 | |
| χ2 | 18.0 | 11.2 | 19.4 | 19.7 | 9.4 | 5.2 | 8.3 | 7.4 | 13.1 | |
| 100k/(50k + n) | −62% | −47% | −78% | −103% | −109% | −112% | 56% | 61% | 86% | |
| CT Mode and Measurement Time | ||||||
|---|---|---|---|---|---|---|
| DE | SE | |||||
| 80 kV (HU) | 140 kV (HU) | 80 kV (HU) | ||||
| HT (%) | 5 h | 24 h | 5 h | 24 h | 5 h | 24 h |
| 0 | 32 ± 10 | 35 ± 7 | 25 ± 10 | 29 ± 7 | 24 ± 5 | 25 ± 4 |
| 20 | 48 ± 4 | 59 ± 9 | 42 ± 7 | 49 ± 6 | 43 ± 7 | 49 ± 10 |
| 40 | 51 ± 9 | 72 ± 14 | 44 ± 9 | 63 ± 16 | 54 ± 17 | 77 ± 21 |
| 60 | 74 ± 14 | 86 ± 11 | 61 ± 11 | 74 ± 9 | 71 ± 10 | 85 ± 18 |
| 80 | 73 ± 9 | 68 ± 13 | 63 ± 11 | 61 ± 9 | 74 ± 15 | 69 ± 13 |
| 100 | 74 ± 6 | 80 ± 4 | 66 ± 6 | 68 ± 4 | 87 ± 4 | 89 ± 7 |
| Platelet | −197 ± 44 | −216 ± 117 | −238 ± 51 | −294 ± 172 | −260 ± 111 | −283 ± 116 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viltužnik, R.; Kaučič, A.; Blinc, A.; Vidmar, J.; Serša, I. Comparing CT and MR Properties of Artificial Thrombi According to Their Composition. Diagnostics 2023, 13, 1802. https://doi.org/10.3390/diagnostics13101802
Viltužnik R, Kaučič A, Blinc A, Vidmar J, Serša I. Comparing CT and MR Properties of Artificial Thrombi According to Their Composition. Diagnostics. 2023; 13(10):1802. https://doi.org/10.3390/diagnostics13101802
Chicago/Turabian StyleViltužnik, Rebeka, Aleš Kaučič, Aleš Blinc, Jernej Vidmar, and Igor Serša. 2023. "Comparing CT and MR Properties of Artificial Thrombi According to Their Composition" Diagnostics 13, no. 10: 1802. https://doi.org/10.3390/diagnostics13101802
APA StyleViltužnik, R., Kaučič, A., Blinc, A., Vidmar, J., & Serša, I. (2023). Comparing CT and MR Properties of Artificial Thrombi According to Their Composition. Diagnostics, 13(10), 1802. https://doi.org/10.3390/diagnostics13101802








