Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm
Abstract
1. Introduction
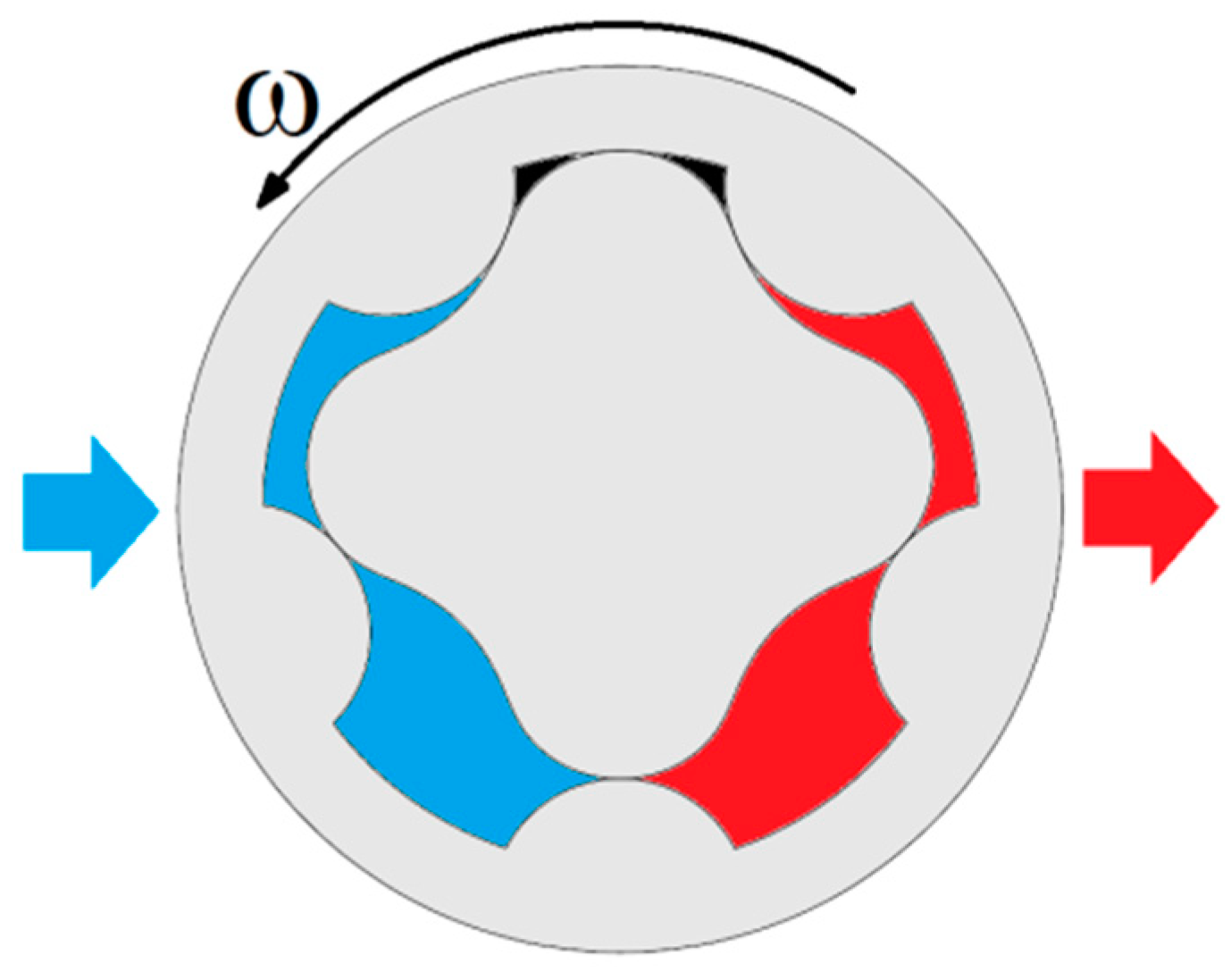
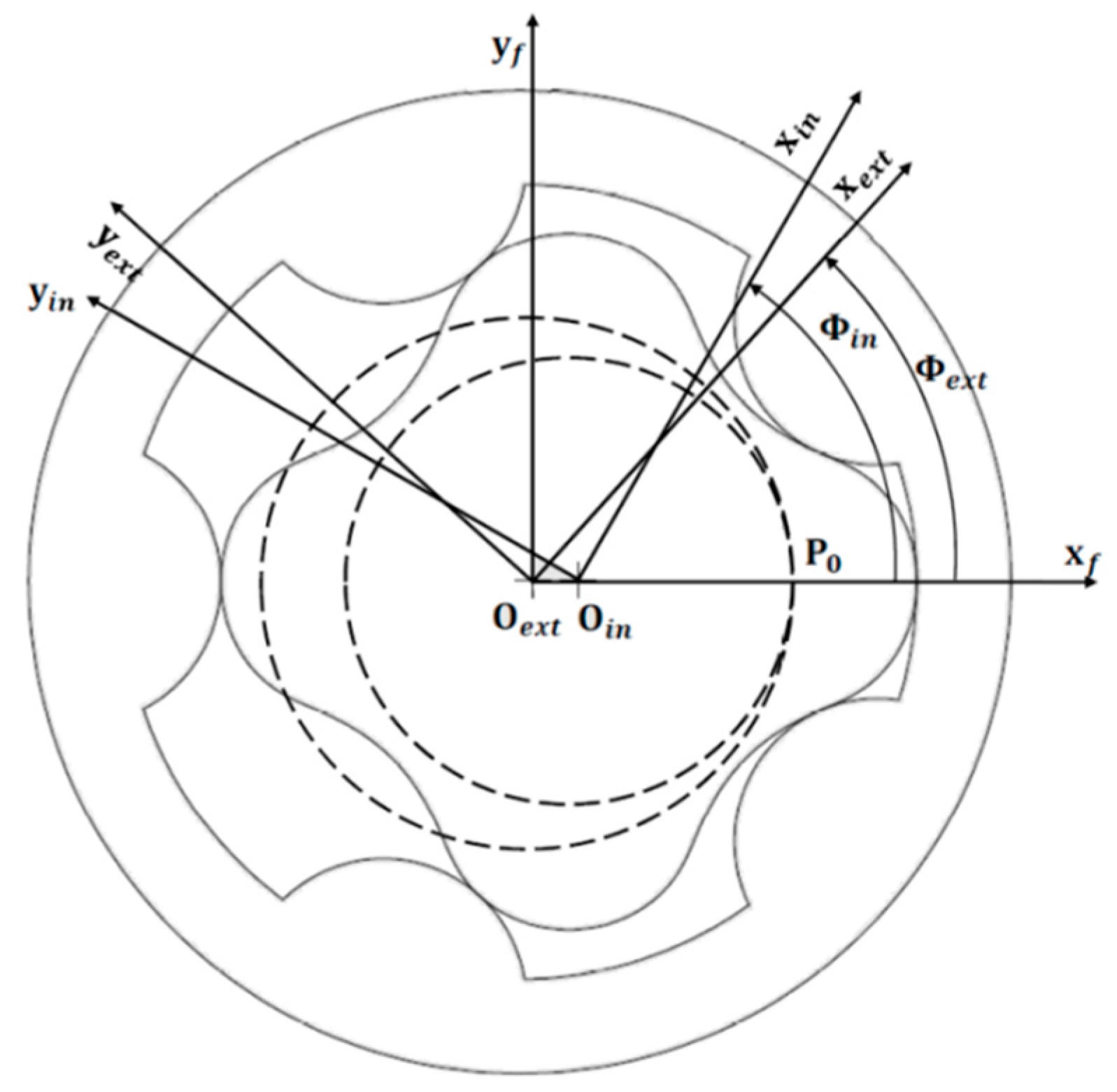
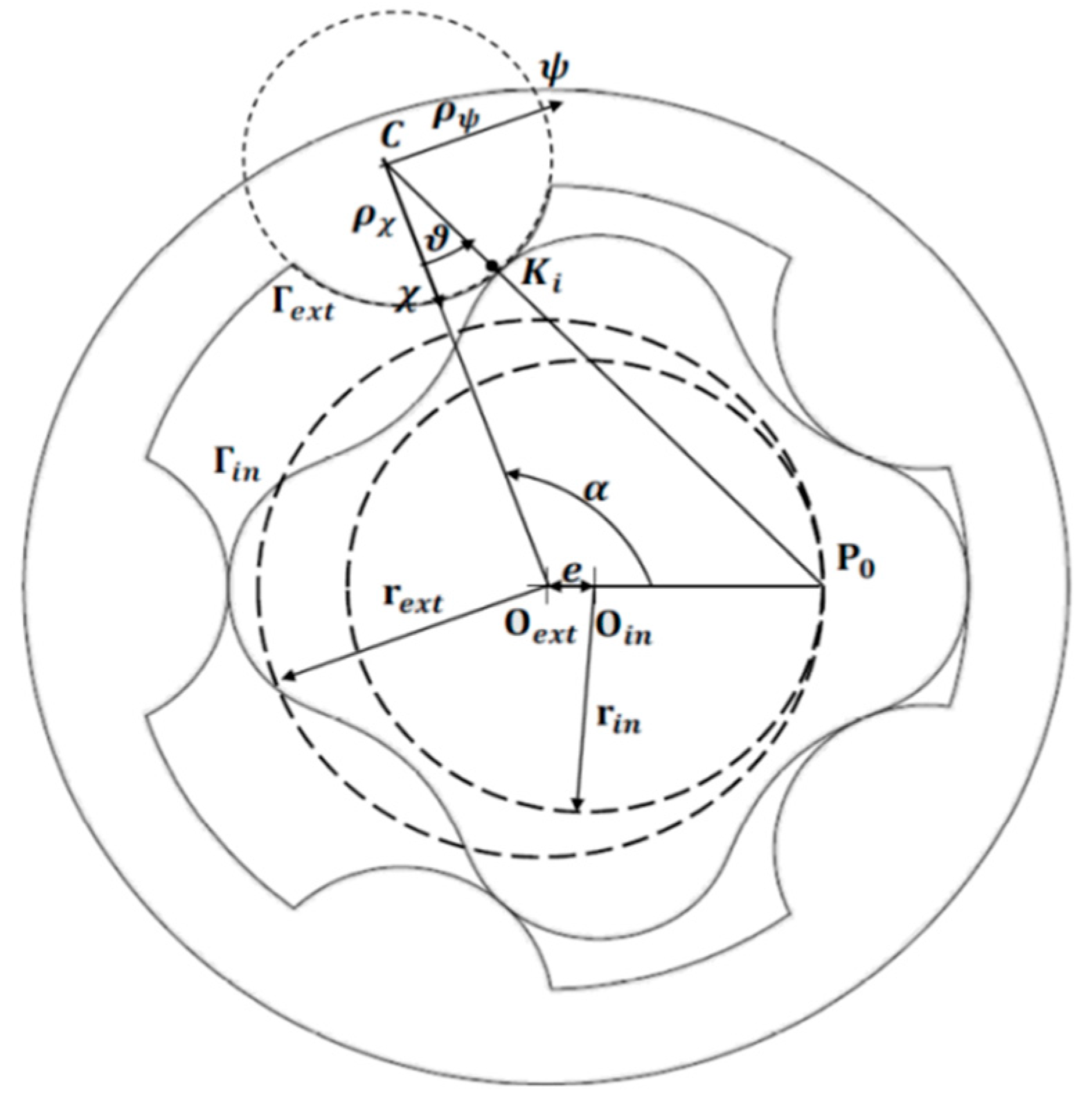
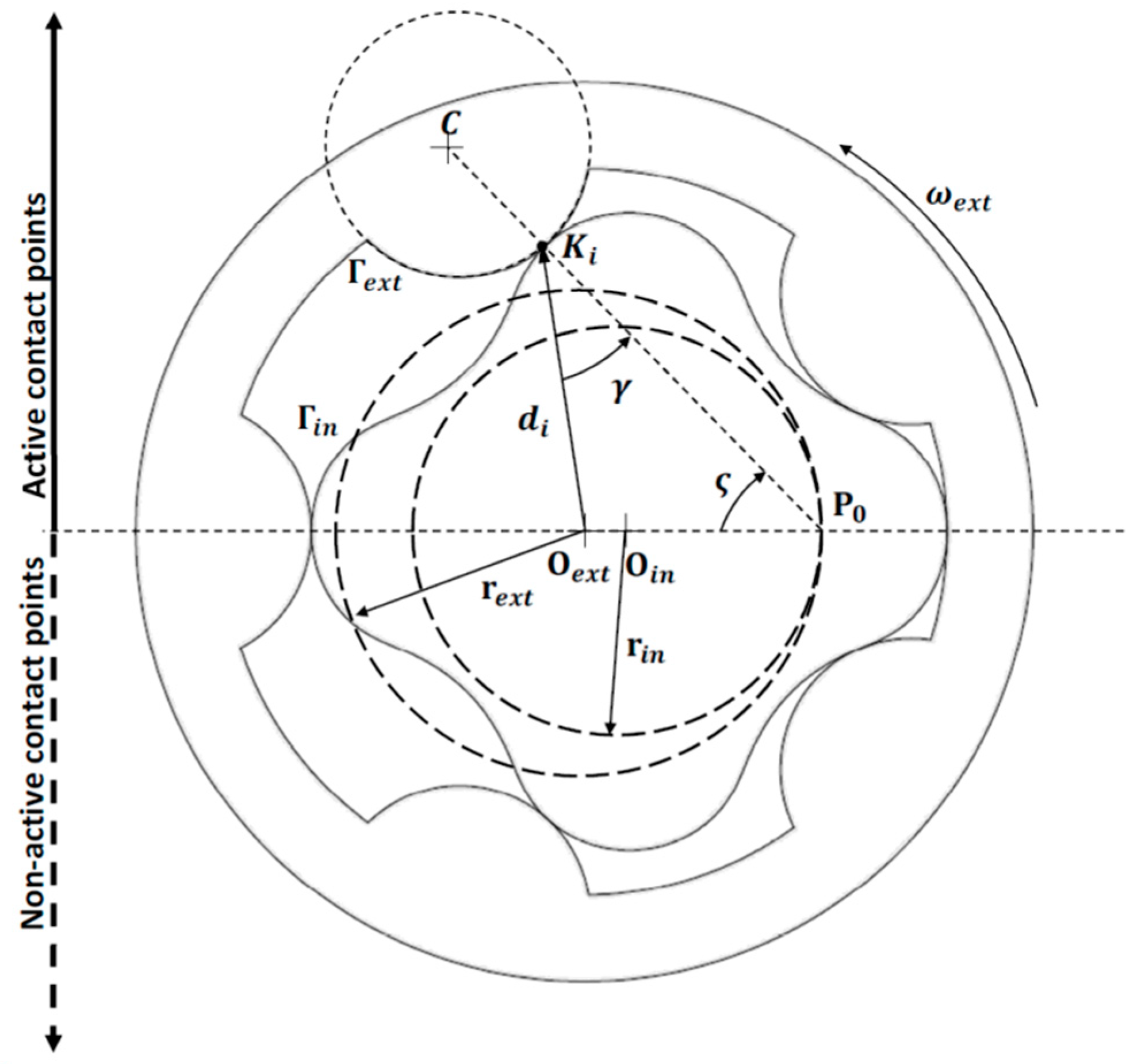
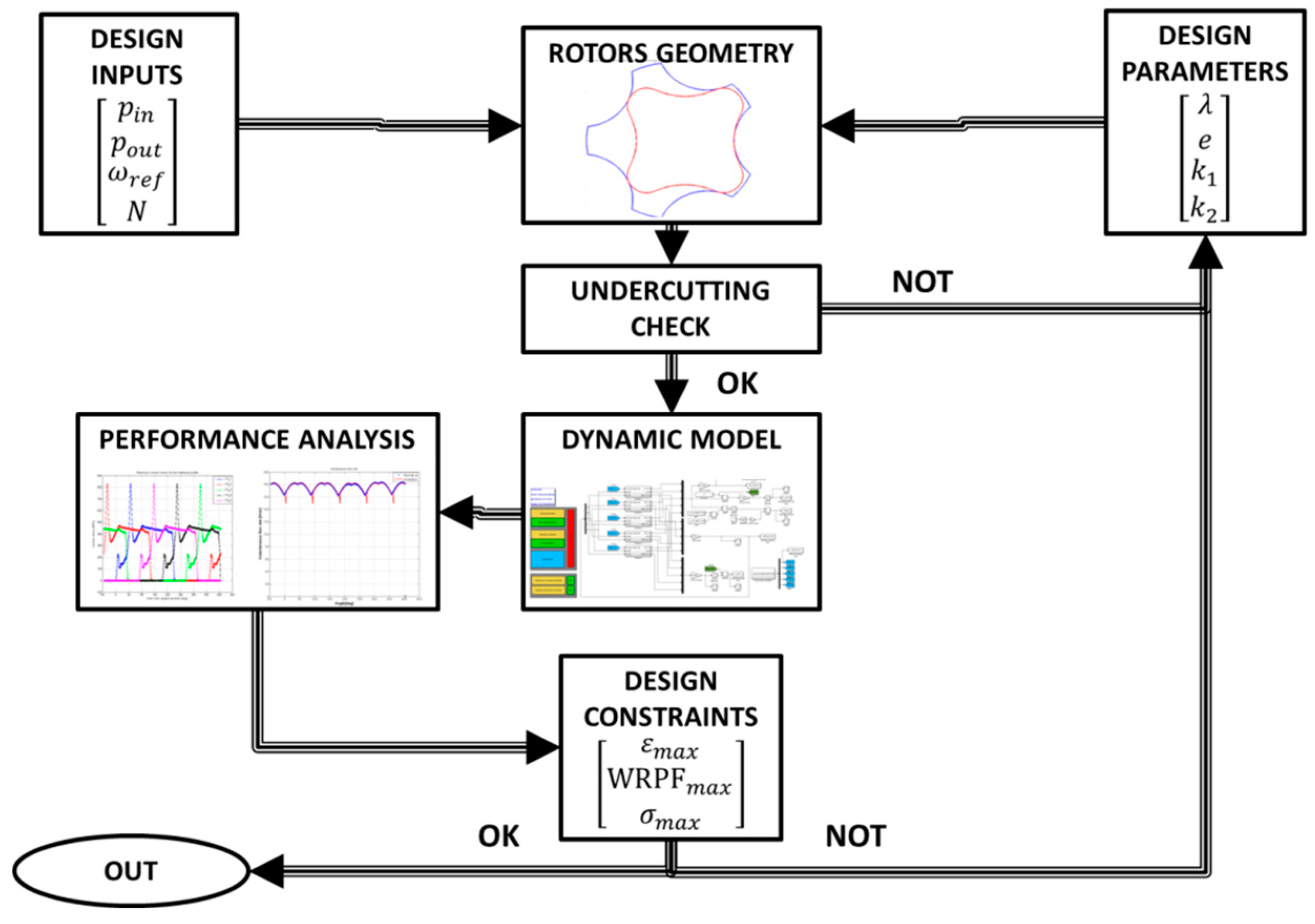
2. General Design Theory for Gerotor Pump Profiles
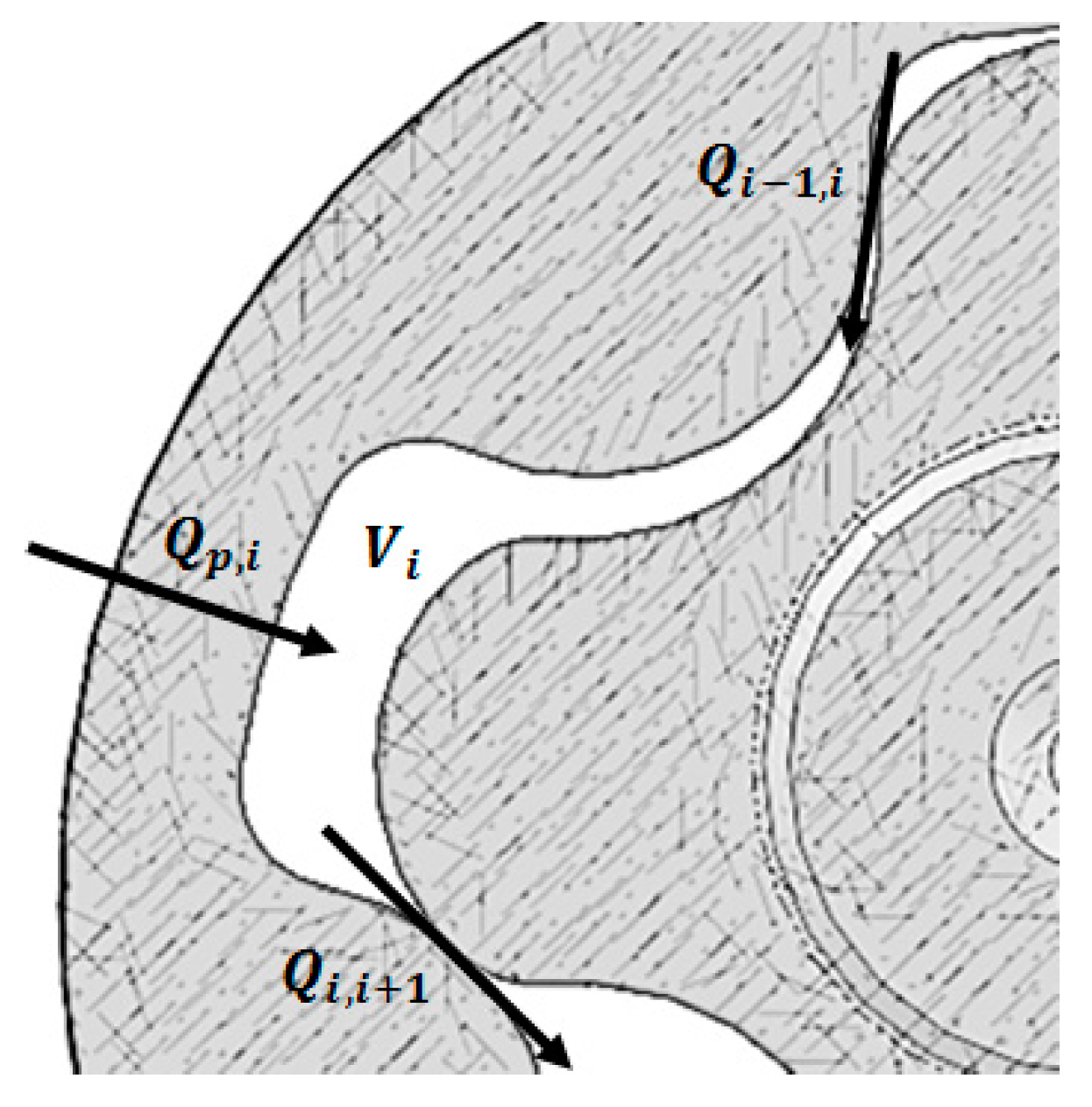
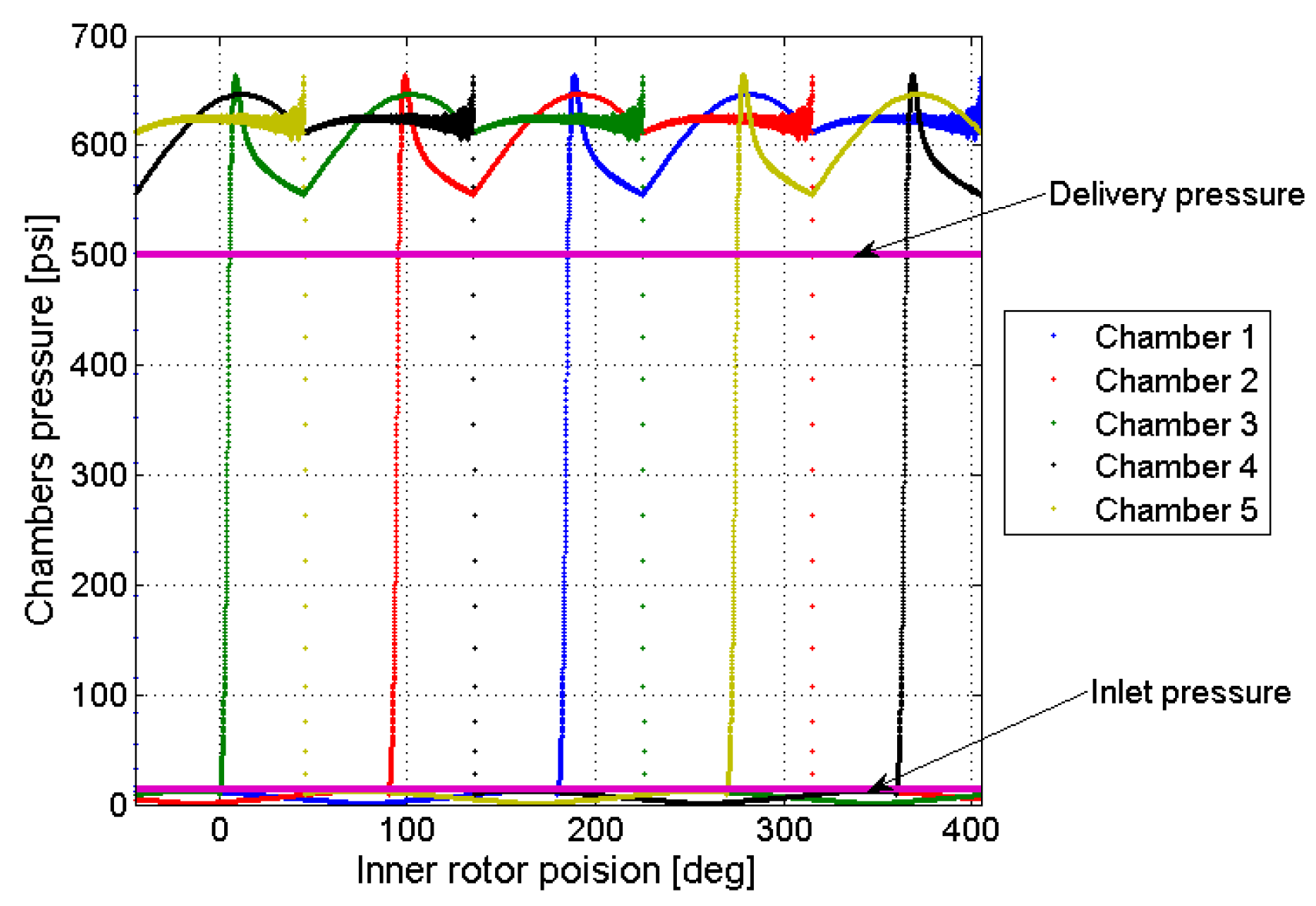
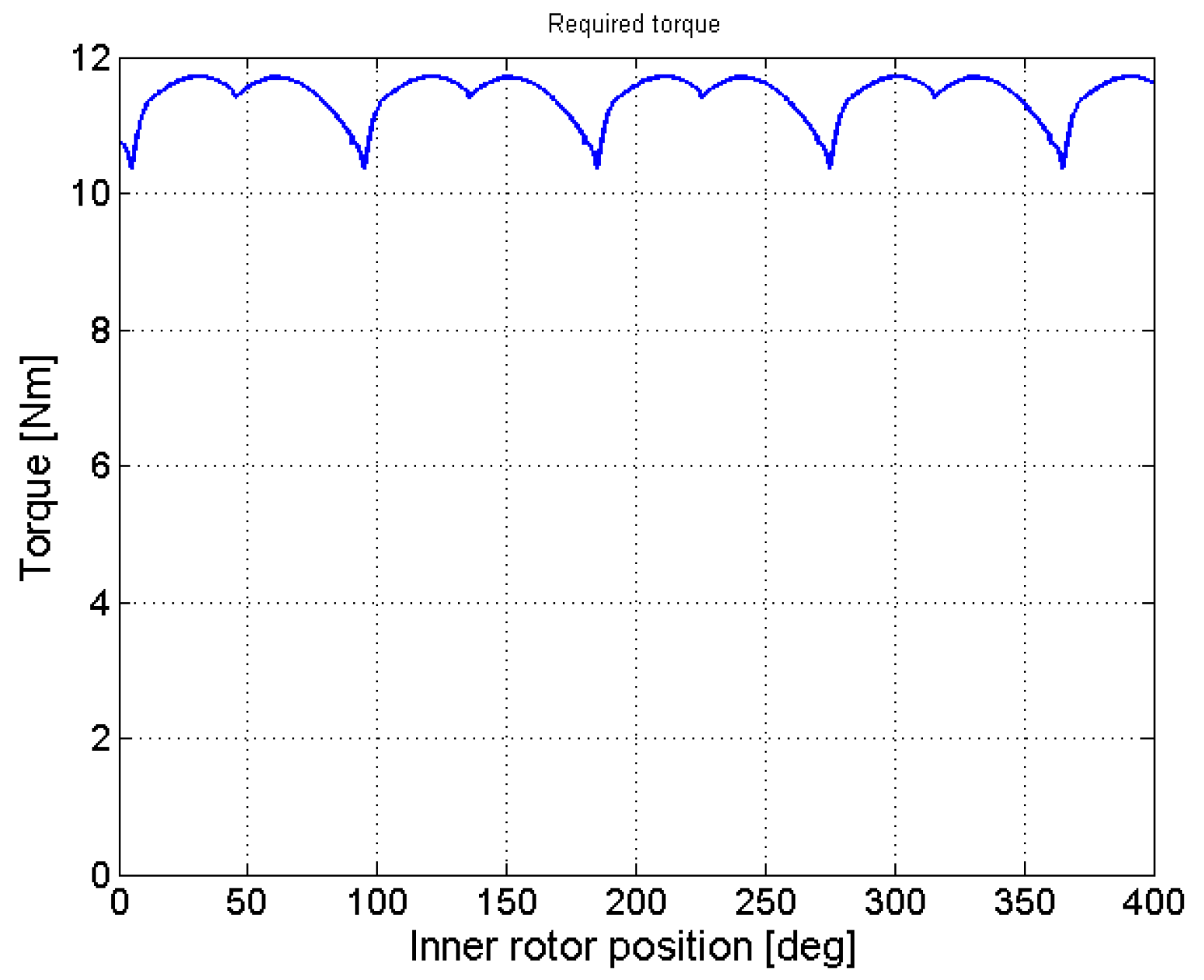
3. Gerotor Dynamic Model
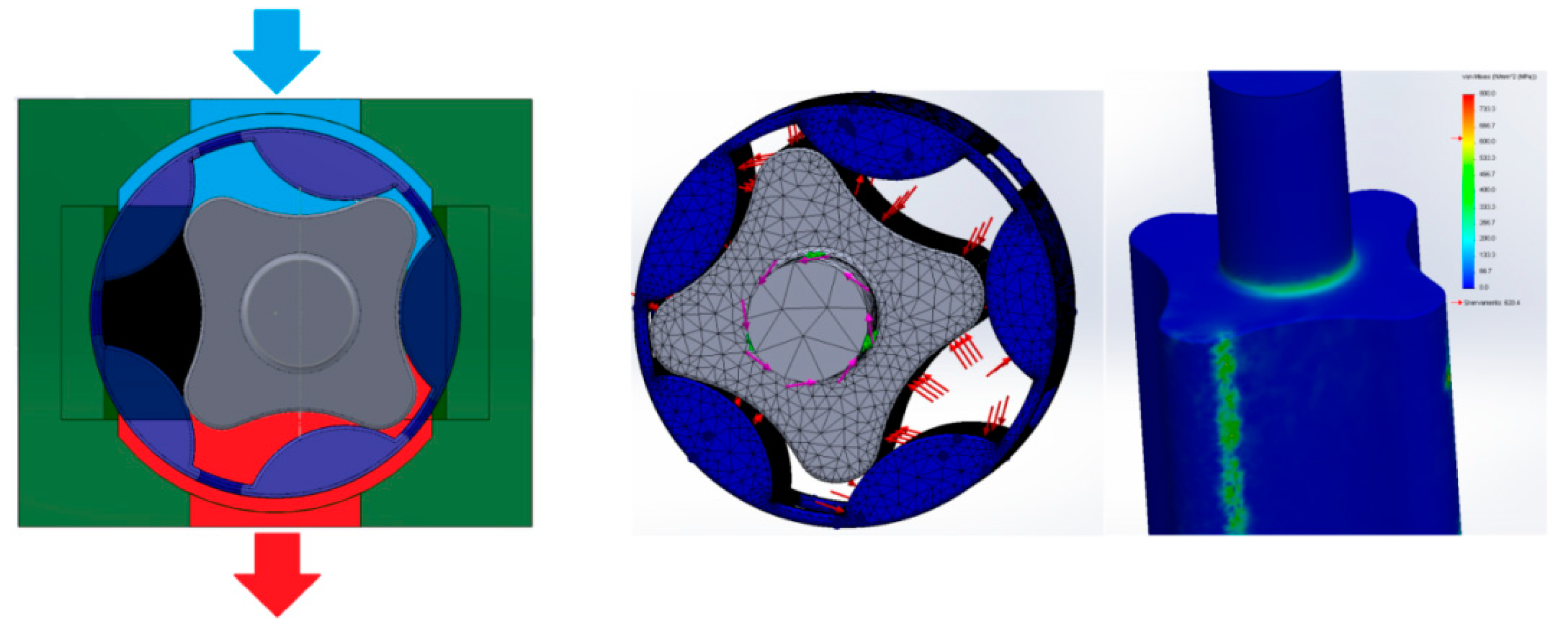
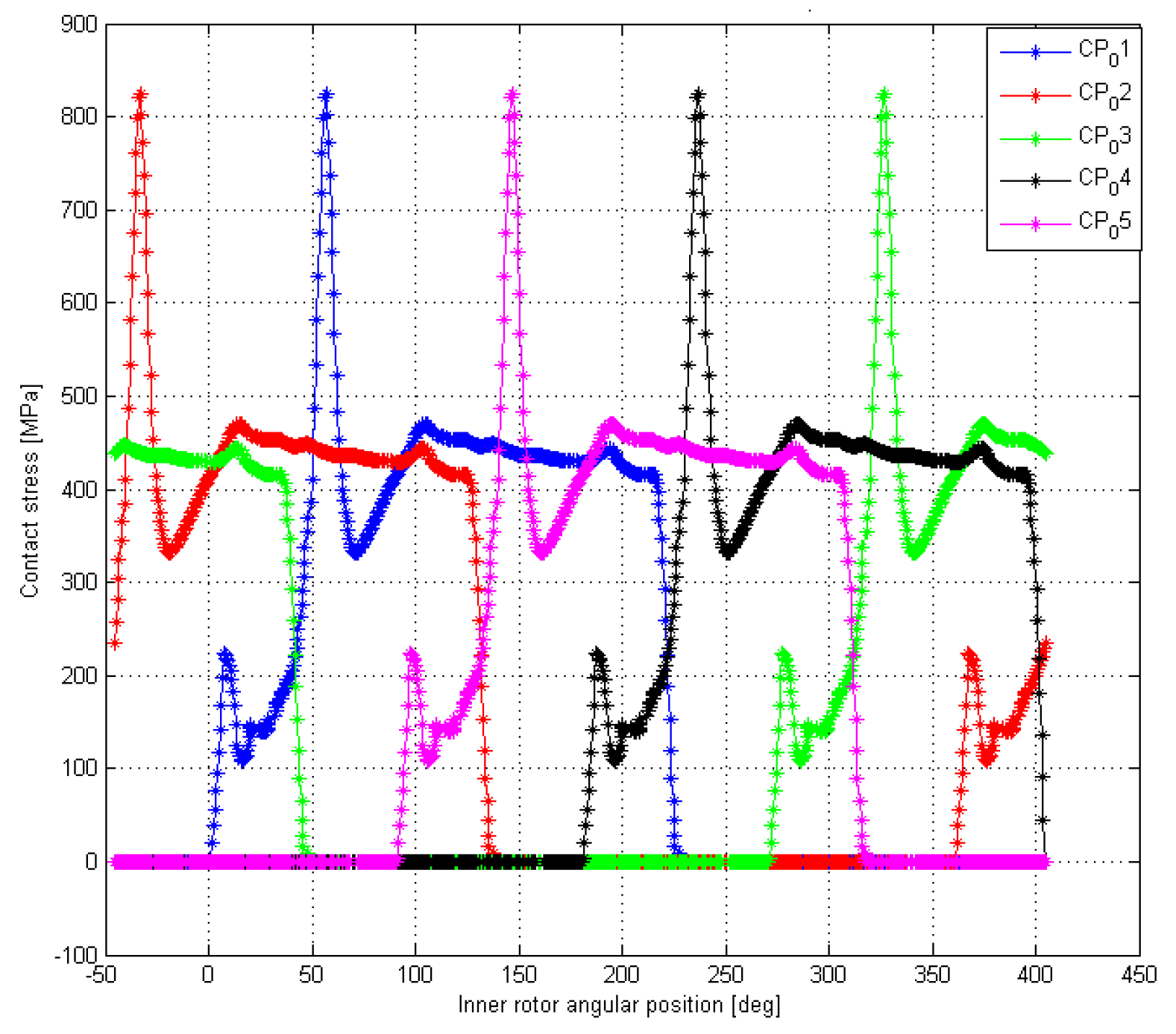
4. Contact Stress Estimation
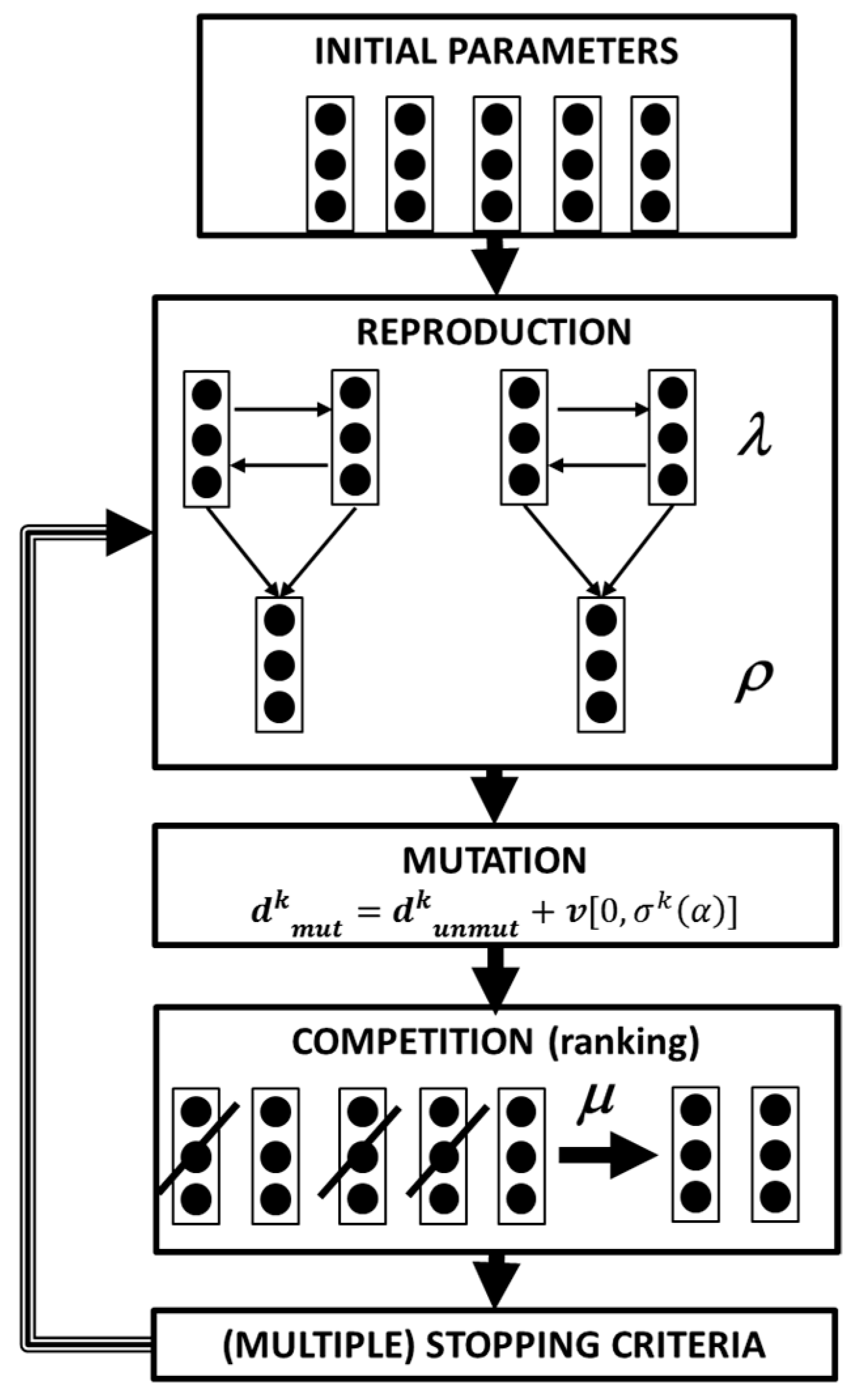
5. Stochastic Optimization Algorithms
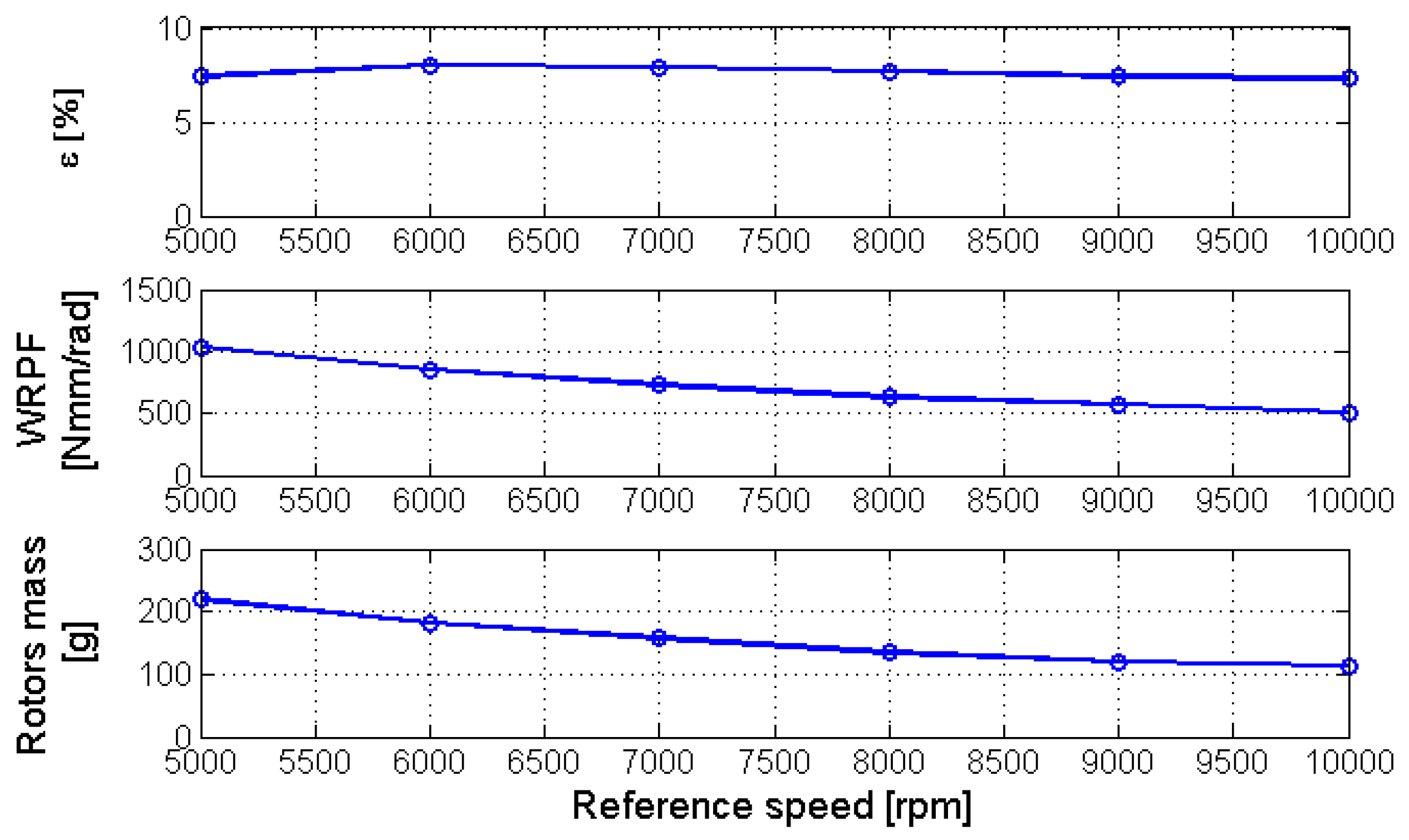
6. Profile Optimization
6.1. Cycloidal Gears Optimization
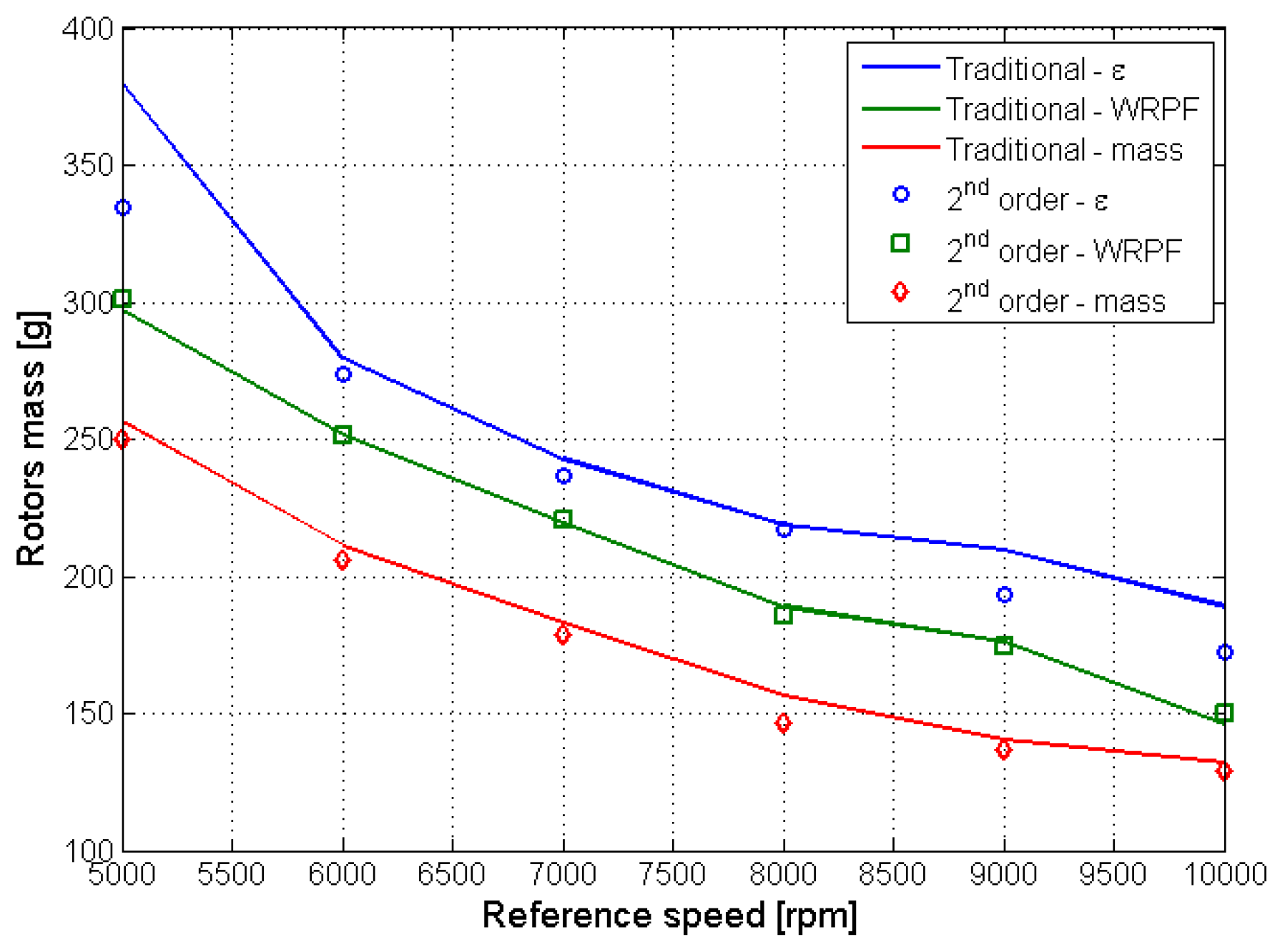
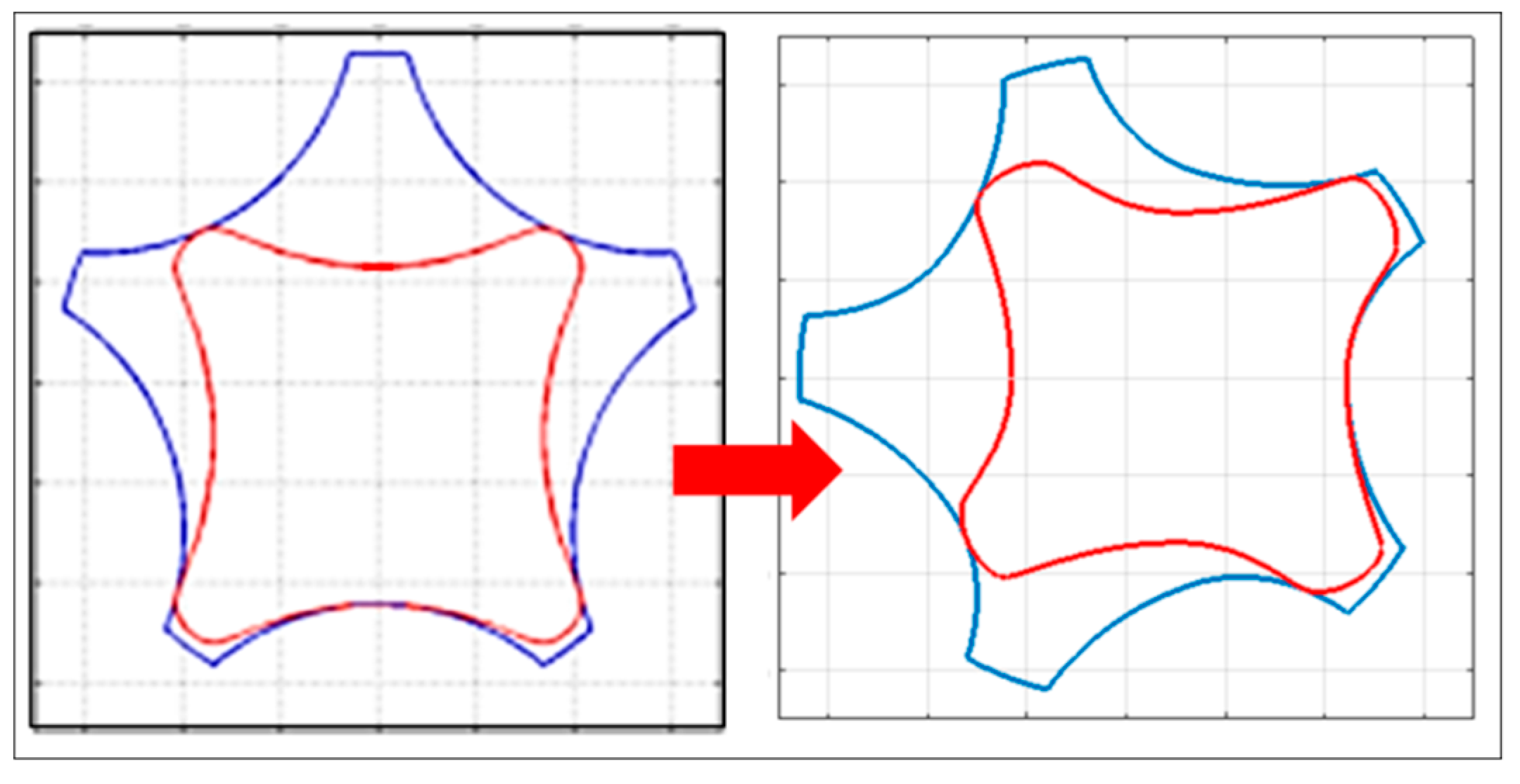
6.2. Second-Order Optimization through Asymmetric Lobes
7. Discussion and Further Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Crossover operator | |
| Fluid bulk modulus | |
| Angular pitch | |
| Flow rate irregularity | |
| Angular parameter for a parametric description of the lobe geometry | |
| Angle between the normal to the contact point and the radial direction | |
| External gear profile in its integral reference system | |
| External gear profile in the inner gear reference system | |
| Inner gear profile in its integral reference system | |
| Angular position of the external gear | |
| Angular position of the inner gear | |
| Non-dimensional design parameter | |
| Number of parents in the evolutionary algorithm | |
| Fluid dynamic viscosity | |
| Number of surviving elements at each iteration of the evolutionary algorithm | |
| Poisson ratio | |
| Profile parameterization | |
| Fluid density | |
| Curvature of the external profile | |
| Curvature of the internal profile | |
| Number of offspring in the evolutionary algorithm | |
| Local radius of the lobe | |
| Angular coordinates for lobe geometry description | |
| Contact stress | |
| Transmission ratio between the gears | |
| Angular speed of the external gear | |
| Angular speed of the inner gear | |
| Profile parameterization | |
| Frontal area of the chamber | |
| Port area | |
| Required port area | |
| Characteristic dimensions of the contact area | |
| Center of the lobe profile | |
| Discharge coefficient | |
| Distance between the gerotor axis and the contact points | |
| “Parent” parameter vector belonging to the k-th generation | |
| Parameter vector for the k+1 generation before mutation | |
| Young’s modulus | |
| Gerotor eccentricity | |
| Contact force | |
| Elliptic parameter | |
| Safety coefficient against cavitation | |
| Height of the leakage path | |
| Axial length of the chambers | |
| Length of the leakage path | |
| Transformation matrix | |
| Tooth number of the external gear | |
| Normal to the external gear profile | |
| Center of the external gear centrode | |
| Center of the inner gear centrode | |
| Mean pressure inside the i-th chamber | |
| Pressure at the inlet port | |
| Pressure at the port | |
| Vapor tension | |
| Pump total flow rate | |
| Net flow rate for the i-th chamber | |
| Flow rate between the i-1th and i − 1th chambers | |
| Average pump flow rate | |
| Flow rate from the port to the i-th variable volume chamber | |
| Fitness of the optimization problem solution | |
| Radius of the external gear centrode | |
| Radius of the internal gear centrode | |
| Limit value of the external gear radius | |
| Limit value of the inner gear radius | |
| Position of the generic point k in the lobe reference system | |
| Driving torque | |
| Volume of the i-th chamber | |
| Limit speed | |
| Sliding speed between mating profiles | |
| Co-penetration between gears profiles | |
| WRPF | Wear rate proportional factor |
| Reference frame integral with the external gear | |
| Fixed reference frame | |
| Reference frame integral with the inner gear |
References
- Mancò, G.; Mancò, S.; Rundo, M.; Nervegna, N. Computerized generation of novel gearings for internal combustion engines lubricating pumps. Int. J. Fluid Power 2000, 1, 49–58. [Google Scholar] [CrossRef]
- Meyr, N.; Cardé, C.; Nitta, C.; Garas, D.; Garrard, T.; Parks, J.; Vaughn, J.; Bangar, C.; Francisco, A.; Duvall, M.; et al. Design and Development of the 2002 UC Davis Future Truck; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2002. [Google Scholar]
- Ippoliti, L.; Hendrick, P. Influence of the supply circuit on oil pump performance in an aircraft engine lubrication system. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar]
- Frosina, E.; Senatore, A.; Buono, D.; Manganelli, M.U.; Olivetti, M. A tridimensional CFD analysis of the oil pump of an high performance motorbike engine. Energy Procedia 2014, 45, 938–948. [Google Scholar] [CrossRef]
- Colbourne, J.R. The geometry of trochoid envelopes and their applications in rotary pumps. Mech. Mach. Theory 1974, 9, 421–435. [Google Scholar] [CrossRef]
- Beard, J.E.; Hall, A.S.; Soedel, W. Comparison of hypotrochoidal and epitrochoidal gerotors. J. Mech. Des. 1991, 113, 133–141. [Google Scholar] [CrossRef]
- Beard, J.E.; Yannitell, D.W.; Pennock, G.R. The effects of the generating pin size and placement on the curvature and displacement of epitrochoidal gerotors. Mech. Mach. Theory 1992, 27, 373–389. [Google Scholar] [CrossRef]
- Adams, G.; Beard, J.E. Comparison of helical and skewed axis gerotor pumps. Mech. Mach. Theory 1997, 32, 729–742. [Google Scholar] [CrossRef]
- Shung, J.B.; Pennock, G.R. Geometry for trochoidal-type machines with conjugate envelopes. Mech. Mach. Theory 1994, 29, 25–42. [Google Scholar] [CrossRef]
- Litivn, F.L. Theory of Gearing; NASA: Washington, DC, USA, 1989.
- Litvin, F.L.; Feng, P.-H. Computerized design and generation of cycloidal gearings. Mech. Mach. Theory 1996, 31, 891–911. [Google Scholar] [CrossRef]
- Vecchiato, D.; Demenego, A.; Argyris, J.; Litvin, F.L. Geometry of a cycloidal pump. Comput. Methods Appl. Mech. Eng. 2001, 190, 2309–2330. [Google Scholar] [CrossRef]
- Hwang, Y.-W.; Hsieh, C.-F. Determination of surface singularities of a cycloidal gear drive with inner meshing. Math. Comput. Model. 2007, 45, 340–354. [Google Scholar] [CrossRef]
- Mimmi, G.; Pennacchi, P. Non-undercutting conditions in internal gears. Mech. Mach. Theory 2000, 35, 477–490. [Google Scholar] [CrossRef]
- Ivanovic, L.; Jositovic, D. Specific sliding of trochoidal gearing profile in the gerotor pumps. FME Trans. 2006, 34, 121–127. [Google Scholar]
- Ivanovic, L.; Devedzic, G.; Cukovic, S.; Miric, N. Modeling of the meshing of trochoidal profiles with clearances. J. Mech. Des. 2012, 134, 041003. [Google Scholar] [CrossRef]
- Ivanovic, L.; Devedzic, G.; Miric, N.; Cukovic, S. Analysis of forces and moments in gerotor pumps. Proc. Inst. Mech. Eng. Part C JMES 2010, 224, 2257–2269. [Google Scholar] [CrossRef]
- Hsieh, C.F. Influence of gerotor performance in varied geometrical design parameters. J. Mech. Des. 2009, 131, 121008. [Google Scholar] [CrossRef]
- Hsieh, C.F. Fluid and dynamic analyses of a gerotor pump using various span angle designs. J. Mech. Des. 2012, 134, 121003. [Google Scholar] [CrossRef]
- Hsieh, C.F.; Hwang, Y.W. Geometric design for a gerotor pump with high area efficiency. J. Mech. Des. 2007, 129, 1269–1277. [Google Scholar] [CrossRef]
- Mimmi, G.; Pennacchi, P. Rotor design and optimization in internal lobe pumps. Appl. Mech. Rev. 1997, 50, 133–141. [Google Scholar] [CrossRef]
- Bonandrini, G.; Mimmi, G.; Rottenbacher, C. Theoretical analysis of an original rotary machine. J. Mech. Des. 2010, 132, 024501. [Google Scholar] [CrossRef]
- Bonandrini, G.; Mimmi, G.; Rottenbacher, C. Design and simulation of meshing of a particular internal rotary pump. Mech. Mach. Theory 2012, 49, 104–116. [Google Scholar] [CrossRef]
- Demenego, D.A.; Vecchiato, F.L.; Litvin, N.; Nervegna, S.; Mancò, S. Design and simulation of meshing of a cycloidal pump. Mech. Mach. Theory 2002, 37, 311–332. [Google Scholar] [CrossRef]
- Chiu-Fan, H. Flow characteristics of gerotor pumps with novel variable clearance design. ASME J. Fluids Eng. 2015, 137, 041107. [Google Scholar]
- Shih-His, T.; Yan, J.; Yang, D.C.H. Design of deviation-function based gerotors. Mech. Mach. Theory 2009, 44, 1595–1606. [Google Scholar]
- Yang, D.C.H.; Yan, J.; Shih-Hsih, T. Flowrate formulation of deviation function based gerotor pumps. J. Mech. Des. 2010, 132, 064503. [Google Scholar] [CrossRef]
- Yan, J.; Yang, D.C.; Shih-Hsih, T. On the generation of analytical noncircular multilobe internal pitch curves. J. Mech. Des. 2009, 130, 092601. [Google Scholar] [CrossRef]
- Litvin, F.L.; Demenego, A.; Vecchiato, D. Formation by branches of envelope to parametric families of surfaces and curves. Comput. Methods Appl. Mech. Eng. 2001, 190, 4587–4608. [Google Scholar] [CrossRef]
- Yan, J.; Shih-Hsih, T.; Yang, D.C.H. A new gerotor design method with switch angle assignability. In Proceedings of the 10th ASME International Power Transmission and Gearing Conference, Las Vegas, NV, USA, 4–7 September 2007. [Google Scholar]
- Choi, T.H.; Kim, M.S.; Lee, G.S.; Yung, S.Y.; Bae, J.H.; Kim, C. Design of rotor for internal gear pump using cycloid and circular-arc curves. J. Mech. Des. 2012, 134, 011005. [Google Scholar] [CrossRef]
- Bae, J.H.; Kwak, H.S.; San, S.; Kim, C. Design and CFD analysis of gerotor with multiple profiles (ellipse-involute-ellipse type and 3-ellipses type) using rotation and translation algorithm. Proc. Inst. Mech. Eng. Part C JMES 2015, 230, 804–823. [Google Scholar] [CrossRef]
- Jung, S.Y.; Bae, J.H.; Kim, M.S.; Kim, C. Development of new gerotor for oil pumps with multiple profiles. Int. J. Precis. Eng. Manuf. 2011, 12, 835–841. [Google Scholar] [CrossRef]
- Lizhen, H. Tooth profiles analysis for internal pump gear with straight line-conjugate curve profile. J. Mech. Transm. 2004, 6, 16–18. [Google Scholar]
- Xu, X.; Song, T.L. Optimization design of internal gear pump with straight line conjugate curve profile. J. Mech. Transm. 2007, 4, 69–71. [Google Scholar]
- Xu, X.Z.; Song, T.L. Analysis of flow characteristics of gear pump with straight line profile. Coal Mine Mach. 2008, 7, 47–49. [Google Scholar]
- Rundo, M. Models for Flow Rate Simulation in Gear Pumps: A review. Energy 2017, 10, 1261. [Google Scholar] [CrossRef]
- Gamez-Montero, P.J.; Castilla, R.; Codina, E.; Freire, J.; Morató, J.; Sanchez-Casas, E.; Flotats, I. GeroMAG: In-House Prototype of an Innovative Sealed, Compact and Non-Shaft-Driven Gerotor Pump with Magnetically-Driving Outer Rotor. Energy 2017, 10, 435. [Google Scholar] [CrossRef]
- Mancò, S.; Nervegna, N.; Rundo, M. Critical issues on performance of lubricating gerotor pumps at high rotational speed. In Proceedings of the 7th Scandinavian International Conference on Fluid Power, Linköping, Sweden, 30 May–1 June 2001; pp. 23–38. [Google Scholar]
- Jacazio, G.; De Martin, A. Influence of rotor profile geometry on the performance of an original low-pressure gerotor pump. Mech. Mach. Theory 2016, 100, 296–312. [Google Scholar] [CrossRef]
- Franc, J.-P. Physics and Control of Cavitation, Chapter in Design and Analysis of High Speed Pumps; NATO RTO Educational Notes; NATO: Washington, DC, USA, 2006. [Google Scholar]
- Singh, T. Design of Vane Pump Suction Porting to Reduce Cavitation at High Operation Speeds; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1991. [Google Scholar]
- Idel’Chik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; Jaico: Mumbai, India, 2008. [Google Scholar]
- Viersma, T.J. Analysis, Synthesis and Design of Hydraulic Servosystems and Pipelines; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Jelali, M.; Kroll, A. Hydraulic Servo-Systems; Springer: Berlin, Germany, 2003. [Google Scholar]
- Gamez-Montero, P.J.; Castilla, R.; Khamashta, M.; Codina, E. Contact problems of a trochoidal-gear pump. Int. J. Mech. Sci. 2006, 48, 1471–1480. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Alotto, P.G.; Eranda, C.; Brandtatter, B.; Furnrtratt, G.; Magele, C.; Molinari, G.; Nervi, M.; Preis, K.; Repetto, M.; Richter, K. Stochastic Algorithms in Electromagnetic Optimization. IEEE Trans. Magn. 1998, 34, 3674–3684. [Google Scholar] [CrossRef]
- Rechenberg, I. Evolutionsstrategie 94; Frommann-Holzboog: Stuttgart, Germany, 1994. [Google Scholar]
- Holland, J.H. Adaption in Natural and Artificial Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1955, 21, 1087–1092. [Google Scholar] [CrossRef]
- Kelner, V.; Léonard, O. Application of genetic algorithms to lubrication pump stacking design. J. Comput. Appl. Math. 2004, 168, 255–265. [Google Scholar] [CrossRef]
- Kim, J.H.; Kim, C.; Chang, Y.J. Optimum design on lobe shapes of gerotor oil pump. J. Mech. Sci. Technol. 2006, 20, 1390–1398. [Google Scholar] [CrossRef]
- Kwon, S.; Kim, C.; Shin, J. Optimal rotor wear design in hypotrochoidal gear pump using genetic algorithm. J. Cent. South Univ. Technol. 2011, 18, 718–725. [Google Scholar] [CrossRef]
- Fogel, D.B. Evolutionary Computation; IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Schwefel, H.P. Numerische Optimierung von Computer-Modellen Mittels der Evolutionsstrategie; Birkhaeuser: Basel, Switzerland, 1977. [Google Scholar]
- Janikow, C.J.; Michalewicz, Z. An experimental comparison of binary and floating point representation in genetic algorithms. In Proceedings of the 4th International Conference Genetic Algorithms, Los Altos, CA, USA, 13–16 July 1991; pp. 31–36. [Google Scholar]
- Back, T.; Schwefel, H.P. An Overview of Evolutionary Algorithms for Parameter Optimization, Evolutionary Computation; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms. In Proceedings of the International Conference on Genetic Algorithm and Their Applications, Pittsburh, PA, USA, 24–26 July 1985. [Google Scholar]
- Fonseca, C.M.; Fleming, P.J. Multiobjective genetic algorithms. In IEE Colloquium on Genetic Algorithms for Control Systems Engineering; IET: London, UK, 1993. [Google Scholar]
- Ivanovic, L.; Stojanovic, B.; Blagojevic, J.; Bogdanovic, G.; Marinkovic, A. Analysis of the flow rate and the volumetric efficiency of the trochoidal pump by application of Taguchi method. Tehnički Vjesnik 2017, 24, 265–270. [Google Scholar]
- Robinson, A.; Vacca, A. Multi-objective optimization of circular-toothed gerotors for kinematics and wear by genetic algorithm. Mech. Mach. Theory 2018, 128, 150–168. [Google Scholar] [CrossRef]
- Horn, J.; Nafpliotis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multiobjective optimization. In Proceedings of the First IEEE Conference on Evolutionary Computation. IEEE World Congress on Computational Intelligence, Orlando, FL, USA, 27–29 June 1994. [Google Scholar]
- Hajela, P.; Lin, C.-Y. Genetic search strategies in multicriterion optimal design. Struct. Optim. 1992, 4, 99–107. [Google Scholar] [CrossRef]
- Murata, T.; Ishibuchi, H. MOGA, multi-objective genetic algorithms. In Proceedings of the 1995 IEEE International Conference on Evolutionary Computation, Perth, WA, Australia, 29 November–1 December 1995. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective optimization using nondominated sorting in genetic algorithms. J. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Corne, D.W.; Knowles, J.D.; Oates, M.J. The Pareto envelope-based selection algorithm for multiobjective optimization. In Proceedings of the Sixth International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000. [Google Scholar]
- Lu, H.; Yen, G.G. Rank-density-based multiobjective genetic algorithm and benchmark test function study. IEEE Trans. Evol. Comput. 2003, 7, 325–343. [Google Scholar]
- Yen, G.G.; Lu, H. Dynamic multiobjective evolutionary algorithm: Adaptive cell-based rank and density estimation. IEEE Trans. Evol. Comput. 2003, 7, 253–274. [Google Scholar] [CrossRef]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the Sixth International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Karamooz Ravari, M.R.; Forouzan, M.R.; Moosavi, H. Flow irregularity and wear optimization in epitrochoidal gerotor pumps. Meccanica 2012, 47, 9178–9928. [Google Scholar]
- Kwon, S.-M.; Kim, M.S.; Shin, J.-H. Analytical wear model of a gerotor pump without hydrodynamic effect. J. Adv. Mech. Des. Syst. Manuf. 2008, 2, 230–237. [Google Scholar] [CrossRef]

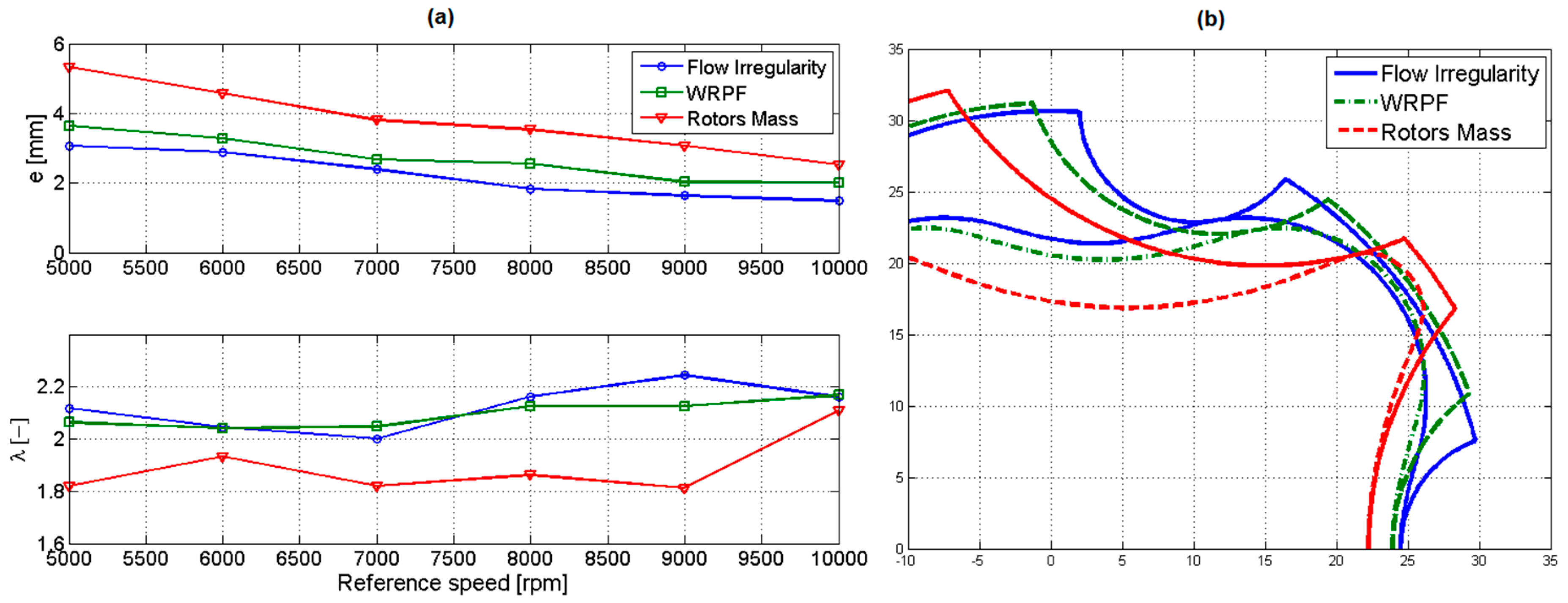
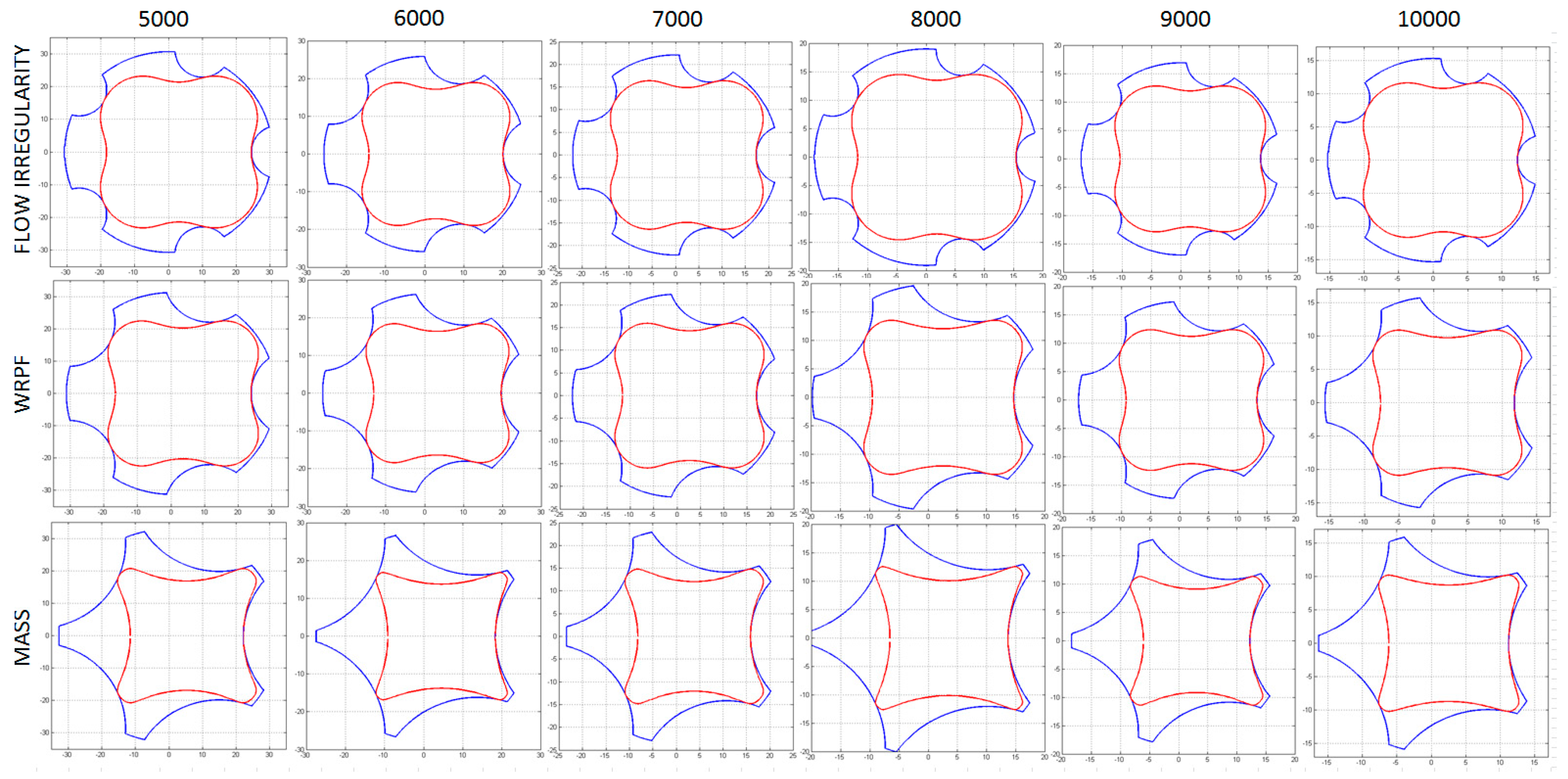
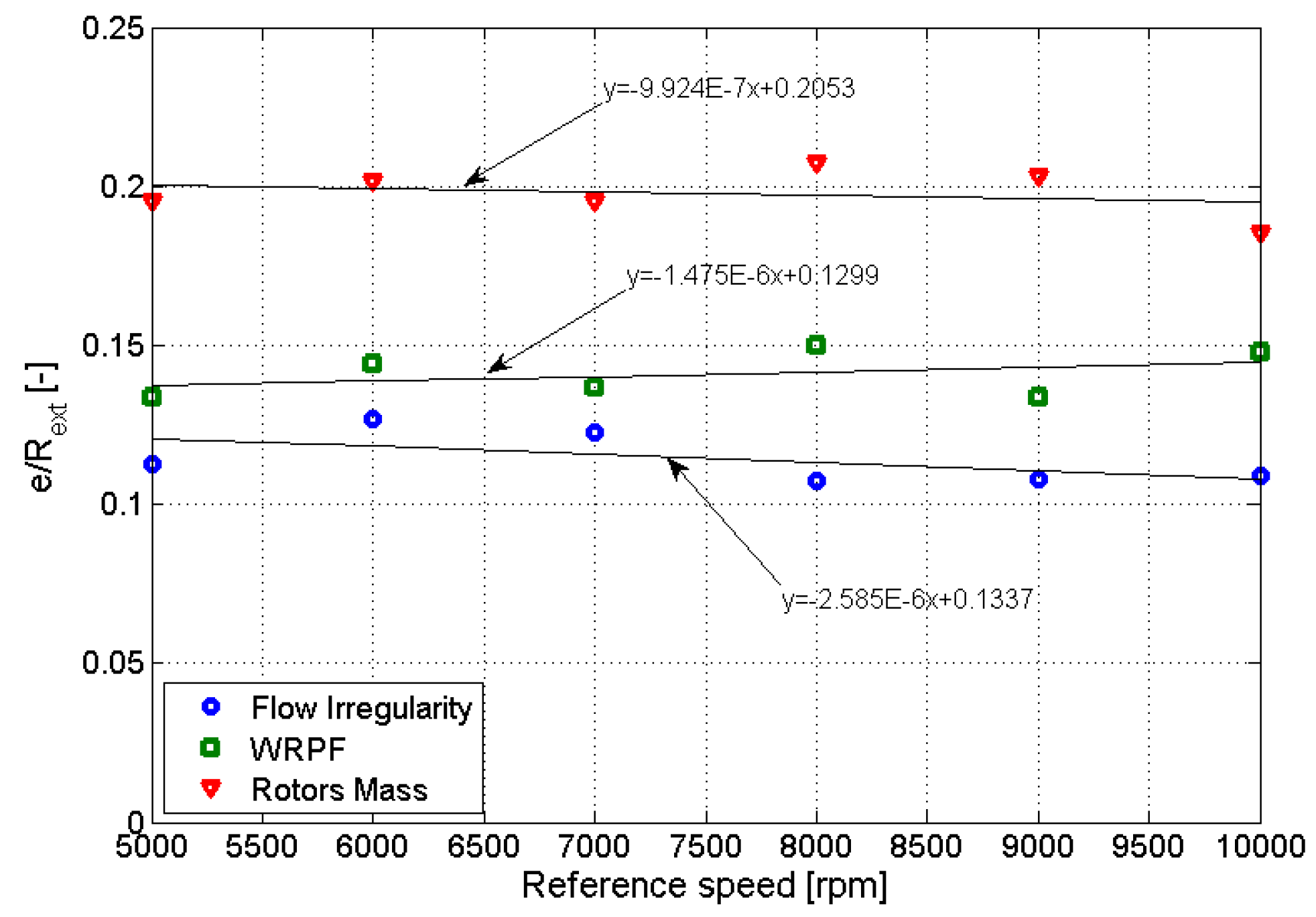
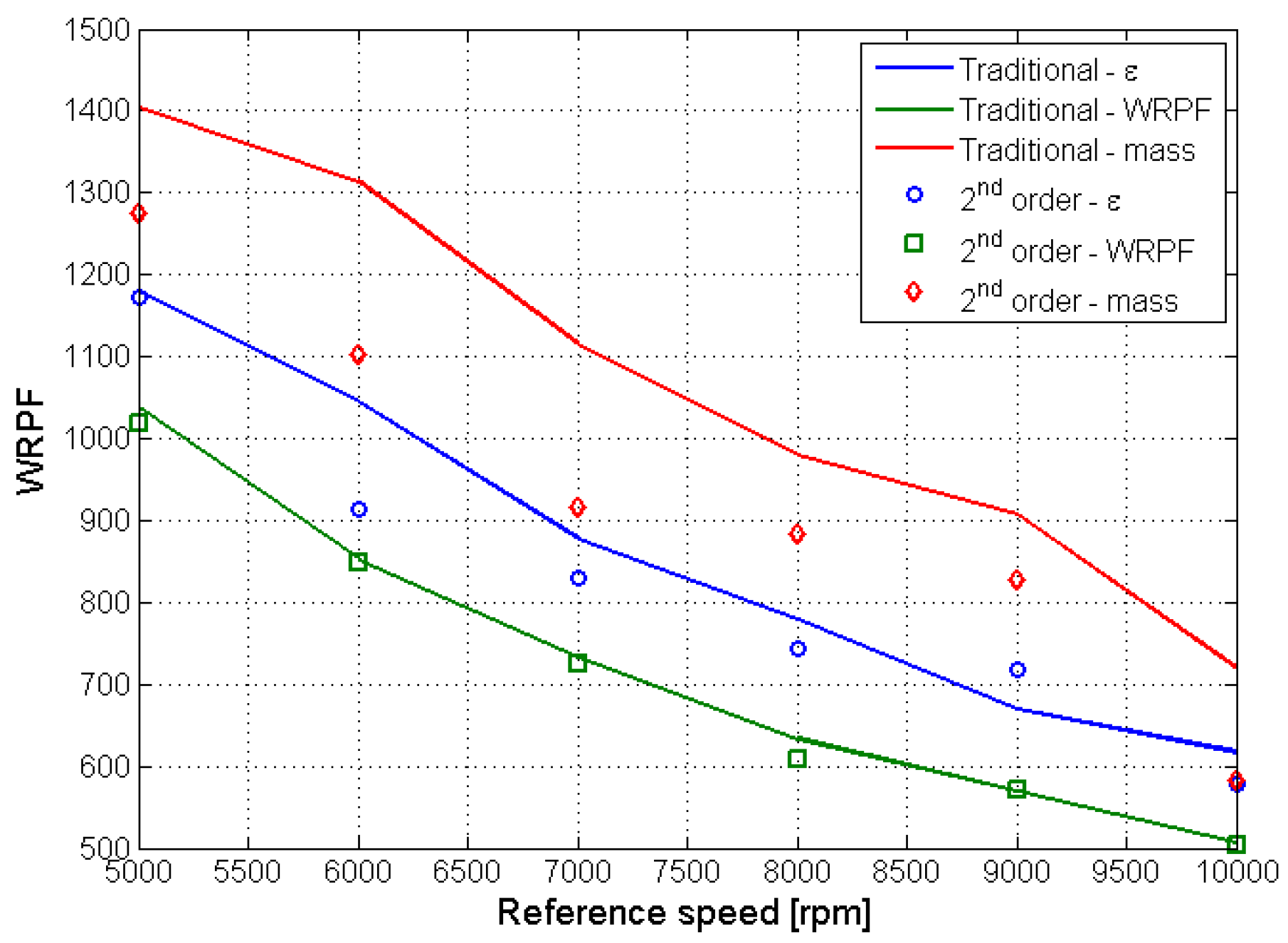
| Speed (rpm) | Objective of the First Optimization Process | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (-) | (mm) | (-) | (-) | (mm) | (-) | (-) | (-) | (mm) | (-) | (mm) | (-) | |
| 5000 | 2.118 | 3.074 | 0.720 | 1.159 | 1.820 | 5.326 | 0.747 | 1.070 | 2.063 | 3.643 | 0.939 | 1.115 |
| 6000 | 2.046 | 2.880 | 0.753 | 1.179 | 1.932 | 4.582 | 0.834 | 1.142 | 2.041 | 3.279 | 0.879 | 1.114 |
| 7000 | 2.000 | 2.388 | 0.775 | 1.037 | 1.821 | 3.807 | 0.780 | 1.091 | 2.047 | 2.671 | 0.851 | 1.099 |
| 8000 | 2.162 | 1.829 | 0.743 | 1.179 | 1.862 | 3.537 | 0.765 | 1.028 | 2.126 | 2.558 | 0.805 | 1.041 |
| 9000 | 2.244 | 1.636 | 0.878 | 1.109 | 1.813 | 3.074 | 0.761 | 1.080 | 2.126 | 2.025 | 0.815 | 1.175 |
| 10,000 | 2.159 | 1.486 | 0.757 | 1.016 | 2.110 | 2.525 | 0.913 | 1.103 | 2.168 | 2.014 | 0.859 | 1.122 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Martin, A.; Jacazio, G.; Sorli, M. Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm. Machines 2019, 7, 17. https://doi.org/10.3390/machines7010017
De Martin A, Jacazio G, Sorli M. Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm. Machines. 2019; 7(1):17. https://doi.org/10.3390/machines7010017
Chicago/Turabian StyleDe Martin, Andrea, Giovanni Jacazio, and Massimo Sorli. 2019. "Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm" Machines 7, no. 1: 17. https://doi.org/10.3390/machines7010017
APA StyleDe Martin, A., Jacazio, G., & Sorli, M. (2019). Optimization of Gerotor Pumps with Asymmetric Profiles through an Evolutionary Strategy Algorithm. Machines, 7(1), 17. https://doi.org/10.3390/machines7010017






