Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train
Abstract
:1. Introduction
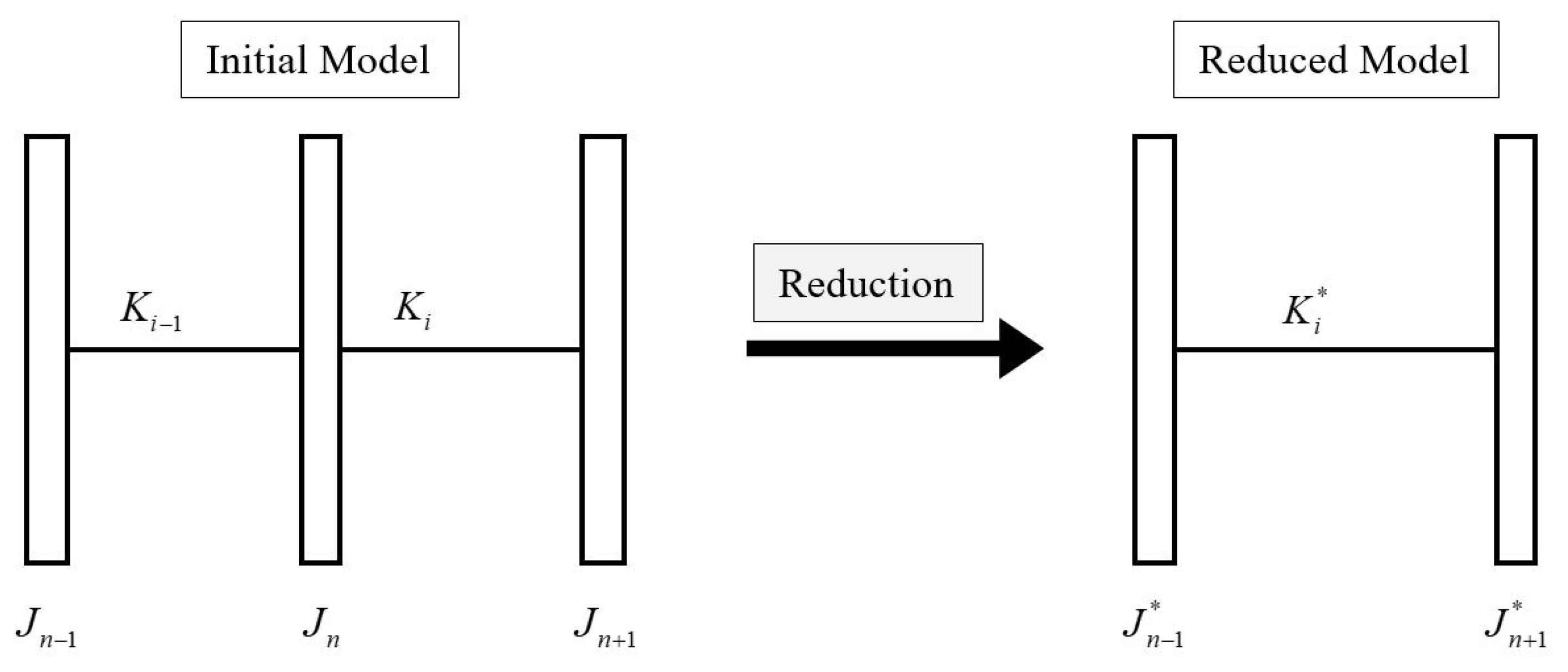
2. Shaft Penetration Factor
3. Experimental Procedure
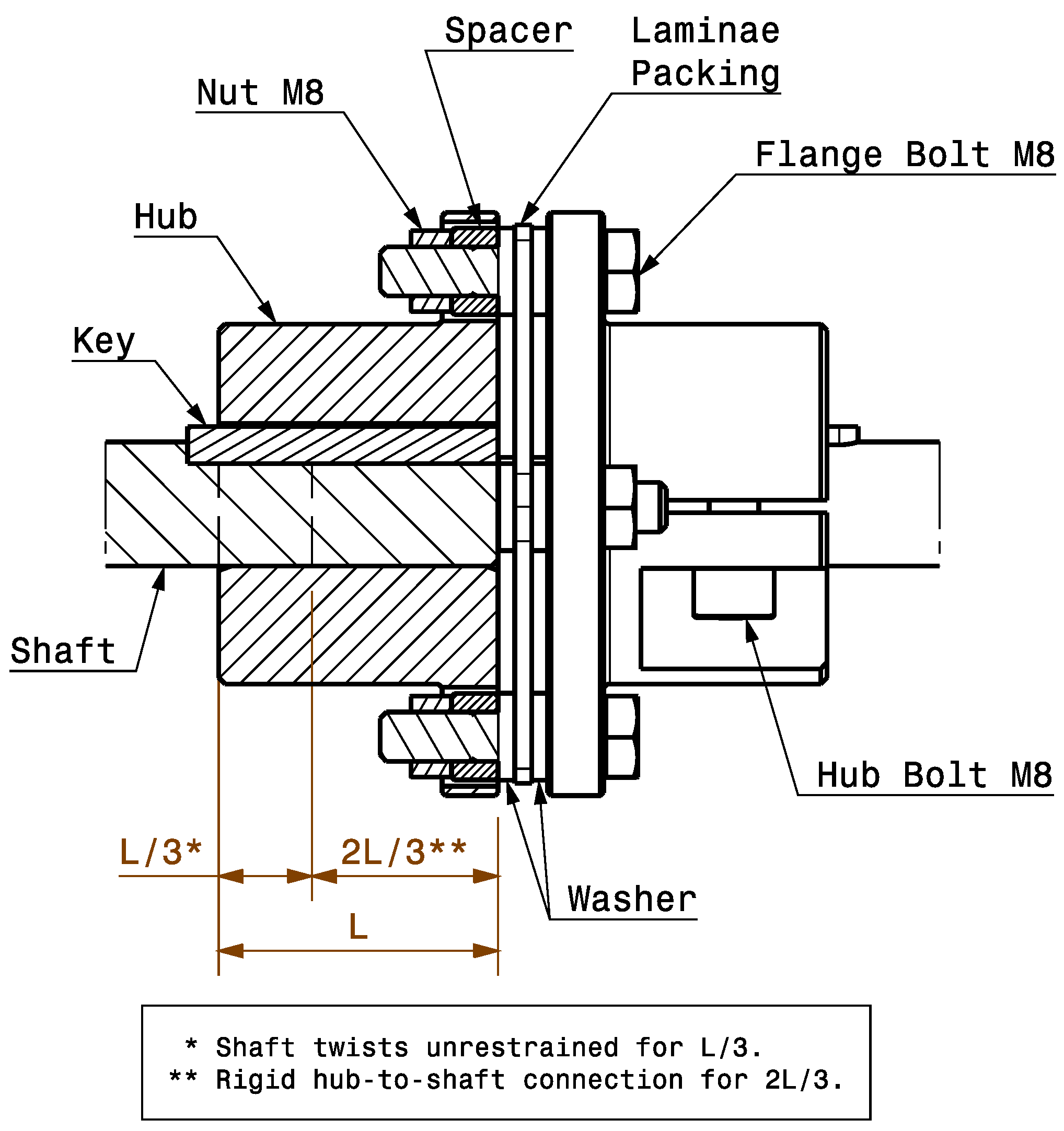
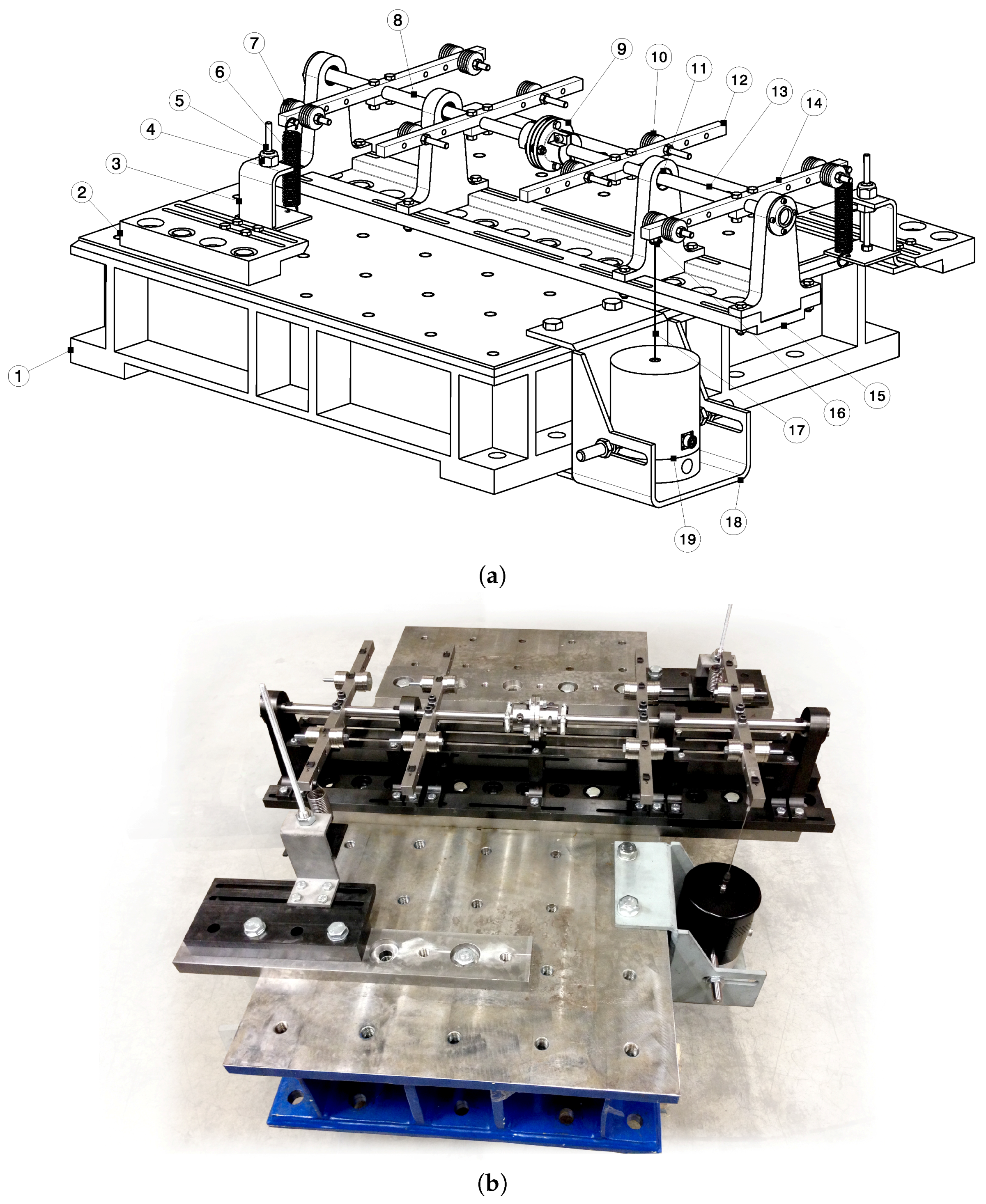
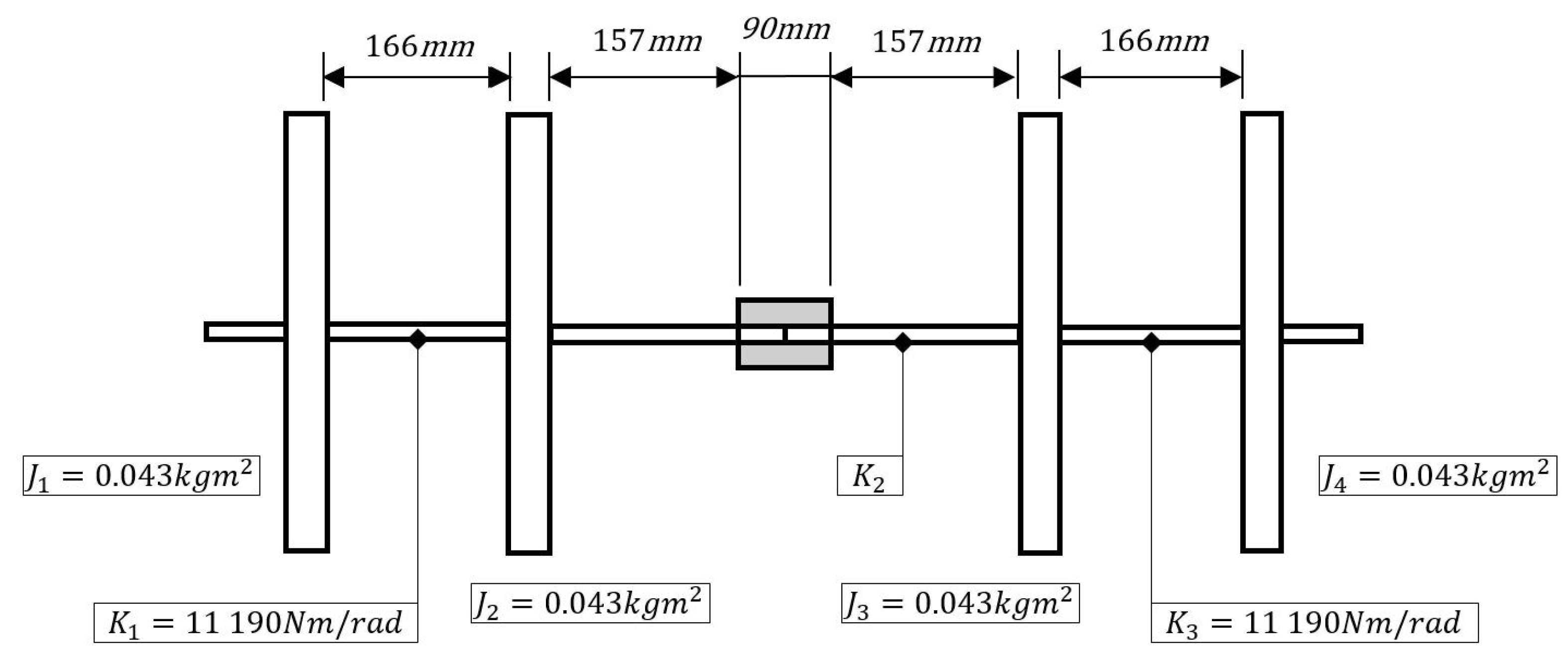
3.1. Test Rig Design
3.2. Test Configurations
- ■
- Configuration A contains the rigid connection by tensioning two M8 bolts to 21.25 kN each.
- ■
- Configuration B sets the tensioning force to 4.25 kN each.
- ■
- Configuration C unties the bolts, so the coupling hub is merely connected to the shaft via a key.
4. Results and Discussion
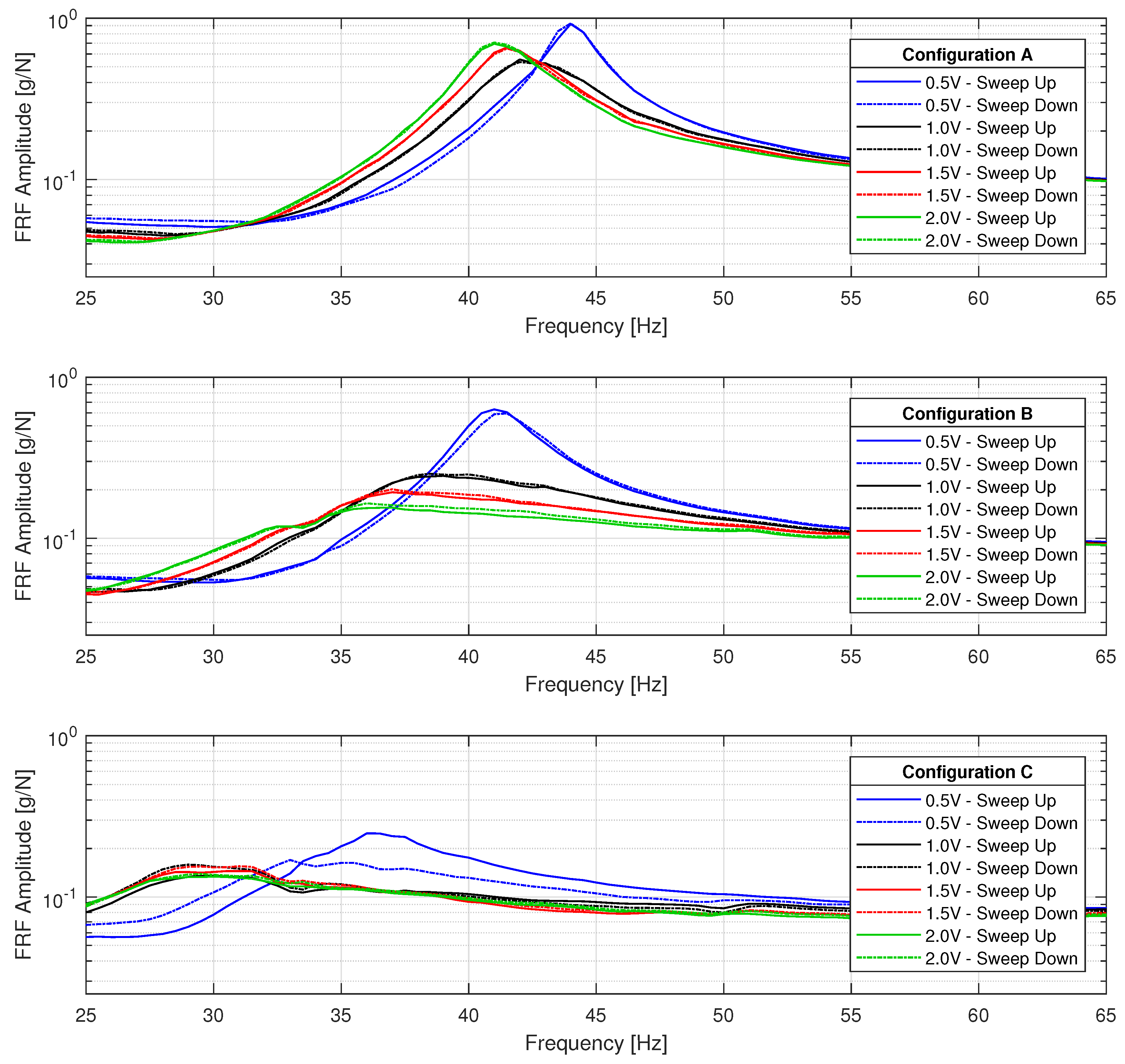
4.1. Experimental Results
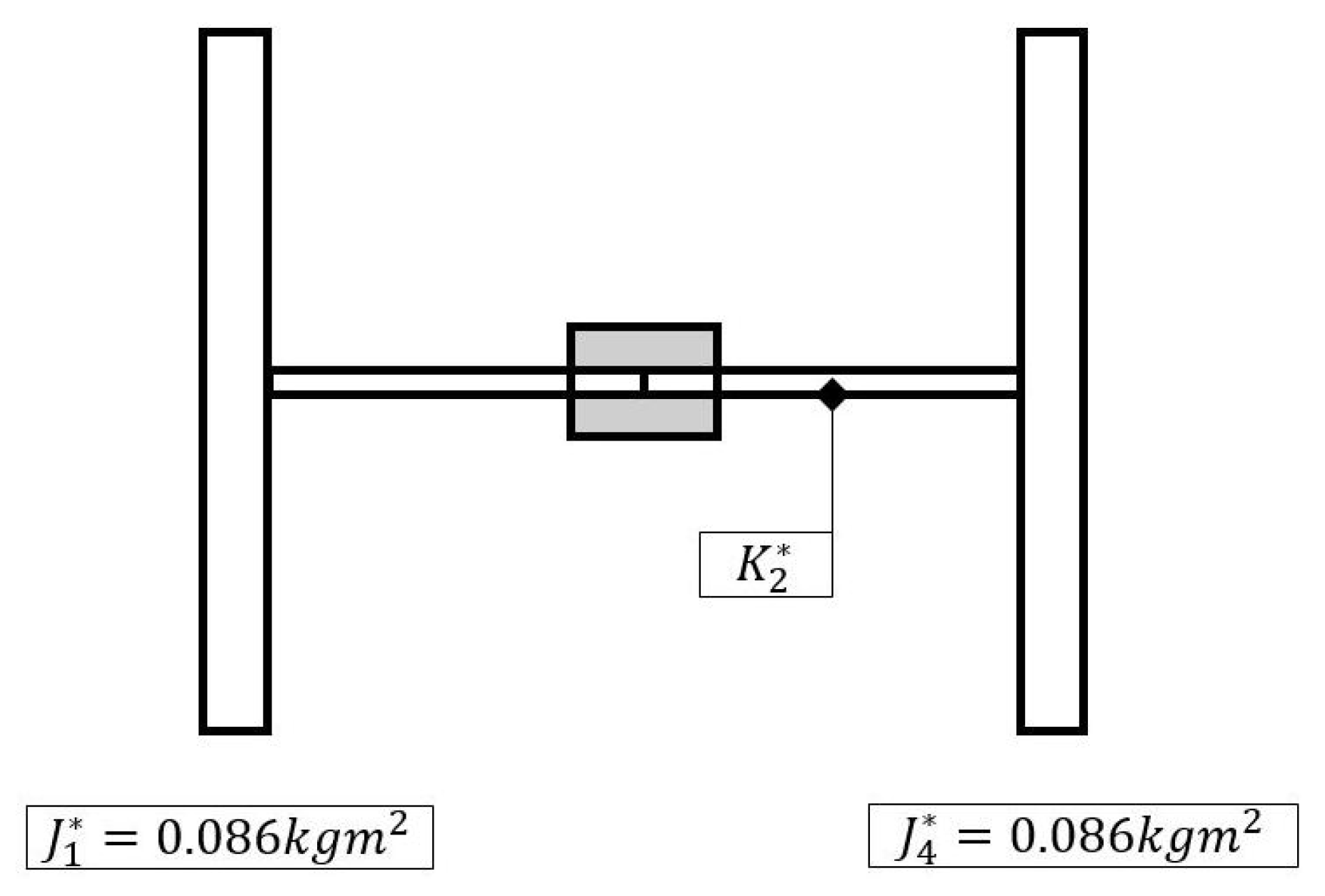
4.2. Analytical Verification of the Torsional Eigenfrequencies
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| API | American Petroleum Institute |
| FRF | Frequency Response Function |
| PolyMAX | Polyreference Least-Squares Complex Frequency-Domain Method |
| SPF | Shaft Penetration Factor |
Appendix A. Instrumentation Data
| Dytran 3023A2H | ||
|---|---|---|
| Type | Accelerometer | |
| General | Weight (g) | 4.0 |
| Case Material | Titanium | |
| Seal | Hermetic | |
| Performance | Sensitivity (mV/g) | 10 (+15%/−10%) |
| Range (g) | ||
| Frequency Response (Hz) | 2 to 10,000 (+/−10%) | |
| Element Natural Frequency (Hz) | 30,000 | |
| Environmental | Max. Shock (g pk) | 5000 |
| Max. Vibration (g pk) | ||
| Temperature Range (C) | −51 to +160 | |
| Coeff. of Thermal Sensitivity (%/C) | 0.015 |
| Dytran 1051C | ||
|---|---|---|
| Type | Dynamic Load Cell | |
| General | Weight (g) | 32.0 |
| Case Material | Stainless Steel | |
| Seal | Welded/Expoxy | |
| Performance | Sensitivity (pC/N) | −80 () |
| Compression Range (kN) | 22.24 | |
| Max. Compression (kN) | 66.72 | |
| Tension Range (kN) | 2.22 | |
| Max. Tension (kN) | 4.45 | |
| Environmental | Max. Shock, unloaded (g pk) | 10,000 |
| Max. Vibration, unloaded (g pk) | ||
| Temperature Range (C) | −73 to +260 | |
| Coeff. of Thermal Sensitivity (%/C) | 0.030 |
| TMS 2100E11 | ||
|---|---|---|
| Type | Electrodynamic Shaker | |
| General | Weight (kg) | 15.0 |
| Dimensions (L × W × H (mm)) | 305 × 305 × 203 | |
| Performance | Output Force, sine pk (N) | 440 |
| Output Force, random RMS (N) | 310 | |
| Stroke Length, pk-pk (mm) | 25.4 | |
| Frequency Range (Hz) | 2–5400 | |
| Max. Acceleration, sine pk (g) | 102 | |
| Environmental | Operating Range (C) | 5 to 35 |
| Continuous Operation (hours) | 8 |
Appendix B. Rivin’s Algorithm
References
- Mirošević, M. The Dynamics of Induction Motor Fed Directly from the Isolated Electrical Grid; InTech: London, UK, 2012; Chapter 3; pp. 73–98. [Google Scholar]
- Vance, J.; Zeidan, F.; Murphy, B. Machinery Vibration and Rotordynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- American Petroleum Institute. Axial and Centrifugal Compressors and Expander-Compressors for Petroleum, Chemical and Gas Industry Services; API Standard 617; American Petroleum Institute: Washington, DC, USA, 2002. [Google Scholar]
- American Petroleum Institute. Tutorial on the API Standard Paragraphs Covering Rotor Dynamics and Balancing: An Introduction to Lateral Critical and Train Torsional Analysis and Rotor Balancing; Standard; American Petroleum Institute: Washington, DC, USA, 2005. [Google Scholar]
- Nestorides, E.J. A Handbook on Torsional Vibration; Cambridge University Press: Cambridge, UK, 1958. [Google Scholar]
- Wilson, W.K. Practical Solution of Torsional Vibration Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1959. [Google Scholar]
- Wachel, J.C.; Szenasi, F.R. Analysis of Torsional Vibrations in Rotating Machinery. In Proceedings of the 22nd Turbomachinery Symposium, Dallas, TX, USA, 14–16 September 1993; Texas A&M University, Turbomachinery Laboratories: College Station, TX, USA, 1993. [Google Scholar]
- Adams, M.L. Rotating Machinery Vibration—From Analysis to Troubleshooting; Marcel Dekker, Inc.: New York, NY, USA, 2001. [Google Scholar]
- Walker, D.N. Torsional Vibration of Turbomachinery; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Calistrat, M.M.; Leaseburge, G.G. Torsional Stiffness of Interference Fit Connections. In Proceedings of the Mechanisms Conference and International Symposium on Gearing and Transmissions, San Francisco, CA, USA, 11–12 October 1972. [Google Scholar]
- Vance, J.; French, R. Measurement of Torsional Vibration in Rotating Machinery. J. Mech. Transm. Autom. Des. 1984, 108, 565–577. [Google Scholar] [CrossRef]
- Murray, B.D.; Howes, B.C.; Chui, J.; Zacharias, V. Sensitivity of Torsional Analyses to Uncertainty in System Mass-Elastic Properties. In Proceedings of the First International Pipeline Conference, Calgary, AB, Canada, 9–13 June 1996; American Society of Mechanical Engineers: NewYork, NY, USA, 1996. [Google Scholar]
- Wang, Q.; Feese, T.D.; Pettinato, B.C. Torsional Natural Frequencies: Measurement vs. Prediction. In Proceedings of the Forty-First Turbomachinery Symposium, Houston, TX, USA, 12–15 September 2012; Texas A&M University, Turbomachinery Laboratories: College Station, TX, USA, 2012. [Google Scholar]
- Peeters, B.; Van der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX Frequency-Domain Method: A New Standard for Modal Parameter Estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- Siemens PLM Software. LMS TestLab Modal Analysis; Siemens PLM Software: Plano, TX, USA, 2015. [Google Scholar]
- Rivin, E.I. Method and Means for Enhancement of Beam Stiffness. U.S. Patent No. 5,533,309, 9 July 1996. [Google Scholar]

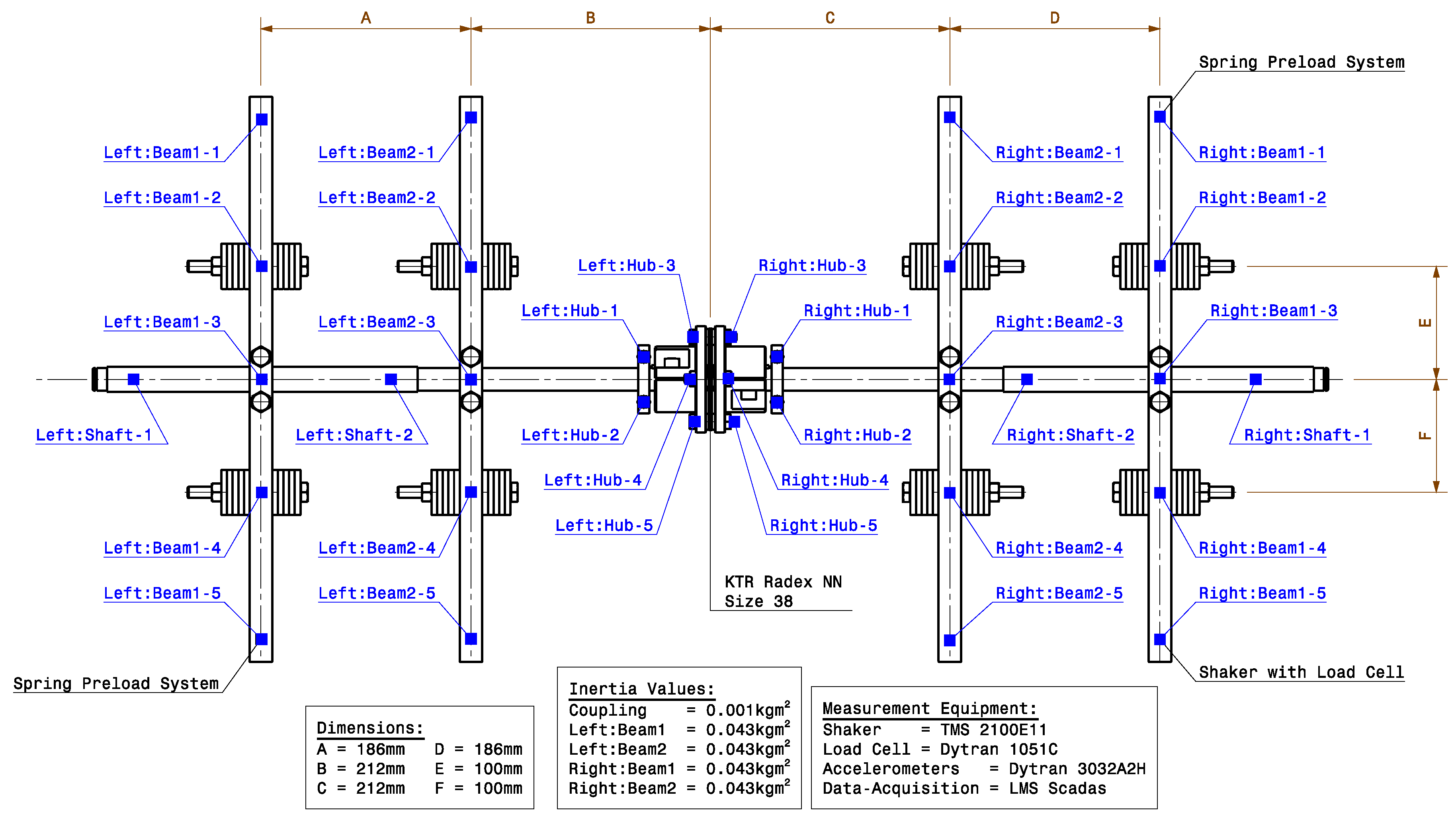

| Dimensions | ||
|---|---|---|
| Setup Envelope | L × W × H (mm) * | 1250 × 1000 × 550 |
| Shaft Sections | Diameter (mm) | 20 |
| Length (mm) | 545 | |
| Bearing Location 1 from Shaft End (mm) | 252.5 | |
| Bearing Location 2 from Shaft End (mm) | 536.5 | |
| Cross-Beams | L × W × H (mm) * | 500 × 20 × 20 |
| Position E wrt center axis (mm) ** | 100, 150, 200 | |
| Position F wrt center axis (mm) ** | 100, 150, 200 | |
| Spring System | Spring Rate (N/mm) | 2.13 |
| Max. Force (N) | 328.4 | |
| Travel of slots (mm) | 280 |
| Measurement Parameters | ||
|---|---|---|
| Swept Sine | Min. Frequency (Hz) | 25 |
| Max. Frequency (Hz) | 65 | |
| Frequency Resolution (Hz) | 0.5 | |
| Sweep Mode (-) | Linear | |
| Sweep Rate, Fixed (Hz/sec) | 0.3 | |
| Number of Sweeps (-) | 3 | |
| Data-Acquisition | FRF Estimator (-) | H1 |
| Max. FRF Sampling Rate (Hz) | 200 |
| Configuration A | Configuration B | Configuration C | ||||
|---|---|---|---|---|---|---|
| Sweep Up Excitation | Eigenfrequency (Hz) | Damping Value (%) | Eigenfrequency (Hz) | Damping Value (%) | Eigenfrequency (Hz) | Damping Value (%) |
| 15 N (0.5 V) | 43.9 | 1.76 | 40.9 | 3.38 | 35.3 | 8.33 |
| 30 N (1.0 V) | 42.0 | 3.63 | 38.5 | 11.78 | 28.7 | 15.59 |
| 45 N (1.5 V) | 41.4 | 3.13 | 36.7 | 11.82 | 28.6 | 14.63 |
| 60 N (2.0 V) | 40.7 | 3.09 | 35.4 | 16.63 | 28.7 | 15.57 |
| Sweep Down Excitation | ||||||
| 15 N (0.5 V) | 44.0 | 1.98 | 41.2 | 3.32 | 33.3 | 12.43 |
| 30 N (1.0 V) | 42.0 | 3.75 | 38.4 | 8.46 | 28.9 | 13.18 |
| 45 N (1.5 V) | 41.6 | 3.17 | 37.0 | 11.97 | 28.9 | 13.67 |
| 60 N (2.0 V) | 41.0 | 2.94 | 35.9 | 14.95 | 28.8 | 15.40 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meeus, H.; Verrelst, B.; Moens, D.; Guillaume, P.; Lefeber, D. Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train. Machines 2018, 6, 31. https://doi.org/10.3390/machines6030031
Meeus H, Verrelst B, Moens D, Guillaume P, Lefeber D. Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train. Machines. 2018; 6(3):31. https://doi.org/10.3390/machines6030031
Chicago/Turabian StyleMeeus, Hans, Björn Verrelst, David Moens, Patrick Guillaume, and Dirk Lefeber. 2018. "Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train" Machines 6, no. 3: 31. https://doi.org/10.3390/machines6030031
APA StyleMeeus, H., Verrelst, B., Moens, D., Guillaume, P., & Lefeber, D. (2018). Experimental Study of the Shaft Penetration Factor on the Torsional Dynamic Response of a Drive Train. Machines, 6(3), 31. https://doi.org/10.3390/machines6030031





