2.1. Two-Degrees of Freedom (DOF) Link Case
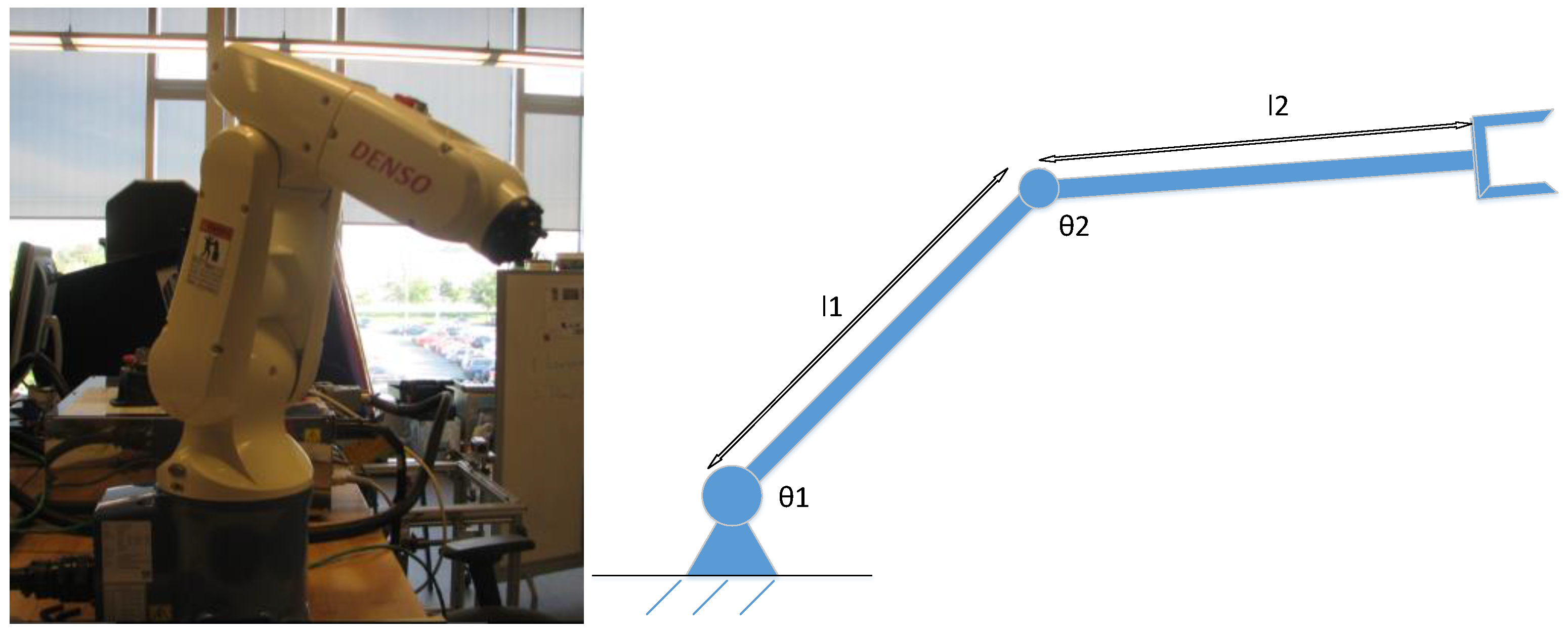
In order to implement PID control of the two-DOF (degrees of freedom) link manipulator case, as shown in
Figure 1, the dynamic equation has to be derived. Here, by using the Lagrange method, the torques applied to the joints are determined:
The kinetic energy and potential energy for link 1 are expressed as:
where
is the mass of link 1 and
is the mass of link 2. For link 2, first write down the coordinates of the end of link 2, then differentiate them with respect to time in order to obtain the kinetic energy. Denote the Cartesian coordinates of the end of link 2 as (
x2,
y2).
Differentiate with respect to time results in:
Therefore, the kinetic energy for link 2 is expressed as:
where
.
The potential energy for link 2 is expressed as:
The total kinetic and potential energy are expressed as:
The Lagrange is obtained as:
Putting them in a matrix form, we can obtain the following:
where
,
,
,
,
.
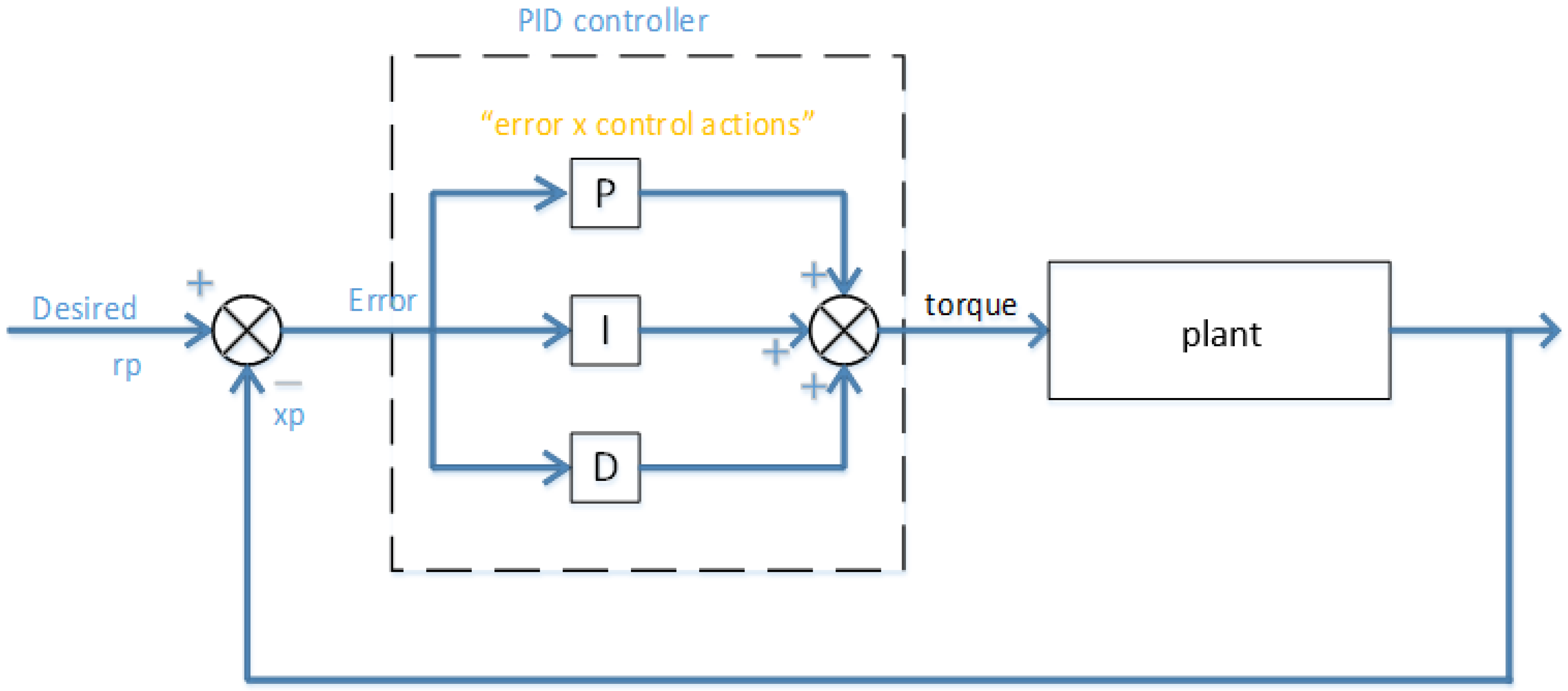
Now apply the PID controller, as shown in
Figure 2, the plant’s output compares with the reference model, which generates a difference. This difference goes via the PID operation (i.e., through “error times control actions”). The output from the PID operation goes to the plant model’s input, and this circle keeps going, up to the point where the difference among the real plant’s output and the ideal one approaches zero. The controller output is the torque; i.e.,
where error
. We know the two-link manipulator M and N matrices, the output from the manipulator (i.e., acceleration of joints 1 and 2) can be determined as follows:
So
After deriving the acceleration of joints 1 and 2, take the time integral to obtain the velocity of joints 1 and 2, and take another integral to obtain the positon of joints 1 and 2.
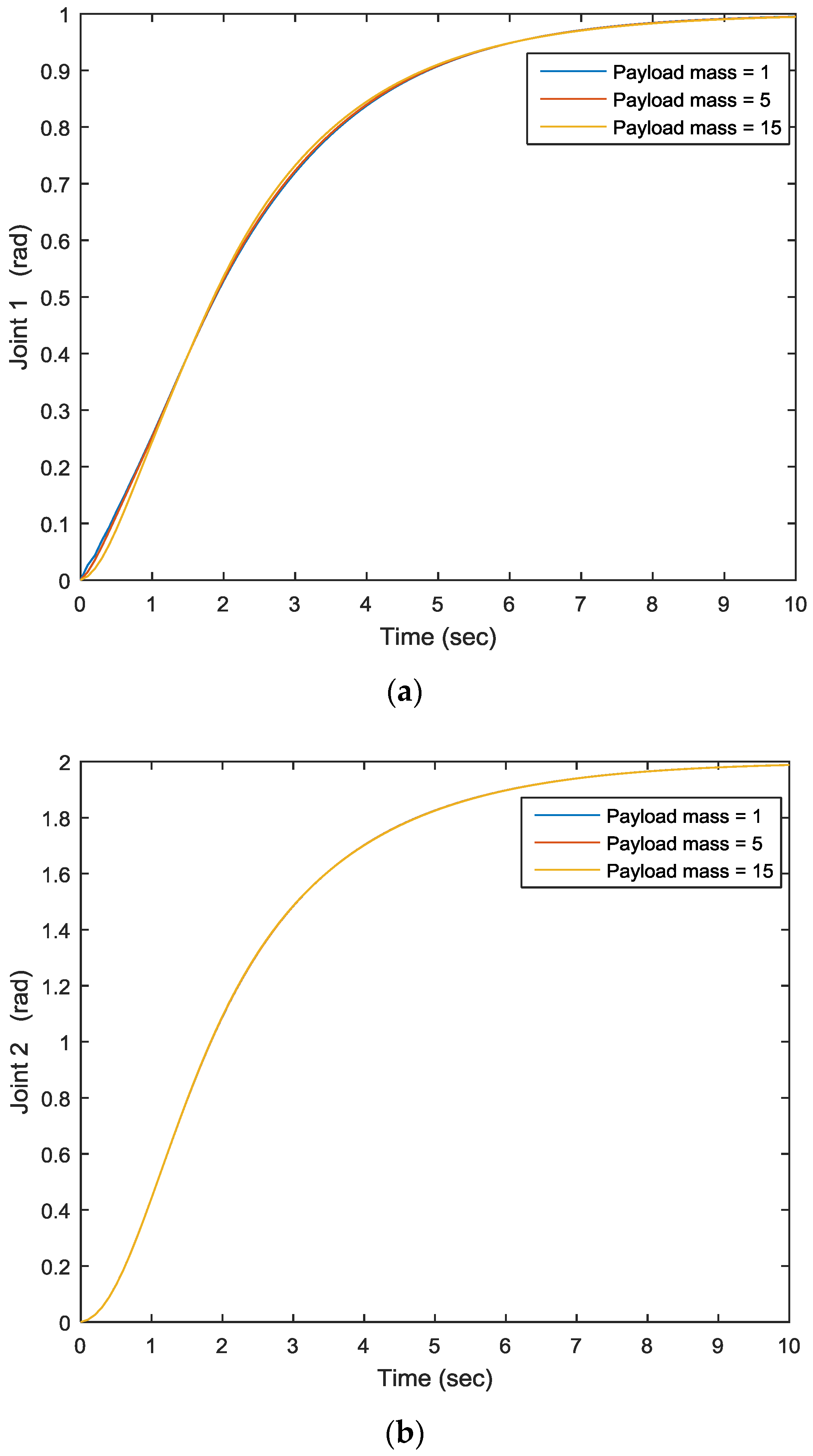
After applying different payload masses, the joints’ motion outputs are illustrated in
Figure 3. For joint 1, when the payload is 0, joint one’s motion is quite steady; however, when the payload increases to 5 and 15, one can see that joint 1’s motion is no longer the same, and the joint output is also going up and down, as shown in
Figure 3. The same applies to joint 2. The output of joint motion varies, which decreases the end-effector positioning accuracy of the robotic arm system. In order to address the above problem, model reference control is applied to compensate the payload variation effect.
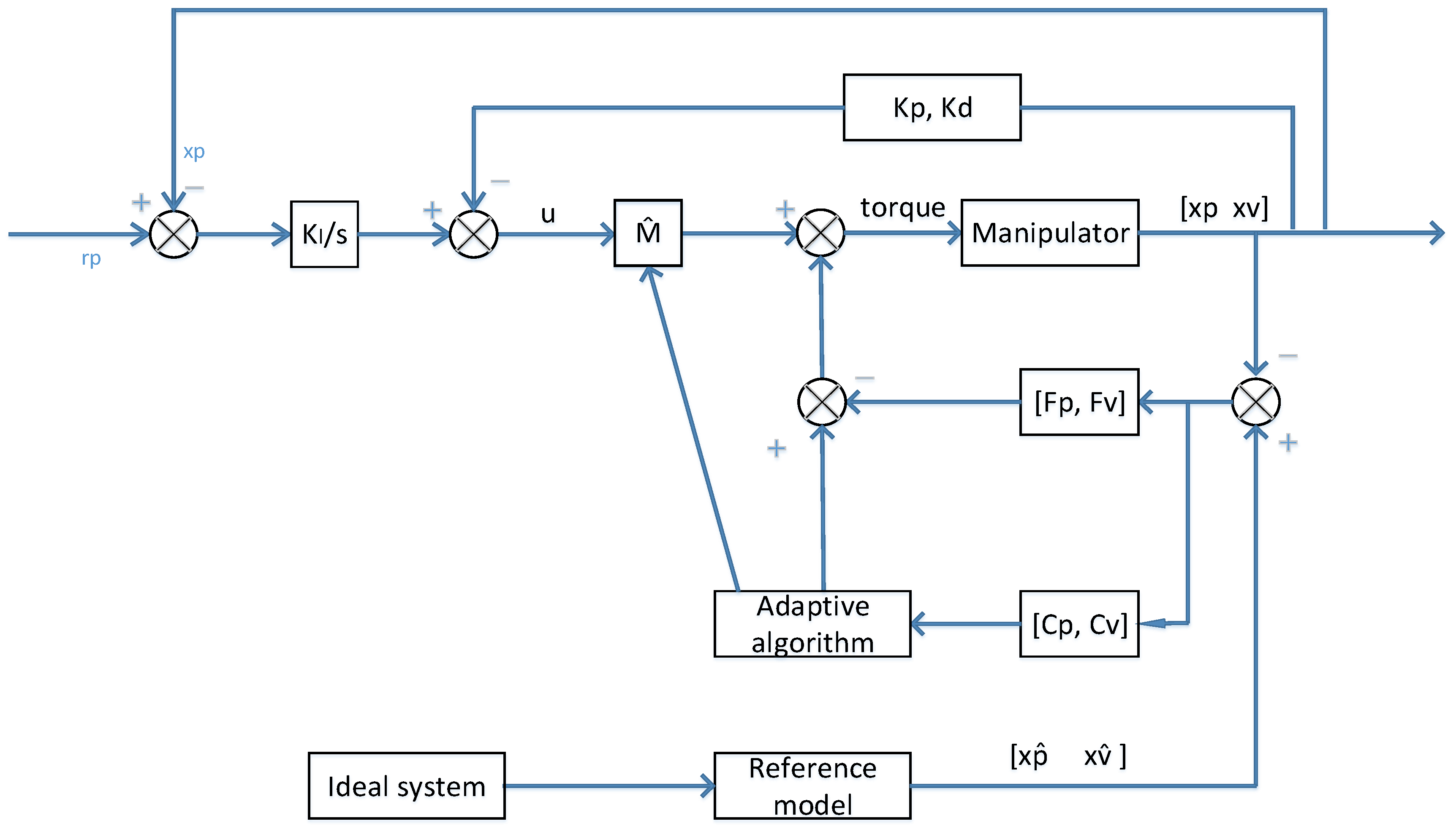
Figure 4 shows a model reference control approach. The output of the reference model will be compared with the output of the manipulator (plant), which produces an error (a difference). The error will go through the adaptation mechanism to adjust the parameters of the dynamic model of the manipulator (i.e., the adaptation process section employed the difference in order to generate the input component that goes to the plant). The matrices F
p, F
v, C
p, and C
v are introduced in order to make the system stable [
4]. At the same time, the plant’s output compares with the desired model, and one can therefore lead to generate another difference. This difference goes through the integration operation, and subsequently deducts the feedback position and velocity. This action resembles the PID control action. This process’ output, times the terms from the adaptation algorithm, then adding the terms from the adaptation algorithm, is the plant’s input. This operation will resume until the difference between the plant’s output and the reference model’s output equals to zero. The ideal system is cut off from the plant, meaning that the plant variables’ feedback values will not participate in handling the reference model’s input. The input to the reference model will be handled from its own output variables. The ideal system is entirely uninfluenced by the plant’s performance. As with the PID control, the output from the controller can be determined as follows. For the model reference adaptive control approach,
where
.
The manipulator dynamic equation is:
So, the output from the manipulator (i.e., acceleration of the joint) is:
After deriving the acceleration of the joint, take the time integral to obtain the velocity of the joint, and take another integral to obtain the positon of the joint. The adaptive algorithm is derived as follows. We now use the Popov’s asymptotic hyper-stability theorem [
4], and set
. Since:
where
, and
. The first term is used to derive the adaptive algorithm for
, and the second term is used to derive the adaptive algorithm for
. For the first term:
and
are the adjusted parameters of the dynamic equation of the manipulator, the matrices Fp, Fv, Cp, and Cv are introduced in order to make the system stable [
4], and
is the output from the Cp and Cv block. Consider the first term in the above equation, and based on Popov’s asymptotic hyper-stability theorem [
4], to prove asymptotic convergence, it must be shown that, for all
T ≥ 0, we need to find
, so that
.
Where γ
2 is a positive constant that is a function of the initial conditions. From
, so by selecting
, one has
Then,
, in order to make the system stable [
4].
Using the same analysis on the other two terms, we obtain
Derivation for M has finished. Now, using the same approach, we can obtain the adaptive algorithm for N as follows:
Figure 5 shows the joints’ output under different payload masses. By using the model reference adaptive control approach, three lines coincide with each other under different payload masses; i.e., the payload mass variation effect has been compensated.
2.2. Three-DOF Link Case
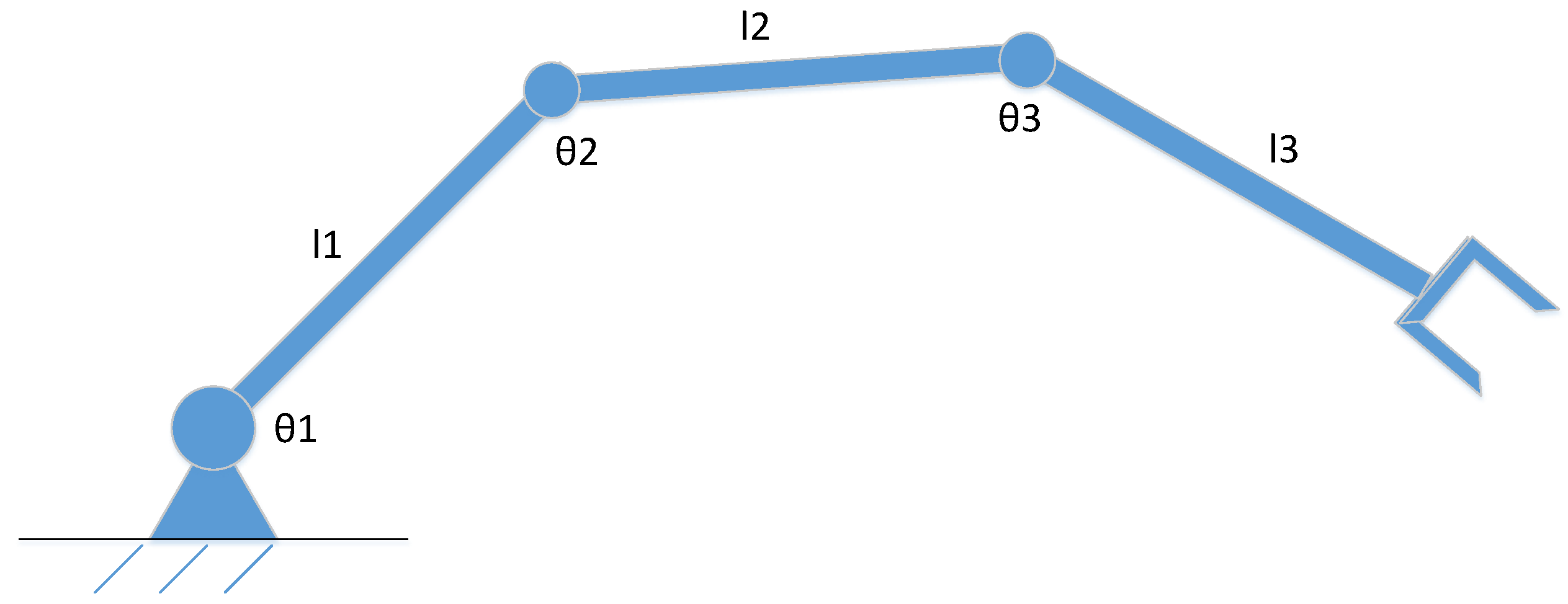
For the 3-DOF link case, as shown in
Figure 6, by using the Lagrange method, the dynamic equation is obtained as follows. Here, we just give the results.
where
,
,
,
,
a = l
1/2, b = l
2/2, c = l
3/2; r
1 = l
1, r
2 = l
2, r
3 = l
3.
Now apply the PID controller, the controller output is the torque,
where error
.
Knowing the two-link manipulator
M and
N matrices, the output from the manipulator (i.e., acceleration of joints 1 and 2) can be determined as follows:
So .
After deriving the acceleration of joints 1 and 2, take the time integral to obtain the velocity of joints 1 and 2, and take another integral to obtain the positon of joints 1 and 2.
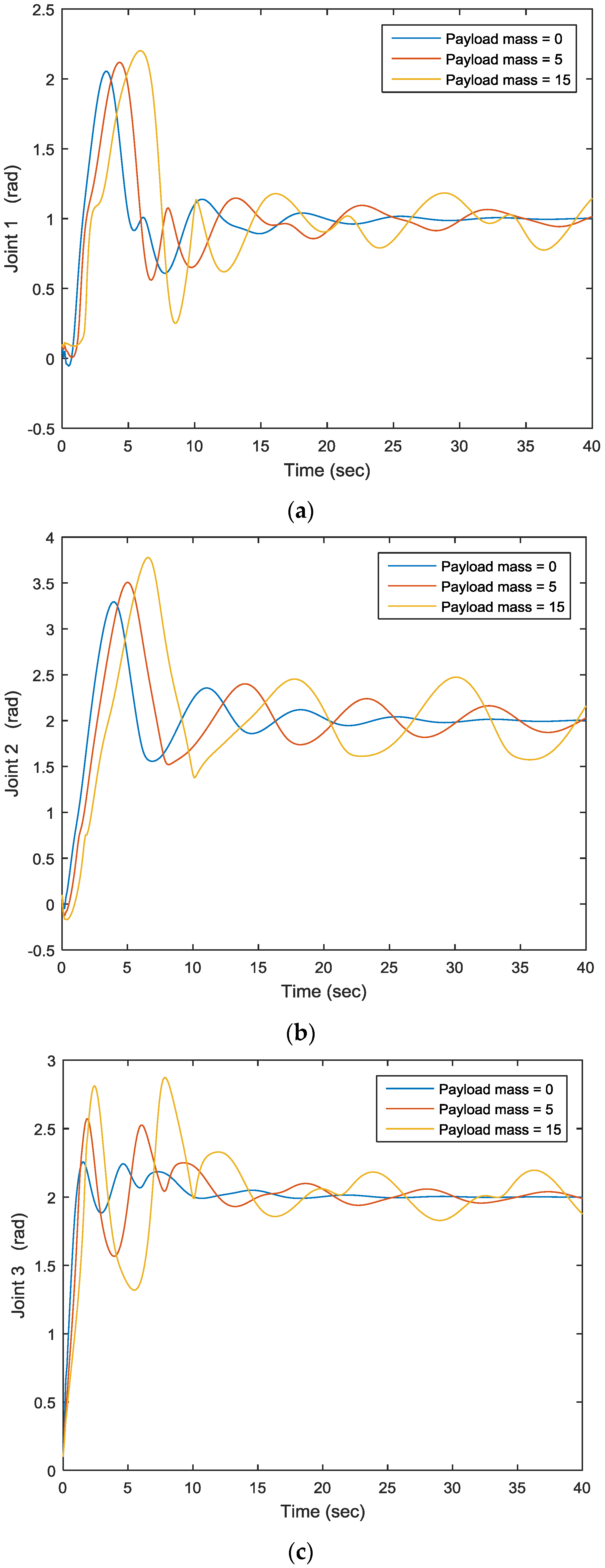
After applying different payload masses, the joints’ motion outputs are illustrated in
Figure 7. For joint 1, when the payload is 0, joint one’s motion is quite steady; however, when the payload increases to 5 and 15, one can see that joint 1’s motion is not the same anymore. The same applies to joints 2 and 3. For the model reference adaptive control approach,
where
.
So, the output from the manipulator (i.e., acceleration of joint) is:
After deriving the acceleration of the joint, take the time integral to obtain the velocity of the joint and take another integral to obtain the positon of the joint. By using the same approach, the adaptive algorithm is derived as follows:
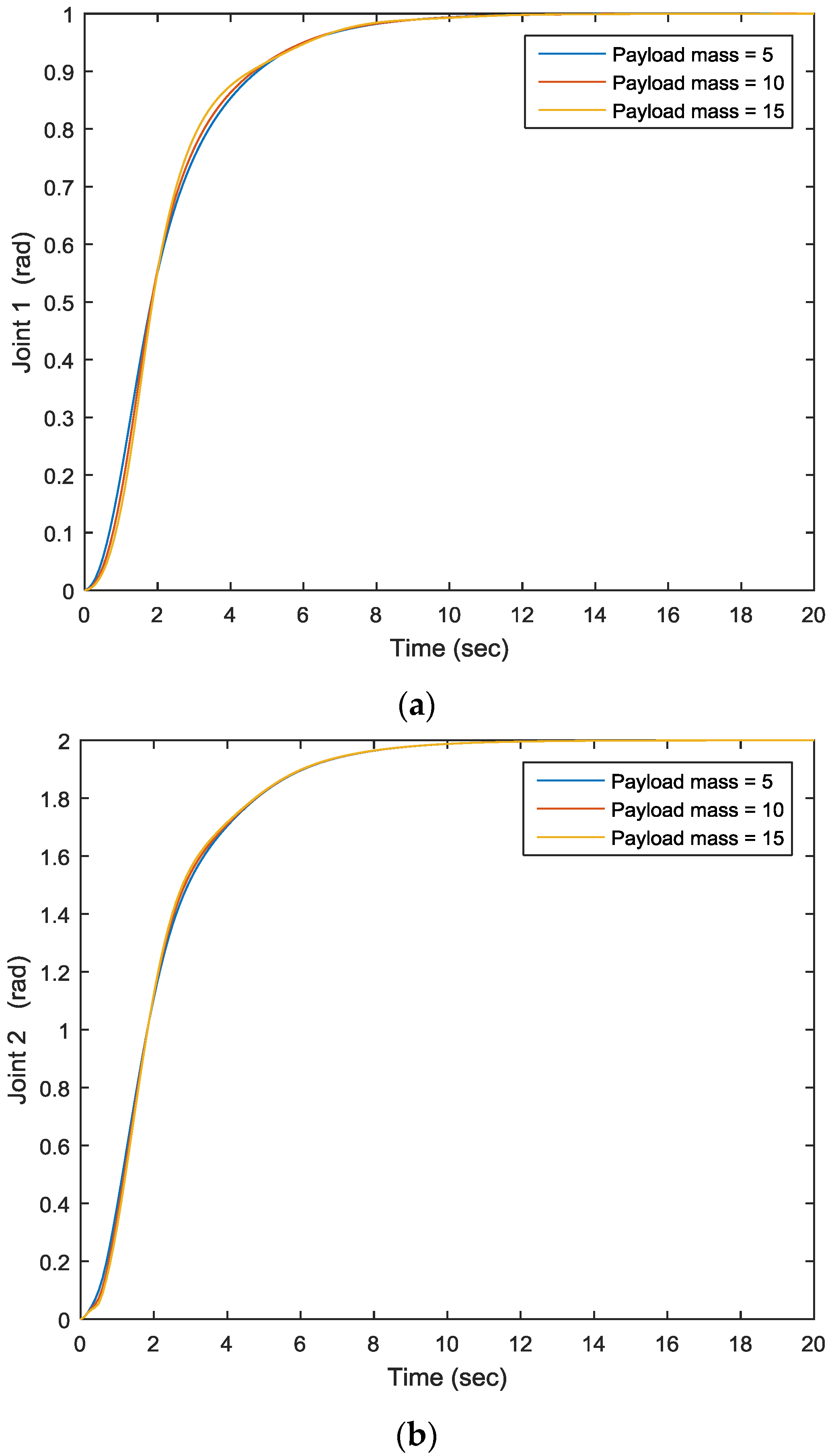
Figure 8 shows the joints’ output under different payload masses. By using the model reference adaptive control approach, the variation effect of payload mass has been resolved. One can see that three lines coincide with each other under different payload masses; i.e., the payload mass variation effect has been compensated.