Vibration Isolation and Trajectory Following Control of a Cable Suspended Stewart Platform
Abstract
:1. Introduction
2. Closed-Form Entire Dynamics of Stewart Platform
2.1. Equation of Driving Force for an Electric Cylinder Leg
- ;
- ;
- ;
- ;
- .
2.2. Dynamics of the Stewart Platform
2.3. Control Law Partition Based Globally Feedback Linearization of the Stewart Platform
3. PID Control Law with Acceleration Feedforward of the Base for the Stewart Platform
3.1. Real-Time Acceleration Estimation of the Base
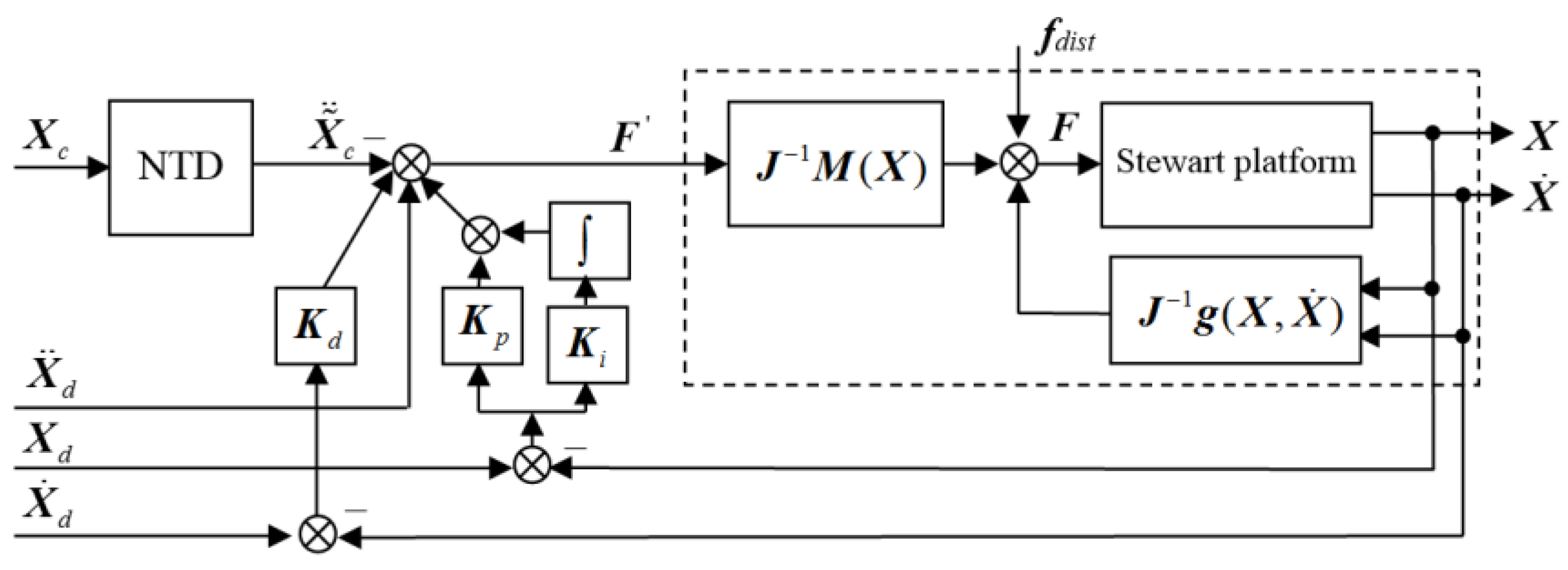
3.2. Controller Design of the Stewart Platform
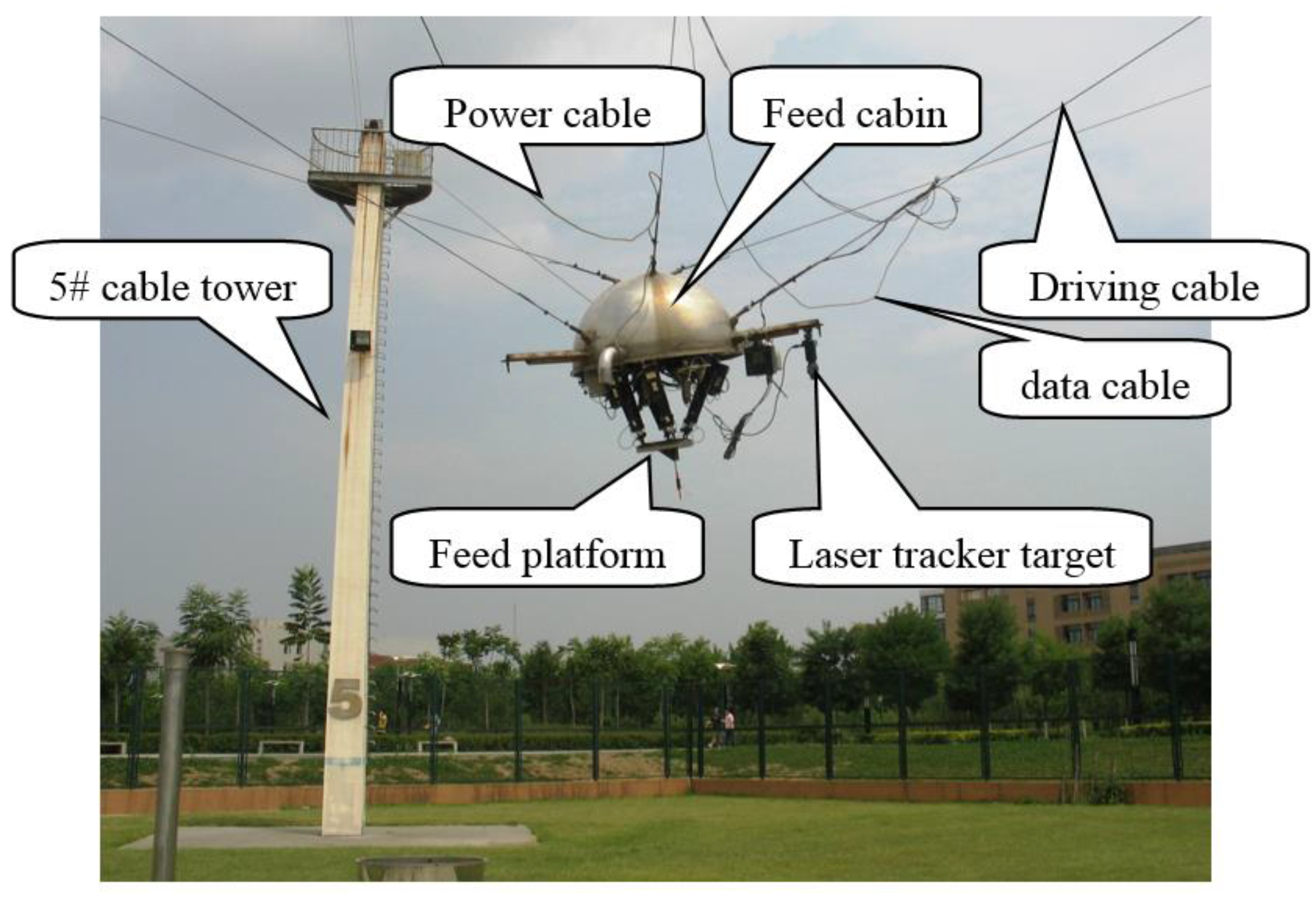
4. Experimental Apparatus
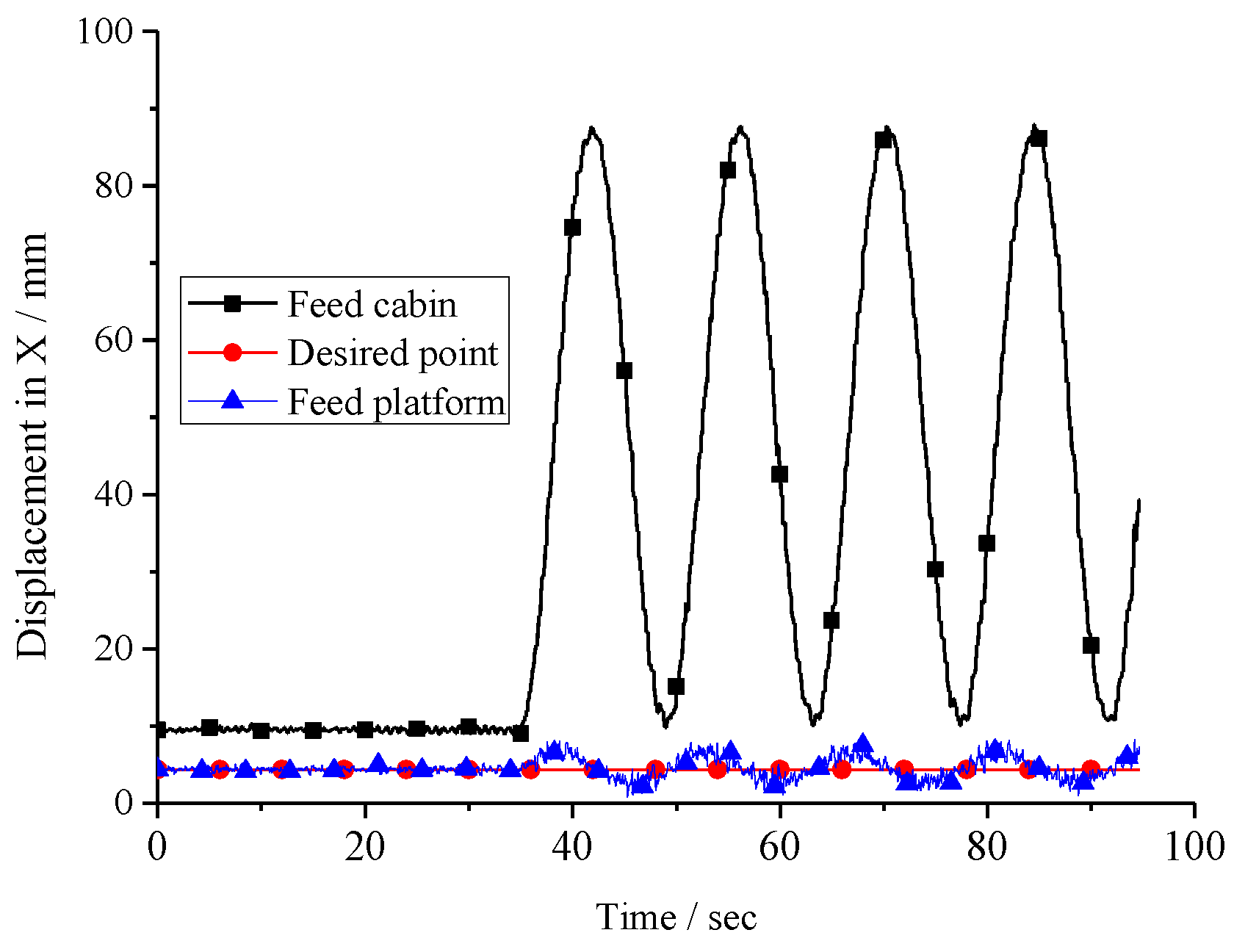
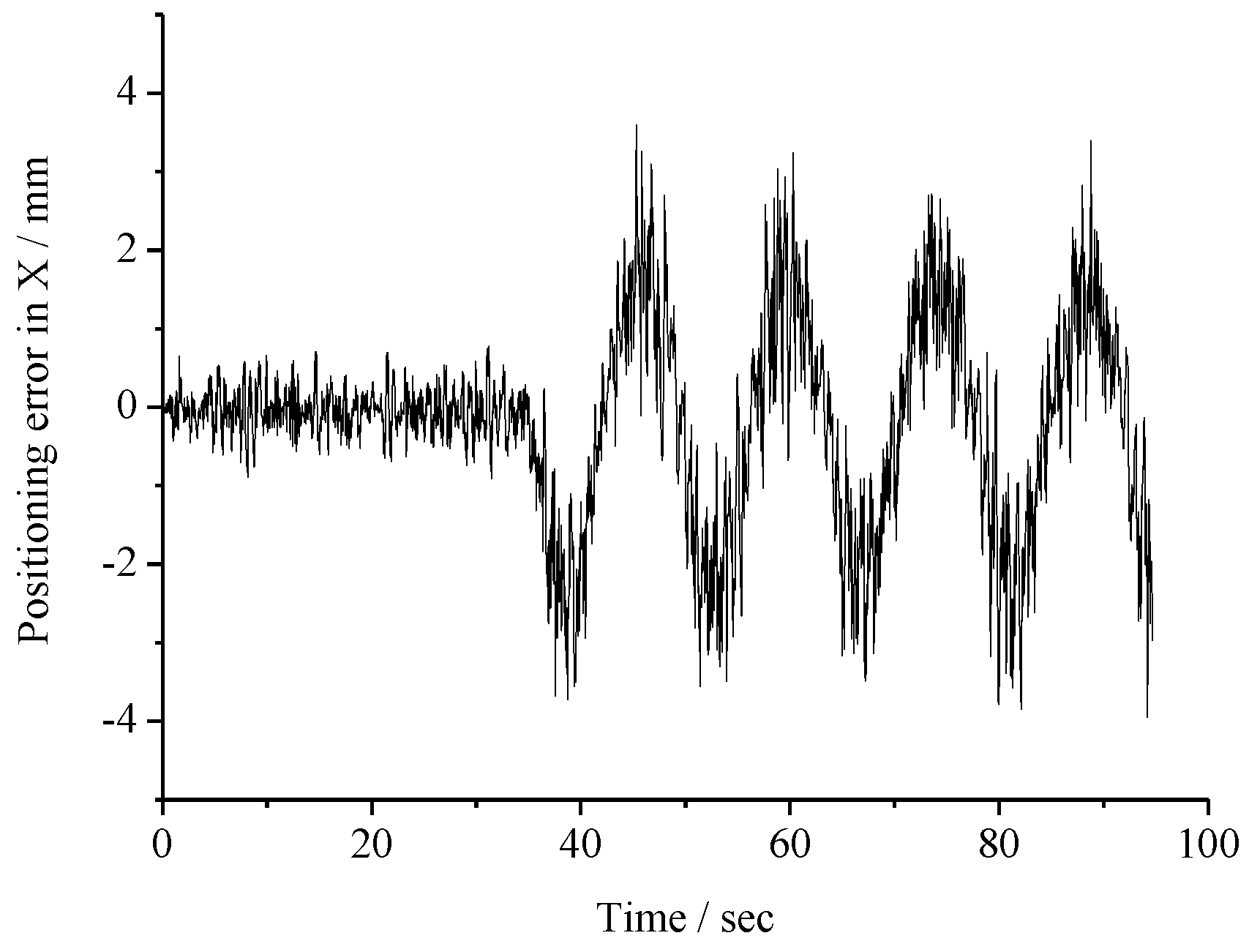
5. Experiments and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nan, R. Five hundred meter aperture spherical radio telescope (FAST). Sci. Chin. G 2006, 49, 129–148. [Google Scholar] [CrossRef]
- Shao, Z.; Tang, X.; Wang, L.; Chen, X. Dynamic modeling and wind vibration control of the feed support system in FAST. Nonlinear Dyn. 2012, 67, 965–985. [Google Scholar] [CrossRef]
- Duan, X.; Qiu, Y.; Mi, J.; Zhao, Z. Motion prediction and supervisory control of the macro-micro parallel manipulator system. Robotica 2011, 29, 1005–1015. [Google Scholar] [CrossRef]
- Duan, X.; Qiu, Y.; Bao, H.; Du, J. Real-time motion planning based vibration control of a macro-micro parallel manipulator system for super antenna. J. Vibroeng. 2014, 16, 694–703. [Google Scholar]
- Du, J.; Bao, H.; Duan, X.; Cui, C. Jacobian analysis of a long-span cable-driven manipulator and its application to forward solution. Mech. Mach. Theory 2010, 45, 1227–1238. [Google Scholar] [CrossRef]
- Qiu, Y.; Duan, B.; Wei, Q. Elimination of force singularity of the cable and cabin structure for the next generation large radio telescope. Mechatronics 2002, 12, 905–918. [Google Scholar] [CrossRef]
- Stewart, D. A platform with six degrees of freedom. Proc. Inst. Mech. Eng. 1965, 180, 371–386. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Huang, Z.; Kong, L.; Fang, Y. Mechanism Theory and Control of Parallel Robot; Machine Industry Press: Beijing, China, 1997. [Google Scholar]
- Dasgupta, B.; Mruthyunjaya, T.S. The Stewart platform manipulator: A review. Mech. Mach. Theory 2000, 180, 15–40. [Google Scholar] [CrossRef]
- Ting, Y.; Chen, Y.; Jar, H.C. Modeling and control for a Gough-Stewart platform CNC machine. J. Rob. Syst. 2004, 21, 609–623. [Google Scholar] [CrossRef]
- Lee, S.H.; Song, J.B.; Choi, W.C.; Hong, D. Position control of a Stewart platform using inverse dynamics control with approximate dynamics. Mechatronics 2003, 13, 605–619. [Google Scholar] [CrossRef]
- Kim, D.; Kang, J.; Lee, K. Robust tracking control design for a 6 DOF parallel manipulator. J. Rob. Syst. 2000, 17, 527–547. [Google Scholar] [CrossRef]
- Ding, B.; Cazzolato, B.S.; Stanley, R.M.; Grainger, S.; Costi, J.J. Stiffness analysis and control of a Stewart platform-based manipulator with decoupled sensor-actuator locations for ultrahigh accuracy positioning under large external loads. J. Dyn. Syst. Meas. Contr. 2014, 136, 061008. [Google Scholar] [CrossRef]
- Chen, S.; Fu, L. Output feedback sliding mode control for a Stewart platform with a nonlinear observer-based forward kinematics solution. IEEE Trans. Control Syst. Technol. 2013, 21, 176–185. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q.; Wang, J. Interpolation for active vibration control of a Stewart platform. J. Tsinghua Univ. 2002, 42, 1473–1476. [Google Scholar]
- Cheng, Y.; Ren, G.; Dai, S. Dynamic control simulation of Stewart platform with flexible suspension. J. Tsinghua Univ. 2003, 43, 1519–1522. [Google Scholar]
- Zhou, Q.; Qi, L.; Zhang, H.; Duan, G. Experiments on active large-amplitude vibration control of a coupled Stewart platform. Chin. Mech. Eng. 2005, 16, 1599–1602. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Duan, X.; Qiu, Y.; Duan, Q.; Du, J. Calibration and Motion Control of a Cable-Driven Parallel Manipulator Based Triple-Level Spatial Positioner. Adv. Mech. Eng. 2014, 2014, 368018. [Google Scholar] [CrossRef]
- Ogata, K. Modern Control Engineering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Angeles, J. Fundamentals of Robotic Mechanical Systems: Theory, Methods, and Algorithms, 4th ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Su, Y.; Duan, B.; Zheng, C. Nonlinear PID control of a six-DOF parallel manipulator. IET Control Theory Appl. 2004, 151, 95–102. [Google Scholar] [CrossRef]
- Dasgupta, B.; Mruthyunjaya, T.S. Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator. Mech. Mach. Theory 1998, 33, 1135–1152. [Google Scholar] [CrossRef]
- Fu, S.; Yao, Y.; Wu, Y. Comments on "A Newton-Euler formulation for the inverse dynamics of the Stewart platform manipulator" by B. Dasgupta and T.S. Mruthyunjaya [Mech. Mach. Theory 33 (1998) 1135–1152]. Mech. Mach. Theory 2007, 42, 1668–1671. [Google Scholar] [CrossRef]
- Han, J. Active Disturbance Rejection Control Technique—the Technique for Estimating and Compensating the Uncertainties; National Defense Industry Press: Beijing, China, 2008. [Google Scholar]
- Han, J. Active disturbances rejection control technique. Front. Sci. 2007, 1, 24–31. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 4th ed.; Prentice Hall: New York, NY, USA, 2002. [Google Scholar]
- Liu, J.K. Control System Design and MATLAB Simulation; Tsinghua University Press: Beijing, China, 2008. [Google Scholar]
- Duan, X.; Qiu, Y.; Mi, J.; Bao, H. On the mechatronic servo bandwidth of a Stewart platform for active vibration isolating in a super antenna. Rob. Comput. Integr. Manuf. 2016, 40, 66–77. [Google Scholar] [CrossRef]


| Symbol | Physical Sense | Value and Unit |
|---|---|---|
| Jm | moment of inertia of the servo motor shaft | 2.2 × 10−5 kg·m2 |
| JL | equivalent moment of inertia of load on ball screw | 2.4 × 10−5 kg·m2 |
| bm | viscous damping coefficient of the motor shaft | 2.5 × 10−3 N·s/rad |
| KL | Equivalent stiffness of the belt and motor shaft | 293.36 Nm/rad |
| bL | viscous damping coefficient of the ball screw | 3.0 × 10−3 N·s/m |
| Ki | current feedback coefficient of the motor armature | 0.02 |
| Ra | resistance of the motor armature | 0.4 Ω |
| La | inductance of the motor armature | 0.0173 H |
| Ce | Coefficient of counter electromotive force | 5.0 × 10−3 V·min/rev |
| Km | Coefficient of electromagnetic force | 0.85 Nm/A |
| KFT | Coefficient of transmission of torque to thrust | 1256.6 |
| Symbol | Physical Sense | Value and Unit |
|---|---|---|
| M | mass of the mobile platform | 5.5 kg |
| r0 | COG of the mobile platform | (0,0,0)T |
| mdi | mass of the upper part of leg | 3.5 kg |
| mui | mass of the lower part of leg | 2.5 kg |
| ru0 | COG of the upper part of leg | (−0.22,0,0)T |
| rd0 | COG of the lower part of leg | (0.16,0,0)T |
| Cui | viscous coefficients at the universal joint | 0.001 |
| Csi | viscous coefficients at the spherical joint | 0.002 |
| angular velocity of the mobile platform | variable | |
| angular acceleration of the mobile platform | variable | |
| external moment acting on the mobile platform in the local frame | variable |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Mi, J.; Zhao, Z. Vibration Isolation and Trajectory Following Control of a Cable Suspended Stewart Platform. Machines 2016, 4, 20. https://doi.org/10.3390/machines4040020
Duan X, Mi J, Zhao Z. Vibration Isolation and Trajectory Following Control of a Cable Suspended Stewart Platform. Machines. 2016; 4(4):20. https://doi.org/10.3390/machines4040020
Chicago/Turabian StyleDuan, Xuechao, Jianwei Mi, and Ze Zhao. 2016. "Vibration Isolation and Trajectory Following Control of a Cable Suspended Stewart Platform" Machines 4, no. 4: 20. https://doi.org/10.3390/machines4040020
APA StyleDuan, X., Mi, J., & Zhao, Z. (2016). Vibration Isolation and Trajectory Following Control of a Cable Suspended Stewart Platform. Machines, 4(4), 20. https://doi.org/10.3390/machines4040020





