On the “Zero of Potential of the Electric Field Produced by the Heart Beat”. A Machine Capable of Estimating this Underlying Persistent Error in Electrocardiography
Abstract
:1. Introduction
- 1)
- Measure the WCT amplitude without the need to encase the patient into a metal structure submerged in water.
- 2)
- Correlate the amplitude of the WCT to the cardinal limb leads.
2. Methods
3. Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Reconstruction of cardinal leads from limb components
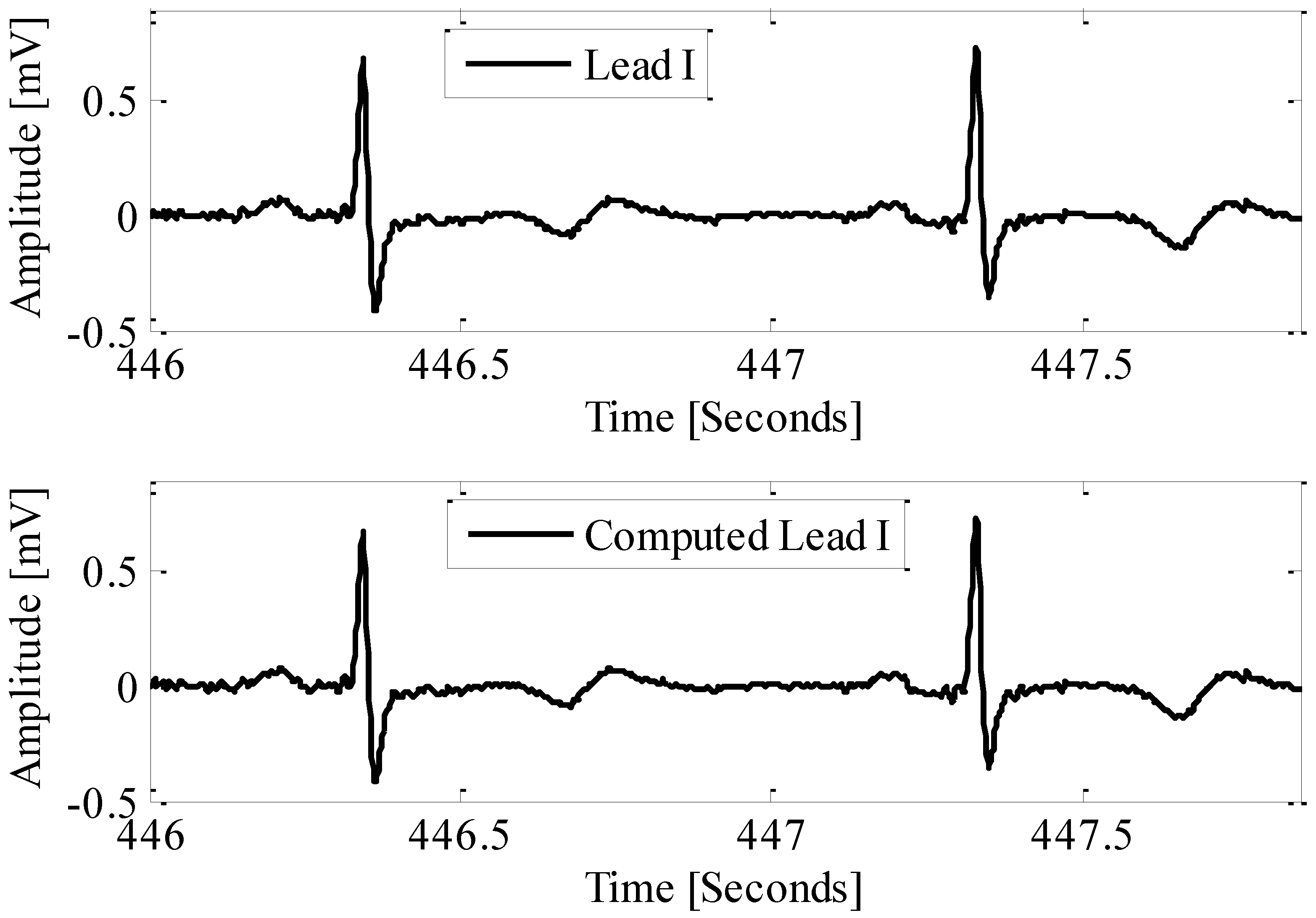
References
- Malmivuo, J.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Frank, E. General theory of heart-vector projection. Circ. Res. 1954, 2, 258–270. [Google Scholar] [CrossRef] [PubMed]
- Bayley, R.H.; Reynolds, E.W.; Kinard, C.L.; Head, J.F. The Zero of Potential of the Electric Field Produced by the Heart Beat: The Problem with Reference to Homogeneous Volume Conductors. Circ. Res. 1954, 2, 4–13. [Google Scholar] [CrossRef] [PubMed]
- Bayley, R.H.; Kinard, C.L. The Zero of Potential of the Electric Field Produced by the Heart Beat: The Problem with Reference to living human subject. Circ. Res. 1954, 2, 104–111. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, P.; Hill, W.; Robinson, I. The Art of Electronics; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Sedra, A.S.; Smith, K.C. Microelectronic Circuits; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Northrop, R.B. Analysis and Application of Analog Electronic Circuits to Biomedical Instrumentation; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Webster, J. Medical Instrumentation: Application and Design; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Enderle, J.D. Bioinstrumentation; Morgan & Claypool: Williston, VT, USA, 2006. [Google Scholar]
- Gargiulo, G.; Bifulco, P.; Calvo, R.A.; Cesarelli, M.; Mcewan, A.; Jin, C.; Ruffo, M.; Romano, M.; Shephard, R.; Schaik, A.V. Giga-ohm high-impedance fet input amplifiers for dry electrode biosensor circuits and systems integrated microsystems: Electronics, photonics, and biotechnology ed k iniewski. In Integrated Microsystems: Electronics, Photonics, and Biotechnology; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Bronzino, J.D. Biomedical Engineering Handbook; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Burger, H.; Van Milaan, J. Heart-vector and leads: Part III geometrical representation. Br. Heart J. 1948, 10, 229–233. [Google Scholar] [CrossRef]
- Burger, H.; Van Milaan, J. Heart-vector and leads. Part II. Br. Heart J. 1947, 9, 154–160. [Google Scholar] [CrossRef] [PubMed]
- Wilson, F.N.; Johnston, F.D.; Rosenbaum, F.F.; Barker, P.S. On einthoven’s triangle, the theory of unipolar electrocardiographic leads, and the interpretation of the precordial electrocardiogram. Am. Heart J. 1946, 32, 277–310. [Google Scholar] [CrossRef]
- Burger, H.C.; Van Milaan, J. Heart-vector and leads. Br. Heart J. 1946, 8, 157–161. [Google Scholar] [CrossRef] [PubMed]
- INA116—Texas Instruments. Available online: http://www.ti.com/lit/ds/symlink/ina116.pdf (accessed on 1 May 2016).
- Gargiulo, G.D.; Tapson, J.; van Schaik, A.; McEwan, A.; Thiagalingam, A. Unipolar ecg circuits: Towards more precise cardiac event identification. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 662–665.
- Gargiulo, G.; Thiagalingam, A.; Mcewan, A.; Cesarelli, M.; Bifulco, P.; Tapson, J.; van Schaik, A. True unipolar ecg leads recording (without the use of wct). Heart Lung Circ. 2013, 22, S102. [Google Scholar] [CrossRef]
- Gargiulo, G.D.; Varaki, E.S.; Hamilton, T.J.; Bifulco, P.; Cesarelli, M.; Romano, M. A 9-independent-leads ecg system from 10 electrodes: A practice preserving wct-less true unipolar ecg system. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4.
- Gargiulo, G.D. True unipolar ecg machine for wilson central terminal measurements. BioMed. Res. Int. 2015, 2015, 586397. [Google Scholar] [CrossRef] [PubMed]
- Gargiulo, G.; McEwan, A.; van Schaik, A.; Jin, C.; Cesarelli, M.; Bifulco, P.; Calvo, R.A. Non-Invasive Electronic Biosensor Circuits and Systems; INTECH Open Access Publisher: Rijeka, Croatia, 2010. [Google Scholar]
- Prance, R.J.; Beardsmore-Rust, S.; Aydin, A.; Harland, C.J.; Prance, H. Biological and medical applications of a new electric field sensor. In Proceedings of the ESA Annual Meeting in Electrostatics, Minneapolis, MN, USA, 17–19 June 2008; pp. 1–4.
- Prance, R.J.; Debray, A.; Clark, T.D.; Prance, H.; Nock, M.; Harland, C.J.; Clippingdale, A.J. An ultra-low-noise electrical-potential probe for human-body scanning. Meas. Sci. Technol. 2000, 11, 291–297. [Google Scholar] [CrossRef]
- CG/CG2 SN Series—Medium to High Surge GDT from Gas Discharge Tubes. Available online: http://www.littelfuse.com/products/gas-discharge-tubes/medium-to-high-surge-gdt/cg-cg2-sn.aspx (accessed on 1 May 2016).
- OPA140 High-Precision, Low-Noise, Rail-to-Rail Output, 11-MHz JFET Op Amp. Available online: http://www.ti.com/lit/ds/symlink/opa4140.pdf (accessed on 1 May 2016).
- Gargiulo, G.D.; Bifulco, P.; Cesarelli, M.; Fratini, A.; Romano, M. Problems in assessment of novel biopotential front-end with dry electrode: A brief review. Machines 2014, 2, 87–98. [Google Scholar] [CrossRef]
- Gargiulo, G.D.; McEwan, A.L.; Bifulco, P.; Cesarelli, M.; Jin, C.; Tapson, J.; Thiagalingam, A.; van Schaik, A. Towards true unipolar bio-potential recording: A preliminary result for ecg. Physiol. Meas. 2012, 34, N1. [Google Scholar] [CrossRef] [PubMed]
- Winter, B.B.; Webster, J.G. Reduction of interference due to common mode voltage in biopotential amplifiers. IEEE Trans. Biomed. Eng. 1983, 30, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Gargiulo, G.; McEwan, A.; Bifulco, P.; Cesarelli, M.; Jin, C.; Tapson, J.; Thiagalingam, A.; Van Schaik, A. Towards true unipolar ecg recording without the wilson central terminal (preliminary results). Physiol. Meas. 2013, 34, 991–1012. [Google Scholar] [CrossRef] [PubMed]
- Akay, M. Wiley Encyclopedia of Biomedical Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hwang, I.-D.; Webster, J.G. Direct interference canceling for two-electrode biopotential amplifier. IEEE Trans. Biomed. Eng. 2008, 55, 2620–2627. [Google Scholar] [CrossRef] [PubMed]
- Gargiulo, G.D.; Bifulco, P.; Cesarelli, M.; McEwan, A.; Wabnitz, A. Open platform, 32-channel, portable, data-logger with 32 PGA control lines for wearable medical device development. Electron. Lett. 2014, 50, 1127–1129. [Google Scholar] [CrossRef]


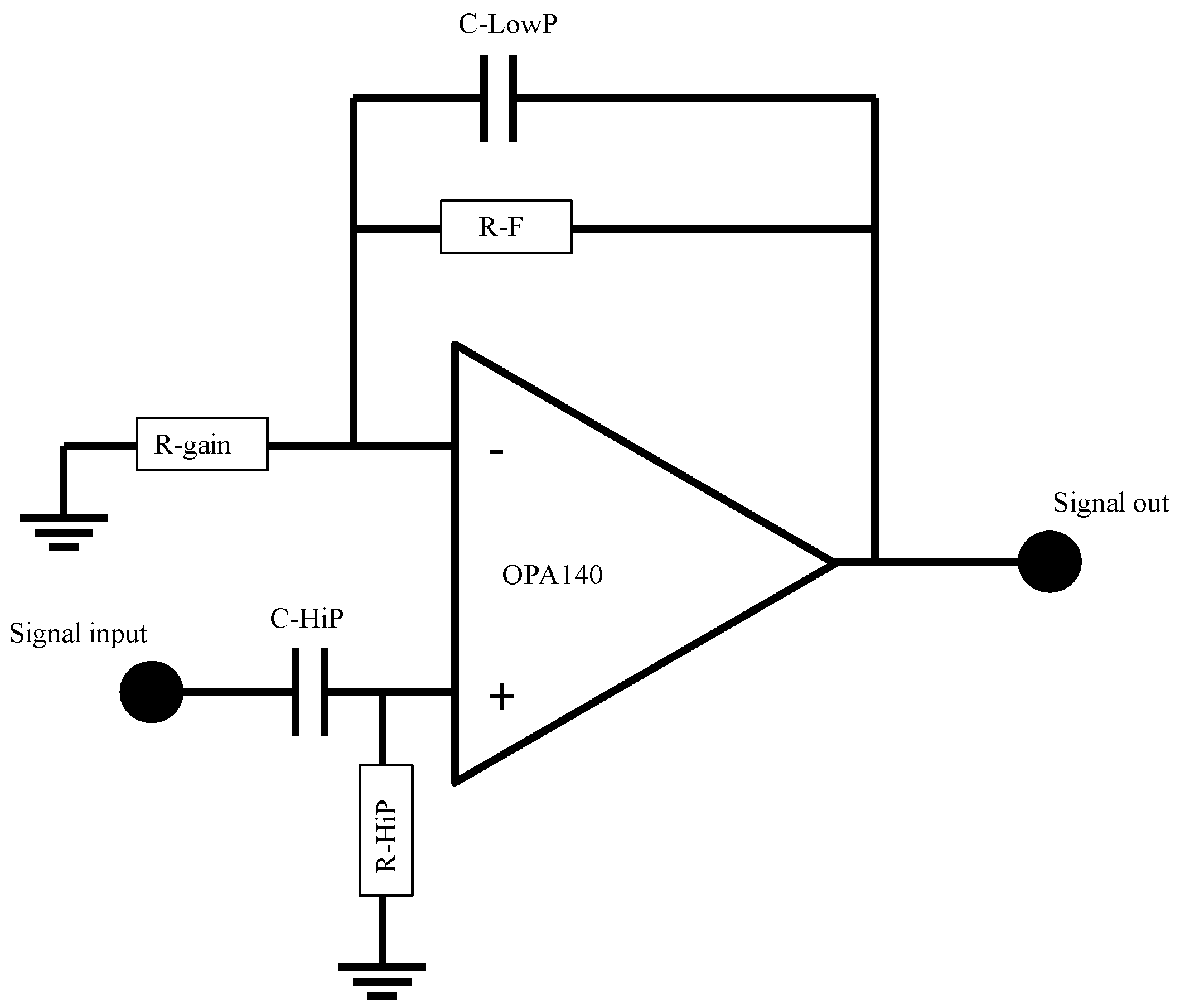

| Component | 10 V/V Gain Version | 100 V/V Gain Version |
|---|---|---|
| C-HiP | 47 µ | 47 µ |
| R-HiP | 100 kΩ | 100 kΩ |
| C-LowP | 15 nF | 1.5 nF |
| R-F | 100 kΩ | 1 MΩ |
| R-gain | 10 kΩ | 10 kΩ |
| Patient ID | Age (y.o.) | Gender | WCT Amplitude As % of Lead II | WCT Polarity | Figure |
|---|---|---|---|---|---|
| P001 | 63 | F | 27 | + | |
| P002 | 51 | F | 40 | + | |
| P003 | 65 | F | 35 | − | |
| P004 | 63 | F | 30 | + | |
| P005 | 88 | F | 90 | + | |
| P006 | 52 | F | 90 | + | |
| P007 | 70 | F | 59 | + | |
| P008 | 55 | F | 44 | + | |
| P009 | 82 | F | 12 | − | |
| P010 | 71 | F | 23 | + | |
| P011 | 69 | F | 19 | + | |
| P012 | 89 | F | 25 | − | |
| P013 | 63 | F | 23 | + | Figure 9 |
| P014 | 70 | F | 41 | N | |
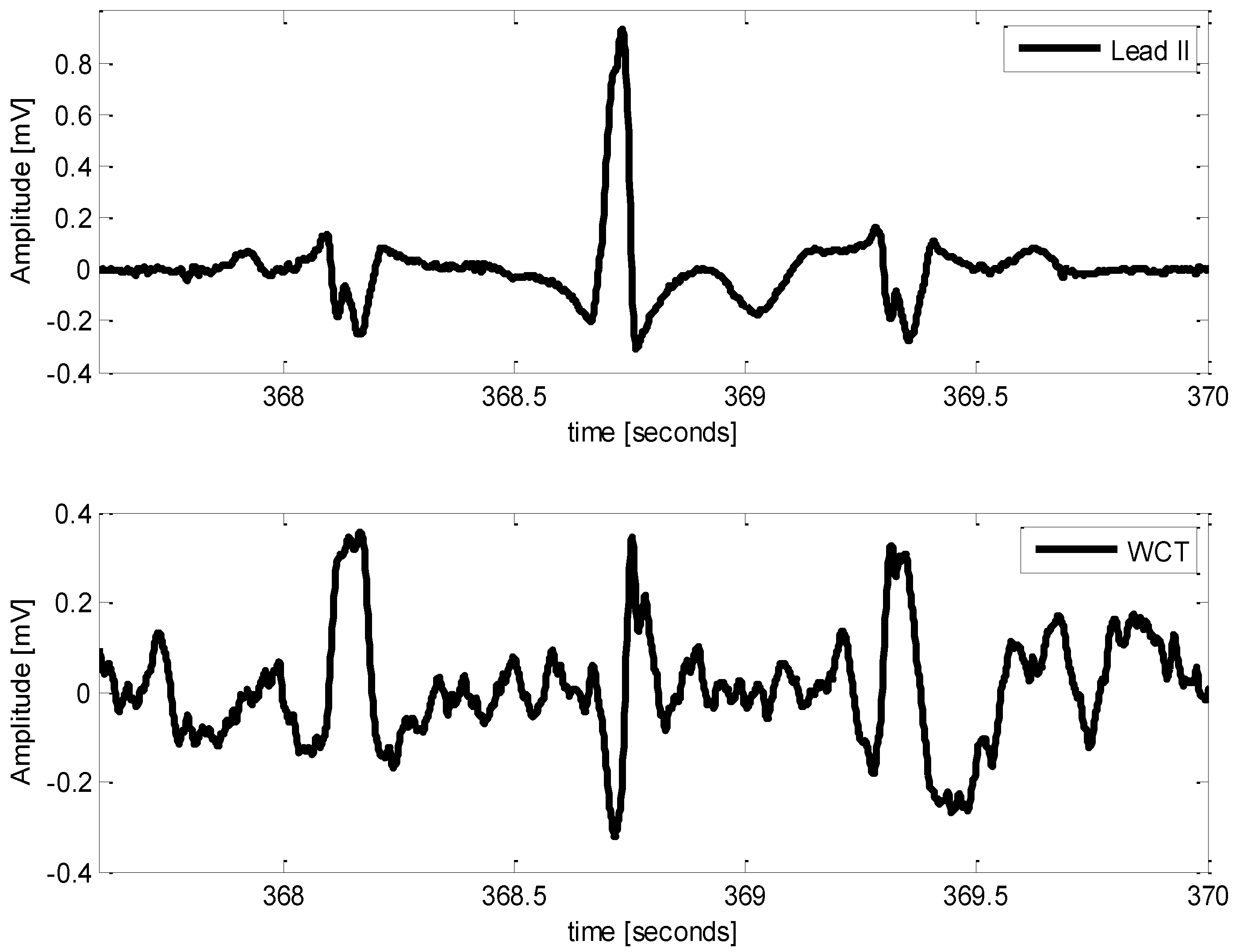
| P015 | 72 | F | 45 | + | Figure 6 |
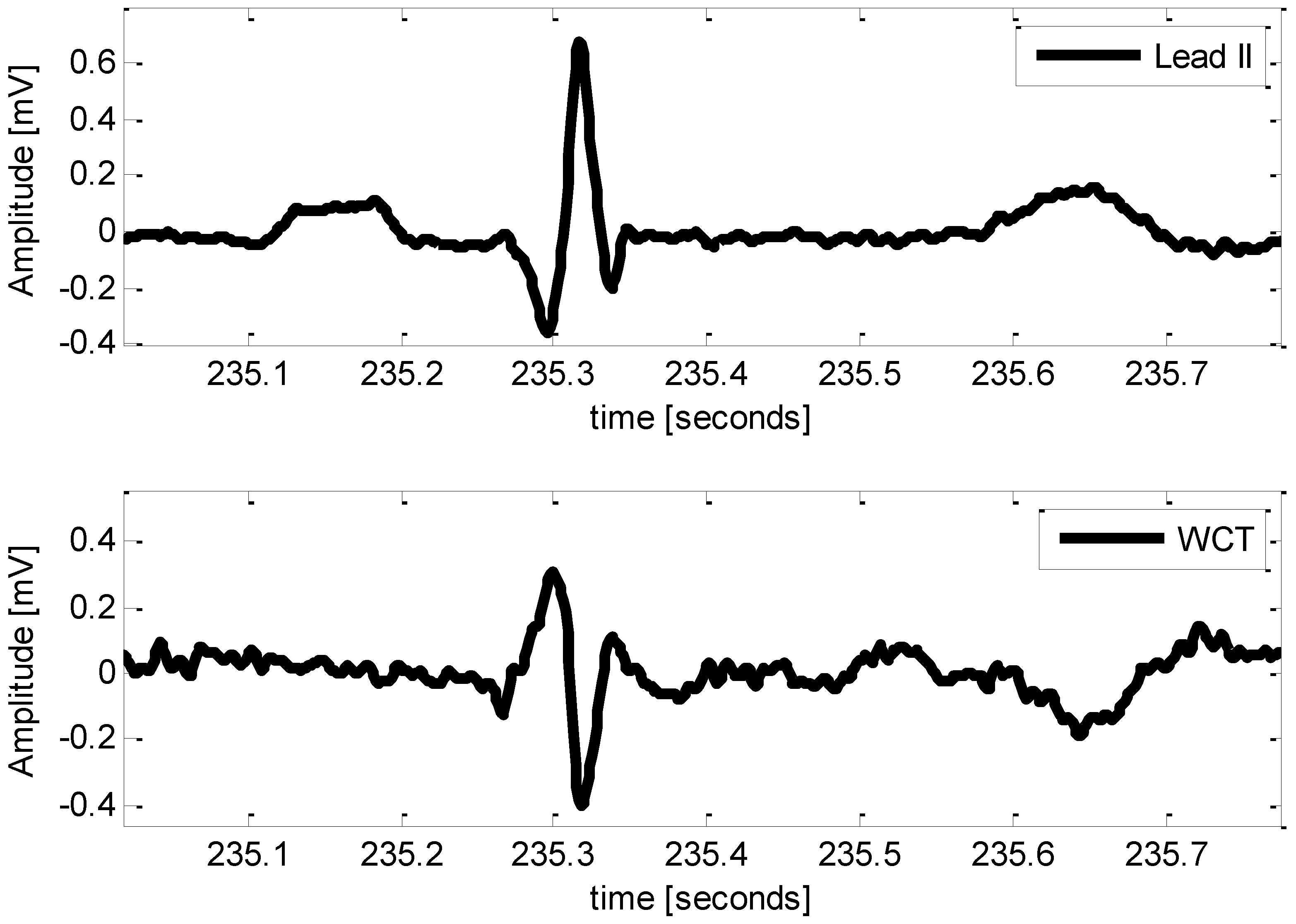
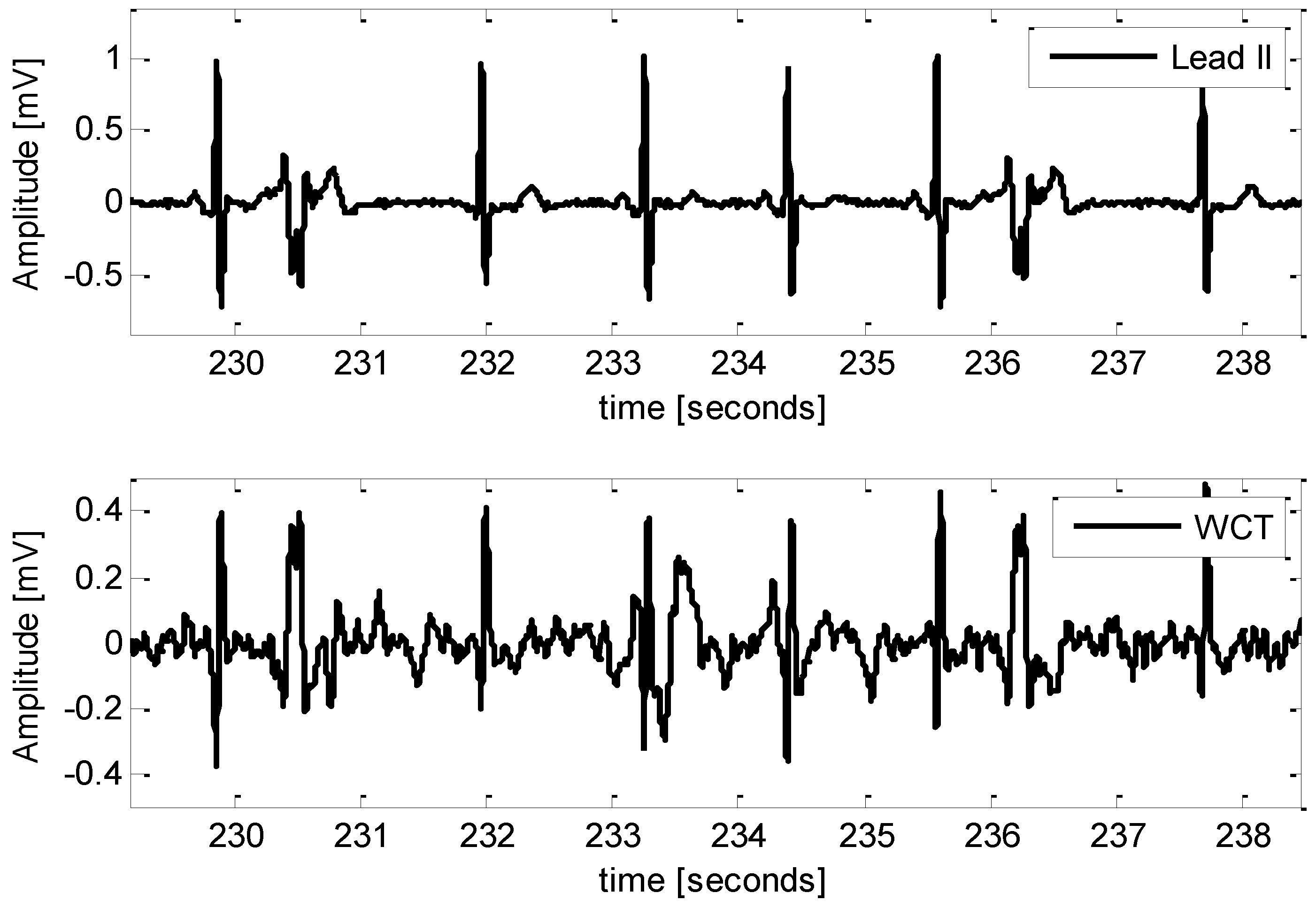
| P016 | 70 | F | 65 | − | Figure 4 |
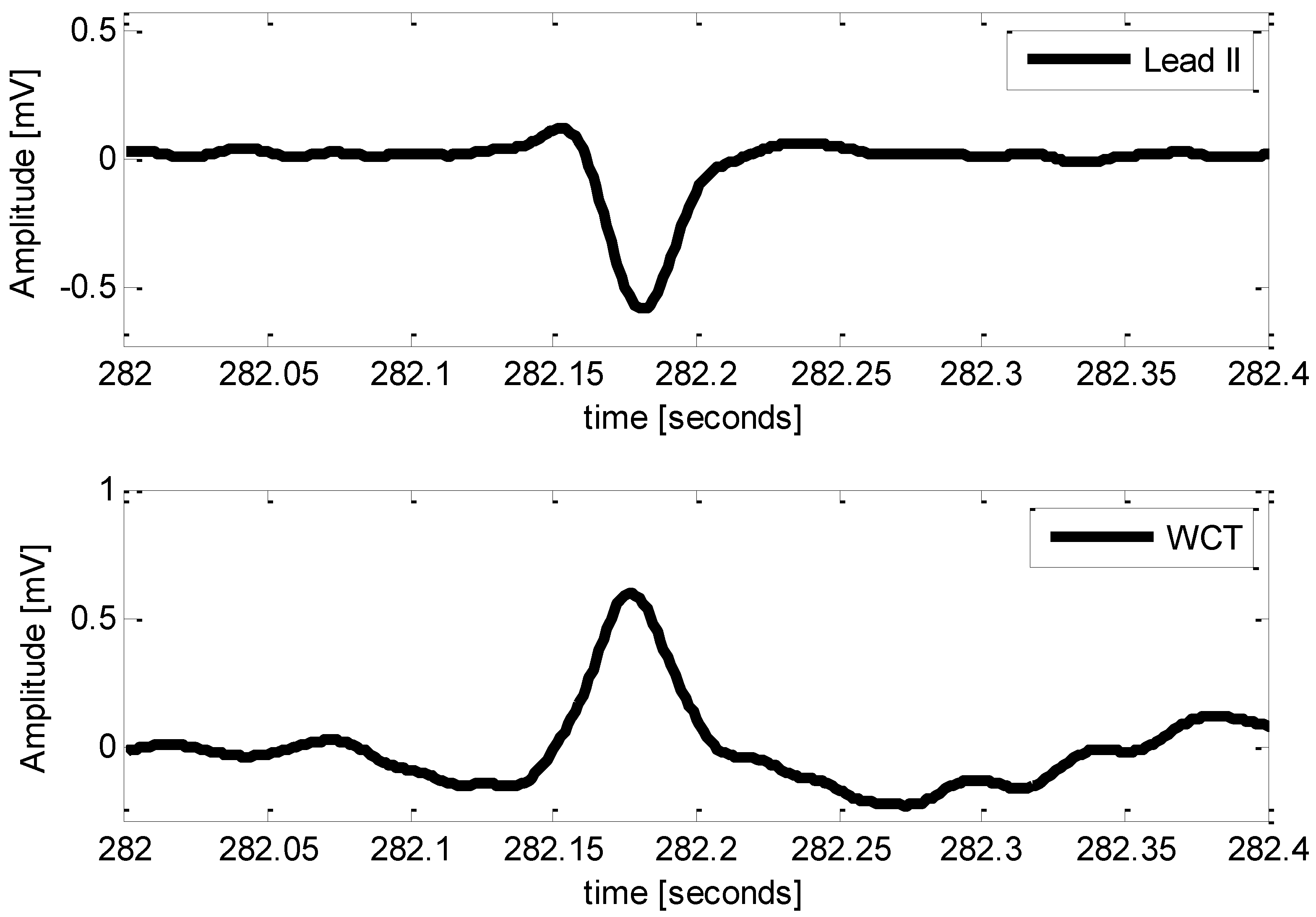
| P017 | 82 | F | 100 | + | Figure 5 |
| P018 | 59 | M | 100 | − | |
| P019 | 68 | M | 33 | − | |
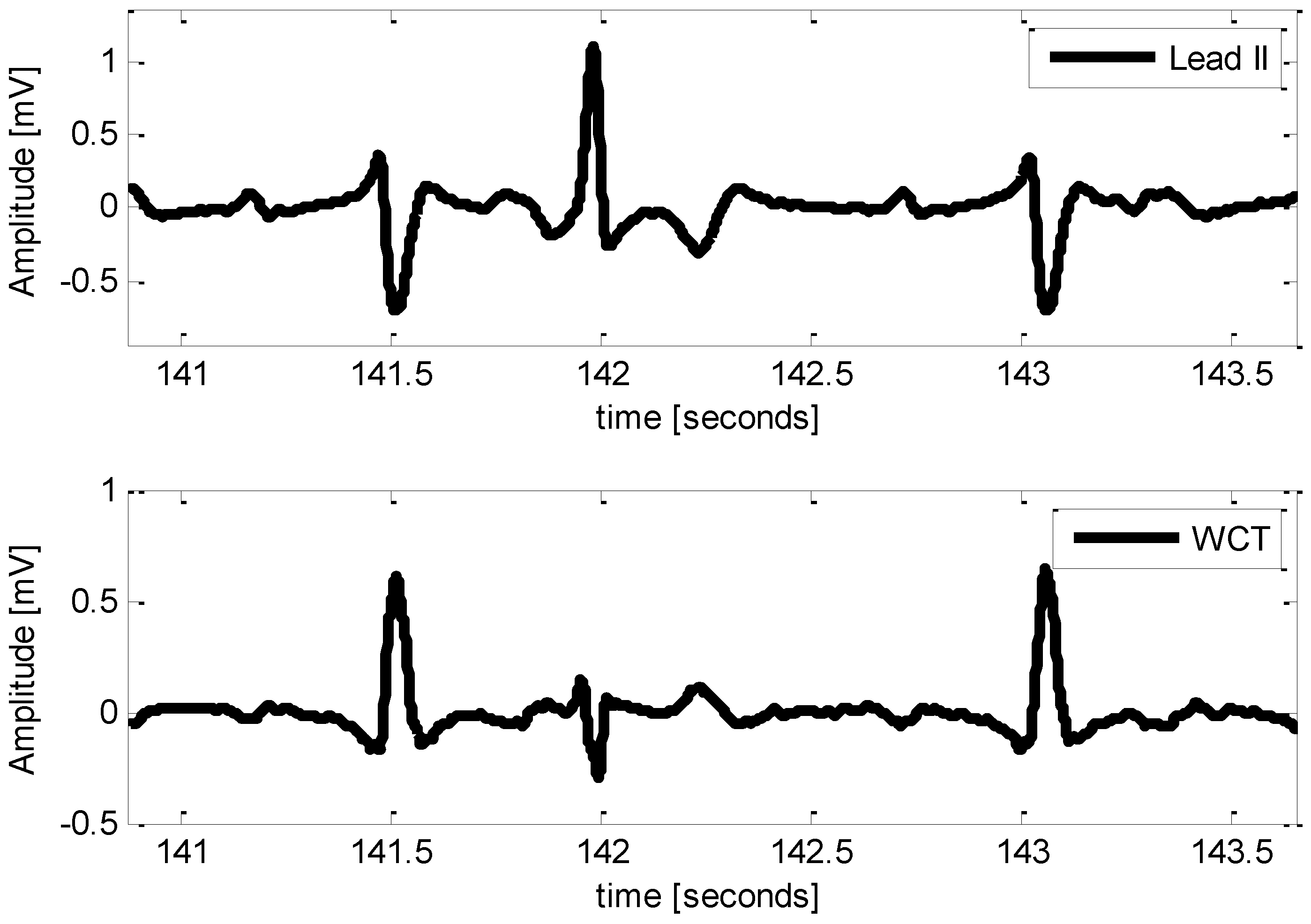
| P020 | 79 | M | 65 | + | Figure 8 |
| P021 | 55 | M | 50 | + | |
| P022 | 71 | M | 40 | N | |
| P023 | 52 | M | 60 | + | |
| P024 | 45 | M | 20 | − | |
| P025 | 79 | M | 50 | + | |
| P026 | 85 | M | 22 | + | |
| P027 | 52 | M | 30 | + | |
| P028 | 62 | M | 41 | − | |
| P029 | 64 | M | 31 | − | |
| P030 | 25 | M | 50 | − | |
| P031 | 76 | M | 46 | − | |
| P032 | 56 | M | 51 | − | |
| P033 | 78 | M | 57 | + | |
| P034 | 73 | M | 100 | + | |
| P035 | 85 | M | 100 | + | Figure 7 |
| P036 | 89 | M | 75 | + | |
| P037 | 72 | M | 25 | + | |
| P038 | 56 | M | 48 | + | |
| P039 | 60 | M | 20 | + | |
| P040 | 65 | M | 27 | + | |
| P041 | 80 | M | 48 | − | |
| P042 | 53 | M | 95 | + | |
| P043 | 53 | M | 100 | + | |
| P044 | 75 | M | 100 | + | |
| Average | 66.8 | 51.2 | |||
| Polarity distribution | N: 4.5%; Negative: 29.5% | ||||
| Total: | 44 | 38% Females |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gargiulo, G.D.; Bifulco, P.; Cesarelli, M.; McEwan, A.L.; Moeinzadeh, H.; O’Loughlin, A.; Shugman, I.M.; Tapson, J.C.; Thiagalingam, A. On the “Zero of Potential of the Electric Field Produced by the Heart Beat”. A Machine Capable of Estimating this Underlying Persistent Error in Electrocardiography. Machines 2016, 4, 18. https://doi.org/10.3390/machines4040018
Gargiulo GD, Bifulco P, Cesarelli M, McEwan AL, Moeinzadeh H, O’Loughlin A, Shugman IM, Tapson JC, Thiagalingam A. On the “Zero of Potential of the Electric Field Produced by the Heart Beat”. A Machine Capable of Estimating this Underlying Persistent Error in Electrocardiography. Machines. 2016; 4(4):18. https://doi.org/10.3390/machines4040018
Chicago/Turabian StyleGargiulo, Gaetano D., Paolo Bifulco, Mario Cesarelli, Alistair L. McEwan, Hossein Moeinzadeh, Aiden O’Loughlin, Ibrahim M. Shugman, Jonathan C. Tapson, and Aravinda Thiagalingam. 2016. "On the “Zero of Potential of the Electric Field Produced by the Heart Beat”. A Machine Capable of Estimating this Underlying Persistent Error in Electrocardiography" Machines 4, no. 4: 18. https://doi.org/10.3390/machines4040018
APA StyleGargiulo, G. D., Bifulco, P., Cesarelli, M., McEwan, A. L., Moeinzadeh, H., O’Loughlin, A., Shugman, I. M., Tapson, J. C., & Thiagalingam, A. (2016). On the “Zero of Potential of the Electric Field Produced by the Heart Beat”. A Machine Capable of Estimating this Underlying Persistent Error in Electrocardiography. Machines, 4(4), 18. https://doi.org/10.3390/machines4040018








