A Framework for Anomaly Detection and Evaluation of Rotating Machinery Based on Data-Accumulation-Aware Generative Adversarial Networks and Similarity Estimation
Abstract
1. Introduction
2. Anomaly Detection and Assessment Framework
2.1. Theoretical Background
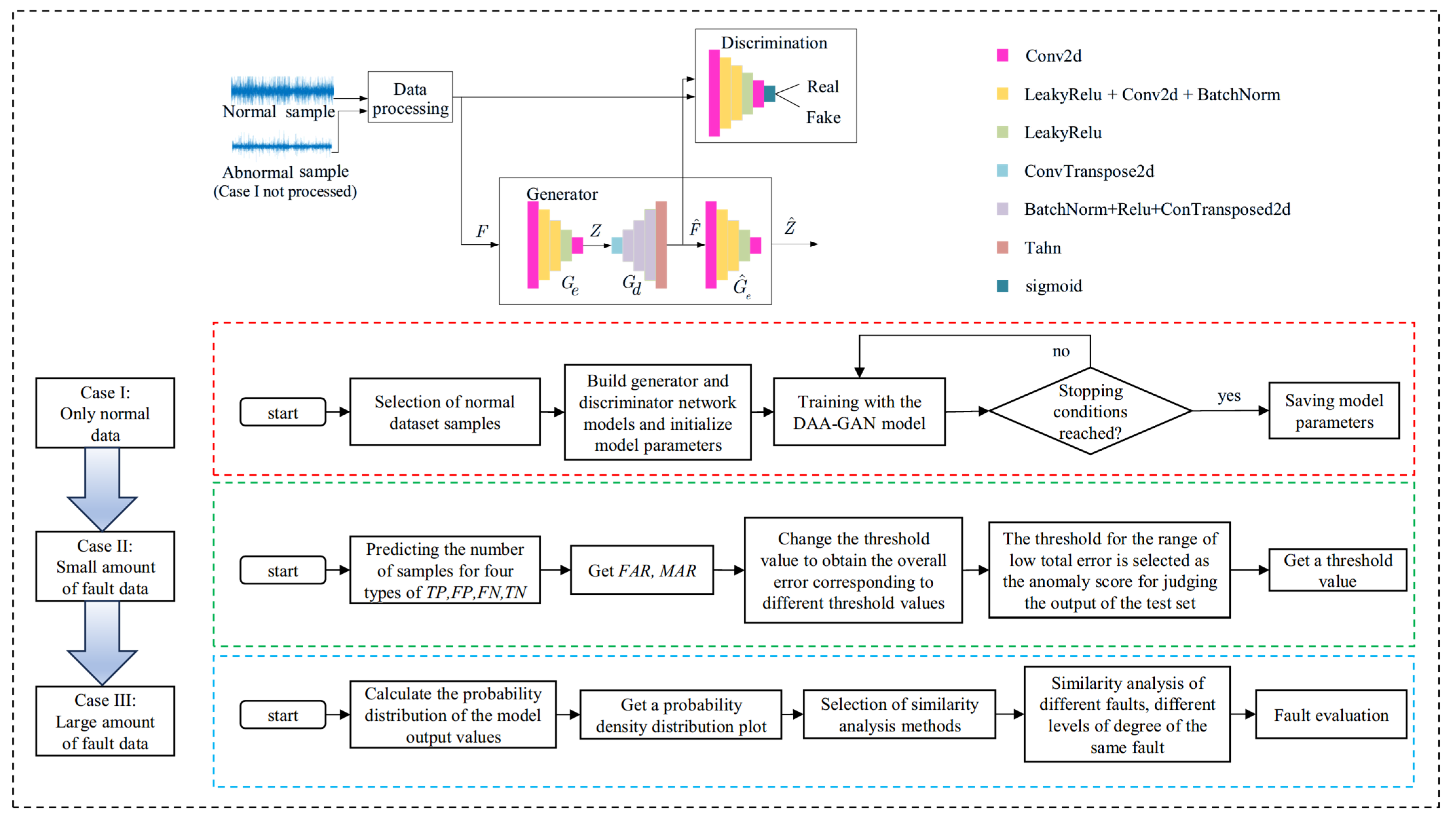
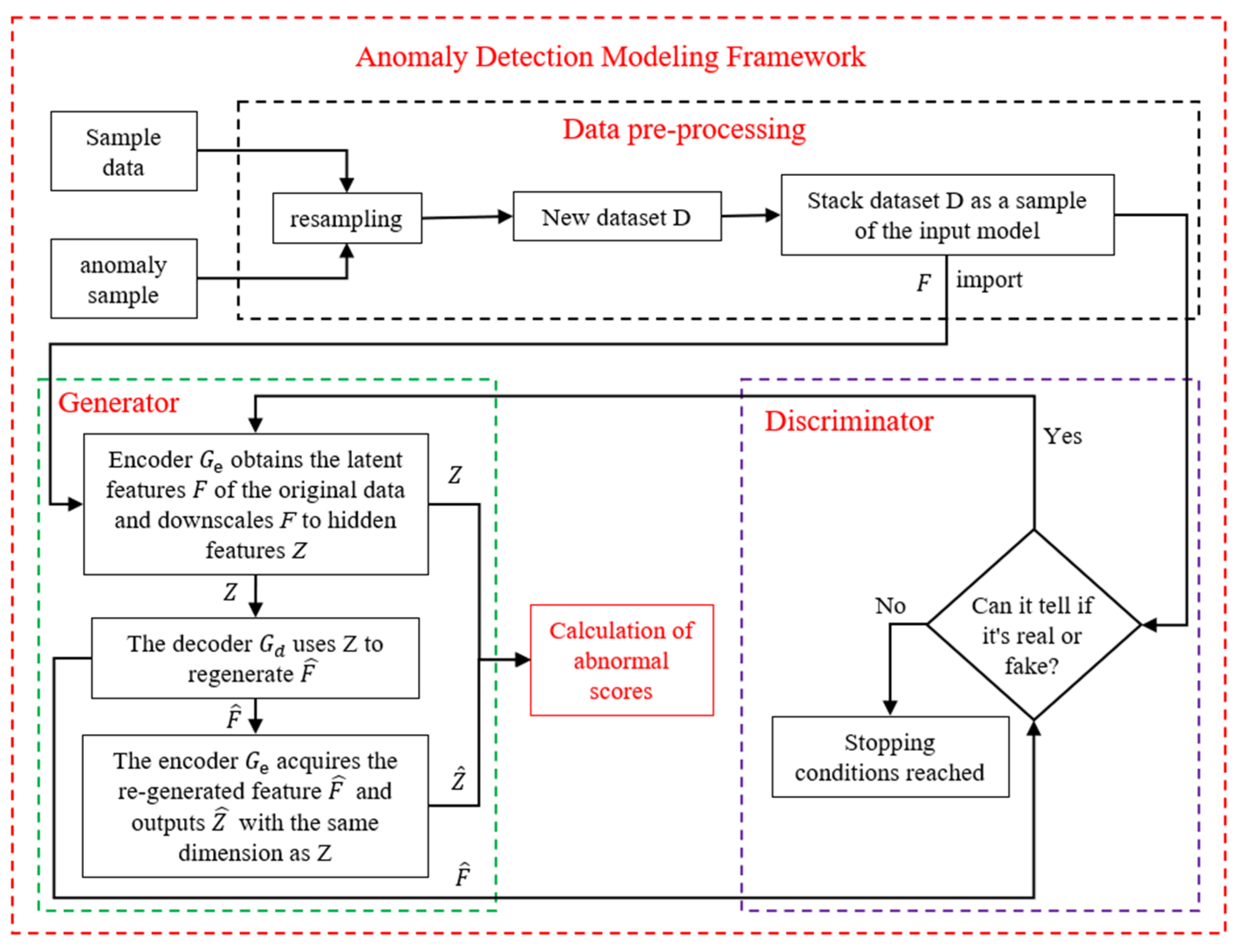
2.2. A Comprehensive Framework for Anomaly Detection and Estimation
2.3. Anomaly Detection Based on DAA-GAN
2.4. Adaptive Threshold Update for DAA-GAN
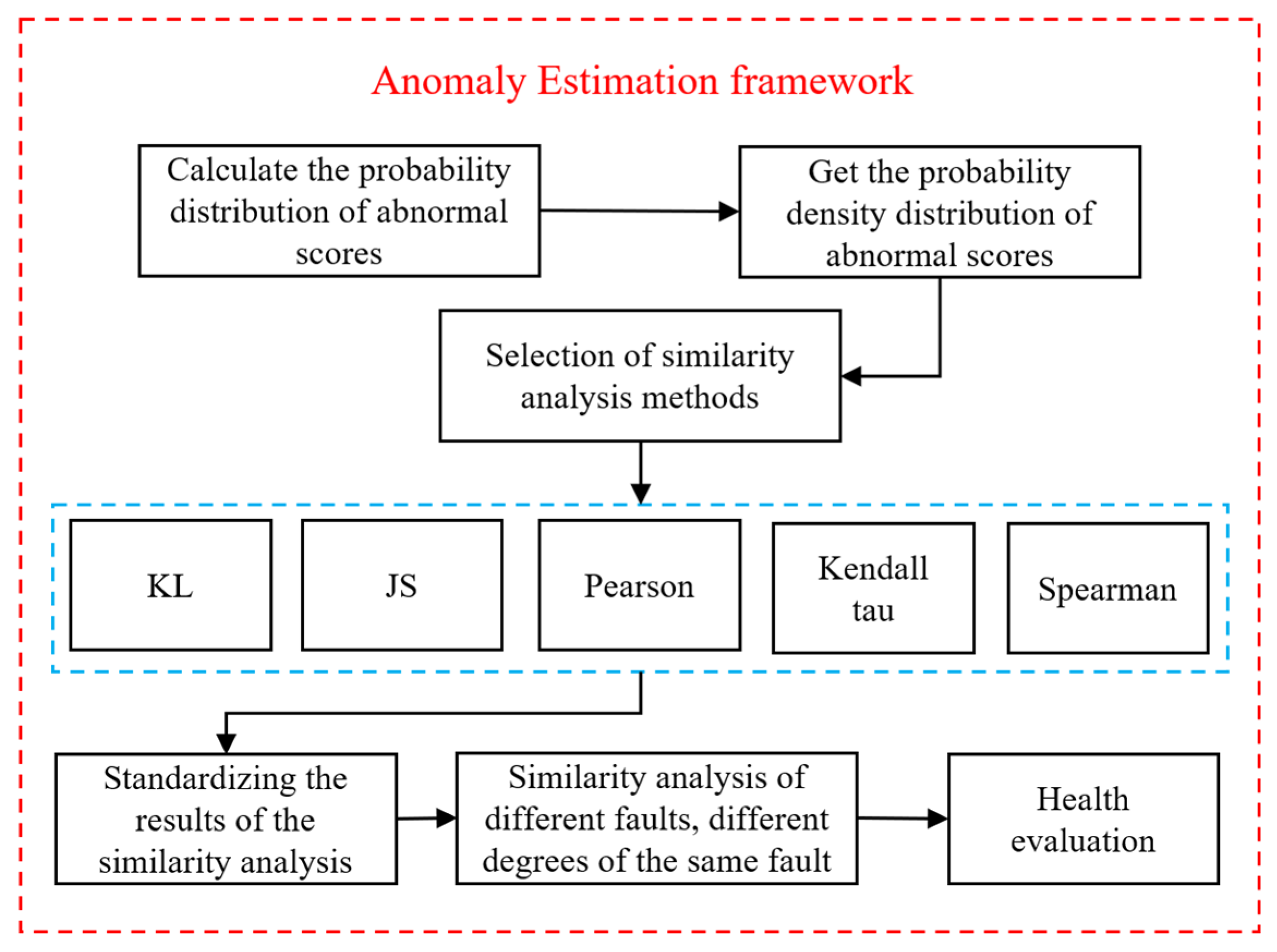
2.5. Similarity Estimation for Anomaly Assessment
| Algorithm 1. Multi-index similarity fusion for Stage III |
| Input: anomaly-score sequence of a test sample and reference anomaly-score sequences for each fault class/severity k. |
| Output: as the identified fault type/severity. |
| Step 1: Estimate the probability density distributions and (e.g., by kernel density estimation or histogram normalization). |
| Step 2: Compute raw metrics for each |
| Step 3 (Directional alignment): Convert divergences to similarities using and convert correlations using |
| Step 4 (Optional normalization): Apply Equation (21) to normalize each aligned similarity vector across k. |
| Step 5 (Fusion): Fuse the aligned-and-normalized similarities by |
| Step 6 (Decision): Output . as the identified fault type/severity. |
3. Validation
3.1. A Simulation Case of the Split-Torque Transmission System
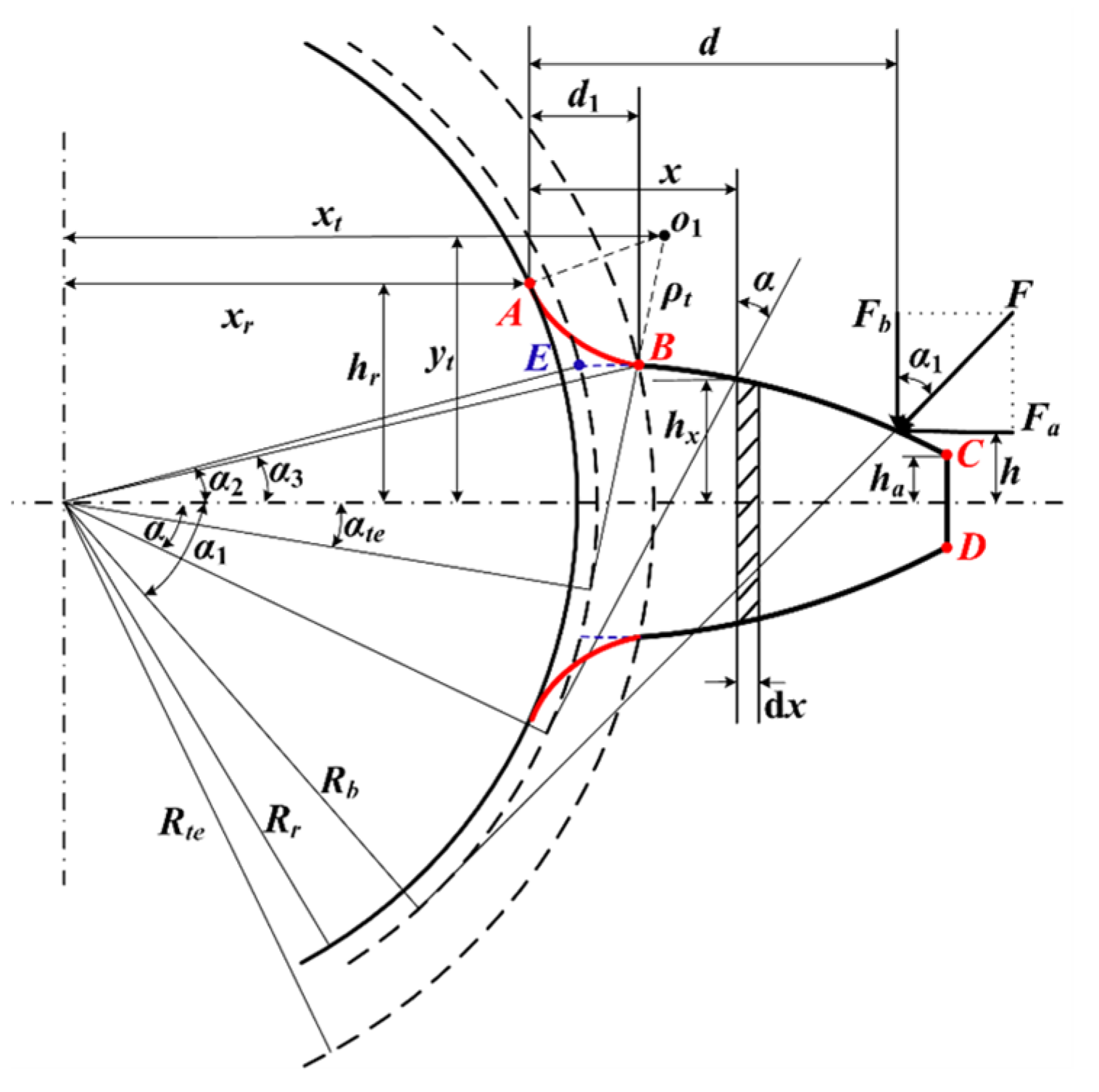
3.1.1. Split-Torque Transmission System and Its Simulation Model
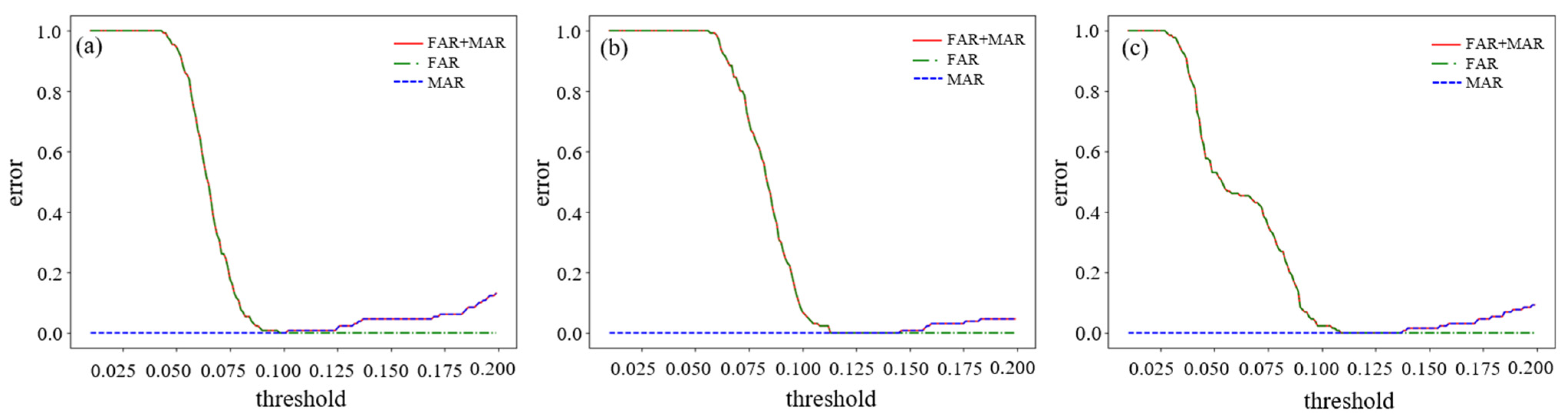
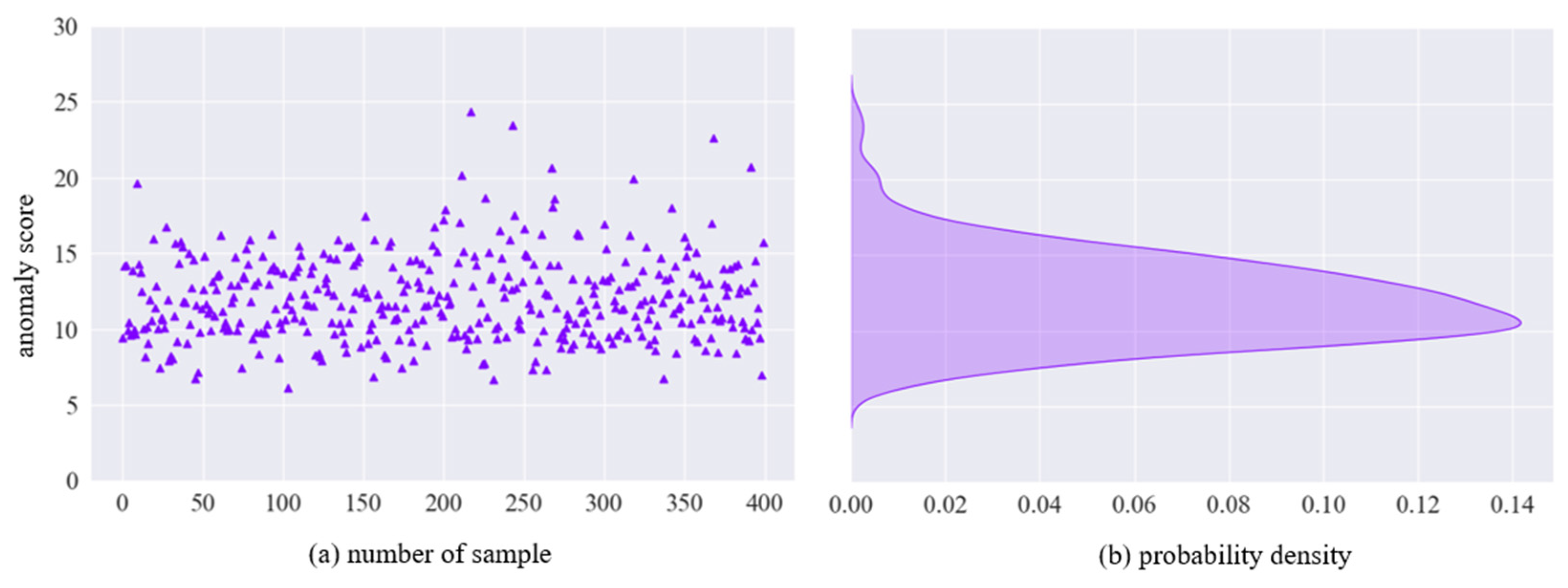
3.1.2. Anomaly Detection and Threshold Optimization
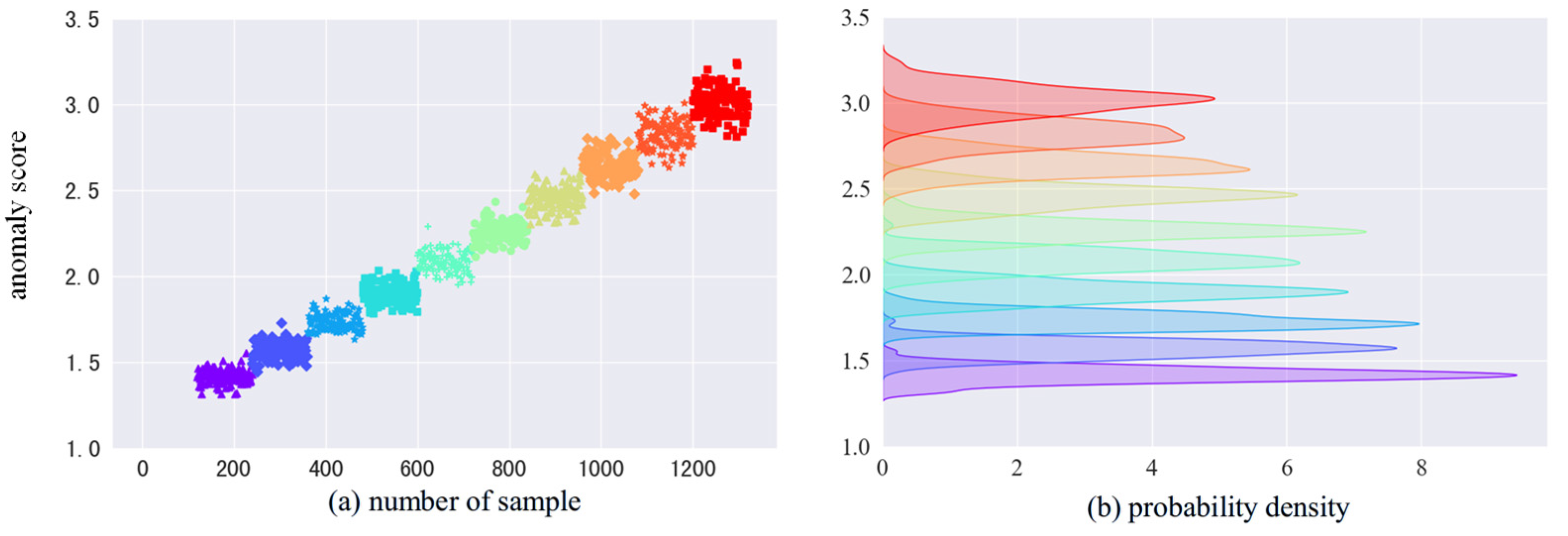
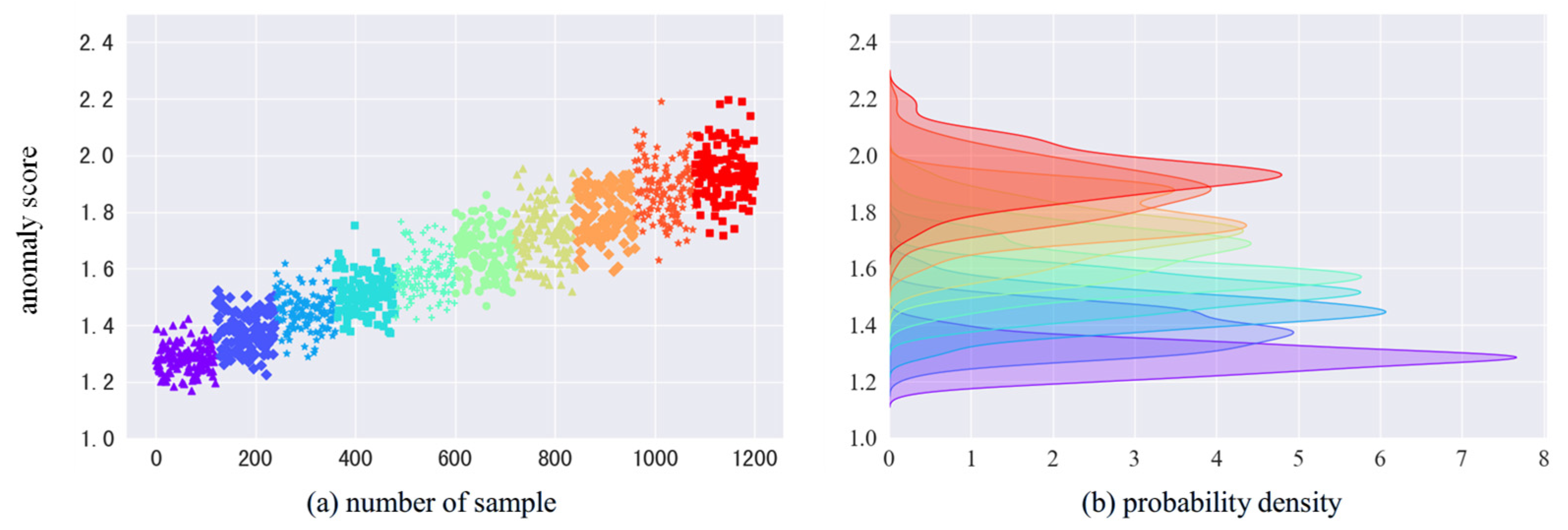
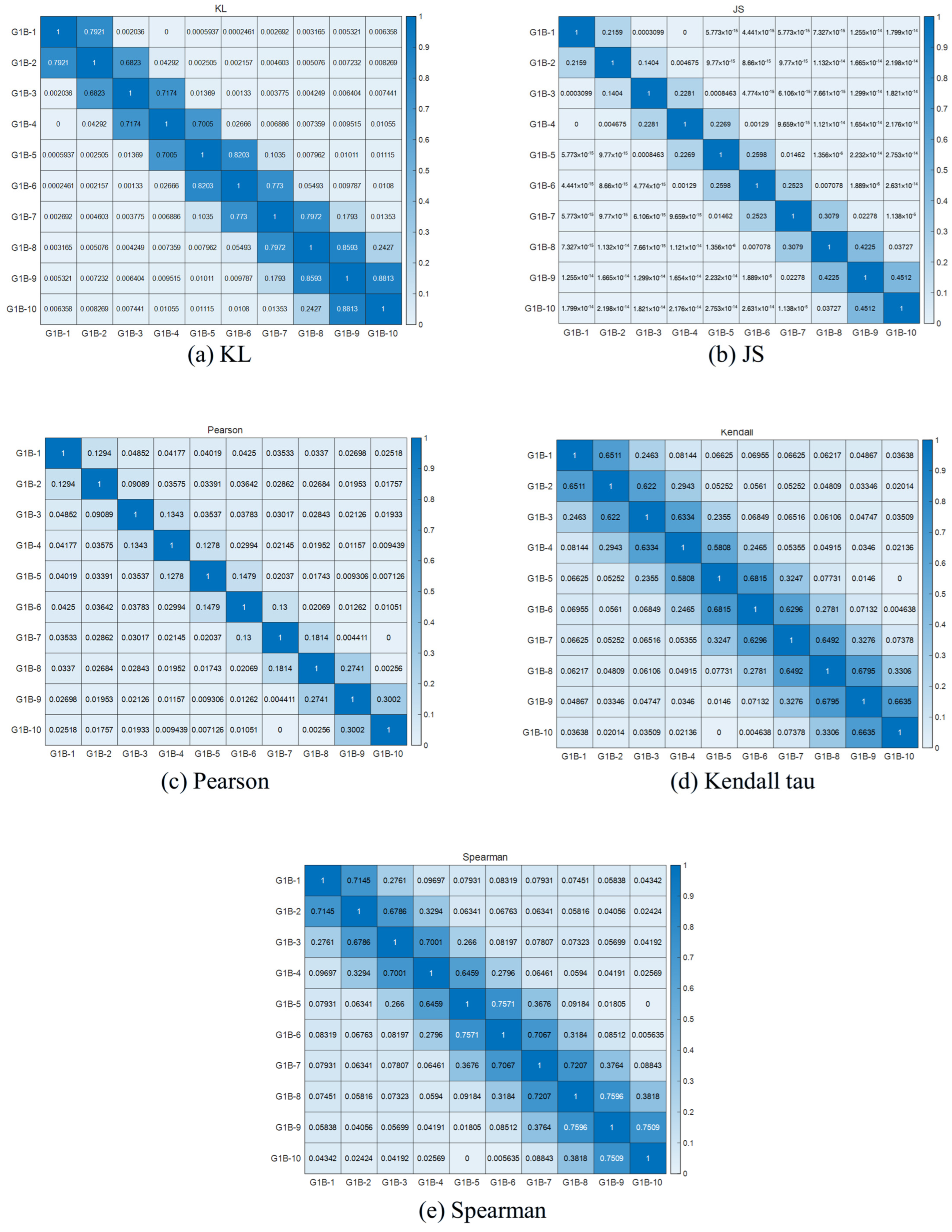
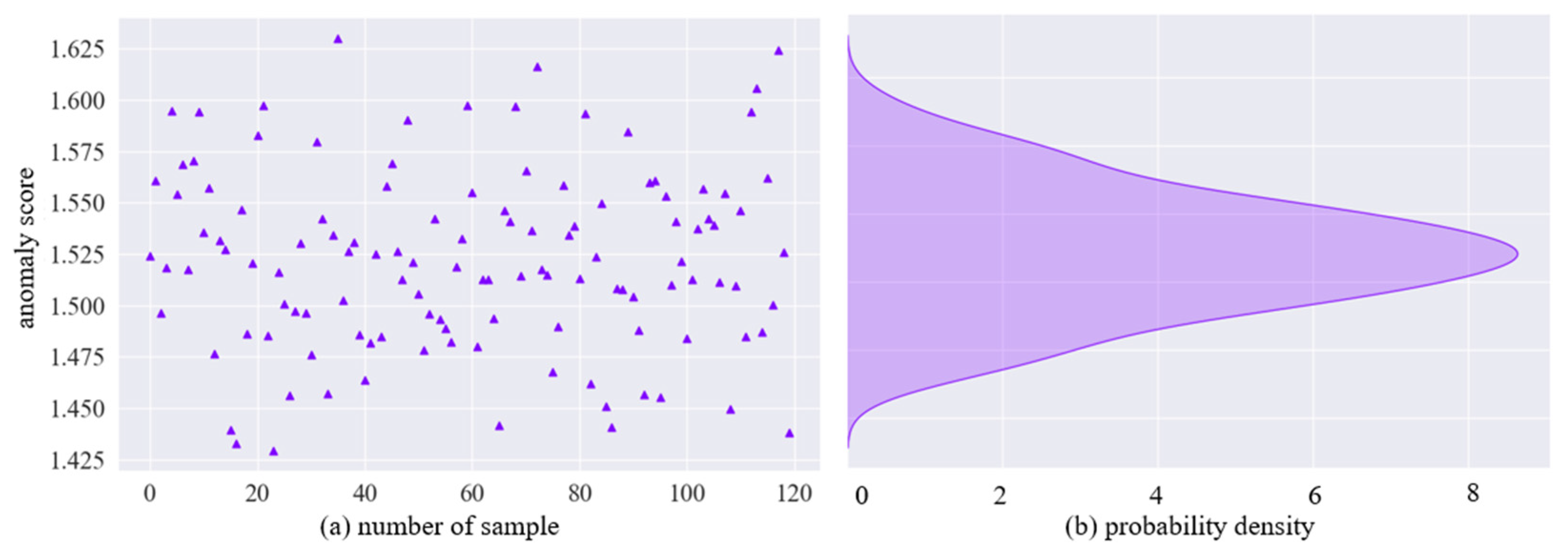
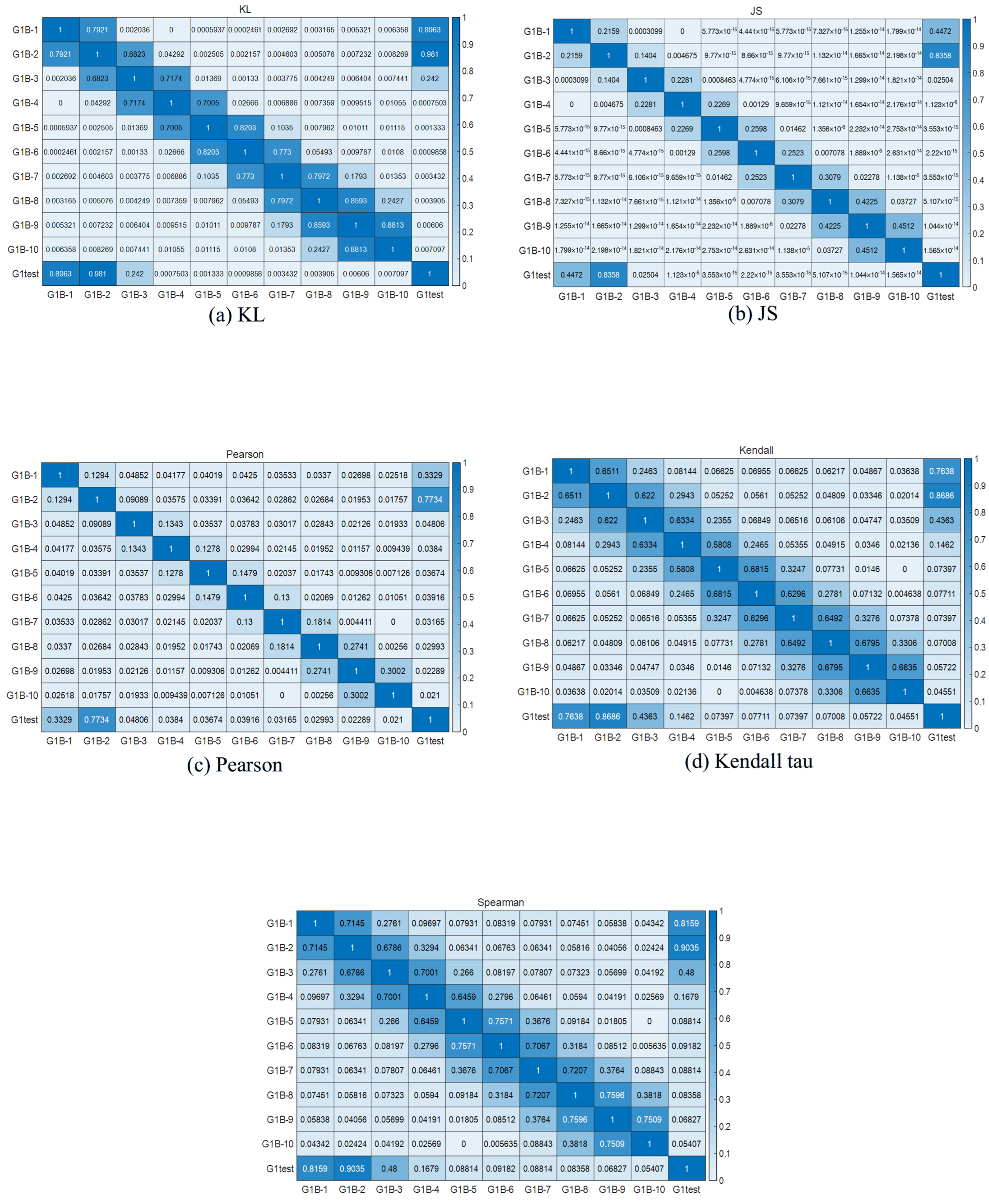
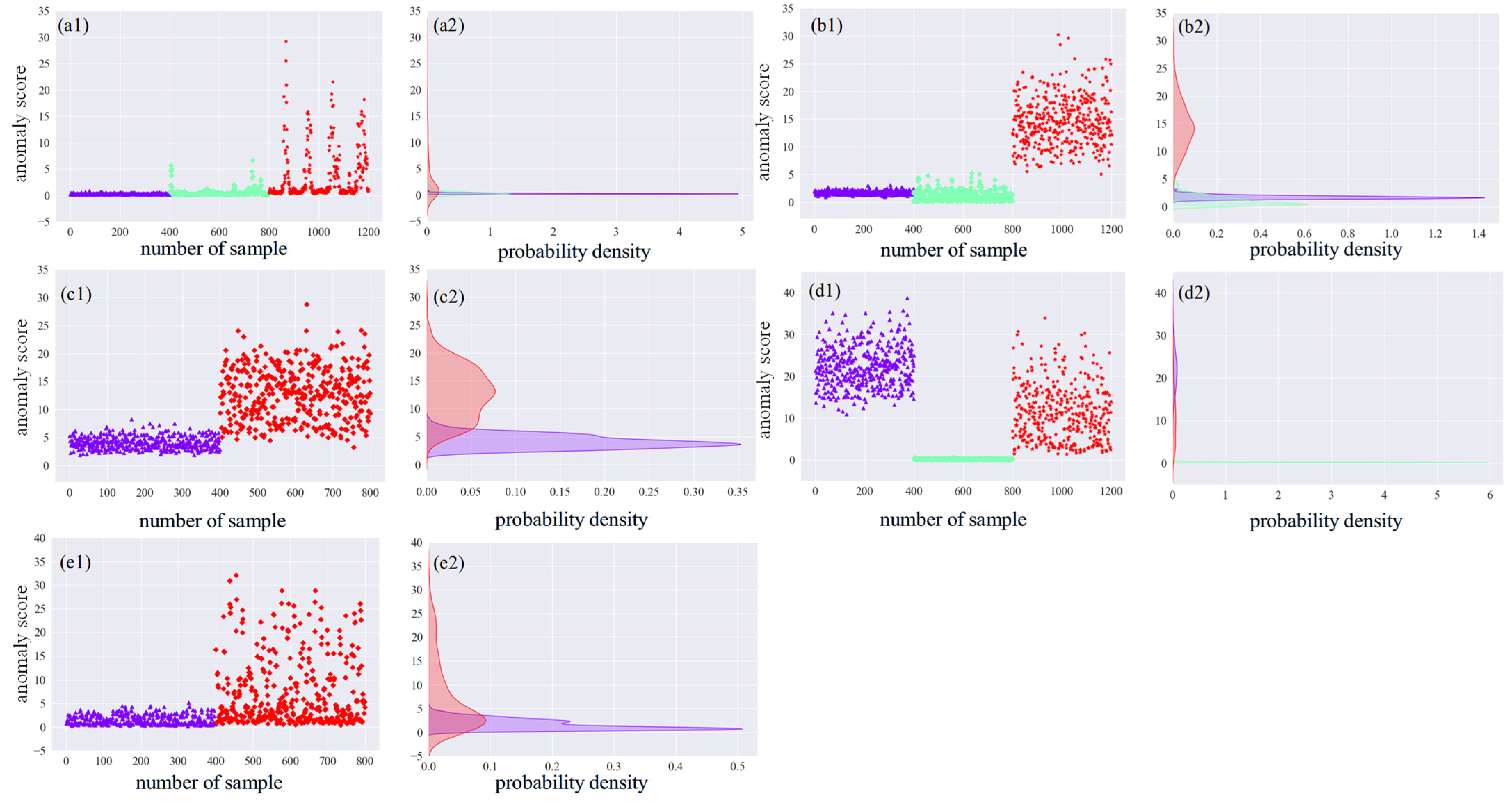
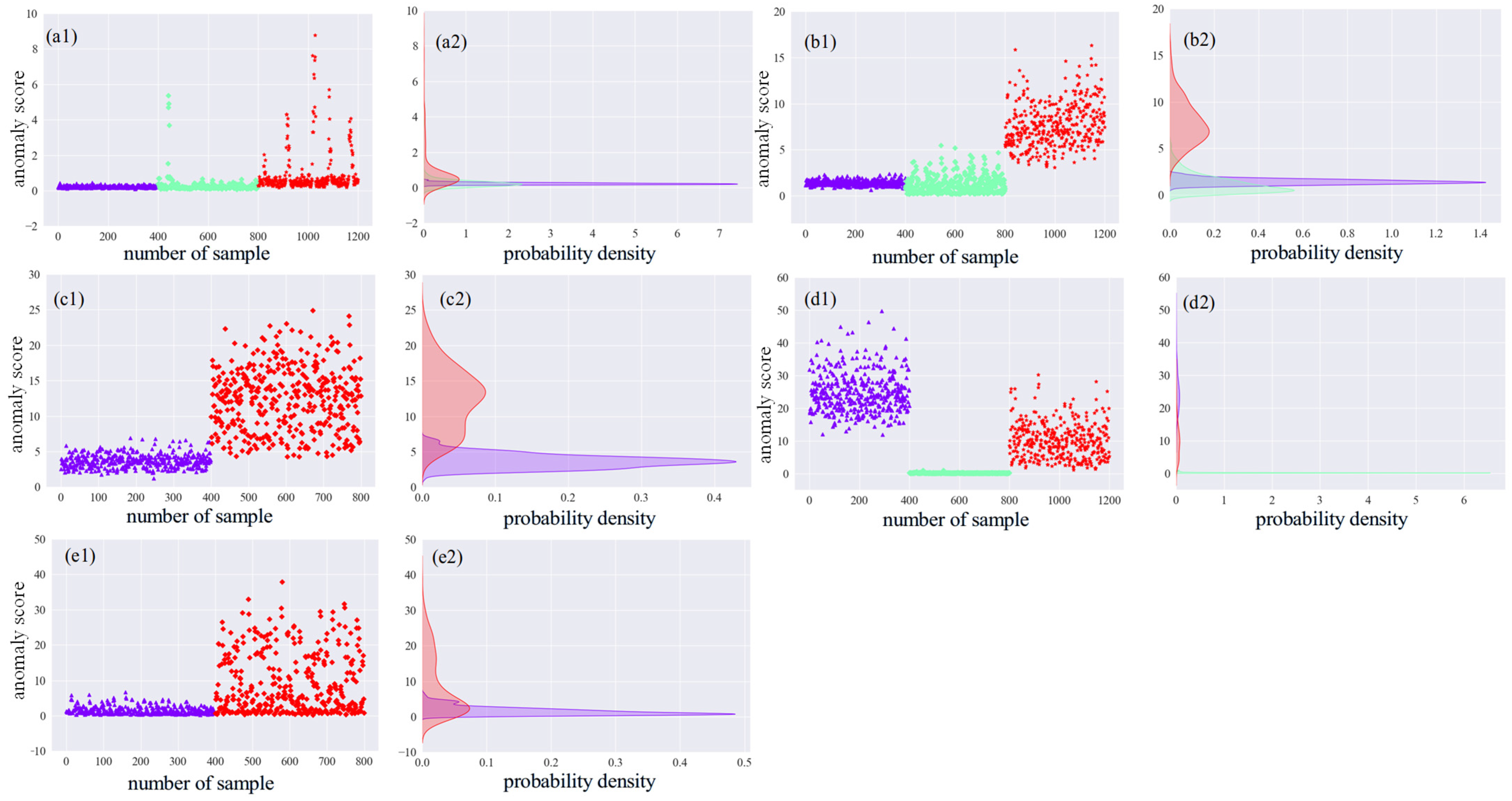
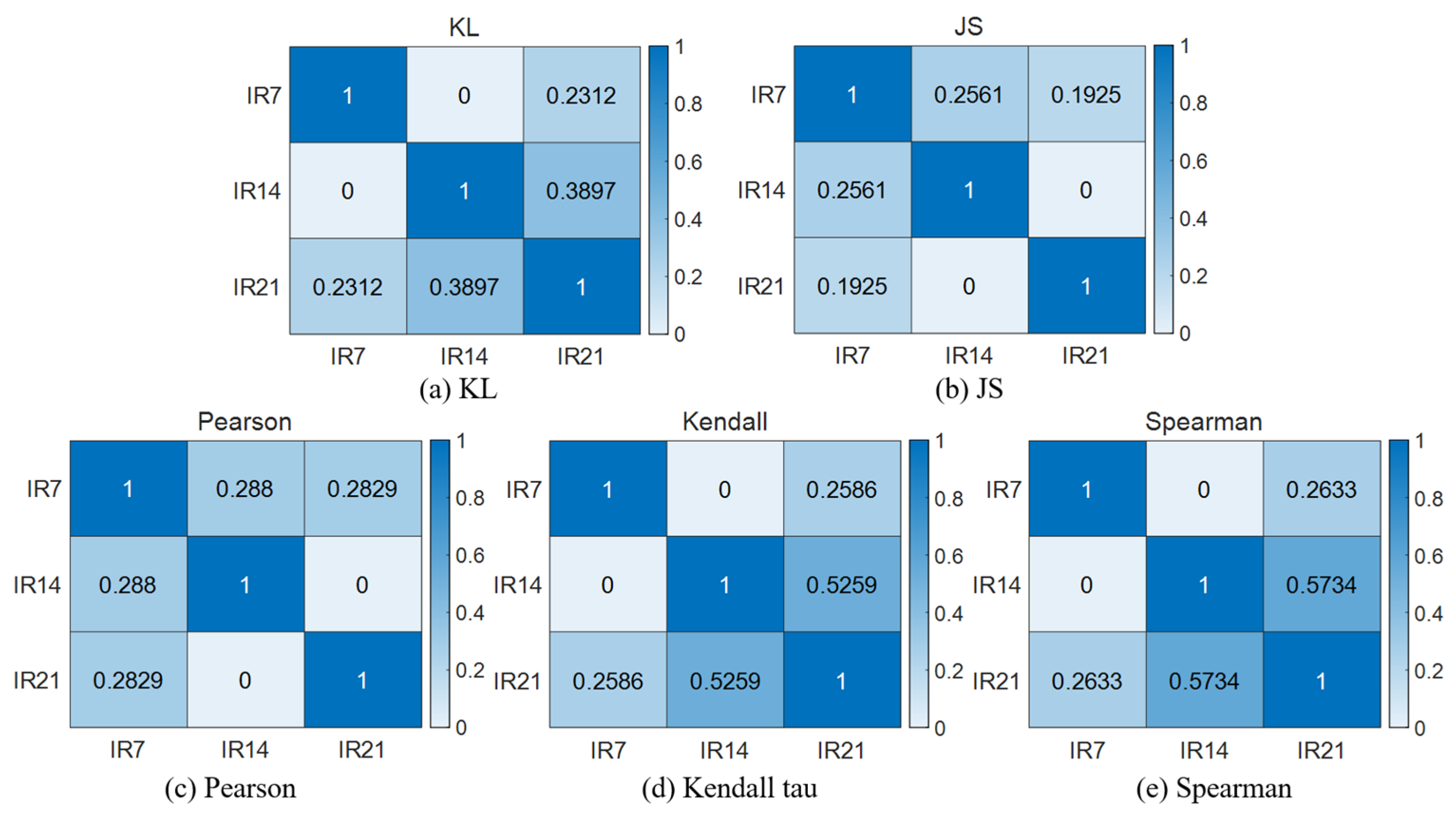
3.1.3. Anomaly Evaluation
3.2. Validation with Popular Open Datasets
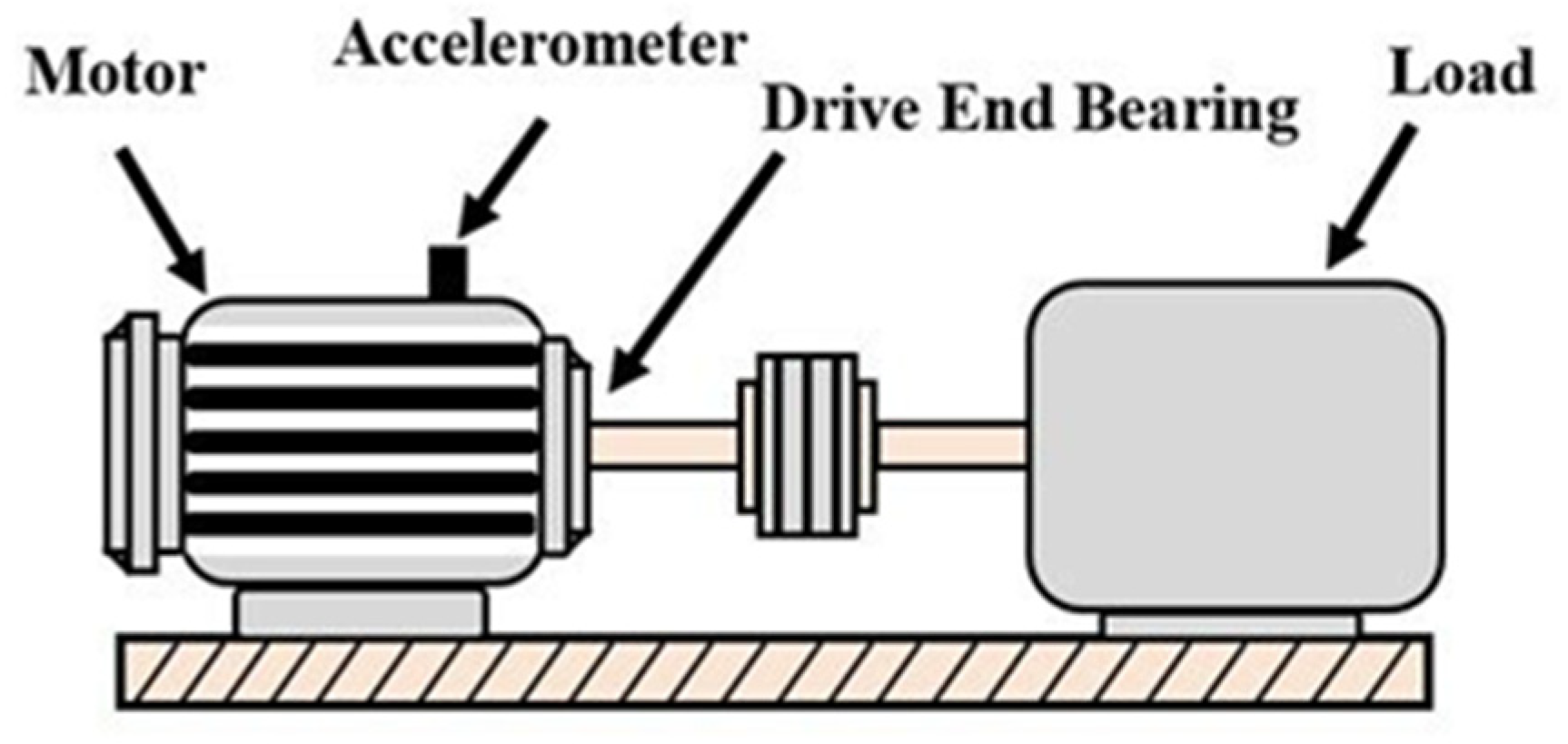
3.2.1. CWRU Dataset
3.2.2. Anomaly Detection and Threshold Optimization
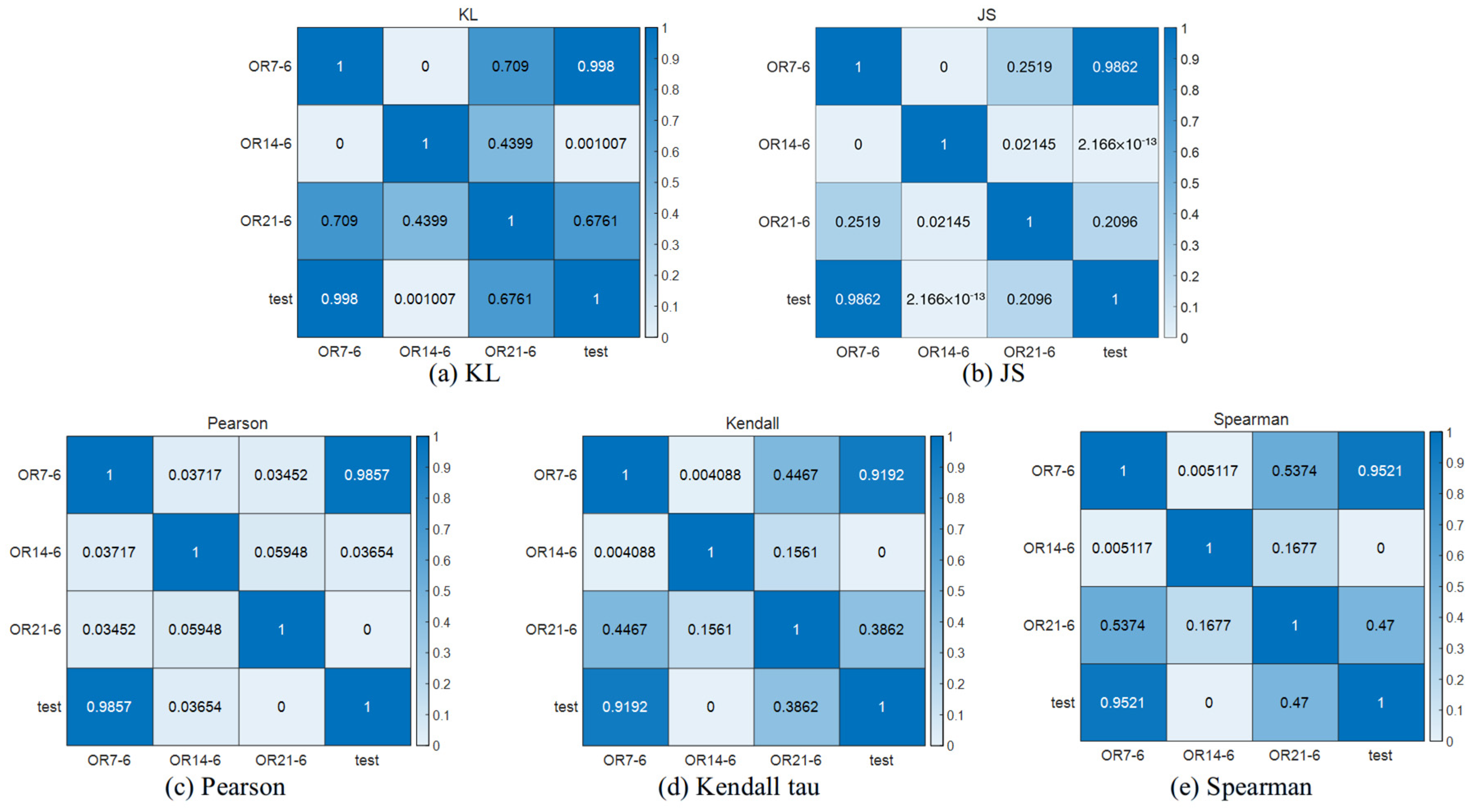
3.2.3. Anomaly Evaluation
3.2.4. Comparison with Related Methods on the CWRU Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
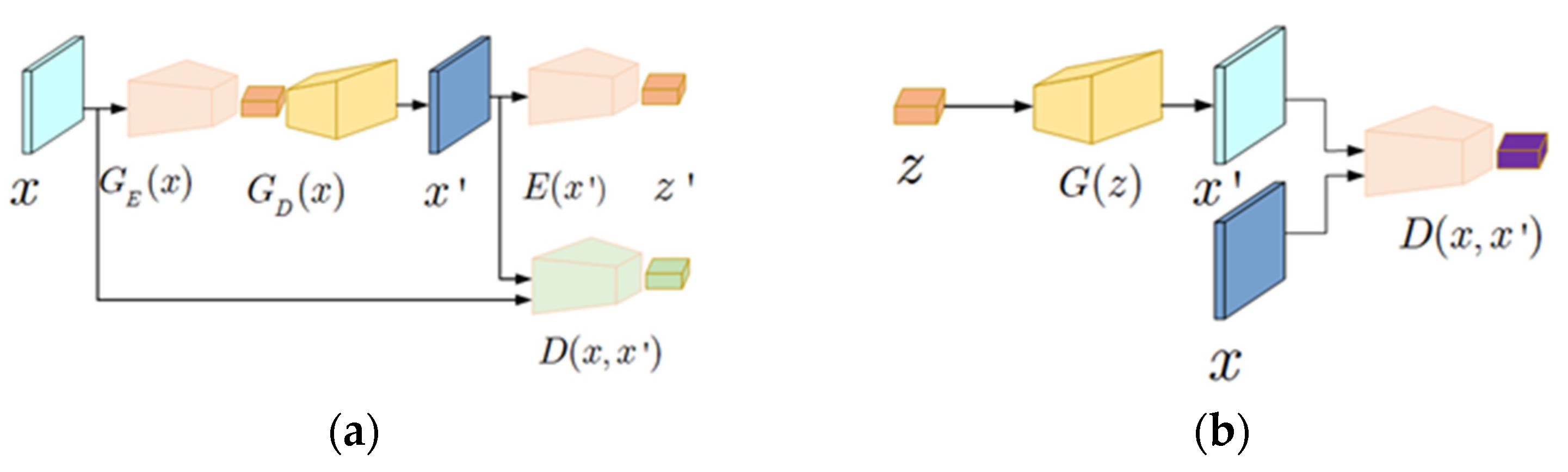
Appendix A. Standard GAN Objective and Background Formulation
Appendix B. Definition of Severity Levels for Fracture-Related Faults in the Split-Torque Simulation
| (a) | |||||
|---|---|---|---|---|---|
| Severity Level | Damage Ratio (–) | Remaining Face Width (mm) | Removed Width (mm) | ||
| Level 1 | 0.10 | 27.0 | 3.0 | ||
| Level 2 | 0.20 | 24.0 | 6.0 | ||
| Level 3 | 0.30 | 21.0 | 9.0 | ||
| Level 4 | 0.40 | 18.0 | 12.0 | ||
| Level 5 | 0.50 | 15.0 | 15.0 | ||
| Level 6 | 0.60 | 12.0 | 18.0 | ||
| Level 7 | 0.70 | 9.0 | 21.0 | ||
| Level 8 | 0.80 | 6.0 | 24.0 | ||
| Level 9 | 0.85 | 4.5 | 25.5 | ||
| Level 10 | 0.90 | 3.0 | 27.0 | ||
| (b) | |||||
| Severity Level | Crack Depth (mm) | Normalized Crack Ratio (–) | |||
| Level 1 | 0.5625 | 0.10 | |||
| Level 2 | 1.1250 | 0.20 | |||
| Level 3 | 1.6875 | 0.30 | |||
| Level 4 | 2.2500 | 0.40 | |||
| Level 5 | 2.8125 | 0.50 | |||
| Level 6 | 3.3750 | 0.60 | |||
| Level 7 | 3.9375 | 0.70 | |||
| Level 8 | 4.5000 | 0.80 | |||
| Level 9 | 5.0625 | 0.90 | |||
| Level 10 | 5.6250 | 1.00 | |||
References
- Deng, W.; Li, Z.; Li, X.; Chen, H.; Zhao, H. Compound Fault Diagnosis Using Optimized MCKD and Sparse Representation for Rolling Bearings. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Ma, J.; Shang, J.; Zhao, X.; Zhong, P. Bayes-DCGRU with bayesian optimization for rolling bearing fault diagnosis. Appl. Intell. 2022, 52, 11172–11183. [Google Scholar] [CrossRef]
- Shao, H.; Xia, M.; Wan, J.; de Silva, C.W. Modified Stacked Autoencoder Using Adaptive Morlet Wavelet for Intelligent Fault Diagnosis of Rotating Machinery. IEEE/ASME Trans. Mechatron. 2022, 27, 24–33. [Google Scholar] [CrossRef]
- Zhou, P.; Hu, X.; Li, P.; Wu, X. Online feature selection for high-dimensional class-imbalanced data. Knowl.-Based Syst. 2017, 136, 187–199. [Google Scholar] [CrossRef]
- Viola, J.; Chen, Y.; Wang, J. FaultFace: Deep convolutional generative adversarial network (DCGAN) based ball-bearing failure detection method. Inf. Sci. 2021, 542, 195–211. [Google Scholar] [CrossRef]
- Zhou, F.; Yang, S.; Fujita, H.; Chen, D.; Wen, C. Deep learning fault diagnosis method based on global optimization GAN for unbalanced data. Knowl.-Based Syst. 2020, 187, 104837. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, T. Imbalanced learning for fault diagnosis problem of rotating machinery based on generative adversarial networks. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 3248–3253. [Google Scholar]
- Huang, K.; Wu, S.; Li, F.; Yang, C.; Gui, W. Fault Diagnosis of Hydraulic Systems Based on Deep Learning Model with Multirate Data Samples. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6789–6801. [Google Scholar] [CrossRef]
- Zareapoor, M.; Shamsolmoali, P.; Yang, J. Oversampling adversarial network for class-imbalanced fault diagnosis. Mech. Syst. Signal Process. 2021, 149, 107175. [Google Scholar] [CrossRef]
- Yan, K.; Su, J.; Huang, J.; Mo, Y. Chiller Fault Diagnosis Based on VAE-Enabled Generative Adversarial Networks. IEEE Trans. Autom. Sci. Eng. 2022, 19, 387–395. [Google Scholar] [CrossRef]
- Spirto, M.; Nicolella, A.; Melluso, F.; Malfi, P.; Cosenza, C.; Savino, S.; Niola, V. Enhancing SDP-CNN for Gear Fault Detection Under Variable Working Conditions via Multi-Order Tracking Filtering. J. Dyn. Monit. Diagn. 2025, 4, 226–238. [Google Scholar] [CrossRef]
- Chen, J.; Li, T.; He, J.; Liu, T. An interpretable wavelet Kolmogorov–Arnold convolutional LSTM for spatial-temporal feature extraction and intelligent fault diagnosis. J. Dyn. Monit. Diagn. 2025, 4, 183–193. [Google Scholar] [CrossRef]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep learning for anomaly detection: A review. ACM Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Ou, X.; Wen, G.; Huang, X.; Su, Y.; Chen, X.; Lin, H. A deep sequence multi-distribution adversarial model for bearing abnormal condition detection. Measurement 2021, 182, 109529. [Google Scholar] [CrossRef]
- Maliuk, A.S.; Prosvirin, A.E.; Ahmad, Z.; Kim, C.H.; Kim, J.-M. Novel bearing fault diagnosis using gaussian mixture model-based fault band selection. Sensors 2021, 21, 6579. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Yang, B.; Zhang, X.; Wang, S.; Chen, X. Time-frequency atoms-driven support vector machine method for bearings incipient fault diagnosis. Mech. Syst. Signal Process. 2016, 75, 345–370. [Google Scholar] [CrossRef]
- Bendjama, H. Bearing fault diagnosis based on optimal Morlet wavelet filter and Teager-Kaiser energy operator. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 392. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Guo, Y. Unknown fault feature extraction of rolling bearings under variable speed conditions based on statistical complexity measures. Mech. Syst. Signal Process. 2022, 172, 108964. [Google Scholar] [CrossRef]
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019, arXiv:1901.03407. [Google Scholar] [CrossRef]
- Hou, Y.; Ma, J.; Wang, J.; Li, T.; Chen, Z. Enhanced generative adversarial networks for bearing imbalanced fault diagnosis of rotating machinery. Appl. Intell. 2023, 53, 25201–25215. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, F.; Wang, B.; Habetler, T.G. Semi-supervised learning of bearing anomaly detection via deep variational autoencoders. arXiv 2019, arXiv:1912.01096. [Google Scholar] [CrossRef]
- Lee, K.; Kim, J.K.; Kim, J.; Hur, K.; Kim, H. Stacked convolutional bidirectional LSTM recurrent neural network for bearing anomaly detection in rotating machinery diagnostics. In Proceedings of the 2018 1st IEEE International Conference on Knowledge Innovation and Invention (ICKII), Jeju, Republic of Korea, 23–27 July 2018; pp. 98–101. [Google Scholar]
- Ahmad, S.; Styp-Rekowski, K.; Nedelkoski, S.; Kao, O. Autoencoder-based condition monitoring and anomaly detection method for rotating machines. In Proceedings of the 2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 10–13 December 2020; pp. 4093–4102. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Schlegl, T.; Seeböck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. In Proceedings of the International Conference on Information Processing in Medical Imaging, Boone, NC, USA, 25–30 June 2017; pp. 146–157. [Google Scholar]
- Donahue, J.; Krähenbühl, P.; Darrell, T. Adversarial feature learning. arXiv 2016, arXiv:1605.09782. [Google Scholar]
- Akçay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-supervised anomaly detection via adversarial training. In Proceedings of the Computer Vision—ACCV, Perth, Australia, 2–6 December 2018; Springer: Cham, The Netherlands, 2018; pp. 622–637. [Google Scholar]
- Jiang, W.; Hong, Y.; Zhou, B.; He, X.; Cheng, C. A GAN-based anomaly detection approach for imbalanced industrial time series. IEEE Access 2019, 7, 143608–143619. [Google Scholar] [CrossRef]
- Hu, W.; Wang, T.; Chu, F. A Wasserstein generative digital twin model in health monitoring of rotating machines. Comput. Ind. 2023, 145, 103807. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved techniques for training gans. ArXiv 2016, arXiv:1606.03498. [Google Scholar]
- Kinga, D.; Adam, J.B. A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; Volume 5. [Google Scholar]
- Case Western Reserve University Bearing Data Center Website. Available online: https://engineering.case.edu/bearingdatacenter/welcome (accessed on 1 January 2025).
- Neupane, D.; Seok, J. Bearing fault detection and diagnosis using case western reserve university dataset with deep learning approaches: A review. IEEE Access 2020, 8, 93155–93178. [Google Scholar] [CrossRef]
- Yan, H.; Si, X.; Liang, J.; Duan, J.; Shi, T. Unsupervised Learning for Machinery Adaptive Fault Detection Using Wide-Deep Convolutional Autoencoder with Kernelized Attention Mechanism. Sensors 2024, 24, 8053. [Google Scholar] [CrossRef]
- Dai, Z.; Jiang, L.; Li, F.; Chen, Y. A Multi-Scale Self-Supervision Approach for Bearing Anomaly Detection Using Sensor Data Under Multiple Operating Conditions. Sensors 2025, 25, 1185. [Google Scholar] [CrossRef]
- Rosa, R.K.; Braga, D.; Silva, D. Benchmarking deep learning models for bearing fault diagnosis using the cwru dataset: A mul-ti-label approach. arXiv 2024, arXiv:2407.14625. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]

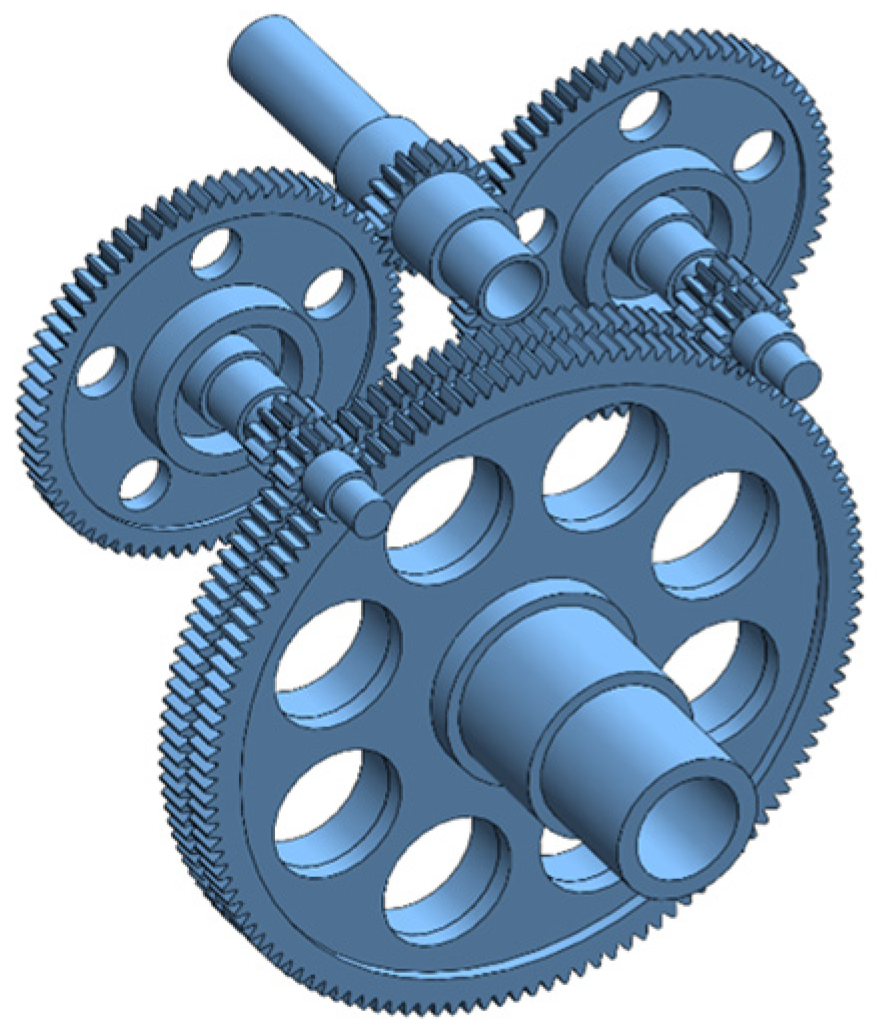
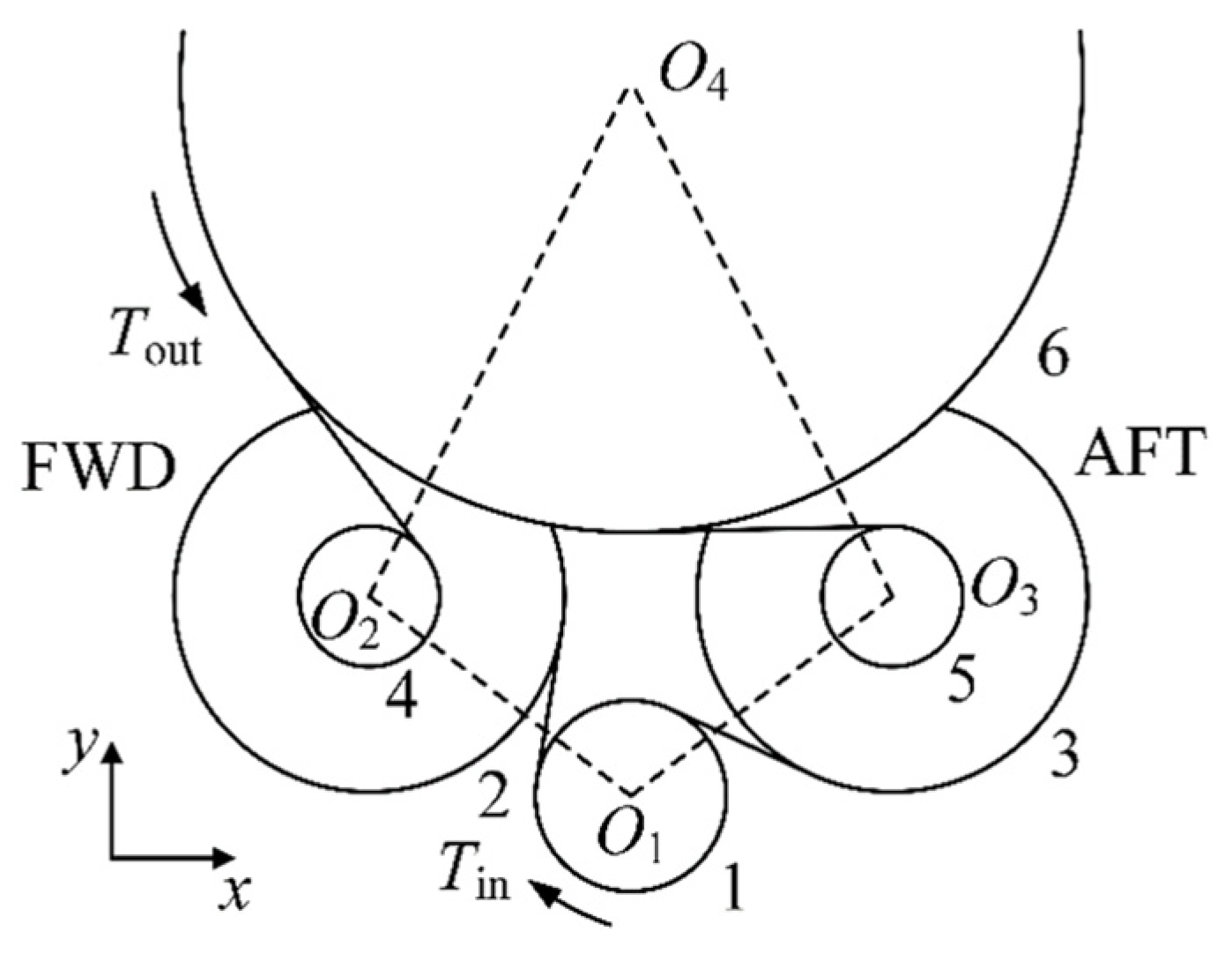





| Parameters | Gear1 | Gear2/Gear3 | Gear2/Gear3 | Gear6 |
|---|---|---|---|---|
| Number of teeth | 21 | 70 | 13 | 126 |
| Pressure angle (°) | 22.5 | 22.5 | 25 | 25 |
| Module (mm) | 4.5 | 4.5 | 4.5 | 4.5 |
| Face width (mm) | 30 | 30 | 80 | 80 |
| Inertia (kg∙mm2) | 1832.1 | 2.26 × 105 | 717.5 | 6.33 × 106 |
| Weight (kg) | 1.64 | 18.24 | 1.68 | >157.56 |
| Bearing stiffness (N/m) | kbx = kby = 1 × 108 | |||
| Subjects | G1B-1 | G1B-2 | G1B-3 | G1B-4 | G1B-5 |
| Similarity | 0.623096 | 0.873446 | 0.198775 | 0.051758 | 0.031555 |
| Subjects | G1B-6 | G1B-7 | G1B-8 | G1B-9 | G1B-10 |
| Similarity | 0.032992 | 0.030805 | 0.029354 | 0.024305 | 0.020541 |
| Parameter | Value |
|---|---|
| Sampling Frequency (kHz) | 12, 48 |
| Motor speed (RPM) | 1730, 1750, 1772, 1797 |
| Fault type | IR, OR, B |
| Fault size(inch) | 0.007, 0.014, 0.021 |
| Fault implantation direction | 3, 6, 12 |
| Accuracy | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fault Type | N | Ball | IR | OR | ||||||||||
| Fault Direction | \ | 07 | 14 | 21 | 07 | 14 | 21 | 3 | 6 | 12 | ||||
| Fault Size | 07 | 21 | 07 | 14 | 21 | 07 | 21 | |||||||
| RPM1730 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.993 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 1.000 |
| RPM1750 | 1.000 | 1.000 | 0.983 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| RPM1772 | 1.000 | 1.000 | 0.955 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 1.000 |
| Mean | 1.000 | 1.000 | 0.979 | 1.000 | 1.000 | 0.998 | 1.000 | 1.000 | 1.000 | 1.000 | 0.999 | 1.000 | 1.000 | 1.000 |
| Std | 0.000 | 0.000 | 0.023 | 0.000 | 0.000 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.000 | 0.000 | 0.000 |
| Subjects | OR7-6 | OR14-6 | OR21-6 |
| Similarity | 0.96824 | 0.007308 | 0.34838 |
| Method | Learning Paradigm | Key Idea | Metric (Reported) | Reported Performance on CWRU |
|---|---|---|---|---|
| FaultFace (DCGAN-aided) [10] | Supervised (GAN-aided) | Data augmentation + CNN classifier | Accuracy (best) | 100% |
| WDCAE-LKA [34] | Unsupervised | Autoencoder + large-kernel attention + dynamic threshold | Average diagnostic accuracy | 90.29% |
| ADBR [35] | Self-supervised | BYOL-style representation + reconstruction | Average fault detection accuracy | 96.97% |
| DAA-GAN (this work) | Unsupervised + staged | DAA-GAN + adaptive threshold + similarity fusion | Average detection accuracy (Table 4) | 99.83% (1730/1750/1772 rpm) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Hu, L.; Tan, L.; Meng, X.; Zeng, J.; Luo, P.; Yang, Y. A Framework for Anomaly Detection and Evaluation of Rotating Machinery Based on Data-Accumulation-Aware Generative Adversarial Networks and Similarity Estimation. Machines 2026, 14, 61. https://doi.org/10.3390/machines14010061
Hu L, Tan L, Meng X, Zeng J, Luo P, Yang Y. A Framework for Anomaly Detection and Evaluation of Rotating Machinery Based on Data-Accumulation-Aware Generative Adversarial Networks and Similarity Estimation. Machines. 2026; 14(1):61. https://doi.org/10.3390/machines14010061
Chicago/Turabian StyleHu, Lei, Lingjie Tan, Xiangyan Meng, Jiyu Zeng, Peng Luo, and Yi Yang. 2026. "A Framework for Anomaly Detection and Evaluation of Rotating Machinery Based on Data-Accumulation-Aware Generative Adversarial Networks and Similarity Estimation" Machines 14, no. 1: 61. https://doi.org/10.3390/machines14010061
APA StyleHu, L., Tan, L., Meng, X., Zeng, J., Luo, P., & Yang, Y. (2026). A Framework for Anomaly Detection and Evaluation of Rotating Machinery Based on Data-Accumulation-Aware Generative Adversarial Networks and Similarity Estimation. Machines, 14(1), 61. https://doi.org/10.3390/machines14010061





