Thermal Error Analysis of Hydrostatic Turntable System
Abstract
1. Introduction
2. Temperature Field Model of Hydrostatic Turntable System
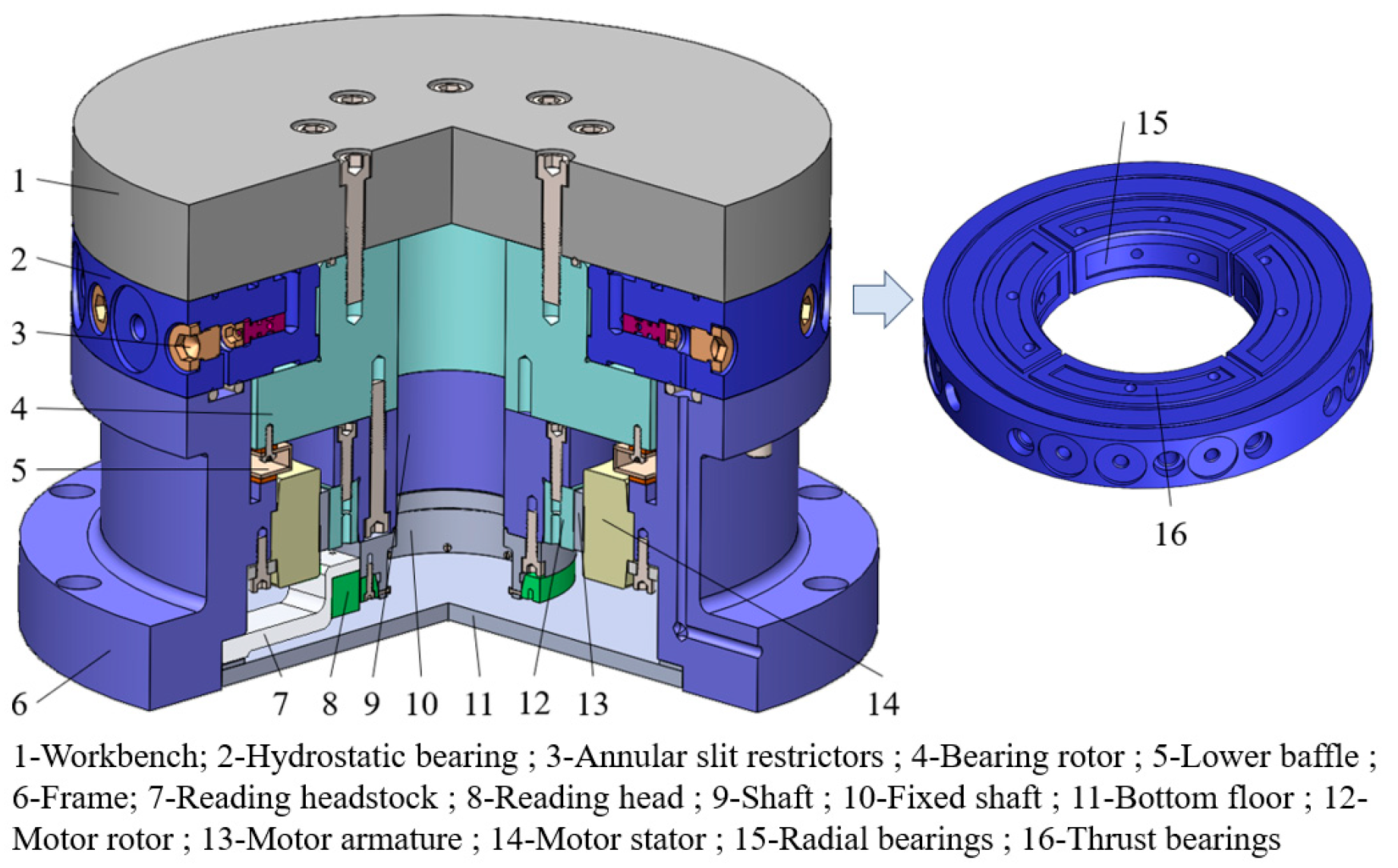
2.1. The Overall Structure of the Hydrostatic Turntable System
2.2. Temperature Field Modeling of Hydrostatic Turntable
- (1)
- Ignoring the heat transfer between the hydraulic oil and the bearing parts; that is, the heat generated by the internal friction of the hydrostatic bearing under the working condition of the hydrostatic rotary table is all used to increase the temperature of the hydraulic oil;
- (2)
- The convective heat transfer coefficient of the fluid of the lubricating medium and the external air does not change with the temperature;
- (3)
- The power consumed by the turntable motor is all converted into heat and absorbed by the lubricating oil;
- (4)
- The process of the hydraulic oil temperature rising caused by the internal friction power follows the law of the conservation of energy.
2.2.1. Temperature Rise Calculation of Radial Bearing
2.2.2. Temperature Rise Calculation of Thrust Bearing
3. Finite Element Analysis of Thermal Characteristics of Turntable System
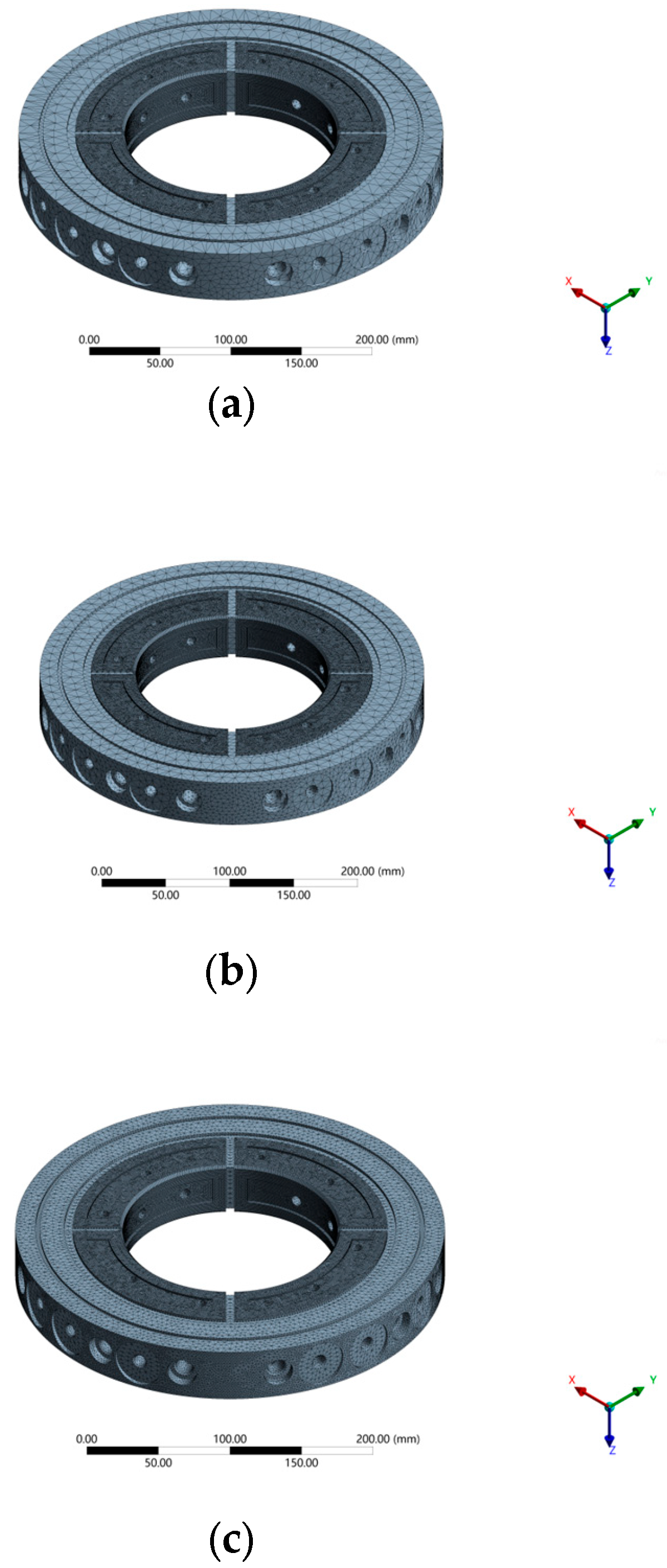
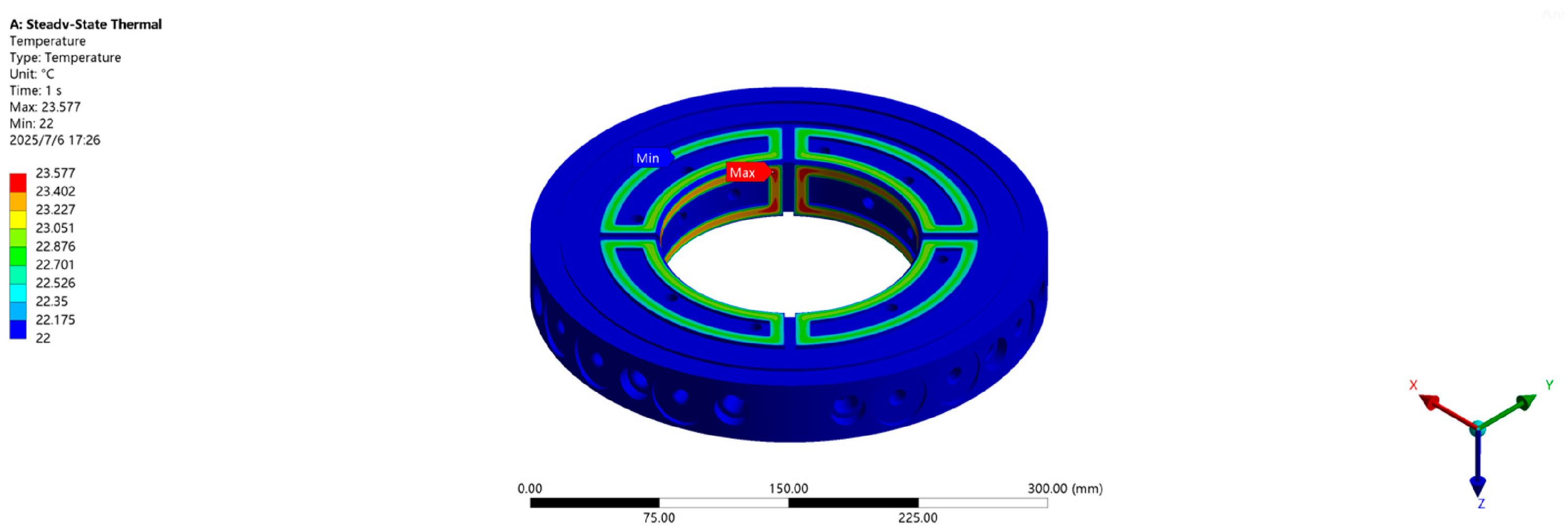
3.1. Finite Element Analysis of Temperature Field of Bearing Bush
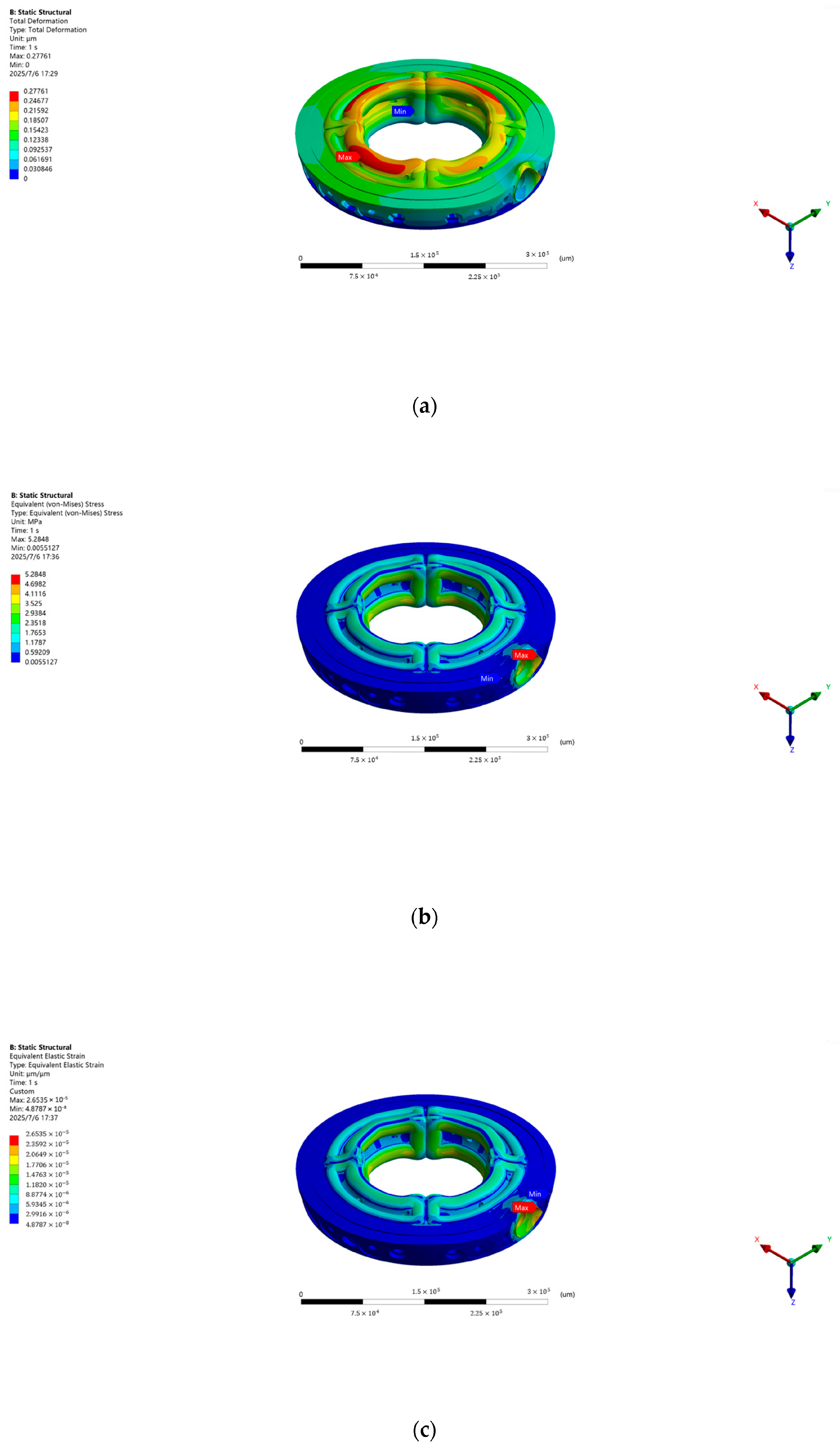
3.2. Thermal Deformation Analysis of Bearing Bush Under Different Working Conditions
4. Conclusions
- (1)
- As the temperature increases, the deformation and strain of the hydrostatic turntable system increase monotonically. For every 1 °C increase, the total deformation of the bearing increases by about 0.285 . This conclusion provides inspiration for the optimal design of the cooling system of the hydrostatic rotary table. For example, the thermal safety limit of the turntable operation can be established according to the quantitative relationship between the temperature and deformation to improve the heat dissipation accuracy of the cooling system.
- (2)
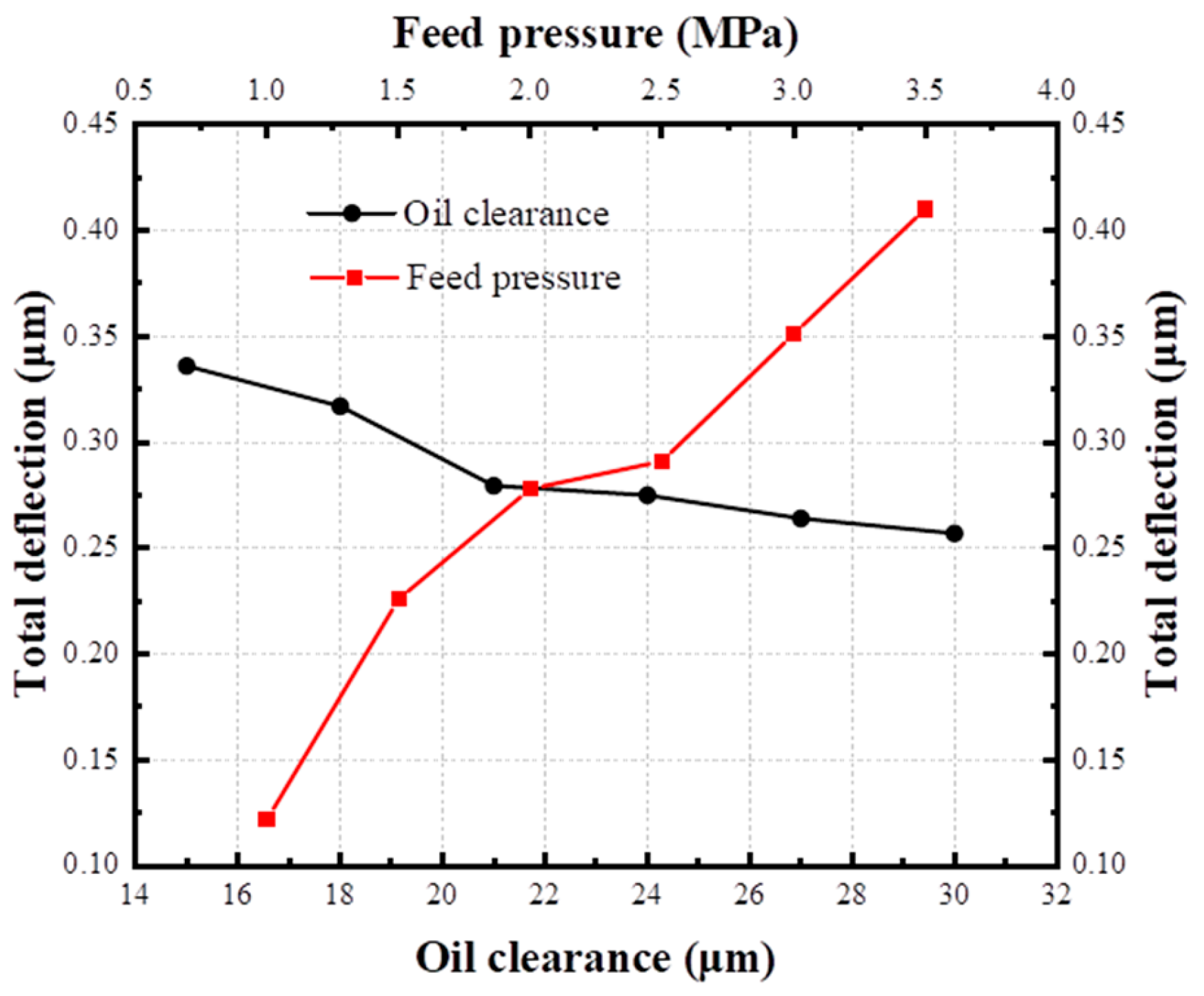
- The temperature rise in the hydrostatic turntable system increases with the increase in the oil supply pressure and decreases with the increase in the oil film clearance. The oil supply pressure has a greater influence on the temperature rise and thermal deformation than the oil film clearance. This conclusion is helpful for the coordinated control of the oil supply pressure and the oil film gap of the hydrostatic turntable. The flow rate can be increased by moderately increasing the oil film gap and the oil supply pressure, thereby reducing the heat generated by the oil film surface during the movement, causing a large amount of heat to be taken away by the hydrostatic oil, so as to reduce the temperature rise in the hydrostatic turntable system and improve the overall accuracy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, X.; Tang, B.; Wang, S.; Han, Z.; Li, S.; Chen, M.; Zhang, R.; Wang, J.; Jiao, J.; Jiang, H. High-speed and heavy-load tribological properties of hydrostatic thrust bearing with double rectangular recess. Int. J. Hydrogen Energy 2022, 47, 21273–21286. [Google Scholar] [CrossRef]
- Zeng, X.; Xiong, W.; Zhang, H.; Li, Y.; Tang, X.; Yuan, S. Research on the grinding rounding mechanism and law of the cylindrical grinding system supported all by hydrostatic spindles. J. Manuf. Process. 2023, 109, 25–37. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, Z.; Zhu, S.; Yang, Z.; Zhang, H.; Chen, G.; Zhang, M. An energy consumption field model considering motion position errors for energy efficient machining on CNC machines:CNC programming perspective. Appl. Energy 2024, 374, 124023. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Yang, Y.; Yang, Y.; Zhao, X.; Shi, H.; Liang, F. Temperature-sensitivity points selection for positioning error modeling of CNC machine tools based on analytic hierarchy process. J. Manuf. Process. 2025, 141, 667–678. [Google Scholar] [CrossRef]
- Lang, S.; Zorzini, M.; Scholze, S.; Mayr, J.; Bambach, M. Sensor placement utilizing a digital twin for thermal error compensation of machine tools. J. Manuf. Syst. 2025, 80, 243–257. [Google Scholar] [CrossRef]
- Dai, B.; Yuan, S.; Xu, Q.; Xu, Q.; Wang, P. Research on thermal error control method for rotary table of five-axis vertical horizontal conversion machining center. J. Phys. Conf. Ser. 2025, 3032, 012050. [Google Scholar] [CrossRef]
- Ma, C.; Mu, R.; Li, M.; He, J.; Hua, C.; Wang, L.; Liu, J.; Totis, G.; Yang, J.; Liu, K.; et al. A multi-scale spatial–temporal interaction fusion network for digital twin-based thermal error compensation in precision machine tools. Expert Syst. Appl. 2025, 286, 127812. [Google Scholar] [CrossRef]
- Michalec, M.; Polnický, V.; Foltýn, J.; Svoboda, P.; Šperka, P.; Hurník, J. The prediction of large-scale hydrostatic bearing pad misalignment error and its compensation using compliant support. Precis. Eng. 2022, 75, 67–79. [Google Scholar] [CrossRef]
- Bian, Q.; Zhang, X.; Wang, X.; Zhao, C.; Jiao, B.; Gao, X. Research on transient temperature rise characteristics of composite cylindrical roller bearings. Tribol. Int. 2024, 195, 109650. [Google Scholar] [CrossRef]
- Siegle, L.; Hilliger, A.; Herbst, S.; Engelmann, F. Analysing the impact of solid contaminants on grease viscosity and the theoretical temperature performance of rolling bearings. J. Loss Prev. Process. Ind. 2025, 94, 105562. [Google Scholar] [CrossRef]
- Ueda, H.; Saito, M.; Kawamura, Y.; Kawada, S.; Miyatake, M. Study on static and dynamic characteristics of water-lubricated hydrostatic thrust bearings – Effect of feed hole inlet shape on bearing characteristics. Tribol. Int. 2023, 191, 109127. [Google Scholar] [CrossRef]
- Marinescu, A.; Cicone, T.; Fatu, A. The study of a novel hydrostatic thrust bearing with a structurally elastic component: Theory and experiments. Tribol. Int. 2023, 189, 108954. [Google Scholar] [CrossRef]
- Zhang, J.; Qiu, M.; Dong, Y.; Yang, C. Investigation of skidding characteristics of high-speed cylindrical roller bearings based on the improved ADORE model with thermal analysis and lubricant distribution. Tribol. Int. 2025, 204, 110523. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Z.; Qiu, C.; Luo, J.; He, L.; Liu, H.; Sa, G.; Jiang, Z.; Tan, J. Machining accuracy prediction and adaptive compensation method of CNC machine tool under absence of machining process sensing. J. Intell. Manuf. 2024, 35, 1–18. [Google Scholar] [CrossRef]
- Fu, Y.; Hong, X.; Wang, D.; Huang, W. Study on static and dynamic characteristics of hydrostatic rotaty table for PM flow controller. J. Mach. Des. 2018, 35, 251–258. [Google Scholar]
- Hu, Q.; Li, M.; Yuan, N. The thermal characteristics control and optimization of a large torque directdrive ultra-precision hydrostatic rotary table. Manuf. Technol. Mach. Tool. 2021, 9, 126–129. [Google Scholar]
- Hu, J.; Liu, C. Effect of working parameters on performance characteristics ofhydrostatic turntable by using FSI-thermal model. J. Cent. South Univ. 2018, 25, 2589–2600. [Google Scholar] [CrossRef]
- Xiong, W.; Fu, M.; Wang, S.; Lü, L. Analyses on Tilted Oil Film Dynamical Characteristics of Hydrostatic Rotary Tables. China Mech. Eng. 2014, 25, 3326–3333. [Google Scholar]
- Yang, C.; Shao, S.; Li, Y.; Zhao, Y.; Ma, H. Performance Analysis and Restrictor Structure Improvement of an Internal Feedback Hydrostatic Turntable Oil Pad Considering Internal Flow. Adv. Theory Simul. 2024, 7, 2300822. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Wu, Y.; Wang, M.; Kong, P. Study of the Lubricity of Oil Film at Constant Cutting Speed Under Different Loads of a Hydrostatic Turntable. Tribol. Trans. 2023, 66, 135–143. [Google Scholar] [CrossRef]
- Ruiz, A.C.; Hooff, V.T.; Blocken, B.; Heijst, G. PIV Measurements and Validation of RANS Solutions for Plane Turbulent Impinging Co-Flowing and Angled Jets at Moderate Reynolds Numbers. Flow Turbul. Combust. 2025, 114, 1113–1147. [Google Scholar] [CrossRef]
- Lam, H.; Berthelon, T.; Balarac, G. Non-dimensional meshing criterion of mean flow field discretization for RANS and LES. Comput. Fluids 2025, 291, 106572. [Google Scholar] [CrossRef]

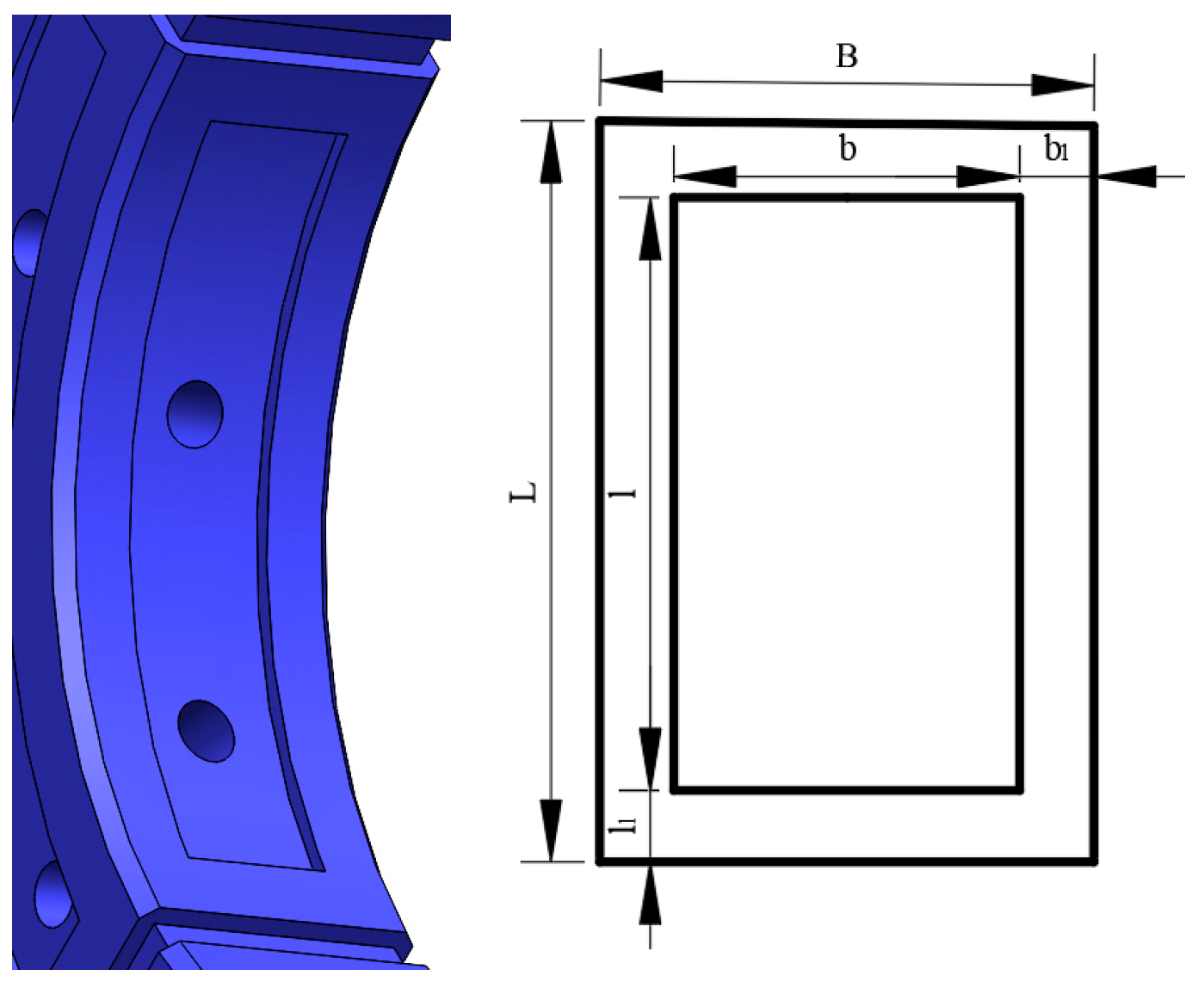
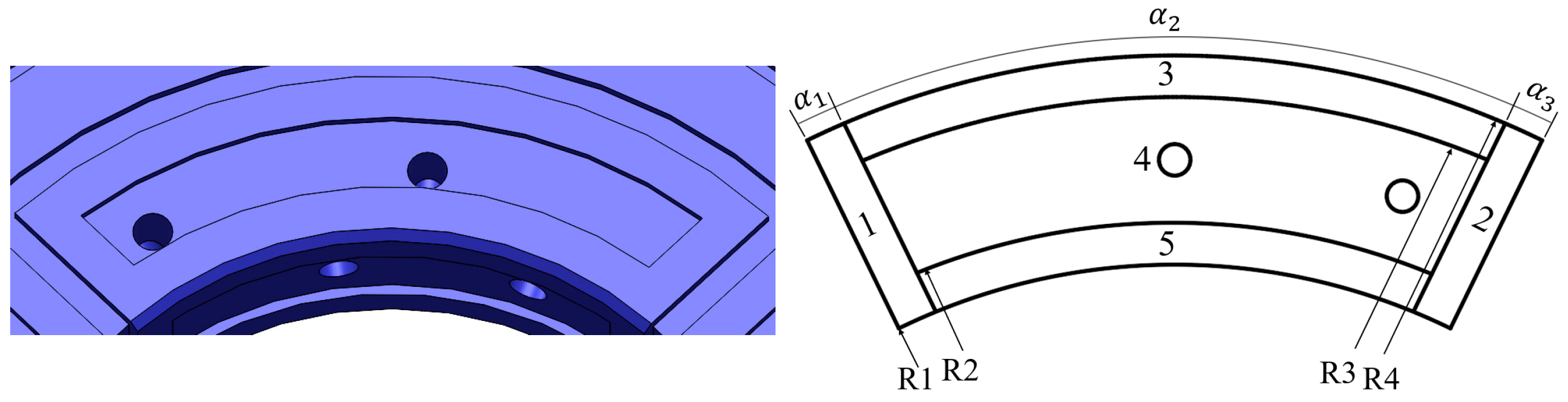


| Symbol | Definition | Parameter Values |
|---|---|---|
| n | Number of oil chambers | 4 |
| Dynamic viscosity of lubricating oil | 28.8 × 10−3 Pa·s | |
| v1 | Spindle speed | 0.39 m/s |
| A1 | The area of the hydraulic support surface of a single oil chamber | 2148.90 mm2 |
| A2 | The area of the hollowing part of a single oil chamber | 2285.91 mm2 |
| h0 | Oil film gap | |
| The depth of the oil chamber | 2 mm | |
| Oil supply pressure | ||
| R | Average radius of oil cavity | 75 mm |
| Pressure of oil chamber | 1 MPa | |
| L | Bearing length | 111.81 mm |
| l | Oil chamber length | 93.81 mm |
| l1 | Axial sealing surface length | 9 mm |
| B | Bearing width | 36 mm |
| b | Oil chamber width | 20 mm |
| b1 | Circumferential sealing surface width | 8 mm |
| b2 | Width of oil return tank | 6 mm |
| Specific heat capacity of lubricating oil | ||
| Lubricating oil density |
| Symbol | Definition | Parameter Values |
|---|---|---|
| Dynamic viscosity of lubricating oil | 28.8 × 10−3 Pa·s | |
| R1 | 77 mm | |
| R2 | 86 mm | |
| R3 | 101 mm | |
| R4 | 110 mm | |
| 0.082 rad | ||
| 1.351 rad | ||
| Oil film gap | ||
| The depth of the oil chamber | 2 mm | |
| Oil supply pressure | ||
| Pressure of oil chamber | ||
| n | Number of oil chambers | 8 |
| Specific heat capacity of lubricating oil | ||
| Lubricating oil density |
| Grid Division Scheme | Overall Meshing Density (mm) | Local Meshing Density (mm) |
|---|---|---|
| a | 8 | 2 |
| b | 5 | 2 |
| c | 2 | 2 |
| Boundary Conditions | Parameter Values |
|---|---|
| Inlet pressure | 2 MPa |
| Oil chamber pressure | 1 MPa |
| Oil outlet pressure | 0 MPa |
| Materials | Structural steel |
| Heat flow of radial bearing | 10.21 W |
| Heat flow of thrust bearing | 19.95 W |
| Ambient temperature | 22 °C |
| Grid Division Scheme | Overall Meshing Density (mm) | Local Meshing Density (mm) | Maximum Temperature Rise (°C) | Error (Relative to b-Meshing Scheme) |
|---|---|---|---|---|
| a | 8 | 2 | 1.616 | 2.5% |
| 6.5 | 2 | 1.590 | 0.8% | |
| b | 5 | 2 | 1.577 | 0 |
| 3.5 | 2 | 1.575 | 0.1% | |
| c | 2 | 2 | 1.576 | 0.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Ke, C.; Hu, K.; Zha, J. Thermal Error Analysis of Hydrostatic Turntable System. Machines 2025, 13, 598. https://doi.org/10.3390/machines13070598
Wang J, Ke C, Hu K, Zha J. Thermal Error Analysis of Hydrostatic Turntable System. Machines. 2025; 13(7):598. https://doi.org/10.3390/machines13070598
Chicago/Turabian StyleWang, Jianlei, Changhui Ke, Kaiyu Hu, and Jun Zha. 2025. "Thermal Error Analysis of Hydrostatic Turntable System" Machines 13, no. 7: 598. https://doi.org/10.3390/machines13070598
APA StyleWang, J., Ke, C., Hu, K., & Zha, J. (2025). Thermal Error Analysis of Hydrostatic Turntable System. Machines, 13(7), 598. https://doi.org/10.3390/machines13070598






