Multi-Physics and Multi-Objective Design of an Axial Flux Permanent Magnet-Assisted Synchronous Reluctance Motor for Use in Electric Vehicles
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
3.1. Optimization of AF-Pma-SynRM
3.2. Mechanical Design and Stress Analyses of the AF-Pma-SynRM Model
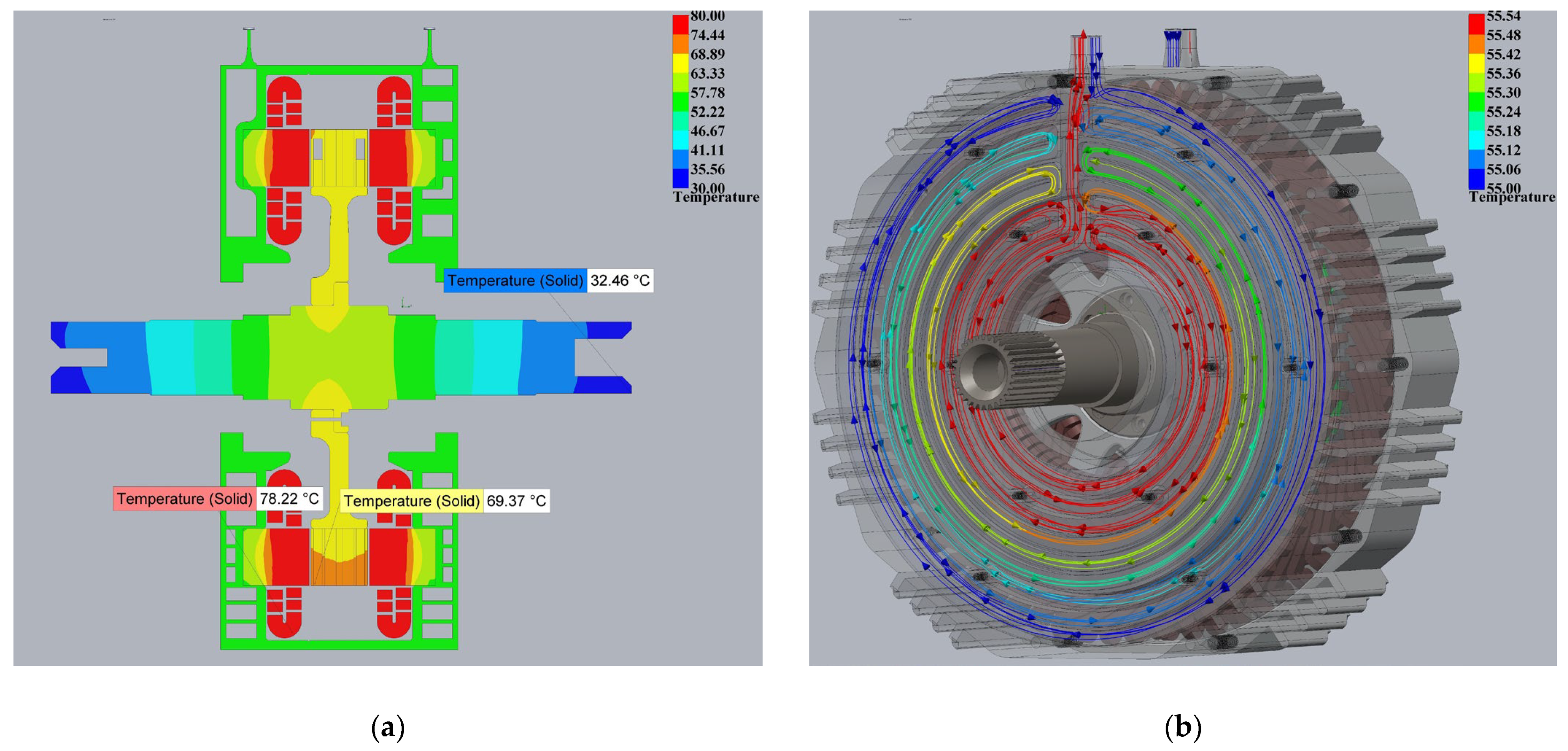
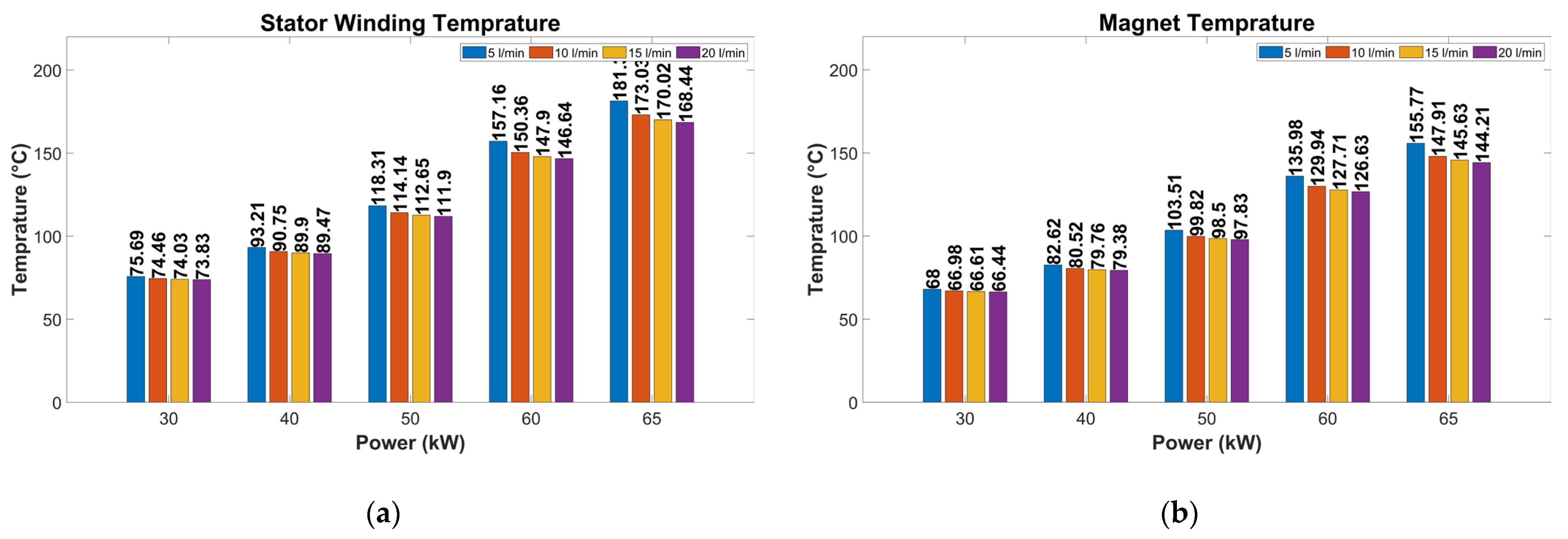
3.3. Thermal Analyses of the AF-Pma-SynRM Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nishanth, F.; Van Verdeghem, J.; Severson, E.L. A Review of Axial Flux Permanent Magnet Machine Technology. IEEE Trans. Ind. Appl. 2023, 59, 3920–3933. [Google Scholar] [CrossRef]
- Shao, L.; Navaratne, R.; Popescu, M.; Liu, G. Design and Construction of Axial-Flux Permanent Magnet Motors for Electric Propulsion Applications—A Review. IEEE Access 2021, 9, 158998–159017. [Google Scholar] [CrossRef]
- Jenkins, C.; Jones-Jackson, S.; Zaher, I.; Pietrini, G.; Rodriguez, R.; Cotton, J.; Emadi, A. Innovations in Axial Flux Permanent Magnet Motor Thermal Management for High Power Density Applications. IEEE Trans. Transp. Electrif. 2023, 9, 4380–4405. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, X.; Xiang, Z.; Xu, L.; Zhang, L.; Lee, C.H.T. Technology trends, challenges, and opportunities of reduced-rare-earth PM motor for modern electric vehicles. Green Energy Intell. Transp. 2022, 1, 100012. [Google Scholar] [CrossRef]
- Gobbi, M.; Sattar, A.; Palazzetti, R.; Mastinu, G. Traction motors for electric vehicles: Maximization of mechanical efficiency—A review. Appl. Energy 2024, 357, 122496. [Google Scholar] [CrossRef]
- Zou, T.; Gerada, D.; Rocca, S.L.; Rocca, A.L.; Walker, A.; Vakil, G.; Arevalo, S.L.; Xu, Z.; Cui, M.; Bardalai, A.; et al. Airgap Length Analysis of a 350 kw PM-Assisted Syn-Rel Machine for Heavy Duty EV Traction. IEEE Trans. Ind. Appl. 2023, 59, 1557–1570. [Google Scholar] [CrossRef]
- Nyitrai, A.; Kuczmann, M. Magnetic equivalent circuit and finite element modelling of anisotropic rotor axial flux permanent magnet synchronous motors with fractional slot distributed winding. IET Electr. Power Appl. 2023, 17, 709–720. [Google Scholar] [CrossRef]
- Katona, M.; Orosz, T. Circular Economy Aspects of Permanent Magnet Synchronous Reluctance Machine Design for Electric Vehicle Applications: A Review. Energies 2024, 17, 1408. [Google Scholar] [CrossRef]
- Yilmaz, M. Limitations/capabilities of electric machine technologies and modeling approaches for electric motor design and analysis in plug-in electric vehicle applications. Renew. Sustain. Energy Rev. 2015, 52, 80–99. [Google Scholar] [CrossRef]
- Adăscăliței, C.; Marțiș, R.A.; Karaisas, P.; Marțiș, C.S. In-Depth Exploration of Design and Analysis for PM-Assisted Synchronous Reluctance Machines: Implications for Light Electric Vehicles. Machines 2024, 12, 361. [Google Scholar] [CrossRef]
- Xing, F.; Zhang, J.; Zhang, M.; Qin, C. Design and Multi-Objective Optimization of an Asymmetric-Rotor Permanent-Magnet-Assisted Synchronous Reluctance Motor for Improved Torque Performance. Appl. Sci. 2024, 14, 6734. [Google Scholar] [CrossRef]
- Huynh, T.-A.; Chen, P.-H.; Hsieh, M.-F. Analysis and Comparison of Operational Characteristics of Electric Vehicle Traction Units Combining Two Different Types of Motors. IEEE Trans. Veh. Technol. 2022, 71, 5727–5742. [Google Scholar] [CrossRef]
- Song, T.; Zhang, Z.; Liu, H.; Hu, W. Multi-objective optimisation design and performance comparison of permanent magnet synchronous motor for EVs based on FEA. IET Electr. Power Appl. 2019, 13, 1157–1166. [Google Scholar] [CrossRef]
- Zhao, J.; Han, Q.; Dai, Y.; Hua, M. Study on the Electromagnetic Design and Analysis of Axial Flux Permanent Magnet Synchronous Motors for Electric Vehicles. Energies 2019, 12, 3451. [Google Scholar] [CrossRef]
- Al-ani, M. Multi-physics design and analyses of dual rotor synchronous reluctance machine. eTransportation 2021, 8, 100113. [Google Scholar] [CrossRef]
- Luo, L.; Chang, J.; Wu, J.; Zhu, B.; Zheng, M.; Zhang, N. Design and Analysis of a Water-Cooling System in a New Yokeless and Segmented Armature Axial In-Wheel Motor for Electric Vehicles. J. Therm. Sci. Eng. Appl. 2021, 13, 051015. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, T.; Geng, W.; Guo, J.; Sun, Y. Cooling System Analysis of an Enclosed Yokeless Stator for High-Power Axial Flux PM Motor With Distributed Winding. IEEE Trans. Ind. Electron. 2024, 71, 2789–2799. [Google Scholar] [CrossRef]
- Ajamloo, A.M.; Ibrahim, M.N.; Sergeant, P. Design, Modelling and Optimization of a High Power Density Axial Flux SRM with Reduced Torque Ripple for Electric Vehicles. Machines 2023, 11, 759. [Google Scholar] [CrossRef]
- Özsoy, M.; Kaplan, O.; Akar, M. FEM-based analysis of rotor cage material and slot geometry on double air gap axial flux induction motors. Ain Shams Eng. J. 2024, 15, 102393. [Google Scholar] [CrossRef]
- Özsoy, M.; Kaplan, O.; Akar, M. The effect of stator slot number and pole number on motor performance in double-sided axial flux induction motors for electric vehicles. Electr. Eng. 2022, 104, 4289–4304. [Google Scholar] [CrossRef]
- Gai, Y.; Kimiabeigi, M.; Chuan Chong, Y.; Widmer, J.D.; Deng, X.; Popescu, M.; Goss, J.; Staton, D.A.; Steven, A. Cooling of Automotive Traction Motors: Schemes, Examples, and Computation Methods. IEEE Trans. Ind. Electron. 2019, 66, 1681–1692. [Google Scholar] [CrossRef]
- Eser, E.; Üstkoyuncu, N. Effects of Permanent Magnets on Different Flux Barriers for the AF-SynRMs. Electr. Power Compon. Syst. 2024, 52, 1936–1945. [Google Scholar] [CrossRef]
- Geng, W.; Wang, J.; Fu, Y.; Guo, J.; Li, W. Design and Performance Analysis of a Novel Axial-flux IPM Machine for Electric Vehicles. IEEE Trans. Transp. Electrif. 2024, 1, 5569–5577. [Google Scholar] [CrossRef]
- Kwon, M.-S.; Lim, D.-K. A Study on the Optimal Design of PMa-SynRM for Electric Vehicles Combining Random Forest and Genetic Algorithm. IEEE Access 2023, 11, 52357–52369. [Google Scholar] [CrossRef]
- Song, T.; Liu, H.; Zhang, Q.; Zhang, Z. Multi-physics and multi-objective optimisation design of interior permanent magnet synchronous motor for electric vehicles. IET Electr. Power Appl. 2020, 14, 2243–2254. [Google Scholar] [CrossRef]
- Wi, C.-H.; Kim, J.-Y.; Choi, J.-W.; Yeo, H.-K.; Lim, D.-K. Optimal Design of PMa-SynRM for Electric Vehicles Using Grain-Oriented Electrical Steel and Surrogate Model Based on Stacking Ensemble. J. Electr. Eng. Technol. 2023, 18, 991–1001. [Google Scholar] [CrossRef]
- Gedara, H. Design Optimization and Performance Improvement of Synchronous Reluctance Machines. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2019. [Google Scholar]
- Özsoy, M. Elektrikli Araçlar için Eksenel Akılı Asenkron Motor Tasarımı, Mekanik ve Isıl Analizi. Ph.D. Thesis, Gazi University, Ankara, Turkey, 2023. [Google Scholar]
- Grace, K.; Galioto, S.; Bodla, K.; El-Refaie, A.M. Design and Testing of a Carbon-Fiber-Wrapped Synchronous Reluctance Traction Motor. IEEE Trans. Ind. Appl. 2018, 54, 4207–4217. [Google Scholar] [CrossRef]
- Madhavan, S.; Raunak Devdatta, P.B.; Gundabattini, E.; Mystkowski, A. Thermal Analysis and Heat Management Strategies for an Induction Motor, a Review. Energies 2022, 15, 8127. [Google Scholar] [CrossRef]
- Roy, R.; Ramasami, S.; Chokkalingam, L.N. Review on Thermal Behavior and Cooling Aspects of Axial Flux Permanent Magnet Motors–A Mechanical Approach. IEEE Access 2023, 11, 6822–6836. [Google Scholar] [CrossRef]
- Konda, Y.R.; Ponnaganti, V.K.; Reddy, P.V.S.; Singh, R.R.; Mercorelli, P.; Gundabattini, E.; Solomon, D.G. Thermal Analysis and Cooling Strategies of High-Efficiency Three-Phase Squirrel-Cage Induction Motors—A Review. Computation 2024, 12, 6. [Google Scholar] [CrossRef]
- IEC 60034-1; Rotating Electrical Machines—Part 11: Thermal Protection. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2020.
- Sun, Y.; Zhang, S.; Chen, G.; Tang, Y.; Liang, F. Experimental and numerical investigation on a novel heat pipe based cooling strategy for permanent magnet synchronous motors. Appl. Therm. Eng. 2020, 170, 114970. [Google Scholar] [CrossRef]
- Avsar, Y.; Fenercioglu, A.; Soyaslan, M. Design Optimization of PM Synchronous Motor: Rail Mounted Belt Drive Elevator Systems. IEEE Trans. Ind. Appl. 2023, 60, 301–311. [Google Scholar] [CrossRef]

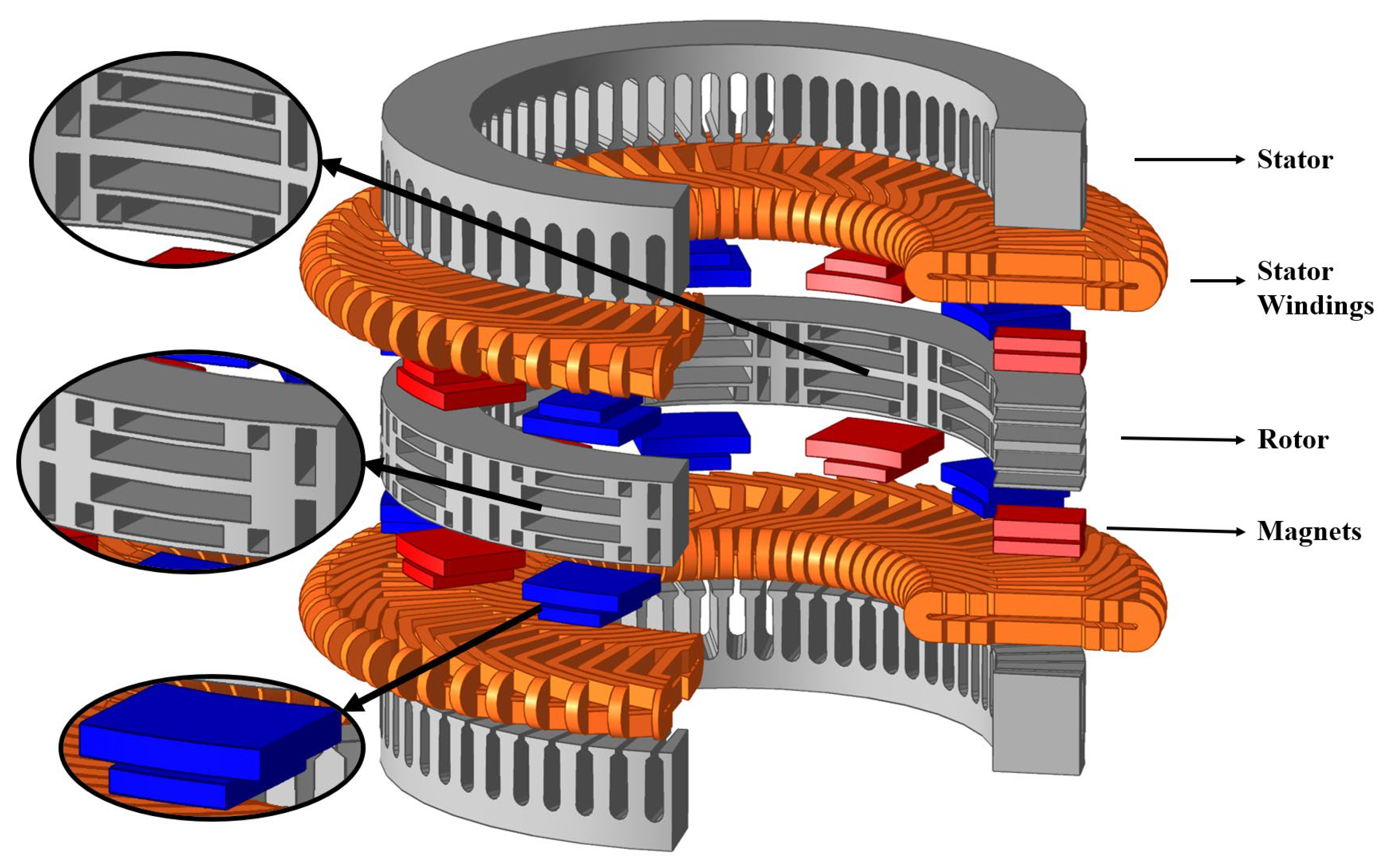
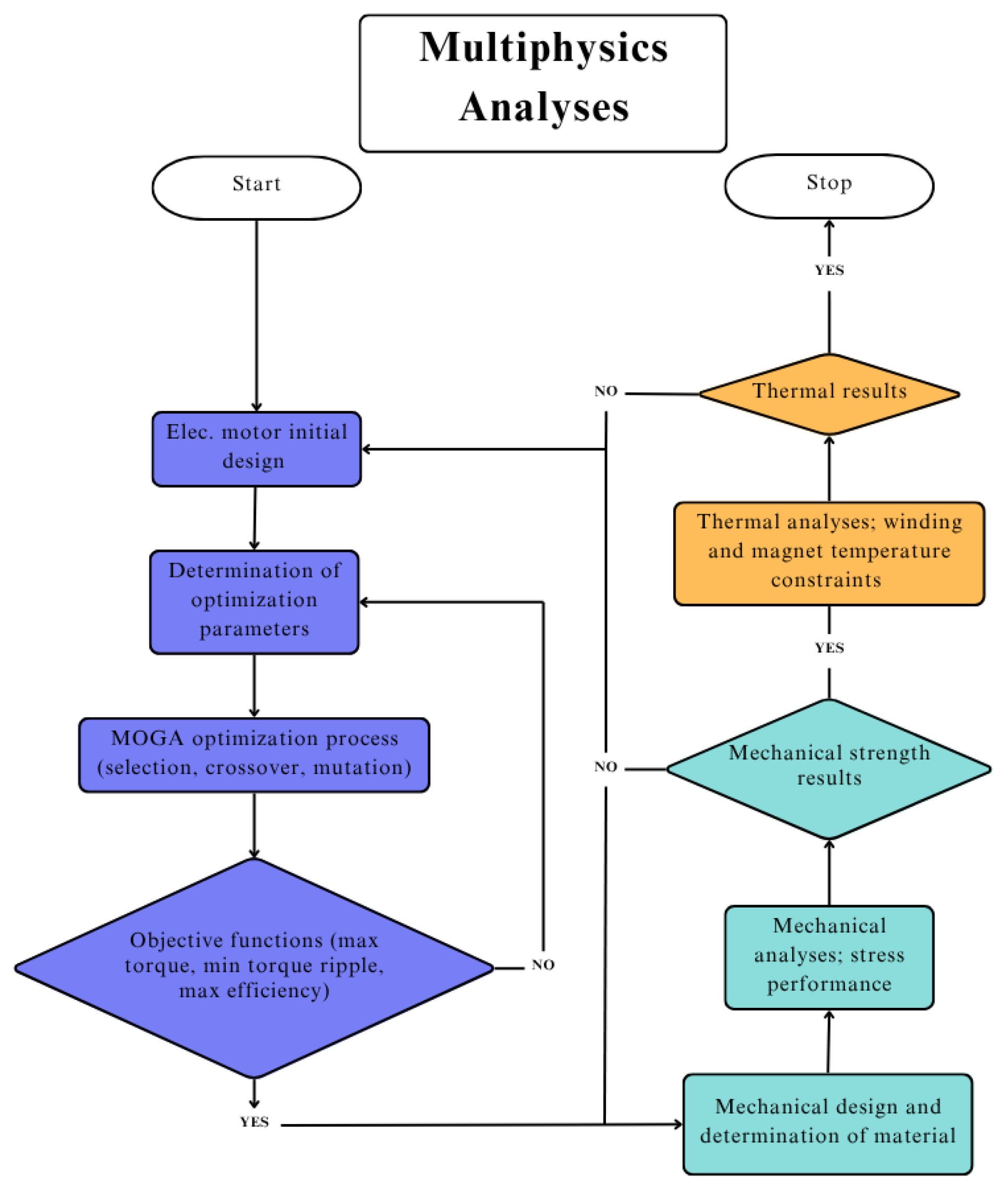
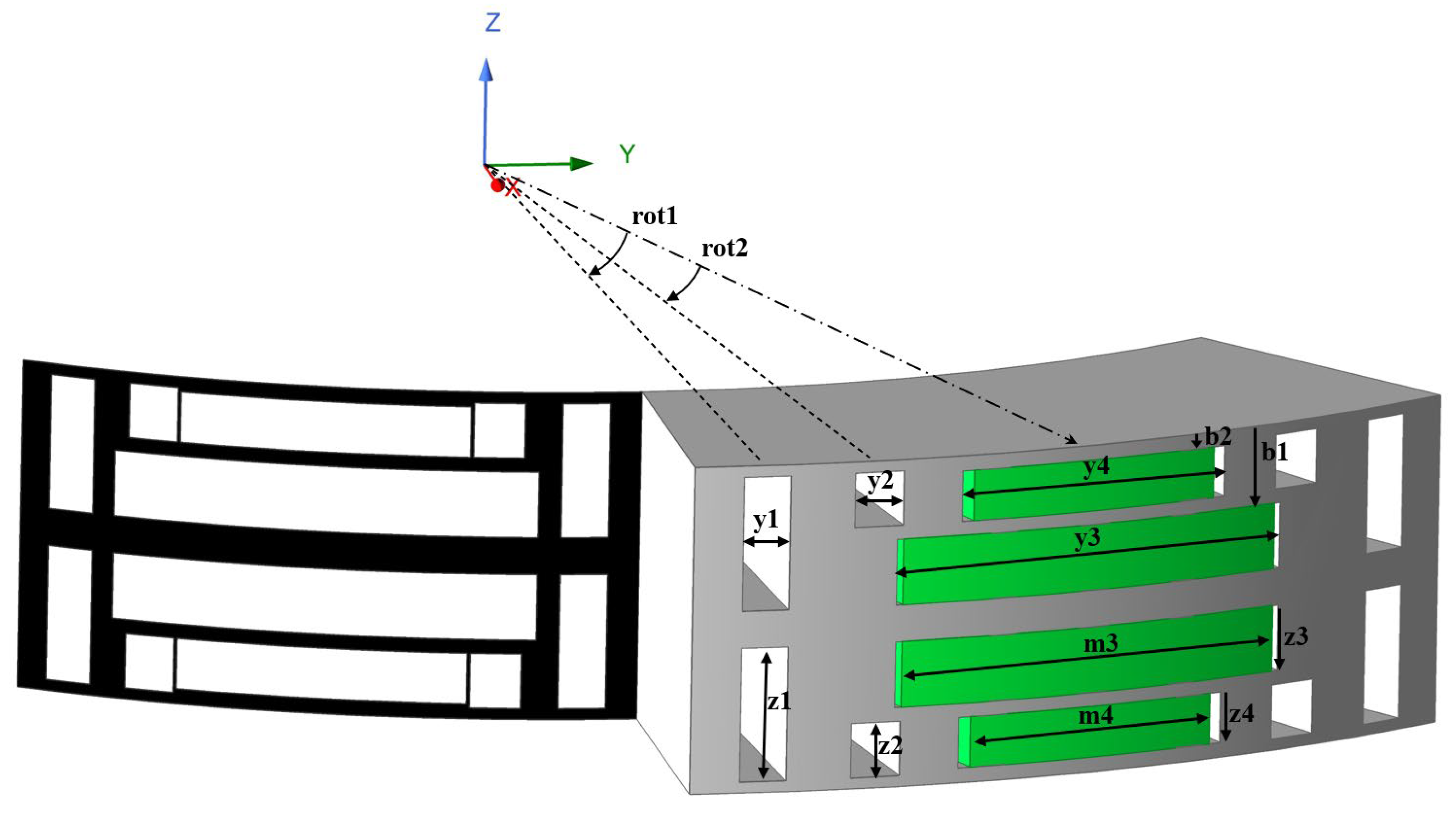
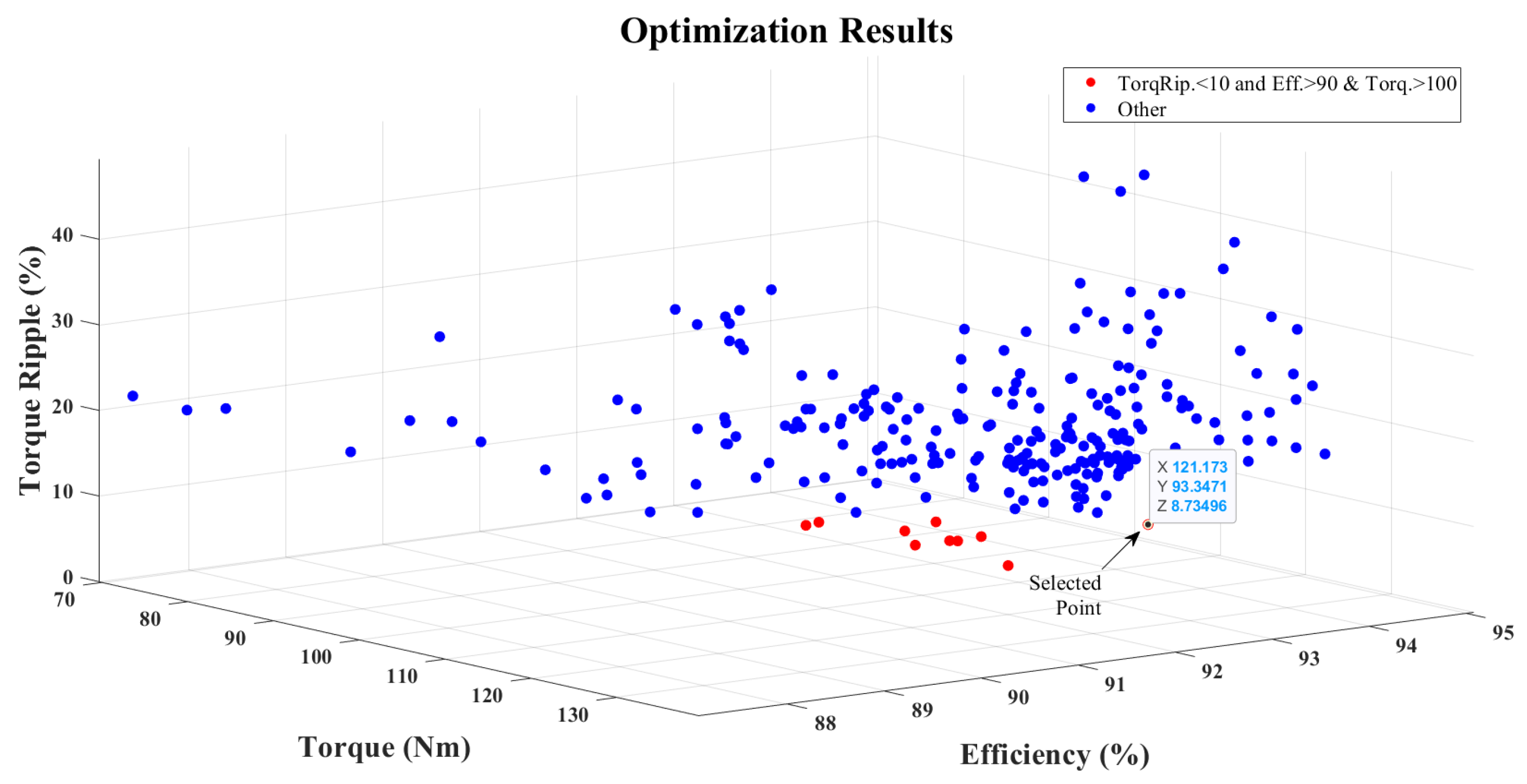
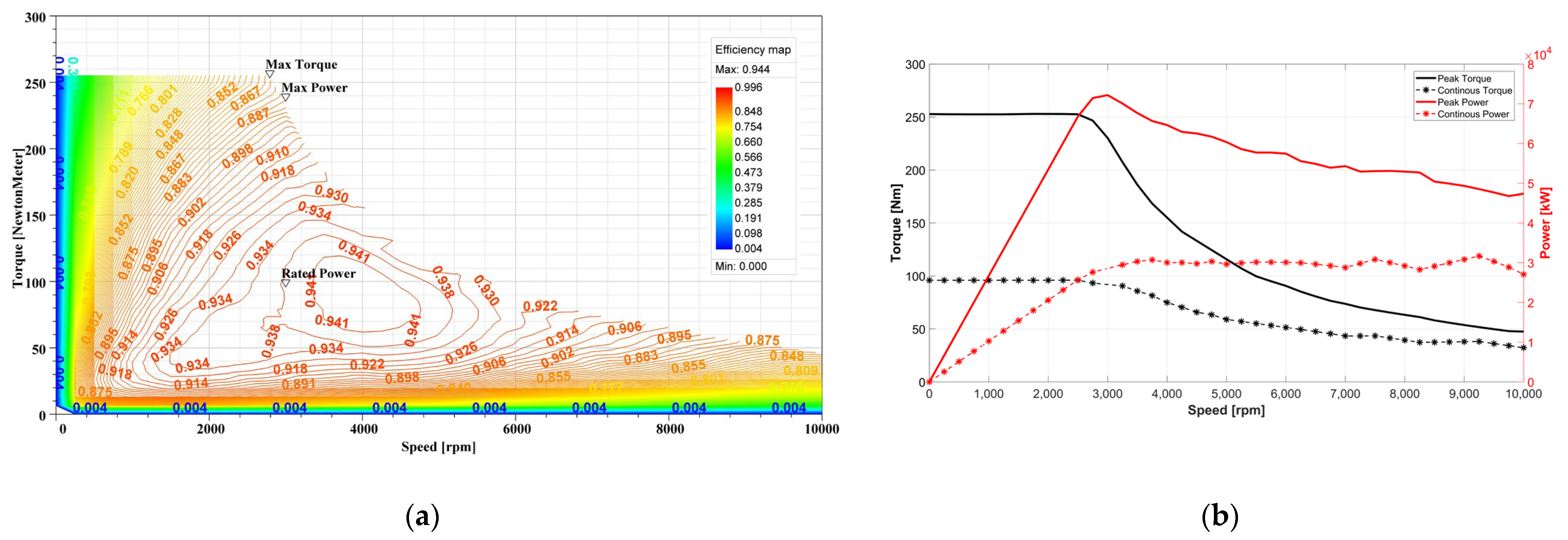

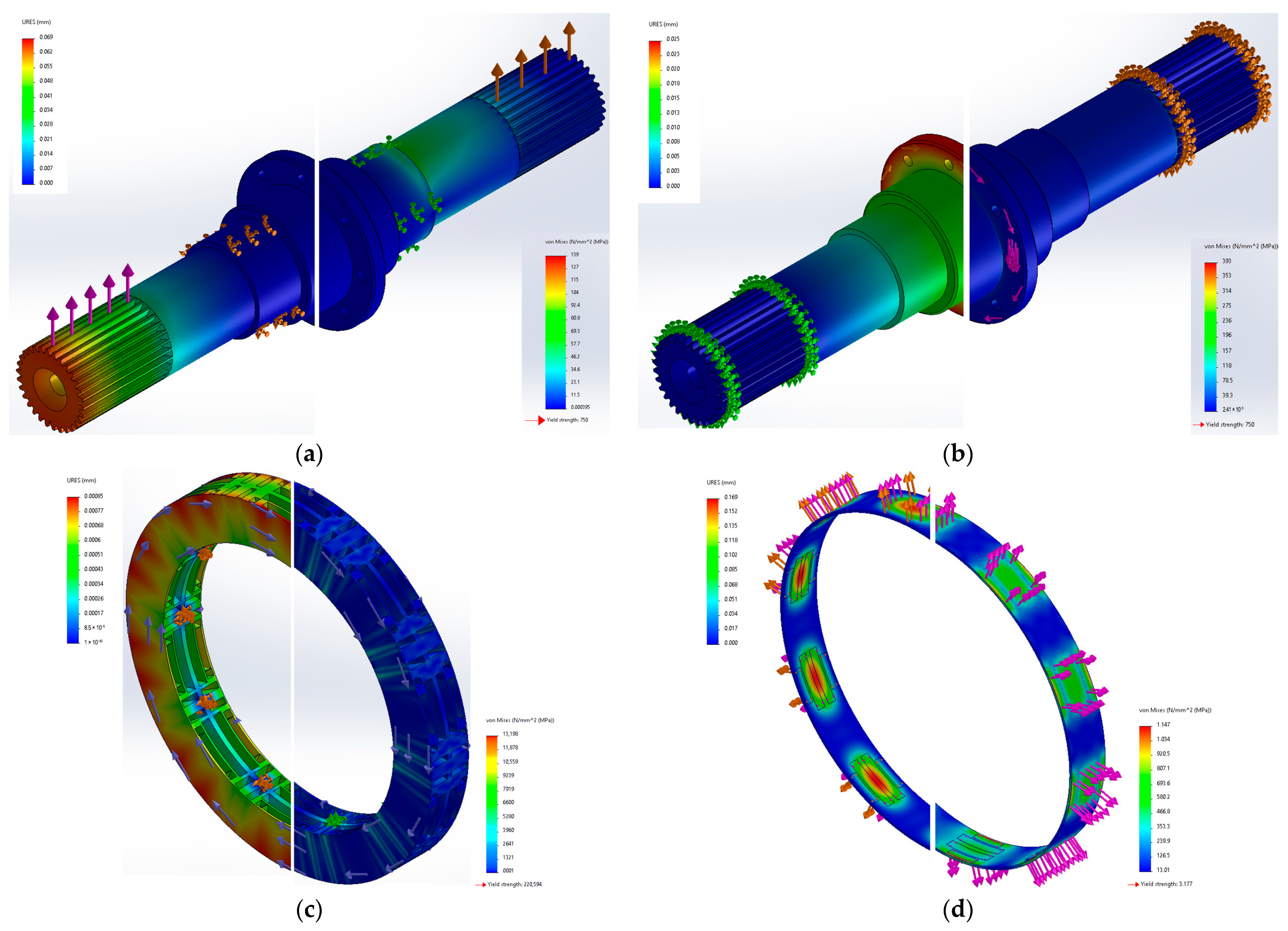
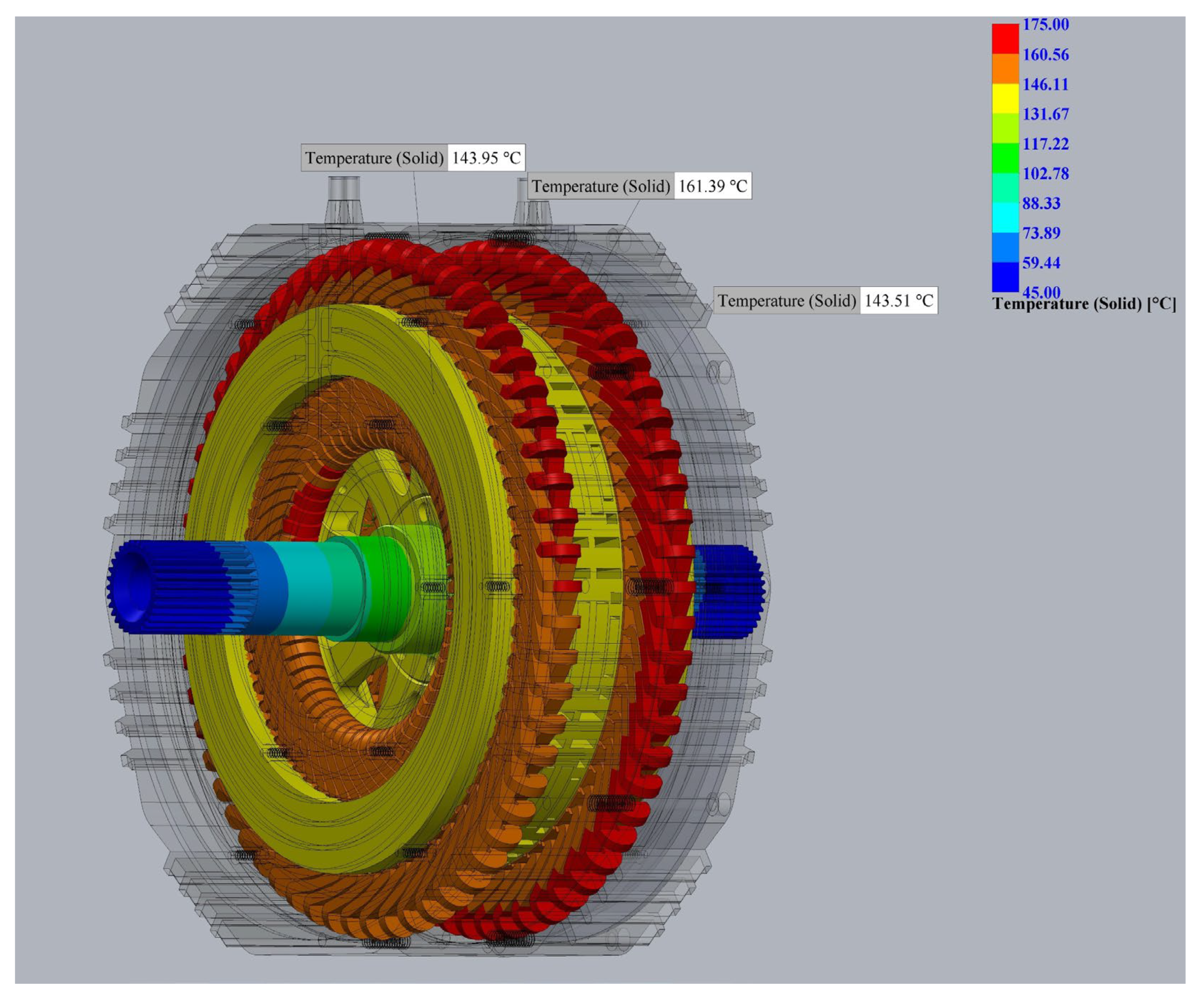
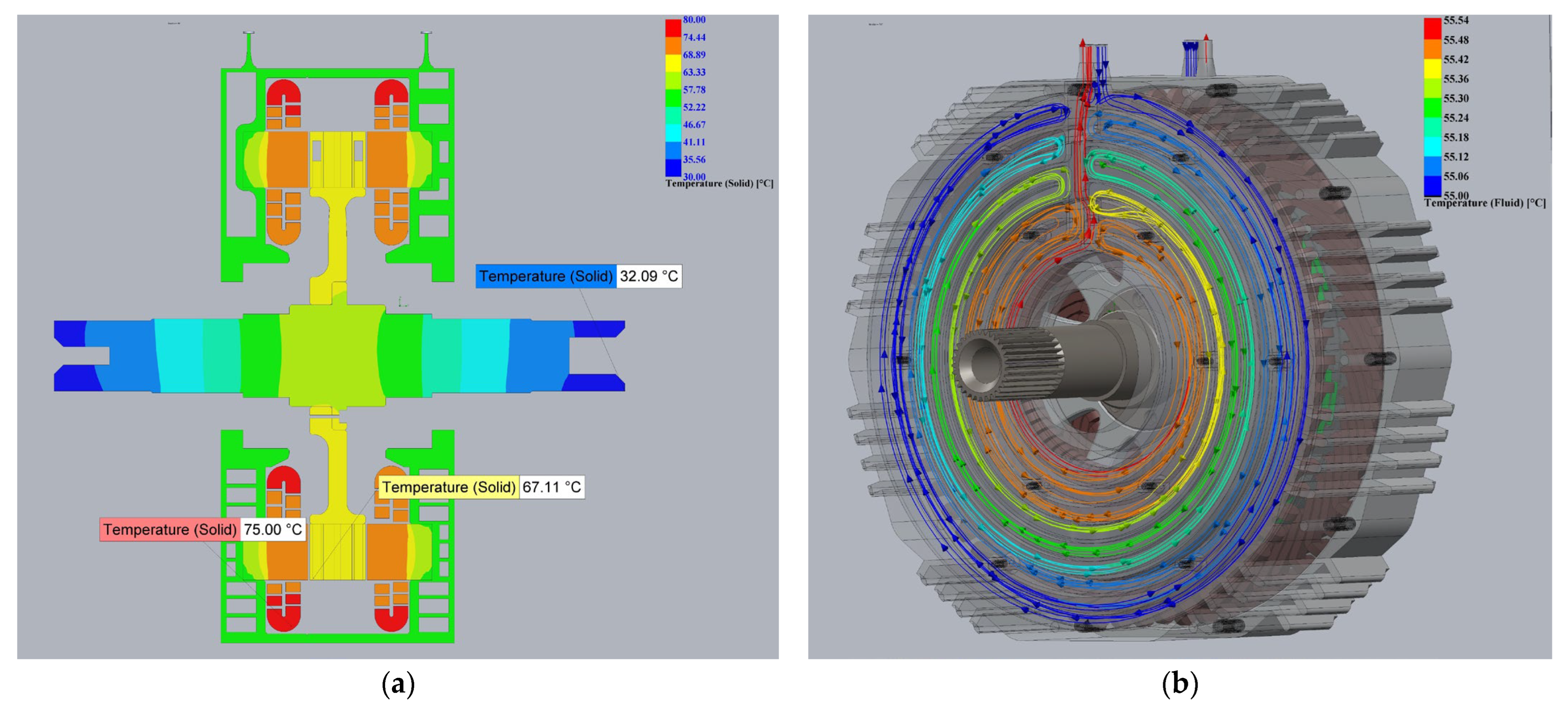

| Parameters | Value |
|---|---|
| Poles/Slot | 10/60 |
| Outer Diameter (mm)/Inner Diameter (mm) | 242/181.5 |
| Stator Axial Length (mm)/Rotor Axial Length (mm) | 35 × 2/30 |
| Airgap Length (mm) | 1 |
| Rated Speed (rpm)/Peak Speed (rpm) | 3000/10,000 |
| Rated Power (kW)/Peak Power (kW) | 30/65 |
| Rated Torque (Nm)/Peak Torque (Nm) | 95/253 |
| Rated Phase Current (Arms)/Peak Phase Current (Arms) | 81.3/200 |
| Stator Material (Laminated)/Rotor Material (Laminated) | JFE_Steel_35JN230 |
| Lamination Stacking Factor | 0.97 |
| Stator Weight (kg)/Rotor Weight (kg) | 6.76/2.26 |
| Magnets | N42SH |
| Magnet 1 (Bottom Barrier) Weight (kg)/Magnet 2 (Top Barrier) Weight (kg) | 0.0517/0.0257 |
| Stator Windings Material | Copper |
| Stator Windings Material Weight (kg) | 9.64 |
| Parameters | Initial Value | Minimum Limit | Maximum Limit | Optimized Value |
|---|---|---|---|---|
| b1 (mm) | 7.5 | 7 | 7.9 | 7.281709009 |
| b2 (mm) | 1.5 | 1 | 2 | 1.359964308 |
| y1 (mm) | 6.2 | 4 | 7 | 4.273731954 |
| y2 (mm) | 3.2 | 3 | 5 | 4.578323399 |
| y3 (mm) | 40 | 30 | 46 | 38.40619239 |
| y4 (mm) | 25 | 20 | 30 | 26.29369015 |
| m3 (mm) | 37 | 25 | 45 | 37.17054926 |
| m4 (mm) | 22 | 15 | 29 | 24.01390593 |
| z3 (mm) | 7 | 5 | 7 | 6.027811951 |
| z4 (mm) | 4 | 3 | 4.9 | 4.654978277 |
| rot1 (degree °) | 14.5 | 14 | 15 | 14.853 |
| rot2 (degree °) | 9.5 | 9 | 10 | 9.94377551 |
| Model | Volume (m3) | Losses W/m3 | ||||
|---|---|---|---|---|---|---|
| 30 kW | 40 kW | 50 kW | 60 kW | 65 kW | ||
| Stator | 8.8862 × 10−4 | 82,625.42 | 94,553.92 | 115,899.93 | 131,152.8 | 138,735.34 |
| Rotor | 2.9702 × 10−4 | 5630.02 | 8885.33 | 10,877.15 | 13,001.78 | 13,898.73 |
| Winding | 8.9461 × 10−6 | 690,053.77 | 1283,911.43 | 2,137,635.39 | 3,474,989.1 | 4,280,021.46 |
| Magnet 1 | 6.8132 × 10−5 | 1210.71 | 1088.1 | 2095.99 | 5540.33 | 7558.55 |
| Magnet 2 | 3.3885 × 10−5 | 3575.83 | 5205.73 | 5382.38 | 6021.31 | 6829.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gözüaçık, E.; Akar, M. Multi-Physics and Multi-Objective Design of an Axial Flux Permanent Magnet-Assisted Synchronous Reluctance Motor for Use in Electric Vehicles. Machines 2025, 13, 555. https://doi.org/10.3390/machines13070555
Gözüaçık E, Akar M. Multi-Physics and Multi-Objective Design of an Axial Flux Permanent Magnet-Assisted Synchronous Reluctance Motor for Use in Electric Vehicles. Machines. 2025; 13(7):555. https://doi.org/10.3390/machines13070555
Chicago/Turabian StyleGözüaçık, Emre, and Mehmet Akar. 2025. "Multi-Physics and Multi-Objective Design of an Axial Flux Permanent Magnet-Assisted Synchronous Reluctance Motor for Use in Electric Vehicles" Machines 13, no. 7: 555. https://doi.org/10.3390/machines13070555
APA StyleGözüaçık, E., & Akar, M. (2025). Multi-Physics and Multi-Objective Design of an Axial Flux Permanent Magnet-Assisted Synchronous Reluctance Motor for Use in Electric Vehicles. Machines, 13(7), 555. https://doi.org/10.3390/machines13070555








