Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Based on Multi-Sensor Information Fusion
Abstract
1. Introduction
- (1)
- It proposes a signal processing method based on MSSDP. The method effectively integrates signals from multiple sensors, providing more comprehensive and richer fault feature information for fault diagnosis. Importantly, it preserves the shape and characteristics of the signals while suppressing the impact of noise.
- (2)
- An adaptive parameter optimization method is proposed. This method of adaptive optimization for the parameters of MSSDP, amplifying the differences between structural fault signals in rotating machinery. It enhances fault features and effectively addresses the difficulty of manually selecting parameters, ensuring more precise and reliable fault diagnosis.
- (3)
- The paper establishes a novel fault diagnosis framework for rotating machinery structures. This framework leverages the ResNet18 neural network to extract and analyze MSSDP feature information. It constructs a robust fault diagnosis model capable of accurately identifying and classifying faults in complex machinery systems.
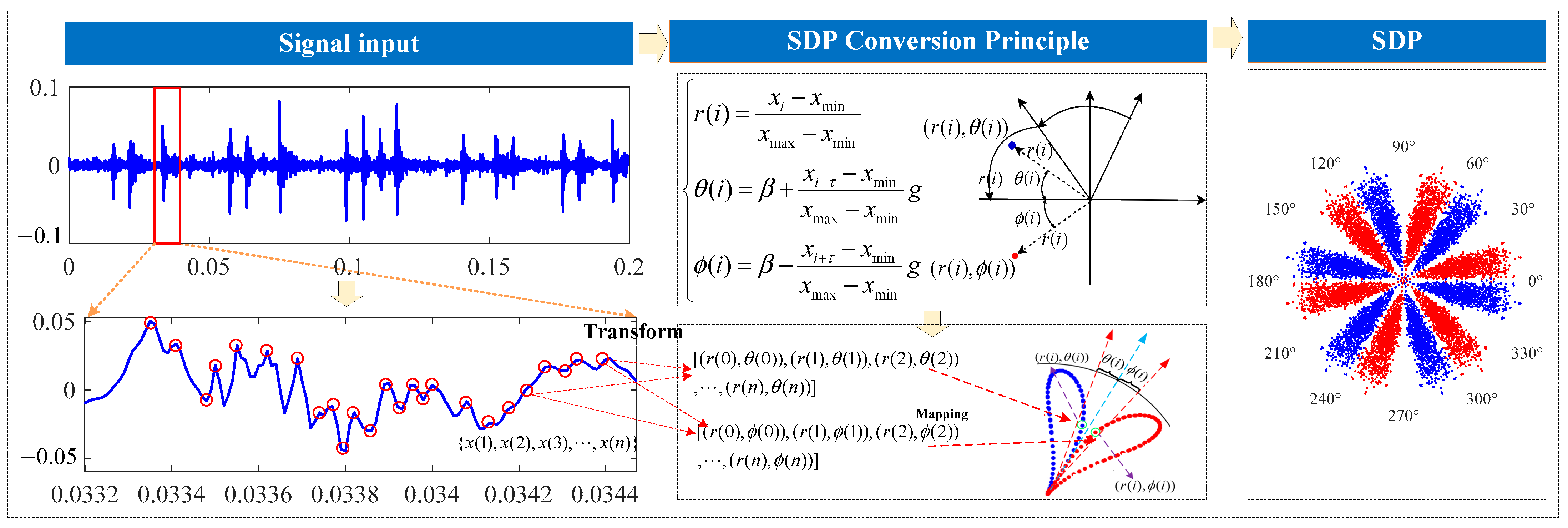
2. Multi-Sensor Savitzky–Golay Symmetric Dot Pattern
2.1. SDP Signal Transformation Method
2.2. Savitzky–Golay Filtering
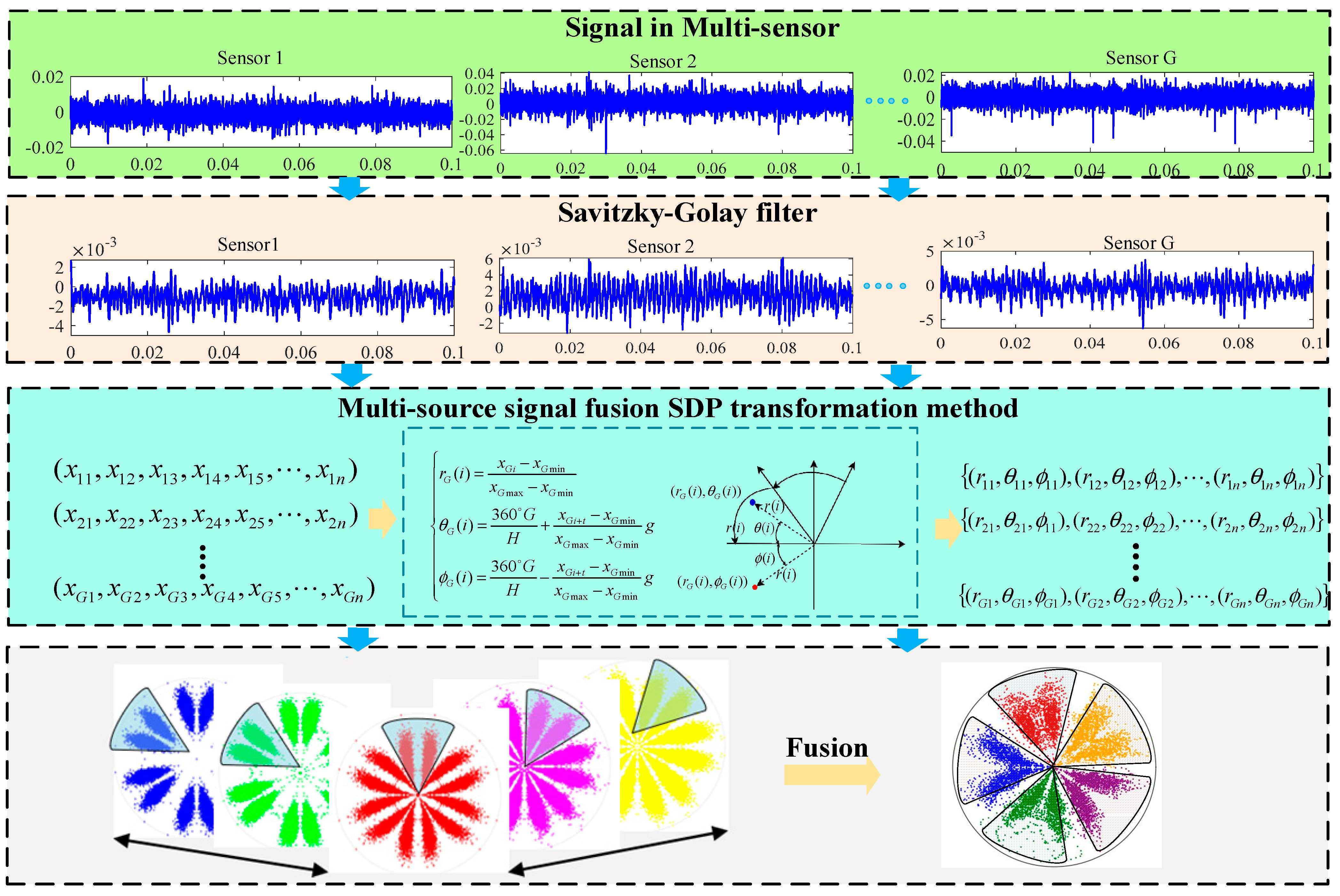
2.3. Multi-Sensor Signal Fusion SDP Signal Transformation Method
2.4. Multi-Sensor Savitzky–Golay Symmetric Dot Pattern Signal Transformation Method
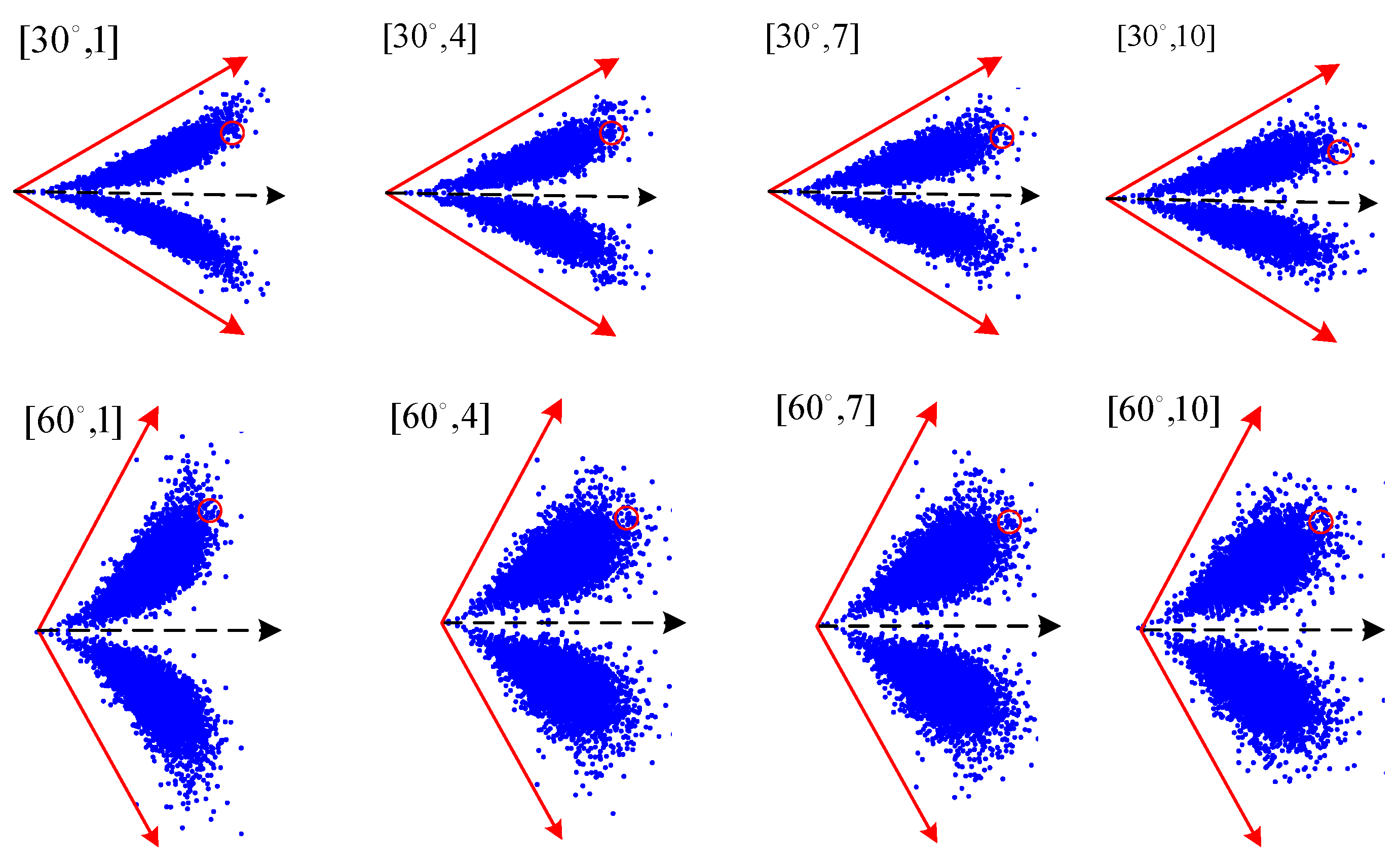
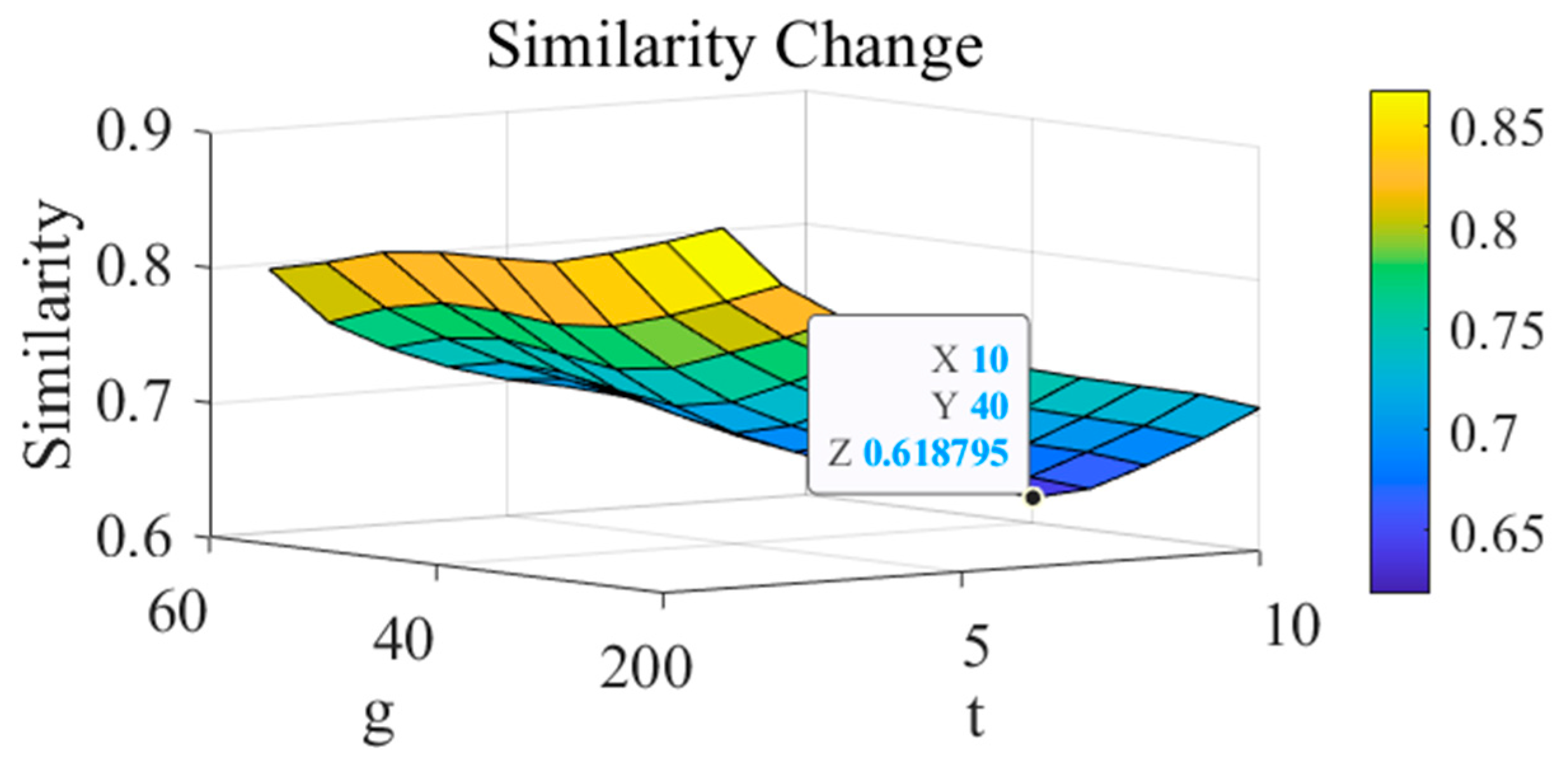
3. Adaptive Parameter Optimization Method
| Algorithm 1: Pseudo-Code Based on Adaptive Parameter Optimization Algorithm |
 |
4. Feature Extraction Method
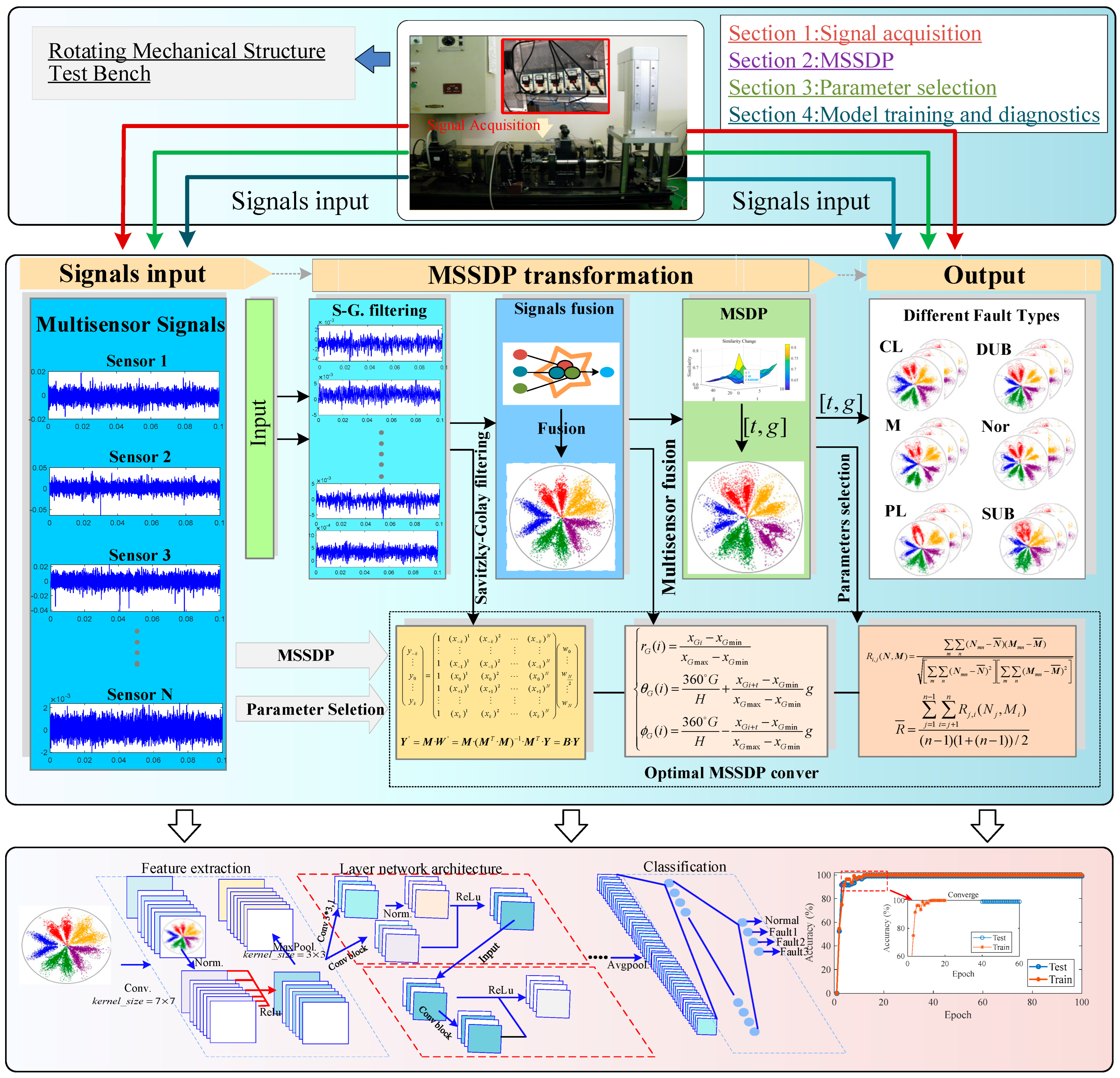
5. Proposed Method
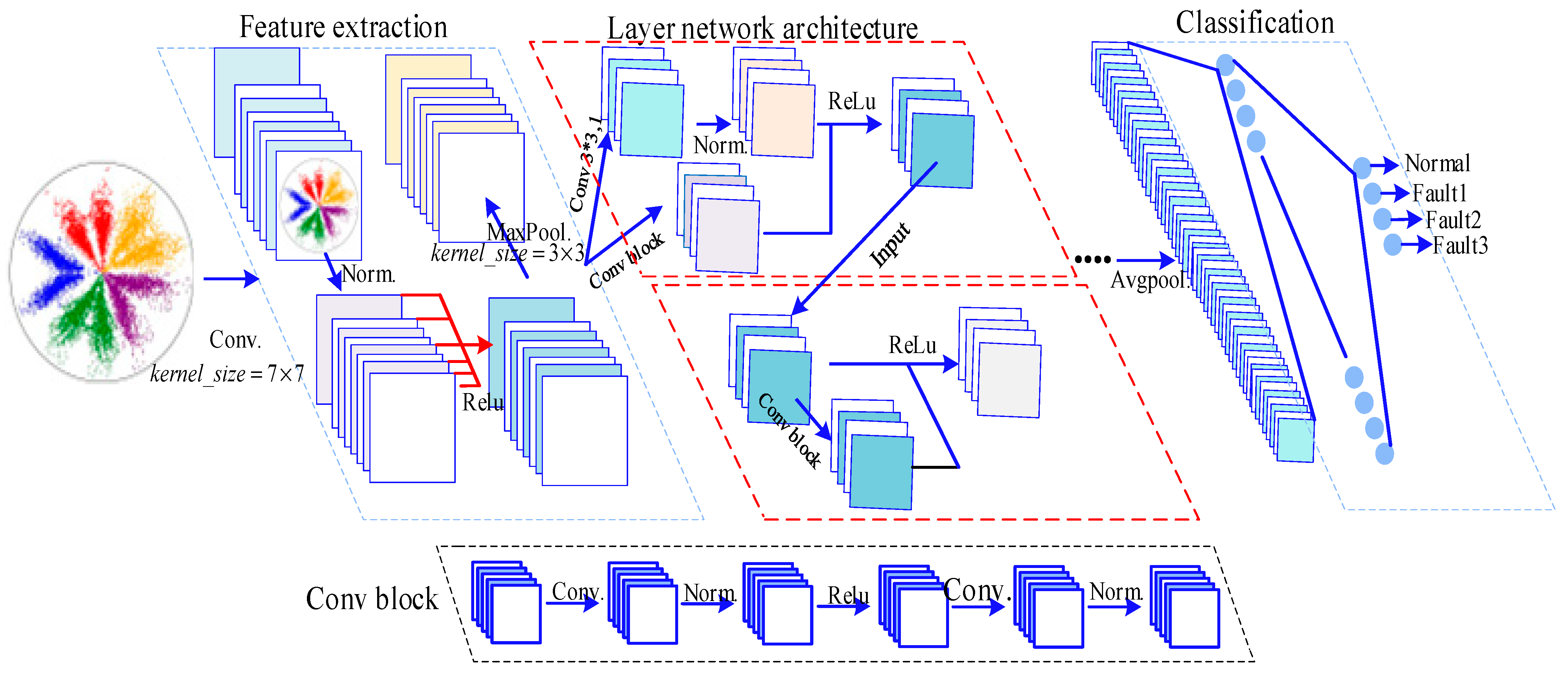
5.1. Resnet18 Neural Network
5.2. Proposed Method Architecture
- (1)
- Use a multi-channel acquisition device to collect signals from different parts of the rotating machinery structure, such as the right vertical, axial, and left vertical positions of the mechanical structure.
- (2)
- The collected signals are segmented into samples, and the MSSDP transformation method is used to obtain MSSDP two-dimensional polar coordinate images.
- (3)
- Use the adaptive optimization algorithm 1 to optimize the parameters of MSSDP for different fault types, obtaining the optimal parameters.
- (4)
- Input the optimal parameters to obtain the optimal MSSDP two-dimensional image.
- (5)
- Divide the samples into training and testing sets and build the ResNet18 fault diagnosis model.
- (6)
- Train the fault diagnosis model using ResNet18 on the training set and use the resulting fault diagnosis model to verify faults on the testing set.
6. Experimental Verification
6.1. Case1
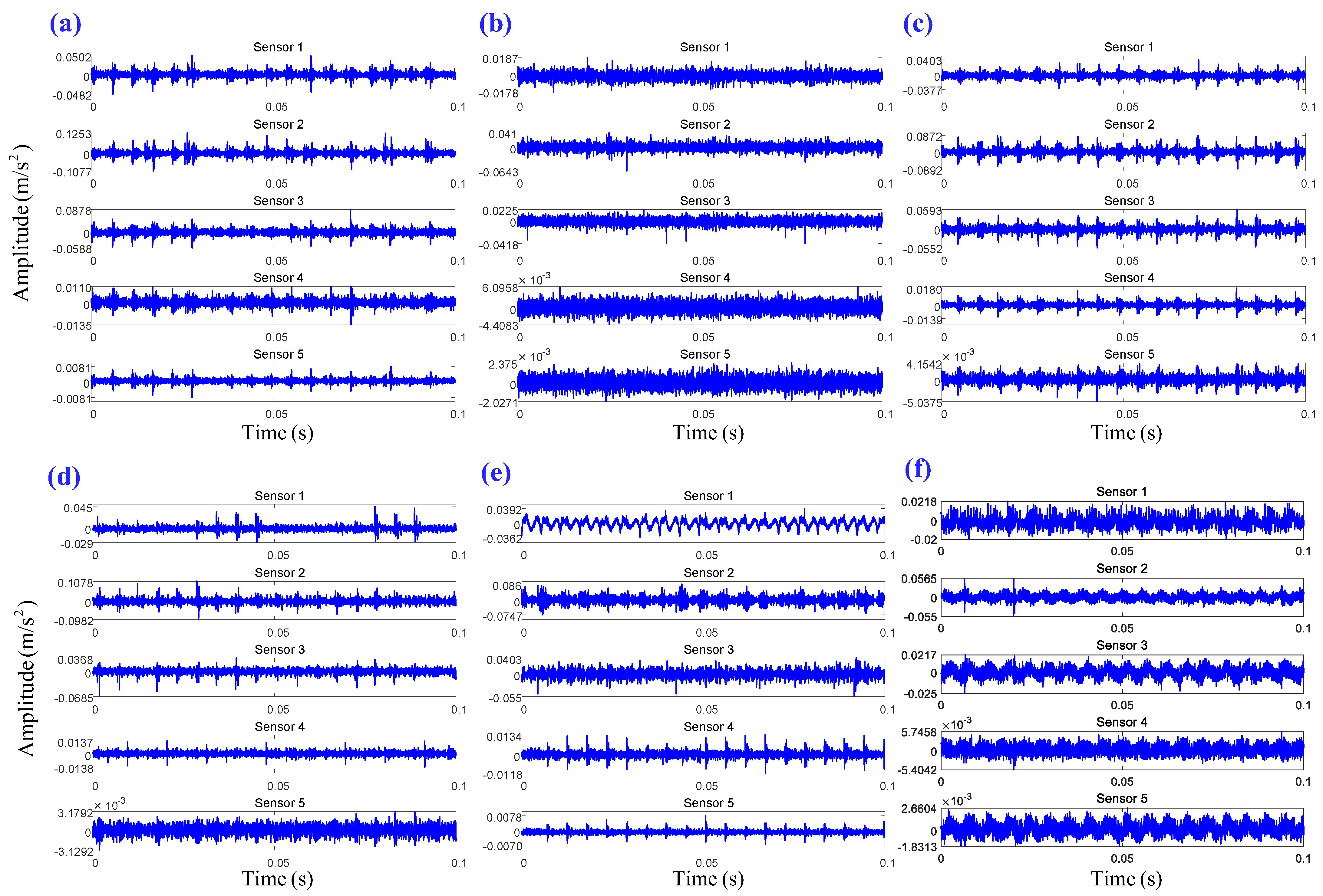
6.1.1. Signal Description and Processing
6.1.2. Parameter Selection and Feature Extraction Method
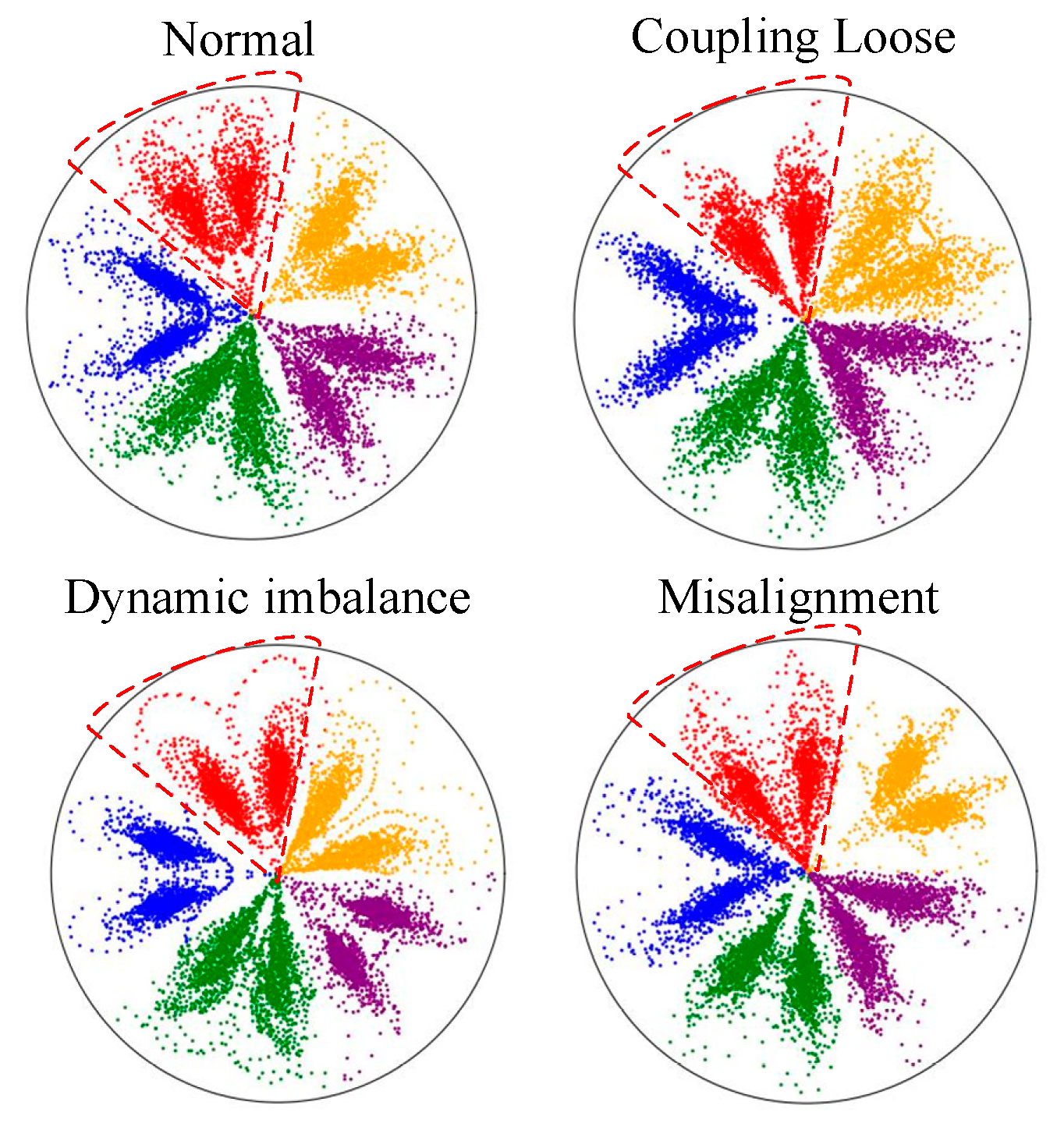
6.1.3. Diagnostic Results
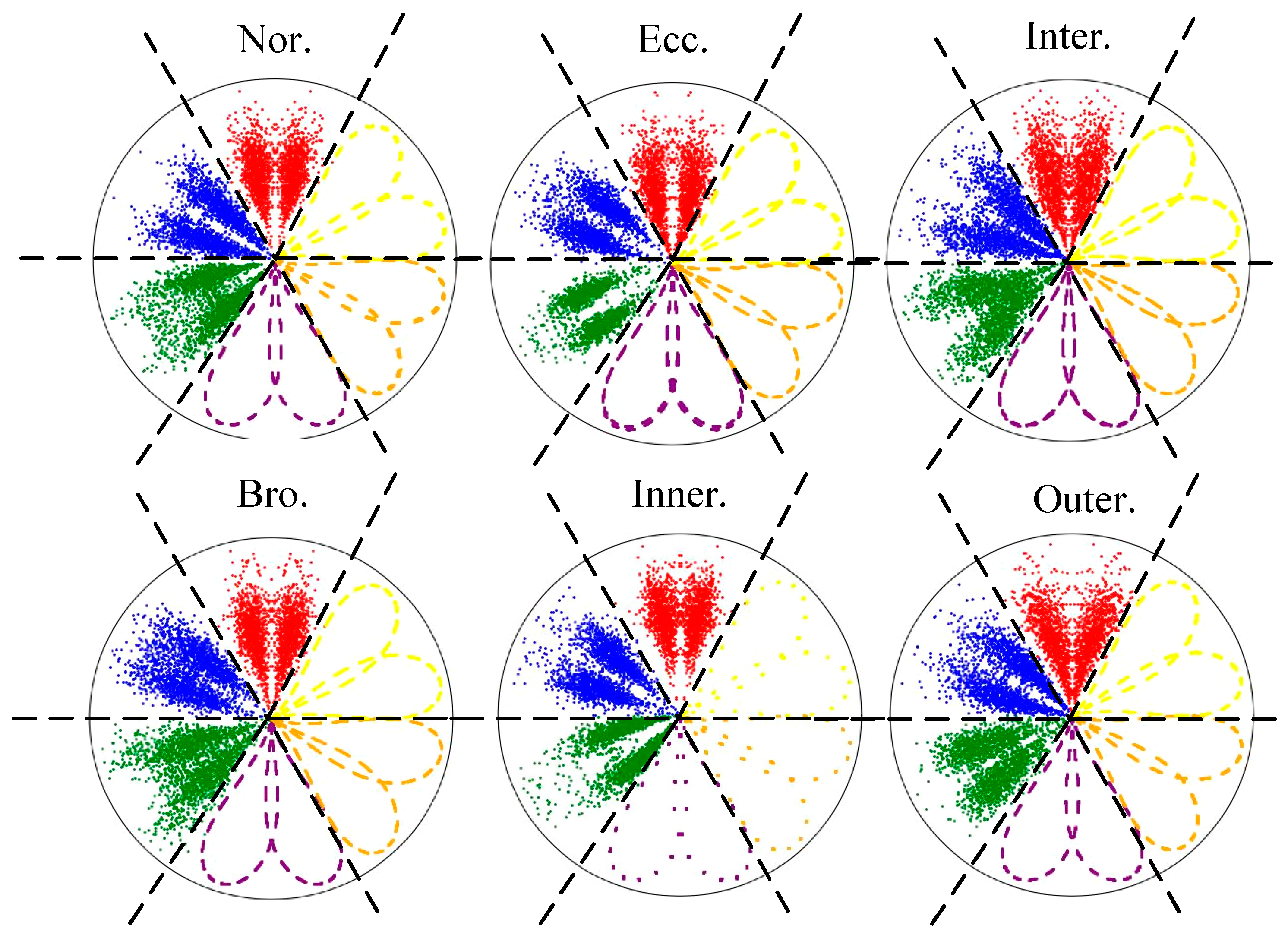
6.2. Case2
6.2.1. Signal Description and Processing
6.2.2. Parameter Selection and Feature Extraction Method
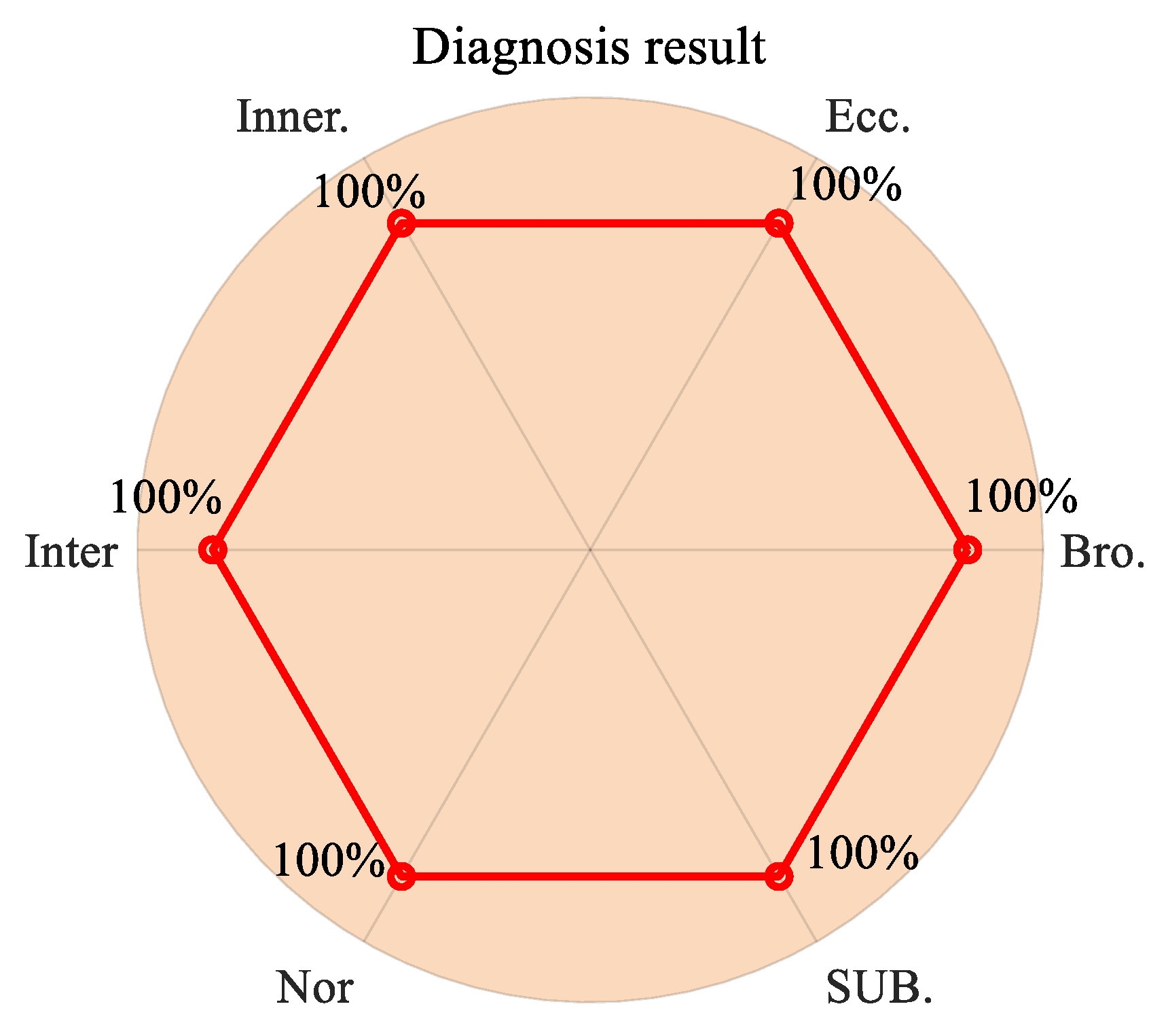
6.2.3. Diagnostic Results
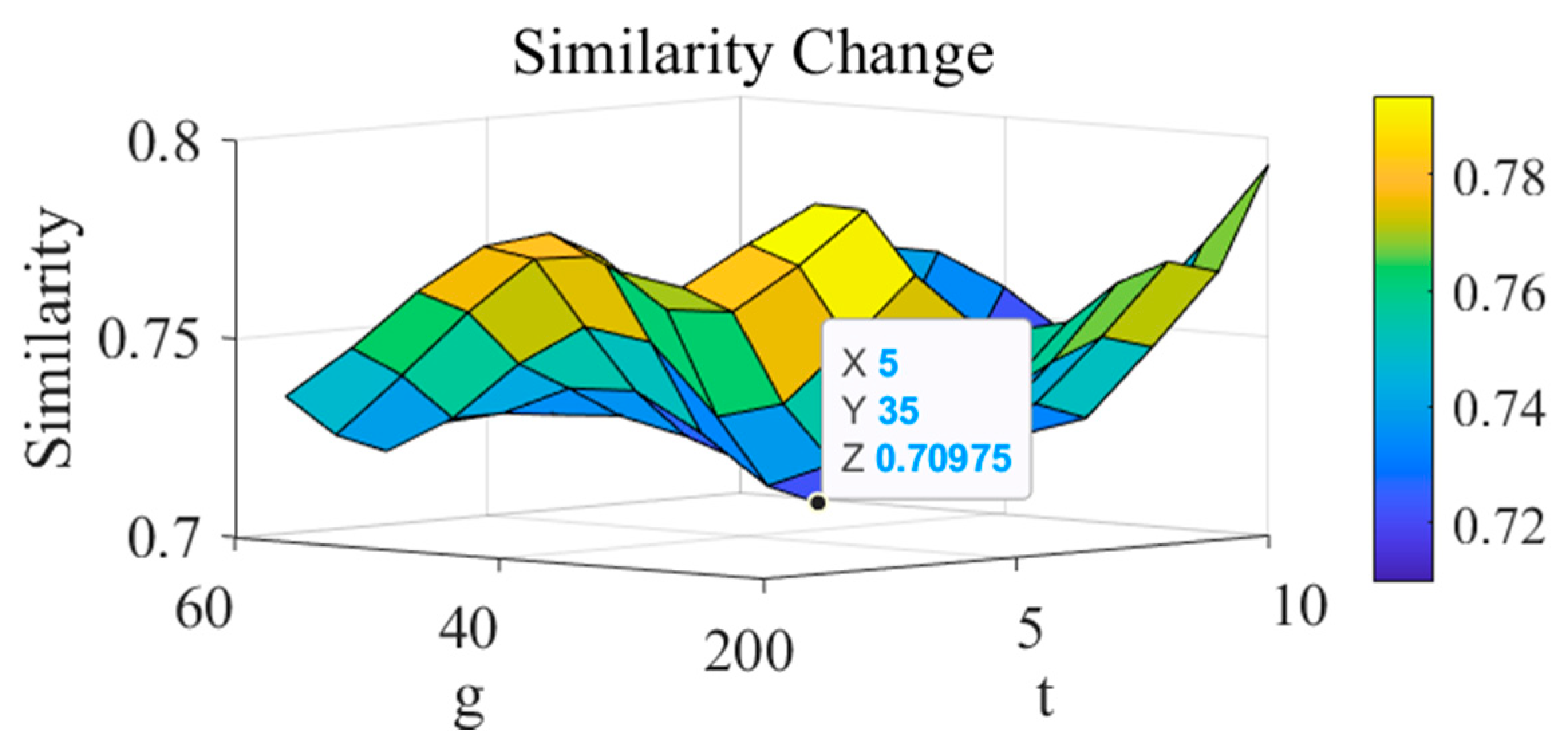
6.3. Parameter Sensitivity Analysis
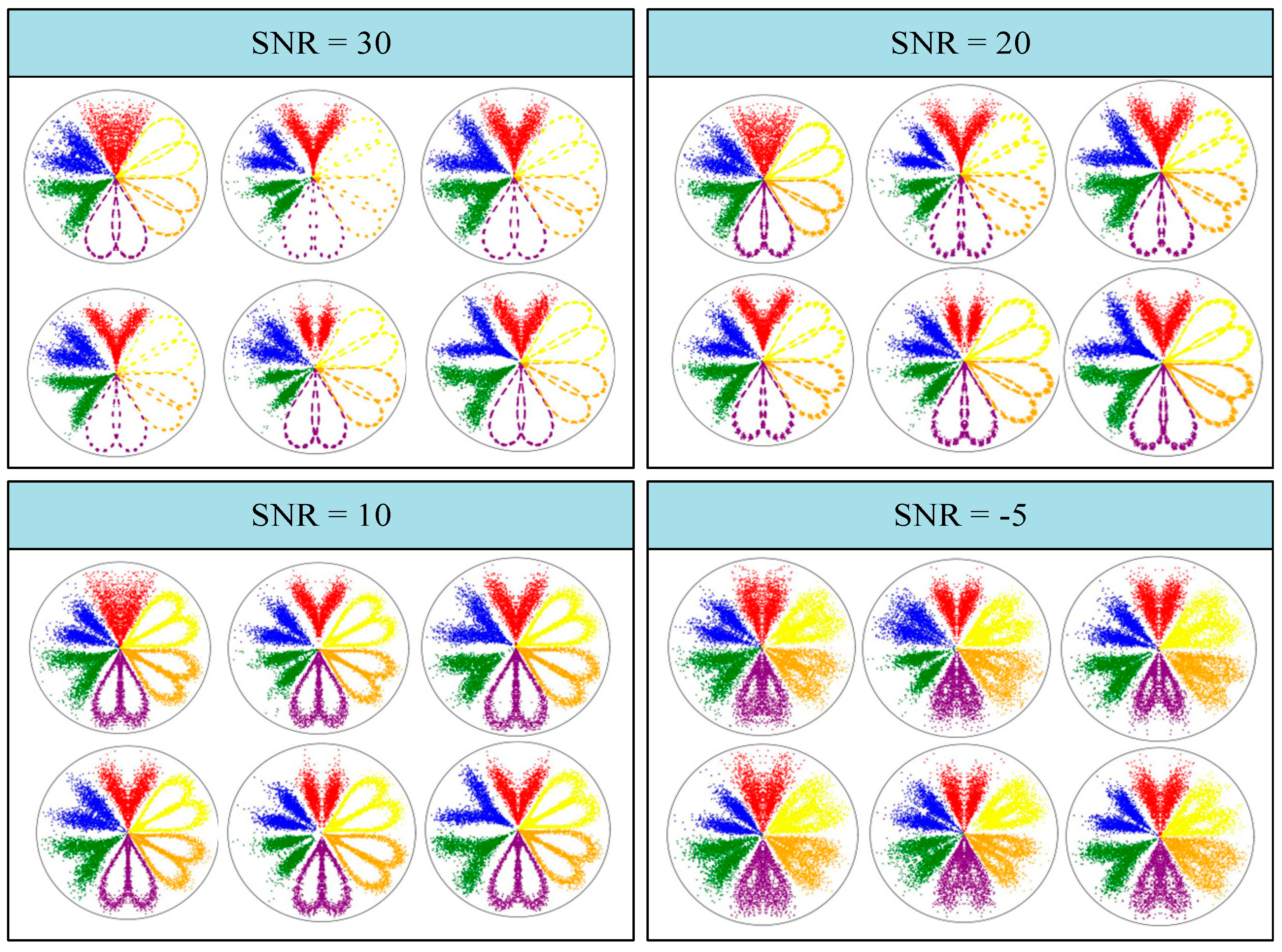
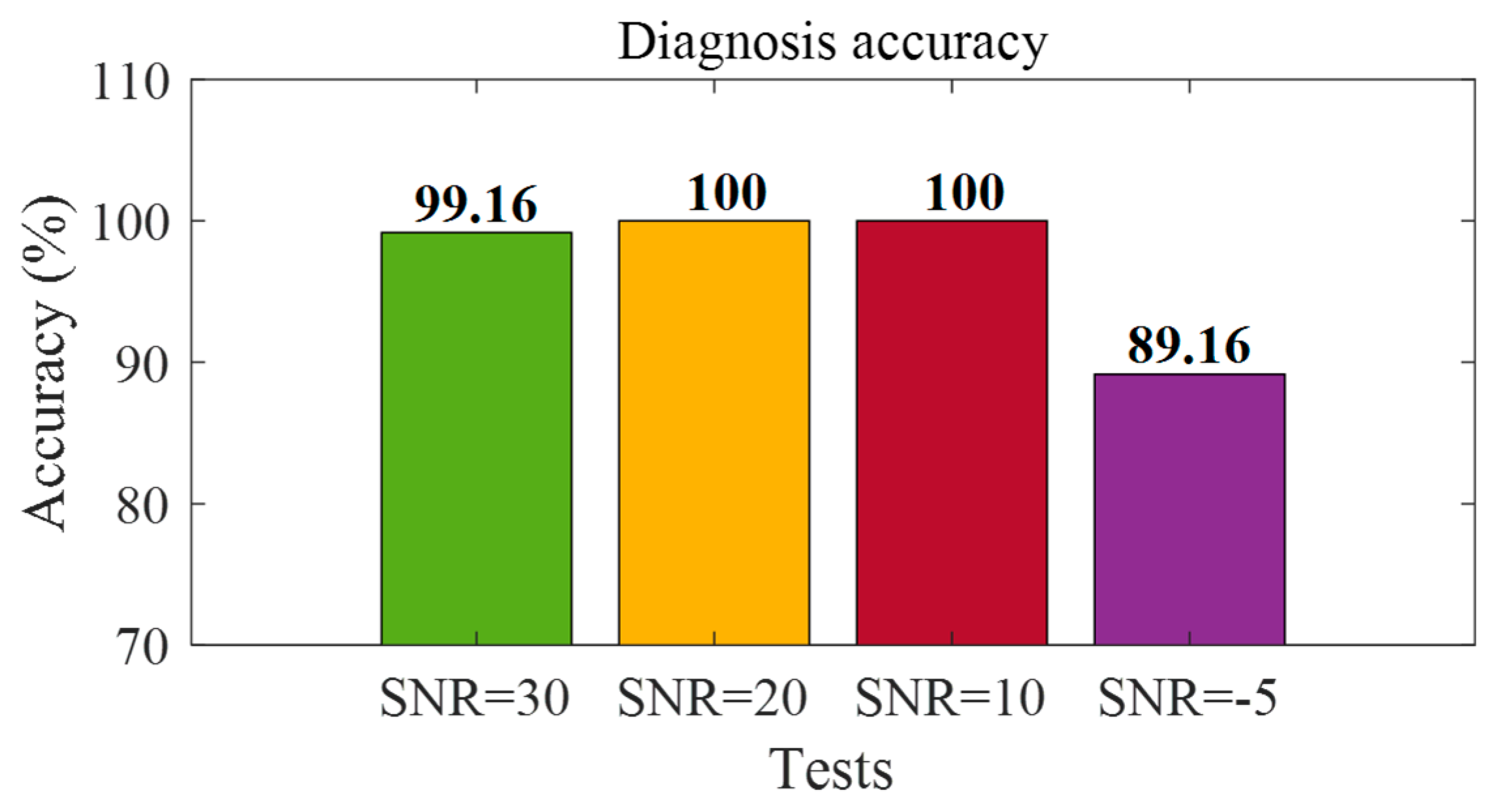
6.4. Noise Adaptability Experiment
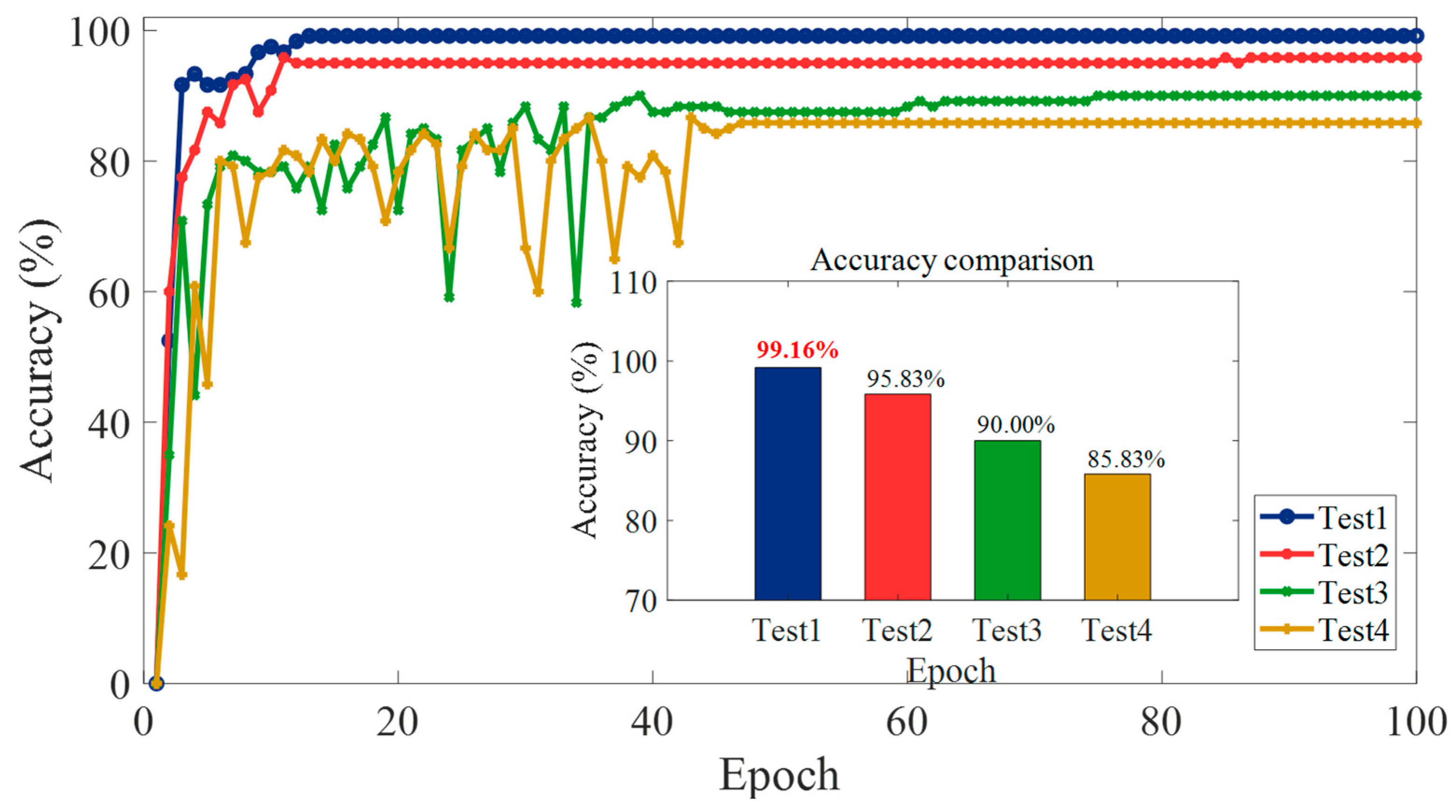
6.5. Ablation Experiments
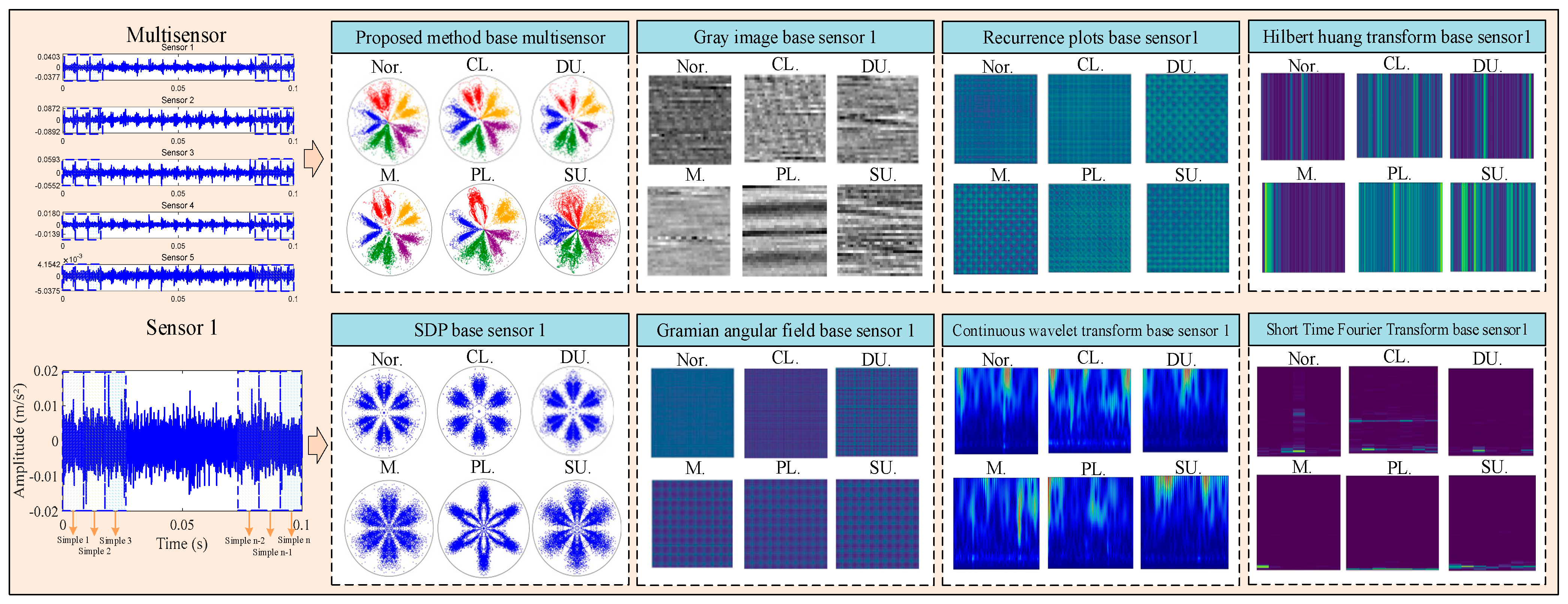
7. Comparison Experiments
7.1. Comparison of Different Models
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, X.; Liao, Z.; Wang, H.; Song, W.; Chen, P. Novel rotating machinery structural faults signal adaptive multiband filtering and automatic diagnosis. Math. Probl. Eng. 2021, 2021, 1497964. [Google Scholar]
- Desnica, E.; Ašonja, A.; Radovanović, L.; Palinkaš, I.; Kiss, I. Selection, dimensioning and maintenance of roller bearings. In International Conference on Organization and Technology of Maintenance; Springer International Publishing: Cham, Switzerland, 2022; pp. 133–142. [Google Scholar]
- Song, L.; Jin, Y.; Lin, T.; Zhao, S.; Wei, Z.; Wang, H. Remaining Useful Life Prediction Method Based on the Spatiotemporal Graph and GCN Nested Parallel Route Model. IEEE Trans. Instrum. Meas. 2024, 73, 3511912. [Google Scholar] [CrossRef]
- Xue, H.; Ding, D.; Zhang, Z.; Wu, M.; Wang, H. A Fuzzy System of Operation Safety Assessment Using Multimodel Linkage and Multistage Collaboration for In-Wheel Motor. IEEE Trans. Fuzzy Syst. 2022, 30, 999–1013. [Google Scholar] [CrossRef]
- Neupane, D.; Bouadjenek, M.R.; Dazeley, R.; Aryal, S. Data-driven machinery fault diagnosis: A comprehensive review. Neurocomputing 2025, 627, 129588. [Google Scholar] [CrossRef]
- Tang, H.; Liao, Z.; Chen, P.; Zuo, D.; Yi, S. A Novel Convolutional Neural Network for Low-Speed Structural Fault Diagnosis Under Different Operating Condition and Its Understanding via Visualization. IEEE Trans. Instrum. Meas. 2021, 70, 3501611. [Google Scholar] [CrossRef]
- Han, T.; Yang, B.-S.; Choi, W.-H.; Kim, J.-S. Fault Diagnosis System of Induction Motors Based on Neural Network and Genetic Algorithm Using Stator Current Signals. Int. J. Rotating Mach. 2006, 2006, 061690. [Google Scholar] [CrossRef]
- Liu, X.; Sun, W.; Li, H.; Hussain, Z.; Liu, A. The Method of Rolling Bearing Fault Diagnosis Based on Multi-Domain Supervised Learning of Convolution Neural Network. Energies 2022, 15, 4614. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, D.; Zhou, P.; Han, Z.; Yuan, Y.; Zhou, W.; Yin, Q. Rotor Fault Diagnosis Using a Convolutional Neural Network with Symmetrized Dot Pattern Images. Measurement 2019, 138, 526–535. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, Z.; Cai, C.; Wang, X.; Xu, J.; Shi, K.; Zhong, X.; Liao, Z.; Li, Q. Rolling bearing fault diagnosis method using time-frequency information integration and multi-scale TransFusion network. Knowl.-Based Syst. 2024, 284, 111344. [Google Scholar] [CrossRef]
- Wang, X.; Gu, H.; Wang, T.; Zhang, W.; Li, A.; Chu, F. Deep Convolutional Tree-Inspired Network: A Decision-Tree-Structured Neural Network for Hierarchical Fault Diagnosis of Bearings. Front. Mech. Eng. 2021, 16, 814–828. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis using 2-D convolutional neural network and motor current signature analysis. Mech. Syst. Signal Process. 2020, 144, 106861. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Wang, S.; Li, W.; Song, K. Fault Diagnosis of Bearings Based on Multi-Sensor Information Fusion and 2D Convolutional Neural Network. IEEE Access 2021, 9, 23717–23725. [Google Scholar] [CrossRef]
- Sun, J.; Gu, X.; He, J.; Yang, S.; Tu, Y.; Wu, C. A Robust Approach of Multi-Sensor Fusion for Fault Diagnosis Using Convolution Neural Network. J. Dyn. Monit. Diagn. 2022, 1, 103–110. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, Y.; Yuan, S. An improved convolutional neural network with an adaptable learning rate towards multi-signal fault diagnosis of hydraulic piston pump. Adv. Eng. Inform. 2021, 50, 101406. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Yang, S.; Xiang, Y.; Long, Z.; Ma, X.; Ding, Q.; Jia, J. Fault Diagnosis of Harmonic Drives Based on an SDP-ConvNeXt Joint Methodology. IEEE Trans. Instrum. Meas. 2023, 72, 3519608. [Google Scholar] [CrossRef]
- Wu, T.-E.; Huang, S.-H.; Lai, C.-H. Helical Gear Defect Detection System Based on Symmetrized Dot Pattern and Convolutional Neural Network. IEEE Access 2024, 12, 171328–171333. [Google Scholar] [CrossRef]
- Wang, L.; Wei, S.; Xi, T.; Li, H. A Symmetrized Dot Pattern Extraction Method Based on Frobenius and Nuclear Hybrid Norm Penalized Robust Principal Component Analysis and Decomposition and Reconstruction. Sensors 2023, 23, 8509. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Li, S.; Wang, Y.; Wang, X. Fault Diagnosis of Rolling Bearing Based on Empirical Mode Decomposition and Improved Manhattan Distance in Symmetrized Dot Pattern Image. Mech. Syst. Signal Process. 2021, 159, 107817. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Li, H. Tool Wear Prediction Method Based on Symmetrized Dot Pattern and Multi-Covariance Gaussian Process Regression. Measurement 2022, 189, 110466. [Google Scholar] [CrossRef]
- Fan, H.; Xue, C.; Ma, J.; Cao, X.; Zhang, X. A novel intelligent diagnosis method of rolling bearing and rotor composite faults based on vibration signal-to-image mapping and CNN-SVM. Meas. Sci. Technol. 2023, 34, 044008. [Google Scholar]
- Han, Y.; Liu, Y.; Huang, Q.; Zhang, Y. SOC estimation for lithium-ion batteries based on BiGRU with SE attention and Savitzky-Golay filter. J. Energy Storage 2024, 90, 111930. [Google Scholar] [CrossRef]
- Pang, B.; Liang, J.; Liu, H.; Dong, J.; Xu, Z.; Zhao, X. Intelligent bearing fault diagnosis based on multivariate symmetrized dot pattern and LEG transformer. Machines 2022, 10, 550. [Google Scholar] [CrossRef]
- Cui, W.; Meng, G.; Gou, T.; Wang, A.; Xiao, R.; Zhang, X. Intelligent Rolling Bearing Fault Diagnosis Method Using Symmetrized Dot Pattern Images and CBAM-DRN. Sensors 2022, 22, 9954. [Google Scholar] [CrossRef]
- Gu, Y.; Zeng, L.; Qiu, G. Bearing Fault Diagnosis with Varying Conditions Using Angular Domain Resampling Technology, SDP and DCNN. Measurement 2020, 156, 107616. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, G.; Tang, S.; Wang, R.; Su, H.; Wang, C. Acoustic Signal-Based Fault Detection of Hydraulic Piston Pump Using a Particle Swarm Optimization Enhancement CNN. Appl. Acoust. 2022, 192, 108718. [Google Scholar] [CrossRef]

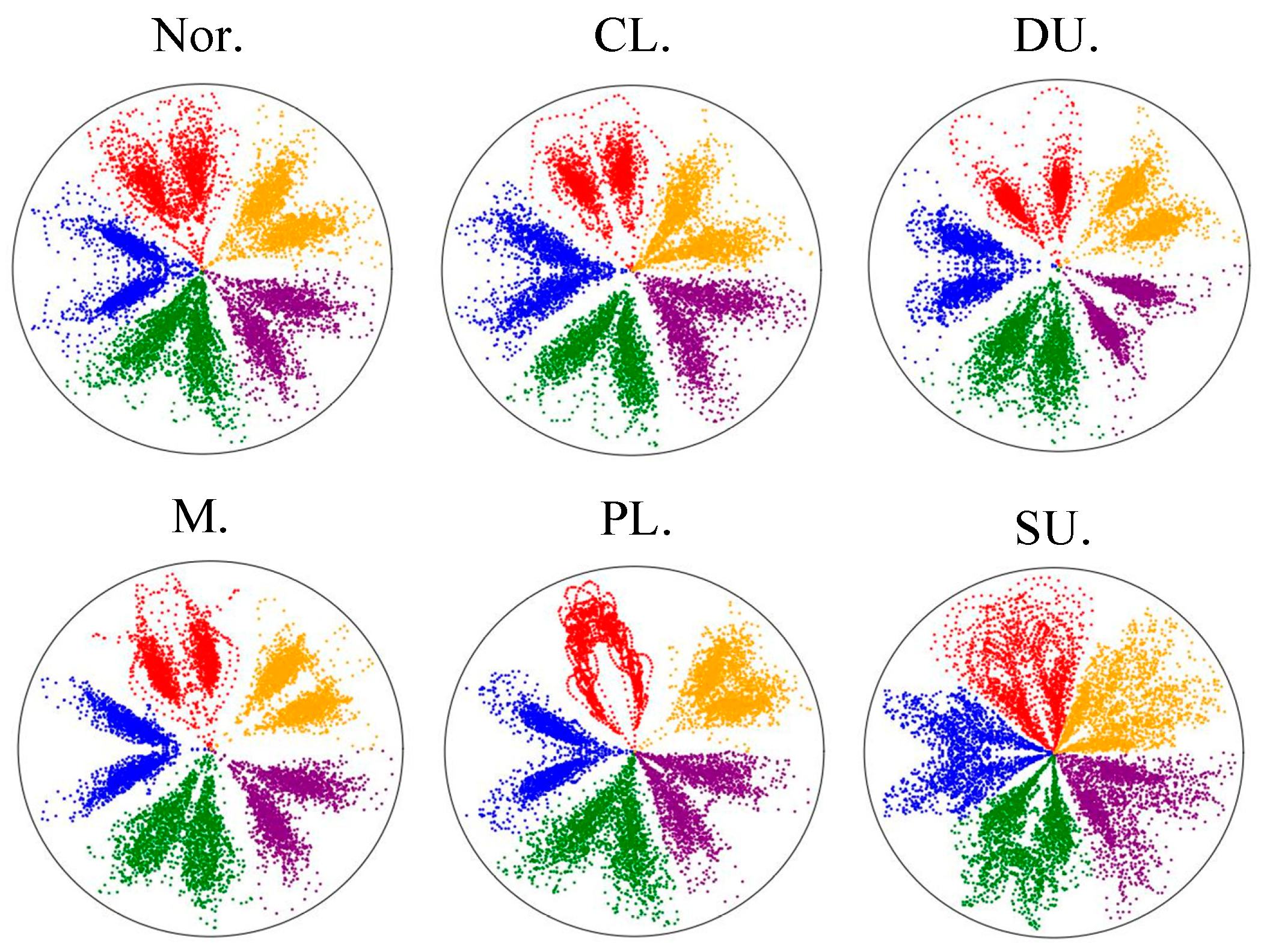
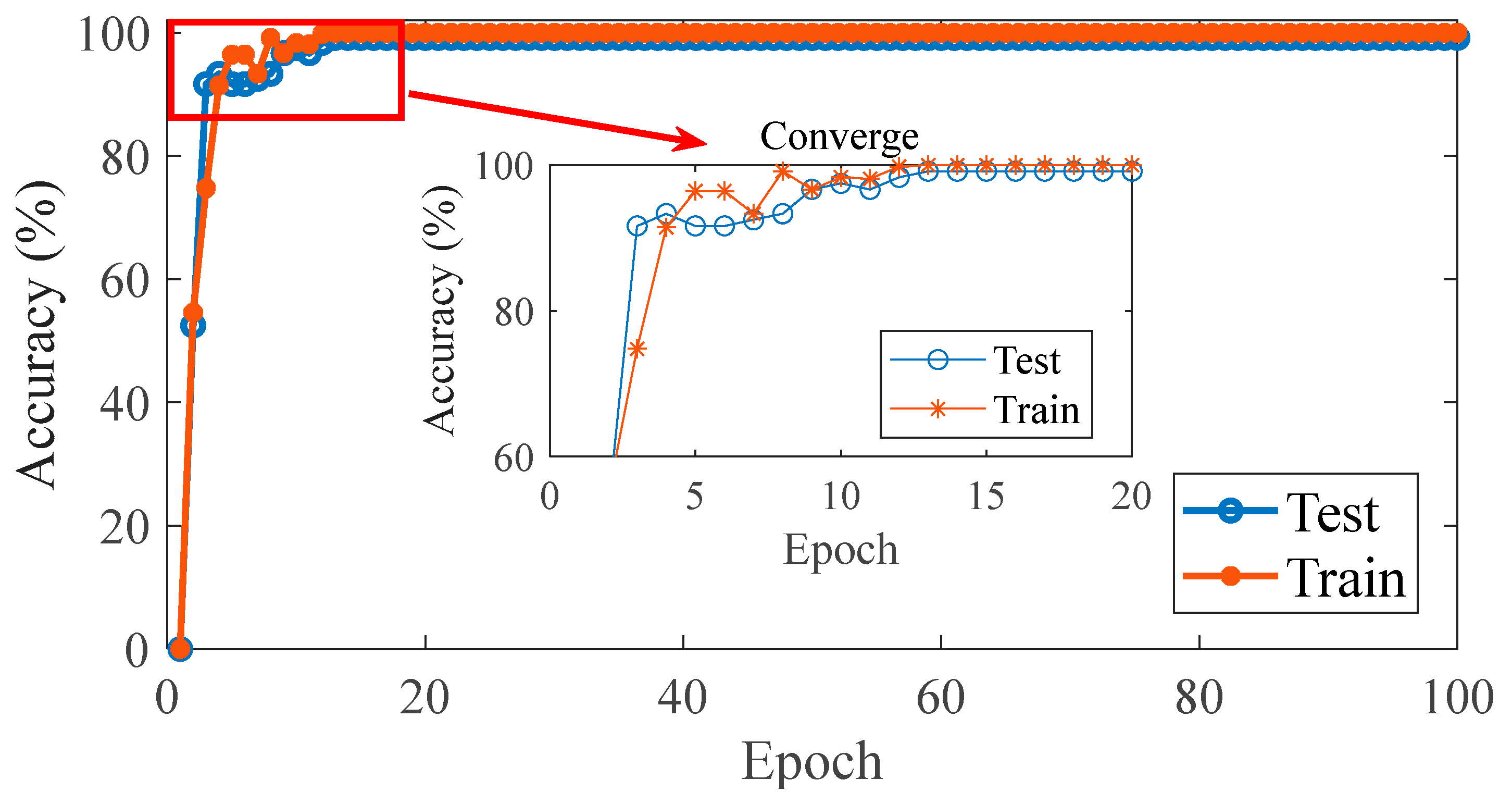
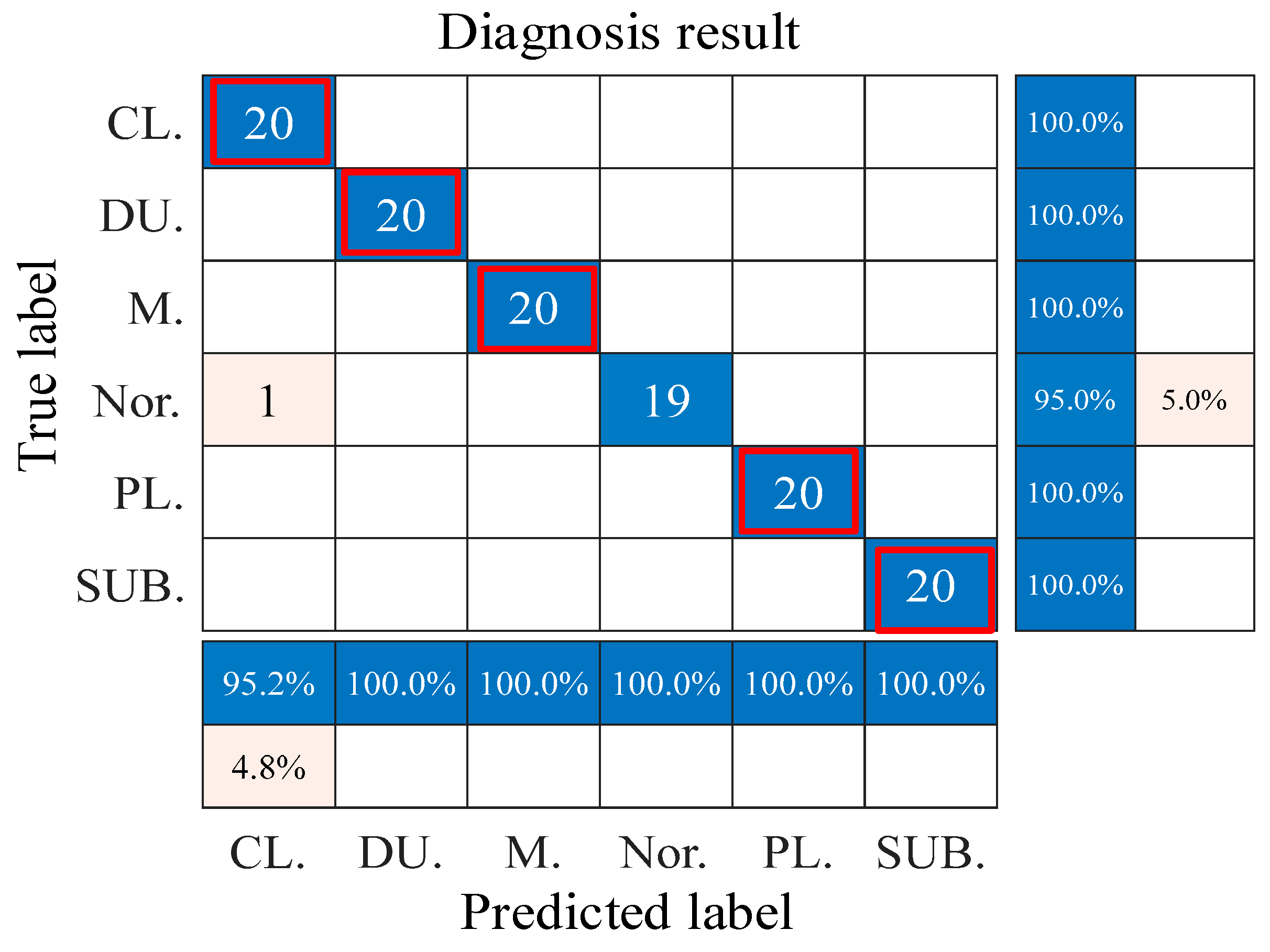

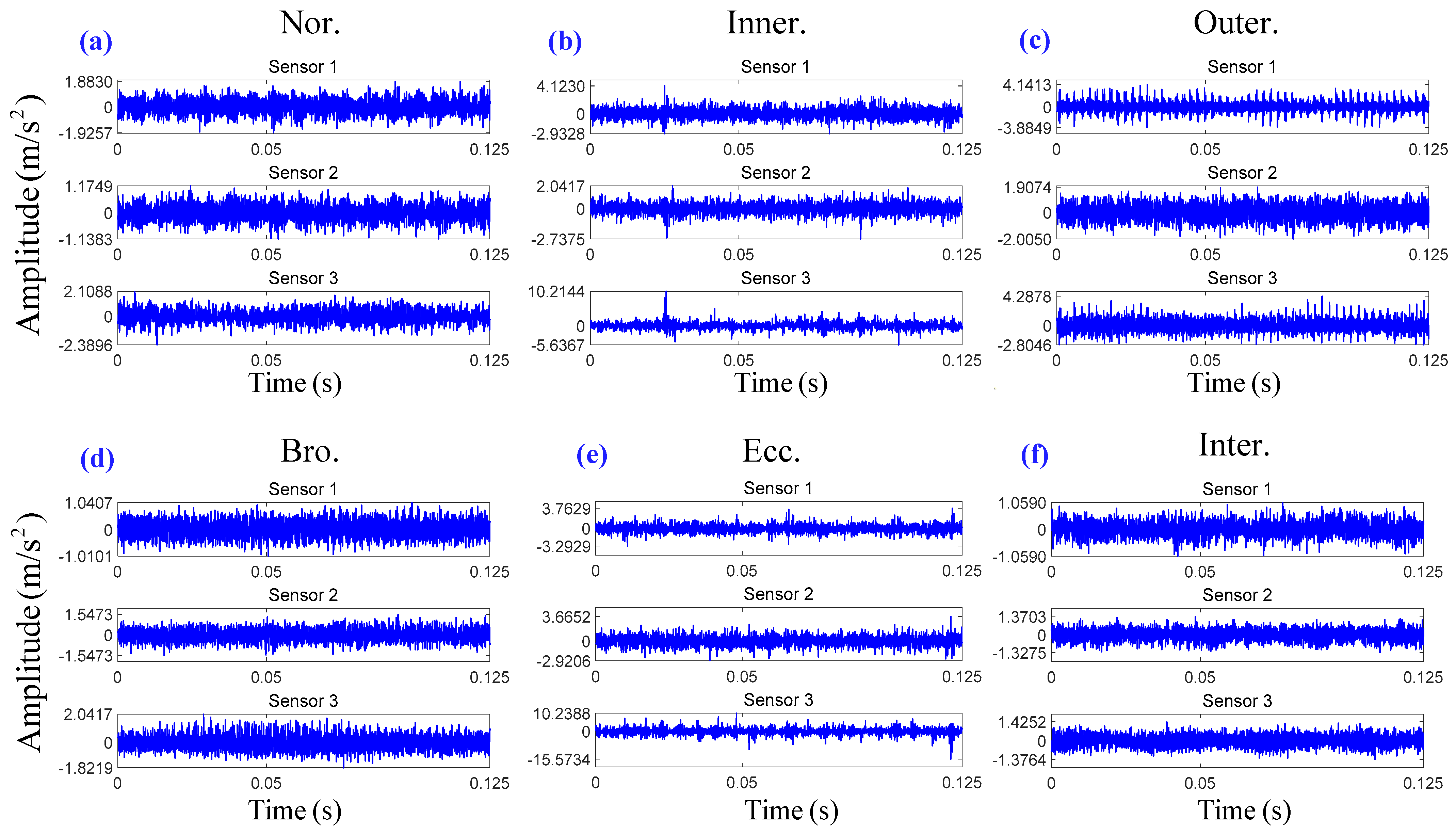



| Rotating Mechanical Structure State | Sample Number | Sample Length | Label |
|---|---|---|---|
| Normal | 100 | 1000 | Nor. |
| Coupling loose fault | 100 | 1000 | CL. |
| Position loose fault | 100 | 1000 | PL. |
| Dynamic unbalance fault | 100 | 1000 | DU. |
| Misalignment fault | 100 | 1000 | M. |
| Static unbalance fault | 100 | 1000 | SU. |
| Rotating Mechanical Structure State | Sample Number | Sample Length | Label |
|---|---|---|---|
| Normal | 100 | 1024 | Nor. |
| Broken strip fault | 100 | 1024 | Bro. |
| Bearing inner race fault | 100 | 1024 | Inner. |
| Bearing outer race fault | 100 | 1024 | Outer. |
| Eccentricity fault | 100 | 1024 | Ecc. |
| Inter-turn fault | 100 | 1024 | Inter. |
| Range | Stride | Iteration Time | Optimal Parameter | Accuracy |
|---|---|---|---|---|
| , | [3, 1] | 119.10 s | 100.00% | |
| , | [5, 1] | 85.61 s | 100.00% | |
| , | [7, 1] | 55.22 s | 99.16% | |
| , | [5, 3] | 28.00 s | 98.33% | |
| , | [5, 1] | 150.10 s | 100.00% | |
| , | [5, 1] | 293.04 s | 100.00% |
| Signal Transformation Methods | Parameter Selection | Dataset Generation Time | Train Time | Model | Accuracy | F1 Score | Label |
|---|---|---|---|---|---|---|---|
| MSSDP | Yes | 30.24 s | 397.62 s | ResNet18 | 99.16% | 0.996 | Test1 |
| MSDP | Yes | 27.60 s | 352.09 s | ResNet18 | 95.83% | 0.977 | Test2 |
| SDP | Yes | 25.08 s | 359.24 s | ResNet18 | 90.00% | 0.942 | Test3 |
| SDP | No | 25.20 s | 367.66 s | ResNet18 | 85.83% | 0.912 | Test4 |
| Signal Transformation Methods | Dataset Generation Time | Model | Accuracy | F1 Score |
|---|---|---|---|---|
| HHT | 374.94 s | ResNet18 | 86.11% | 0.916 |
| MSSDP | 32.04 s | ResNet18 | 99.16% | 0.996 |
| STFT | 15.48 s | ResNet18 | 96.29% | 0.979 |
| GRAY | 17.52 s | ResNet18 | 88.80% | 0.900 |
| RP | 38.76 s | ResNet18 | 88.30% | 0.875 |
| SDP | 31.44 s | ResNet18 | 83.30% | 0.820 |
| GAF | 31.62 s | ResNet18 | 85.00% | 0.824 |
| CWT | 34.38 s | ResNet18 | 95.00% | 0.958 |
| Signal Transformation Methods | Train Time | Inference Time | Diagnosis Model | Accuracy | F1 Score |
|---|---|---|---|---|---|
| MSSDP | 315.57 s | 0.59 s | CNN | 98.33% | 0.991 |
| MSSDP | 397.62 s | 0.64 s | ResNet18 | 99.16% | 0.996 |
| MSSDP | 282.14 s | 0.53 s | Alex | 93.33% | 0.963 |
| MSSDP | 748.81 s | 1.18 s | DenseNet | 96.66% | 0.982 |
| MSSDP | 1378.43 s | 1.42 s | VGG | 97.50% | 0.986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, B.; Liang, G.; Huang, Z.; Song, X.; Liao, Z. Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Based on Multi-Sensor Information Fusion. Machines 2025, 13, 553. https://doi.org/10.3390/machines13070553
Jia B, Liang G, Huang Z, Song X, Liao Z. Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Based on Multi-Sensor Information Fusion. Machines. 2025; 13(7):553. https://doi.org/10.3390/machines13070553
Chicago/Turabian StyleJia, Baozhu, Guanlong Liang, Zhende Huang, Xuewei Song, and Zhiqiang Liao. 2025. "Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Based on Multi-Sensor Information Fusion" Machines 13, no. 7: 553. https://doi.org/10.3390/machines13070553
APA StyleJia, B., Liang, G., Huang, Z., Song, X., & Liao, Z. (2025). Rotating Machinery Structural Faults Feature Enhancement and Diagnosis Based on Multi-Sensor Information Fusion. Machines, 13(7), 553. https://doi.org/10.3390/machines13070553






