A Neural Network-Based Approach to Estimate Printing Time and Cost in L-PBF Projects
Abstract
1. Introduction
2. Research Background
2.1. Machine Learning
ML in Production Techniques
- Data Collection: Gather relevant data from various sources pertinent to the AM process, such as sensor data and production logs.
- Storage: Collected data and the model’s weights must be stored securely on an available server, ensuring they are organized for easy access during model training.
- Model Training: Training an ML algorithm with adequate data. This includes selecting algorithms, model selection, training, setting, and validating model performance.
- Model Registration: After training, another critical step in streamlining the model lifecycle from development to production deployment is managing machine learning model versions, particularly if a continual learning iteration is planned within the production pipeline.
- API Gateway: The system must implement a web service and RESTful API to interact with and serve client calls.
- Continual Learning: A solution to avoid the deterioration over time of the model’s performance. This is due to the dynamic nature of the AM production environment, where the high variability in material properties and process parameters demands adaptive learning models capable of real-time adjustments.
- Monitoring: Monitoring and logging are essential for analyzing job status (such as training job failures and successes), platform health, and various metrics (including inference error rates, data drift, and training loss).
- Model Endpoint: The trained model is deployed as an endpoint, a web service tool that allows real-time predictions based on incoming requests routed through an API Gateway.
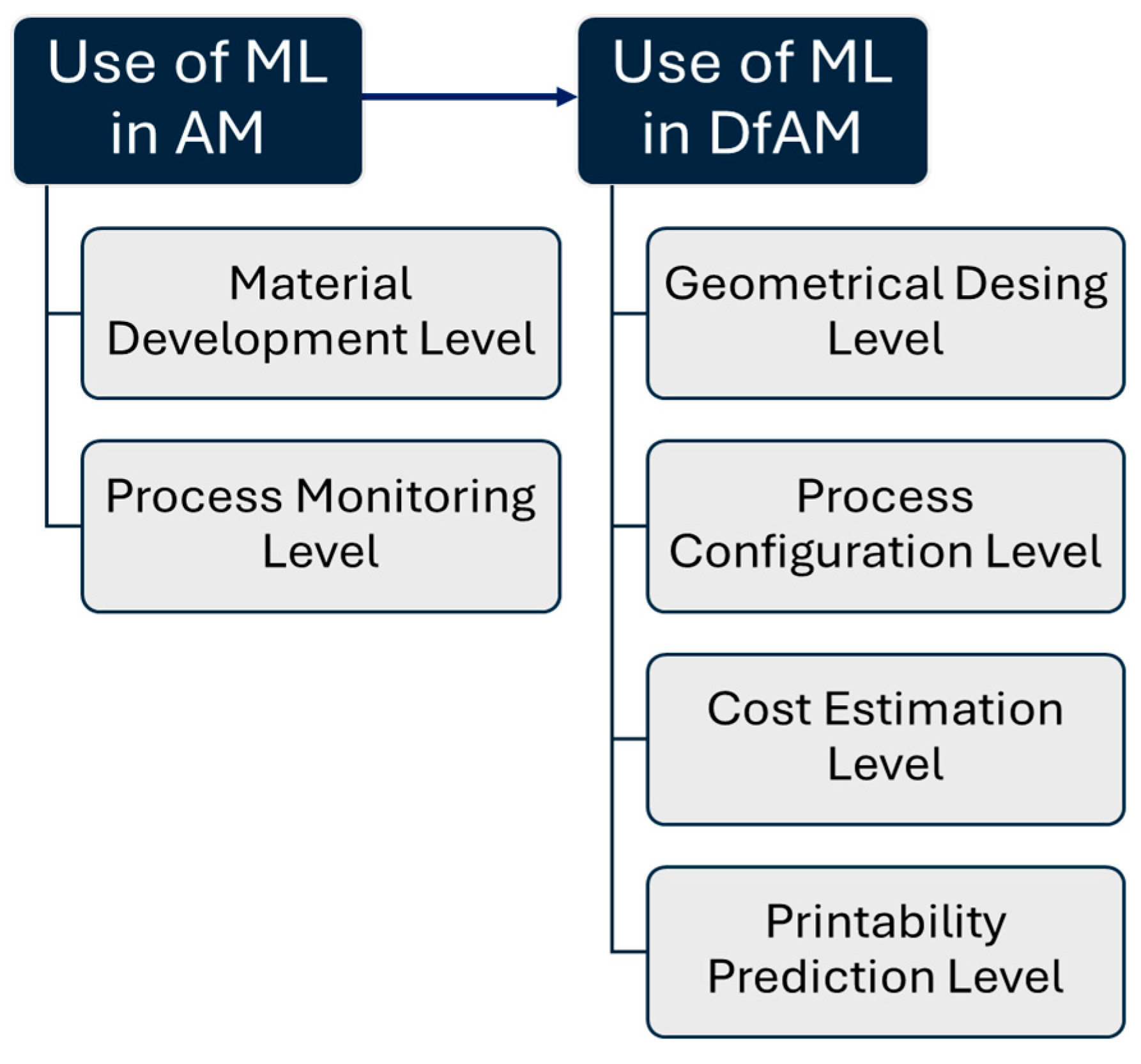
2.2. Machine Learning Applications in Design for Additive Manufacturing
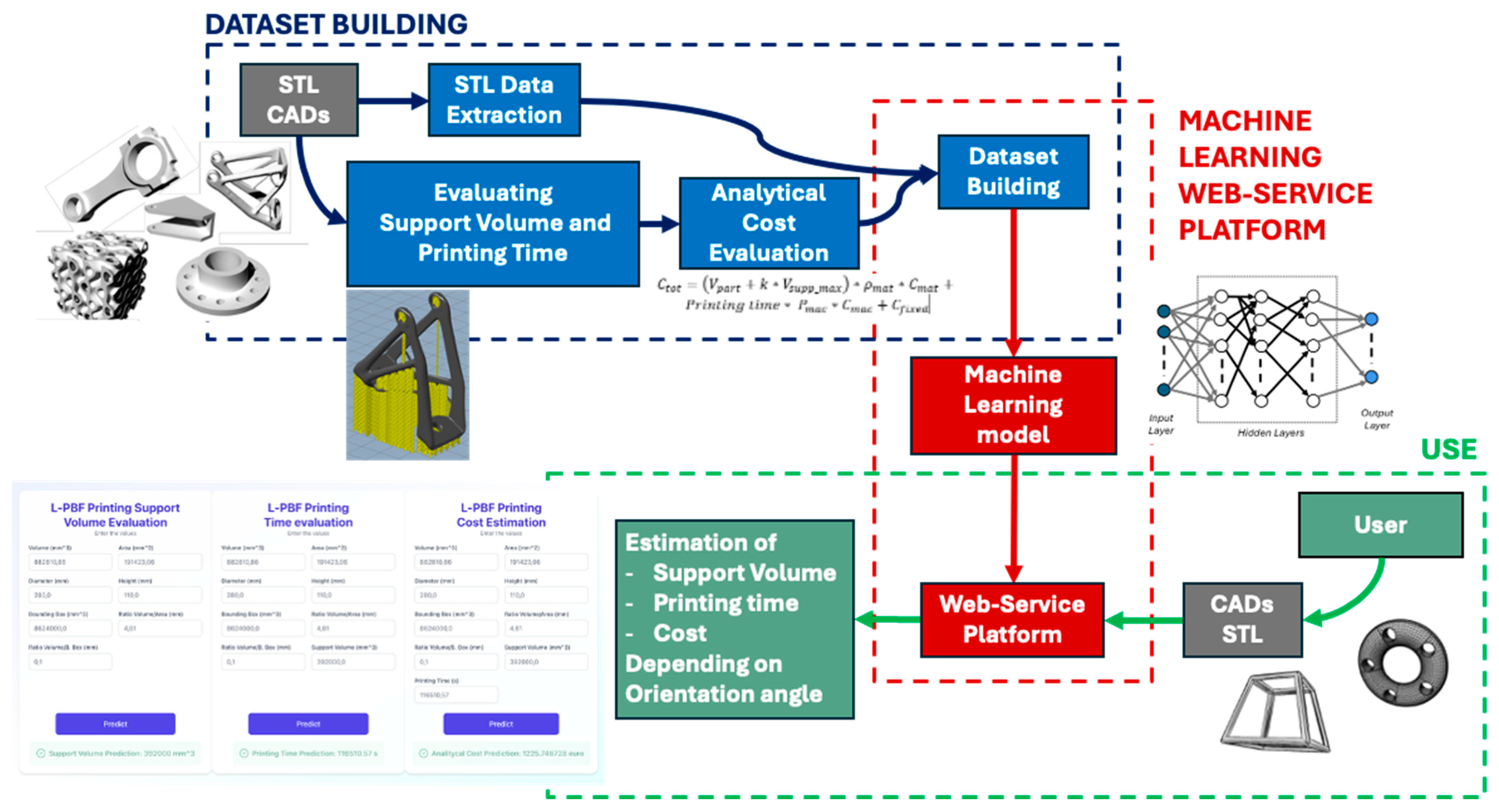
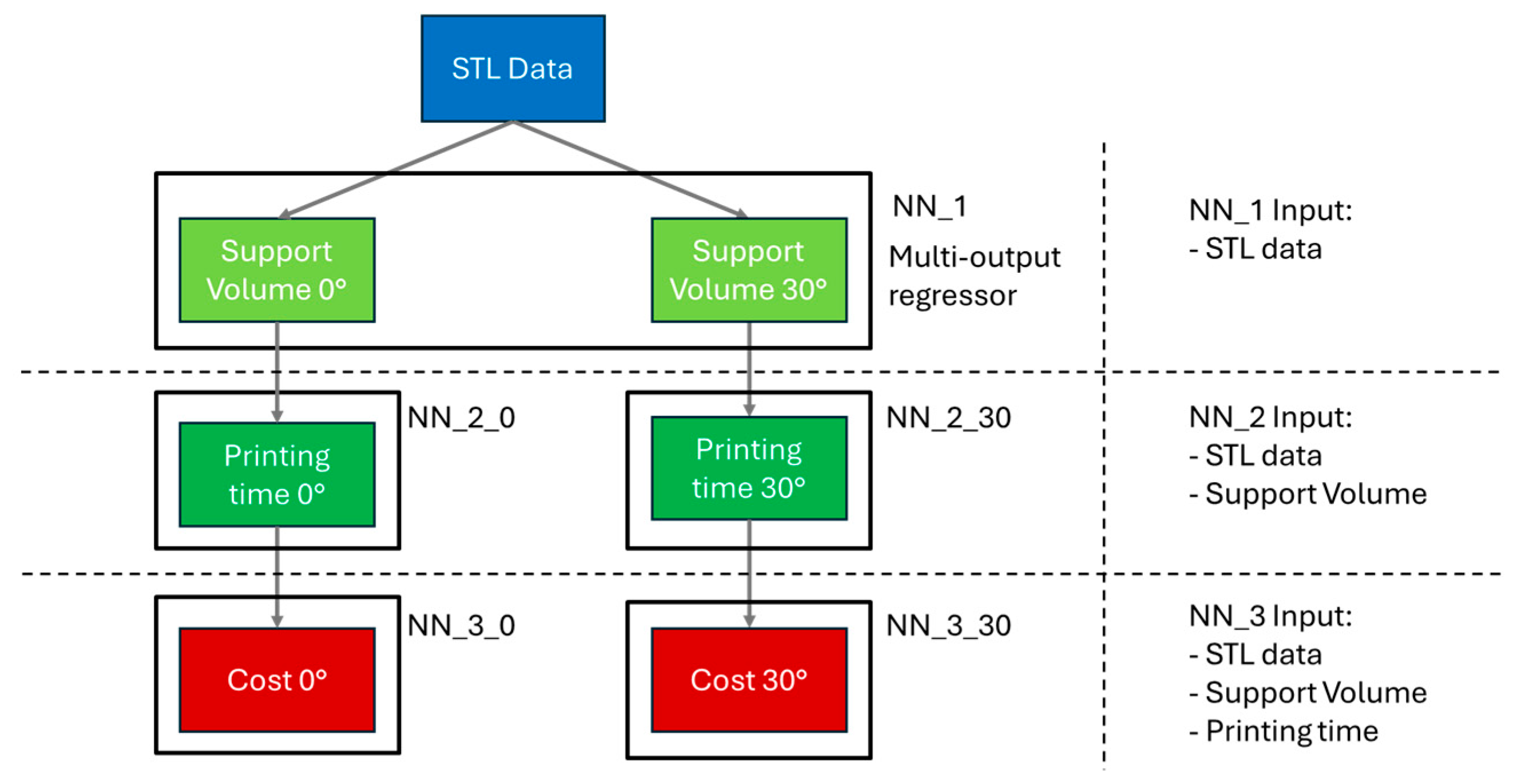
3. Proposed Approach
4. Case Study
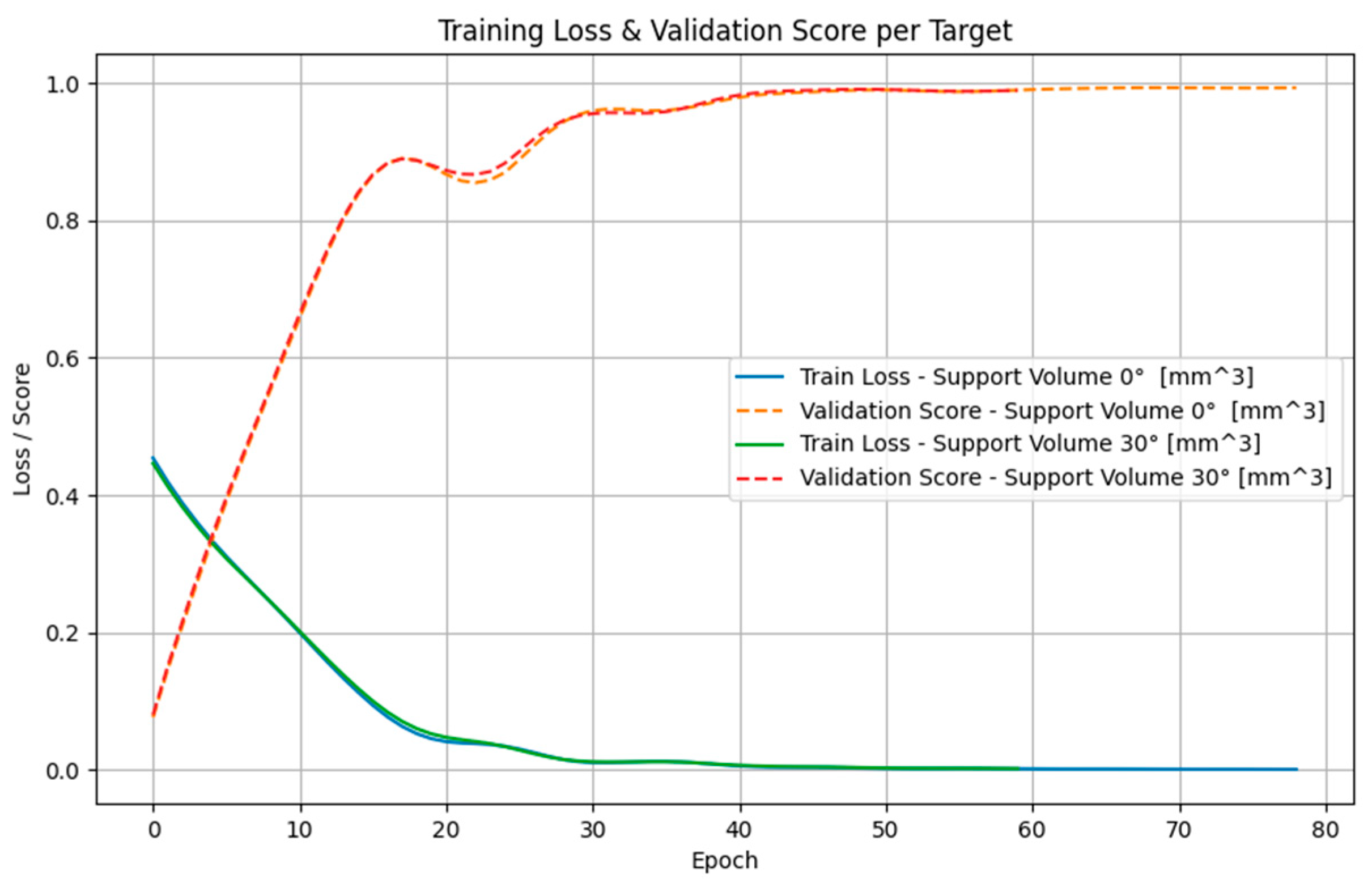
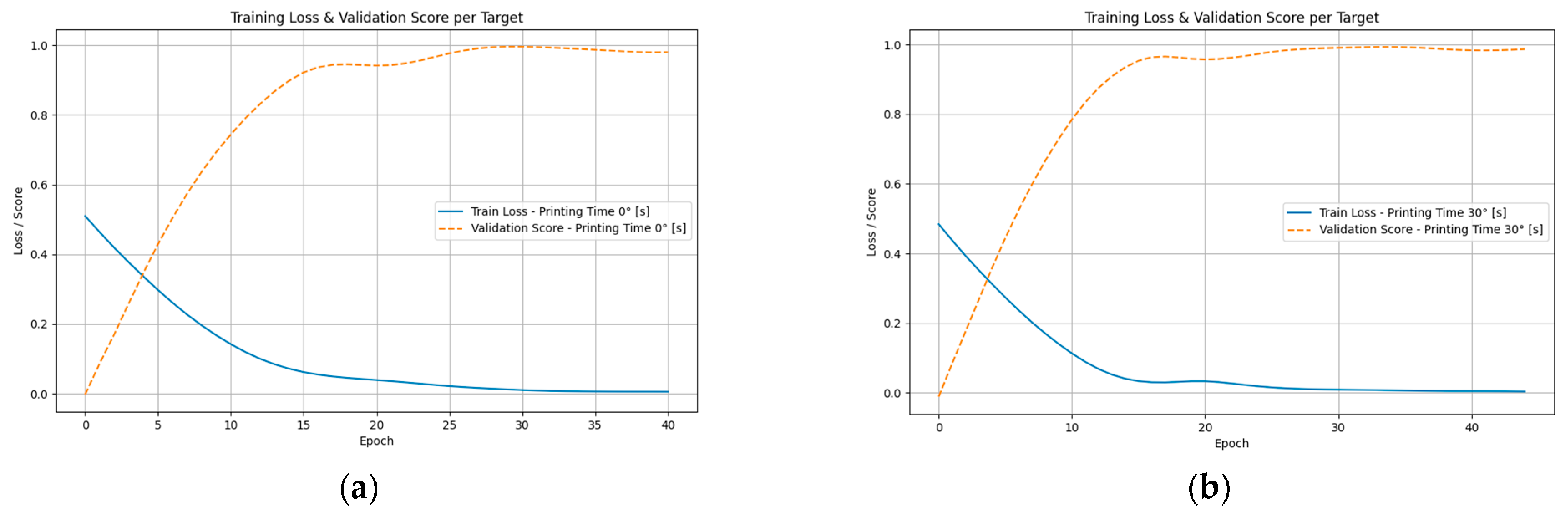
4.1. Training Results
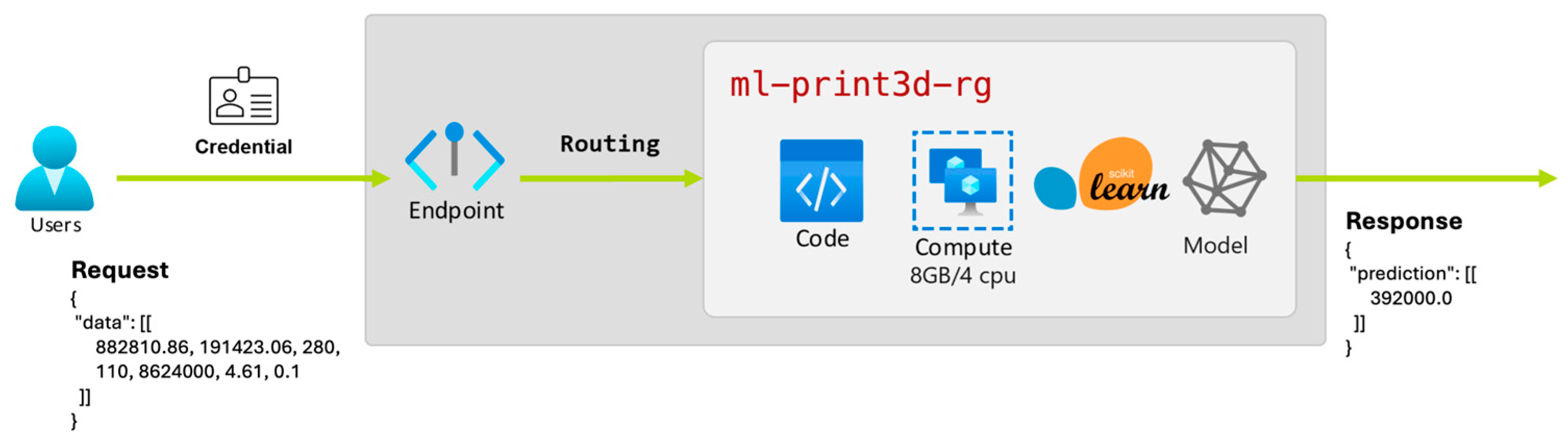
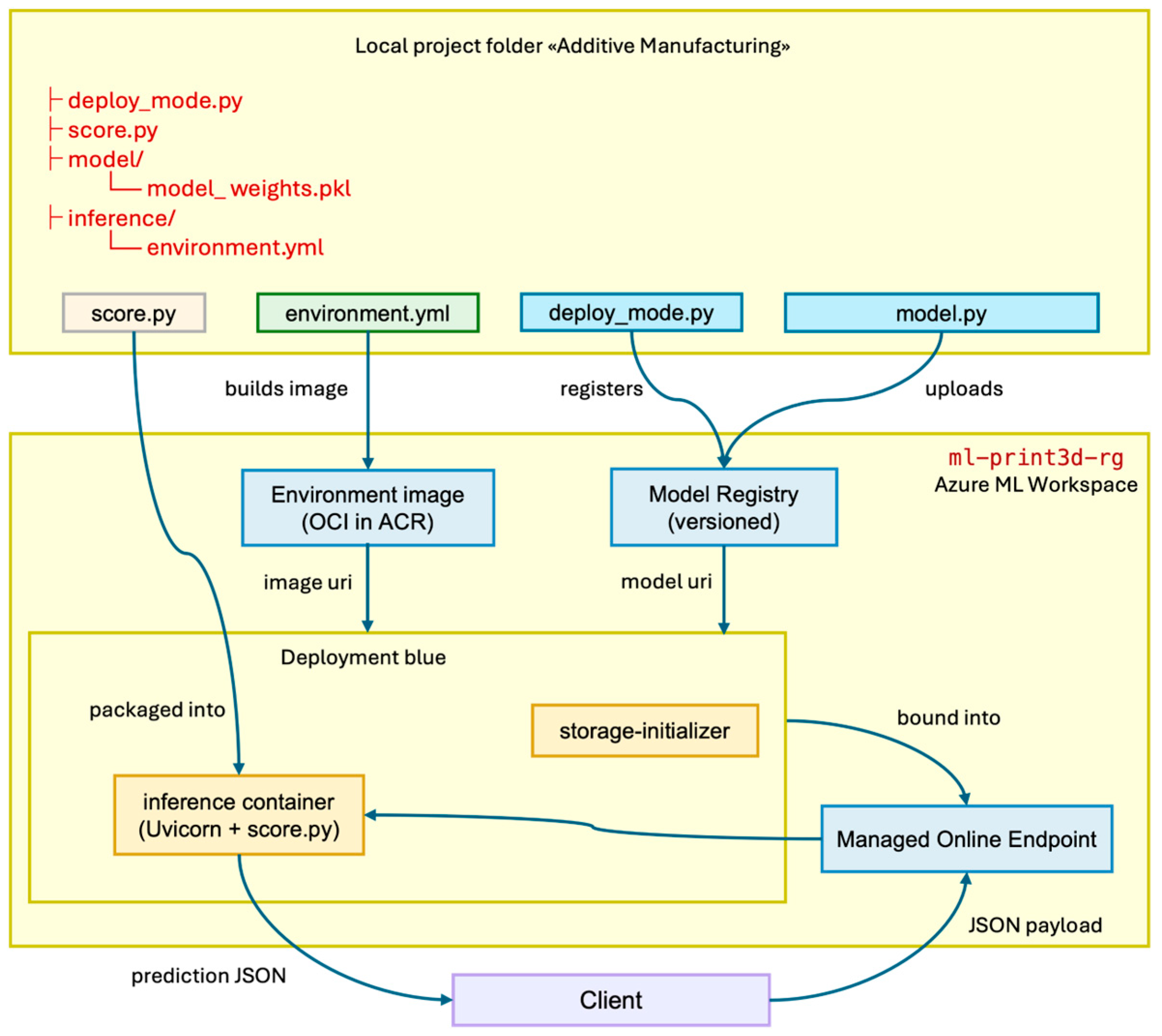
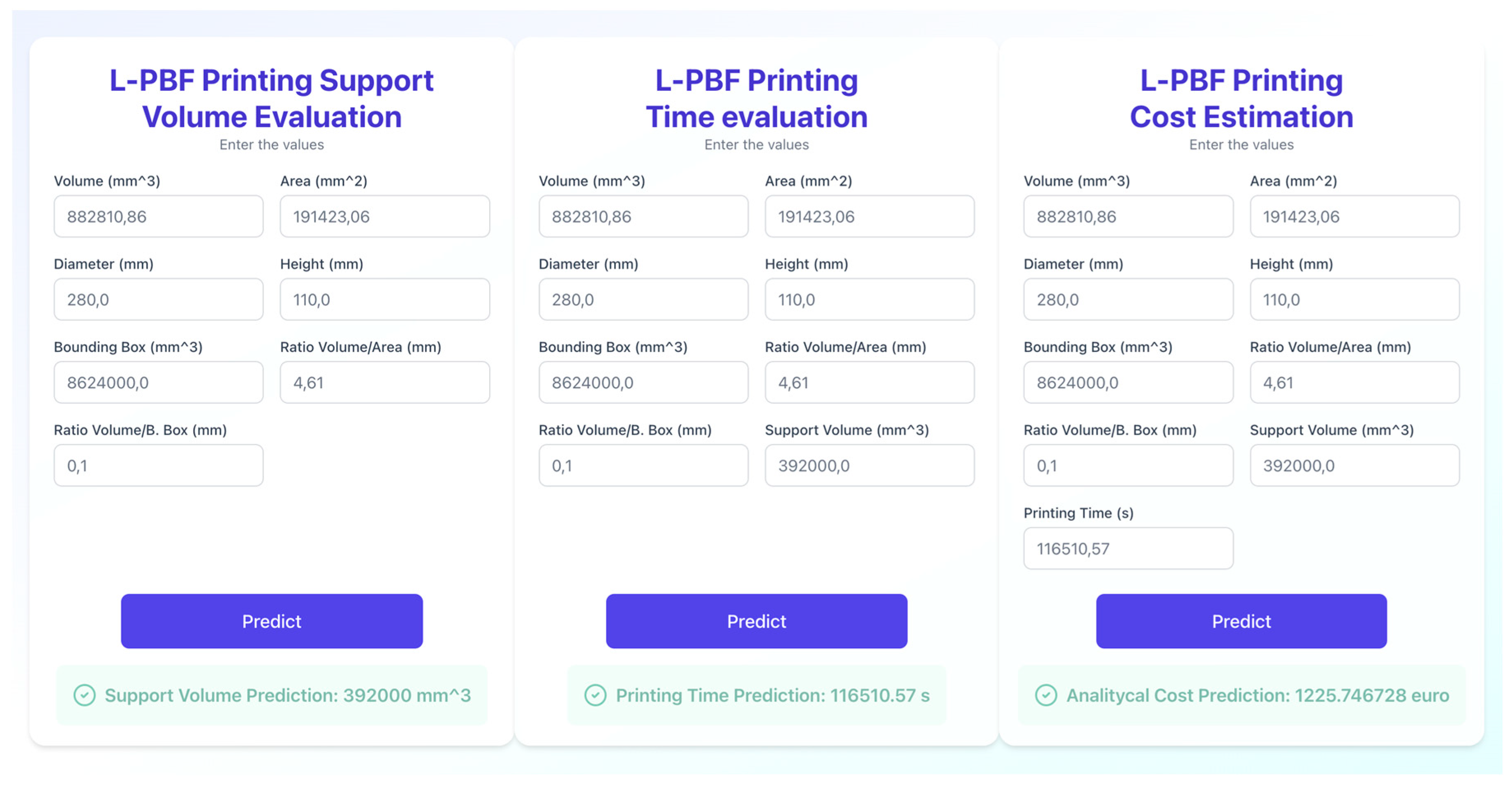
4.2. Web-Service Platform Development
- Code: the score.py script that implements init() (model loading) and run() (prediction).
- Compute: a dedicated container instance with 8 GB RAM and 4 vCPU, provisioned from the Stock Keeping Unit (SKU) selected during deployment creation.
- Scikit-learn runtime: the framework layer installed via the Azure ML Environment image.
- Model: the serialized estimator, which resides in the container’s mounted storage and is loaded into memory at start-up.
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonnard, R.; Hascoët, J.-Y.; Mognol, P.; Zancul, E.; Alvares, A.J. Hierarchical object-oriented model (HOOM) for additive manufacturing digital thread. J. Manuf. Syst. 2019, 50, 36–52. [Google Scholar] [CrossRef]
- Dilberoglu, U.M.; Gharehpapagh, B.; Yaman, U.; Dolen, M. The Role of Additive Manufacturing in the Era of Industry 4.0. Procedia Manuf. 2017, 11, 545–554. [Google Scholar] [CrossRef]
- Mies, D.; Marsden, W.; Warde, S. Overview of Additive Manufacturing Informatics: “A Digital Thread”. Integr. Mater. Manuf. Innov. 2016, 5, 114–142. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2021; Additive Manufacturing—General Principles—Fundamentals and Vocabulary. ISO/ASTM International: Geneva, Switzerland, 2021.
- Shi, Y.; Zhang, Y.; Baek, S.; De Backer, W.; Harik, R. Manufacturability analysis for additive manufacturing using a novel feature recognition technique. Comput.-Aided Des. Appl. 2018, 15, 941–952. [Google Scholar] [CrossRef]
- Haines, M.P.; Peter, N.J.; Babu, S.S.; Jägle, E.A. In-situ synthesis of oxides by reactive process atmospheres during L-PBF of stainless steel. Addit. Manuf. 2020, 33, 101178. [Google Scholar] [CrossRef]
- Vaneker, T.; Bernard, A.; Moroni, G.; Gibson, I.; Zhang, Y. Design for additive manufacturing: Framework and methodology. CIRP Ann. 2020, 69, 578–599. [Google Scholar] [CrossRef]
- Lynn, R.; Saldana, C.; Kurfess, T.; Reddy, N.; Simpson, T.; Jablokow, K.; Tucker, T.; Tedia, S.; Williams, C. Toward Rapid Manufacturability Analysis Tools for Engineering Design Education. Procedia Manuf. 2016, 5, 1183–1196. [Google Scholar] [CrossRef]
- Trovato, M.; Cicconi, P. Design tools for metal additive manufacturing: A critical and perspective overview. Procedia CIRP 2023, 119, 1084–1090. [Google Scholar] [CrossRef]
- Kaščák, Ľ.; Varga, J.; Bidulská, J.; Bidulský, R.; Manfredi, D. Weight Factor as a Parameter for Optimal Part Orientation in the L-PBF Printing Process Using Numerical Simulation. Materials 2024, 17, 3604. [Google Scholar] [CrossRef]
- Dixit, S.; Liu, S.; Murdoch, H.A.; Smith, P.M. Investigating build orientation-induced mechanical anisotropy in additive manufacturing 316L stainless steel. Mater. Sci. Eng. A 2023, 880, 145308. [Google Scholar] [CrossRef]
- Bianchi, I.; Forcellese, A.; Forcellese, P.; Mancia, T.; Mignanelli, C.; Simoncini, M.; Verdini, T. Effect of Printing Orientation Angle and Heat Treatment on the Mechanical Properties and Microstructure of Binder-Jetting-Printed Parts in 17-4 PH Stainless Steel. Metals 2024, 14, 1220. [Google Scholar] [CrossRef]
- Rabalo, M.A.; Rubio, E.M.; Agustina, B.; Camacho, A.M. Hybrid additive and subtractive manufacturing: Evolution of the concept and last trends in research and industry. Procedia CIRP 2023, 118, 741–746. [Google Scholar] [CrossRef]
- Schmitz, T.; Corson, G.; Olvera, D.; Tyler, C.; Smith, S. A framework for hybrid manufacturing cost minimization and preform design. CIRP Ann. 2023, 72, 373–376. [Google Scholar] [CrossRef]
- Sharifani, K.; Amini, M. Machine Learning and Deep Learning: A Review of Methods and Applications. World Inf. Technol. Eng. J. 2023, 10, 3897–3904. [Google Scholar]
- Jiang, Y.; Li, X.; Luo, H.; Yin, S.; Kaynak, O. Quo vadis artificial intelligence? Discov. Artif. Intell. 2022, 2, 4. [Google Scholar] [CrossRef]
- Mahesh, B. Machine Learning Algorithms—A Review. Int. J. Sci. Res. 2020, 9, 381–386. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised Learning. In Machine Learning Techniques for Multimedia: Case Studies on Organization and Retrieval; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. [Google Scholar]
- Dayan, P. Unsupervised Learning. In The MIT Encyclopedia of the Cognitive Sciences; Wilson, R.A., Keil, F., Eds.; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Luo, F.M.; Xu, T.; Lai, H.; Chen, X.H.; Zhang, W.; Yu, Y. A survey on model-based reinforcement learning. Sci. China Inf. Sci. 2024, 67, 121101. [Google Scholar] [CrossRef]
- Joshi, M.; Flood, A.; Sparks, T.; Liou, F.W. Applications of supervised machine learning algorithms in additive manufacturing: A review. In 2019 International Solid Freeform Fabrication Symposium; University of Texas at Austin: Austin, TX, USA, 2019. [Google Scholar]
- Zhang, Y.; Safdar, M.; Xie, J.; Li, J.; Sage, M.; Zhao, Y.F. A systematic review on data of additive manufacturing for machine learning applications: The data quality, type, preprocessing, and management. J. Intell. Manuf. 2022, 34, 3305–3340. [Google Scholar] [CrossRef]
- García-Moreno, A.-I.; Alvarado-Orozco, J.-M.; Ibarra-Medina, J.; Martínez-Franco, E. Image-based porosity classification in Al-alloys by laser metal deposition using random forests. Int. J. Adv. Manuf. Technol. 2020, 110, 2827–2845. [Google Scholar] [CrossRef]
- Kumar, P.; Jain, N.K. Surface roughness prediction in micro-plasma transferred arc metal additive manufacturing process using K-nearest neighbors algorithm. Int. J. Adv. Manuf. Technol. 2022, 119, 2985–2997. [Google Scholar] [CrossRef]
- Vandecasteele, M.; Heylen, R.; Iuso, D.; Thanki, A.; Philips, W.; Witvrouw, A.; Verhees, D.; Booth, B.G. Towards material and process agnostic features for the classification of pore types in metal additive manufacturing. Mater. Des. 2023, 227, 111757. [Google Scholar] [CrossRef]
- Banadaki, Y.M.; Razaviarab, N.; Fekrmandi, H.; Li, G.; Mensah, P.; Bai, S.; Sharifi, S. Automated Quality and Process Control for Additive Manufacturing using Deep Convolutional Neural Networks. Recent Prog. Mater. 2021, 4, 5. [Google Scholar] [CrossRef]
- Xiao, S.; Li, J.; Wang, Z.; Chen, Y.; Tofighi, S. Advancing Additive Manufacturing Through Machine Learning Techniques: A State-of-the-Art Review. Future Internet 2024, 16, 419. [Google Scholar] [CrossRef]
- Baturynska, I.; Semeniuta, O.; Martinsen, K. Optimization of Process Parameters for Powder Bed Fusion Additive Manufacturing by Combination of Machine Learning and Finite Element Method: A Conceptual Framework. Procedia CIRP 2018, 67, 227–232. [Google Scholar] [CrossRef]
- Mattera, G.; Piscopo, G.; Longobardi, M.; Giacalone, M.; Nele, L. Improving the Interpretability of Data-Driven Models for Additive Manufacturing Processes Using Clusterwise Regression. Mathematics 2024, 12, 2559. [Google Scholar] [CrossRef]
- Song, L.; Huang, W.; Han, X.; Mazumder, J. Real-Time Composition Monitoring Using Support Vector Regression of Laser-Induced Plasma for Laser Additive Manufacturing. IEEE Trans. Ind. Electron. 2017, 64, 633–642. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, F.; Guo, C.; Wang, Z.; Dong, T.; Li, H. Prediction of melt pool shape in additive manufacturing based on machine learning methods. Opt. Laser Technol. 2023, 159, 108964. [Google Scholar] [CrossRef]
- Equbal, M.A.; Equbal, A.; Khan, Z.A.; Badruddin, I.A. Machine learning in Additive Manufacturing: A Comprehensive insight. Int. J. Lightweight Mater. Manuf. 2025, 8, 264. [Google Scholar] [CrossRef]
- Ciccone, F.; Bacciaglia, A.; Ceruti, A. Optimization with artificial intelligence in additive manufacturing: A systematic review. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 303. [Google Scholar] [CrossRef]
- Trovato, M.; Belluomo, L.; Bici, M.; Prist, M.; Campana, F.; Cicconi, P. Machine learning in design for additive manufacturing: A state-of-the-art discussion for a support tool in product design lifecycle. Int. J. Adv. Manuf. Technol. 2025, 137, 2157–2180. [Google Scholar] [CrossRef]
- Trovato, M.; Belluomo, L.; Bici, M.; Campana, F.; Cicconi, P. Machine Learning Trends in Design for Additive Manufacturing. In Design Tools and Methods in Industrial Engineering III; Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2024; pp. 109–117. [Google Scholar]
- Johnson, N.S.; Vulimiri, P.S.; To, A.C.; Zhang, X.; Brice, C.A.; Kappes, B.B.; Stebner, A.P. Invited review: Machine learning for materials developments in metals additive manufacturing. Addit. Manuf. 2020, 36, 101641. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Demir, K.; Gu, G.X. Machine Learning for Advanced Additive Manufacturing. Matter 2020, 3, 1541–1556. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, G.S.; Ye, D.; Zhu, K.; Fuh, J.Y.H. Extraction and evaluation of melt pool, plume and spatter information for powder-bed fusion AM process monitoring. Mater. Des. 2018, 156, 458–469. [Google Scholar] [CrossRef]
- Pandiyan, V.; Masinelli, G.; Claire, N.; Le-Quang, T.; Hamidi-Nasab, M.; de Formanoir, C.; Esmaeilzadeh, R.; Goel, S.; Marone, F.; Logé, R.; et al. Deep learning-based monitoring of laser powder bed fusion process on variable time-scales using heterogeneous sensing and operando X-ray radiography guidance. Addit. Manuf. 2022, 58, 103007. [Google Scholar]
- Ye, D.; Hong, G.S.; Zhang, Y.; Zhu, K.; Fuh, J.Y.H. Defect detection in selective laser melting technology by acoustic signals with deep belief networks. Int. J. Adv. Manuf. Technol. 2018, 96, 2791–2801. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Krish, S. A practical generative design method. Comput.-Aided Des. 2011, 43, 88–100. [Google Scholar] [CrossRef]
- Amicarelli, M.; Trovato, M.; Cicconi, P. Lightweight Design of a Connecting Rod Using Lattice-Structure Parameter Optimisations: A Test Case for L-PBF. Machines 2025, 13, 171. [Google Scholar] [CrossRef]
- Hsiao, S.-W.; Tsai, H.-C. Applying a hybrid approach based on fuzzy neural network and genetic algorithm to product form design. Int. J. Ind. Ergon. 2005, 35, 411–428. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, T.; Jiang, H.; Kara, L.B. TopologyGAN: Topology Optimization Using Generative Adversarial Networks Based on Physical Fields Over the Initial Domain. J. Mech. Des. 2021, 143, 031715. [Google Scholar] [CrossRef]
- Yüksel, N.; Eren, O.; Börklü, H.R.; Sezer, H.K. Mechanical properties of additively manufactured lattice structures designed by deep learning. Thin-Walled Struct. 2024, 196, 111475. [Google Scholar] [CrossRef]
- Uriati, F.; Nicoletto, G. A comparison of Inconel 718 obtained with three L-PBF production systems in terms of process parameters, as-built surface quality, and fatigue performance. Int. J. Fatigue 2022, 162, 107004. [Google Scholar] [CrossRef]
- Zhang, W.; Mehta, A.; Desai, P.S.; Higgs III, C.F. Machine learning enabled powder spreading process map for metal additive manufacturing (AM). In Proceedings of the 2018 Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, Austin, TX, USA, 13–15 August 2018. [Google Scholar]
- Bao, H.; Wu, S.; Wu, Z.; Kang, G.; Peng, X.; Withers, P.J. A machine-learning fatigue life prediction approach of additively manufactured metals. Eng. Fract. Mech. 2021, 242, 107508. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. Machine learning based fatigue life prediction with effects of additive manufacturing process parameters for printed SS 316L. Int. J. Fatigue 2021, 142, 105941. [Google Scholar] [CrossRef]
- Chan, S.L.; Lu, Y.; Wang, Y. Data-driven cost estimation for additive manufacturing in cybermanufacturing. J. Manuf. Syst. 2018, 46, 115–126. [Google Scholar] [CrossRef]
- Mycroft, W.; Katzman, M.; Tammas-Williams, S.; Hernandez-Nava, E.; Panoutsos, G.; Todd, I.; Kadirkamanathan, V. A data-driven approach for predicting printability in metal additive manufacturing processes. J. Intell. Manuf. 2020, 31, 1769–1781. [Google Scholar] [CrossRef]
- Ntousia, M.; Fudos, I.; Moschopoulos, S.; Stamati, V. Predicting geometric errors and failures in additive manufacturing. Rapid Prototyp. J. 2023, 29, 1843–1861. [Google Scholar] [CrossRef]
- Trovato, M.; Cicconi, P. A Decision Tree approach for an early evaluation of 3D models in Design for Additive Manufacturing. Procedia CIRP 2024, 128, 96–101. [Google Scholar] [CrossRef]
- Su, J.; Mo, Y.; Shangguan, P.; Panwisawas, C.; Jiang, F.; Sing, S.L. Additive manufacturing-by-design for support structures: A critical review. Int. J. Extrem. Manuf. 2025, 7, 052002. [Google Scholar] [CrossRef]
- numpy-stl 3.2.0. PyPI—Python Package Index. Available online: https://pypi.org/project/numpy-stl/ (accessed on 11 May 2025).
- StandardScaler. Scikit-Learn Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html# (accessed on 11 May 2025).
- Azure Machine Learning. Microsoft Learn. Available online: https://learn.microsoft.com/en-us/azure/machine-learning/?view=azureml-api-2 (accessed on 11 May 2025).





| Model | When to Use | AM Applications |
|---|---|---|
| Support Vector Machine (SVM) | SVM is effective in solving classification problems involving datasets with numerous features, especially when using the kernel trick to handle complex, non-linear decision boundaries. It performs well on small datasets, especially when classes are separable. | Print success estimation, defect detection, process optimization, and material property analysis [21]. |
| Decision Tree (DT) | DT can be useful for datasets with numerical and categorical features and can handle non-linear decision boundaries. DT performs optimally with small to medium-sized datasets and can also be used with imbalanced data. However, it is susceptible to overfitting, particularly when the tree becomes excessively deep. | Defect classification, process parameter optimization, print quality analysis, and manufacturability prediction [22]. |
| Random Forest (RF) | RF excels at handling datasets with numerous features and complex non-linear interactions. | Image-based porosity classification [23]. |
| K-Nearest Neighbors (KNN) | KNN does not assume any predefined distribution for the underlying data. It is non-parametric and suitable for datasets with arbitrary distributions. It works well with numerical and categorical features. It requires careful tuning and can be computationally intensive for large datasets. | Surface roughness prediction [24]. |
| Naive Bayes (NB) | NB performs effectively with relatively small datasets, with good results for text classification or categorical data. The algorithm functions optimally with clean, noise-free datasets, and it can handle imbalanced data by estimating class probabilities. | Defect classification, material composition analysis, printability prediction, and anomaly detection [25]. |
| Convolutional Neural Networks (CNN) | CNNs excel at automatically learning spatial hierarchies of features, making them suitable for datasets with strong local patterns or visual characteristics. They are ideal for large datasets because they can generalize well. | Quality and process control [26]. |
| Recurrent Neural Network (RNN) | RNNs are designed to handle sequential data, making them suitable for datasets with critical temporal or sequential dependencies. RNNs are effective for datasets where the current input is influenced by previous states, allowing the model to capture dynamic patterns over time. | Process monitoring, fault detection over time, predictive maintenance, and real-time monitoring [27]. |
| Model | When to Use | AM Applications |
|---|---|---|
| Linear Regression (LR) | LR works best with numerical datasets that are well-structured, clean, and free from significant outliers. The method is sensitive to extreme values and unsuitable for datasets with strong non-linear patterns. It performs well with small to moderately sized datasets. | Process parameter optimization [28]. |
| Polynomial Regression (PR) | PR is particularly suitable for small to moderately sized datasets where polynomial terms of the independent variables can approximate the non-linearity. This method works best when the dataset is clean and free from outliers, as higher-degree polynomials are sensitive to noise and overfitting. | Process parameter modeling and optimization [29]. |
| Support Vector Regression (SVR) | SVR excels with small to moderately sized datasets, especially when the data has many features and the relationships are non-linear. SVR can capture intricate, non-linear. SVR is sensitive to noise and outliers. | Real-time monitoring for defect detection [30]. |
| Gradient Boosting Machines (GBM) | GBMs are well-suited for moderately sized datasets with diverse feature types, including numerical and categorical variables. GBR performs well even with noisy data or datasets with missing values, as the boosting mechanism reduces bias and variance. | Melt pool shape prediction with process parameters data [31]. |
| Deep Neural Networks (DNN) | DNNs excel in scenarios with high-dimensional data and multiple features, especially when sufficient labeled data is available to train the network effectively. They perform best with clean, well-preprocessed datasets, as they are sensitive to noise and can overfit smaller datasets without proper regularization techniques, such as dropout or weight decay. | Print time prediction, defect severity estimation, material property, and multi-parameter optimization [32]. |
| Recurrent Neural Network (RNN) | RNN is ideal for datasets with ordered structures, such as sensor data, production logs, process monitoring logs, or sequential datasets. The model requires large, clean, sequential datasets to learn effectively, as they are sensitive to noise and data quality. | Time-series prediction for print times, process monitoring and optimization, fault prediction, and tracking of material property evolution [33]. |
| Hyperparameter | Value/Type |
|---|---|
| Hidden layers | 5 |
| Neuron per hidden layer | 25, 50, 100, 50, 25 |
| Activation function | ReLU |
| Solver | Adam |
| Maximum iteration | 1000 |
| NN_1 | Train Metrics | Test Metrics |
|---|---|---|
| Support Volume 0° | R2: 0.9975 | R2: 0.9973 |
| MSE: 0.0022 | MSE: 0.0037 | |
| MAE: 0.0338 | MAE: 0.0416 | |
| Support Volume 30° | R2: 0.9930 | R2: 0.9912 |
| MSE: 0.0062 | MSE: 0.0125 | |
| MAE: 0.0602 | MAE: 0.0704 |
| NN_2 | Train Metrics | Test Metrics |
|---|---|---|
| NN_2_0: Printing Time 0° | R2: 0.9799 | R2: 0.9864 |
| MSE: 0.0191 | MSE: 0.0163 | |
| MAE: 0.0992 | MAE: 0.1036 | |
| NN_2_30: Printing Time 30° | R2: 0.9865 | R2: 0. 9846 |
| MSE: 0.0122 | MSE: 0.0212 | |
| MAE: 0.0811 | MAE: 0.1023 |
| NN_3 | Train Metrics | Test Metrics |
|---|---|---|
| NN_3_0: Analytical Cost 0° | R2: 0.9984 | R2: 0.9965 |
| MSE: 0.0015 | MSE: 0.0044 | |
| MAE: 0.0284 | MAE: 0.0457 | |
| NN_3_30: Analytical Cost 30° | R2: 0.9983 | R2: 0.9937 |
| MSE: 0.0015 | MSE: 0.0044 | |
| MAE: 0.0295 | MAE: 0.0527 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trovato, M.; Amicarelli, M.; Prist, M.; Cicconi, P. A Neural Network-Based Approach to Estimate Printing Time and Cost in L-PBF Projects. Machines 2025, 13, 550. https://doi.org/10.3390/machines13070550
Trovato M, Amicarelli M, Prist M, Cicconi P. A Neural Network-Based Approach to Estimate Printing Time and Cost in L-PBF Projects. Machines. 2025; 13(7):550. https://doi.org/10.3390/machines13070550
Chicago/Turabian StyleTrovato, Michele, Michele Amicarelli, Mariorosario Prist, and Paolo Cicconi. 2025. "A Neural Network-Based Approach to Estimate Printing Time and Cost in L-PBF Projects" Machines 13, no. 7: 550. https://doi.org/10.3390/machines13070550
APA StyleTrovato, M., Amicarelli, M., Prist, M., & Cicconi, P. (2025). A Neural Network-Based Approach to Estimate Printing Time and Cost in L-PBF Projects. Machines, 13(7), 550. https://doi.org/10.3390/machines13070550








