Abstract
In this paper, an enhanced deep reinforcement learning approach is presented for unmanned aerial vehicles (UAVs) operating in dynamic and potentially hazardous environments. Initially, the capability to discern obstacles from visual data is achieved through the application of the Yolov8-StrongSort technique. Concurrently, a novel data storage system for deep Q-networks (DQN), named dynamic data memory (DDM), is introduced to hasten the learning process and convergence for UAVs. Furthermore, addressing the issue of UAVs’ paths veering too close to obstacles, a novel strategy employing an artificial potential field to adjust the reward function is introduced, which effectively guides the UAVs away from proximate obstacles. Rigorous simulation tests in an AirSim-based environment confirm the effectiveness of these methods. Compared to DQN, dueling DQN, M-DQN, improved Q-learning, DDM-DQN, EPF (enhanced potential field), APF-DQN, and L1-MBRL, our algorithm achieves the highest success rate of 77.67%, while also having the lowest average number of moving steps. Additionally, we conducted obstacle avoidance experiments with UAVs with different densities of obstacles. These tests highlight fast learning convergence and real-time obstacle detection and avoidance, ensuring successful achievement of the target.
1. Introduction
Drone technology is widely used in various industries, and its application scope and influence are showing a significant and growing trend. Achieving autonomous obstacle avoidance in dynamically changing environments poses a significant challenge within the field of UAV technological research. The studies related to the navigation of autonomous UAVs through sensors installed onboard have always been successful in static environments [1,2,3,4,5]. However, dynamic environments are associated with many complexities, as numerous moving objects interfere with UAVs navigation. The unpredictable trajectories of such obstacles require detailed planning, since treating these obstacles as non-moving would lead to a lack of reaction time and the possibility of collisions by the UAV near their approach to them. Thus, attributes of these obstacles should be included into navigation methods as characteristics of a dynamic environment. Addressing dynamic obstacles efficiently and accurately presents a formidable challenge, especially given the constraints of the onboard computational resources tasked with environment sensing, navigation, and localization. Systems designed for obstacle detection and avoidance in dynamic settings [6,7,8,9,10] typically employ detection and tracking of moving objects (DATMO) [11] to ascertain the motion states of dynamic entities and adapt their trajectory accordingly. Nonetheless, these strategies often fall short in effectively detecting or circumventing dynamic obstacles.
In recent years, particularly the last half-decade, the performance of online multi-object tracking (MOT) facilitated by deep learning technologies has not met the efficiency levels of methods based on sparse principal component analyses [12,13]. This contrast becomes evident as we witness significant strides being made in the domain of neural networks, notably with the evolution from traditional convolutional neural networks (CNNs) to more sophisticated deep convolutional neural networks (DCNNs). These advancements have catalyzed substantial improvements in various computational tasks, including target detection and the tracking of multiple objects, thereby fostering progress in online MOT systems [14,15,16]. The deployment of DCNNs in analyzing natural scenes for object detection and tracking underscores their potent feature extraction prowess and the intricacies of their network architecture, which collectively enhance their ability to perform detailed and efficient image analyses [17,18]. In contrast, the detection-based tracking methodology (TBD) relies on the utilization of video-based detectors that identify targets, subsequently orchestrating and linking trajectories of objects post-identity verification based on the initial detection results [19]. Addressing the complexities introduced by employing multiple cameras in online MOT settings, various optimizations and enhancements in detection and tracking methods have been implemented. In a parallel vein, offline MOT implementations that leverage single-camera tracking strategies have demonstrated superior performance, although they are often hindered by the limited scope of their viewing angles. These single-camera setups prove more suitable for offline MOT scenarios [12,20], as they navigate the inherent limitations of viewing angles, which frequently lead to issues such as the misidentification of objects, occlusions, and challenges with debris motion [21,22].
Currently, references [23] and [24] provide comprehensive reviews of multi-object tracking literature based on visual tracking and detection technologies, rather than focusing specifically on deep learning methods for online multi-object tracking (MOT). SORT [25] incorporates a Kalman filter (KF) to approximate inter-frame displacement, while other models [26,27] focus on distinguishing appearance features to enhance matching accuracy. The tracker [28] utilizes the regression component of Faster R-CNN [29] to predict object displacement between consecutive frames. FFT [30] further integrates optical flow to assist with backward displacement estimation. In addition, the center tracking approach [31] develops a dedicated tracking branch specifically to predict motion.
Substantial progress has been made in UAV navigation through environments cluttered with both dynamic and static obstacles, with numerous investigations employing classical techniques such as the artificial potential field (APF) [32], rapidly exploring random trees (RRTs) [33], the A* algorithm [34], Voronoi diagrams (VDs) [35], and probabilistic roadmaps (PRMs) [36]. These traditional path planning approaches are favored for their straightforward implementation. Nonetheless, they often suffer from high time complexity and reduced efficacy in scenarios involving complex, high-dimensional spatial navigation. Alternatively, intelligent optimization algorithms such as the genetic algorithm (GA) [37], particle swarm optimization (PSO) [38], gray wolf optimization (GWO) [39], and differential evolution (DE) [40] have been adopted. These methodologies, while simple to deploy for UAV route optimization, boast extensive search capabilities and robustness in addressing large-scale problems. Despite these advantages, they are hampered by significant computational demands, performance sensitivity to parameter settings, and slow convergence rates. To mitigate these drawbacks, recent studies have pivoted to employing deep reinforcement learning techniques for autonomous navigation and collision avoidance (ANCA) challenges. For instance, a study in the literature [41] introduced a UAV obstacle avoidance strategy utilizing a deep recurrent q-network enhanced with temporal attention, enabling monocular camera-equipped quadrotors to autonomously navigate complex indoor environments. Another contribution [42] enhanced the deep Q-network (DQN) for path planning to address the overestimation biases commonly associated with Q-networks. One study outlined in the literature [43] developed a dual deep Q-network (DQN) leveraging a dueling architecture to enhance image-based ANCA for mobile robots, using Kinect sensors within a simplified simulation setting. Despite certain advancements, DQN-based methodologies still face challenges in navigating complex image environments effectively. As the environmental complexity escalates, both the convergence rate and the efficacy of the DQN are adversely impacted. To bolster the image navigation capabilities, the integration of convolutional neural network (CNN)-based target detection algorithms with DQN techniques is being explored. As detailed in the literature [44], a method for monocular visual obstacle avoidance in quadrotor UAVs employing deep learning techniques has been introduced. Furthermore, the literature [45] discusses a DQN strategy enhanced with YOLO for autonomous navigation in lawnmowers, where YOLO excels in identifying specific markers from camera-captured images, which are then seamlessly integrated into the DQN to facilitate autonomous navigation functionalities. Another study highlighted in the literature [46] introduces a distance estimation methodology based on deep learning, employing YOLOv3 to identify, categorize, and pinpoint target objects within images, followed by an evaluation of its efficacy using both DNN and CNN. However, the processing of detection results by these algorithms tends to be somewhat limited, failing to adequately address the dynamic and uncertain conditions typical of unmanned aerial vehicle (UAV) operations. To enhance the effectiveness in complex environments, where poor convergence and slower convergence rates are prevalent, optimizing the sampling probability of experiences in the replay memory is essential. The literature [47] discusses a strategy termed combined classical experience replay (ER), which incorporates the most recent experiences into the training batches from the replay buffer. Additionally, as described in the literature [48], an approach involves calculating the discrepancy between the action’s output and its estimated value for each experience, then setting the sampling probability accordingly based on this error magnitude. In scenarios involving dynamic, unknown UAV tasks, this method increases the computational demands and slows down training due to the continuous calculation of new parameters for each experience. Moreover, the frequent storage of experiences significantly enlarges the memory usage, thereby restricting the method’s utility and efficiency.
To tackle the issues identified above, this research presents improved deep reinforcement learning strategies that combine the Yolov8-StrongSort model with a new DQN data storage method. The key contributions of this research are outlined as follows:
- Considering the negative impact of dynamic obstacles, the reward function is set up using an artificial potential field to circumvent obstacles and approach the target so that the UAV can obtain the optimal path.
- We introduce a data storage mechanism that alters the distribution of the experience types in the replay memory, thereby accelerating the convergence of the proposed method.
- Based on the scenarios, we apply the Yolov8-StrongSort model to consider dynamic obstacle trajectories and the background of the image output from the model, thereby reducing the difficulty of training the UAV.
- For efficient target tracking, we choose OSNet, a lightweight yet powerful network architecture with exceptional target reidentification capabilities, ensuring stable performance even in complex environments.
This paper is structured as follows. The following sections provide an organized introduction to the paper. Section 2 describes the UAV ANCA problem in detail. Section 3 describes the system framework, the optimization of StrongSort, a detailed description of the playback memory data storage mechanism, and a mathematical analysis of collision avoidance. In Section 4, we describe and analyze the results and present a discussion. Finally, in Section 5, we summarize the results of this paper and propose future research directions.
2. Reinforcement Learning for the UAV ANCA Problem
This section defines the state, action, and reward foundations within the context of reinforcement learning and then develops a model of the environment that suits the frameworks of reinforcement learning. In particular, the problem of UAV collision avoidance is formulated as a Markov decision process.
2.1. States and Actions
To enhance the resolution of the UAV ANCA issue, it is essential to precisely define the input state and the corresponding action , where t symbolizes time. During mission execution, the UAV’s available states include its own state , the target’s state , and visual data . The state , comprising coordinates and velocities , is derived from GPS and gyroscopic measurements, with and denoting the trajectory and heading angle, respectively; the target state , predetermined before the mission or adjusted in real-time through UAV communications, consists of ; represents imagery from the onboard camera, utilized primarily for collision avoidance. Both the UAV and target states, and , are described within the inertial coordinate framework. This approach ensures that the methodology remains effective, even in varying scenarios. Moreover, any intervention studies involving animals or humans, along with other studies requiring ethical approval, must clearly state the authority granting this approval and include the relevant ethical approval code.
In this context, represents the variance between the current and minimum set flight altitudes. Meanwhile, measures the altitude differential relative to the destination. The parameters and specify the UAV’s relative positioning to its destination along the XOY and XOZ planes, respectively. Given these inputs , the corresponding action is defined as , with and controlling the UAV’s trajectory and heading angle, respectively.
2.2. Reward Function Design Based on Artificial Potential Field Method
We adopted an artificial potential field-based approach to design the reward function because it combines simplicity, adaptability, and effectiveness, and can naturally integrate navigation and obstacle avoidance targets into a unified framework. At the same time, it is compatible with reinforcement learning methods. The core idea of this method is to guide drones to efficiently reach targets and safely avoid obstacles in complex environments through the interaction of attraction and repulsion.
As the UAV advances towards its target, the reward function is bifurcated into two components based on the concept of an artificial potential field. The first segment encompasses the positional reward function, which itself is divided into the target acquisition reward and the obstacle avoidance reward. The target acquisition reward aims to expedite the UAV’s journey to the target location, whereas the obstacle avoidance reward ensures the UAV maintains a safe distance from any obstructions. The second segment pertains to the directional reward function, which is crucial for effective navigation. Given that the resultant force direction in the artificial potential field aligns well with the UAV’s trajectory, this directional reward is crafted to steer the UAV precisely towards the designated target point. In developing the positional reward function, the gravitational potential field method is initially employed to formulate the target reward function.
Here, represents the constant in the gravitational reward function and refers to the distance from the current location to the target point.
The obstacle avoidance reward function is developed in part by integrating a repulsive potential field function. This function assigns increasingly negative rewards as the UAV’s proximity to an obstacle decreases.
In this context, represents the constant associated with the repulsive reward function, specifies the distance from the UAV to the nearest obstacle, and denotes the maximum distance at which an obstacle exerts its influence.
In the directional reward function, the resultant force influencing the robot aligns with its intended trajectory. The angular disparity between the robot’s actual and intended directions is quantified as follows.
Here, represents the intended direction, indicates the actual direction, φ is the angle that measures the deviation between the intended and actual directions, and represents the directional reward constant, which controls the weight of directional consistency. Consequently, the directional reward function can be articulated as follows.
By synthesizing Equations (2), (3) and (5), the comprehensive reward function is formulated as follows.
The parameters and in the reward function control the weights of different reward components, reflecting the importance of target attractiveness, obstacle repulsion, and navigation directionality. By adjusting the weights of parameters and based on the environment, balancing obstacle avoidance and a quick arrival at the destination, the optimized reward function exhibits a high success rate and navigation efficiency in the task.
Consequently, the total reward function for the mobile robot is delineated as follows.
Here, is defined as the radius surrounding the target point that constitutes the target area, while is the radius around the obstacle defining the collision area, where the reward value for drones is , and the reward value for drones is .
To evaluate the efficacy of the reward function based on the artificial potential field, the setting of the reward function takes into account only the distance between the mobile robot and the target point for comparative purposes. The configuration of the reward function is presented as follows:
2.3. Markov Decision Process
During a task, the UAV intelligently selects a move based on the current state at time step t. Following the implementation of action , the state transitions from to , at which point the UAV receives an environmental reward . The UAV’s decision-making process in selecting actions is inherently Markovian, hence it is described as a Markov decision process [43]. This process is characterized by a set of components known as a quaternion.
Here, comprises the entire state space, with indicating the state at time step t; represents the action space, with denoting the action taken at time step t. , the probability of state transition, signifies the likelihood of moving to the new state and receiving the reward after action is carried out in state . serves as the reward function, while is the reward accrued from executing action in state .
2.4. Examples
In this section, we present a simple example scenario and calculation. We assume that the UAV needs to reach the target point from the starting point and an obstacle at needs to be avoided during the path planning process. The UAV’s state space includes its position, velocity, target distance (), and obstacle distance (). Initially, these values are set as:
The UAV can perform two types of maneuvers: moving forward or changing direction. The path planning strategy is guided by a reward function consisting of three components: target attraction, obstacle avoidance, and heading consistency. The total reward function is defined as:
Target attraction reward (encourages moving toward the goal):
Obstacle avoidance reward (prevents UAV from getting too close to obstacles):
Heading consistency reward (ensures the UAV maintains an optimal direction):
The total initial reward calculation is:
3. Methods
3.1. System Framework
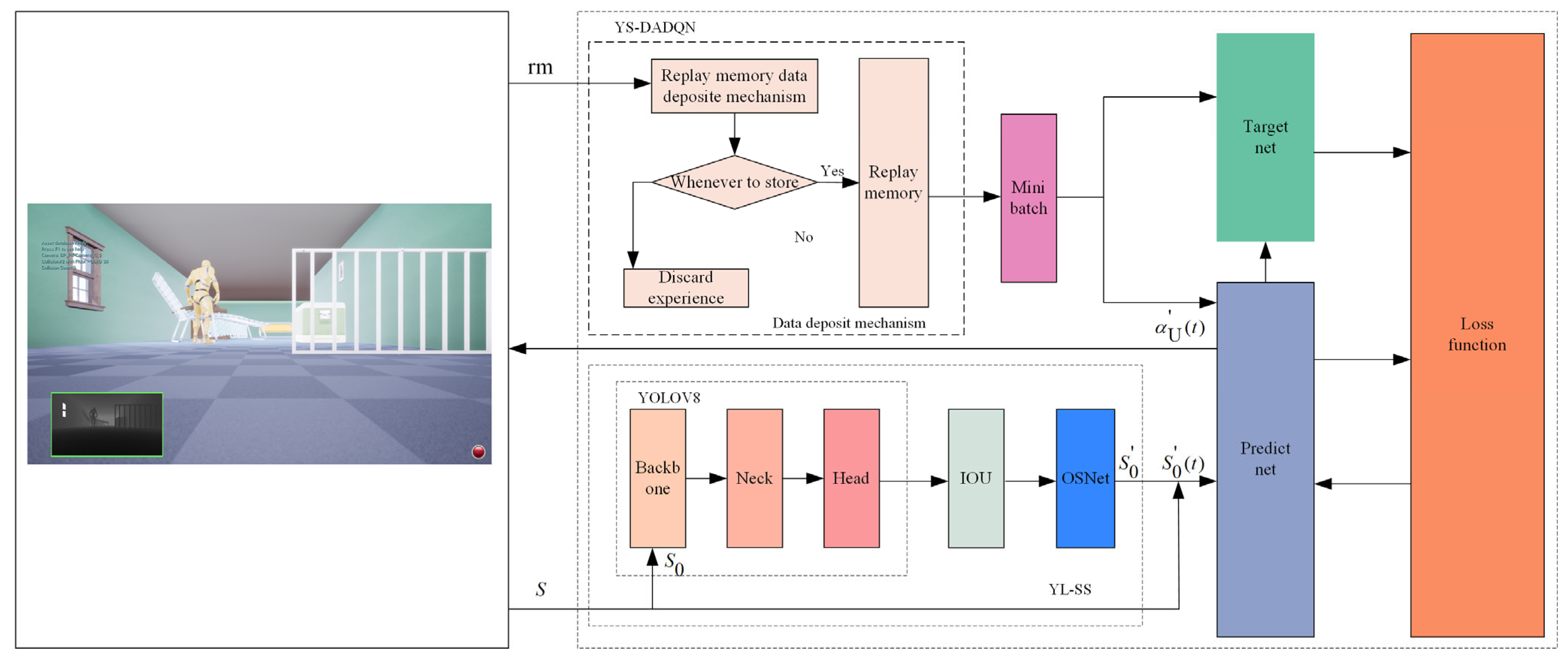
Figure 1 illustrates the YS-DADQN architecture. In this setup, the UAV gathers state information using onboard sensors and provides an enhanced image to the advanced Yolov8-StrongSort model. This model processes the image for feature extraction and subsequently identifies obstacle data . Integrating these data with positional details, the updated state is fed into the predictive network. From state , this network predicts the optimal maneuver . Upon implementing , the system receives the updated state S(t + 1) along with the associated reward . Subsequently, the current experience tuple is assessed for storage in the replay memory based on specific criteria; if it does not meet these, it is discarded. The filtering process adjusts the distribution of experiences within the replay memory, ensuring a balanced sampling likelihood for each experience category. Random sets of experiences are then drawn from the replay memory, inputted into both the predictive and target networks, followed by error evaluation via the loss function. Using the computed error, the gradient descent method refines the predictive network. During training, both the direction and distance to obstacles and targets are calculated, and the reward value is derived from the reward function of the artificial potential field. After extensive training and optimization, an intelligent entity capable of ANCA is developed.
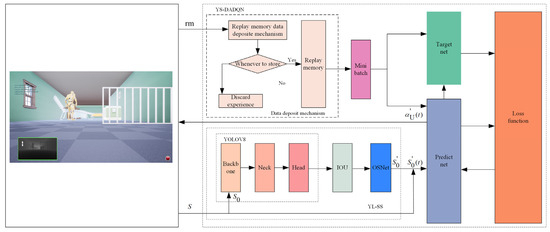
Figure 1.
YS-DADQN structure and data flow.
3.2. Obstacle Detection and Tracking
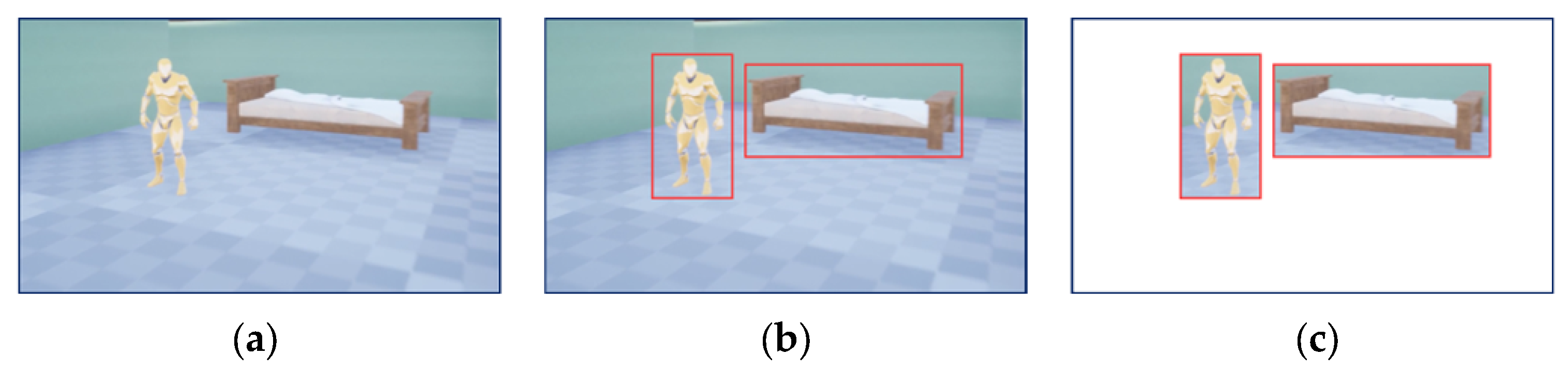
To mitigate collisions with dynamic obstacles, the initial step involves identifying the status of these obstacles through detection and tracking. As depicted in Figure 2, the process starts by using RGBD images to identify 2D areas of potential motion in objects (illustrated in Figure 2a). Given the UAV’s limited computational capabilities, the lightweight Yolov8-StrongSort neural network is utilized for this task. This method offers greater resilience and less sensitivity to alterations in algorithmic settings and environmental conditions compared to point-cloud-based clustering techniques [49,50]. It also achieves higher efficiency and accuracy. The images processed for tracking and recognition (as in Figure 2b) are further utilized to isolate obstacle information by removing background elements (as shown in Figure 2c).
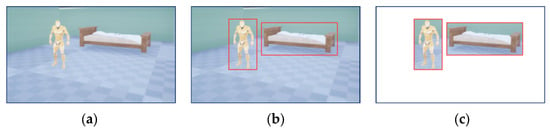
Figure 2.
(a) Raw RGB image. (b) Obstacle tracking and identification. (c) Background elimination of obstacle tracking identification. Red boxes are detected obstacles.
Following the outcomes of the object detection, tracking is conducted using the StrongSort algorithm, which involves calculating the pairwise distances among detected objects in images captured at successive time steps. This technique supports the correlation of information across multiple frames, thereby enhancing the tracking of objects. Additionally, leveraging the camera’s pose, it is possible to estimate the velocity, trajectory, and other dynamic states of an object over a defined period. An object’s motion state is defined by its velocity. If the computed velocity consistently surpasses a pre-established threshold, , the object is classified as moving; if not, it is regarded as part of the static environment.
Our obstacle avoidance planning system is predicated on forecasting the forthcoming paths of dynamic obstacles. Exploring future trajectories of objects is a compelling subject that has been approached in various ways [51,52,53]. Nonetheless, considering the demands of UAV flight control, the prediction models need to be streamlined for efficacy. Building on the methodology proposed by Eppenberger [54], we adopt a conservative motion model to predict the velocity and imminent trajectory of any detected dynamic obstacle. When a dynamic obstacle moves on a horizontal plane, its velocity can be accurately estimated using a Kalman filter (KF). For such an obstacle, its state vector = [, , , ] captures its position and velocity in the plane. The measurement input for the KF at time t, denoted as , represents the center of mass of the object on this plane. We define the dynamics of the system and the measurement model accordingly.
In this model, A represents the state transition matrix, while H serves as the observation matrix, with Q and R modeling the system and measurement noise, respectively.
Based on a priori knowledge, the noise coefficients in the Kalman filters were selected as = 0.05 (position), = 0.00625 (velocity), and = 0.05 (motion).
This framework supports the real-time, short-term forecasting of the movement paths of dynamic obstacles. It should be noted that during the tracking phase, if there is a significant discrepancy between the actual observed position of the target and the position estimated by the Kalman filter (KF), this is indicative of a tracking error. In such instances, the prior results are discarded and the tracking sequence is reinitiated.
3.2.1. Yolov8
YOLOv8s is a streamlined version of the YOLOv8 algorithm, featuring a lightweight parameter structure. It includes a backbone network, a neck network, and a prediction output header. The backbone network performs convolutional operations on RGB (red, green, blue) images to extract multi-scale features. The neck network’s function is to integrate these features from the backbone. A common method used for this integration is the feature pyramid network (FPN), which combines lower-level features into more abstract representations. The prediction header is tasked with classifying the target categories and employing three different-sized sets of detection sensors to identify and select relevant image content.
YOLOv8s is a streamlined version of the YOLOv8 algorithm, featuring a lightweight parameter structure. It includes a backbone network, a neck network, and a prediction output header. The backbone network performs convolutional operations on RGB (red, green, blue) images to extract multiscale features. The neck network’s function is to integrate these features from the backbone. A common method used for this integration is the feature pyramid network (FPN), which combines lower-level features into more abstract representations. The prediction header is tasked with classifying the target categories and employing three different-sized sets of detection sensors to identify and select relevant image content.
3.2.2. Optimization of StrongSort
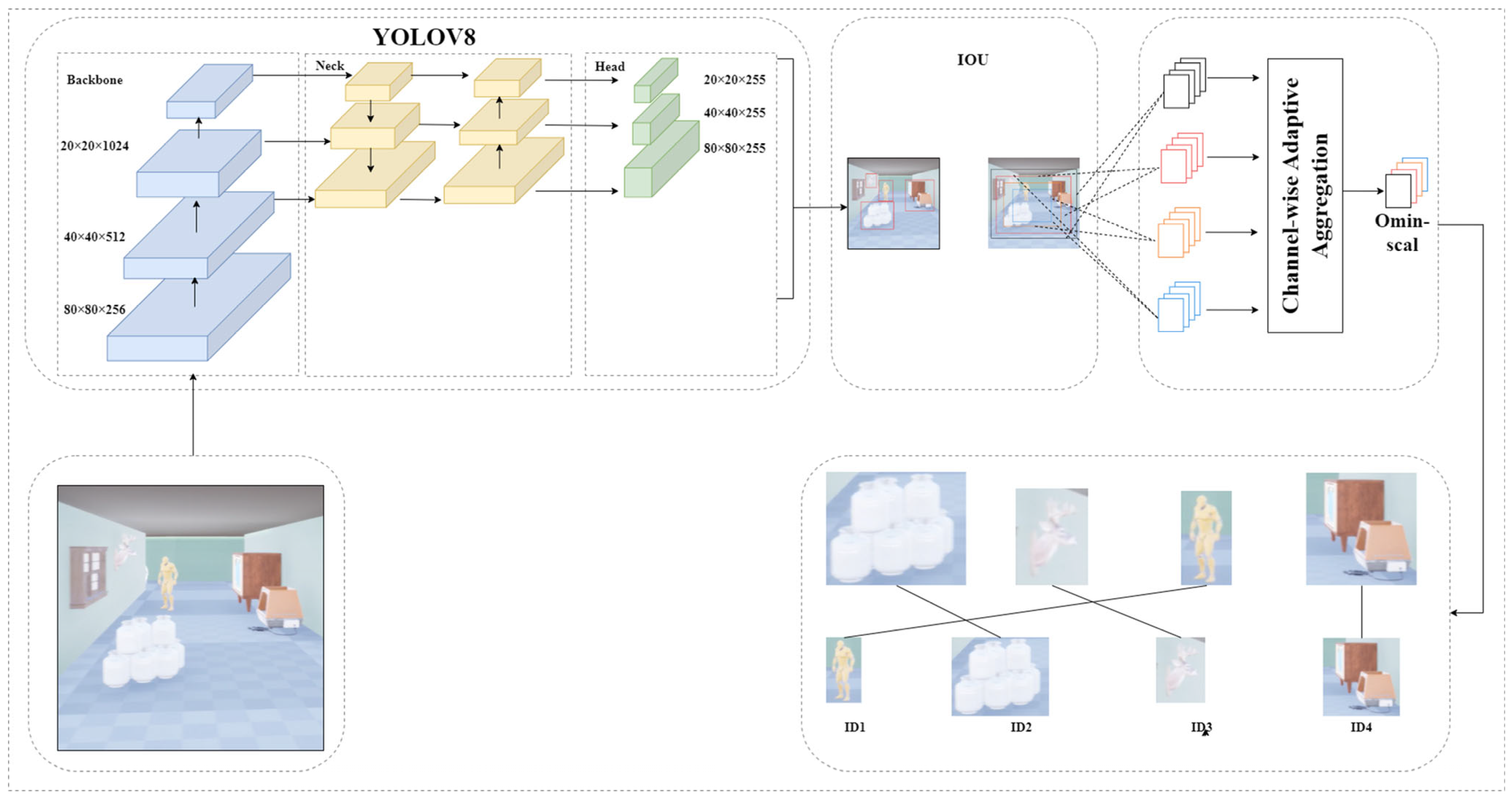
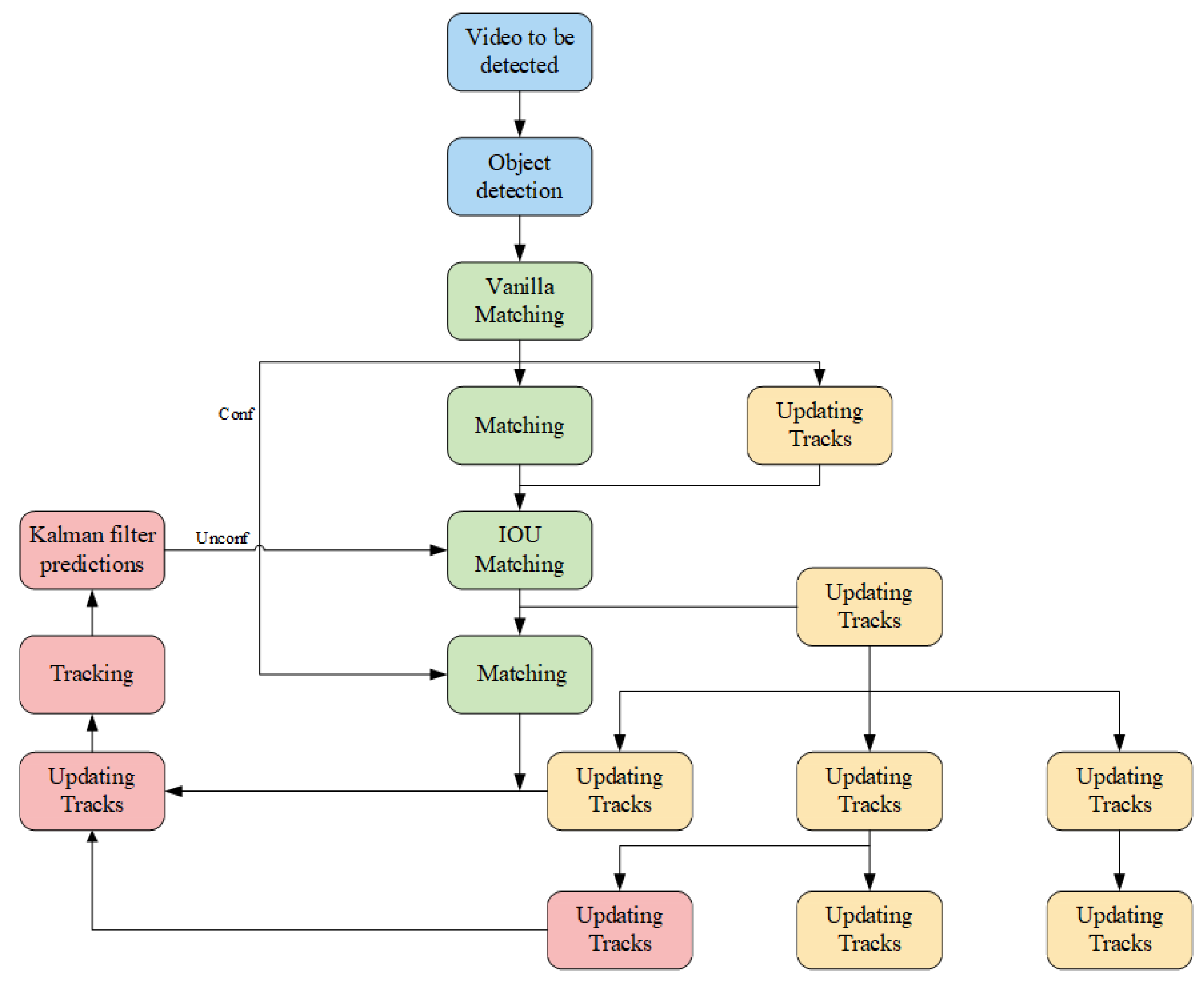
The architecture of the Yolov8-StrongSort algorithm is depicted in Figure 3. Initially, videos to be analyzed pass through the target detection module, utilizing YOLOv8 as the detector, which identifies and outputs details about the target boxes. Subsequently, within the tracking module, a comprehensive network (OSNet) serves as a feature extraction network, pulling the appearance features of the targets. Concurrently, the NSA Kalman method in this module updates and forecasts the location data of the targets, while in state estimation, observation noise impacts the accuracy of measurements. The measurement noise covariance R is utilized to quantify the noise scales associated with the measurements. In Kalman’s algorithm, the noise scale is a constant matrix. However, different measurements have varying noise scales, which should be adjusted with the detection confidence. Equation (21) introduces an adaptive approach for determining the noise covariance. The outputs from the target detection are then integrated with the tracking predictions using both vanilla and IOU matching techniques. If the vanilla matching confirms a match, the next frame is updated and predicted immediately. If a matched target vanishes but reappears within N frames, its tracking is reaffirmed and the next frame is forecasted. For newly appearing targets without prior tracking frames, IOU matching is employed, and if three consecutive matches succeed, the tracking state is established as confirmed. The procedural flowchart of this algorithm is illustrated in Figure 4.
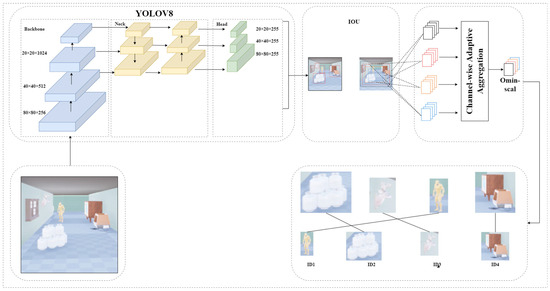
Figure 3.
Yolov8-StrongSort algorithm framework.
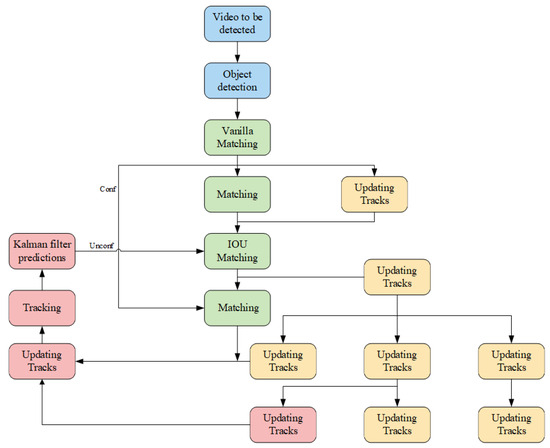
Figure 4.
Flowchart of Yolov8-StrongSort algorithm.
- NSA Kalman (Noise-Scale Adaptive Kalman Algorithm)
Traditional Kalman filters [55] utilize recursive algorithms to predict past, present, and future states of detection boxes, serving as a robust, efficient method for state estimation that is widely applied in engineering challenges. Nevertheless, in dynamic multi-target tracking environments typical for UAVs, issues such as environmental shifts, sensor errors, and fluctuating noise levels present significant hurdles. The standard practice of applying a consistent measurement noise level across all detection boxes, without considering their detection quality, may not yield precise motion estimations. Consequently, within the camera module, we implemented an enhanced correlation co-efficient maximization (ECC) [56] technique, which incorporates camera motion compensation as described in Equation (20).
Here, ∥·∥ signifies the Euclidean norm, represents the deformation parameter, and and are the zero-mean normalized forms of the reference image ir and the warped image , respectively. To address the issue of image alignment, an iterative method, which could either be positive additive or inverse composite, was employed to minimize the function . The ECC algorithm [57] provides an effective strategy for mitigating the impact of UAV motion noise, establishing its utility as a dependable tool for such applications.
Later, Du and Y introduced the NSA Kalman algorithm [58], which enhances the detection accuracy by dynamically adjusting the noise scale based on the quality of the detected target box. The adaptive modification of the noise covariance , as specified in Equation (21), is determined through specific metrics that assess the detection quality.
In this model, represents the constant measurement noise covariance, and it also indicates the detection confidence score for state k. A lower noise level correlates with a higher detection confidence score , resulting in a reduced value of . A decrease in signifies an increased influence of detection data in the state update process and vice versa. This methodology significantly enhances the precision of state updates.
- Target Reidentification
ResNet50 [59], known for its robust performance in the ImageNet large-scale image classification competition, is extensively utilized across a variety of image processing applications [60,61,62]. Nonetheless, the considerable size and parameter count of ResNet50 contribute to increased image processing durations and heightened computational demands, rendering it less optimal for resource-limited UAV platforms. Conversely, OSNet is tailor-made for specific applications such as target reidentification, delivering superior performance characterized by enhanced efficiency and adaptability. Consequently, we opted for OSNet over ResNet50 in the StrongSORT algorithm and conducted training with a specific dataset.
We incorporated the feature storage and update mechanism outlined in [63], which leverages both multiple frame data and variations between frames. This approach is particularly adept for enhancing the correlation between detection and tracking within intricate environments. In this methodology, the appearance state of the trajectory in frame t within the feature extraction segment is updated using an exponential moving average (EMA). The corresponding formula is depicted in Equation (22).
In this model, represents the appearance embedding corresponding to the detected match, and the value for α (representing the motion vector) is set at 0.9. By employing the EMA method for updates, this strategy enhances the matching accuracy and concurrently decreases the computational time required.
3.3. Path Planning
This section introduces an enhanced version of the DQN method, tailored for scenarios involving UAVs using only onboard camera images for autonomous navigation. To augment the image-based navigation capabilities, the Yolov8-StrongSort model is integrated within the DQN framework, hence forming the YOLO-StrongSort-enhanced DQN approach. Furthermore, traditional experience replay techniques have become ineffective due to changing scene features, adversely affecting the UAV training outcomes. To address this, an innovative experience replay mechanism called the data-driven memory (DDM) model is proposed, incorporating Yolov8-StrongSort into a data storage mechanism, referred to as YS-DADQN.
3.3.1. DQN
Developed by the DeepMind team, the DQN [64] framework represents an advanced deep reinforcement learning approach that melds Q-learning with deep neural networks and an empirical replay mechanism, facilitating the generation of action–value functions across an extensive state space. Within the DQN architecture, the prediction network and its counterpart, the target network , share identical structures. To evaluate and optimize the approximation quality, the networks’ loss function is articulated in Equation (23). Furthermore, Equation (24) delineates the computation of the gradient for the parameter θ, which is subsequently refined using the gradient descent technique to ascertain the optimal action–value function after thorough training.
This paper identifies two significant challenges in adapting the traditional DQN framework to the current study’s scenarios: the absence of robust image-based autonomous navigation capabilities for ANCA and the ineffectiveness of traditional empirical replay techniques. To address these issues, this work introduces the YS-DADQN model, which modifies the conventional structure of the DQN method.
3.3.2. Playback Memory Data Storage Mechanism
In light of the scenarios outlined in this study, traditional experience replay methods used within DQN frameworks have proved inadequate, inhibiting the attainment of superior training outcomes for artificial intelligences. Consequently, this paper introduces an innovative DDM approach specifically designed to refine the experience playback mechanism in the DQN context.
This research outlines task scenarios marked by three distinct aspects: (A) their complexity; (B) the drone speed is low compared to the scene area; (C) a reward mechanism that only acknowledges the final action in each sequence. Such characteristics contribute to a disproportionate distribution of experiences within the replay memory—predominantly storing intermediate, non-rewarding states and fewer critical, rewarding end states. This disproportionality hinders the training efficacy of UAVs. Moreover, DQN training involves enhancing the decision-making capabilities of autonomous systems through randomly sampling small subsets of experiences from the significantly larger replay memory (for instance, a replay memory of 1000 while only 64 experiences are sampled at a time). The skewed experience representation coupled with the minimal exposure to diverse scenarios during each sampling event challenges the enhancement of UAV training outcomes.
Consequently, we introduce a replay memory dynamic deposit model (DDM) designed to reduce the computational complexity while adjusting the sampling probability of various experiences. This model classifies experiences and allocates a specific deposit ratio to each category. By using this ratio, the proportion of each experience type within the replay memory is recalibrated, ensuring that every category of experience has an opportunity to be included in smaller sample batches.
In addressing the UAV ANCA issue, the empirical replay memory (RM) is archived within the playback memory. This archive is composed of the actions executed, represented by , along with the .
Here, represents the sequence number of the experience data. The symbol α- indicates the time step one αU prior to the execution of the operation, while α+ signifies the time step one αU after the execution. The capacity of the replay memory is denoted as . In this scenario, the state following the operation in the experience also corresponds to the state prior to the operation in the experience .
Based on the analysis of the state data, the task scenario is defined by as follows:
where [∙][∙] denotes the task situation represented by the state. The parameters are used to define this scenario; indicates the detection of an obstacle by the agent, signifies a collision, represents crossing a boundary, and denotes reaching the destination. The values and definitions for are listed in Table 1.

Table 1.
System description parameters.
Based on the aforementioned mission scenario, the states obtained by the agent can be classified as follows: , where the drone neither detects obstacles nor collides, crosses boundaries, or reaches the destination; , where the drone detects an obstacle without colliding, crossing boundaries, or arriving at the destination; , where the drone collides with an obstacle; , where the drone crosses the boundary; , where the drone reaches its destination.
In addition, experiences are classified according to the type of state in the replay memory as follows, where .
(1) A resulting experience (RE) refers to the type of experience gained by an agent at the conclusion of each episode within the simulation. This experience is subdivided into three specific categories: the arrival experience, denoted as ; the collision experience, referred to as ; and the experience of exceeding the boundary limits, labeled as .
All three types of experiences provide non-zero rewards, enabling the intelligent agent to learn effective strategies. Positive rewards guide the agent to navigate towards its destination, while negative rewards teach it to avoid collisions and crossing boundaries. Additionally, since RE-type experiences are only generated at the end of each episode, they are relatively infrequent compared to the replay memory capacity. Therefore, a higher deposit rate should be assigned to RE-type experiences.
(2) Dangerous experiences (DE) occur when the agent detects an obstacle. In such cases, the drone approaches the obstacle, requiring the intelligent agent to decide whether to avoid it. The agent must determine an appropriate obstacle avoidance action based on the positions of both the obstacle and the destination.
In this context, RE represents the experience where the agent detects an obstacle before taking action and no longer detects it afterward. Conversely, DE indicates an experience where the agent does not detect any obstacle before the action but detects it afterward. Additionally, it includes the experience where obstacles are detected both before and after executing the action.
The DE and experience types both relate to obstacles but serve different purposes. experiences teach the UAV to avoid collisions when near an obstacle, while DE experiences enable the intelligent agent to learn collision avoidance strategies. During training, DE experiences are generated when the UAV approaches obstacles. As the training progresses and the UAV becomes adept at avoiding obstacles, the frequency of these experiences increases as the UAV navigates more effectively between obstacles. Consequently, the replay memory may contain a higher number of DE experiences, necessitating a lower deposit ratio, , for these experiences.
(3) A safety experience (SE) represents an intermediate state, where the drone is navigating towards its destination while avoiding obstacles.
In the research presented here, the employment of a positive reinforcement mechanism at the culmination of each episode significantly aided in training the artificial intelligence agents to proficiently pilot a drone towards its intended target. The investigation encompassed scenarios that involved extensive tasks, thereby accumulating a substantial volume of SE (successful experience) instances. Given this abundance, it is advisable to establish a minimal deposit ratio, denoted as , for these types of experiences to optimize the learning efficiency.
As part of the training protocol, variable deposit ratios were applied to different categories of experiences, as previously outlined. Subsequently, a selective proportion of each experience category was incorporated into the replay memory. This approach led to a recalibrated quantitative composition of the assorted experience types within the revised replay memory structure.
The notation |∙| signifies the count of designated experience types present in the replay memory, while RM′ represents the collection of all experiences stored within the newly updated replay memory. Details regarding the operation of this data storage process are illustrated in Algorithm A1, appended to this document.
3.4. Mathematical Analysis of Collision Avoidance
To ensure the safety of the proposed method, we provide a mathematical framework to guarantee collision avoidance. The analysis includes a theoretical derivation based on the Markov decision process framework, a proof based on Lyapunov stability, and a worst-case evaluation.
3.4.1. Security Assurance in the Framework of the Markov Decision Process
The UAV path planning problem can be represented as a Markov decision process, defined as a tuple:
where is the state space, including the UAV position and obstacle position; is the action space, representing the possible directions of movement of the UAV; is the state transfer probability function; is a reward function designed to penalise collisions and encourage safe navigation; is the discount factor.
Assigning a large penalty value for collisions ensures that the optimal policy learned by reinforcement learning avoids entering a collision state. Specifically, we define:
where is a large penalty constant and represents the Euclidean distance to the goal. Theorem 1 proves that under this reward setting, the learned policy is able to avoid collisions, and the detailed proof is given in Appendix A.
Theorem 1.
(Collision avoidance in the form of Markov decision process. For detailed certification see 2. Certification in Appendix A.) The optimal policy obtained by reinforcement learning is satisfied for a sufficiently large value of the reward function:
3.4.2. Safe Path Planning Based on a Lyapunov Stability Analysis
We use the Lyapunov function V(s) to analyze the stability of the UAV trajectory, where V(s) represents the extent to which the UAV deviates from the optimal path. The definition is as follows:
where denotes the distance to the obstacle, and t is the weight that balances the target point optimization and obstacle avoidance. Its time derivative is satisfied:
This ensures asymptotic stability, i.e., the drone can navigate along a safe trajectory and reduce the risk of collision.
3.4.3. Worst-Case Scenario Assessment
To evaluate the worst-case performance, we consider the scenario where obstacles move randomly at high speeds. We derive an upper bound on the collision probability based on the worst-case state transfer model:
Combined with the theoretical analysis, we can conclude that:
By optimizing the obstacle avoidance strategy and reducing the probability of visiting the collision region, we were able to keep the value within acceptable limits.
4. Results and Discussion
4.1. Experimental Environment
The experimental setup comprised Ubuntu 18.04, TensorFlow 1.4.0, and CUDA 11.0, running on an Intel i9-14900KF processor. The simulation was conducted using the Airsim platform, where an indoor experimental setup was designed to validate the effectiveness of the proposed YS-DADQN algorithm in 3D environments. The experimental environment was arranged with various sizes of furniture as static obstacles and five walking figures inside the house as dynamic obstacles, as illustrated in Figure 5. We set the starting and target positions to train unmanned aerial vehicles in obstacle avoidance. The dynamic obstacles moved randomly within a 10 m radius at a speed of 0.7 m/s. In this mission scenario, the UAV’s speed and maximum heading angular velocity were configured to 0.7 m/s and 0.84 rad/s, respectively.

Figure 5.
Snapshot of the test environment in UE4.
4.2. Comparative Experiments with Yolov8-StrongSort
To train the Yolov8-StrongSort model, we constructed our own dataset called SDO by combining it with the environment. A total of four video clips were recorded, resulting in 2390 extracted frames. The dataset, containing 1920 × 1280 pixel images, was segmented into training and validation groups with allocation rates of 80% and 20%, respectively. Specifically, the training group was equipped with 1912 images, whereas the validation group was furnished with 478 images.
In the realm of dynamic multi-target tracking, a comparison was conducted between Deep-SORT, ByteTrack, StrongSort, and the enhanced YL-SS algorithm. Each of these models was trained under identical conditions, employing pre-trained weights and utilizing our SDO dataset. The trackers were evaluated based on several metrics, including IDF1, false positives (FP), ID switches (IDSW), and the detection time. The experimental results are presented in Table 2.

Table 2.
Comparative results for different models. Here, ↓ indicates better performance (lower is better) and ↑ indicates better performance (higher is better).
The data presented in Table 2 reveal that the ByteTrack algorithm achieves the highest detection speed among all algorithms, surpassing the YL-SS algorithm. It is essential to recognize, however, that this increased speed comes with a significant rise in ID switches by 125%, and a 52.02% increase in total false positives. Moreover, there are reductions in ID tracking precision and recall by 5.31% and 3.12%, respectively. On the other hand, the YL-SS algorithm offers consistent real-time performance and notably improves upon key metrics such as the ID switching, tracking accuracy, and recall, particularly when benchmarked against the Deep-SORT algorithm. This makes the YL-SS algorithm a reliable option for demanding tracking tasks. Figure 6 shows the detection tracking effect. Additionally, while the YL-SS algorithm exhibits a slight decline in accuracy relative to the precision-oriented StrongSort algorithm, it compensates with a 34.7% enhancement in detection speed.
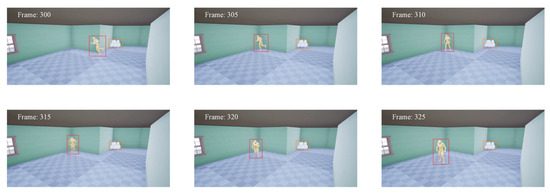
Figure 6.
Detection tracking effect. Red boxes are detected obstacles.
4.3. UAV Path Planning
4.3.1. Experimental Setup
Over a series of 950 training episodes, we evaluated the performance of four algorithms: DQN, DDM-DQN, APF-DQN, and YS-DADQN. We evaluated each model’s ability to avoid obstacles, measured success rates, and analyzed how training influenced the performance. The parameters of the algorithm during experimental training are shown in Table 3.

Table 3.
Training parameters and values.
4.3.2. UAV Indoor Obstacle Avoidance
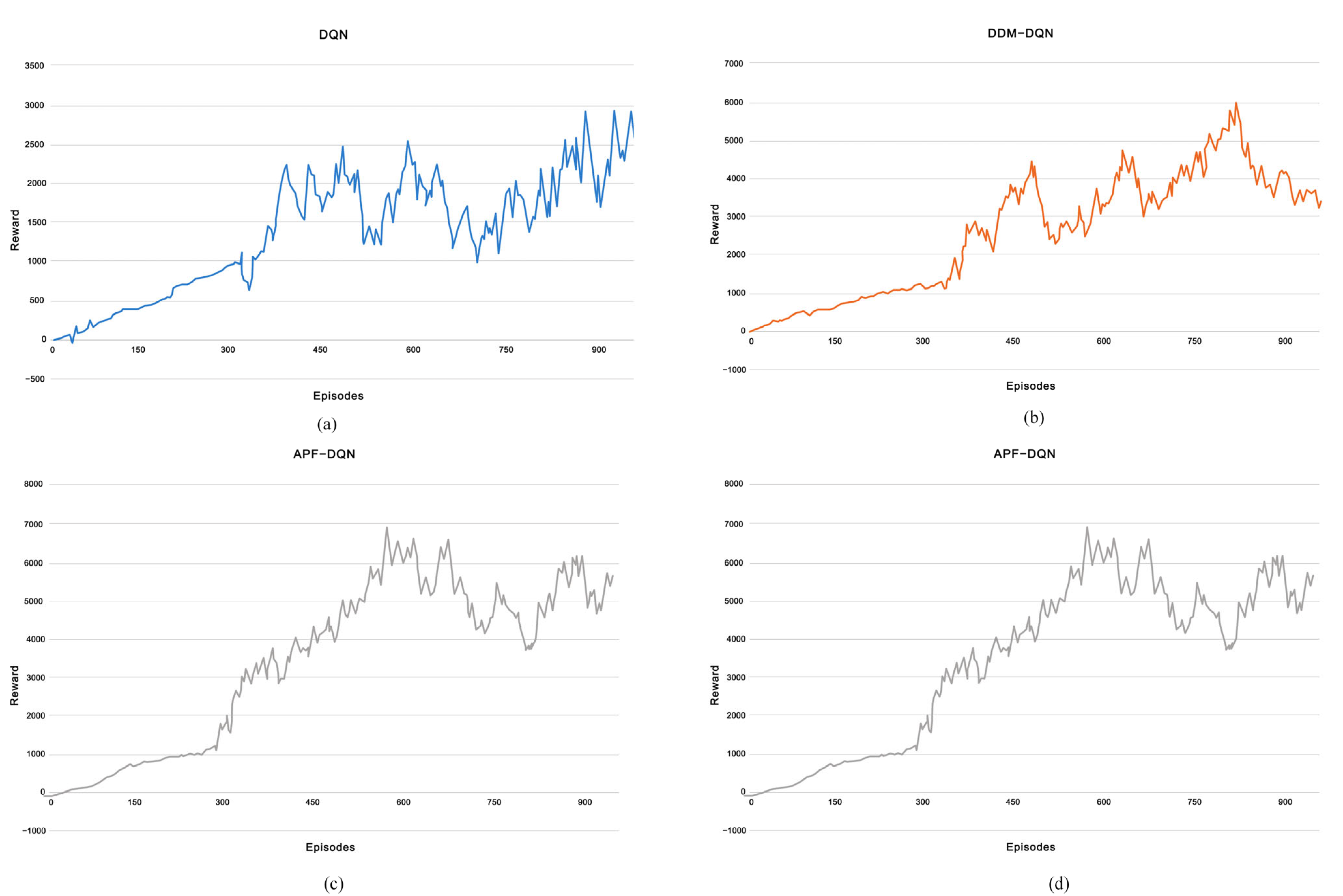
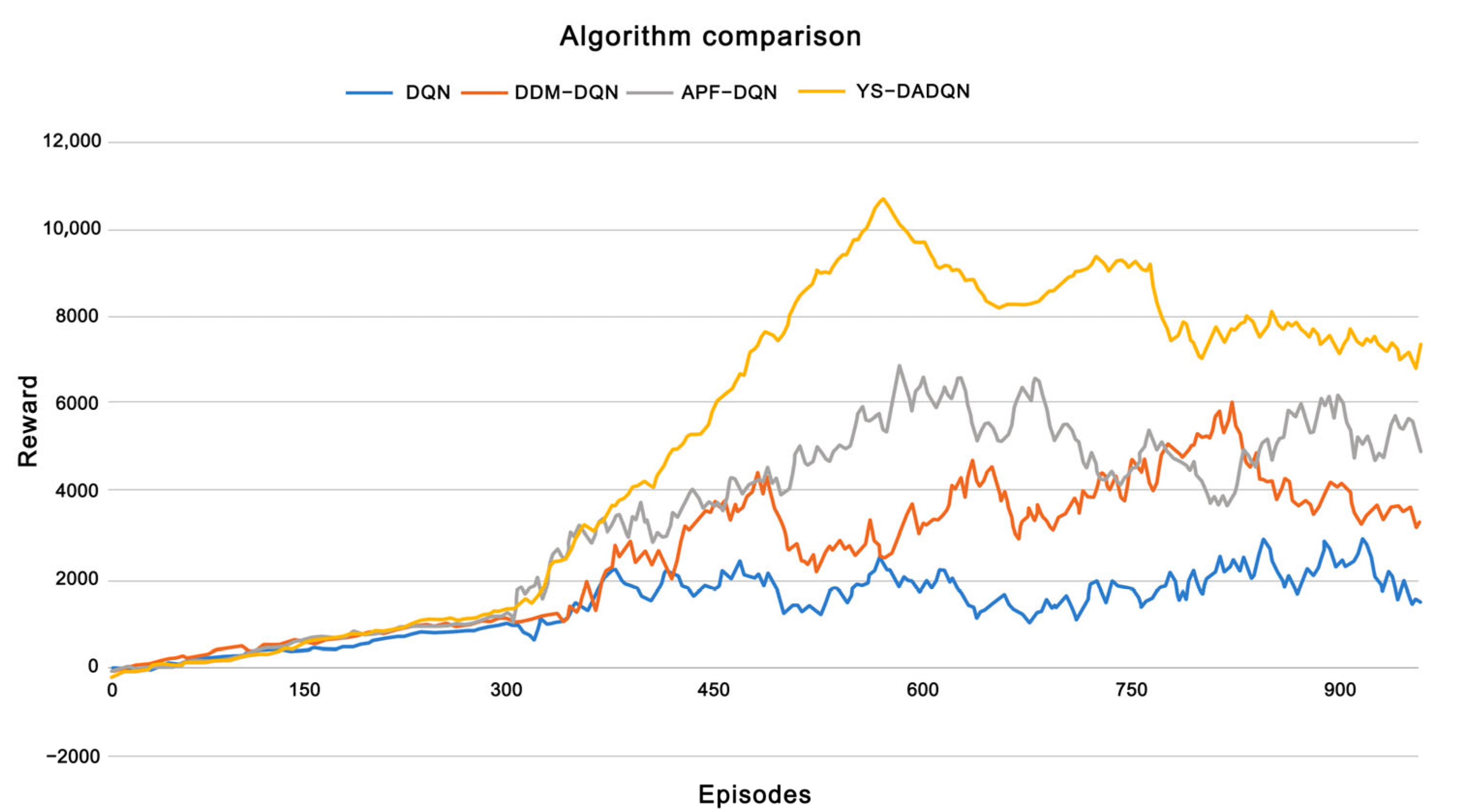
In this research, Figure 7 illustrates the relationship between episodes and rewards in path planning for dynamic and static environments across four models: DQN, DDM-DQN, APF-DQN, and YS-DADQN. Each algorithm was tested over 950 episodes to compare convergence speeds. The curves in Figure 8 represent the reward per UAV round. Initially, the UAV lacks the experience needed to reach the goal efficiently, spending the first 300 episodes primarily exploring the environment rather than directly achieving the goal. As a result, the UAV receives low rewards early on but gradually converges in later rounds, indicating that it learns to avoid obstacles by sensing its surroundings and adjusting its behavior accordingly. Figure 8 clearly shows the performance improvements of each algorithm after the initial learning phase. It is evident that DDM-DQN, APF-DQN, and YS-DADQN adapt more rapidly than the standard DQN. Specifically, DDM-DQN enhances its learning efficiency by selectively emphasizing significant experiential data and diminishing its dependence on less impactful experiences. Meanwhile, APF-DQN accelerates its advancement by employing a reward function tailored to promote strategies that prioritize collision avoidance and optimal path discovery. YS-DADQN learns faster than other algorithms, attributed to its superior capabilities in accurate target detection and environmental sensing. This model effectively enables UAVs to navigate and make decisions more efficiently, optimizing both the exploration phase and the route optimization process. The final analysis, as presented in Figure 8, shows that the ultimate reward achievements differ markedly. DQN plateaus at a reward of 2200; DDM-DQN and APF-DQN ascend to 4000 and 5000, respectively; while YS-DADQN reaches peak performance with a reward tally of 8000. These data underscore YS-DADQN’s superior efficiency in navigating and formulating more effective path strategies compared to its counterparts.
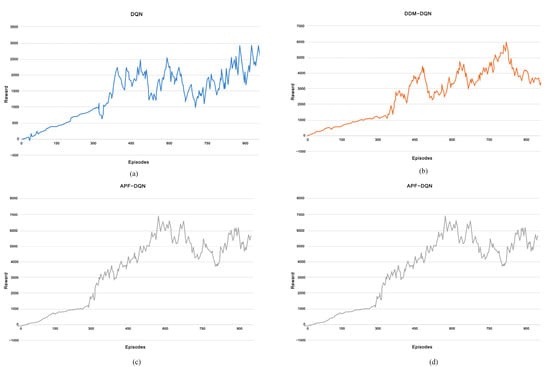
Figure 7.
Reward for each episode of the UAV based on four algorithms. (a–d) respectively represent the relationship between Reward and Episodes for DQN, DDM-DQN, APF-DQN, and YS-DADQN.
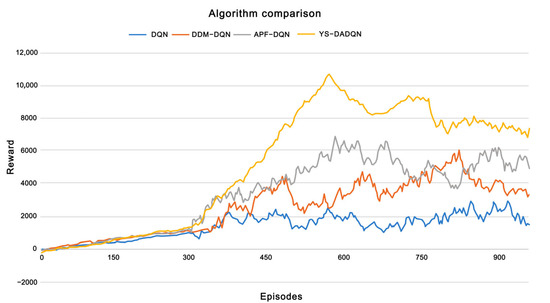
Figure 8.
Comparison of four algorithms.
We captured two scenes during the UAV flight process. In the first scenario, the drone detects an obstacle from a distance, as shown in Figure 9a, and chooses to fly to the left based on the trained YS-DADQN. Figure 9b shows the drone beginning to change direction and yaw to the left. In Figure 9c, the drone moves to the left of the obstacle and successfully bypasses it, as shown in Figure 9d. The drone successfully evades the obstacle. In the second scenario, the drone navigates through a corridor. From the depth map (Figure 9e), it is evident that the drone needs to turn right, and there is sufficient space available. As the drone gradually approaches the corridor (Figure 9f), the gap between the two walls becomes wide enough for the drone to pass through. The drone adjusts its path to maintain a safe distance from the walls, gradually adapting to the open area as in Figure 9g. Ultimately, the drone successfully crosses the corridor, as shown in Figure 9h.

Figure 9.
The obstacle avoidance process of the UAV: (a–d) the UAV avoiding obstacles; (e–h) crossing an indoor corridor.
In the experimental setup, we designated two target points within the environment, allowing the UAVs to navigate autonomously between these points to explore the area. To assess the effectiveness of the proposed algorithm, we conducted several simulations and compared the results with other path planning algorithms. Table 4 presents the outcomes of 300 episodes of experiments, evaluated using three metrics: the average number of moves to reach the target, the number of successful arrivals, and the success rate. All simulations were conducted on the same computer under identical conditions to determine the UAV path planning success rate. The results indicate that the YS-DADQN algorithm achieves the highest success rate of 77.67%, outperforming several existing methods. It improves the success rates by 19% over improved Q-learning, 23.34% over traditional DQN, 22% over dueling DQN, 20.67% over M-DQN, 17% over DDM-DQN, 12.67% over EPF, 8% over APF-DQN, and 5.34% over L1-MBRL. These results clearly demonstrate the proposed algorithm’s superiority, as it not only converges faster than its counterparts but also reaches the target more efficiently compared to the existing studies.

Table 4.
Algorithm comparison results. Here, —— represents an indication of non-participation.
In this study, the YS-DADQN algorithm performs well on these metrics, an advantage that is mainly attributed to its improvements in environment perception and target detection, which enable the UAV to make faster and more accurate decisions in dynamic environments, thereby avoiding obstacles and optimizing the path selection process when planning paths. Compared to traditional DQN algorithms, YS-DADQN can make more effective use of experiences and real-time feedback to rapidly improve its learning efficiency and reduce unnecessary exploration phases. For the enhanced potential field method, although the method performs well in dynamic obstacle avoidance, its effectiveness usually relies on accurate velocity models and obstacle prediction. For the L1-MBRL algorithm, the L1-MBRL adaptive control strategy enhances the robustness of the model, and especially excels in handling system uncertainties and external perturbations. However, the method relies on accurate system modelling and requires constant adjustment of the control inputs to adapt to environmental changes. Compared to other algorithms, YS-DADQN not only improves the convergence speed but also reaches the goal in a shorter time and exhibits a higher success rate of path planning. YS-DADQN demonstrates the ability to flexibly cope with dynamic environments through the combination of reinforcement learning and intelligent perception modules, and is able to avoid obstacles and optimize paths efficiently. In addition, reasonable hyper-parameter settings, such as the learning rate, discount factor, and exploration strategy, also positively affect the algorithm’s performance, enabling YS-DADQN to achieve faster convergence in training and demonstrate higher efficiency and stability in experiments. Through the optimization of these experimental parameters, YS-DADQN is able to quickly adjust its path when facing dynamic environments, demonstrating its superiority in complex environments.
4.3.3. Algorithm Performance with Different Obstacle Densities
To evaluate the impact of obstacle density on UAV performance, we tested YS-DADQN in environments with varying obstacle densities (10%, 30%, and 50% area coverage). Table 5 presents success rates of 85%, 78%, and 72%, respectively, demonstrating the model’s adaptability to increasingly complex environments.

Table 5.
The impacts of different obstacle densities on algorithms.
5. Conclusions
We introduce an innovative approach for autonomous navigation and collision avoidance in dynamic environments for quadcopter UAVs, utilizing the YS-DADQN framework. This method incorporates Yolov8-StrongSort for enhanced dynamic obstacle detection. Additionally, a novel data storage mechanism for replay memory has been developed to boost the efficacy of training processes. Furthermore, we have crafted a reward function inspired by artificial potential fields that optimizes the UAV’s trajectory by considering both the proximity to the target and the avoidance of obstacles. Our empirical results show that the proposed YS-DADQN outperforms DQN, DDM-DQN, APF-DQN, EPF, and L1-MBRL in terms of its higher success rate, with YS-DADQN achieving a success rate of 77.67%, which outperforms the other methods for navigation in complex environments. In addition, we also conducted experiments with different obstacle densities, and the success rate of YS-DADQN is 85% in low-density environments, 78% in medium-density environments, and still 72% in high-density environments. YS-DADQN has good robustness and adaptability, and maintains a high task success rate, even in complex environments with more obstacles.
Although traditional and some modern methods have certain advantages in specific scenarios, their respective limitations (e.g., easy to fall into local optima, dependence on accurate modelling, high computational complexity, etc.) make them deficient in dealing with complex, dynamic, and unknown environments. YS-DADQN, however, effectively overcomes these shortcomings by virtue of the dynamic adjustment and global optimization capabilities of reinforcement learning, providing a more efficient solution for autonomous UAV navigation and obstacle avoidance.
Future studies could significantly benefit from a detailed examination of integrating multi-source heterogeneous data into sensor-based obstacle avoidance systems. The development of sophisticated algorithms for data fusion alongside enhanced decision-making strategies for intelligent obstacle navigation could markedly improve the systems’ environmental perception and navigation capabilities.
Author Contributions
Conceptualization, J.L.; methodology, J.L.; software, G.Z.; validation, J.L., R.L. and W.L.; formal analysis, W.L. and G.Z.; investigation, R.L.; data curation, R.L.; writing—original draft preparation, G.Z.; writing—review and editing, J.L.; visualization, R.L.; supervision, W.L.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Innovation Project Fund of North China Institute of Aerospace Engineering (No. YKY-2024-90).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
- Algorithm A1.
| Algorithm A1. Replay memory data storage mechanism method |
| 1. Experencestorage(rm) |
| 2. Initialize experience storage flags, experience deposit ratio pRE, pDE, pSE |
| 3. Generate a random value p′, and p′ ∈ [0, 1] |
| 4. Type(rm) ← Determine the type of experience rm |
| 5. if Type(rm) is RE do |
| 6. if p′ < pRE do |
| 7. Fstorage ← true |
| 8. end if |
| 9. else if Type(rm) is DE do |
| 10. if p′ < pRE do |
| 11. Fstorage ← true |
| 12. end if |
| 13. else if Type(rm) is SE do |
| 14. if p′ < pRE do |
| 15. Fstorage ← true |
| 16. end if |
| 17. end if |
| 18. Return Fstorage |
- 2.
- Certification
Proof of Theorem 1.
Let be the optimal value function be computed based on the reward function, i.e.,:
Since the reward for a collision state is , for any policy , the chosen action leads to a collision state:
In order to minimize negative rewards, the optimal policy chooses actions that avoid collisions as much as possible so that the probability of visiting a collision state tends to zero, i.e.,:
This demonstrates that reinforcement learning can learn collision avoidance strategies when designed with appropriate rewards. □
References
- Chen, G.; Sun, D.; Dong, W.; Sheng, X.; Zhu, X.; Ding, H. Computationally efficient trajectory planning for high speed obstacle avoidance of a quadrotor with active sensing. IEEE Robot. Autom. Lett. 2021, 6, 3365–3372. [Google Scholar] [CrossRef]
- Falanga, D.; Kim, S.; Scaramuzza, D. How fast is too fast? the role of perception latency in high-speed sense and avoid. IEEE Robot. Autom. Lett. 2019, 4, 1884–1891. [Google Scholar] [CrossRef]
- Gao, F.; Wu, W.; Gao, W.; Shen, S. Flying on point clouds: Online trajectory generation and autonomous navigation for quadrotors in cluttered environments. J. Field Robot. 2019, 36, 710–733. [Google Scholar] [CrossRef]
- Tordesillas, J.; Lopez, B.T.; How, J.P. Faster: Fast and safe trajectory planner for flights in unknown environments. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 1934–1940. [Google Scholar]
- Zhou, X.; Wang, Z.; Ye, H.; Xu, C.; Gao, F. Ego-planner: An esdf-free gradient-based local planner for quadrotors. IEEE Robot. Autom. Lett. 2020, 6, 478–485. [Google Scholar] [CrossRef]
- Chen, G.; Dong, W.; Sheng, X.; Zhu, X.; Ding, H. An active sense and avoid system for flying robots in dynamic environments. IEEE/ASME Trans. Mechatron. 2021, 26, 668–678. [Google Scholar] [CrossRef]
- Chen, G.; Peng, P.; Zhang, P.; Dong, W. Risk-aware trajectory sampling for quadrotor obstacle avoidance in dynamic environments. IEEE Trans. Ind. Electron. 2023, 70, 12606–12615. [Google Scholar] [CrossRef]
- Lin, J.; Zhu, H.; Alonso-Mora, J. Robust vision-based obstacle avoidance for micro aerial vehicles in dynamic environments. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2682–2688. [Google Scholar]
- Wang, Y.; Ji, J.; Wang, Q.; Xu, C.; Gao, F. Autonomous flights in dynamic environments with onboard vision. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 1966–1973. [Google Scholar]
- Zhu, H.; Alonso-Mora, J. Chance-constrained collision avoidance for mavs in dynamic environments. IEEE Robot. Autom. Lett. 2019, 4, 776–783. [Google Scholar] [CrossRef]
- Wang, C.C.; Thorpe, C.; Thrun, S.; Hebert, M.; Durrant-Whyte, H. Simultaneous localization, mapping and moving object tracking. Int. J. Robot. Res. 2007, 26, 889–916. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Chen, Y. Online multi-object tracking using CNN-based single object tracker with spatial-temporal attention mechanism. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1472–1481. [Google Scholar]
- Wojke, N.; Bewley, A. Simple online and realtime tracking. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3464–3468. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Milan, A.; Leal-Taixé, L.; Reid, I.; Roth, S.; Schindler, K. MOT16: A benchmark for multi-object tracking. arXiv 2016, arXiv:1603.00831. [Google Scholar]
- Kang, K.; Li, H.; Yan, J.; Zeng, X.; Yang, B.; Xiao, T.; Zhang, C.; Wang, Z.; Wang, R.; Wang, X.; et al. T-cnn: Tubelets with convolutional neural networks for object detection from videos. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2896–2907. [Google Scholar] [CrossRef]
- Pal, S.K.; Pramanik, A.; Maiti, J.; Mitra, P. Deep learning in multi-object detection and tracking: State of the art. Appl. Intell. 2021, 51, 6400–6429. [Google Scholar] [CrossRef]
- Sahu, C.K.; Young, C.; Rai, R. Artificial intelligence (AI) in augmented reality (AR)-assisted manufacturing applications: A review. Int. J. Prod. Res. 2021, 59, 4903–4959. [Google Scholar] [CrossRef]
- Dendorfer, P.; Osep, A.; Milan, A.; Schindler, K.; Cremers, D.; Reid, I.; Roth, S.; Leal-Taixé, L. Motchallenge: A benchmark for single-camera multiple target tracking. Int. J. Comput. Vis. 2021, 129, 845–881. [Google Scholar] [CrossRef]
- Yang, B.; Nevatia, R. An online learned CRF model for multi-object tracking. In Proceedings of the CVPR 2011, Providence, RI, USA, 16–21 June 2011; pp. 1397–1404. [Google Scholar]
- Wang, M.; Liu, Y. Learning a neural solver for multiple object tracking. In Proceedings of the CVPR 2019, Long Beach, CA, USA, 15–20 June 2019; pp. 7304–7312. [Google Scholar]
- Wang, D.; Fang, W.; Chen, W.; Sun, T.; Chen, T. Model update strategies about object tracking: A state of the art review. Electronics 2019, 8, 1207. [Google Scholar] [CrossRef]
- Fiaz, M.; Mahmood, A.; Jung, S.K. Tracking noisy targets: A review of recent object tracking approaches. arXiv 2018, arXiv:1802.03098. [Google Scholar]
- Bewley, A.; Ge, Z.; Ott, L.; Ramos, F.; Upcroft, B. Simple online and realtime tracking. In Proceedings of the ICIP 2016, Phoenix, AZ, USA, 25–28 September 2016; pp. 3464–3468. [Google Scholar]
- Pang, J.; Qiu, L.; Li, X.; Chen, H.; Li, Q.; Yu, F. Quasi-dense similarity learning for multiple object tracking. In Proceedings of the CVPR 2021, Nashville, TN, USA, 20–25 June 2021; pp. 164–173. [Google Scholar]
- Wang, Q.; Zheng, Y.; Pan, P.; Xu, Y. Multiple object tracking with correlation learning. In Proceedings of the CVPR 2021, Nashville, TN, USA, 20–25 June 2021; pp. 3876–3886. [Google Scholar]
- Bergmann, P.; Meinhardt, T.; Leal-Taixe, L. Tracking without bells and whistles. In Proceedings of the ICCV 2019, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 941–951. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the NIPS 2015, Montreal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Zhang, J.; Zhou, S.; Chang, X.; Wan, F.; Wang, J.; Wu, Y.; Huang, D. Multiple object tracking by flowing and fusing. arXiv 2020, arXiv:2001.11180. [Google Scholar]
- Zhou, X.; Koltun, V.; Krähenbühl, P. Tracking objects as points. In Proceedings of the ECCV 2020, Glasgow, UK, 23–28 August 2020; pp. 474–490. [Google Scholar]
- Wu, Z.; Dong, S.; Yuan, M.; Cui, J.; Zhao, L.; Tong, C. Rotate artificial potential field algorithm toward 3D real-time path planning for unmanned aerial vehicle. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2023, 237, 940–955. [Google Scholar] [CrossRef]
- Yang, K.; Gan, S.K.; Sukkarieh, S. A Gaussian process-based RRT planner for the exploration of an unknown and cluttered environment with a UAV. Adv. Robot. 2013, 27, 431–443. [Google Scholar] [CrossRef]
- Liang, H.; Bai, H.; Sun, R.; Sun, R.; Li, C. Three-dimensional path planning based on DEM. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 5980–5987. [Google Scholar]
- Baek, J.; Han, S.I.; Han, Y. Energy-efficient UAV routing for wireless sensor networks. IEEE Trans. Veh. Technol. 2020, 69, 1741–1750. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Zou, A.; Cai, J.; He, H.; Tan, T. Path planning for UAV based on improved PRM. Energies 2022, 15, 7267. [Google Scholar] [CrossRef]
- Roberge, V.; Tarbouchi, M.; Labonte, G. Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Trans. Ind. Inform. 2013, 9, 132–141. [Google Scholar] [CrossRef]
- Geng, Q.; Zhao, Z. A kind of route planning method for UAV based on improved PSO algorithm. In Proceedings of the 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 2328–2331. [Google Scholar]
- Qu, C.; Gai, W.; Zhong, M.; Zhang, J. A novel reinforcement learning based grey wolf optimizer algorithm for unmanned aerial vehicles (UAVs) path planning. Appl. Soft Comput. 2020, 89, 106099. [Google Scholar] [CrossRef]
- Chai, X.; Zheng, Z.; Xiao, J.; Yan, L.; Qu, B.; Wen, P.; Wang, H.; Zhou, Y.; Sun, H. Multi-strategy fusion differential evolution algorithm for UAV path planning in complex environment. Aerosp. Sci. Technol. 2022, 121, 107287. [Google Scholar] [CrossRef]
- Singla, A.; Padakandla, S.; Bhatnagar, S. Memory-based deep reinforcement learning for obstacle avoidance in UAV with limited environment knowledge. IEEE Trans. Intell. Transp. Syst. 2021, 22, 107–118. [Google Scholar] [CrossRef]
- Feng, S.; Shu, H.; Xie, B. 3D environment path planning based on improved deep reinforcement learning. Comput. Appl. Softw. 2021, 38, 250–255. [Google Scholar]
- Ruan, X.G.; Ren, D.Q.; Zhu, X.Q.; Huang, J. Mobile robot navigation based on deep reinforcement learning. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; IEEE Press: Piscataway, NJ, USA, 2019; pp. 6174–6178. [Google Scholar]
- Zhang, W.; Zhang, W.; Song, F.; Long, L. Monocular vision obstacle avoidance method for quadcopter based on deep learning. J. Comput. Appl. 2019, 39, 1001. [Google Scholar]
- Taghibakhshi, A.; Ogden, N.; West, M. Local navigation and docking of an autonomous robot mower using reinforcement learning and computer vision. In Proceedings of the 2021 13th International Conference on Computer and Automation Engineering (ICCAE), Melbourne, Australia, 20–22 March 2021; pp. 10–14. [Google Scholar]
- Lai, Y.-C.; Huang, Z.-Y. Detection of a moving UAV based on deep learning-based distance estimation. Remote Sens. 2020, 12, 3035. [Google Scholar] [CrossRef]
- Zhang, S.; Sutton, R.S. A deeper look at experience replay. arXiv 2017, arXiv:1712.01275. [Google Scholar]
- Li, X.J.; Liu, H.; Li, J.Q.; Li, Y. Deep deterministic policy gradient algorithm for crowd-evacuation path planning. Comput. Ind. Eng. 2021, 161, 107621. [Google Scholar] [CrossRef]
- Jafari, O.H.; Mitzel, D.; Leibe, B. Real-time RGB-D based people detection and tracking for mobile robots and head-worn cameras. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 5636–5643. [Google Scholar]
- Oleynikova, H.; Honegger, D.; Pollefeys, M. Reactive avoidance using embedded stereo vision for MAV flight. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 50–56. [Google Scholar]
- Pfeiffer, M.; Paolo, G.; Sommer, H.; Nieto, J.I.; Siegwart, R.; Cadena, C. A data-driven model for interaction-aware pedestrian motion prediction in object cluttered environments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 5921–5928. [Google Scholar]
- Wang, C.; Wang, Y.; Xu, M.; Crandall, D.J. Stepwise goal-driven networks for trajectory prediction. IEEE Robot. Autom. Lett. 2022, 7, 2716–2723. [Google Scholar] [CrossRef]
- Wulfmeier, M.; Rao, D.; Wang, D.Z.; Ondruska, P.; Posner, I. Large-scale cost function learning for path planning using deep inverse reinforcement learning. Int. J. Robot. Res. 2017, 36, 1073–1087. [Google Scholar] [CrossRef]
- Eppenberger, T.; Cesari, G.; Dymczyk, M.; Siegwart, R.; Dubé, R. Leveraging stereo-camera data for real-time dynamic obstacle detection and tracking. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 10528–10535. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. Trans. ASME–J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Evangelidis, G.D.; Psarakis, E.Z. Parametric image alignment using enhanced correlation coefficient maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1858–1865. [Google Scholar] [CrossRef]
- Baker, S.; Matthews, I. Equivalence and efficiency of image alignment algorithms. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2001), Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Du, Y.; Wan, J.; Zhao, Y.; Zhang, B.; Tong, Z.; Dong, J. Giaotracker: A comprehensive framework for mcmot with global information and optimizing strategies in visdrone 2021. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2809–2819. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Du, Y.; Zhao, Z.; Song, Y.; Zhao, Y.; Su, F.; Gong, T.; Meng, H. Strongsort: Make deepsort great again. IEEE Trans. Multimed. 2023, 25, 8725–8737. [Google Scholar] [CrossRef]
- Hu, Y.; Tang, H.; Pan, G. Spiking deep residual networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 5200–5205. [Google Scholar] [CrossRef]
- Sun, H.; Demanet, L. Beyond correlations: Deep learning for seismic interferometry. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 3385–3396. [Google Scholar] [CrossRef]
- Qiao, S.; Chen, L.C.; Yuille, A. Detectors: Detecting objects with recursive feature pyramid and switchable atrous convolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 10213–10224. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Jiang, W.; Bao, C.; Xu, G.; Wang, Y. Research on autonomous obstacle avoidance and target tracking of UAV based on improved dueling DQN algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 5110–5115. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Vieillard, N.; Pietquin, O.; Geist, M. Munchausen reinforcement learning. In Proceedings of the Advances in Neural Information Processing Systems, Virtual, 6–12 December 2020; Volume 33, pp. 4235–4246. [Google Scholar]
- Tu, G.-T.; Juang, J.-G. UAV path planning and obstacle avoidance based on reinforcement learning in 3d environments. Actuators 2023, 12, 57. [Google Scholar] [CrossRef]
- Choi, D.; Kim, D.; Lee, K. Enhanced potential field-based collision avoidance in cluttered three-dimensional urban environments. Appl. Sci. 2021, 11, 11003. [Google Scholar] [CrossRef]
- Sung, M.; Karumanchi, S.H.; Gahlawat, A.; Hovakimyan, N. Robust model based reinforcement learning using L1 adaptive control. In Proceedings of the 12th International Conference on Learning Representations (ICLR 2024), Vienna, Austria, 7–11 May 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).