Condition-Based Maintenance for Degradation-Aware Control Systems in Continuous Manufacturing
Abstract
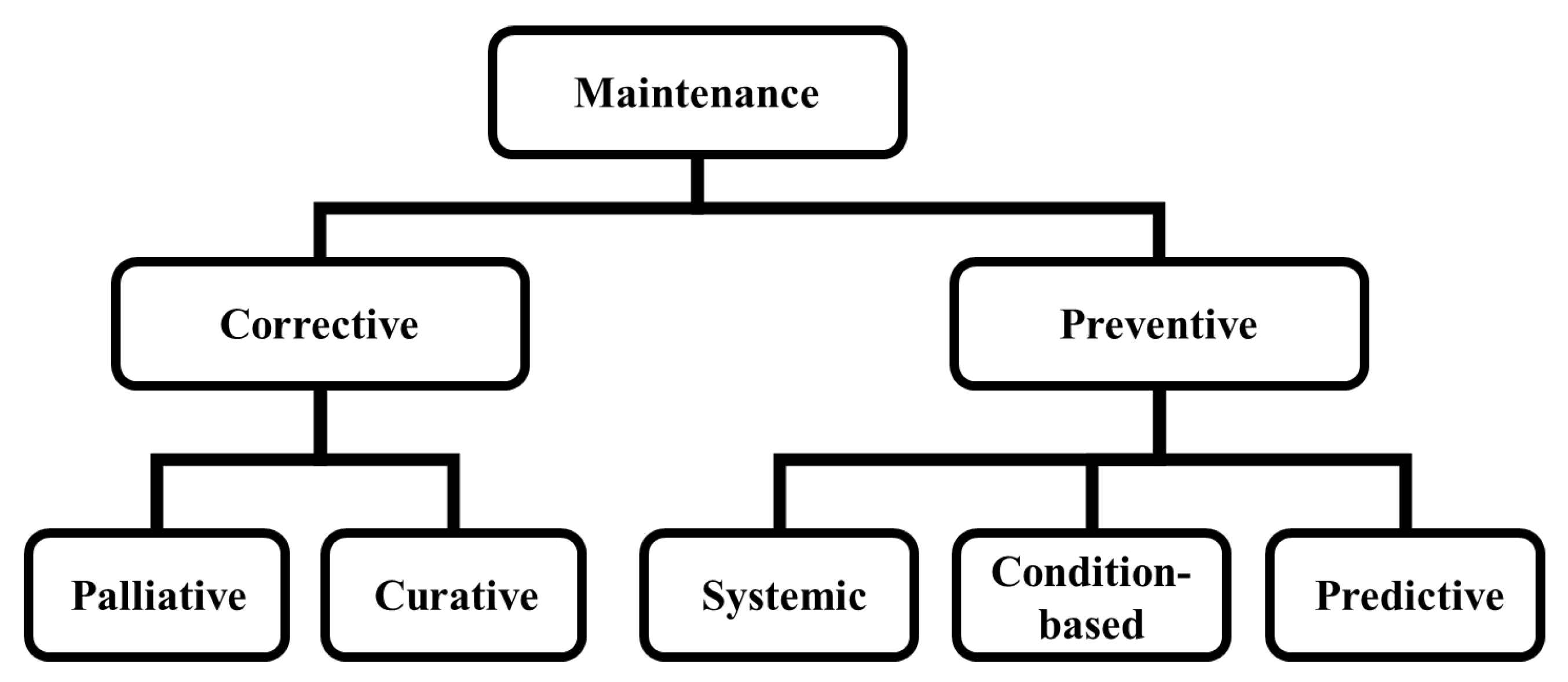
1. Introduction
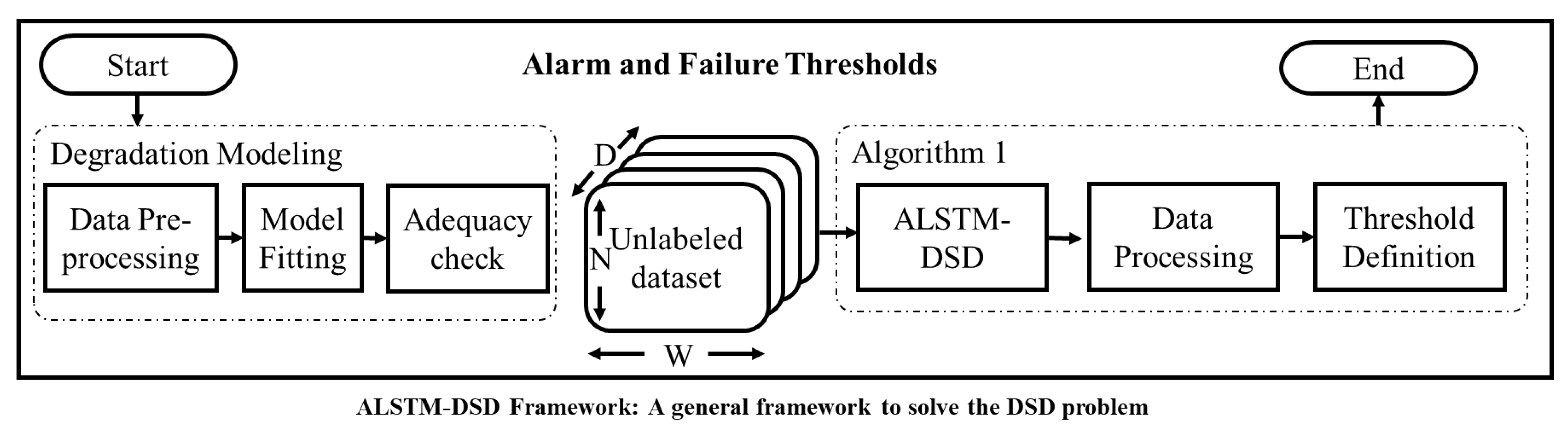
2. Materials and Methods
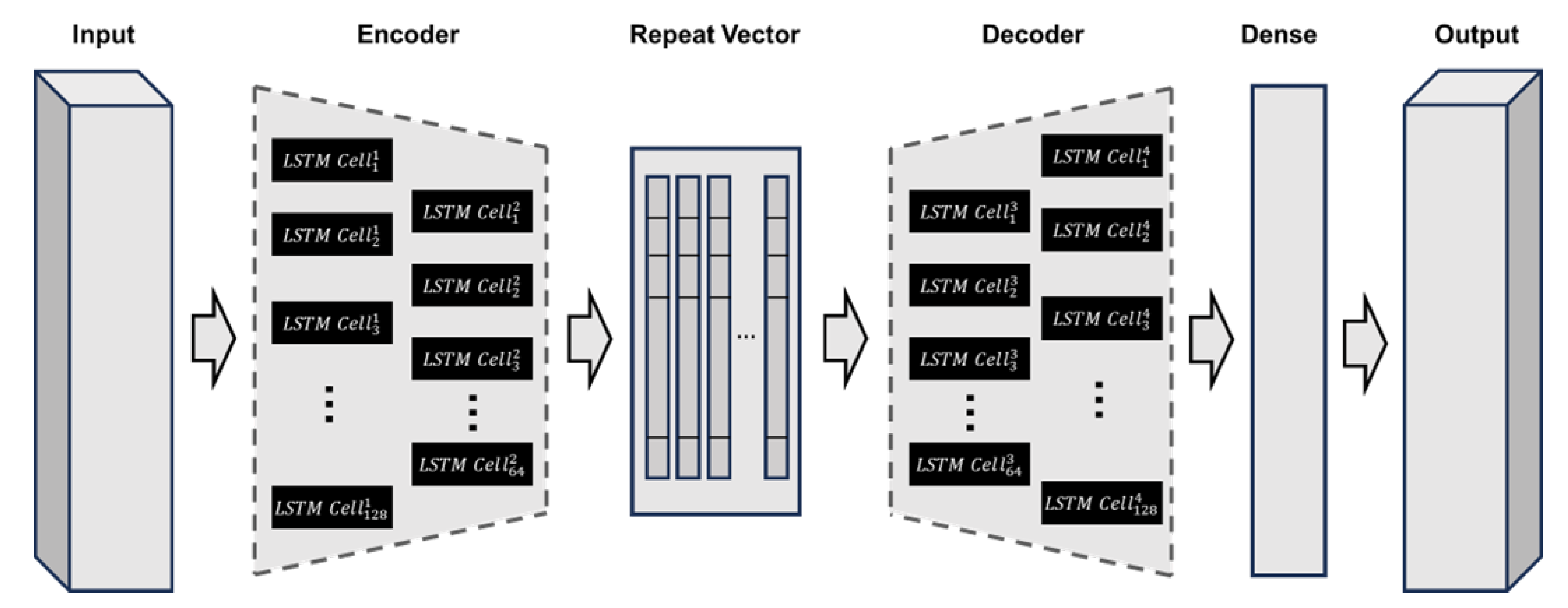
2.1. Degradation Modeling
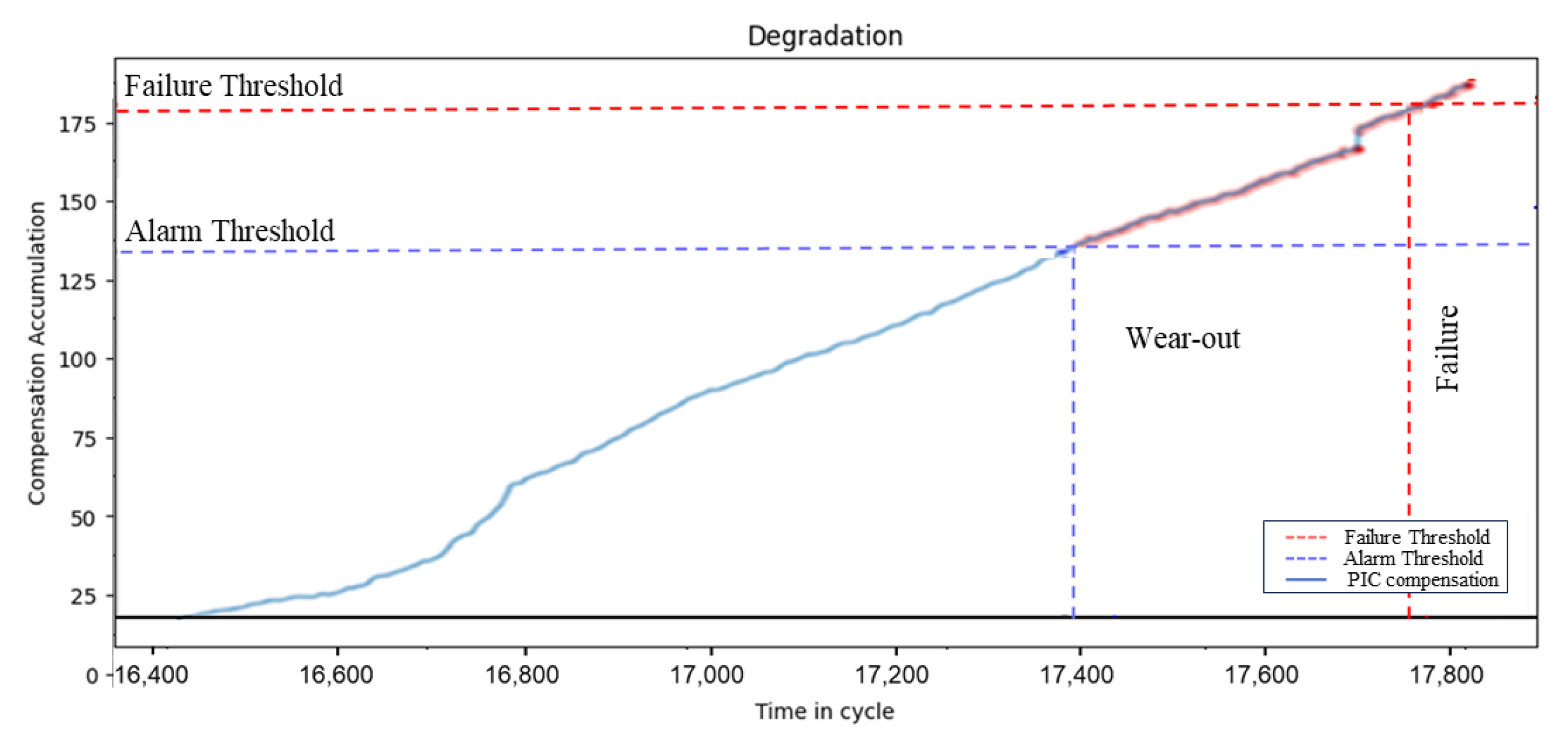
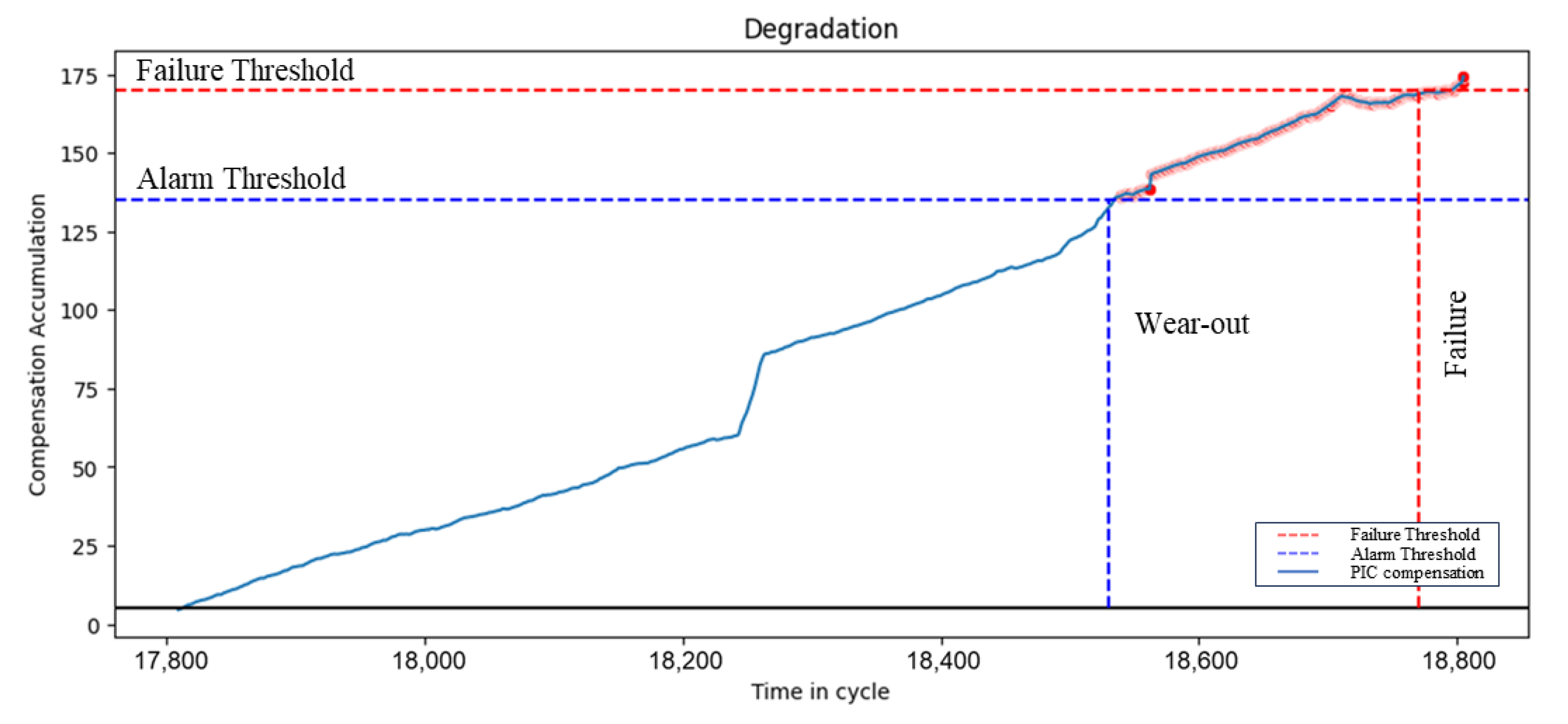
2.2. Threshold Setup
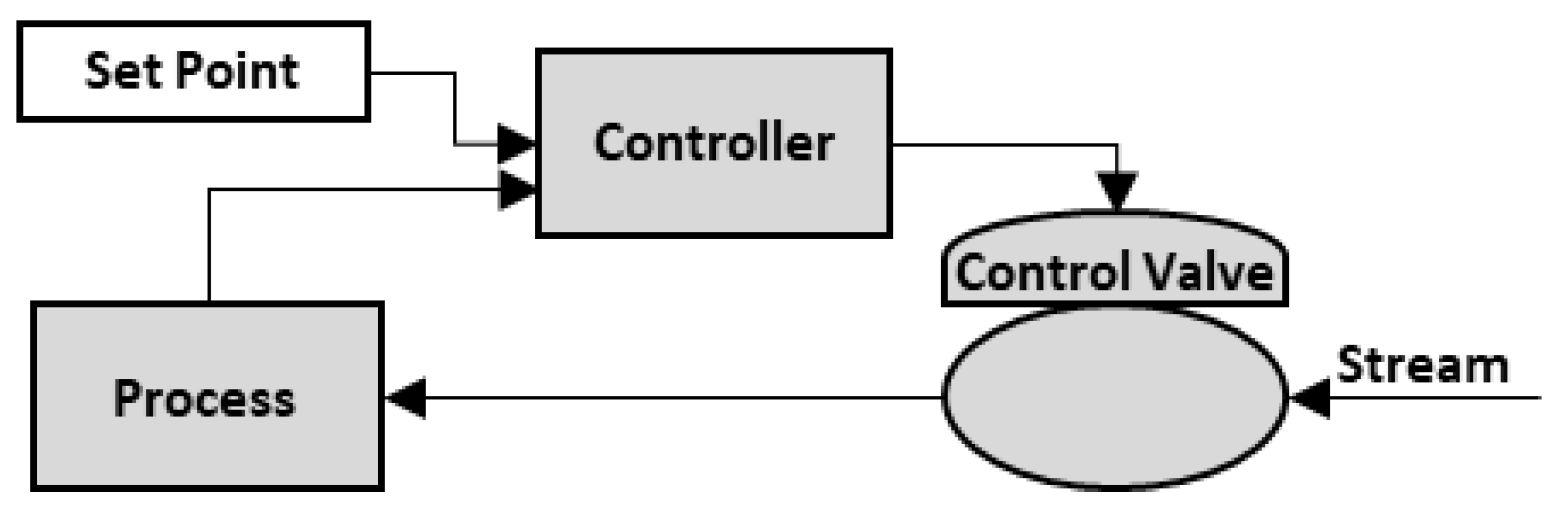
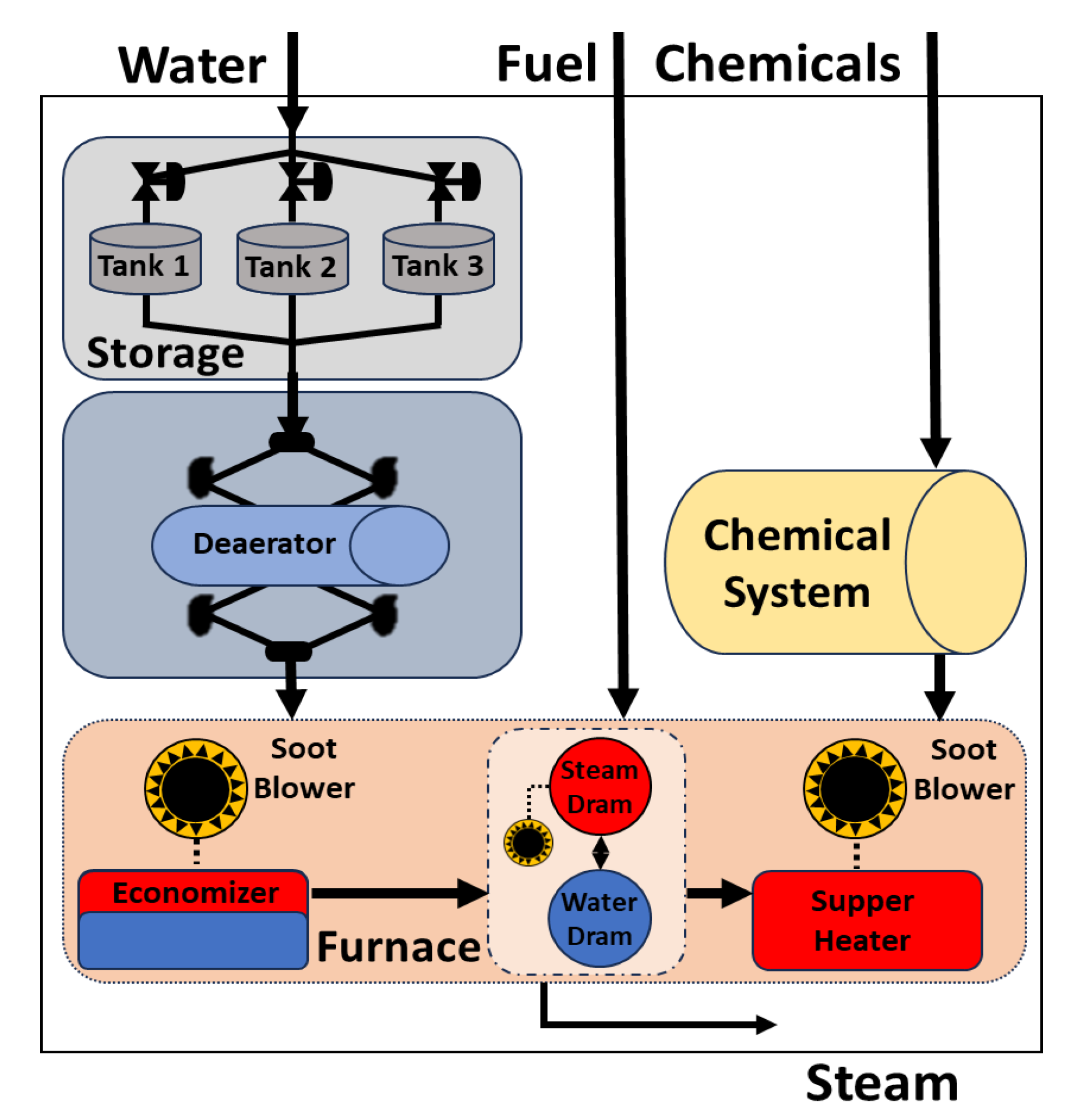
3. System Description
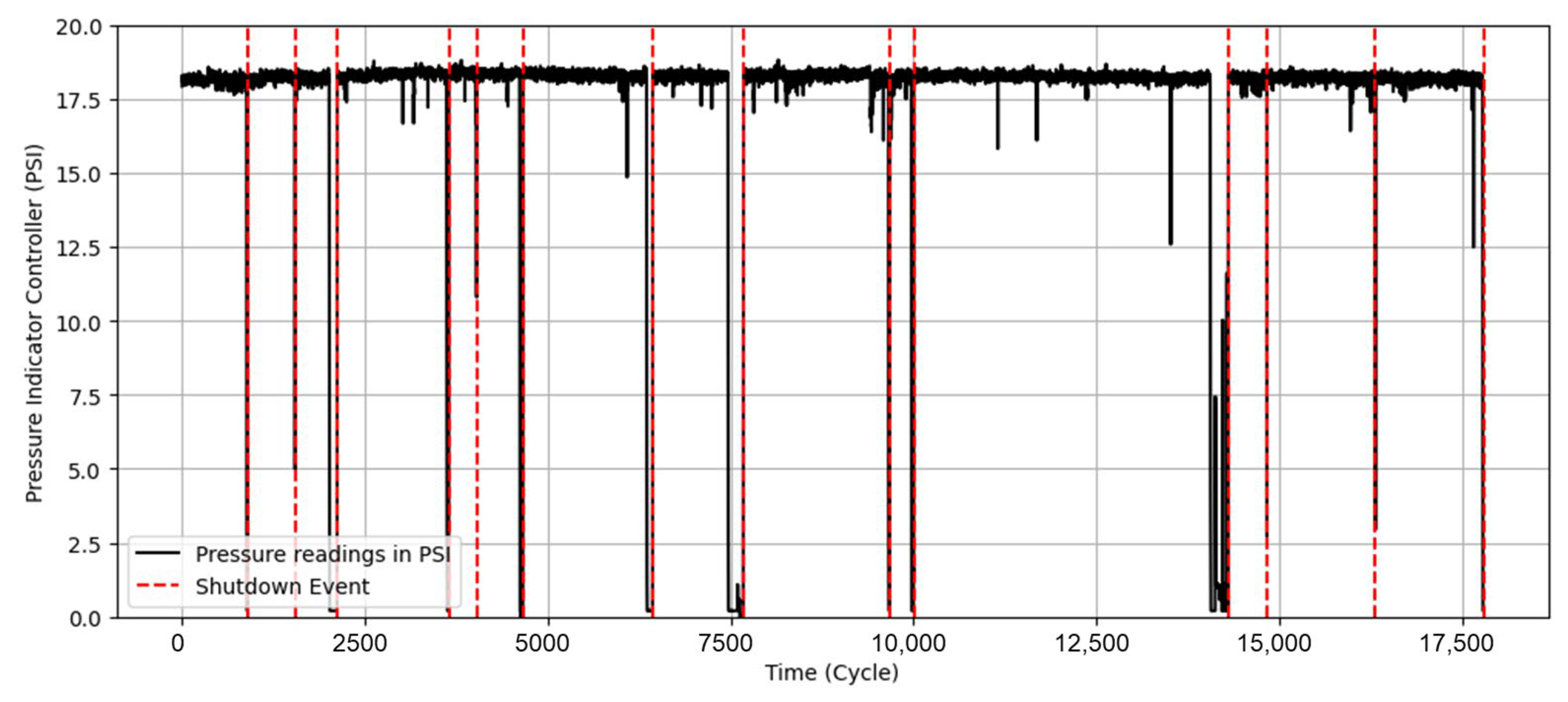
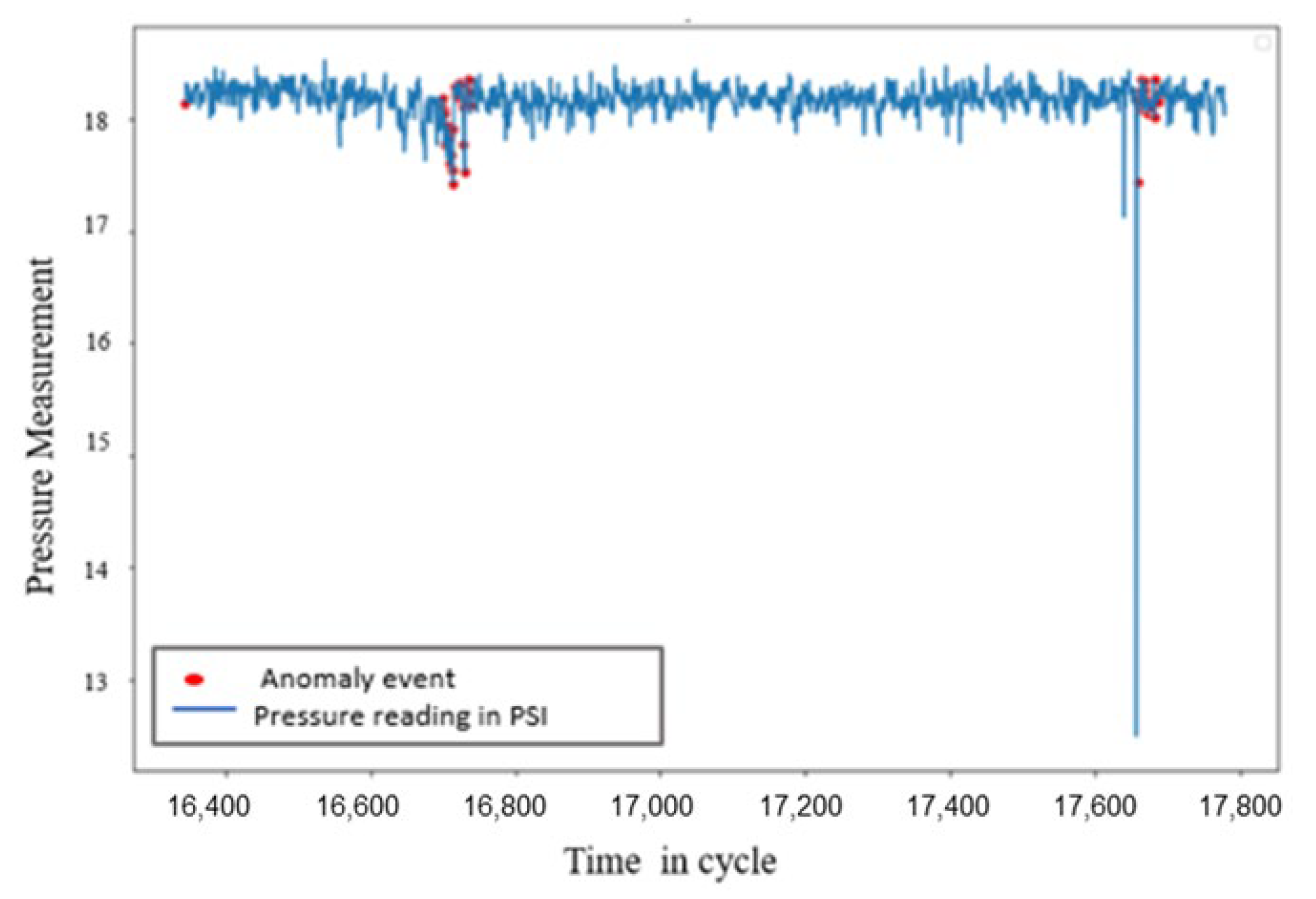
Dataset
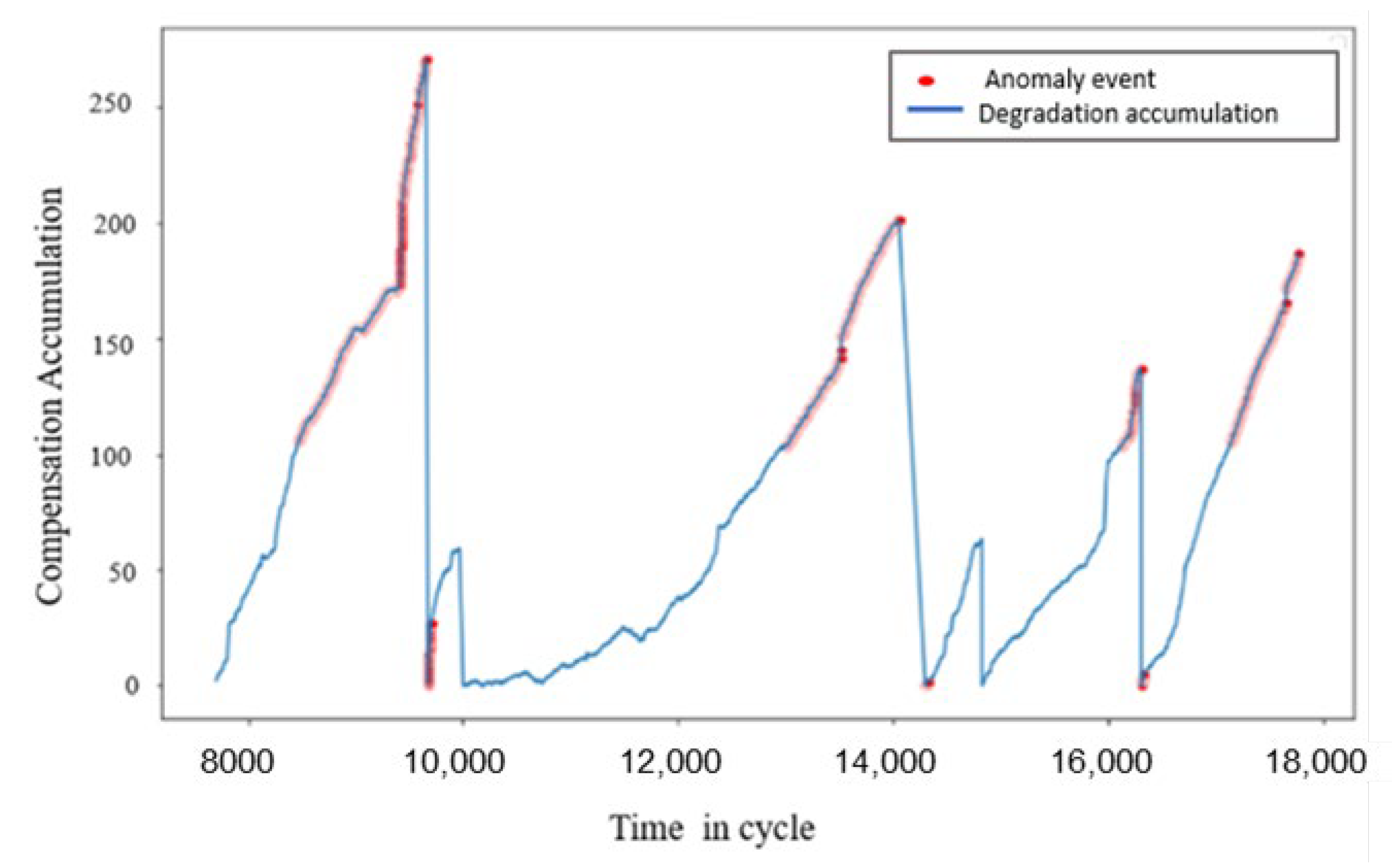
4. Results and Discussion
Performance Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| A-LSTMA-DSD | Long Short-Term Memory Autoencoder-Degradation Stage Detector |
| CBM | Condition-based maintenance |
| Machine Learning | ML |
| Artificial Intelligence | AL |
| PIC | Pressure Indicator Controller |
| PLC | Programable Logic Control |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| ARIMA | Autoregressive Integrated Moving Average |
| FP | Facebook Prophet |
| CNN | Convolutional Neural Network |
| ANN | Artificial Neural Network |
| LSTM | Short Long-Term Memory |
| RUL | Remaining Useful Life |
| DCS | Distributed Control System |
| PSI | Pounds per square inch |
References
- Bengtsson, M. On Condition-Based Maintenance and Its Implementation in Industrial Settings. Ph.D. Dissertation, Mälardalens högskola, Vasteras, Sweden, 2007. [Google Scholar]
- Ding, F.; Tian, Z. Opportunistic maintenance optimization for wind turbine systems considering imperfect maintenance actions. Int. J. Reliab. Qual. Saf. Eng. 2011, 18, 463–481. [Google Scholar] [CrossRef]
- Chen, N.; Ye, Z.-S.; Xiang, Y.; Zhang, L. Condition-based maintenance using the inverse Gaussian degradation model. Eur. J. Oper. Res. 2015, 243, 190–199. [Google Scholar] [CrossRef]
- Al-Najjar, B.; Alsyouf, I. Selecting the most efficient maintenance approach using fuzzy multiple criteria decision making. Int. J. Prod. Econ. 2003, 84, 85–100. [Google Scholar] [CrossRef]
- Nguyen, K.-A.; Do, P.; Grall, A. Multi-level predictive maintenance for multi-component systems. Reliab. Eng. Syst. Saf. 2015, 144, 83–94. [Google Scholar] [CrossRef]
- Sophie, S.; Adolf, T.; Lucke, D.; Haug, R.; Boulet, P.; García-Sedano, J. Supreme sustainable predictive maintenance for manufacturing equipment. In Proceedings of the European Congress, 2014, the 22nd Euromaintenance Conference, Helsinki, Finland, 5–8 May 2014. [Google Scholar]
- Jardine, A.K.; Lin, D.; Banjevic, D. A review on machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Zhang, N.; Si, W. Deep reinforcement learning for condition-based maintenance planning of multi-component systems under dependent competing risks. Reliab. Eng. Syst. Saf. 2020, 203, 107094. [Google Scholar] [CrossRef]
- Chen, J.; Patton, R.J. Robust Model-Based Fault Diagnosis for Dynamic Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 3. [Google Scholar]
- Gorjian, N.; Ma, L.; Mittinty, M.; Yarlagadda, P.; Sun, Y. A review on degradation models in reliability analysis. In Engineering Asset Lifecycle Management: Proceedings of the 4th World Congress on Engineering Asset Management (WCEAM 2009), Athens, Greece, 28–30 September 2009; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Vickers, N.J. Animal communication: When i’m calling you, will you answer too? Curr. Biol. 2017, 27, R713–R715. [Google Scholar] [CrossRef]
- Funyufunyu, D.D. The Development of an Equipment Management System for a Parts Distribution Centre. Bachelor’s Thesis, University of Pretoria, Pretoria, South Africa, 2009. Available online: https://repository.up.ac.za/handle/2263/13935 (accessed on 11 February 2025).
- Le, T.T. Contribution to Deterioration Modeling and Residual Life Estimation Based on Condition Monitoring Data. Ph.D. Dissertation, Université Grenoble Alpes, Grenoble, France, 2015. Available online: https://theses.hal.science/tel-01242995/ (accessed on 11 February 2025).
- Zagorowska, M.; Wu, O.; Ottewill, J.R.; Reble, M.; Thornhill, N.F. A survey of models of degradation for control applications. Annu. Rev. Control 2020, 50, 150–173. [Google Scholar] [CrossRef]
- Fink, O.; Zio, E.; Weidmann, U. Predicting component reliability and level of degradation with complex-valued neural networks. Reliab. Eng. Syst. Saf. 2014, 121, 198–206. [Google Scholar] [CrossRef]
- Giorgio, M.; Guida, M.; Pulcini, G. An age- and state-dependent Markov model for degradation processes. IIE Trans. 2011, 43, 621–632. [Google Scholar] [CrossRef]
- Zhang, Z.; Si, X.; Hu, C.; Kong, X. Degradation modeling–based remaining useful life estimation: A review on approaches for systems with heterogeneity. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2015, 229, 343–355. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, Q.; King, C.B.; Hong, Y. A General Accelerated Destructive Degradation Testing Model for Reliability Analysis. IEEE Trans. Reliab. 2019, 68, 1272–1282. [Google Scholar] [CrossRef]
- Xie, Y.; King, C.B.; Hong, Y.; Yang, Q. Semiparametric Models for Accelerated Destructive Degradation Test Data Analysis. Technometrics 2018, 60, 222–234. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Zhou, D.-H. Remaining useful life estimation—A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Ye, Z.; Xie, M. Stochastic modelling and analysis of degradation for highly reliable products. Appl. Stoch. Model. Bus. Ind. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Siu, N. Risk assessment for dynamic systems: An overview. Reliab. Eng. Syst. Saf. 1994, 43, 43–73. [Google Scholar] [CrossRef]
- Labeau, P.; Smidts, C.; Swaminathan, S. Dynamic reliability: Towards an integrated platform for probabilistic risk assessment. Reliab. Eng. Syst. Saf. 2000, 68, 219–254. [Google Scholar] [CrossRef]
- Park, K. Condition-based predictive maintenance by multiple logistic function. IEEE Trans. Reliab. 1993, 42, 556–560. [Google Scholar] [CrossRef]
- Maillart, L.; Pollock, S. Cost-optimal condition-monitoring for predictive maintenance of 2-phase systems. IEEE Trans. Reliab. 2002, 51, 322–330. [Google Scholar] [CrossRef]
- Yang, S. A condition-based failure-prediction and processing-scheme for preventive maintenance. IEEE Trans. Reliab. 2003, 52, 373–383. [Google Scholar] [CrossRef]
- Li, W.; Pham, H. An Inspection-Maintenance Model for Systems with Multiple Competing Processes. IEEE Trans. Reliab. 2005, 54, 318–327. [Google Scholar] [CrossRef]
- Xu, Z.; Ji, Y.; Zhou, D. Real-time Reliability Prediction for a Dynamic System Based on the Hidden Degradation Process Identification. IEEE Trans. Reliab. 2008, 57, 230–242. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Isermann, R.; Ballé, P. Trends in the application of model-based fault detection and diagnosis of technical processes. Control Eng. Pr. 1997, 5, 709–719. [Google Scholar] [CrossRef]
- Blanke, M.; Izadi-Zamanabadi, R.; Bøgh, S.A.; Lunau, C.P. Fault-tolerant control systems—A holistic view. Control Eng. Pract. 1997, 5, 693–702. [Google Scholar] [CrossRef]
- Zhang, D.; Yu, L. Fault-Tolerant Control for Discrete-Time Switched Linear Systems with Time-Varying Delay and Actuator Saturation. J. Optim. Theory Appl. 2012, 153, 157–176. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, X. Fault-tolerant control systems: A comparative study between active and passive approaches. Annu. Rev. Control 2012, 36, 60–72. [Google Scholar] [CrossRef]
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A survey of fault detection, isolation, and reconfiguration methods. IEEE Trans. Control Syst. Technol. 2009, 18, 636–653. [Google Scholar] [CrossRef]
- Muenchhof, M.; Beck, M.; Isermann, R. Fault-tolerant actuators and drives—Structures, fault detection principles and applications. Annu. Rev. Control 2009, 33, 136–148. [Google Scholar] [CrossRef]
- Mhaskar, P.; Liu, J.; Christofides, P.D. Fault-Tolerant Process Control: Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Milosavljevic, P.; Cortinovis, A.; Marchetti, A.G.; Faulwasser, T.; Mercangoz, M.; Bonvin, D. Optimal load sharing of parallel compressors via modifier adaptation. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016. [Google Scholar]
- Rahman, S.; Rahman, M.; Abdullah-Al-Wadud, M.; Al-Quaderi, G.D.; Shoyaib, M. An adaptive gamma correction for image enhancement. EURASIP J. Image Video Process. 2016, 2016, 35. [Google Scholar] [CrossRef]
- Sontag, E.D. Mathematical Control Theory, Volume 6 of Texts in Applied Mathematics; Springer: New York, NY, USA, 1998. [Google Scholar]
- Kamali Mohammadzadeh, A.; Allen, C.L.; Masoud, S. VR Driven Unsupervised Classification for Context Aware Human Robot Collaboration. In Proceedings of the International Conference on Flexible Automation and Intelligent Manufacturing, Porto, Portugal, 18–22 June 2023; Springer Nature: Cham, Switzerland, 2023; pp. 3–11. [Google Scholar]
- Jahanmahin, R.; Masoud, S.; Rickli, J.; Djuric, A. Human-robot interactions in manufacturing: A survey of human behavior modeling. Robot. Comput. Manuf. 2022, 78, 102404. [Google Scholar] [CrossRef]
- Lanier, D.; Roush, C.; Young, G.; Masoud, S. Predictive Analysis of Endoscope Demand in Otolaryngology Outpatient Settings. BioMedInformatics 2024, 4, 721–732. [Google Scholar] [CrossRef]
- Emakhu, J.; Etu, E.-E.; Monplaisir, L.; Aguwa, C.; Arslanturk, S.; Masoud, S.; Tenebe, I.T.; Nassereddine, H.; Hamam, M.; Miller, J. A hybrid machine learning and natural language processing model for early detection of acute coronary syndrome. Health Anal. 2023, 4, 100249. [Google Scholar] [CrossRef]
- Eghbali-Zarch, M.; Masoud, S. Application of machine learning in affordable and accessible insulin management for type 1 and 2 diabetes: A comprehensive review. Artif. Intell. Med. 2024, 151, 102868. [Google Scholar] [CrossRef] [PubMed]
- Mohammadzadeh, A.K.; Salah, H.; Jahanmahin, R.; Hussain, A.E.A.; Masoud, S.; Huang, Y. Spatiotemporal integration of GCN and E-LSTM networks for PM2.5 forecasting. Mach. Learn. Appl. 2024, 15, 100521. [Google Scholar] [CrossRef]
- Masoud, S.; Mariscal, N.; Huang, Y.; Zhu, M. A sensor-based data driven framework to investigate PM 2.5 in the greater Detroit area. IEEE Sens. J. 2021, 21, 16192–16200. [Google Scholar] [CrossRef]
- Chowdhury, B.D.B.; Masoud, S.; Son, Y.J.; Kubota, C.; Tronstad, R. A dynamic data driven indoor localisation framework based on ultra-high frequency passive RFID system. Int. J. Sens. Netw. 2020, 34, 172–187. [Google Scholar] [CrossRef]
- Chowdhury, B.D.B.; Masoud, S.; Son, Y.-J.; Kubota, C.; Tronstad, R. A Dynamic HMM-Based Real-Time Location Tracking System Utilizing UHF Passive RFID. IEEE J. Radio Freq. Identif. 2021, 6, 41–53. [Google Scholar] [CrossRef]
- Ta, Q.-B.; Huynh, T.-C.; Pham, Q.-Q.; Kim, J.-T. Corroded Bolt Identification Using Mask Region-Based Deep Learning Trained on Synthesized Data. Sensors 2022, 22, 3340. [Google Scholar] [CrossRef]
- Ta, Q.-B.; Pham, Q.-Q.; Pham, N.-L.; Huynh, T.-C.; Kim, J.-T. Smart Aggregate-Based Concrete Stress Monitoring via 1D CNN Deep Learning of Raw Impedance Signals. Struct. Control Health Monit. 2024, 2024, 5822653. [Google Scholar] [CrossRef]
- Soualhi, A.; Razik, H.; Clerc, G.; Doan, D.D. Prognosis of Bearing Failures Using Hidden Markov Models and the Adaptive Neuro-Fuzzy Inference System. IEEE Trans. Ind. Electron. 2013, 61, 2864–2874. [Google Scholar] [CrossRef]
- Dao, F.; Zeng, Y.; Qian, J. Fault diagnosis of hydro-turbine via the incorporation of bayesian algorithm optimized CNN-LSTM neural network. Energy 2024, 290, 130326. [Google Scholar] [CrossRef]
- Borré, A.; Seman, L.O.; Camponogara, E.; Stefenon, S.F.; Mariani, V.C.; Coelho, L.D.S. Machine Fault Detection Using a Hybrid CNN-LSTM Attention-Based Model. Sensors 2023, 23, 4512. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.S.; Kolarik, W.J. Real-time conditional reliability prediction from on-line tool performance data. Int. J. Prod. Res. 1992, 30, 1831–1844. [Google Scholar] [CrossRef]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R.; Ryan, J.K. Residual-life distributions from component degradation signals: A Bayesian approach. IIE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Liberzon, D.; Morse, A. Hysteresis-based switching algorithms for supervisory control of uncertain systems. Automatica 2003, 39, 263–272. [Google Scholar] [CrossRef]
- Morse, A.S. Supervisory control of families of linear set-point controllers-part i. exact matching. IEEE Trans. Autom. Control 1996, 41, 1413–1431. [Google Scholar] [CrossRef]
- Na, G.; Jo, N.H.; Eun, Y. Performance degradation due to measurement noise in control systems with disturbance observers and saturating actuators. J. Frankl. Inst. 2019, 356, 3922–3947. [Google Scholar] [CrossRef]
- Trinh, H.D.; Zeydan, E.; Giupponi, L.; Dini, P. Detecting Mobile Traffic Anomalies Through Physical Control Channel Fingerprinting: A Deep Semi-Supervised Approach. IEEE Access 2019, 7, 152187–152201. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsaedi, F.; Masoud, S. Condition-Based Maintenance for Degradation-Aware Control Systems in Continuous Manufacturing. Machines 2025, 13, 141. https://doi.org/10.3390/machines13020141
Alsaedi F, Masoud S. Condition-Based Maintenance for Degradation-Aware Control Systems in Continuous Manufacturing. Machines. 2025; 13(2):141. https://doi.org/10.3390/machines13020141
Chicago/Turabian StyleAlsaedi, Faisal, and Sara Masoud. 2025. "Condition-Based Maintenance for Degradation-Aware Control Systems in Continuous Manufacturing" Machines 13, no. 2: 141. https://doi.org/10.3390/machines13020141
APA StyleAlsaedi, F., & Masoud, S. (2025). Condition-Based Maintenance for Degradation-Aware Control Systems in Continuous Manufacturing. Machines, 13(2), 141. https://doi.org/10.3390/machines13020141




