Development of Electrohydraulic Proportional Valve Model for Precise Steering Control in Autonomous Tractors

Abstract

Autonomous tractors are emerging as a pivotal technology in agricultural automation. Precise steering control in these tractors requires high-performance electrohydraulic proportional valves (EHPVs). To optimize EHPV performance and reduce development costs and time, simulation analysis serves as a valuable pre-testing tool. This study aimed to develop a simulation model capable of predicting the hydraulic characteristics of EHPVs under real-world operating conditions. The model was created using AMESim, incorporating actual tractor operating conditions and valve control signals. The proposed model was validated through experiments conducted on a tractor equipped with an EHPV, evaluating hydraulic characteristics across various engine speeds and steering angular velocities. The simulation model was utilized to analyze the priority valve control flow characteristics of the automatic steering system and the hydraulic response of the EHPV under step inputs at specific engine speed points. The results indicate that the simulation model demonstrated a mean absolute percentage error (MAPE) ranging from 7.45% to 9.79% for hydraulic power. A t-test analysis of hydraulic power indicated no statistically significant difference between the simulation and experimental values under all test conditions. The proposed EHPV simulation model can be utilized for the optimal future design of EHPV systems.

1. Introduction

Agricultural tractors are vital machines for open-field farming, performing a wide range of tasks through various implement attachments. Tractors not only have the highest annual usage hours among agricultural machines but are also the most widely produced [1]. The global tractor market is projected to reach USD 69 billion by 2029, representing 35% of the entire agricultural machinery market [2]. With rapid advancements in communication and sensor technologies, the agriculture machinery sector, including tractors, has seen the introduction of innovative technologies aimed at enhancing precision agriculture practices [3]. Among these innovations, autonomous driving technology is the most actively researched field globally [4]. This technology for tractors includes several key components, such as automatic steering, environmental perception, and driving and work path generation [5]. Automatic steering was the primary focus during the early stages of autonomous tractor development [6]. It has rapidly evolved from basic straight-line guidance to integrated turn and path-following functions, combining environmental perception with GPS technology [7]. These automatic steering functions have been commercialized in various forms, including as built-in features in new tractors and add-on kits for existing models [8].

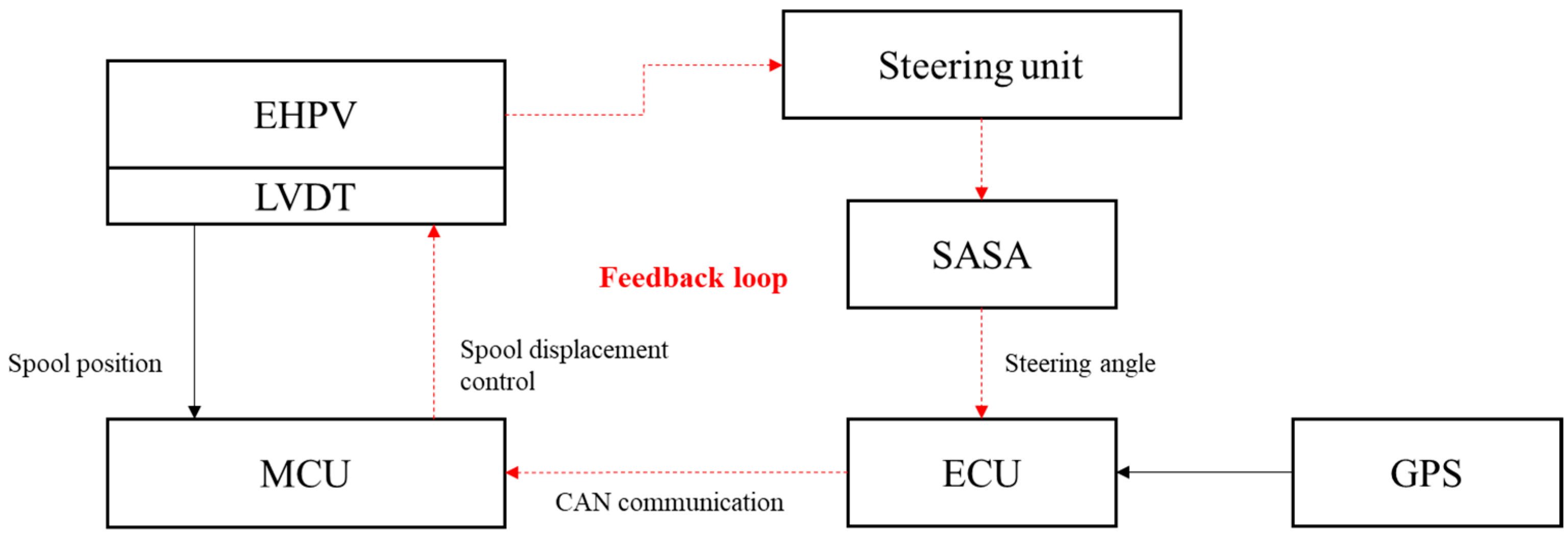
In agricultural tractors, electronically controlled hydraulic steering systems, which include electrohydraulic proportional valves (EHPVs), are commonly used for automatic steering. Over time, steering systems have evolved in various ways. In passenger vehicles, electric power steering (EPS) systems with motors or steer-by-wire technologies that eliminate mechanical connections have become standard. However, in large trucks, construction machinery, and agricultural equipment, electronically controlled hydraulic steering systems are preferred due to their stability under load and high reliability [9]. An electronically controlled hydraulic steering system operates by regulating the steering pump through an electronic control unit (ECU) or by managing fluid flow through electronically controlled valves. Integrating an EHPV into a tractor’s automatic steering system offers two main benefits. First, it provides design flexibility by eliminating the need for a separate steering pump. Second, the EHPV enables the continuous, precise control of fluid flow and is usually connected to a controller with a feedback loop [10]. The precise control enhances the steering responsiveness and performance of the automatic steering system [11].

Research on tractor automatic steering systems incorporating EHPVs has predominantly focused on control algorithms. Challenges faced by electronically controlled hydraulic steering systems include low precision, often due to the nonlinearity and hysteresis inherent in hydraulic systems [12]. Qiu et al. (2001) developed a fuzzy steering controller for tractors equipped with an EHPV [13]. The study introduced methods for evaluating the steering system using hardware-in-the-loop (HIL) simulation and field experiments. Liu et al. (2016) extended traditional steering systems with an EHPV-based automatic steering system [14]. To meet the demands of automatic steering, the researchers added a steering angle sensor, proposed a PID control concept, and developed a discrete PID control method suitable for digital applications. Bo et al. (2018) formulated the state equation for an EHPV in an automatic steering system and conducted computer simulations to assess flow control and pressure compensation [15]. The vehicle-based experiments conducted by the researchers validated the system, revealing an average steering angle error of up to 2.4°. Lee et al. (2022) compared the performance of EPS and EHPV systems using an HIL simulator [9]. The findings of the study showed that EHPVs performed better than EPS systems, with further evaluation conducted using RTK-GPS in field experiments. However, research on the impact of actual tractor operating conditions on the hydraulic characteristics of EHPVs remains limited. Understanding the variations in flow rate and pressure under different operational conditions is crucial for designing and predicting the performance of EHPVs in real-world scenarios. The accurate control of fluid flow is essential, particularly if EHPVs are used as extensions of existing steering systems, to ensure that they match the capacity of the pump and actuators. To address this gap, this study aimed to develop a simulation analysis model for EHPVs in tractor automatic steering systems. The specific objectives were to (1) conduct field measurements on an automatic steering system equipped with an EHPV, (2) develop a simulation analysis model for an EHPV, (3) compare the results of field measurements with those of simulation analysis, and (4) validate the EHPV simulation model.

Computer-aided engineering (CAE) has proven to be a valuable tool in various industries, including agricultural machinery, for product design and capacity selection [16,17,18]. CAE-based simulation analysis can reduce the costs and time associated with performance prediction and the optimal design of EHPVs. Recently, studies integrating machine learning models with CAE-based approaches have been actively conducted to enhance the prediction of hydraulic characteristics [19,20,21]. These computational resource-driven techniques enable more efficient and accurate modeling by learning complex nonlinear behaviors in hydraulic systems, complementing traditional physics-based simulations. By leveraging data-driven insights, these hybrid approaches contribute to improved control precision and system reliability in EHPV-equipped tractor steering systems.

2. Materials and Methods

2.1. Agricultural Tractor

The tractor used in this study was equipped with a 4-cylinder diesel engine that delivered a rated power of 93.2 kW. The tractor had a total weight of 4072 kg. The front tires adhered to the 13.6 R24 specification, with a front wheel track width of 1680 mm. Detailed specifications of the tractor are provided in

Table 1. Specifications of the tractor used in this study.

Item		Specifications
Tractor	Dimensions (L × W × H) (mm)	4670 × 2250 × 2770
	Wheelbase (mm)	2370
	Front track width (mm)	1680
	Rear track width (mm)	1790
	Weight (kg)	4072
Engine	Number of cylinders	4
	Displacement (cc)	3409
	Rated power (kW)	93.2 (@ 2200 rpm)
Front-wheel tire	Section width (mm)	345
	Type	Radial
	Rim diameter (mm)	610
	Overall diameter (mm)	1184
Rear-wheel tire	Section width (mm)	467
	Type	Radial
	Rim diameter (mm)	864
	Overall diameter (mm)	1666
Steering actuator	Piston diameter of the actuator (mm)	70
	Rods diameter of the actuator (mm)	35
	Length of stroke (mm)	274

.

2.2. Hydraulic Steering System

The tractor featured a non-load reaction type electrohydraulic power steering system. The steering pump was a gear pump directly connected to the engine, with a gear ratio of 1:1. The pump had a displacement of 21 cc/rev and the steering oil tank had a capacity of 11 L. The steering oil used was ISO VG 46 standard oil.

As illustrated in Figure 1, the developed automatic steering system was integrated into the existing tractor steering system. This system comprised an EHPV, priority valve, cutoff valve, solenoid valve, relief valve, and EHPV controller, designed as an add-on component to the existing steering mechanism. The priority valve managed the internal flow up to 25 LPM based on the steering pump’s discharge rate, while the EHPV controlled the steering direction and input flow according to the solenoid valve’s signals. The cutoff valve served as a safety feature, blocking the discharge flow from the directional control valve to the steering cylinder in response to the on/off solenoid valve’s operation. The controller was connected to the steering angle sensors on both the steering shaft and the steering angle sensor of the front axle and adjusted the proportional control valve according to the steering algorithm. The specifications of the proportional control valve are detailed in

Table 2. Specifications of the hydraulic steering system.

Item		Specifications
Steering pump	Type	Gear pump
	Gear ratio of the engine	1:1
	Displacement (cc/rev)	21
Steering oil	Oil tank capacity (L)	11
	Standard	ISO VG 46
	Density (kg/m3)	860 (at 40 °C)
EHPV	Maximum flow rate (LPM)	60
	Maximum control flow rate (LPM)	25
	Relief valve pressure (bar)	210 bar (at 25 LPM)
	Temperature range (°C)	−40 to 120

.

The control flow of the automatic steering system is illustrated in Figure 2. The microcontroller unit (MCU) of the steering system was connected to the LVDT installed on the directional control valve spool of the EHPV to measure the spool displacement. A Steering Angle Sensor Assembly (SASA) was mounted on the tractor’s steering column, providing steering angle data of the tractor measured by the left and right axle sensors. The MCU received steering angle, tractor motion, and GPS position information via CAN communication. Upon initiation of the automatic steering sequence, a target steering angle was generated by a GPS-based steering algorithm, and the spool was controlled accordingly. The spool feedback control was executed by utilizing real-time steering angle feedback from the SASA sensor.

2.3. Measurement System

The measurement system for assessing the flow rate and pressure characteristics of the EHPV under various operating conditions is illustrated in Figure 3. This system included two flow meters, two pressure sensors, two angle sensors, and a data acquisition (DAQ) system. The flow meters (Hysense PR130, Hydrotechnik, Limburg an der Lahn, Germany) and pressure sensors (Hysense QG100, Hydrotechnik, Limburg an der Lahn, Germany) were mounted on each hydraulic hose connecting the EHPV to the steering cylinder. Steering angle sensors (424A, Elobau, Leutkirch, Germany) were attached to the left and right front wheels of the tractor. Measurement data were collected and stored on a PC via the DAQ system (Q.brixx A107, Gantner, Nuziders, Austria), with the sampling rate set at 1000 Hz. The specifications of the measurement system are provided in

Table 3. Specifications of the measurement system.

Item		Specifications
Flow meter (Hysense QG100)	Type	Gear type
	Measurement range (LPM)	0.7 to 70
	Geometric gear volume (L)	0.00222
	Resolution (LPM)	0.133
	Accuracy (%)	±0.4
Pressure sensor (Hysense PR130)	Pressure type	Relative pressure
	Measuring type	Piezo-resistive
	Measurement range (bar)	0 to 250
	Accuracy (%)	±0.5
Angle sensor (424A)	Measurement range (°)	90
	Resolution (°)	0.1
	Accuracy (%)	±1
DAQ (Q.brixx A107)	Number of channels	4 universal input
	Resolution	24 bits
	Sample rate (kHz)	10
	Filter	IIR, low pass, high pass, 4th order
	Accuracy (%)	0.01%

.

2.4. Simulation Model

In this study, a simulation model was developed to analyze the hydraulic characteristics of the EHPV. The model was created using Simcenter AMESim (version 2021.2, Siemens Digital Industries Software, Munich, Germany), a 1-D CAE software. The tractor’s steering system was simplified into a configuration consisting of a steering pump, the developed EHPV-based automatic steering system, and the steering actuator. The EHPV controller unit was implemented as a simplified control signal input model within AMESim. The control signal input model was designed to evaluate the hydraulic characteristics of the valve using a spool position control step input signal and validate the simulation model by applying the same spool control signals as those used in actual vehicle experiments. Each model component reflected the specifications of actual components, and certain parameters for simulation analysis were approximated using empirical experimental data.

Table 4. Simulation parameters of the EHPV analysis model.

Parameters	Value
Fractional spool position function of priority valve	0.025(x-y)
Pilot pressure of priority valve (bar)	10
Orifice diameter of priority valve (mm)	1.5
Axial load of the steering actuator mass model (kN/(m/s))	64.81

includes the spool dynamics equation estimated based on the maximum opening pressure of the priority valve, as well as the estimated axial load applied to the steering cylinder to compensate for the operating pressure of the EHPV. The simulation fluid parameters were applied in accordance with the viscosity characteristics of ISO VG 46 hydraulic fluid, considering temperature variations, as presented in

Table 5. Simulation parameters for fluid viscosity based on oil temperature.

Oil Temperature (°C)	Kinematic Viscosity (cSt)	Absolute Viscosity (cP)
40	46	40
50	28	25
60	20	17
80	9	8
100	5	4.5

.

The simulation model development and verification procedure are illustrated in Figure 4. The automatic steering system was developed through two stages: creating individual component models based on actual specifications and performing system integration (SI) to develop the integrated model. The developed model underwent hydraulic characteristic evaluation using step input signals and was validated by verifying its hydraulic power prediction accuracy against actual vehicle data.

2.5. Test Methods

We conducted experiments on an EHPV mounted on an actual tractor. The experimental conditions were determined by two factors: engine speed and steering angular speed. Engine speed affected the rotational speed of the steering pump, which, in turn, influenced the operating flow rate of the EHPV. The steering angular speed affected the flow rate and pressure at the steering cylinder via the EHPV. Engine speeds were tested at three levels: 900 rpm (idle speed), 1400 rpm (maximum torque speed), and 2200 rpm (rated speed). The steering angular velocities were set to 0.16, 0.21, and 0.26 rad/s. Each angular velocity corresponded to 30%, 70%, and 100% of the maximum front wheel steering angle, with target steering angles set at 16°, 38°, and 54°, respectively. These values represented the initial angular velocity inputs in the steering control algorithm. The experimental site was covered with urethane, and the tractor remained stationary during the experiment, with no additional attachments installed. The hydraulic power of the EHPV was computed using Equation (1), with the hydraulic efficiency set at 0.9, as reported in previous research [22].

$${\mathrm{P}}_{\mathrm{h}}={\mathsf{\eta }}_{\mathrm{v}}\times {\displaystyle \frac{\mathrm{P}\times \mathrm{Q}}{0.6}},$$

(1)

where ${\mathrm{P}}_{\mathrm{h}}$ is the hydraulic power requirement (W), ${\mathsf{\eta }}_{\mathrm{v}}$ is the hydraulic efficiency (%), $\mathrm{P}$ is the pressure (bar), and $\mathrm{Q}$ is the flow rate (LPM).

2.6. Analysis Method

The flow response characteristics of the developed automatic steering system model were analyzed in response to a step signal. We evaluated several performance metrics:

• Steady-state error: This measured the discrepancy between the flow rate of the simulation model once it had stabilized and the value measured under identical conditions.
• Rise time: This was the time required for the flow rate to increase from 10% to 90% of the target flow rate.
• Settling time: This was the duration needed for the flow response to stay within 5% of the target flow rate without deviating.
• Overshoot: This represented the extent to which the peak flow response exceeded the target value, calculated using Equation (2).

To validate the simulation model, we compared it with actual experimental data. Parameters such as flow rate, pressure, and hydraulic power were assessed, and the simulation model’s accuracy was evaluated using the following metrics [20,21]:

• Mean absolute percentage error (MAPE): This represented the absolute error between experimental and simulation values as a percentage of the experimental values, calculated using Equation (3).
• Root mean square error (RMSE): This was the square root of the average squared differences between experimental and simulation values, calculated using Equation (4).
• Normalized RMSE (NRMSE): This was obtained by normalizing the RMSE by dividing it by the mean of the observed values, as calculated using Equation (5).
• Coefficient of determination (R²): This indicated the degree of agreement between the experimental and simulation values, calculated using Equation (6).

Additionally, a T-test was performed to determine if there was a statistically significant difference between the experimental and simulation results, with significance set at p < 0.05.

$$\mathrm{O}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{t}=\left({\displaystyle \frac{{\mathrm{y}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{y}}_{\mathrm{s}\mathrm{s}}}{{\mathrm{y}}_{\mathrm{s}\mathrm{s}}}}\right)\times 100\mathrm{\%},$$

(2)

where ${\mathrm{y}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum flow rate (LPM) and ${\mathrm{y}}_{\mathrm{s}\mathrm{s}}$ is the steady-state flow rate (LPM).

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{\mathrm{N}}}{\sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{N}}\left|{\displaystyle \frac{1}{{\mathrm{y}}_{\mathrm{i}}}}({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}})\right|\times 100\mathrm{\%},$$

(3)

where ${\mathrm{y}}_{\mathrm{i}}$ is the experimental value and ${\widehat{\mathrm{y}}}_{\mathrm{i}}$ is the simulation value.

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{\mathrm{N}}}{\sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{N}}({({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}})}^2},$$

(4)

where ${\mathrm{y}}_{\mathrm{i}}$ is the experimental value and ${\widehat{\mathrm{y}}}_{\mathrm{i}}$ is the simulation value.

$$\mathrm{N}\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}}{\overline{\mathrm{y}}}},$$

(5)

where $\overline{\mathrm{y}}$ is the average of the experimental values.

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{N}}{\left({\widehat{\mathrm{y}}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2}{{\sum }_{\mathrm{i}=1}^{\mathrm{i}=\mathrm{N}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2}},$$

(6)

where ${\mathrm{R}}^2$ is the coefficient of determination, ${\widehat{\mathrm{y}}}_{\mathrm{i}}$ is the simulation value, ${\overline{\mathrm{y}}}_{\mathrm{i}}$ is the average of the experimental values, and ${\mathrm{y}}_{\mathrm{i}}$ is the experimental value.

3. Results

3.1. Development of the EHPV Simulation Model

A simulation model of the EHPV was developed, as shown in Figure 5. To simplify the hydraulic pump, a motor was used instead of an engine. The pump delivered flow rates of 18.9, 29.4, and 46.2 LPM at engine speeds of 900, 1400, and 2200 rpm, respectively. The EHPV model was designed based on actual valve specifications and design data. The main directional control valve in the EHPV was simplified to a signal input system using a proportional control solenoid valve. The control signals were modeled exactly as in the experimental setup. The steering unit employed a double-acting actuator model, excluding the standard tractor steering structure.

Figure 6 illustrates the simulation analysis results of the priority valve control flow rate according to the engine speed and EHPV spool opening ratio. The priority valve functioned to discharge more flow to the outlet line as the input flow from the steering pump increased. The simulation results showed that the control flow rate of the priority valve increased non-linearly as the engine speed increased. However, when the EHPV spool openings corresponded to 25%, 50%, and 75% of the maximum displacement, the control flow rate demonstrated a linear increase starting at engine speeds of 2091, 2494, and 2697 rpm, respectively. This indicated that the priority valve reached its maximum opening position, referred to as the full-stroke point, at these engine speeds.

As the EHPV spool opening ratio decreased, the pressure in the priority valve increased, providing sufficient pilot pressure to compress the priority valve spring to its full displacement, even under lower input flow conditions. The priority valve control flow rates corresponding to various EHPV spool opening ratios at key engine operating points (idle speed, maximum torque, rated speed, and maximum speed) are summarized in

Table 6. Flow rate response of the priority valve for different spool opening ratios at key engine speeds.

Engine Speed (rpm)		Flow Rate (LPM)
		900	1400	2200	2800
Spool opening (%)	25	7.22	8.60	10.74	13.68
	50	11.70	14.25	17.30	20.79
	75	14.19	17.61	21.66	24.40
	100	15.58	19.58	24.33	27.02

.

Figure 7 illustrates the control flow characteristics of the priority valve under various hydraulic oil temperature conditions. As the operating oil temperature increased, the viscosity of the steering oil decreased, leading to an increase in pilot circuit pressure due to the rise in internal flow resistance within the valve. Consequently, the control flow rate of the priority valve exhibited an increasing trend with rising oil temperature, with the maximum flow rate also showing an upward tendency. Notably, beyond approximately 60 °C, the rate of increase in control flow diminished significantly, and the difference in control flow between 80 °C and 100 °C was numerically negligible. Specifically, the control flow rate of the priority valve increased from 24.33 LPM at 40 °C to approximately 25.4 LPM as the temperature rose. The detailed characteristics of priority valve flow rates under different hydraulic oil temperature conditions are presented in

Table 7. Control flow characteristics of the priority valve according to hydraulic oil temperature.

Engine Speed (rpm)	Oil Temperature (°C)	Control Flow Rate (LPM)	Maximum Flow Rate (LPM)	Spool Opening (%)
2200	40	24.33	27.59	79.26
	50	25.05	27.91	83.60
	60	25.26	28.00	85.01
	80	25.36	28.04	85.66
	100	25.36	28.04	85.66

.

Figure 8 illustrates the response characteristics of flow rate, pressure, and hydraulic power to step input changes in the spool displacement of the electro-hydraulic proportional valve (EHPV). These characteristics served as critical indicators for analyzing the system performance requirements associated with spool movement and were closely linked to the dynamic behavior of the valve.

In the experiment, step input signals were applied to displace the spool to 25%, 50%, and 75% positions relative to the maximum spool displacement of 4 mm. Although this step input did not perfectly replicate the physical behavior of the spool, it effectively approximated the rapid response of the proportional control valve and facilitated the evaluation of the maximum flow rate variation at specific spool openings. In actual experimental results, the spool opening was observed to remain below 50%. The simulation results for a 75% opening predict the potential hydraulic characteristics of the EHPV when the tractor exhibited extremely high steering angular velocity behavior.

At an engine speed of 900 rpm, the system exhibited minimal overshoot. Under the 1400 rpm condition, overshoot exceeded 5% in all cases except for one. At 2200 rpm, overshoot increased significantly, reaching 12.2% or higher. The overshoot in pressure was more pronounced than that in flow rate, and the hydraulic power demonstrated a maximum overshoot of 45.9%. The rise time of the system decreased as the engine speed increased, which could be attributed to the higher supply flow rate allowing the system to reach the target flow rate more rapidly. Conversely, the settling time tended to increase with engine speed, as more overshoot required more time for the system to stabilize.

When the hydraulic stiffness of the system was sufficiently high, increasing the supply flow rate enabled the target flow rate to be achieved more quickly, resulting in a shorter rise time. Additionally, a higher supply flow rate increased fluid inertia while reducing hydraulic resistance. Due to fluid inertia, under rapidly changing conditions such as a step input, flow rate and pressure could exceed the control setpoint, leading to overshoot. The increased inertia reduced the damping ratio of the hydraulic system, thereby diminishing the damping effect and prolonging the time required for system stabilization. Consequently, more overshoot tended to result in a longer settling time. Detailed results on the hydraulic response characteristics of the EHPV can be found in

Table 8. Simulation analysis results of EHPV response characteristics.

Engine Speed (rpm)		900			1400			2200
Spool Open (%)		25	50	75	25	50	75	25	50	75
Flow rate (LPM)	Steady-state value	7.22	11.7	14.2	8.7	14.5	18.1	11.3	17.8	22.5
	Max. value	7.35	11.7	14.2	9.5	15.5	18.9	12.2	20.4	25.3
	Overshoot (%)	1.73	0.079	0.044	8.74	6.24	4.75	8.63	14.4	12.7
	Steady-state error (%)	0.306	0.796	1.247	0.304	0.910	1.550	0.261	1.045	1.839
	Settling time (s)	0.26	0.26	0.25	0.55	0.46	0.20	0.52	0.61	0.57
	Rise time (s)	0.20	0.19	0.19	0.17	0.17	0.16	0.18	0.16	0.15
Pressure (bar)	Steady-state value	27.7	62.0	81.0	39.1	83.7	110	58.7	109	144
	Max. value	28.6	62.0	81.1	46.0	93.5	119	68.7	139	177
	Overshoot (%)	3.29	0.108	0.172	17.7	11.7	8.18	17.1	28.2	23.2
	Steady-state error (%)	0.652	1.084	1.717	0.568	0.874	1.373	0.569	0.675	1.047
	Settling time (s)	0.31	0.33	0.35	0.66	0.6	0.54	0.65	0.77	0.72
	Rise time (s)	0.23	0.24	0.25	0.19	0.20	0.21	0.20	0.18	0.19
Power (W)	Steady-state value	300	1088	1726	510	1827	2990	992	2905	4854
	Max. value	315	1088	1727	653	2162	3373	1259	4237	6675
	Overshoot (%)	5.04	0.029	0.047	27.9	18.4	12.8	26.9	45.9	37.5
	Steady-state error (%)	0.346	0.287	0.469	0.264	0.037	0.179	0.308	0.370	0.794
	Settling time (s)	0.46	0.34	0.36	0.7	0.65	0.59	0.69	0.81	0.74
	Rise time (s)	0.22	0.24	0.25	0.17	0.18	0.19	0.18	0.15	0.16

.

Figure 9 presents the results of a regression analysis on the settling time and rise time of flow rate, pressure, and hydraulic power responses with respect to engine speed. In theory, higher engine speeds and greater spool openings should lead to an increased rate of change in flow per unit time, thereby reducing both the settling time and response time. However, several factors caused deviations from this expected trend.

First, when overshoot occurred, the system required additional time for the increased flow rate and pressure to stabilize near their steady-state values. As a result, the effect of overshoot-induced settling time prolongation outweighed the reduction in settling time caused by higher engine speeds. Consequently, in conditions where overshoot was present, an increase in engine speed led to a longer settling time.

Additionally, in the case of a 25% spool opening step input, an unusual trend was observed: at 2200 rpm, the settling time was shorter and the rise time was longer compared to 1400 rpm. This suggested a distinctive behavior in EHPV operation under high engine speeds. When supplying high flow rates to the EHPV at lower spool openings, the system reached the maximum deliverable flow capacity of the valve more rapidly. Despite the increase in overshoot, this effect could lead to a shorter settling time, highlighting a unique characteristic of the system’s response dynamics.

3.2. Comparison of Hydraulic Power Characteristics of the EHPV Between Field Tests and Simulation Analysis

Figure 10 presents the hydraulic power characteristics of the EHPV as obtained from both field experiments and simulation analysis. The simulation analysis was conducted using the same control signals applied during the field tests. The hydraulic power characteristics were evaluated up to the point where the EHPV reached its maximum power under steering angular velocity conditions. Each data point was collected at a sampling rate of 1000 Hz, corresponding to 1 ms.

In the field experiments, the hydraulic power characteristics were influenced by various factors, including the nonlinear behavior of the hydraulic system. The maximum hydraulic power increased with higher engine speeds and larger steering angular velocities. However, the average hydraulic power did not always follow this trend consistently. While the simulation model effectively captured the overall trend of hydraulic power increase, localized variations and irregularities inherent in real hydraulic systems introduced small discrepancies between field test results and simulations. These discrepancies stemmed from the dynamic response of the system, where real-time control algorithms adjusted flow rates nonlinearly based on feedback, leading to variations in the timing and magnitude of hydraulic power output. Despite these localized fluctuations, the general trend of increasing hydraulic power with higher engine speeds and larger steering angular velocities was consistently well predicted by the simulation.

Table 9. Statistical analysis results of the EHPV hydraulic power characteristics.

Steering Direction	Steering Angular Speed (rad/s)	Type	Experimental Value (W)			Simulation Value (W)			MAPE * (%)
			Engine Speed (rpm)			Engine Speed (rpm)			Engine Speed (rpm)
			900	1400	2200	900	1400	2200	900	1400	2200
Left turn	0.16	Max.	291	437	678	287	466	674	7.89	8.49	7.45
		Avg.	139	199	265	138	203	270
	0.21	Max.	377	575	809	397	605	790	9.32	9.17	9.39
		Avg.	208	290	345	218	291	335
	0.26	Max.	491	718	1027	518	720	1033	9.77	9.61	9.41
		Avg.	270	349	377	289	339	372
Right turn	0.16	Max.	235	468	648	254	467	682	8.99	9.87	8.56
		Avg.	148	168	318	147	171	316
	0.21	Max.	482	671	833	508	707	848	9.42	9.04	9.69
		Avg.	272	272	381	285	270	380
	0.26	Max.	689	877	1084	686	887	1105	9.56	9.76	9.79
		Avg.	342	336	438	353	328	448

* MAPE = mean absolute percentage error.

provides the statistical analysis results of the EHPV’s hydraulic power characteristics. Field experiments showed maximum hydraulic power values ranging from 235 to 1084 W, with average values between 139 and 438 W. The simulation model predicted maximum power values of 254 to 1105 W and average values from 138 to 448 W. The hydraulic power characteristics demonstrated an MAPE ranging from 7.45% to 9.79%.

3.3. Validation of EHPV Simulation Model

3.3.1. t-Test Results of the Simulation Analysis

Table 10. Mann–Whitney U test results for the EHPV hydraulic power characteristics.

Direction	Engine Speed (rpm)	Angular Speed (rad/s)	Experimental Value (W)	Simulation Value (W)	Mann–Whitney U Test
			Avg. ± Std.	Avg. ± Std.	U-Statistic	Sample Size	p
Left turn	900	0.16	139 ± 91	137 ± 92	29705	245	0.845
		0.21	208 ± 109	218 ± 119	36405	263	0.296
		0.26	269 ± 143	288 ± 144	18668	186	0.187
	1400	0.16	199 ± 134	203 ± 143	17834	188	0.878
		0.21	290 ± 164	290 ± 177	19760	199	0.972
		0.26	348 ± 218	338 ± 227	27843	239	0.635
	2200	0.16	264 ± 202	270 ± 209	37858	274	0.863
		0.21	345 ± 252	334 ± 254	39052	284	0.514
		0.26	376 ± 312	372 ± 318	39550	284	0.691
Right turn	900	0.16	147 ± 66	147 ± 74	39131	277	0.684
		0.21	271 ± 149	284 ± 153	46461	297	0.260
		0.26	342 ± 207	353 ± 219	26786	228	0.573
	1400	0.16	167 ± 151	170 ± 152	39437	280	0.902
		0.21	272 ± 210	269 ± 212	40643	286	0.898
		0.26	336 ± 276	327 ± 273	33790	263	0.649
	2200	0.16	318 ± 215	315 ± 219	39385	282	0.846
		0.21	380 ± 264	380 ± 261	23693	217	0.910
		0.26	437 ± 342	447 ± 358	34916	263	0.849

presents the results of a Mann–Whitney U test comparing the experimental and simulated values of the EHPV hydraulic power. Because the experimental and simulation values were derived from different methods based on input signals to the EHPV controller, a non-parametric Mann–Whitney U test was conducted. The experimental and simulation values exhibited a heavy-tailed distribution due to the initial delay in hydraulic power increase and a light-tailed distribution as a result of stabilization in the later phase. Therefore, a non-parametric test was conducted.

The p-values for the hydraulic power across all operating conditions ranged from 0.187 to 0.972, indicating no statistically significant difference between the experimental and simulation values at a significance level of 0.05. This suggested that the simulation model effectively captured the overall trend of hydraulic power response, despite inherent variations in the experimental conditions. Additionally, the consistency of the U-statistics across different engine speeds and angular velocities implied that the model maintained stable predictive capability across a range of operating conditions.

Furthermore, while no significant deviations were observed, variations in the U-statistics and sample sizes suggested that discrepancies could arise under specific conditions, particularly at higher angular speeds, where transient effects become more pronounced. This highlights the importance of refining the model to improve accuracy in capturing rapid dynamic changes in hydraulic power response.

3.3.2. Evaluation of Hydraulic Power Prediction Accuracy in the EHPV Simulation Model

To assess the accuracy of hydraulic power predictions in the EHPV simulation model, an identity line fitting was conducted, as illustrated in Figure 11. In the figure, the dashed line represents the 1:1 line, where experimental values are plotted on the x-axis and simulation values on the y-axis. The red line shows the linear fit of the simulation data. The degree to which the linear fit deviated from the 1:1 line highlighted potential bias or nonlinearity in the simulation model.

In most cases, the linear fit line lay above the 1:1 line in the higher hydraulic power range, suggesting that the EHPV simulation model tended to slightly overestimate the maximum required hydraulic power. The model exhibited an MAPE of 7.45% to 9.87%. Even when the linear fit aligned with the 1:1 line (such as in cases (B₁₆) or (E₁₆)), the MAPE was still 8.49% or higher. This discrepancy was attributed to pressure fluctuations during actual experiments that were not included in the simulation model, indicating that the EHPV simulation model maintained consistent predictive accuracy despite these fluctuations.

The RMSE, which measured the accuracy of the simulation model in terms of watts (W) for each condition, was sensitive to outliers and could increase the higher maximum hydraulic power values. To address this, the NRMSE was calculated by dividing the RMSE by the mean of the experimental values, allowing for a relative comparison of the RMSE across conditions. The R² reflected the explanatory power of the simulation model concerning the experimental values. R² values ranged from 0.986 to 0.999, indicating that the simulation model accurately predicted the trends in the EHPV’s hydraulic power characteristics.

Overall, the MAPE and RMSE/NRMSE assessed the errors and outliers between the experimental and simulation values, while R² measured the model’s ability to explain variability in the experimental data. The EHPV simulation model was evaluated as effectively capturing hydraulic power fluctuations, with an MAPE of less than 10%.

4. Discussion

The primary source of error in the EHPV simulation model stemmed from pressure fluctuations and instability in the tractor’s hydraulic system connected to the EHPV. Despite this, the simplified model, which included only the pump, EHPV, and actuator, demonstrated statistically significant accuracy. The proposed simulation model effectively predicted hydraulic characteristics within the first 0.3 s of EHPV control under specified tractor operating conditions. Enhancing the model’s complexity by incorporating detailed mechanical steering structures, valve geometries, and adjustments to hydraulic parameters could reduce these errors. Such improvements would be particularly valuable for evaluating instantaneous hydraulic characteristics at specific points. However, the current study has limitations as it only predicted the EHPV’s hydraulic characteristics while the tractor was stationary. In reality, steering power requirements change when a tractor is in motion, with the steering load generally increasing at higher speeds due to greater inertia. Furthermore, steering load is significantly influenced by soil conditions, which affect repeatability in experimental results [23,24]. Therefore, future research is needed to understand the impact of soil conditions on EHPV performance. Future studies should focus on predicting the hydraulic characteristics of EHPVs in tractors operating in diverse road and working conditions.

5. Conclusions

We developed a simulation model for an automatic steering system for tractors including an EHPV. The developed model was validated by evaluating the initial input–output behavior of the valve based on control signal inputs and comparing the results with field experiments. The model’s hydraulic power prediction performance was assessed using various statistical models. The simulation results of the priority valve provided design guidelines for the automatic steering system’s valve to be applied to the steering system of conventional tractors. The results showed that the priority valve reached its full-stroke point under high engine speed conditions when the EHPV spool opening was low. This indicated a potential insufficiency in the input flow control of the automatic steering system during high-speed operations, highlighting the need for design modifications to meet the target flow control performance.

The response characteristics of the EHPV to step input signals were evaluated through simulation analysis based on overshoot, settling time, and rise time. These metrics demonstrated the control performance of the automatic steering system and can be utilized to develop controllers suited to the dynamic behavior of the valve.

The MAPE of the simulation model for hydraulic power ranged from 7.45% to 9.87%. The t-test results indicated that the experimental and simulation values of the EHPV hydraulic power had statistically equivalent means under all operating conditions, with similar variances in most cases. This suggests a high level of reliability for the EHPV simulation model results. Furthermore, the coefficient of determination (R²) ranged from 0.986 to 0.999, reflecting an excellent fit to the identity line and an effective representation of the actual hydraulic power trends.

In conclusion, the proposed EHPV simulation model closely aligned with the actual hydraulic characteristics of the EHPV, with an error margin of less than 10%. This model is expected to be useful for optimizing the EHPV design to achieve high-performance steering control in autonomous tractors.